当前, 我国经济已从高速增长阶段转向高质量发展阶段, 正处在转变发展方式、优化经济结构、转换增长动力的攻关期. 迫切要求物流业以供给侧结构性改革为主线, 推动物流产业质量变革、效率变革和动力变革, 实现高质量发展. 物流业的核心部分为车辆配送, 而车辆路径规划问题(vehicle routing problem, VRP)[1]. 是其中重要的一部分. 传统的VRP是指由配送中心向一系列客户交付货物, 并规划合理的行驶路线, 目标是满足客户的需求. 随着环保意识的增强和物流双向流通的发展, 送取货的车辆路径问题也不断得到重视. 为了提升企业的服务质量和客户的满意度, 还需要将客户能接受的服务时间考虑在内. 因此, 研究带时间窗和同时送取货的车辆路径问题(VRPSPDTW)具有重要的理论和实践意义.
VRPSPDTW问题是VRP的扩展, 已被证明是一个NP-hard问题[2]. VRPSPDTW的求解算法主要分为两类, 一类是运筹学算法, 包括动态规划、分支定价等[3,4]. 主要采用几何分析和线性代数作为基本方法, 利用目标函数和约束项结构信息来求解问题. Angelelli等[4]采用了分支定价法得到了小规模问题的最优解. 当数据规模变大时, VRPSPDTW的求解会更加复杂, 甚至可能需要数天才能得到满意解. 另一类为智能算法[5–9], 包括遗传算法、布谷鸟算法、粒子群算法等. 这类算法不依赖问题的结构, 通过对解的编码解码处理约束, 不断生成新的可行解. 往往只需要较短的时间, 便可得到不同规模问题的满意解决方案. 因此, 使用智能算法来解决VRPSPDTW问题, 是非常必要且合理的. Wang等[10]设计了协同遗传算法完成了对VRPSPDTW问题的求解, 并设计了64组VRPSPDTW测试算例. 黄务兰等[11]改进了人工鱼群算法, 优化了算法的搜索能力, 降低了计算复杂度, 并通过实验验证了算法的可行性. 王超等[12]提出了布谷鸟算法离散化来求解VRPSPDTW问题, 并刷新了国际最优解. Belgin等[13]通过将局部搜索算法与变邻域下降搜索相结合, 求解了VRPSPDTW问题. Lagos等[14]采用改进的粒子群算法完成了VRPSPDTW问题的寻优. Wang等[15]在VRPSPDTW的基础上添加了多配送中心限制, 并采用聚类算法得到满意解. 根据以上文献可知, 1)大多数求解VRP的方法仍然是元启发式算法; 2)在算法的局部搜索过程中, 大多采用固定的顺序执行插入操作, 难以实现种群的深入搜索.
灰狼算法(grey wolf optimization, GWO)是澳大利亚学者Mirjalili等[16]提出的一种群体智能优化算法. 该算法是根据灰狼的捕食行为而开发的一种优化算法, 它具有收敛性强、参数少、易实现等特点. 然而GWO最初是为了优化连续问题而设计的, 在求解连续优化问题方面有着广泛的应用, 但在车辆路径优化等离散问题上的应用较少. 为了能将GWO应用于离散优化问题, 黄戈文等[17]设计了一种采用灰狼整数编码的自适应灰狼更新策略来求解CVRP问题. 姜天华[18]针对车间调度问题, 设计了一种离散灰狼算法进行求解, 该算法采用两段式编码, 建立GWO连续空间与离散空间的映射关系. 顾九春等[19]针对作业车间节能调度问题, 设计了一种多目标离散灰狼算法进行求解, 该算法基于速度-工序的离散整数编码方式, 并引入跟踪和搜寻模式. 综上所述, 现有文献采用GWO解决离散组合优化问题(特别是VRP)的研究非常有限. 除此之外, 现有的文献针对离散优化问题所设计的离散灰狼优化算法存在局限性, 主要体现在算法对GWO的原有机制过于保留, 在个体位置更新时, 算法的离散化不够彻底, 影响算法的运行效率.
因此, 本文构建了以最小化车辆行驶距离为优化目标的VRPSPDTW数学模型, 并提出了一种离散灰狼优化算法(discrete grey wolf optimization, DGWO)对其求解. 首先, 通过个体与决策个体的离散交叉操作, 实现算法在离散域中的更新, 提高了算法的运行效率. 然后, 引入了带评分策略的邻域搜索, 与单一的邻域操作相比, 评分策略能积累优质解信息并引导邻域搜索尽快到达优质解区域. 最后, 引入移除-插入机制对路径进行优化, 提高了解的多样性, 从而更好地进行全局寻优. 实验结果表明, 本文所提出的DGWO算法能有效缩短物流配送路径长度, 节约配送成本, 为求解VRPSPDTW问题提供有效的解决方案.
1 问题描述及数学模型 1.1 问题描述VRPSPDTW问题如图1所示, 其中正方形表示配送中心, 带编号的圆点表示客户编号, 箭头表示车辆配送路径. 若干相同类型的车辆从配送中心出发, 对一系列客户进行送货、取货服务, 在服务完所有客户后返回配送中心. 要求配送中心规划出一条合理的路线, 以最小的成本(如车辆数目、最短行驶距等)满足所有客户的需求, 并满足以下假设.
(1)车辆到达客户点后, 需要先对客户送货再取货.
(2)每个客户的需求量和接受服务的时间窗为已知的.
(3)每辆车的载重量不能超过车辆最大容量.
(4)每个客户只能被一辆车服务, 且客户的需求不能被拆分完成.
(5)每个客户只在时间窗内接受服务.
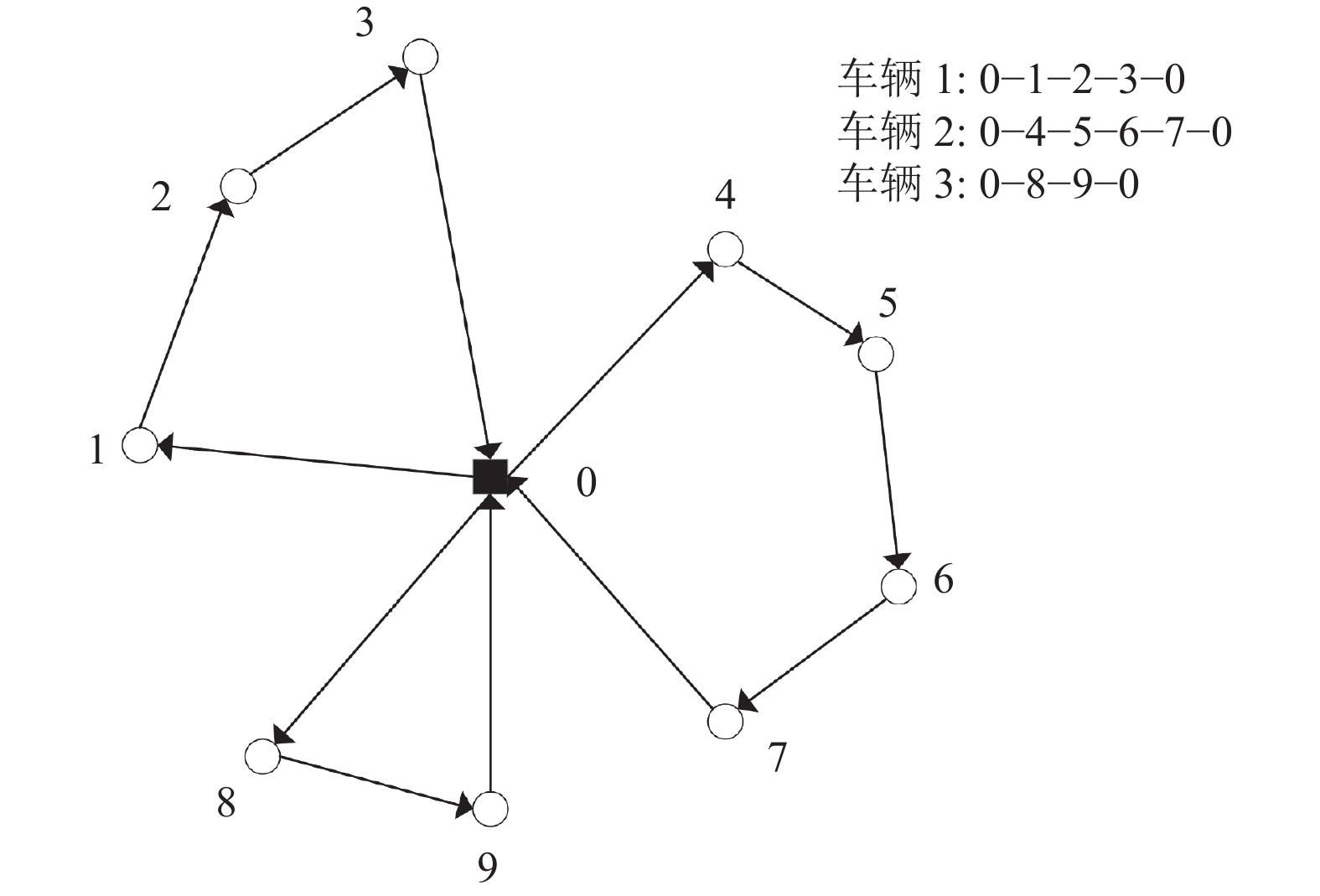
|
图 1 VRPSPDTW图例 |
1.2 参数定义
为了能准确地描述模型, 本文所设计的参数和变量符号如表1所示.
| 表 1 符号表 |
1.3 数学模型
根据问题描述和参数定义, 建立如下的VRPSPDTW模型.
| min | (1) |
| \sum\limits_{k = 1}^m {\sum\limits_{j = 1}^n {{x_{0jk}} \leqslant m} } | (2) |
| \sum\limits_{k = 1}^m {\sum\limits_{i = 1}^n {{x_{ijk}}} = 1} , \; j = 1, 2, \cdots , n | (3) |
| \sum\limits_{j = 1}^n {{x_{0jk}} = \sum\limits_{i = 1}^n {{x_{i0k}}, \; k = 1, 2, \cdots , m} } | (4) |
| {y_{ijk}} \leqslant {x_{ijk}}Q, \; i, j = 1, 2 , \cdots , n; \; k = 1, 2 , \cdots , m | (5) |
| \sum\limits_{j = 1}^n {y_{0jk}^{} = \sum\limits_{i = 1}^n {{D_j}} \sum\limits_{i = 0}^n {{x_{ijk}} \leqslant Q, \; k = 1, 2, \cdots , m} } | (6) |
| \sum\limits_{j = 1}^n {y_{i0k}^{} = \sum\limits_{i = 1}^n {{P_i}} \sum\limits_{i = 0}^n {{x_{ijk}} \leqslant Q, \; k = 1, 2, \cdots , m} } | (7) |
| {T_j} = {T_i} + {s_i} + \frac{{{d_{ij}}}}{v}, \; i, j = 1, 2, \cdots , n | (8) |
| E{T_j} \leqslant {T_j} \leqslant L{T_j}, \; j = 1, 2, \cdots , n | (9) |
| {y_{ijk}} \geqslant 0, \; i, j = 1, 2, \cdots , n; \; k = 1, 2, \cdots , m | (10) |
| {x_{ijk}} = \left\{ {0, 1} \right\}, \; i, j = 1, 2, \cdots , n, \; k = 1, 2, \cdots , m | (11) |
其中, 式(1)为目标函数, 即车辆行驶距离最小; 式(2)表示配送中心派出的车辆数目不超过最大车辆数目; 式(3)表示每个客户点只接受一辆车的服务; 式(4)表示每辆车需要从配送中心开始服务, 在完成配送任务后返回配送中心; 式(5)表示配送车辆在任意时刻的装载量均满足容量限制; 式(6)表示当车辆离开配送中心时, 负载量应满足所有配送客户的需求; 式(7)表示车辆返回配送中心时, 载重量为所服务的客户总的取货量; 式(8)表示车辆从客户
由建立的模型可知, 相对于传统的VRP问题, VRPS-PDTW将时间窗和同时送取货考虑在内, 使模型的约束得到增加, 复杂了问题的求解空间. 随着客户数量的增加, VRPSPDTW的求解空间和时间也呈指数增长.
1.4 构建带惩罚系数的适应度函数对种群解码所得到的路径方案不一定都是可行的. 针对VRPSPDTW中存在的容量约束和时间窗约束, 将2种约束转化为具有惩罚值的软约束项. 在算法的更新过程中允许出现非可行解, 可采用适应度函数
| F(x) = f(x) + aq(x) + bt(x) | (12) |
其中,
GWO的优化过程包括等级分层、跟踪、包围和攻击猎物等步骤, 具体步骤如下.
等级分层: 计算种群的适应度, 将适应值最好的3匹狼设置为
| \vec X(t + 1) = {\vec X_p}(t) - \vec A \cdot \left| {\vec C \cdot {{\vec X}_p}(t) - \vec X(t)} \right| | (13) |
| \vec A = 2\vec a \cdot {r_1} - \vec a | (14) |
| \vec C = 2{r_2} | (15) |
其中,
猎物的搜索过程主要是依靠
| \left\{ \begin{gathered} {{\vec D}_\alpha } = \left| {{{\vec C}_1} \cdot {{\vec X}_\alpha } - \vec X} \right| \\ {{\vec D}_\beta } = \left| {{{\vec C}_2} \cdot {{\vec X}_\beta } - \vec X} \right| \\ {{\vec D}_\delta } = \left| {{{\vec C}_3} \cdot {{\vec X}_\delta } - \vec X} \right| \\ \end{gathered} \right. | (16) |
| \left\{ \begin{gathered} {{\vec X}_1} = \left| {{{\vec X}_\alpha } - {{\vec A}_1} \cdot {{\vec D}_\alpha }} \right| \\ {{\vec X}_2} = \left| {{{\vec X}_\beta } - {{\vec A}_2} \cdot {{\vec D}_\beta }} \right| \\ {{\vec X}_3} = \left| {{{\vec X}_\delta } - {{\vec A}_3} \cdot {{\vec D}_\delta }} \right| \\ \end{gathered} \right. | (17) |
| \vec X(t + 1) = \frac{{{{\vec X}_1} + {{\vec X}_2} + {{\vec X}_3}}}{3} | (18) |
其中,
本文提出了一种离散灰狼优化算法(DGWO)解决上述VRPSPDTW问题. DGWO的算法流程如图2所示, 在DGWO的初始化阶段, 为了提高初始种群的质量和算法的收敛性能, 提出了两种规则用于生成初始解. 在保留灰狼算法搜索机制的基础上, 设计了离散域的灰狼位置更新策略. 在局部搜索阶段, 采用6种有效的邻域操作, 并设计了改进的评分机制评价不同邻域操作的性能, 增强算法的局部寻优能力. 在全局搜索阶段, 将最不合理的路径剔除, 对优质解区域进行深入搜索. 本文后续将对DGWO各环节依次介绍.
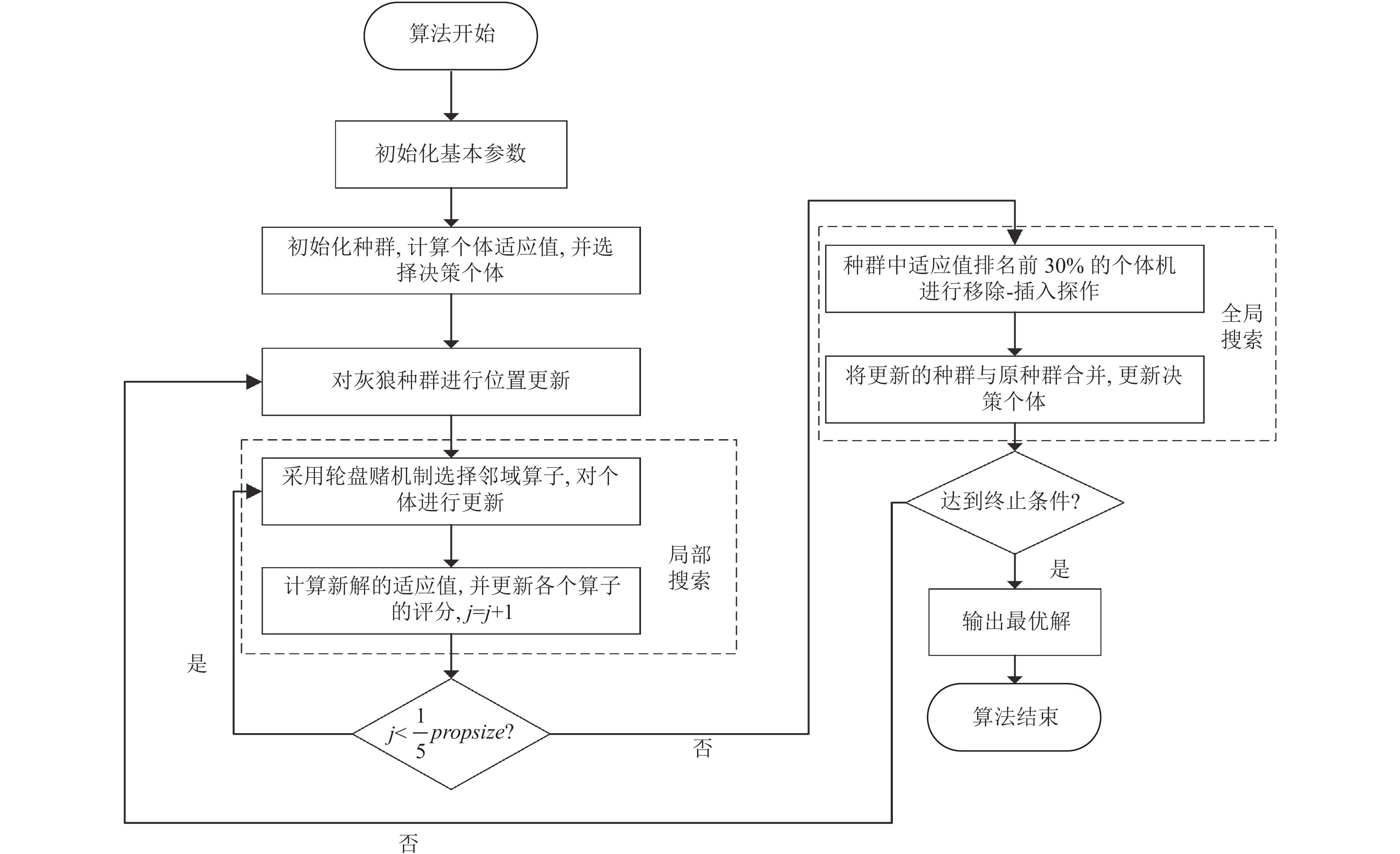
|
图 2 DGWO算法流程图 |
3.1 编码与解码
本文采用整数编码, 若总的客户数目为
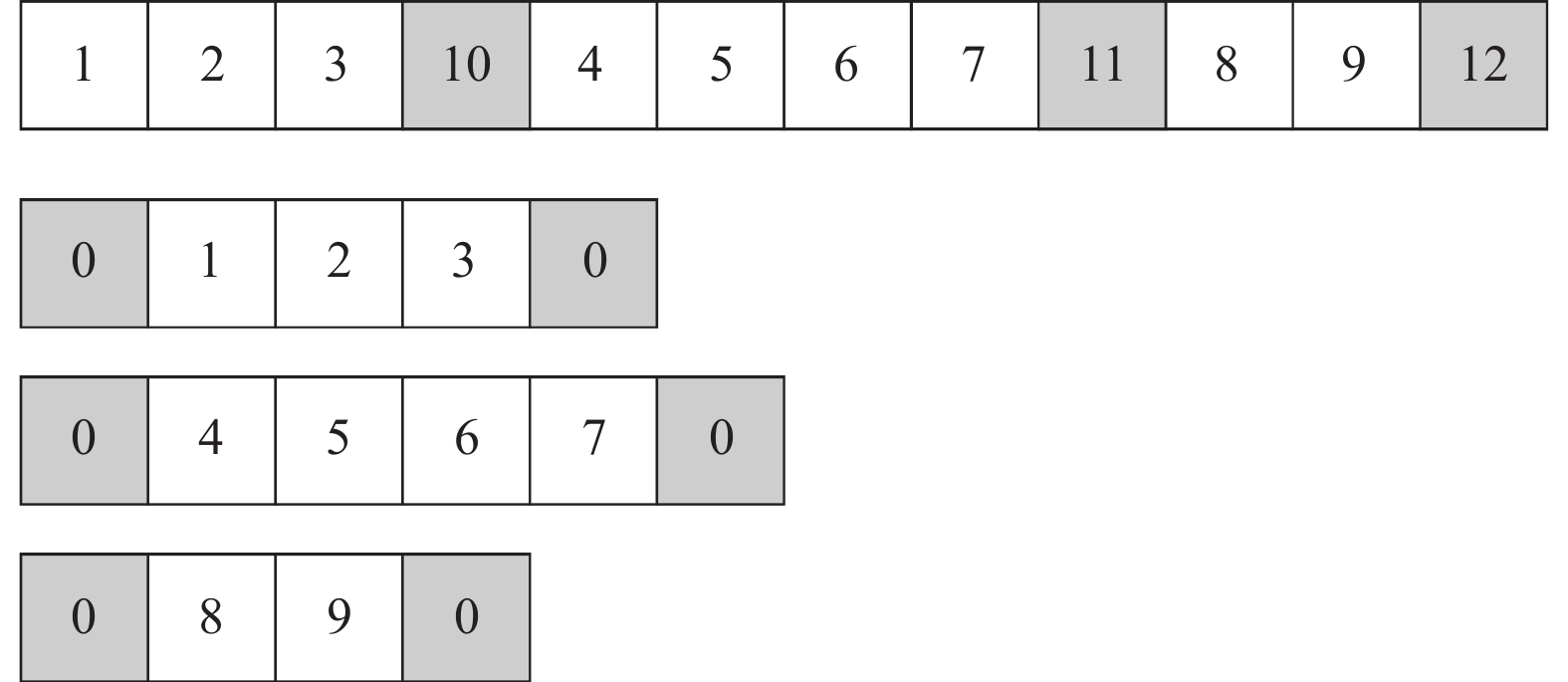
|
图 3 解的编码与解码 |
路径编码: 以车辆编号为结尾并包含客户点的一组数据序列; 路径解码: 车辆10依次服务客户1、2、3; 车辆11依次服务客户4、5、6、7; 车辆12依次服务客户8、9.
采用以上的编码和解码方式能在一定程度上降低模型的复杂程度, 提高算法的运行效率.
3.2 种群初始化初始化解的好坏直接影响算法的全局收敛性能和解的质量. 为了保证解的多样性和分散性, 本文采用2种规则构造初始解, 使用距离最短规则生成1个个体, 其余个体采用随机规则生成.
距离最短规则: 车辆从配送中心出发, 选择距离最短的客户
随机规则: 采用随机的方式生成初始解, 随机规则应遵循两项原则. 1)不允许产生相同的种群; 2)随机产生的个体与已产生个体的适应度函数值应不小于数值
在种群初始化中允许初始种群违反时间窗约束和容量约束, 即允许出现非可行解. 在算法的搜索过程中加入非可行解, 以增大算法的搜索范围, 避免算法陷入局部最优, 使算法在迭代过程中找到更优解.
3.3 离散灰狼优化机制在基本的灰狼算法中, 根据式(16)–式(18)来更新灰狼的位置, 参数
标准的GWO的参数和位置更新公式无法直接应用于离散优化问题, 因此对GWO中的参数
| SN = S \times \left(1 - abs\left(\frac{A}{2}\right)\right) | (19) |
| OS = round({r_3}(S - SN)) | (20) |
| OD = round\left(\frac{C}{2}(SN - OS)\right) | (21) |
其中,
假设
| X_i^{t + 1} = \left\{ \begin{gathered} LOX(X_i^t, X{_\alpha }, {\textit{SN}}, OS, OD),\;\; rand < \frac{1}{3} \\ LOX(X_i^t, X{_\beta }, {\textit{SN}}, OS, OD),\;\; \frac{1}{3} \leqslant rand \leqslant \frac{2}{3} \\ LOX(X_i^t, X{_\delta }, {\textit{SN}}, OS, OD),\;\; rand > \frac{2}{3} \\ \end{gathered} \right. | (22) |
其中,
在求解组合优化问题时, DGWO在离散域直接对灰狼位置向量进行更新, 不仅能保证解的收敛性和多样性, 并且能减少算法的额外计算量.
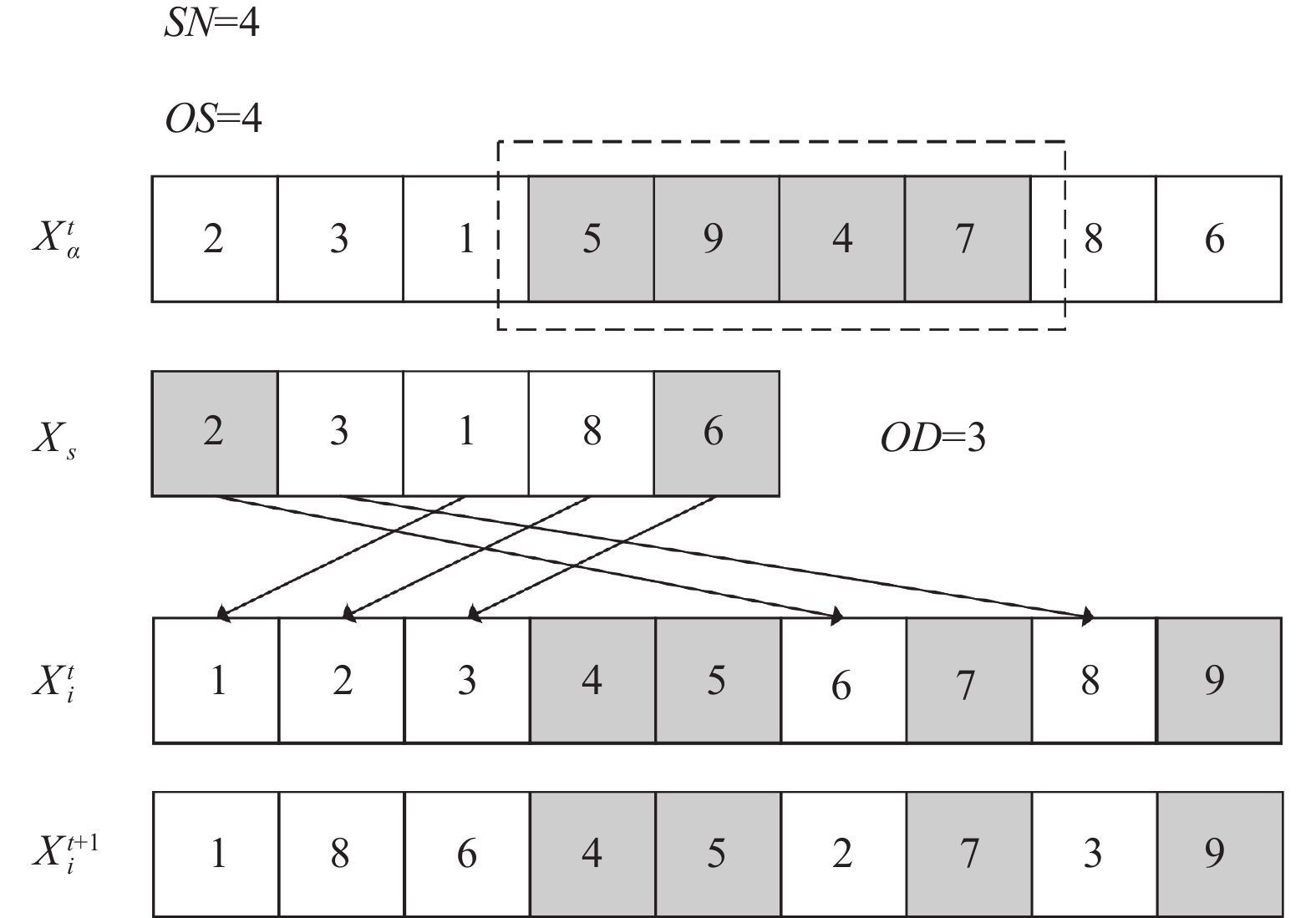
|
图 4 LOX交叉 |
3.4 局部搜索
采用单一的邻域操作容易陷入该结构的局部最优. 故采用多种邻域操作相结合的邻域结构进行探索, 从而更容易获得优质解, 减少搜索的盲目性. 针对VRPSPDTW的具体问题, 本文采用了路径内与路径间相结合的邻域操作进行局部搜索. 根据算子在算法中的表现, 不断调整每个算子的权重, 提高优异算子的选中概率. 探索能力较强的算子将会有更高的概率被选择, 而其他算子也有一定的概率被选择, 这能形成众多新的邻域组合结构. 下面对各种邻域操作进行介绍.
路径内:
(1) 2-opt算子: 先随机选取一条车辆路径r, 在r中任意选取两个客户点, 将两个客户间的顺序进行逆转. 如图5所示, 选择0-1-2-3-4-0路径中的客户点1和客户点4, 进行2-opt操作, 得到新路径0-1-3-2-4-0.
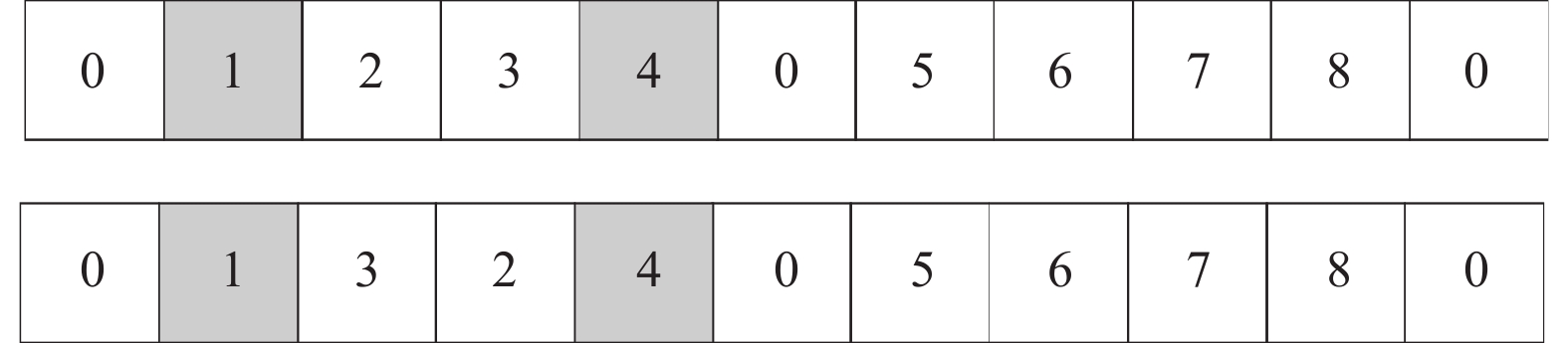
|
图 5 2-opt算子 |
(2) exchange算子: 随机选取一条车辆路径r, 在路径r任意选取两个客户点进行交换, 形成一条新路径.
(3) relocate算子: 随机选取一条路径r, 在路径r中随机选取m个连续客户点, 将这m个客户点重新定位到该路径中.
路径间:
(4) shift算子: 首先随机选取两条路径r1和r2, 并从r1中随机选择一个客户点
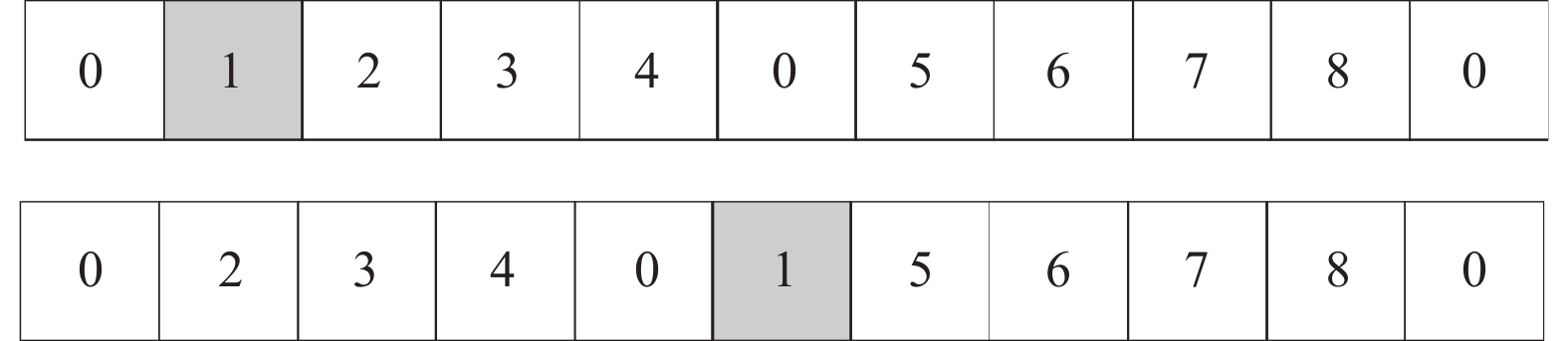
|
图 6 shift算子 |
(5) swap算子: 随机选取2条路径r1和r2, 分别在2条路径中选取一个客户点, 交换2个客户点的位置.
(6) gene算子: 随机选取2条路径r1和r2, 并随机选取一条路径中的一个客户点, 插入到另一条路径中, 插入位置为距离该客户点最近的2个节点之间.
在执行完任意一种局部操作后, 若产生的解为可行解且优于原解, 则采用新解代替原解, 否则, 不接受该解.
3.5 自适应选择邻域策略采用不同形式的邻域操作, 有助于避免陷入局部最优并提高解的搜索质量. 在算法的每次迭代中, DGWO采用轮盘赌的机制选择多种邻域结构来实现路径的更新. 根据更新后路径的优劣, 对每个邻域结构进行评分. 假设每个算子的初始得分为
| P_i^j = P_i^{j - 1} + \sigma \frac{{F(x)}}{{F(x')}} - 1 | (23) |
其中,
| P_i^j = \left\{ \begin{gathered} {P_{\max }}, \; P_i^j > {P_{\max }} \\ {P_{\min }}, \; P_i^j < {P_{\min }} \\ \end{gathered} \right. | (24) |
为了能在较短的时间内平衡算法搜索的广度和深度, 选择适应值前10%的种群和适应值后10%的种群进行局部搜索.
3.6 移除-插入操作路径寻优过程中, 采用移除算子和插入算子全局优化路径. 移除算子将部分客户点从路径中移除, 再通过插入算子, 将移除的客户点插入到合理的路径中, 得到新路径. 如图7所示, 黑色圆点为移除的客户点, 将客户点重新插入路径中, 形成了新路径, 新路径与原路径相比减少了总距离. 下面对本文采用的移除-插入机制进行介绍.
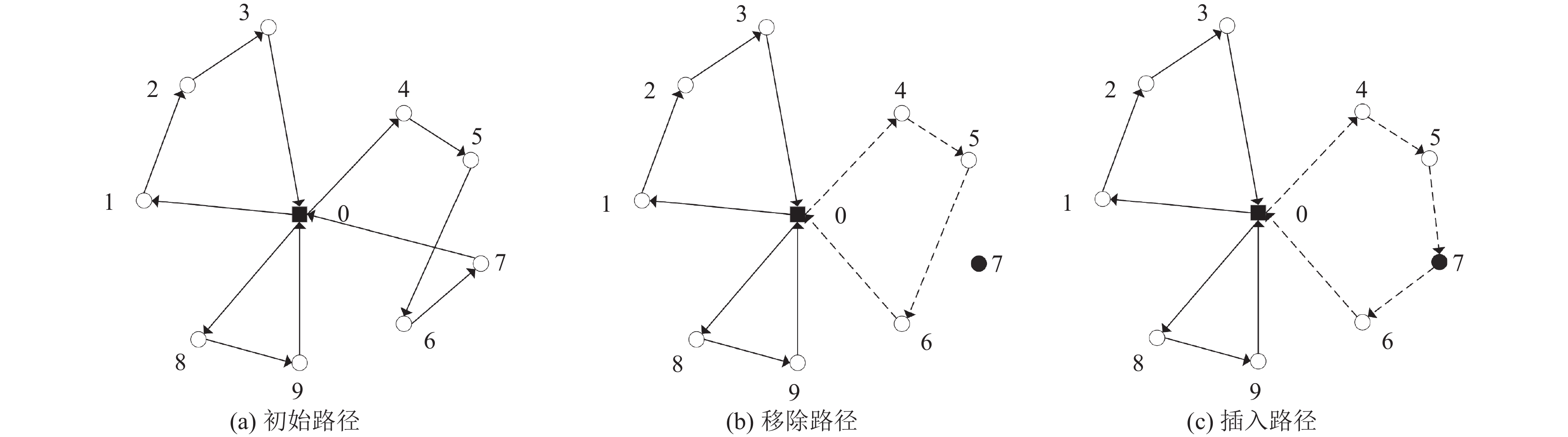
|
图 7 移除-插入操作 |
(1)选择最不经济的一条路线, 即平均行驶距离最大的一条路线. 将最不经济的一条路线移除该路线上的所有客户点为待插入客户点. 平均行驶距离的计算公式如下:
| {A_k} = \frac{{D(k)}}{{{N_k}}} | (25) |
其中,
(2)令所有待插入客户点的集合为R, 在满足时间窗和容量约束的基础上, 记录每个插入点的距离增量. 若将客户点
(3)选择距离增量小的位置插入, 并将该客户点从R中移除, 重复操作直到R为空集.
与随机移除算子相比, 本文选用的算子考虑了路线的整体性. 随机移除算子随机性强, 跳出局部搜索能力较强, 但容易将正确位置的客户点移除, 产生无效操作. 若选择最不经济的一条路线进行移除, 则会集中移除一条路线中的客户点, 策略简单, 且不易陷入局部最优.
3.7 迭代终止条件算法存在两种终止条件. 1)算法设置最大迭代次数, 若当前算法的迭代次数大于算法最大迭代次数, 则算法终止; 2)令
实验运行环境如下: 计算机为Lenovo XiaoXin Air 15ARE 2021, 处理器为AMD Ryzen 7 4800U with Radeon Graphics, 主频为1.80 GHz, 内存为16.0 GB. 采用Matlab R2020b软件进行模拟仿真. 算法的参数设置如下:
为了测试多规则初始化种群策略、自适应选择邻域策略和移除-插入机制的有效性, 在本实验中, 我们研究DGWO的相关变体.
(1) Variant-1: DGWO采用随机策略构造初始解.
(2) Variant-2: DGWO无自适应选择邻域策略.
(3) Variant-3: DGWO无移除-插入机制.
以标准数据集中的Rdp101为例, 分析DGWO和Variant-1的收敛性能. DGWO和Variant-1的最优结果迭代过程如图8所示. 以Cdp2问题为例, 表2对比了DGWO和Variant运行20次的最优值、平均值和最差值.
从图8中看出, DGWO迭代到75次左右, 算法收敛到最优解1646.20; Variant-1迭代到85次左右, 算法收敛到最优解1649.57. 这说明采用多策略构造初始种群能提高初始解的质量并增强初始解的多样性, 加快种群的收敛并保持良好寻优能力.
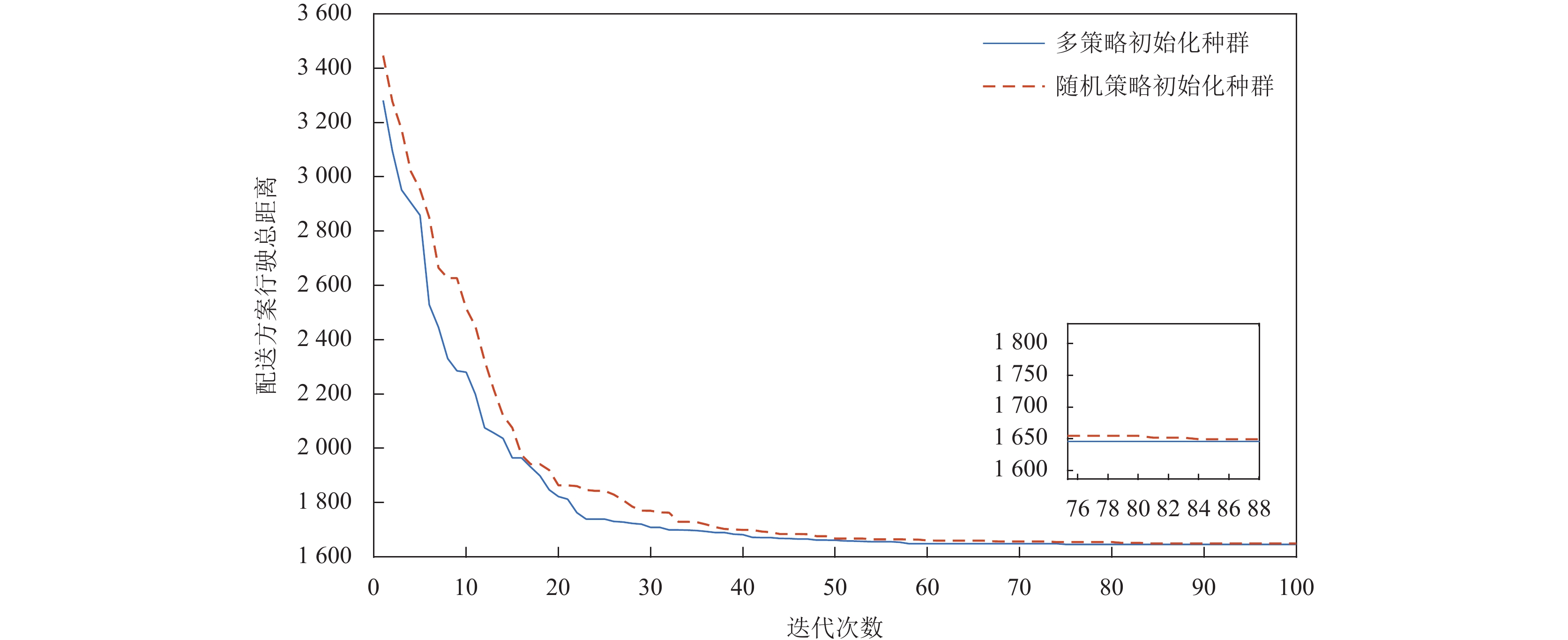
|
图 8 DGWO和Variant-1在Rdp101算例上的收敛曲线图 |
| 表 2 DGWO和Variant-2、Variant3的比较结果 |
从表2中可以看出, DGWO的最优值、平均值和最差值均优于Variant-2和Variant-3, 这表明DGWO拥有更好的稳定和收敛性能. 以Cdp202为例, DGWO最优值相比Variant-2提高了0.3%, 这表明引入自适应选择邻域策略, 动态构造了丰富的邻域结构, 能增强算法在优质解区域的探索深度.
以Cdp202为例, DGWO最优值相比Variant-3提高了1.77%, 这表明移除-插入机制能有效地跳出局部最优, 提升算法的综合性能.
因此3种策略对于算法的优化存在积极作用.
4.2 小规模算例实验分析选用Wang等[10]设计的9种中小规模算例进行测试, 包括3组10个客户点规模, 3组25个客户点规模和3组50个客户点规模的算例. 表3列出了DGWO、p-SA[21]、IGAFSA[11]和DCS[12]在小规模算例的最优解对比结果.
| 表 3 小规模算例实验结果对比 |
表3的实验结果表明, 在客户点规模较小的时候, DGWO、p-SA、IGAFSA和DCS都能得到问题的最优解. 当数据规模变大时, 数据的计算复杂程度会显著增加. 当数据规模扩展到25时, 只有DGWO均能得到问题的最优解. 当数据规模扩展到50时, 只有DGWO和IGAFSA能每次都准确得到问题的最优解. 这验证了DGWO在处理小规模算例的有效性.
4.3 大规模算例实验分析选取Wang等[10]针对VRPSPDTW问题设计的测试集作为验证算例. 共56个数据集, 由6种不同的问题类型组成, 分别为Rdp1、Rdp2、Cdp1、Cdp2、RCdp1和RCdp2, 每个算例都包含100个客户点. 其中Rdp1和Rdp2的客户点为随机分配, Cdp1和Cdp2的客户点满足聚类分布, Rcdp1和Rcdp2的客户点混合了随机和聚类分布. 记录DGWO算法20次独立运行中的最优结果. 将实验结果与p-SA算法[11]、DCS算法[12]、VNS-BSTS算法[21]、SA-ALNS算法[22]进行对比. DGWO与上述算法在Cdp, Rdp, RCdp算例的对比结果分别如表4–表6所示, 其中粗体表示更优值.
| 表 4 Cdp算例实验结果对比 |
(1)从表4可以看出, 在Cdp105、Cdp106算例中, DGWO的实验结果最优; 在Cdp109算例中, VNS-BSTS的实验结果最优; 在其余Cdp1算例中, SA-ALNS均能获得最优解. 总的来说, DGWO在处理Cdp1算例上的求解性能弱于SA-ALNS. 在Cdp2算例中, DGWO均能获得最优解. 从表5可以看出, 在RCdp103、RCdp201、RCdp202、RCdp203、RCdp205、RCdp206和RCdp207上, DGWO均刷新了当前已知最优解. 在其余RCdp问题上, DGWO的优化性能略弱于SA-ALNS和VNS-BSTS. 从表6可以看出, 除了Rdp103、Rdp104、Rdp105、Rdp110、Rdp111和Rdp112, DGWO在其余Rdp算例中均更新了当前已知最优解.
| 表 5 Rdp算例实验结果对比 |
| 表 6 RCdp算例实验结果对比 |
(2)在56个算例中, DGWO在85.7%的算例上优于p-SA, 在83.9%的算例上优于DCS, 在83.9%的算例上优于VNS-BSTS, 在73.2%的算例上优于SA-ALNS. 这表明本算法在求解VRPSPDTW问题上具有较好的性能, 整体性能优于p-SA、DCS、VNS-BSTS和SA-ALNS.
(3)对比实验表明DGWO算法在满足随机分布的算例中表现优异, 输出结果稳定. 图9分别给出了算例Rdp、RCdp和Cdp的部分路径图. 图10给出了Rdp108算例的收敛曲线, 这表明DGWO能以较快的收敛速度寻找到更优解.
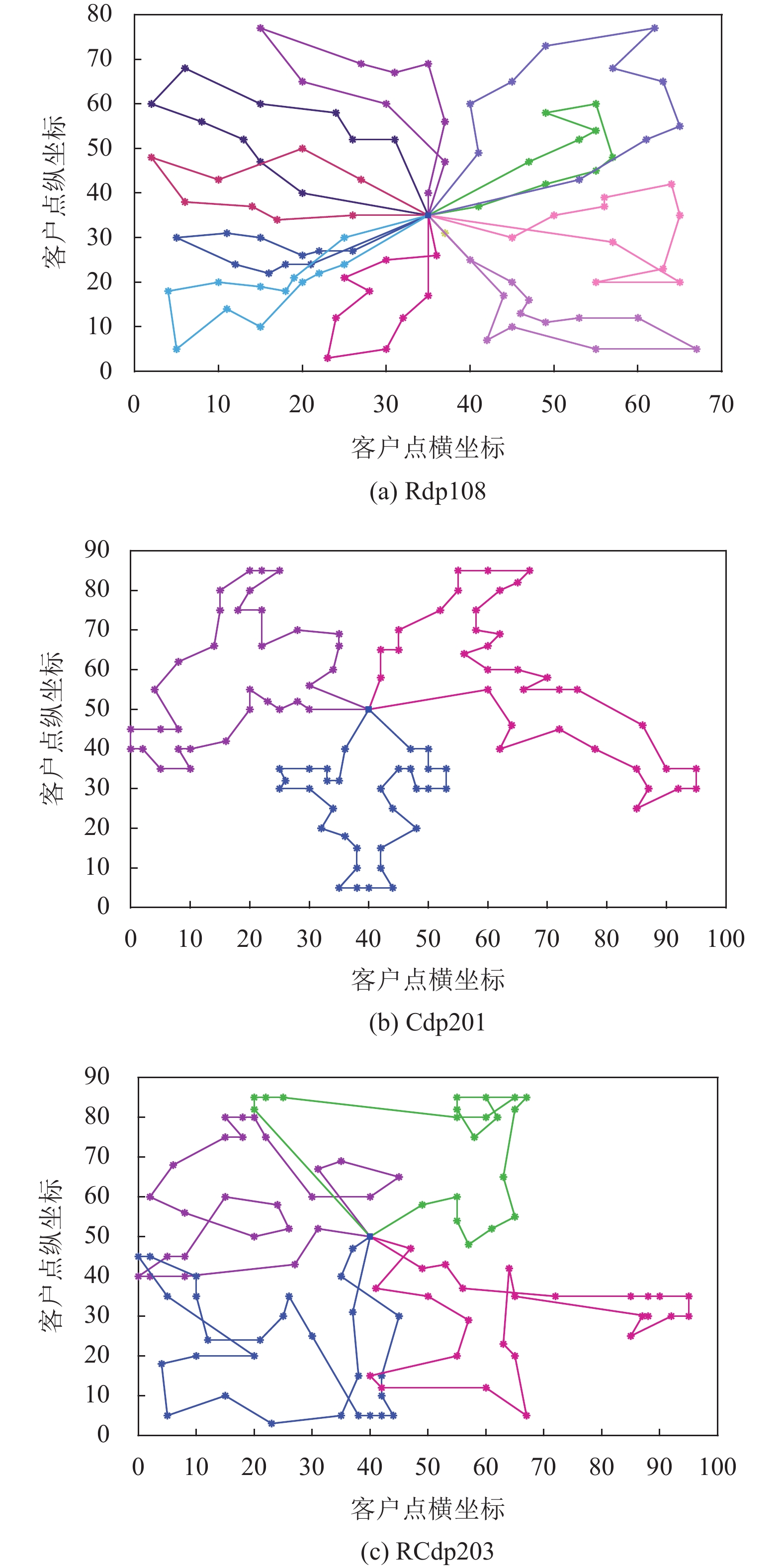
|
图 9 部分算例最优路线 |
综上表明, 本文提出的DGWO算法具有较好的收敛性和可行性, 在求VRPSPDTW问题中具有良好的效果同时也说明不同的机制组合很大程度上法的性能.
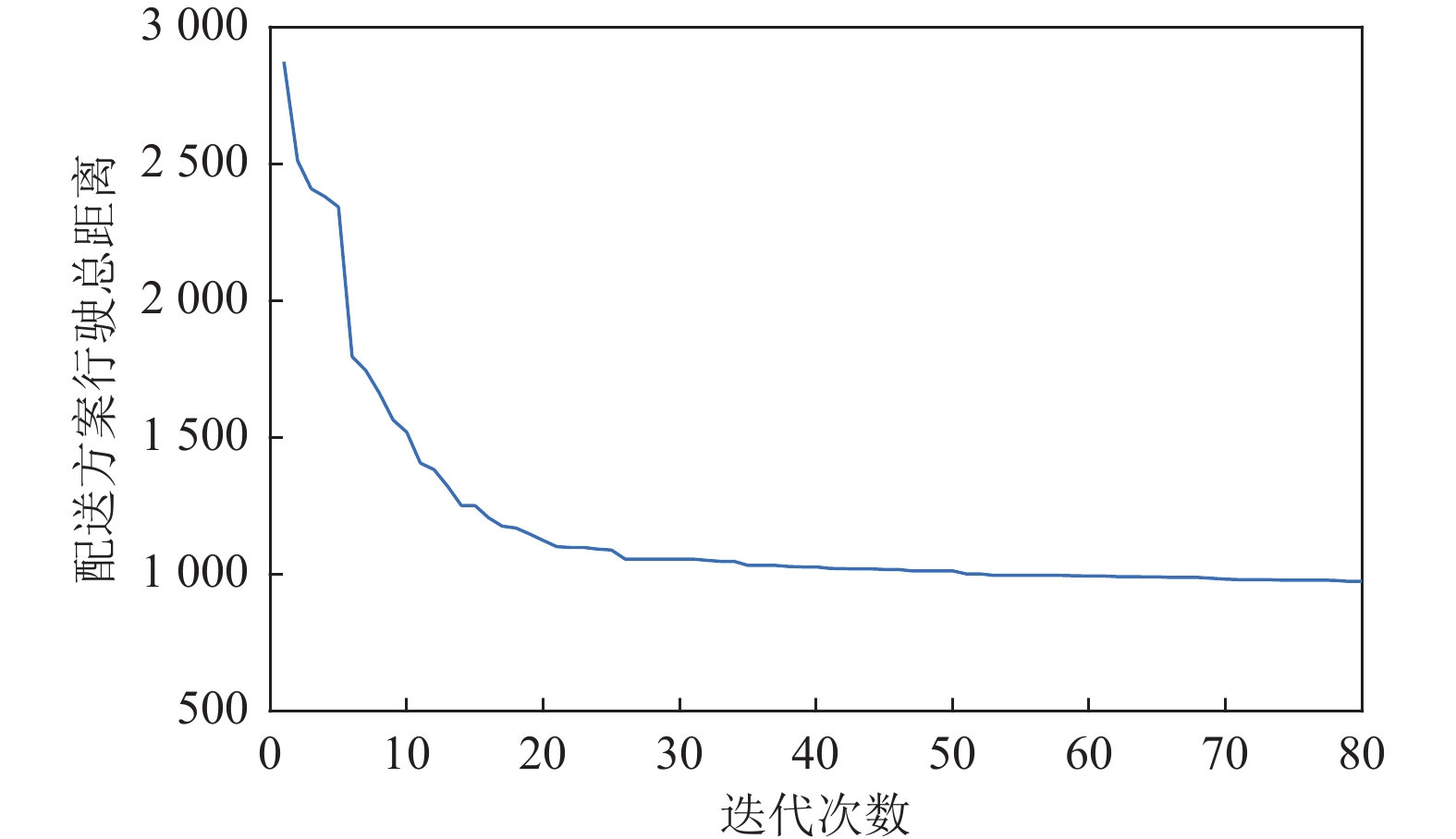
|
图 10 Rdp108收敛曲线 |
4.4 应用案例分析
为了验证本算法的实际有效性, 本文选择南京市某一连锁超市的部分数据, 包括1个配送中心和18个需要配送的连锁店. 参与配送的车辆共4台, 且车辆类型统一. 放了方便研究, 本文对18个连锁店进行了1, 2, …, 18编号处理, 数字0表示配送中心. 各连锁店的具体数据如表7所示. 配送车辆的最大载重量为3吨, 在不考虑交通拥堵的情况下, 假设车辆平均行驶速度为50 km/h. 本文的主要目标是最小化总行驶距离. 图11为车辆最优配送路线, 图12为算法的收敛曲线, 可以看出DGWO能在较短的时间内获得最优解, 这表明DGWO能应用于实际问题.
| 表 7 各连锁店的数据信息 |
5 结束语
本文针对带时间窗和同时取送货的车辆路径优化问题, 建立了以行驶距离最小为目标的车辆优化模型, 设计离散灰狼优化算法DGWO进行求解. DGWO具有以下优点: 1)在种群初始化中允许加入非可行解, 增大算法的搜索范围; 2)设计了在离散空间中灰狼的位置更新策略, 使GWO能处理离散优化问题; 3)采用评分机制丰富了邻域操作, 拓展了搜索深度, 从而改善了算法的性能; 4)采用移除-插入操作, 平衡了算法的搜索深度和广度, 加速的解的收敛. 通过仿真实验和对比, 验证了DGWO是求解VRPSPDTW问题的有效算法, 该算法能在较短时间内获得最优解. 后续将进一步研究基于模糊需求的车辆路径优化问题, 并设计有效算法来求解.
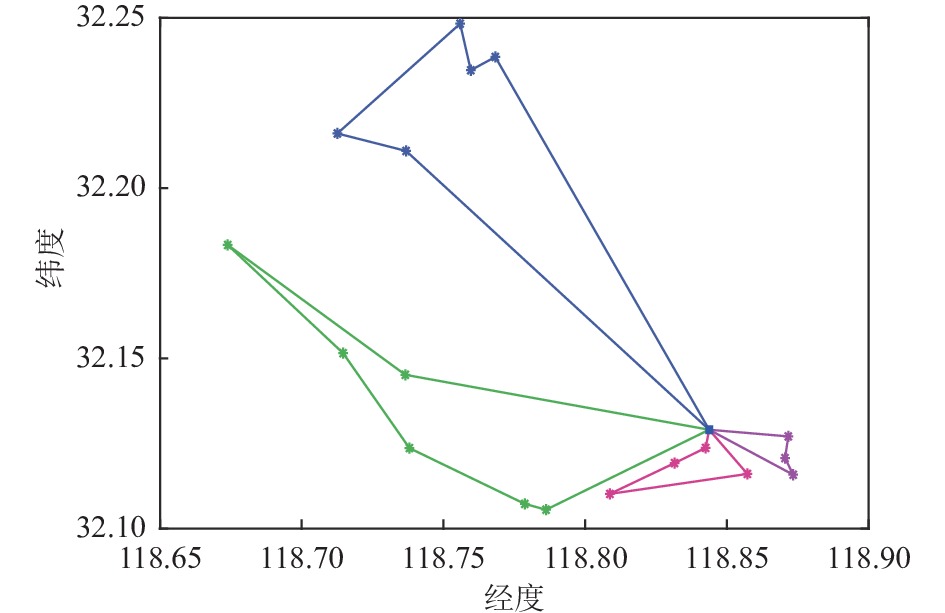
|
图 11 最优配送路线 |
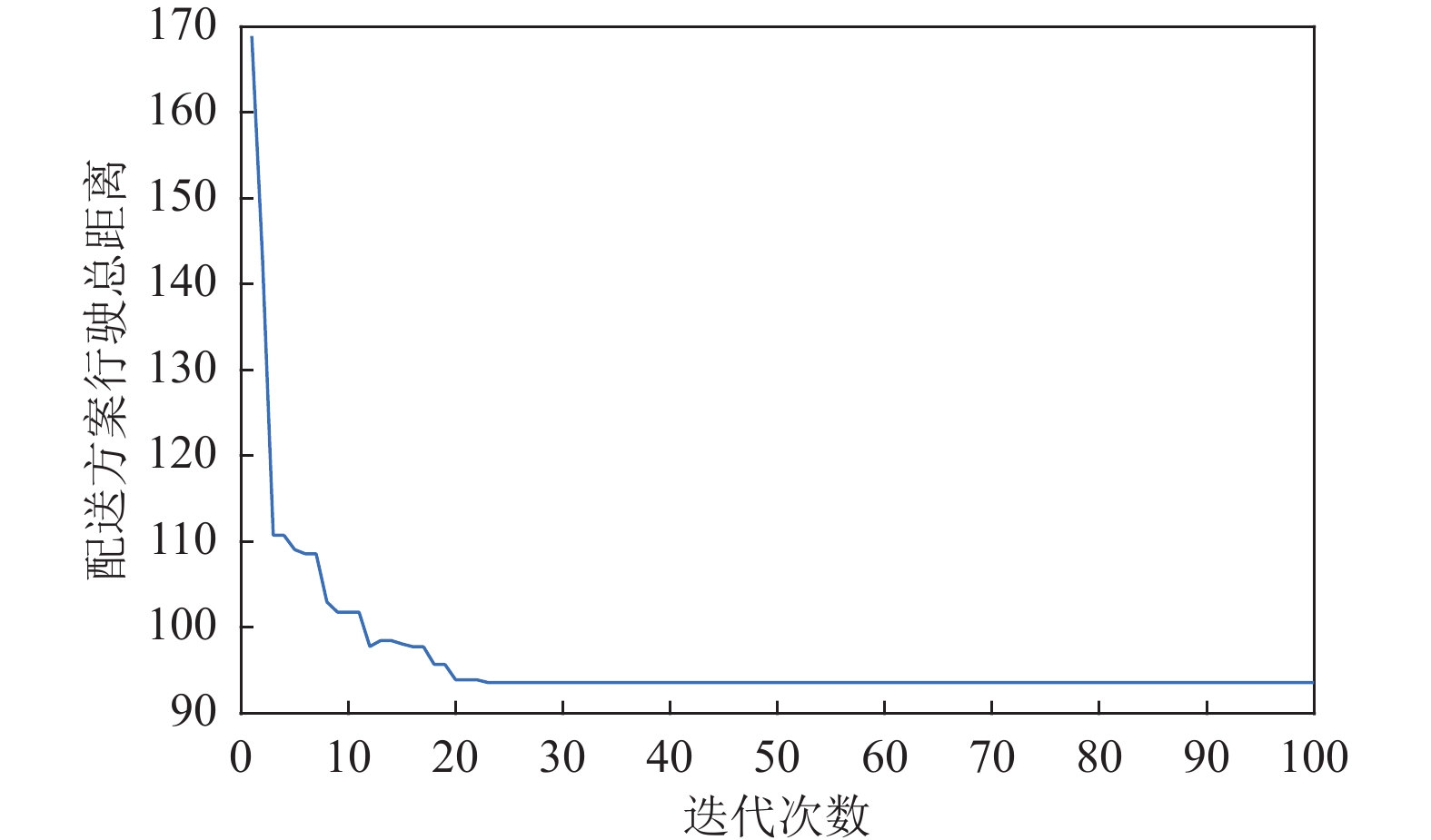
|
图 12 收敛曲线 |
| [1] |
Zhang SQ, Mu D, Wang C. A solution for the full-load collection vehicle routing problem with multiple trips and demands: An application in Beijing. IEEE Access, 2020, 8: 89381–89394.
|
| [2] |
Pureza V, Morabito R, Reimann M. Vehicle routing with multiple deliverymen: Modeling and heuristic approaches for the VRPTW. European Journal of Operational Research, 2012, 218(3): 636-647. DOI:10.1016/j.ejor.2011.12.005 |
| [3] |
Alyasiry AM, Forbes M, Bulmer M. An exact algorithm for the pickup and delivery problem with time windows and last-in-first-out loading. Transportation Science, 2019, 53(6): 1695-1705. DOI:10.1287/trsc.2019.0905 |
| [4] |
Angelelli E, Mansini R. The vehicle routing problem with time windows and simultaneous pick-up and delivery. In: Klose A, Speranza MG, Wassenhove LN, eds. Quantitative Approaches to Distribution Logistics and Supply Chain Management. Berlin Heidelberg: Springer , 2002. 249–267.
|
| [5] |
Bettinelli A, Cacchiani V, Crainic TG, et al. A branch-and-cut-and-price algorithm for the multi-trip separate pickup and delivery problem with time windows at customers and facilities. European Journal of Operational Research, 2019, 279(3): 824-839. DOI:10.1016/j.ejor.2019.06.032 |
| [6] |
Sitek P, Wikarek J, Rutczyńska-Wdowiak K, et al. Optimization of capacitated vehicle routing problem with alternative delivery, pick-up and time windows: A modified hybrid approach. Neurocomputing, 2021, 423: 670-678. DOI:10.1016/j.neucom.2020.02.126 |
| [7] |
张九龙, 王晓峰, 芦磊, 等. 若干新型智能优化算法对比分析研究. 计算机科学与探索, 2022, 16(1): 88-105. |
| [8] |
钟倩漪, 钱谦, 伏云发, 等. 粒子群优化算法在关联规则挖掘中的研究综述. 计算机科学与探索, 2021, 15(5): 777-793. |
| [9] |
李丹. 改进群智能优化算法的海上物流配送路径优化方法. 舰船科学技术, 2020, 42(16): 184-186. |
| [10] |
Wang HF, Chen YY. A genetic algorithm for the simultaneous delivery and pickup problems with time window. Computers & Industrial Engineering, 2012, 62(1): 84-95. |
| [11] |
黄务兰, 张涛. 基于改进全局人工鱼群算法的VRPSPDTW研究. 计算机工程与应用, 2016, 52(21): 21-29. |
| [12] |
王超, 刘超, 穆东, 等. 基于离散布谷鸟算法求解带时间窗和同时取送货的车辆路径问题. 计算机集成制造系统, 2018, 24(3): 570-582. |
| [13] |
Belgin O, Karaoglan I, Altiparmak F. Two-echelon vehicle routing problem with simultaneous pickup and delivery: Mathematical model and heuristic approach. Computers & Industrial Engineering, 2018, 115: 1-16. |
| [14] |
Lagos C, Guerrero G, Cabrera E, et al. An improved particle swarm optimization algorithm for the VRP with simultaneous pickup and delivery and time windows. IEEE Latin America Transactions, 2018, 16(6): 1732-1740. DOI:10.1109/TLA.2018.8444393 |
| [15] |
Wang Y, Li Q, Guan XY, et al. Collaborative multi-depot pickup and delivery vehicle routing problem with split loads and time windows. Knowledge-based Systems, 2021, 231: 107412. DOI:10.1016/j.knosys.2021.107412 |
| [16] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [17] |
黄戈文, 蔡延光, 戚远航, 等. 自适应遗传灰狼优化算法求解带容量约束的车辆路径问题. 电子学报, 2019, 47(12): 2602-2610. |
| [18] |
姜天华. 混合灰狼优化算法求解柔性作业车间调度问题. 控制与决策, 2018, 33(3): 503-508. |
| [19] |
顾九春, 姜天华, 朱惠琦. 多目标离散灰狼优化算法求解作业车间节能调度问题. 计算机集成制造系统, 2021, 27(8): 2295-2306. |
| [20] |
Della Croce F, Tadei R, Volta G. A genetic algorithm for the job shop problem. Computers & Operations Research, 1995, 22(1): 15-24. |
| [21] |
Ma YF, Li ZM, Yan F, et al. A hybrid priority-based genetic algorithm for simultaneous pickup and delivery problems in reverse logistics with time windows and multiple decision-makers. Soft Computing, 2019, 23(15): 6697-6714. DOI:10.1007/s00500-019-03754-5 |
| [22] |
Shi Y, Zhou YJ, Boudouh T, et al. A lexicographic-based two-stage algorithm for vehicle routing problem with simultaneous pickup-delivery and time window. Engineering Applications of Artificial Intelligence, 2020, 95: 103901. DOI:10.1016/j.engappai.2020.103901 |
 2023, Vol. 32
2023, Vol. 32



