2. 广东石油化工学院 自动化学院, 茂名525000
2. School of Automation, Guangdong University of Petrochemical Technology, Maoming 525000, China
近年来, 深度学习图像分类领域随着卷积神经网络(CNN)和Transformer等模型的逐步发展, 已经取得了显著的成果, 但图像分类算法仍然面临着大量超参数优化问题. 超参数的设置会直接影响模型性能[1–3], 因此超参数优化显得至关重要. 超参数优化包括经验调参、网格搜索、贝叶斯优化、群智能算法优化等方法. He等人[4]通过经验调参法提高图像分类模型精度. 虽然经验调参法可以提高模型性能, 但需要花费巨大的时间成本, 且很难找到最优的模型. 文献[5, 6]通过网格搜索优化超参数, 提高网络模型性能. 网格搜索方法简单易行, 能够找到给定取值范围内的最优解, 但是计算效率低下, 并且需要人为确定超参数的取值范围. 文献[7, 8]通过贝叶斯优化超参数, 获得高性能的分类模型, 但是贝叶斯优化超参数计算复杂度高. 文献[9–13]中通过群智能算法优化超参数, 实验表明, 该方法可以有效地提高分类模型的精度. 群智能算法优化不仅能够处理大规模的复杂问题, 不需要预先定义参数取值范围, 并且具有全局优化能力. 综上所述, 群智能优化超参数存在优越性, 故文中选取秃鹰搜索(bald eagle search, BES)算法[14]优化CNN网络结构中的超参数, 提高网络分类模型精度. 秃鹰搜索算法为2020年提出的一种新型的元启发算法, 虽然算法具有结构简单、收敛速度快、全局搜索能力较强等优点, 在解决各类数值优化问题方面非常有效, 但缺点是易陷入局部最优解, 且跳出局部最优解的能力较弱, 即算法在全局最优探索和局部利用之间存在不协调. 针对原算法存在的缺点, 学者通过Tent混沌映射[15–17]、Sinusoidal 映射[18]、levy飞行策略[19]等方法代替随机初始化种群, 扩大种群前期的多样性; 通过自适应t分布[16]、反向学习机制[17,20]、自适应惯性权重[15,20,21]等策略来提高算法全局搜索能力, 同时平衡算法的收敛速度与局部寻优能力.
为了解决BES存在的问题, 文中引入了正余弦搜索机制、惯性权重自适应策略、萤火虫搜索机制对BES位置更新公式进行修改, 提出一种基于BES的新型秃鹰搜索算法. 实验表明, 改进后的新型秃鹰搜索算法可以有效地改善全局搜索与局部搜索的不协调, 提高算法寻优准确率和收敛速度. 最后, 将改进后的算法应用于优化CNN的超参数学习率, 有效地提高分类模型的性能.
2 背景知识秃鹰搜索算法整体思路是对秃鹰捕获猎物的行为进行模拟, 整个算法可分为选择空间、搜索空间、俯冲这3个阶段.
1) 选择搜索空间阶段. 该行为数学模型为:
| Xi,new=Xbest+α×r×(Xmean−Xi) | (1) |
其中, 秃鹰当前位置为
2) 搜索空间猎物阶段. 相关公式如下:
| θ(i)=a×π×rand | (2) |
| r(i)=θ(i)+R×rand | (3) |
| xr(i)=r(i)×sin[θ(i)] | (4) |
| yr(i)=r(i)×cos[θ(i)] | (5) |
| x(i)=xr(i)/xr(i)max(|xr|)max(|xr|) | (6) |
| y(i)=yr(i)/yr(i)max(|yr|)max(|yr|) | (7) |
| Xi,new=Xi+x(i)×(Xi−Xmean)+y(i)×(Xi−Xi+1) | (8) |
其中,
3) 俯冲阶段. 极坐标方程描述运动数学模型, 具体如下:
| θ(i)=a×π×rand | (9) |
| r(i)=θ(i) | (10) |
| x1r(i)=r(i)×sinh[θ(i)] | (11) |
| y1r(i)=r(i)×cosh[θ(i)] | (12) |
秃鹰当前位置更新的数学模型如下:
| x2(i)=x1r(i)max(|x1r|)×(Xi−c1×Xmean) | (13) |
| y2(i)=y1r(i)max(|y1r|)×(Xi−c2×Xbest) | (14) |
| Xi,new=rand×Xbest+x2+y2 | (15) |
其中,
正余弦算法(sine cosine algorithm, SCA)[22]作为一种新型的随机搜索算法, 具有随机搜索算法的共性, 其优化过程分为探索与利用两个阶段, 具有较强地搜索空间、逃避局部最优的能力. 其数学模型具体如下:
| Xt+1i={Xti+r1×sin(r2)×|r3×Pti−Xti|,r4<0.5Xti+r1×cos(r2)×|r3×Pti−Xti|,r4⩾ | (16) |
| {r_1} = h - h \times t/ T | (17) |
其中,
秃鹰搜索算法通过一组随机值来求解全局最优解, 寻优过程中起始阶段的最优值和位置状态会直接影响下一阶段寻优结果, 如果起始状态以较少的随机值或局部最优范围内的随机值来启动算法, 则较易陷入局部最优. 因此利用正余弦优化机制具有高探索性和局部最优避免性来修正秃鹰搜索算法选择搜索空间阶段的位置更新公式, 具体数学模型如下:
| {X_{i, {\rm{new}}}} = \left\{ \begin{aligned} & \left( {{X_{{\rm{mean}}}} - {X_i}} \right) \times {r_5} + {r_1}\sin \left( {{r_2}} \right) \times \left| {{r_3}{X_{{\rm{best}}}} - {X_i}} \right|, \\ &\qquad\qquad {r_4} < 0.5 \\ & \left( {{X_{{\rm{mean}}}} - {X_i}} \right) \times {r_5} + {r_1}\cos \left( {{r_2}} \right) \times \left| {{r_3}{X_{{\rm{best}}}} - {X_i}} \right|, \\ &\qquad\qquad {r_4} \geqslant 0.5 \end{aligned} \right. | (18) |
其中,
群智能搜索算法通过适应度值来评估解的优劣性, 然而随着迭代次数的增加, 陷入局部最优的概率增大. 因此需要通过适应度值, 不断调整位置更新公式的权重参数值, 平衡局部开发与全局搜索之间存在的冲突, 防止陷入局部最优, 加快求得全局最优解.
为了加强BES算法全局探索与后期局部利用能力, 修改惯性权重自适应公式. 改进后数学公式如下:
| w_i^t = \left\{ \begin{aligned} & {w_{\min }} + \left( {{w_{\max }} - {w_{\min }}} \right)\frac{{fit\left( {X_i^t} \right) - fi{t_{\min }}\left( {{X^t}} \right)}}{{fi{t_{{\rm{mean}}}}\left( {{X^t}} \right) - fi{t_{\min }}\left( {{X^t}} \right)}}, \\ &\qquad\qquad fit\left( {X_i^t} \right) \leqslant fi{t_{{\rm{mean}}}}\left( {{X^t}} \right)\\ & {{w_{\max }} + {r_6}{{\rm{e}}^{{{T - t} / T}}}, fit\left( {X_i^t} \right) > fi{t_{{\rm{mean}}}}\left( {{X^t}} \right)} \end{aligned} \right. | (19) |
其中,
利用式(19)改进BES算法搜索空间阶段的权重参数, 调整个体和群体之间的联系强度. 具体数学公式如下:
| {X_{i, {\rm{new}}}} = {X_i} + x\left( i \right) \times \left( {{X_i} - {X_{{\rm{mean}}}}} \right) + w_i^t \times y\left( i \right) \times \left( {{X_i} - {X_{i + 1}}} \right) | (20) |
其中,
萤火虫算法(firefly algorithm, FA)[23]作为新型搜索算法, 性能处于粒子群优化算法与随机搜索算法之间. 数学模型具体如下:
| X_i^{t + 1} = {X_i} + {\beta _0}{{\rm{e}}^{ - \gamma r_{i, j}^2}}\left( {{X_i} - {X_j}} \right) + \sigma \left( {rand - 0.5} \right) | (21) |
| \sigma = {\sigma _0} \times {\theta ^t} | (22) |
其中,
由于BES算法存在全局探索与局部利用不平衡性问题, 而萤火虫算法具有非常有效的求解方式, 可以有效地找到全局最优解[23]. 因此利用式(19)和式(21)优化BES俯冲阶段的位置更新公式, 具体数学模型如下:
| {X_{i, {\rm{new}}}} = {X_i} + {x_2}\left( i \right) \times {{\rm{e}}^{ - w_i^t\gamma y_2^2\left( i \right)}} \times \left( {{X_i} - {X_{{\rm{best}}}}} \right) + \alpha \times \left( {rand - 0.5} \right) | (23) |
其中,
| {X_{i, {\rm{new}}}} = {X_i} + {x_2}\left( i \right) \times \frac{{\left( {{X_i} - {X_{{\rm{best}}}}} \right)}}{{1 + w_i^t\gamma y_2^2\left( i \right)}} + \alpha \times \left( {rand - 0.5} \right) | (24) |
将经过以上改进后的秃鹰算法命名为新型秃鹰搜索 (new bald eagle search, NBES).
3.4 NBES算法步骤新算法流程图如图1所示, 具体步骤为Step1–Step6. Step1: 种群初始化、算法参数设置. 种群数量设为
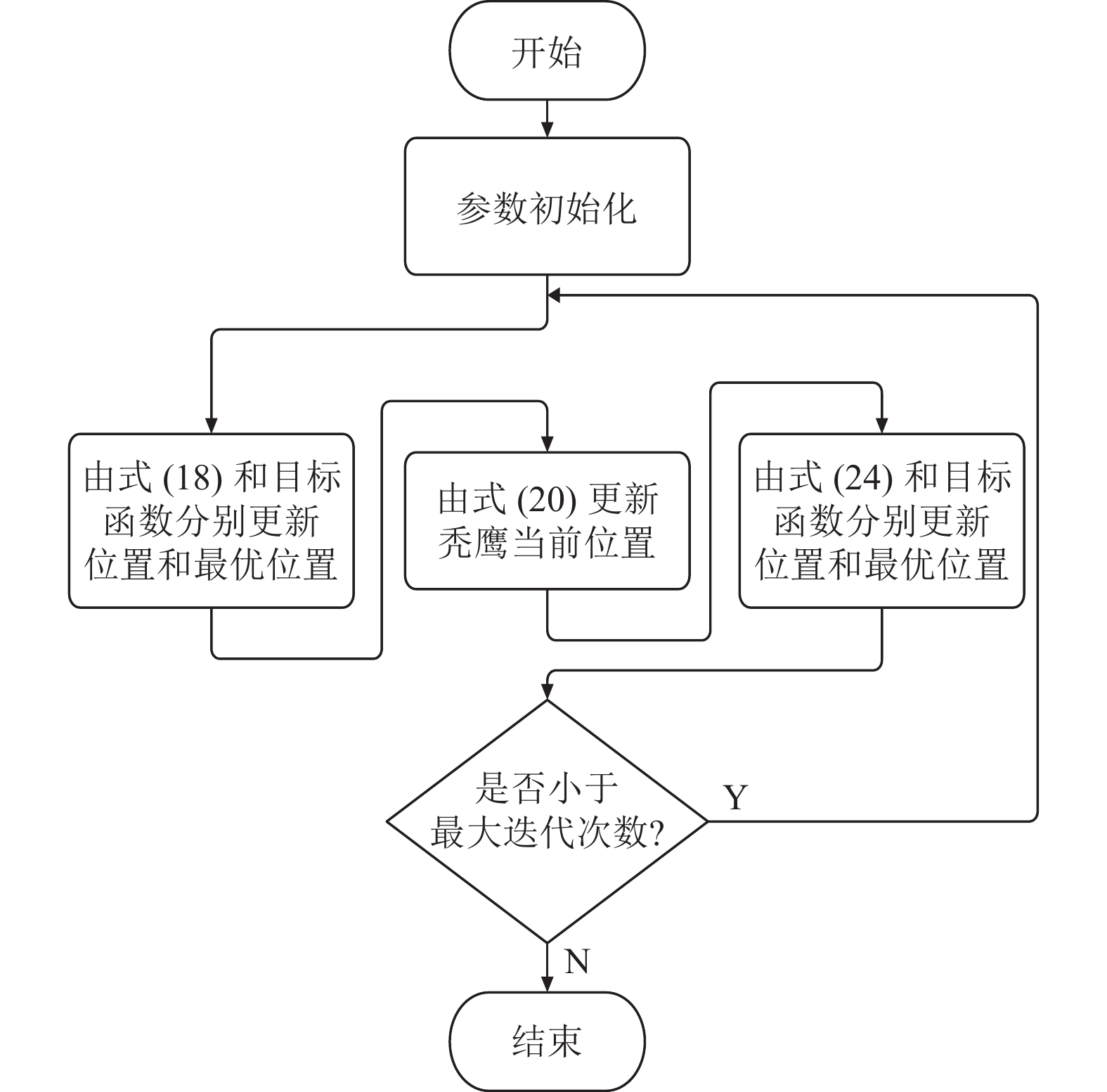
|
图 1 NBES算法流程图 |
4 算法实际应用
对图像分类模型进行研究时, CNN模型则扮演了一个非常重要的角色. 构建CNN模型时, 超参数的设置会直接影响模型性能. 由于CNN模型具有复杂性高、超参数多等现象, 人们往往需要通过试错策略和经验来选择最佳的超参数. 这种方法既耗时又费力, 并且不一定能够获得最优结果. 因此, 研究人员开始尝试在CNN模型中应用群智能算法对超参数进行自动化优化, 从而提高模型性能. 群智能算法通过对超参数进行优化搜索, 可以在短时间内找到最优的超参数值, 从而提高CNN模型的性能和训练效率. 具体应用场景包括医疗图像和人脸识别等领域. 因此, 群智能算法的应用在CNN模型性能优化中发挥着重要的作用, 它可以帮助我们更快地找到最优模型的超参数, 进一步提高图像分类的准确性和鲁棒性.
文中将通过多种群智能算法优化超参数学习率, 提高图像分类的识别精度. 同时对比不同群智能算法改进后的分类精度, 证明新算法NBES的实际应用价值.
4.1 模型构建首先需要选取优质的医疗影像数据集, 文中使用的数据集为Chest X-ray Database[24,25]. 其次对选取的医疗影像数据集进行预处理, 处理方式主要包括数据集划分、数据清洗、数据增强. 最后根据医疗影像数据集搭建适合的卷积神经网络结构. 为了方便后期将模型进行FPGA (field programmable gate array)硬件部署, 则搭建小型的网络模型训练医疗影像数据集. 其模型结构如图2所示.

|
图 2 网络模型结构图 |
4.2 模型优化
模型优化方法包括数据优化、结构优化、损失函数优化、超参数优化等[4]. 为了降低通过经验优化模型的难度与时间成本, 使用群智能算法优化学习率, 使学习率随模型的损失函数值变化而自动更新, 从而得到最优模型. 其中涉及的相关数学公式如下所示:
| {\textit{MSE}}\left( {y\_ {} , y} \right) = \frac{1}{n}{\sum\limits_{i = 1}^n {\left( {y - y\_ {} } \right)} ^2} | (25) |
| {W_{t + 1}} = {W_t} - {I_{r, i}} \times \frac{{\partial {\textit{MSE}}}}{{\partial {W_t}}} | (26) |
| {I_{r, i}} = \frac{1}{n}\sum\limits_{i = 1}^n {{X_{i, {\rm{best}}}}} | (27) |
| b = \sum\limits_{i = 1}^D {i \times X_i^8 + rand} | (28) |
| d = \frac{1}{{1 + {{\rm{e}}^{ - {\textit{MSE}}}}}} | (29) |
| {\textit{fitness}}5 = 0.5 + \frac{{{{\left( {\sin \left( {{b^2} + {d^2}} \right)} \right)}^{0.5}}}}{{{{\left( {1 + 0.001 \times \left( {{b^2} + {d^2}} \right)} \right)}^2}}} | (30) |
| R = \frac{{TP}}{{TP + FN}} | (31) |
| P = \frac{{TP}}{{TP + FP}} | (32) |
其中, 均方误差
| 表 1 混淆矩阵 |
模型优化具体流程图如图3所示. 首先根据医疗图像数据集构建适合的深度神经网络, 模型每次epoch训练过程中, 会根据式(25)和式(26)输出当前的loss值和权重值, 将每次输出的loss值代入式(30)中求出适应度值, 以适应度值为指标不断更新模型的学习率, 其次判断当前模型训练次数是否小于设定的模型训练次数, 判断成立则将学习率输入卷积神经网络中继续训练, 反之结束模型训练并保存当前最优模型.
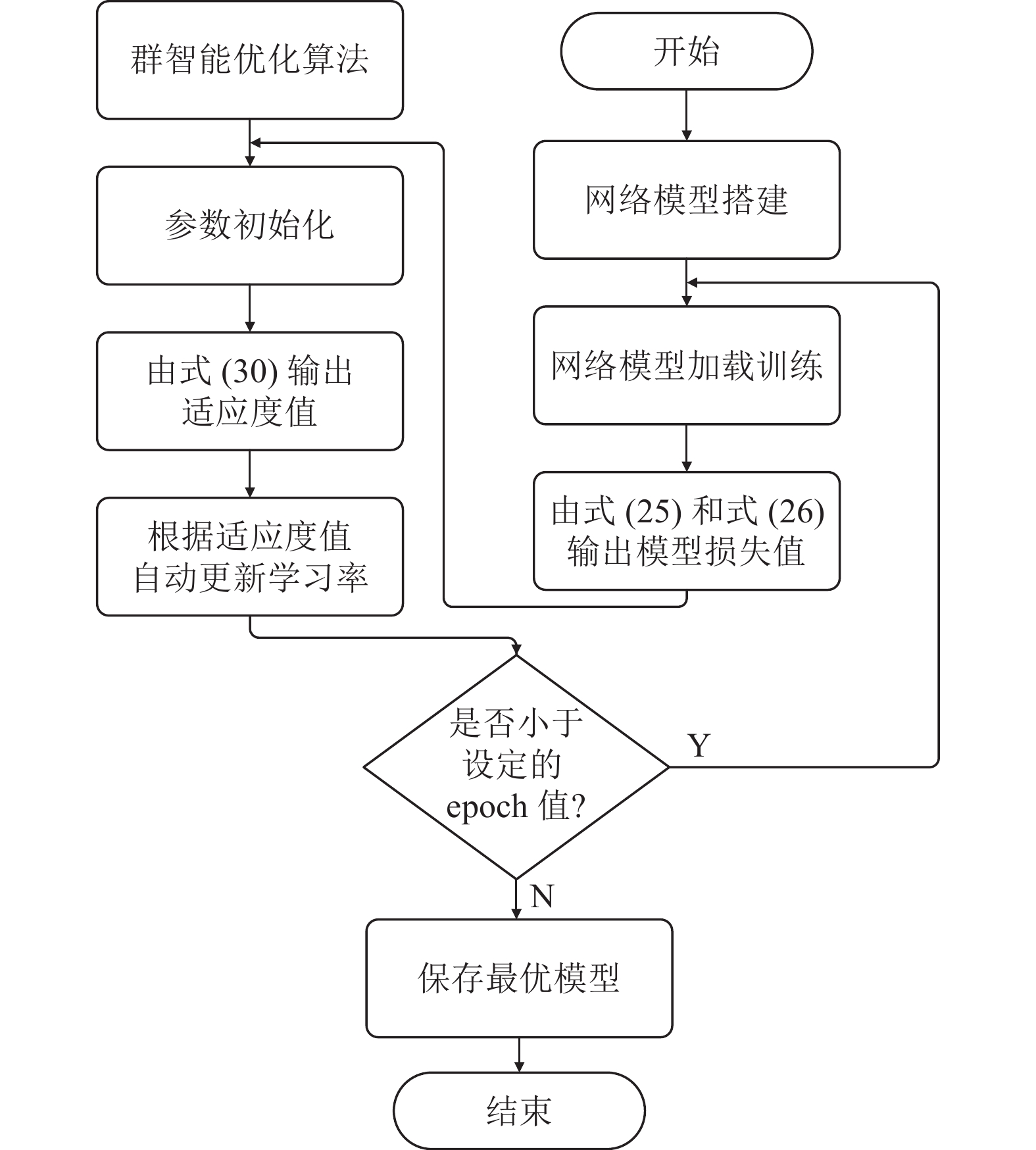
|
图 3 模型优化流程图 |
5 实验结果与分析
通过多种对比实验验证NBES算法性能. 首先对比BES算法在不同改进方案的效果, 保证改进方案的有效性, 将效果最好的算法记为NBES; 其次将NBES算法与BES、GSCBES[21]、人工蜂群算法(ABC)、粒子群算法(PSO)进行实验结果对比, 展现NBES算法性能. 最后利用BES、NBES、GSCBES优化超参数学习率, 通过对比实验效果, 展现NBES的应用性能.
5.1 改进方案有效性分析为了体现出不同改进方案对算法性能的影响, 使用表2中11个标准测试函数[26]作为算法的目标函数. 其中
| 表 2 标准测试函数 |
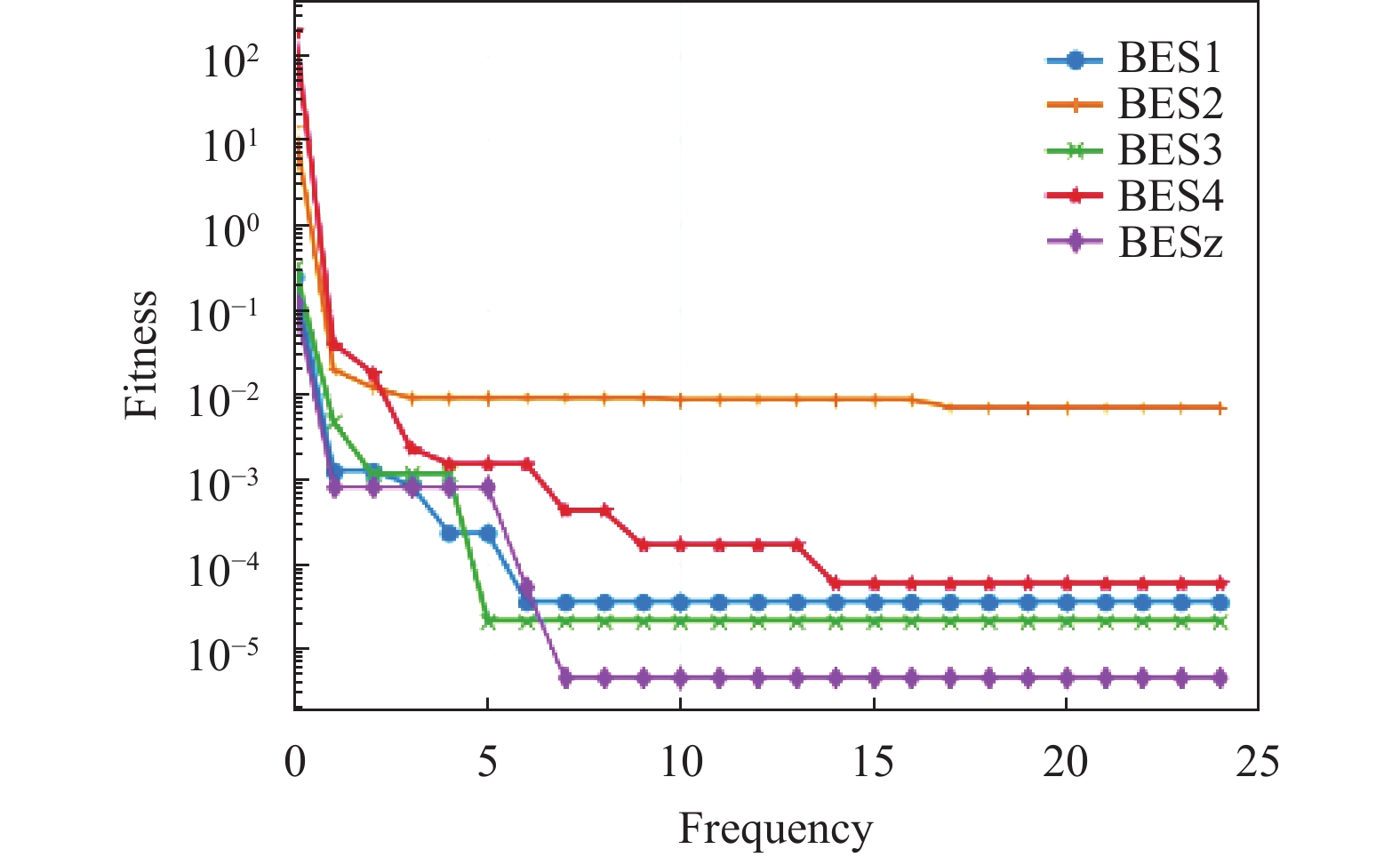
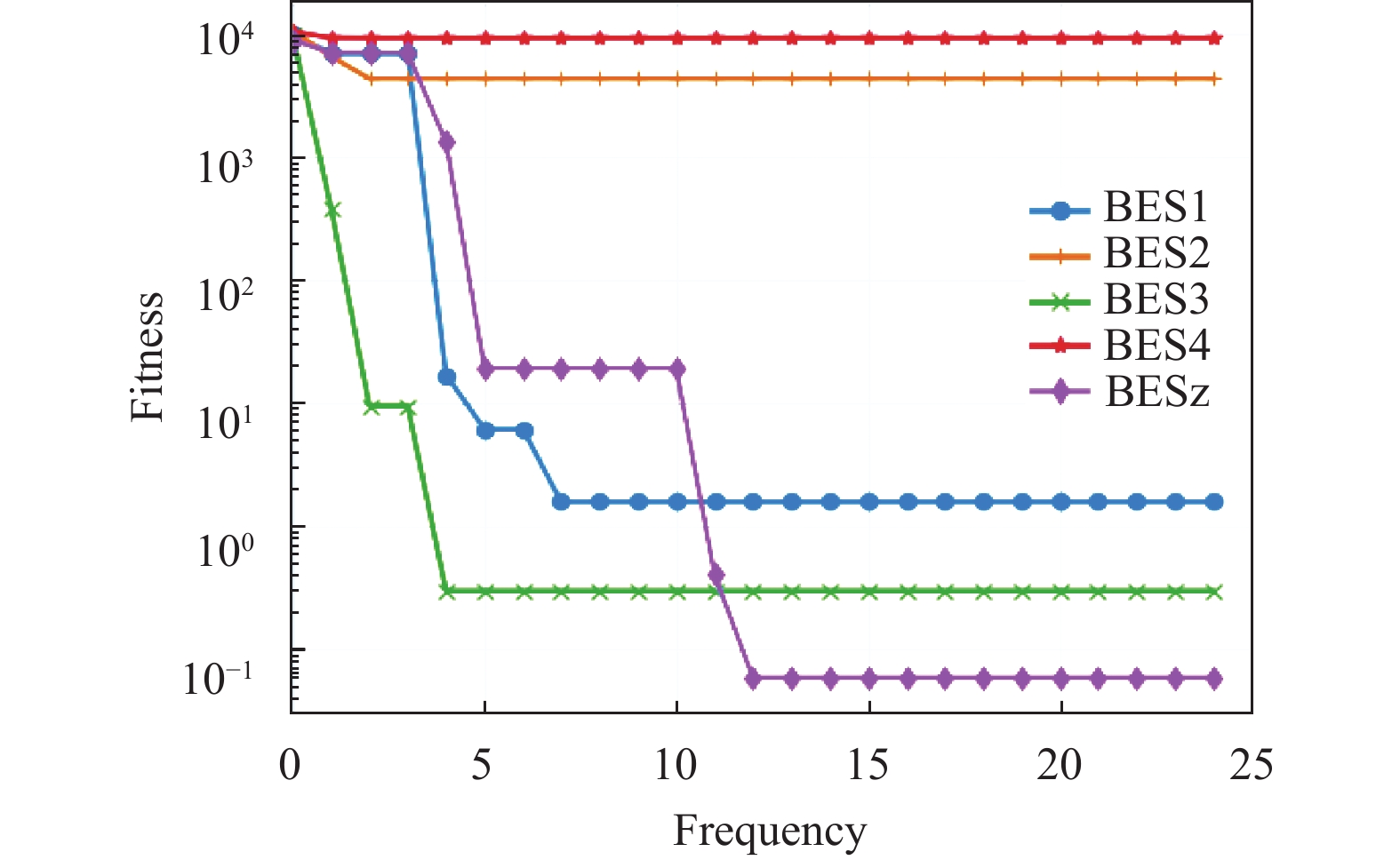
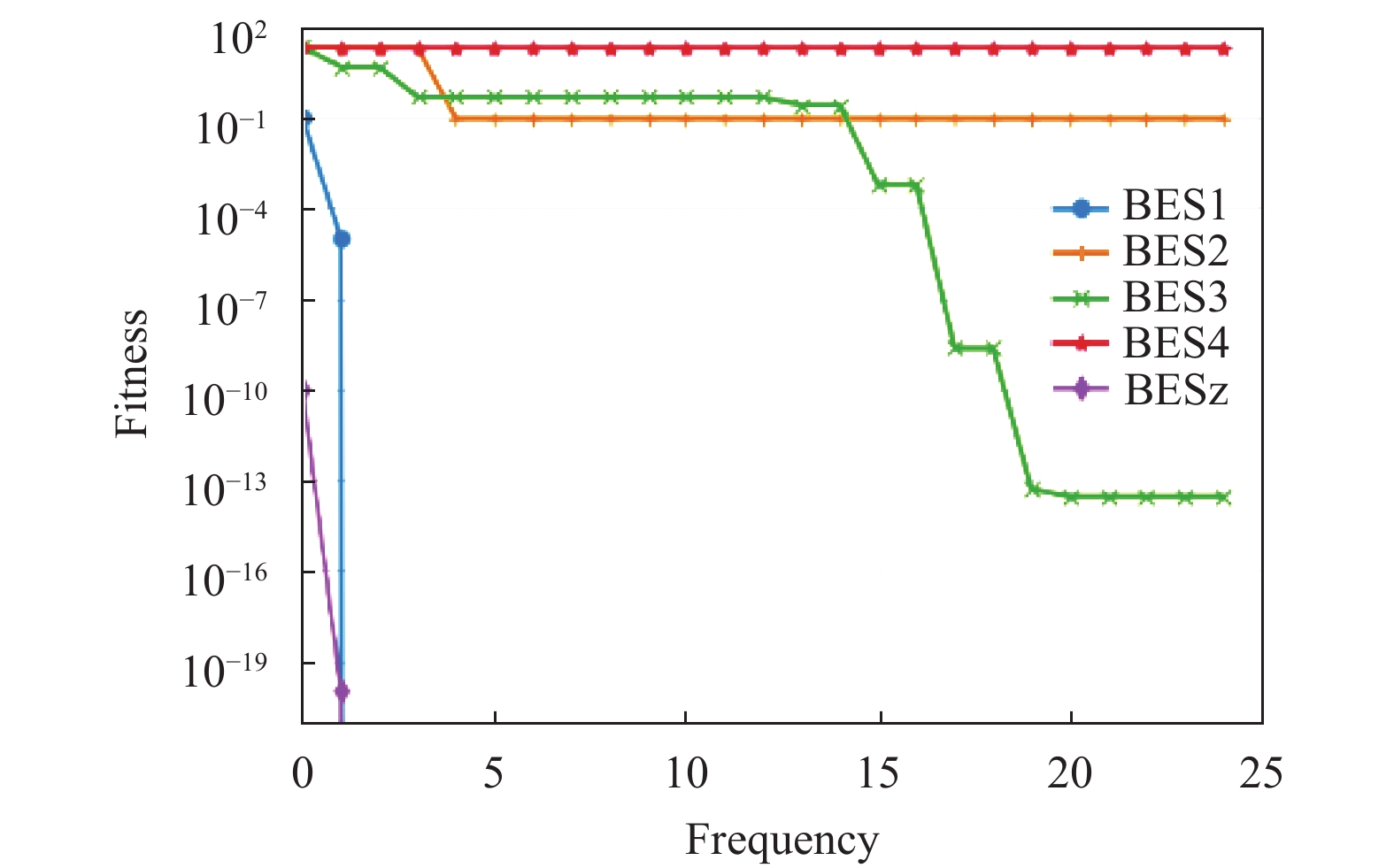
记BES算法加上正余弦优化机制为BES1; BES算法加上惯性权重自适应位置更新策略为BES2; BES算法加上正余弦优化机制和惯性权重自适应位置更新策略为BES3; BES算法加上惯性权重自适应位置更新策略和萤火虫优化机制为BES4; BES算法加上正余弦优化机制、惯性权重自适应策略、萤火虫优化机制为BESz (NBES). 为了体现每次改进方案的有效性, 对比BES1、BES2、BES3、BES4、BESz (NBES)算法的实验效果. 同理为了实验的公平性与专业性, 对不同算法的共有参数设置为相同值, 且进行50次重复性实验取均值. 具体的实验效果如表3所示.
| 表 3 改进方案效果对比 |
由实验结果可知, 不同改进方案下的算法在标准测试函数上都展现出不同层次的优越性. 例如其中BES1、BES3、BESz (NBES)对测试函数寻优的稳定性和精准性都优于原算法, 证明这3种改进方案不仅提高了原算法的全局寻优能力, 也提高了算法逃脱局部最优的能力. BES2在
为了突显出不同算法对于标准测试函数的寻优性能, 选取5个测试函数进行图像展示, 其中包括3个单峰函数和2个多峰函数. 由图4–图8可知, BESz (NBES)算法对于测试函数的寻优准确率和寻得最优解的速度都远优于BES1、BES2、BES3、BES4. 为了使得线图标记更加清晰, 能够快速的区分出不同算法所对应的线条, 对迭代次数进行20倍等比例缩小, 实际迭代次数(frequency)为500次. 综上所述NBES算法的整体寻优性能最为优越.
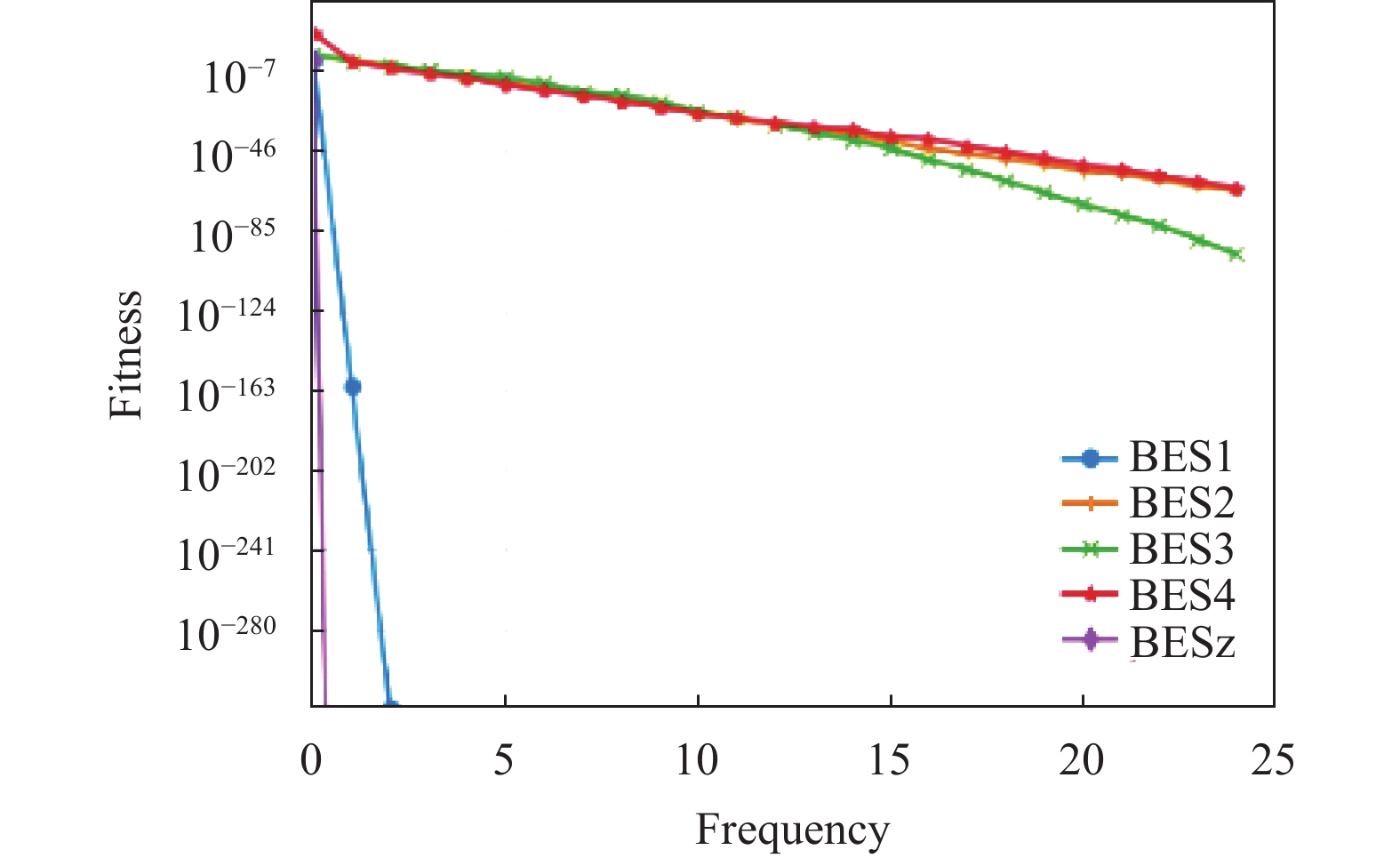
|
图 4 |
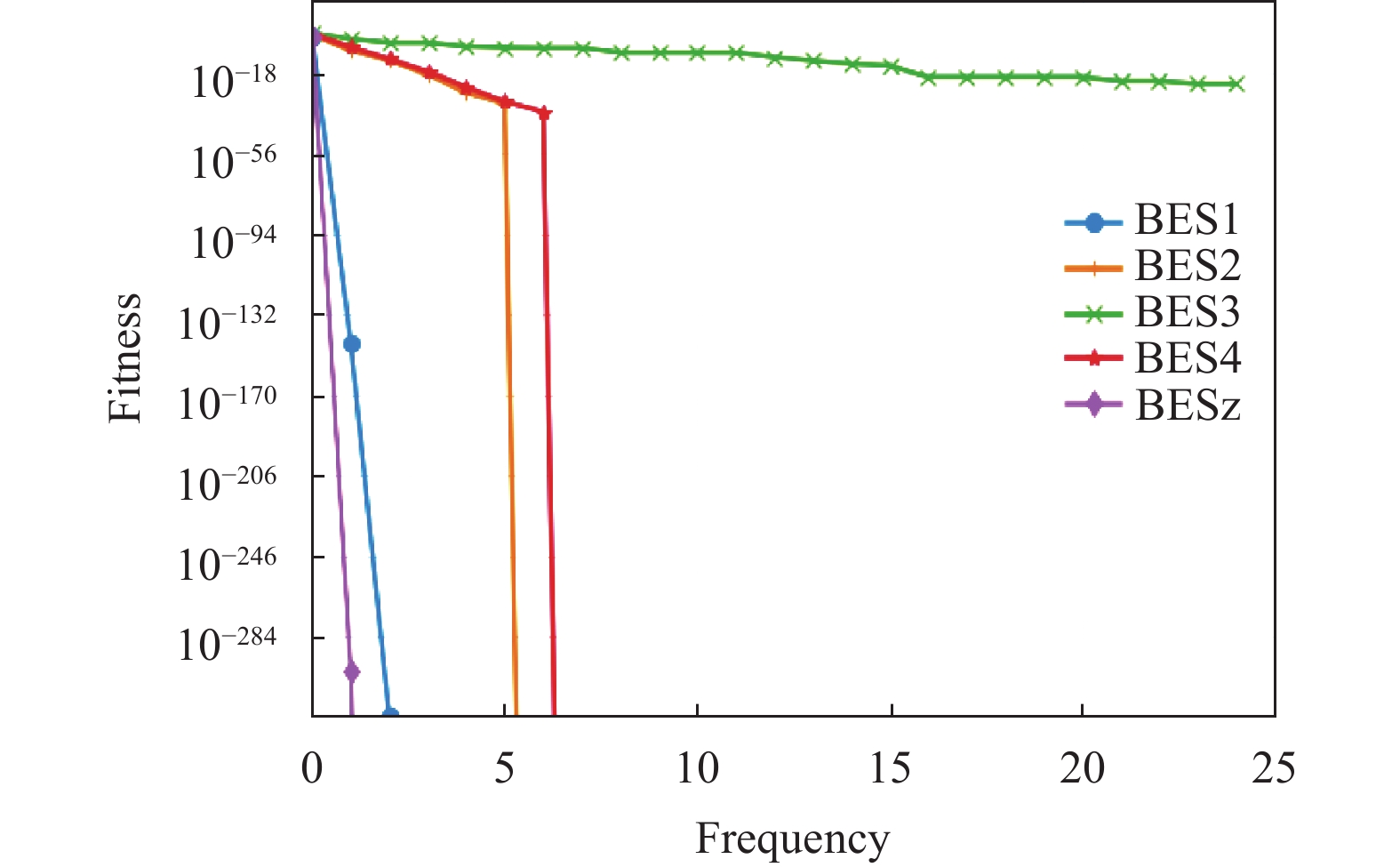
|
图 5 |
|
图 6 |
|
图 7 |
|
图 8 |
5.2 与不同群智能算法对比
在维度为30与100的条件下, 对比NBES、PSO、ABC、GSCBES、BES算法的实验效果, 验证新算法的性能. 具体的实验效果如表4所示.
| 表 4 不同的维度和算法效果对比 |
首先从相同算法但不同维度的角度分析实验结果. 随着维度的不断增大, 群智能优化算法的整体性能会呈现下降趋势, 这是由于随着维度的增大求解空间随着变大, 导致其求解难度也加大. 其中PSO、ABC、GSCBES、BES算法随着维度增大, 其对测试函数求解的稳定性、准确性、收敛速率都变差; 而NBES算法在
通过实验结果展现群智能算法在图像分类领域的应用价值, 设计原理如图3所示.
当未使用群智能算法优化学习率时, 模型经过100轮次训练后, 得到分类精度稳定在0.788. 经过BES、GSCBES、NBES优化后的CNN, 将其分别记为BES_CNN、GSCBES_CNN、NBES_CNN. 表5中的“Best accuracy”指进行100轮次模型训练的过程中, 测试集中出现的最高分类精度. “Final accuracy”则指代100轮次模型训练后, 在测试集上达到的最终稳定的分类精度. “Test loss”表示测试集的损失值. “Avg accuracy”为3次重复实验, 测试集精度的平均值. “R”表示查全率. “P”表示查准率. 由实验可知, 当以不同的算法优化学习率或以不同的目标函数作为寻优指标时, 可以得到不同的分类模型精度. 由表5的实验结果可知, 当以
| 表 5 不同的算法优化效果对比 |
6 结语
本文基于秃鹰搜索算法提出一种新型算法, 该算法在原算法的基础上融合正余弦优化机制、惯性权重自适应位置更新策略、萤火虫优化机制, 使得算法前期全局探索范围增大, 中后期平衡全局探索与局部利用, 使算法不仅拥有极强地全局探索能力和局部利用能力, 且算法稳定性、准确性、收敛性都极强. 为了体现新算法的实用性, 利用新算法优化卷积神经网络的超参数学习率, 达到自动寻找最佳的分类模型, 并将模型用于医疗影像病理性分类预测中, 实验表明, 新算法NBES的模型优化效果优于其他群智能算法.
NBES不仅可以用于优化分类模型的超参数, 也可以优化分割模型、识别模型、检测模型中的各种超参数. 例如优化超参数正则化参数、小批量数据大小、模型训练次数、神经网络层数和神经元个数等.
| [1] |
Feurer M, Hutter F. Hyperparameter optimization. Automated Machine Learning: Methods, Systems, Challenges. Cham: Springer, 2019. 3–33.
|
| [2] |
Kohavi R, John GH. Automatic parameter selection by minimizing estimated error. Proceedings of the 1995 Conference on Machine Learning. Amsterdam: Elsevier. 1995. 304–312.
|
| [3] |
Yang L, Shami A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing, 2020, 415: 295-316. DOI:10.1016/j.neucom.2020.07.061 |
| [4] |
He T, Zhang Z, Zhang H, et al. Bag of tricks for image classification with convolutional neural networks. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 558–567.
|
| [5] |
Liu RM, Liu EQ, Yang J, et al. Optimizing the hyper-parameters for SVM by combining evolution strategies with a grid search. Proceedings of the 2006 International Conference on Intelligent Computing on Intelligent Control and Automation. Kunming: Springer, 2006. 712–721.
|
| [6] |
Prabu S, Thiyaneswaran B, Sujatha M, et al. Grid search for predicting coronary heart disease by tuning hyper-parameters. Computer Systems Science and Engineering, 2022, 43(2): 737-749. DOI:10.32604/csse.2022.022739 |
| [7] |
Klein A, Falkner S, Bartels S, et al. Fast Bayesian optimization of machine learning hyperparameters on large datasets. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale: PMLR, 2017. 528–536.
|
| [8] |
Wu J, Chen XY, Zhang H, et al. Hyperparameter optimization for machine learning models based on Bayesian optimization. Journal of Electronic Science and Technology, 2019, 17(1): 26-40. |
| [9] |
Aszemi NM, Dominic PDD. Hyperparameter optimization in convolutional neural network using genetic algorithms. International Journal of Advanced Computer Science and Applications, 2019, 10(6): 269-278. |
| [10] |
Ayumi V, Rere LMR, Fanany MI, et al. Optimization of convolutional neural network using microcanonical annealing algorithm. Proceedings of the 2016 International Conference on Advanced Computer Science and Information Systems (ICACSIS). Malang: IEEE, 2016. 506–511.
|
| [11] |
Serizawa T, Fujita H. Optimization of convolutional neural network using the linearly decreasing weight particle swarm optimization. Proceedings of the 36th Annual Conference of the Japanese Society for Artificial Intelligence. Kyoto: JSAI, 2022. 1–5.
|
| [12] |
Singh P, Chaudhury S, Panigrahi BK. Hybrid MPSO-CNN: Multi-level particle swarm optimized hyperparameters of convolutional neural network. Swarm and Evolutionary Computation, 2021, 63: 100863. DOI:10.1016/j.swevo.2021.100863 |
| [13] |
Yamasaki T, Honma T, Aizawa K. Efficient optimization of convolutional neural networks using particle swarm optimization. Proceedings of the 3rd IEEE International Conference on Multimedia Big Data (BigMM). Laguna Hills: IEEE, 2017. 70–73.
|
| [14] |
Alsattar HA, Zaidan AA, Zaidan BB. Novel meta-heuristic bald eagle search optimisation algorithm. Artificial Intelligence Review, 2020, 53(3): 2237-2264. DOI:10.1007/s10462-019-09732-5 |
| [15] |
丁容, 高建瓴, 张倩. 融合自适应惯性权重和柯西变异的秃鹰搜索算法. 小型微型计算机系统, 2023, 44(5): 910-915. |
| [16] |
耿棒棒, 王勇. 基于改进秃鹰搜索算法的Kubernetes资源调度应用. 计算机系统应用, 2023, 32(4): 187-196. DOI:10.15888/j.cnki.csa.009034 |
| [17] |
莫仕勋, 杨皓, 蒋坤坪, 等. 基于改进秃鹰搜索算法的变压器J-A模型参数辨识. 电工电能新技术, 2022, 41(4): 67-74. |
| [18] |
杨国华, 冯骥, 柳萱, 等. 基于改进秃鹰搜索算法的含分布式电源配电网分区故障定位. 电力系统保护与控制, 2022, 50(18): 1-9. |
| [19] |
黄维, 吕丽平. 基于改进秃鹰搜索算法的工业机器人几何参数标定方法. 机械设计与研究, 2022, 38(6): 21-24, 33. |
| [20] |
陈将宏, 胡炀, 饶佳黎, 等. 基于自适应反向学习秃鹰搜索算法的最优潮流计算. 电工材料, 2023(1): 85-93. |
| [21] |
赵沛雯, 张达敏, 张琳娜, 等. 融合黄金正弦算法和纵横交叉策略的秃鹰搜索算法. 计算机应用, 2023, 43(1): 192-201. |
| [22] |
Mirjalili S. SCA: A sine cosine algorithm for solving optimization problems. Knowledge-based Systems, 2016, 96: 120-133. DOI:10.1016/j.knosys.2015.12.022 |
| [23] |
Yang XS, He XS. Firefly algorithm: Recent advances and applications. International Journal of Swarm Intelligence, 2013, 1(1): 36-50. DOI:10.1504/IJSI.2013.055801 |
| [24] |
Jaeger S, Karargyris A, Candemir S, et al. Automatic tuberculosis screening using chest radiographs. IEEE Transactions on Medical Imaging, 2014, 33(2): 233-245. DOI:10.1109/TMI.2013.2284099 |
| [25] |
Candemir S, Jaeger S, Palaniappan K, et al. Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration. IEEE Transactions on Medical Imaging, 2014, 33(2): 577-590. DOI:10.1109/TMI.2013.2290491 |
| [26] |
Yao X, Liu Y, Lin GM. Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, 1999, 3(2): 82-102. DOI:10.1109/4235.771163 |
 2023, Vol. 32
2023, Vol. 32



