随着计算机技术的快速发展, 软件系统已经成为人们生活中的重要组成部分, 对软件安全的需求也越来越高[1]. 软件系统的可靠性对于国家的安全、生产的稳定以及人们的生活存在直接或间接的影响, 因此软件系统中潜藏的错误可能带来不可估量的后果.
虽然人们在软件开发中进行了常规测试以提高其可靠性, 但软件的复杂性、代码量和测试成本的增加使软件测试的局限性变得更加明显. 软件测试只能检测错误, 不能完全保证软件的安全性和正确性, 因此, 需要找到更可靠、更高效的工业应用方法和工具.
不幸的是, 软件安全问题时常发生, 不仅国内外频频出现, 而且对生产和人们的生活造成严重影响. 例如, 2013年9月, 美国联合航空公司的网站发生了票务错误, 导致机票几乎免费, 引发了乘客的不安情绪, 局势失控. 同样, 2014年中国一家票务网站的信息被泄露, 大量用户账户密码和相关信息遭到侵犯. 2016年1月, 一颗运行了15年的卫星发生故障, 尽管只有13 μs, 但对追踪系统造成了重大影响. 此外, 汽车制造商因为软件控制系统的质量问题而被迫频繁召回车辆, 这阻碍了无人驾驶汽车的发展. 这些事件表明, 软件安全问题仍然是一个重要的挑战, 需要采取更加可靠措施来解决这个问题.
为了解决上述问题, 先前的研究者采用了传统的软件测试作为提高软件可靠性的手段. 然而, 传统的软件测试方法只能覆盖一些执行频率高的关键路径, 无法覆盖所有路径, 所覆盖的路径仅涉及安全风险. 因此, 软件测试只能检测错误, 不能完全保证软件的安全性和正确性, 在理论和工具的不断进步的推动下, 工业界和学术界的研究人员已积极参与到软件验证的国际大挑战中.
作为这一挑战的一部分, Jones等人[1]提出了对FreeRTOS[2]进行验证, 这是一种使用C编写的嵌入式抢占式多任务实时操作系统, 验证属性包括内存安全和功能正确性. 他们针对FreeRTOS涉及的大量指针, 堆操作程序的自动验证[3]提出使用分离逻辑, 并支持关于共享复杂数据结构的推理. seL4[4,5]和CertiKOS[6,7]是验证重新设计的目标内核, 它们的算法和数据结构是独立开发的, 以便简化验证过程. 然而, 在这些操作系统内核验证项目中, 复杂内核数据结构程序的形式化描述和验证仍然需要进一步的探索.
Murray等人[8]主要对seL4进行验证, 其中重要的数据结构就是双向链表. 在验证的过程中, 他们采用的方式是用有序列表结构近似模拟双向链表, 但是这种模拟方式没办法知道双向链表内部不同指针的指向情况. 为了进一步提高操作系统的形式化验证, Klein团队在不同方向上开展了研究, 如系统验证、缓存验证[9]和实时验证[10].
耶鲁大学Flint实验室的一系列论文[11–14]提出了在编译器上进行验证的有效方法, 这些方法从编译过程中抽象出数据结构状态, 描述并验证程序迁移过程中的状态. Ironclad项目[15]将应用程序、运行时库和内核作为一个整体, 验证其运行行为是否符合正式的应用层规范. Hyperkernel[16]和Serval[17]也是类似的自动验证项目, 它们都假定系统接口的特殊性, 而其程序不包含复杂算法.
国内对嵌入式操作系统的验证同样进行了大量的工作[18–20]. 姜菁菁等人[21]使用Coq进行需求层建模工作, 针对需求层模型的性质以及操作系统模型的性质进行分析, 将两者匹配起来, 从而确保这两部分具有一致性, 但是, 该工作不包括代码层工作, 也不包括验证各种代码层功能与全局性质的匹配.
综合上述工作中的局限性, 我们认为现阶段操作系统内核形式化工作的难点主要有两个方面, 一方面是操作系统内核中代码层涉及很多全局性质, 在验证过程中, 需要通过全局不变式对全局性质进行形式化的描述, 并在不同的函数中进行验证, 从而证明各个函数符合操作系统内核的全局性质; 另一方面是操作系统内核中存在很多复杂数据结构程序, 尤其是多种形状耦合在一起的不规则数据结构程序, 极大增加了验证的难度. 本文的主要贡献有以下两点.
(1)根据操作系统内核满足的全局性质, 对其中的部分关键代码, 进行形式化验证. 通过规范语言给出不变式性质的断言, 以函数为单位对其功能和行为进行形式化描述, 并根据推理规则在原型系统中实现程序的自动验证.
(2)针对操作系统内核中经常使用的复杂数据结构程序, 本文通过扩展形状图理论, 提出嵌套形状图逻辑的方法, 分开定义主数据结构和次数据结构, 并对分离前后的嵌套形状图进行一致性证明. 运用该方法, 验证了该内核中关于任务创建与调度, 消息队列创建与操作相关的代码.
2 原型系统介绍在Hoare逻辑[22]出现之后, 大量的研究工作迅速展开, 但是Hoare逻辑有一个严重的缺陷, 即不能处理别名问题. 在程序验证过程中, 指针别名出现频率很高, 于是研究人员设计了很多在Hoare逻辑基础上进行扩展的逻辑, 使得Hoare能够处理更复杂的程序. 我们课题组实现的原型系统是以Hoare逻辑为基础, 引入形状图逻辑[23]来解决指针别名相关问题, 扩大了Hoare逻辑的处理范围, 但又不会增加证明的负担. 下面将对原型系统的验证流程以及形状分析模块进行详细地阐释.
2.1 原型系统现状简介本文使用原型系统[24], 分为4个主要模块: 前端、验证条件生成器、形状分析和验证条件证明器.
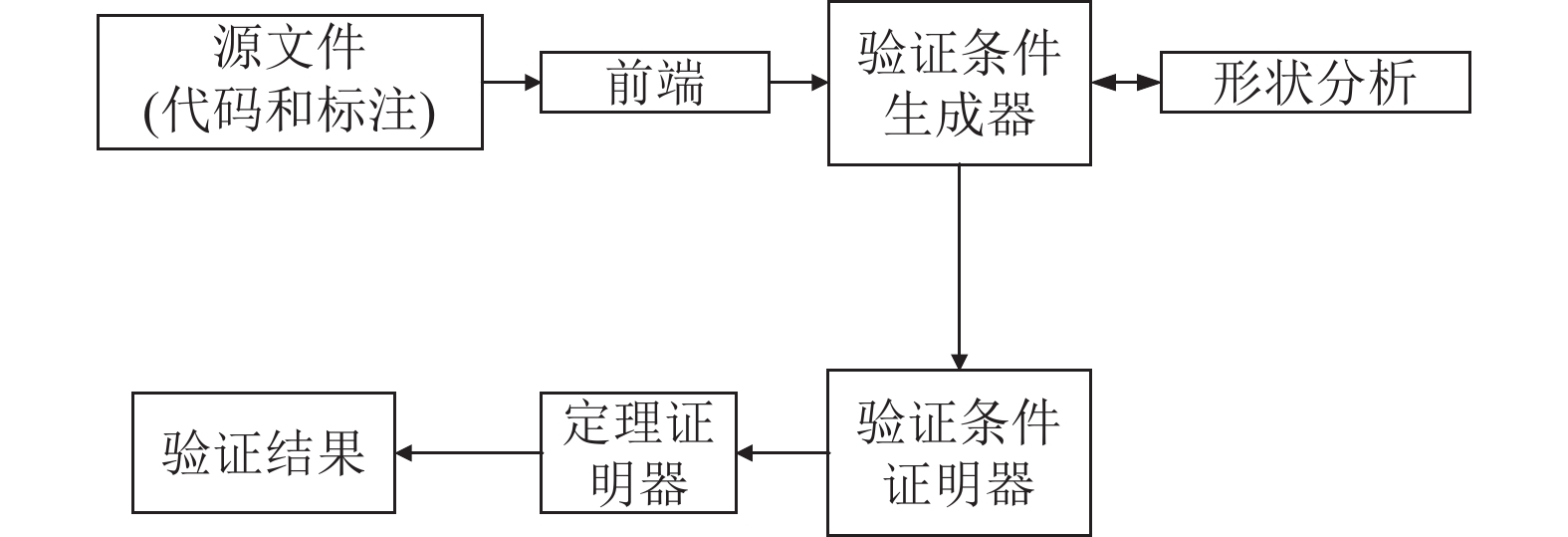
图1显示了系统的框架, 整个过程是将C源文件和安全C规范注释传递到前端, 在那里进行静态检查, 收集一些重要的信息, 并将这些信息生成对应的语法树; 验证条件生成器向前遍历语法树, 堆指针相关操作留给形状分析. 形状分析是根据形状图逻辑, 对应到各个程序点生成对应的形状图. 验证条件证明器需要用到最强的后条件推理, 通过此方法, 能够生成对应的验证条件, 可用
|
图 1 原型系统框架 |
2.2 形状分析
形状图是对程序运行时复杂数据结构状态的图形化描述. 它采用有向图的形式进行描述, 主要是程序中的声明堆指针变量, 但不包括节点数据域. 相应的节点类型在图2中展示, 分别为声明节点, 结构节点, NULL节点, 悬挂节点, 浓缩节点, 谓词节点.

|
图 2 形状图的节点类型 |
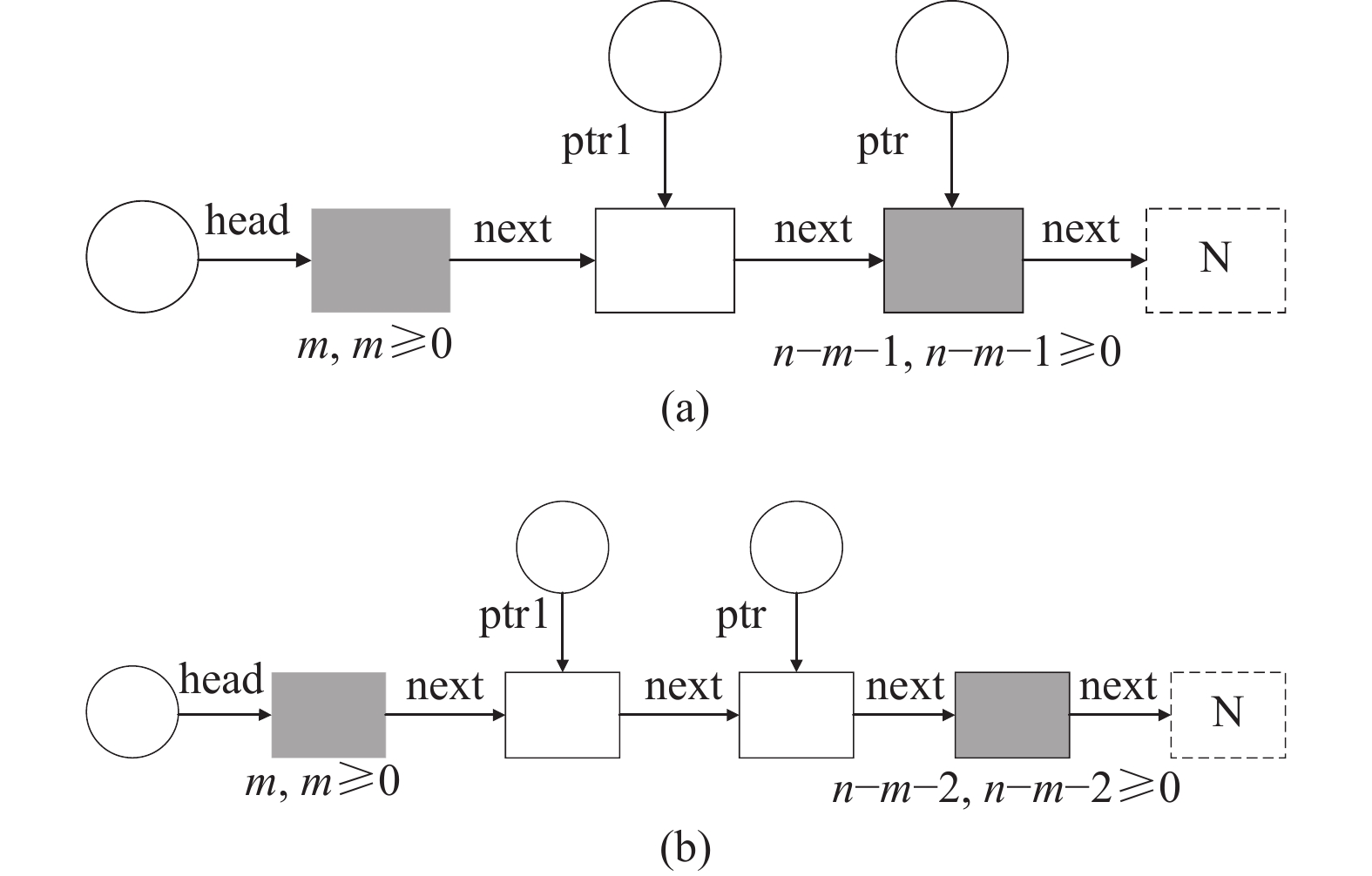
为了更好地描述与形状图相关的内容, 本文通过单向链表的两个形状图(见图3)进行介绍, 对应的单向链表部分程序代码见图4. 其中, 图3(a)中的形状图表示程序片段的循环不变属性, 而图3(b)中的形状图则表示程序代码循环体中第1条指令之前的程序点.
|
图 3 形状图的两个例子 |
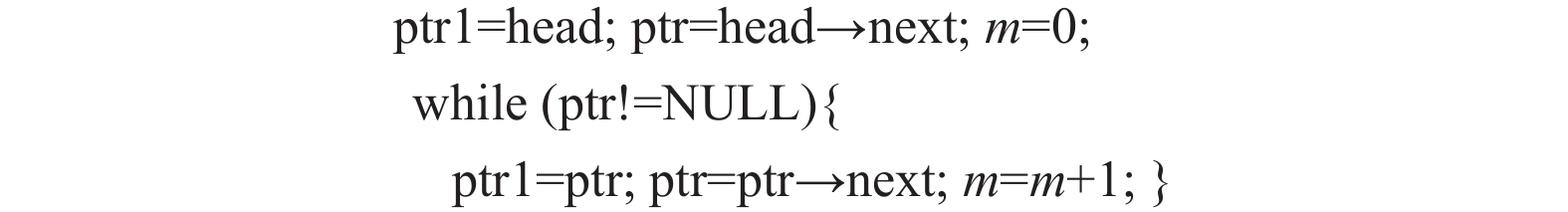
|
图 4 单向链表部分程序 |
本文的原型系统结合形状图的等价转换规则与程序, 实现了以下具体步骤.
首先, 在满足循环条件ptr!=NULL时, 结构节点由图3(a)中右边的浓缩节点展开, 得到图3(b).
其次, 在循环中, 执行第1条语句ptr1=ptr后, 图3上的ptr1重新指向, 所指的为ptr节点的指针; 执行第2条语句ptr=ptr→next后, 图3上的ptr1重新指向, 所指的为右边那个浓缩节点; 执行第3条语句m=m+1后, 程序中的循环体已经结束, 对应的形状图也会重新调整.
最后, 调整过程中发现, ptr1最初指向的结构节点现在没有指针, 就可以对形状图进行简化, 将其折叠到右边的浓缩节点中, 再次产生图3(a)中的形状图.
3 操作系统内核全局性质的验证操作系统内核中存在不同的模块, 这些模块里有多种多样的数据结构, 它们相互之间并不独立, 而是存在着一定的耦合关系. 本节针对这些全局性质, 详细描述语法和推理规则, 用断言的形式对内核不变式进行形式化定义并验证.
3.1 操作系统内核形式化定义操作系统内核中的绝大多数系统调用都是用C语言等高级语言实现的, 其中, 本文的研究对象μCOS-II在代码层的系统调用部分就是用C语言编写的. 这里采用的验证方法包括3个步骤: (1)认真分析系统调用中的自然语言规范, 并从这里面整理出相应的全局性质, 然后通过后文中定义的语法对这些全局性质逐个进行描述. (2)将(1)中描述的内容作为安全C规范注释, 并将其增加到程序中合适的位置上, 增加的内容包括有前后置条件, 循环不变式等. (3)在插入相应的安全C规范注释之后, 使用原型系统对其进行验证. 如果它能够验证通过, 那么该程序就满足对应的全局性质; 如果不能够验证通过, 需要对相应的安全C规范注释进行修正并再次验证.
3.1.1 语法图5所示的语法中, 该语法中包含有变量, 基本的表达式, 类型表达式, 二元运算符, 一元运算符, 函数和语句.

|
图 5 操作系统内核形式化定义语法 |
3.1.2 推理规则
在验证过程中, 针对操作系统内核的共享数据结构, 我们需要为其编写对应的不变式. 本文将Hoare三元组形式{p}s{q}相应扩展为INV{p}s{q}, 其中, INV用来表示全局不变式对应的断言描述, p为前条件, q为后条件, s是程序执行时的语句. 通俗来说, 该四元组的含义是: 在INV符合的情况下, 如果运行语句s之前, 程序状态能够满足前条件p, 那么, 在执行语句s之后, 程序状态就会满足后条件q.
图6展示了一些一般的推理规则, 这些推理规则与Hoare逻辑推理规则相似. 其中, 比较特殊的推理规则有ENCRIT和EXCRIT, 它们分别对应于内核操作的关闭和开启中断. 当中断关闭期间, 程序在运行的过程中能够访问到全局共享数据结构, 因此, 相应的指令被赋予INV不变式; 当中断开启期间, 程序不再能继续访问共享数据结构, 保证了全局不变式的不变性, 因此, 前条件蕴含着INV不变式.
3.2 内核不变式本节细化内核中的全局性质, 并将其用断言不变式的形式描述出来.

|
图 6 推理规则 |
性质1: 任何时刻系统正在执行的任务只有一个. 断言是根据正在运行任务的优先级i, 将系统中的任务分成两类: 优先级小于i的任务和优先级大于i的任务, 当优先级为i的任务处于运行状态时, 这两类任务都不能处于运行状态. 对应表1中的性质1.
性质2: 如果在任务创建操作中要调用任务调度, 为任务调度选择的任务总是在就绪态的任务集中具有最高优先级的任务. 系统中任务的优先级与其在OSTC-BPrioTbl中的下标相等, 且处于0–OS_LOWEST_PRIO范围内. 对应表1中的性质2.
性质3: 任务就绪表两个变量OSRdyGrp和OSRdyTbl[]之间的一致性关系.
(1)如果OSRdyTbl的第i个元素为0, 则OSRdyGrp第i位为0.
(2)如果OSRdyGrp的第i位为0, 则OSRdyTbl第i个元素为0.
对应表1中的性质3.
性质4: 空闲任务永远处于就绪态, 为保证系统始终都有就绪态的任务, 空闲任务不允许被挂起. 对应表1中的性质4.
性质5: 任务就绪表和任务优先级表之间存在蕴涵关系, 就绪表中的任务的状态一定是就绪态. 对应表1中的性质5.
| 表 1 全局性质断言描述 |
性质6: 若i是最高优先级, 针对小于i的优先级, 当且仅当它们在就绪表中对应的位为0, i对应的位为1. 对应表1中的性质6.
性质7: 消息队列中的任务等待列表和消息列表不能同时不为空. 当消息队列中存在等待消息的任务, 则将消息发给等待消息的任务, 否则将消息放入消息列表中. 所以任务等待列表和消息列表不能同时不为空. 对应表1中的性质7.
性质8: 消息队列中记录等待任务列表的两个数据域OSEventGrp和OSEventTbl具有一致性. 对应表1中的性质8.
4 内核复杂数据结构程序的验证方法在验证的过程中, 除了对内核相关性质进行形式化描述, 还需要对数据结构程序进行更精确的刻画. 但是, 在实际的验证工作中, 内核中经常会使用一些复杂数据结构程序, 这极大增加了验证的难度. 本节我们对原型系统中的形状图进行扩展, 针对复杂数据结构程序中多种形状耦合在一起的情况, 提出嵌套形状图的验证方法, 并对此方法进行正确性证明. 通过运用扩展后的嵌套形状图, 成功刻画并验证了操作系统内核中, 部分重要的复杂数据结构程序.
4.1 嵌套形状图的扩展 4.1.1 嵌套形状图语义描述扩展形状图中的语义描述见图7. 其中, C-declaration是对形状图进行声明; shape_desc是对形状进行描述, 若仅有主数据结构, 则只用shape描述; 若还有次数据结构, 需要用shape和property描述; shape为嵌套形状图中允许的基本形状, 分别为单链表、循环单链表、双链表、循环双链表、树; property描述形状属性, 分别用primary和secondary分别表示主数据结构和次数据结构. 在进行结构体声明的过程中, 域指针都附有形状声明. 在描述的过程中, 如果有且仅有主数据结构, 那么, 用于描述的结构体类型就只有shape; 若同时包含有主数据结构和次数据结构, 则用于描述的结构体类型必须有shape和feature.

|
图 7 嵌套形状图语义 |
4.1.2 嵌套形状图编程原则
针对嵌套形状图, 限定易于保证形状正确性的主数据结构和次数据结构编程原则, 主要包括有: (1)针对访问路径从主数据结构声明指针开始, 并且只存在primary指针域的情况, 本文将其称之为主数据结构访问路径; 同理, 我们可以定义次数据结构访问路径. 在程序中, 需要严格规范访问路径, 即只允许出现主数据结构访问路径和次数据结构访问路径, 不允许出现混淆的访问路径. (2)针对主数据结构上的节点, 我们可以通过主数据结构指针对其进行生成; 当它不同时为次数据结构的节点时, 同样可以通过主数据结构指针对其进行释放. (3)主数据结构和次数据结构分别操作, 互不影响.
4.1.3 验证方法在扩展的形状系统中, 为减少对原系统的改动, 在进行访问路径的别名计算和产生交给Z3的验证条件之前, 仍然用断言和形状图上进行等式推理的方式. 同时, 采用本节的验证方法将嵌套形状图进行分离, 使得主数据结构和次数据结构变换为基本数据结构, 后面的别名计算和产生验证条件等工作仍然可以用原系统. 在扩展的形状图中, 我们对不同的形状类别进行了形状定义, 分别是标准形状, 可接受形状, 不安全形状. 在这3个类别当中, 标准形状的限制较多, 不仅需要对应前文描述的基本形状, 还需要满足最多只有一个次数据结构域指向该复杂数据结构; 可接受形状限制稍稍有所放宽, 能够允许一个以上的次数据结构域指向该复杂数据结构; 不安全形状就是除了前面两种形状之外, 其他的复杂数据结构, 在本文的研究范围内, 这样的复杂数据结构不具备安全性, 所以不进行讨论.
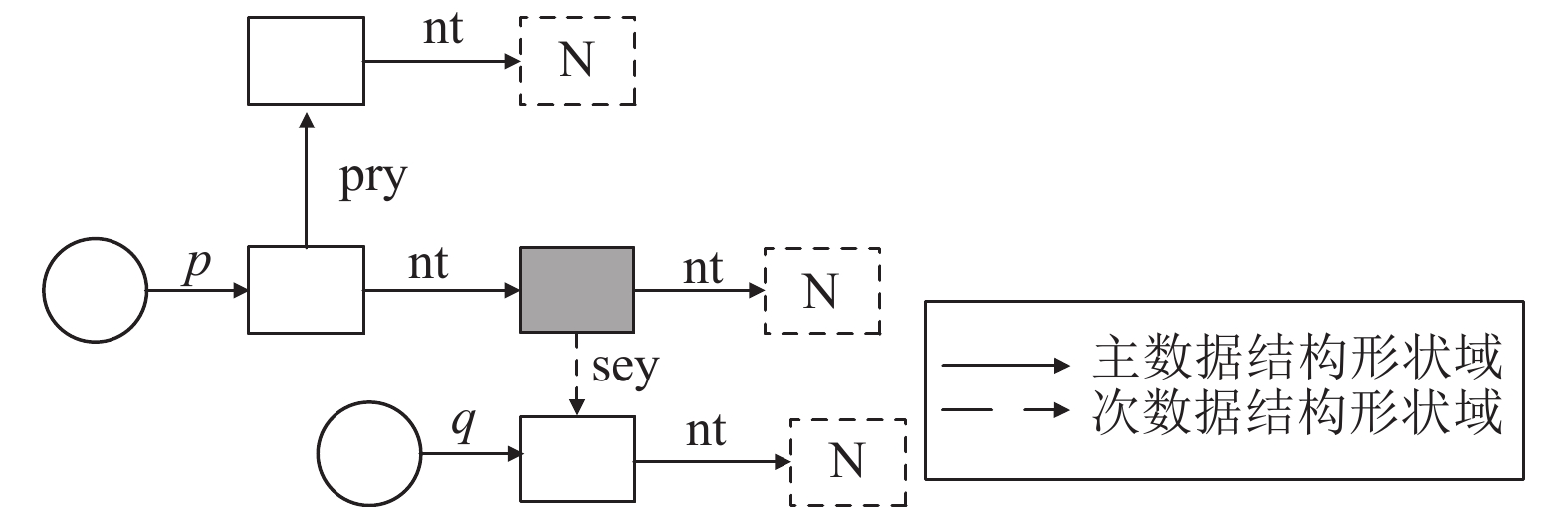
在操作系统内核中, 常会出现复杂数据结构程序, 尤其是主数据结构和次数据结构嵌套在一起. 针对这样的情况, 我们将其称为嵌套形状图, 具体如图8所示, 与此同时, 这种嵌套的结构也极大地增加了具体程序的验证难度.
|
图 8 嵌套形状图实例 |
所以, 本节针对嵌套形状图, 扩展了原有的形状系统, 接下来将详细介绍嵌套形状图验证方法的具体思路: (1)通过嵌套形状图分离的方法将复杂数据结构程序中的不同数据结构进行分离, 分离后的主数据结构和次数据结构都通过集合保存各自的信息. (2)对主数据结构的形状特性进行分析, 结合相应的规则确定其对应形状定义的类别. (3)针对已经通过步骤(2)的嵌套形状图, 进一步分析次数据结构指针的指向, 综合分析主数据结构和次数据结构对应形状定义的类别, 进行形状图判定后得到最终的形状定义的类别.
综上, 根据上述步骤, 一方面判定出嵌套形状图是否符合形状定义的类别, 能够及时发现该复杂数据结构在原型系统中的安全性; 另一方面, 将验证多种基本形状耦合在一起的嵌套形状图进行分离, 从而达到问题分解的目的, 最后可以简化为验证多个基本形状图, 极大地降低了验证的复杂程度. 具体步骤见算法1.
算法1. NestShape
输入: 嵌套形状图X
输出: 嵌套形状图形状定义类别M
while NestShape(X, M) do
SplitShape(X.A, X.O);
if AnalyseShape(X.F.f) then
InferShape(X.A);
end
end
return M[A];
(1)嵌套形状图分离
在嵌套形状图分离过程中, 需要关注次数据结构的指针指向关系, 并将其通过集合的方式保存在对应的形状图信息里面. 本文用<T, F, L, S, D>五元组表示形状图信息, 其中T是复杂数据结构程序所声明的形状定义, F是主数据结构形状域的起始节点集合, L是主数据结构形状域的目标节点集合, S表示次数据结构形状域的起始节点集合, D表示次数据结构形状域的目标节点集合.
算法2中首先使用GetShapeDef函数获取节点O的形状定义类别, 并且将其保存在前面定义的五元组T中. 为了方便操作, 需要创建一个队列, 并将形状节点O加入到这个队列当中, 接着采用循环遍历的方式, 一直重复操作, 直到队列当中没有数据. 在循环体中, 通过PrimaryField函数判断当前节点是否存在主数据结构形状域, 若该节点存在, 则分别放入主数据结构形状域的起始节点集合L和目标节点集合S中. 通过SecondaryField函数判断当前节点是否存在次数据结构形状域, 若该节点存在, 则对次数据结构形状域的信息进行保存, 分别放到起始节点集合S以及目标节点集合D中. 该循环将不断迭代直至队列为空时终止.
算法2. SplitShape
输入: 形状图信息A, 形状节点O
A.T ← GetShapeDef(O);
Q ←CreateQueue();
Enqueue(Q, O);
while isEmpty(Q) == False do
cur ← Dequeue(Q);
if PrimaryField<cur> == truethen
Insert(A.F, node of primary point-in field);
Insert(A.L, node of primary point-out fileld);
end
else if SecondaryField<cur> == truethen
Insert(A.S, node of secondary point-in fileld);
Insert(A.D, node of secondary point-out field);
end
end
return M[A];
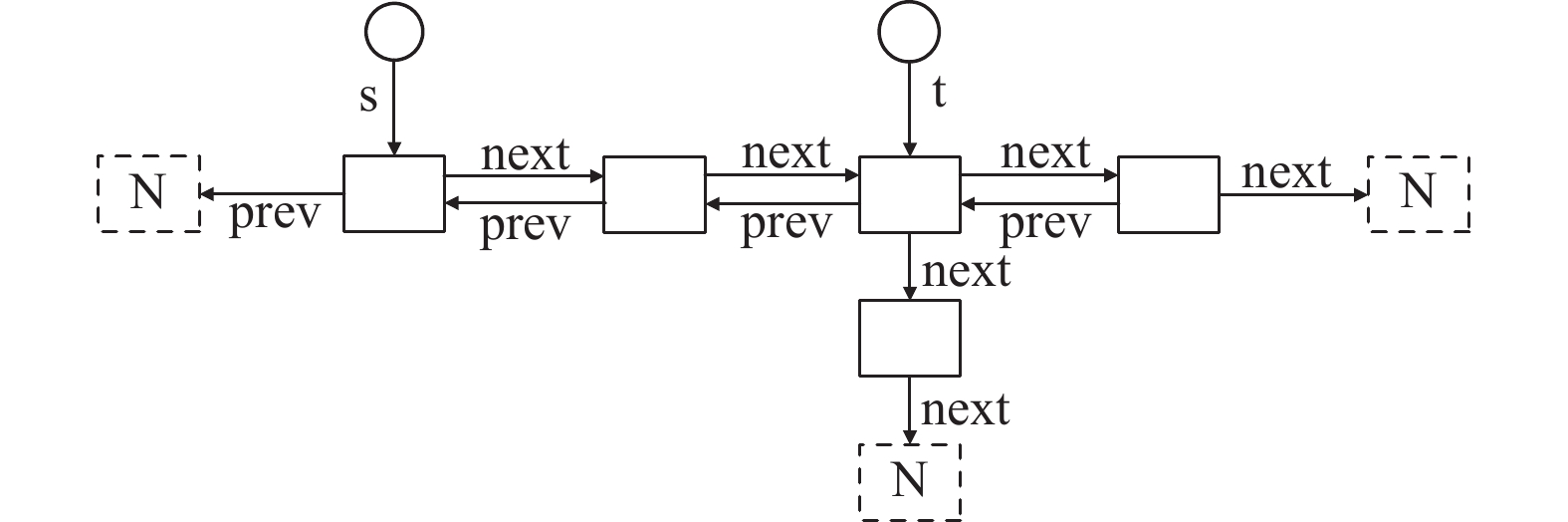
针对算法2中嵌套形状图分离前后的情况, 可以用图9表示分离前的数据结构示意图, 图10是形状系统分离后主数据结构对应的示意图, 图11是形状系统分离后次数据结构对应的示意图, 其中, s和t表示分离前后形状图中的具体元素. 在验证过程中, 实际的形状图可能比上述情况更为复杂, 因为主数据结构和次数据结构在完成插入或删除操作的时候, 往往都需要多条程序才能够实现.
|
图 9 分离前的数据结构示意图 |

|
图 10 分离后的主数据结构 |

|
图 11 分离后的次数据结构 |
(2)嵌套形状图分析
根据前面提出的形状属性约束规则, 如果经过形状图分析后, 复杂数据结构不符合约束规则, 就可以判定其为不安全形状. 算法3中函数HeadNode, TailNode, NormalNode分别是判断表头节点, 表尾节点, 其他节点的入度和出度. 接着采用循环遍历的方式对主数据结构节点进行操作, 并用队列依次取出节点进行分析. 此处使用函数IsEnd来判断函数是否终止, 针对不同的基本形状, 往往有不同的判断标准. 比如单向链表或者双向链表, 需要判断它的后指针何时指向的是NULL; 二叉树需要判断队列中的数据是否是空; 循环单向链表或者循环双向链表, 需要判断它的前指针指向的那个节点是否为起始节点.
算法3. AnalyseShape
输入: 形状入口节点f (集合F中元素)
输出: 复杂数据结构是否通过嵌套形状图分析
if isEmpty(Q) == False do
return False;
end
Q ← QueueCreate();
EnqueueNextNode(Q, cur);
cur ← R;
while IsEnd(cur, f, Q) == False do
cur ← Dequeue(Q);
if NormalNode(cur) == False then
return False;
end
EnqueueNextNode(Q, cur);
end
if TailNode(cur, f) == False do
return False;
end
return True;
(3)嵌套形状图判定
嵌套形状分析阶段预先判断了嵌套形状图中主数据结构对应形状定义的类别, 嵌套形状图判定会进一步分析次数据结构指针的指向和信息. 综合分析主数据结构和次数据结构对应形状定义的类别, 并根据嵌套形状图内置规则(见表2), 得到最后判定.
| 表 2 嵌套形状图内置规则 |
算法4中首先使用函数AnalyseShape判定形状信息N对应的主数据结构的形状定义, 若判定形状定义为不安全形状, 则无需继续推断其次数据结构的形状定义; 若判定主数据结构的形状定义类别不是不安全形状, 需要通过函数SecondaryStructure获取其次数据结构, 递归调用InferShape得到次数据结构的形状定义. 最后, 结合分析主数据结构和次数据结构的形状定义, 对比嵌套形状图内置规则可以得到最终嵌套形状图的形状定义.
算法4. InferShape
输入: 形状信息A和形状定义M
输出: 判定得到的形状定义
K ← AnalyseShape(A);
M[A] ← K;
if K == INACCURACY do
return M[A];
end
for n in SecondaryStructure(A) do
if K==STANDARD && SK==ACCURACY then
M[A] ← ACCURACY;
K ← ACCURACY;
end
if SK == INACCURACY || (K==ACCURACY &&
SK == ACCURACY && HasSecondaryPointInField
(the node which points to n) == False) && SK==ACCURACY
M[A] ← INACCURACY;
break;
end
end
return M[A];
4.2 嵌套形状图的正确性证明针对嵌套形状图验证方法的正确性, 非形式的说, 在任何程序点, 分离后的形状图声明指针和域指针之间的关系都准确表达并且和分离前的嵌套形状图保持一致, 那么, 该验证方法是正确的. 针对动态分配的各堆块的地址, 为了方便证明, 本文首先假设它们分别拥有不一样的抽象值, 然后在处理栈和堆块上存储单元的时候, 前者用声明指针表示, 后者用域指针表示, 那么, 此时的机器抽象状态就很容易通过函数的形式进行呈现. 本文将此时未分离的状态记为
| {sd:DecVar→AbsValue∪{N,D}sf:AbsValue×FieldVar→AbsValue∪{N,D} |
其中,
针对上述两个函数, 本文需要分别对
扩展后的嵌套形状图中涉及主数据结构与次数据结构. 本文将分离后的状态记为
| {s′dp:DecPrimary→AbsValue∪{N,D}s′ds:DecSecondary→AbsValue∪{N,D}s′fp:AbsValue×PrimaryFieldVar→AbsValue∪{N,D}s′fs:AbsValue×SecondaryFieldVar→AbsValue∪{N,D} |
针对上述4个函数, 本文分别对DecPrimary, DecSecondary,
定义1. 状态
(1)函数
(2)函数
若
若
若
(3)函数
若
若
若
定义2. 状态
(1)函数
(2)函数
若
若
若
(3)函数
若
若
若
在有了相应的定义之后, 我们需要证明
首先证明
根据形状分离算法, 操作过程中不会丢弃由次数据结构表述的关系, 而是将其保存于形状信息中. 这里用<T, F, L, S, D>五元组表示, 其中里面的元素有不同的含义, 分别是复杂数据结构的形状类别定义, 主数据结构的起始节点集合, 主数据结构的目标节点集合, 次数据结构的起始节点集合, 次数据结构的目标节点集合. 这些形状图信息体现在状态
| {DecPrimary⊆DecVarDecSecondary⊆DecVarPrimaryFieldVar⊆FieldVarSecondaryFieldVar⊆FieldVar |
满足定义1中的条件(1), (2), (3), 得到
然后证明
同理可得:
| {DecVar⊆DecPrimary∪DecSecondaryFieldVar⊆PrimaryFieldVar∪SecondaryFieldVar |
满足定义2中的条件(1), (2), (3), 得到
综上可得
μCOS-II在原型系统验证时, 认真分析程序中的自然语言规范, 并从这里面提取出相应的性质, 接着将这些性质用前面定义的语法用断言形式描述出来, 添加到C语言程序中对应的位置. 本节选取函数OSTaskCreate为例, 详细分析如何从该函数中提取性质并验证.
函数OSTaskCreate(task, p_arg, OS_STK, ptos, prio) 中有多个参数, 下面对各个参数表示的含义详细介绍.
(1) task是指针类型, 指向的是任务代码.
(2) p_arg是指针类型, 指向的是可选择数据区域, 当任务第1次运行时, 会给其传递相关的参数信息.
(3) ptos是指针类型, 指向的是任务栈栈顶.
(4) prio代表着该任务的优先级.
在验证的过程中, 我们需要分析函数参数的情况, 并将重要的信息用前置条件进行描述, 这里前置条件都是放在(requires…)的相关语句中. 同理, 后置条件应放在(ensures…)的相关语句中. 对应的断言描述见表3.
| 表 3 OSTaskCreate前后置条件 |
在完成了上述针对前后置条件断言描述之后, 我们还需要在函数安全C规范注释中增加相应的全局性质. 如在上述OSTaskCreate函数调用中, 满足全局性质1, 2, 3, 5. 添加性质后的代码如算法5所示.
算法5. OSTaskCreate 代码
/*@requires 0 ≤ OSTaskCtr ≤ OS_MAX_TASKS +OS_N_SYS_TASKS;
/*@ensures \result > 0 &&
OSScheduleCount > \old(OSScheduleCount)&& \result == 0;
/*@strong global invariant only_one:
(
/*@strong global invariant OSRdyTbl_OSRdyGrp_Consistency:
INT8U OSTaskCreate(void (*task)(void *p_arg),
void *p_arg, OS_STK *ptos, INT8U prio)
{ OS_ENTER_CRITICAL();
if (OSIntNesting > 0 u) {OS_EXIT_CRITICAL();
return (OS_ERR_TASK_CREATE_ISR);}
/*@strong global invariant prio_range:
/*@strong global invariant correspondence:
& (1 << (i&0x07u))) > 0
if (OSTCBPrioTbl[prio] == (OS_TCB *)0)
OSTCBPrioTbl[prio] = OS_TCB_RESERVED;
OS_EXIT_CRITICAL();
psp = OSTaskStkInit(task, p_arg, ptos, 0u);
err = OS_TCBInit(prio, psp, (OS_STK *)0, 0u, 0u, (void *)0, 0u)
if (err == OS_ERR_NONE)
{if (OSRunning == OS_TRUE) { OS_Sched();}
} else { OS_ENTER_CRITICAL();
OSTCBPrioTbl[prio] = (OS_TCB *)0;
OS_EXIT_CRITICAL(); }return (err);}
除了上述任务创建函数, 其他函数以及对应全局性质的证明工作如表4所示, 文中主要是以函数为单位逐个进行验证.
5.2 函数中复杂内核数据结构的验证在进行内核复杂数据结构程序验证之前, 我们需要先对μCOS-Ⅱ操作系统内核中的部分数据结构进行详细说明. 执行过程中, 当建立了任务之后, OS_TCB将会被赋值, 在操作系统内核中, OS_TCB具有很重要的作用, 里面用来存储任务的相关参数. 包括有TCB双向链表的前后指针, 空闲TCB的数组指针, 此处省略部分与具体验证分析中无关的代码, 对应的结构体见图12.
| 表 4 函数中全局性质证明工作 |

|
图 12 TCB结构体 |
系统在调用函数OSInit()之后, 马上就对μCOS-II系统进行了初始化. 紧接着会建立数组OSTCBTbl[], 这个数组里的元素就是前面所说的OS_TCB, 这里的OS_TCB会进行链接, 从而形成了链表(见图13). 我们将此链表命名为任务控制块空闲链表.
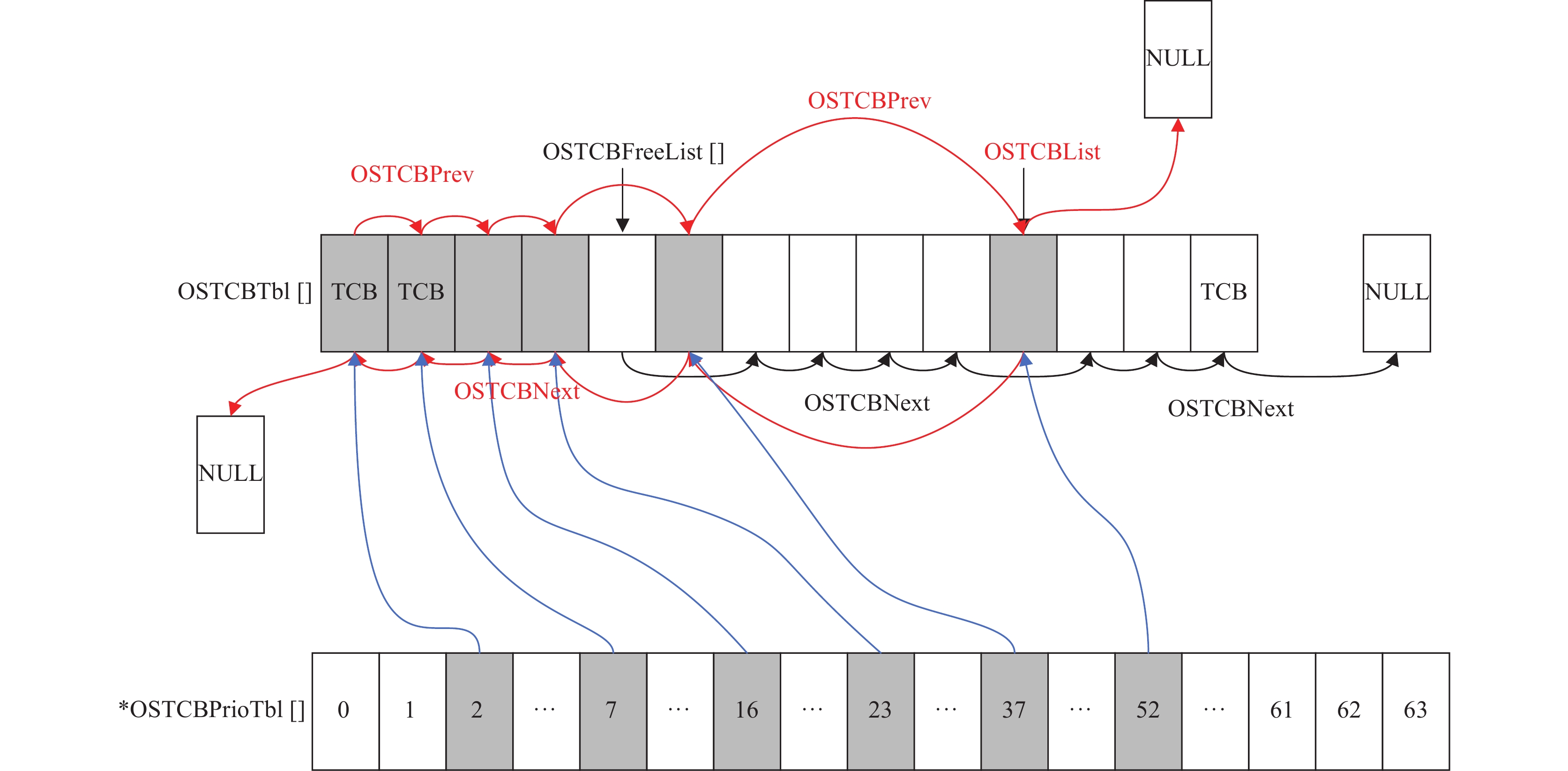
同时, 在任务调度过程中, 常需要同时用到任务控制块链表和空闲任务控制块链表, 并且根据全局一维指针数组任务优先级表OSTCBPrioTbl[]指向相对应优先级任务的TCB, 如图14所示.
本节通过一个实验用例分析嵌套形状图的验证方法, 添加断言后的代码如算法6所示, 对应的嵌套形状图见图15. 其中, OSTCBList指向主数据结构的双向链表, 代表着内核中任务控制块链表的头指针, OSTCBPrev代表着前指针, OSTCBNext代表着后指针; OSTCBFreeList指向次数据结构的双向链表, 代表着内核中任务控制块空闲链表的头指针, 前后指针用OSTCBPrev和OSTCBNext进行表示.

|
图 13 任务控制块空闲链表 |
|
图 14 任务控制块链表和任务控制块空闲链表 |

|
图 15 嵌套形状图示例 |
根据断言描述, 在具体操作过程中, 这里主数据结构的前置条件描述清楚待删除的ptcb位于双向链表OSTCBList中, 其头节点的OSTCBPrev为空, OSTCBList指向的节点到待删除的ptcb为一个双向链表表段, 此处双向链表的长度为n, 并限制条件n大于等于1, 双向链表的最后一个节点一定为空闲任务. 后置条件描述清楚当删除成功时, 以OSTCBList指向的节点为头节点构成双向链表, 双向链表长度变为n–1且限制原先链表长至少为2, 已删除节点的OSTCBNext, OSTCBPrev域为空, 此时双向链表最后一个节点仍为空闲任务; 当删除失败时, 原有的数据结构保持不变.
次数据结构的前置条件定义待插入的节点指针的OSTCBNext为空, 此时空闲链表为双向链表, 长度为0, 并使用自定义的逻辑变量记录函数入口处的变量. 后置条件描述清楚当插入成功时, 双向链表长度加1, 之前待插入节点称为单向链表的头节点, 原先的头节点变为双向链表的第2个节点; 当插入失败时, 原有数据结构保持不变.
在介绍完相关断言描述之后, 下面需要详细说明嵌套形状图逻辑验证方法的工作流程. 在形状分离阶段, 原型系统会将形状图的次数据结构分离, 并把相应的节点和指针信息放在集合中. 其中, 主数据结构的相关信息体现在F, L集合中, 次数据结构的相关信息体现在S, D集合中, 分离后的主数据结构见图16, 次数据结构见图17. 在形状图分析阶段, 采用广度优先遍历方式对主数据结构节点进行遍历, 遍历过程中易知它为双向链表, 需要判断表头节点, 表尾节点和其他节点的入度与出度, 得出主数据结构的形状定义是标准形状. 在形状图判定阶段, 进一步分析次数据结构的形状定义为标准形状, 并且指针的指向为存在一个次数据结构域指向主数据结构的非入口节点. 通过前面的分析, 我们能够得到主数据结构和次数据结构的形状定义和指针指向, 再根据嵌套形状图内置规则得到嵌套形状图的形状定义为可接受形状, 符合预期的形状定义, 就可以顺利的分别对主数据结构和次数据结构完成插入或删除等操作.

|
图 16 主数据结构示例 |

|
图 17 次数据结构示例 |
除了前面详细介绍的任务删除函数验证步骤, 其他函数中复杂数据结构程序证明工作如表5所示.
| 表 5 函数中复杂数据结构程序证明工作 |
6 总结
操作系统内核的形式化验证一直是学术界和工业界共同关注的焦点, 研究人员试图在全局不变式的定义, 复杂数据结构程序的形式化描述方面降低验证的复杂度, 同时提高证明工作的效率.
本文针对这些问题, 一方面, 通过对操作系统内核以函数为单位进行形式化验证, 首先提取出操作系统内核中重要的8条全局性质, 然后采用全局不变式进行定义, 最后在对应的函数中进行验证. 验证结果表明, 这些函数符合操作系统内核的8条全局性质.
另一方面, 针对操作系统内核中使用的复杂数据结构程序, 通过扩展形状图理论, 提出嵌套形状图逻辑的验证方法, 将嵌套形状图分离为主数据结构和次数据结构, 达到问题分解的目的, 并证明了分离前后形状图的一致性, 有效地简化了操作系统内核中复杂数据结构程序的验证. 验证结果表明, 该方法成功刻画并验证了操作系统内核中关于任务创建与调度, 消息队列创建与操作相关的代码.
算法6. OSTaskDel代码
typedef struct OSTCB{
struct OSTCB *OSTCBNext;
struct OSTCB *OSTCBPrev;
struct OSTCB *OSTCBFreeList;
} OS_TCB;
/*@shape OSTCBNext, OSTCBPrev: dlist, primary
shape OSTCBNext, OSTCBPrev: dlist, secondary*/
/*@requires OSTCBList→OSTCBPrev == \null
ensures \result == OS_ERR_NONE
ptcb→OSTCBNext→OSTCBPrev = (OS_TCB *)0;
OSTCBList = ptcb→OSTCBNext;}
else{ptcb→OSTCBPrev→OSTCBNext = ptcb→OSTCBNext;
ptcb→OSTCBNext→OSTCBPrev = ptcb→OSTCBPrev; }
/*@requires ptcb→OSTCBNext == \null
ensures \dlist(OSTCBFreeList)
ptcb→OSTCBNext = OSTCBFreeList;
OSTCBFreeList = ptcb;
| [1] |
Jones C, O’Hearn P, Woodcock J. Verified software: A grand challenge. Computer, 2006, 39(4): 93-95. DOI:10.1109/MC.2006.145 |
| [2] |
The FreeRTOS project website. http://www.freetos.org. [2023-03-11].
|
| [3] |
Sagiv M, Reps T, Wilhelm R. Parametric shape analysis via 3-valued logic. ACM Transactions on Programming Languages and Systems, 2002, 24(3): 217-298. DOI:10.1145/514188.514190 |
| [4] |
Klein G, Elphinstone K, Heiser G, et al. seL4: Formal verification of an OS kernel. Proceedings of the 22nd ACM SIGOPS Symposium on Operating Systems Principles. Big Sky: ACM, 2009. 207–220.
|
| [5] |
Klein G, Andronick J, Elphinstone K, et al. Comprehensive formal verification of an OS microkernel. ACM Transactions on Computer Systems, 2014, 32(1): 2. |
| [6] |
Gu RH, Koenig J, Ramananandro T, et al. Deep specifications and certified abstraction layers. ACM SIGPLAN Notices, 2015, 50(1): 595-608. DOI:10.1145/2775051.2676975 |
| [7] |
Costanzo D, Shao Z, Gu RH. End-to-end verification of information-flow security for C and assembly programs. ACM SIGPLAN Notices, 2016, 51(6): 648-664. DOI:10.1145/2980983.2908100 |
| [8] |
Murray T, Matichuk D, Brassil M, et al. seL4: From general purpose to a proof of information flow enforcement. Proceedings of the 2013 IEEE Symposium on Security and Privacy. Berkeley: IEEE, 2013. 415–429.
|
| [9] |
Syeda HT, Klein G. Formal reasoning under cached address translation. Journal of Automated Reasoning, 2020, 64(5): 911-945. DOI:10.1007/s10817-019-09539-7 |
| [10] |
Heiser G, Klein G, Murray T. Can we prove time protection? Proceedings of the 2019 Workshop on Hot Topics in Operating Systems. Bertinoro: ACM, 2019. 23–29.
|
| [11] |
Leroy X. Formal certification of a compiler back-end or: Programming a compiler with a proof assistant. Proceedings of the 33rd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. Charleston: Association for Computing Machinery, 2006. 42–54.
|
| [12] |
Song Y, Cho M, Kim D, et al. CompCertM: CompCert with c-assembly linking and lightweight modular verification. Proceedings of the ACM on Programming Languages, 2020, 4(POPL): 23. |
| [13] |
Wang YT, Xu XZ, Wilke P, et al. CompCertELF: Verified separate compilation of C programs into ELF object files. Proceedings of the ACM on Programming Languages, 2020, 4(OOPSLA): 197. |
| [14] |
Koenig J, Shao Z. CompCertO: Compiling certified open C components. Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation. Association for Computing Machinery, 2021. 1095–1109.
|
| [15] |
Hawblitzel C, Howell J, Lorch JR, et al. Ironclad APPs: End-to-end security via automated full-system verification. Proceedings of the 11th USENIX Conference on Operating Systems Design and Implementation. Broomfield: USENIX Association, 2014. 165–181.
|
| [16] |
Nelson L, Sigurbjarnarson H, Zhang KY, et al. Hyperkernel: Push-button verification of an OS kernel. Proceedings of the 26th Symposium on Operating Systems Principles. Shanghai: ACM, 2017. 252–269.
|
| [17] |
Nelson L, Bornholt J, Gu RH, et al. Scaling symbolic evaluation for automated verification of systems code with Serval. Proceedings of the 27th ACM Symposium on Operating Systems Principles. Huntsville: ACM, 2019. 225–242.
|
| [18] |
顾海博, 付明, 乔磊, 等. SpaceOS中若干全局性质的形式化描述和验证. 小型微型计算机系统, 2019, 40(1): 141-148. |
| [19] |
郭建, 丁继政, 朱晓冉. 嵌入式实时操作系统内核混合代码的自动化验证框架. 软件学报, 2020, 31(5): 1353-1373. DOI:10.13328/j.cnki.jos.005957 |
| [20] |
孙海泳. 嵌入式操作系统的形式化验证方法研究[博士学位论文]. 成都: 电子科技大学, 2020.
|
| [21] |
姜菁菁, 乔磊, 杨孟飞, 等. 基于Coq的操作系统任务管理需求层建模及验证. 软件学报, 2020, 31(8): 2375-2387. DOI:10.13328/j.cnki.jos.005961 |
| [22] |
Hoare CAR. An axiomatic basis for computer programming. Communications of the ACM, 1969, 12(10): 576-580. DOI:10.1145/363235.363259 |
| [23] |
张昱, 陈意云, 李兆鹏. 形状图理论的定理证明. 计算机学报, 2016, 39(12): 2460–2480.
|
| [24] |
张志天, 李兆鹏, 陈意云, 等. 一个程序验证器的设计和实现. 计算机研究与发展, 2013, 50(5): 1044-1054. DOI:10.7544/issn1000-1239.2013.20101611 |
| [25] |
de Moura L, Bjørner N. Z3: An efficient SMT solver. Proceedings of the 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Budapest: Springer, 2008. 337–340.
|
 2023, Vol. 32
2023, Vol. 32



