图像补全的主要工作是将受损图像补全, 获得语义连贯和纹理契合的完整图像. 而相应的图像补全技术则广泛应用于目标移除、老照片修复、刑事侦查等研究领域, 该类技术具有切实的应用场景.
传统的图像补全方法, 依据最邻近与最相似原则, 搜寻与缺失区域内容最接近的块以填补对应的缺失区域[1]. 该类算法擅长修复小孔洞缺失, 但不适用于大面积受损的图片, 因而这类方法逐渐被鲁棒性更强的深度学习方法取代.
实验表明, 具有全局感知能力的网络能够高效地整合图像的上下文信息, 提高生成图像的真实性. 为此, 许多基于深度学习的图像补全方法[2–5]利用重复的空洞卷积操作, 试图在网络深层获取全局感知能力, 进而优化网络性能. 然而这种设计不利于远端像素间的信息交互, 部分远端像素难以在浅层网络实现有效地信息传递. 此外, 卷积操作倾向于借助邻近可见像素信息修复缺失区域, 当待补全图像的可见像素非常少时, 远离可见信息的补全区域内容在契合度上表现不佳.
考虑到上述问题, 多名研究人员提出替代方案, 试图通过建立像素间的长距离依赖来整合全局信息. Li等人[6]在其补全网络添加了改进后的自注意力机制, 实现远端像素信息的有效传递, 然而作为网络的关键模块, 自注意力的加入让整体模型产生
针对上述模型局限, 本文提出基于快速傅里叶变换[8]以及选择性卷积核网络[9]的图像补全算法. 快速傅里叶变换属于在谱域和空域的域间转换, 该模块具备实质性的全局感受野, 能够有效建立像素间的长距离依赖. 此外, 快速傅里叶变换操作充分利用了傅里叶变换的周期性和对称性等特点, 并采取了分治的计算策略, 因此相较于自注意力和Transformer模块有更高的参数效率. 最后, 本文还在快速傅里叶变换模块中引入选择性卷积核网络, 并根据补全任务的特点改进此网络模块, 以进一步提升整体网络的性能和精度.
1 相关工作 1.1 图像补全传统的图像补全方法可分为基于扩散的方法和基于块的方法. 基于扩散的方法根据已知区域像素对未知区域进行扩散式填补[10]. 这类方法基于平滑限制的像素生成方式有效地规范了空洞的填补过程, 因此适用于填补狭小的缺失孔洞, 但该类算法处理难以修复较大的缺失孔洞, 且容易生成模糊的内容. 而另一种基于块的合成方法, 通过搜寻相似图像的相似块, 填补到相应缺失区域的方式实现图像补全[11,12]. 该类补全方法能够修复稍大的孔洞, 但需要承担最紧邻搜寻算法计算相似度带来的昂贵计算花销. 此外, 这类方法仅在纹理上获得顺滑效果但在结构上契合度不佳.
图像补全研究进入深度学习阶段, 研究人员提出了大量基于GAN[13]的图像补全算法. Nazeri等人[2]提出了Edge Connect算法, 该算法以边缘检测结果作为引导, 提高了补全精确度. 随后, Patel等人[3]提出了部分卷积补全算法, Yu等人[14]提出了门控卷积算法. 这类算法通过对补全后的特征进行提取和重利用, 帮助深度补全网络处理图像的不规则缺失. 紧接着, Iizuka等人[15]提出了全局-局部一致性的生成对抗网络, 实现了图像的全局与局部一致性补全. 这类基于GAN的深度学习方法在生成质量上有一定的提高, 但它们的生成器局限于狭小的感受野, 未能在大面积受损的图像上获得好的表现. 此外, 这类方法不仅缺乏随机性, 它们采用的上下文注意力模块在计算时还需要消耗大量的内存和时间. 针对大面积不规则掩膜的任务挑战, Zeng等人[16]提出了AOT GAN模型, 该算法通过聚合多尺度上下文特征帮助模型还原更多结构细节, 增强网络对缺失区域外像素的利用. 但AOT GAN模型训练时需要根据待补全图像的尺度调整AOT模块的分支数和扩张率, 不具备灵活的自适应能力. 上述方法取得了一定的性能提升, 但未实质性地建立像素的长距离依赖, 未能充分利用缺失区域远端的像素信息. 针对以上不足, 本文模型提出在网络中加入快速傅里叶变换模块的方法. 该方法将借助快速傅里叶变换模块建立像素的长距离依赖, 以应对图像中大面积缺失孔洞带来的挑战.
1.2 注意力机制注意力机制[17]主要在网络中实现两个功能目标, 一是决定需要关注待处理对象的哪些部分, 二是将有限的信息处理资源分配给待处理对象中的重要部分. 因此, 注意力机制能有选择地关注关键信息, 忽略非关键信息, 从而提高网络的运行效率. 此外经过针对性设计的注意力机制能够提高补全模型的效率, 同时提升补全结果的质量. Liang等人[11]提出了将网络生成的图像块与已知图像块进行匹配的上下文注意力机制, 将空间位置上彼此位于远端的图像块联系起来, 提升了生成图片的契合度. 而Liu等人[18]设计的连贯语义注意力机制(CSA)建立了孔洞区域内部特征间的语义相关, 确保了生成像素的连续性. 实验结果表明, 在网络中加入针对性设计的注意力机制可以有效提升整体模型的效率和性能. 然而, 这类算法未能解决不规则缺失补全以及补全过程细节信息丢失等问题. 为此, 本文引进了选择性卷积核注意力机制, 增强网络的扰动抗性, 同时帮助模型学习到更多的细节特征.
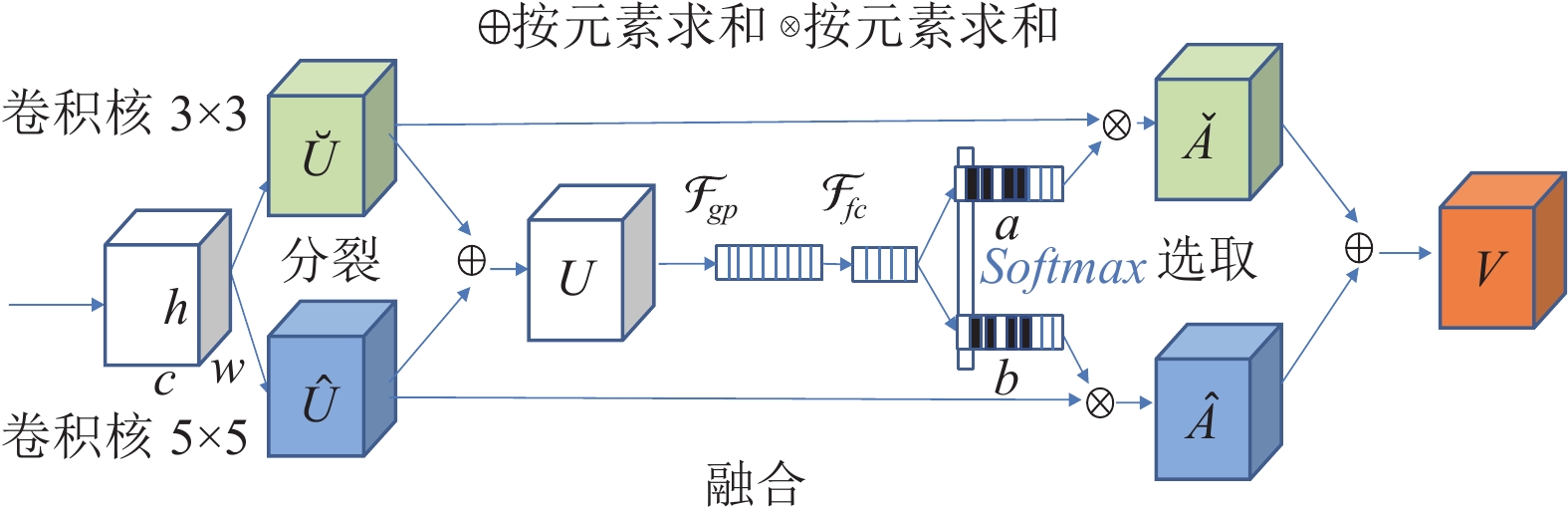
1.3 选择性卷积核网络模块选择性卷积核网络模块(SKNET)[9]包含分裂(split)、融合(fuse)以及选择(select)这3个操作步骤. 如图1所示, 该模块的操作流程为: 设卷积网络任意给定的输出特征图为
|
图 1 SKNET示意图 |
SKNET模块对所有分支特征矩阵按元素求和, 融合特征信息, 以帮助模型自适应地调节感受野:
| U=˘U+ˆU | (1) |
接着, 模块通过平均池化将融合后得到的特征U压缩成一个1×1×c的序列, 第c层特征图的平均池化计算过程如下:
| Sc=Fgp(Uc)=1H×W∑Hi=1∑Wj=1Uc(i,j) | (2) |
为了提升网络复杂度, SKA模块执行一个全连接操作获得一个特征序列
| z=Ffc(s)=B(δ(WS)) | (3) |
其中,
| ac=e(Acz)/(eAcz+eBcz) | (4) |
| bc=eBcz/(eAcz+eBcz) | (5) |
选择性卷积核网络的设计思想来源于SE注意力[19], 其主要特点在于获得多尺度表征后, 有选择地赋予不同卷积核权重以帮助模型调节感受野. 为增强模型鲁棒性, 本文将引入选择性卷积核网络(SKNET), 并根据补全任务的特点对其进行针对性改进.
1.4 快速傅里叶变换快速傅里叶变换(FFT)[8]是一种高效、快速的跨域算法. 该算法主要针对离散傅里叶变换, 将信号从一个域转换到另一个域. 在计算机视觉领域, FFT能够帮助图像在傅里叶(即频率)域和空间域之间进行转换. 谱域转换是以全员像素更新的方式进行的, 因此FFT能够帮助模型将感受野扩展到图像的全部像素, 即获得全局感受野, 提高全员像素的信息关联度, 最终实现远端像素信息的高效交流.
本文采用库利-图基快速傅里叶变换算法(Cooley-Tukey FFT算法)[20]进行谱域变换. 尽管快速傅里叶变换和卷积操作都涉及大量复杂的数据计算, 但快速傅里叶变换更加高效. 快速傅里叶变换算法采取分治的策略将一个长度为N的离散傅里叶变换过程分解成多个序列长度较短的离散傅里叶变换, 并利用快速傅里叶变换的周期性和对称性, 对重复计算进行删减, 从而减少了计算量. 该算法的时间复杂度为O(
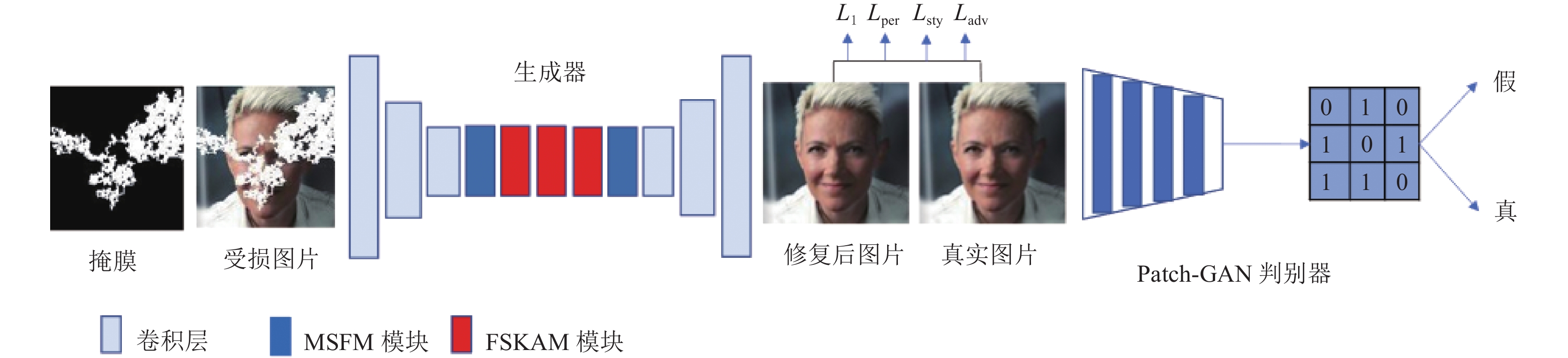
单纯由卷积堆叠而成的补全网络无法有效建立像素间的长距离依赖, 因此在大面积区域受损的图片上表现不佳. 一些工作提出了实现像素远距离信息交互的补全方案, 一定程度提高局部像素的连续性, 但其参数效率不高. 因此有必要设计一种兼具效率与全局信息联动的补全方案. 为此, 本文提出一种以生成对抗网络[13]为主体架构的图像补全模型, 并以快速傅里叶变换作为关键模块. 如图2, 生成器参照真实图像生成补全图像, 而Patch-GAN[21]判别器负责判断生成器补全图像的真假. 该训练过程以判别器无法分辨真实图像与生成图像作为结束条件. 与普通生成对抗网络不同, Patch-GAN利用卷积将输入特征映射成N×N矩阵, 并以矩阵代替单个值来判断整张图, 矩阵中每个点代表原图像的一小块区域(即Patch).
|
图 2 总体模型框架 |
2.1 编码器-解码器架构
本模型的生成网络采用编码器-解码器框架. 该网络首先利用3层卷积处理掩膜与受损图像在通道维度拼接而成的输入, 得到一个低维度特征图, 并传递给高度模块化的瓶颈层. 瓶颈层的多尺度卷积融合模块(multi-scale convolution fusion module, MSFM)嵌入其前端和末端, 而中间部分则以多个基于快速傅里叶变换的选择性注意力模块(fast Fourier transform and selective kernels attention module, FSKAM) 串联而成. 此外, FSKAM模块又内嵌了聚合型选择性注意力网络模块(aggregative selective kernels network, ASKNET). 编码特征图经过上述模块处理后, 由生成网络末端的解码器升维输出.
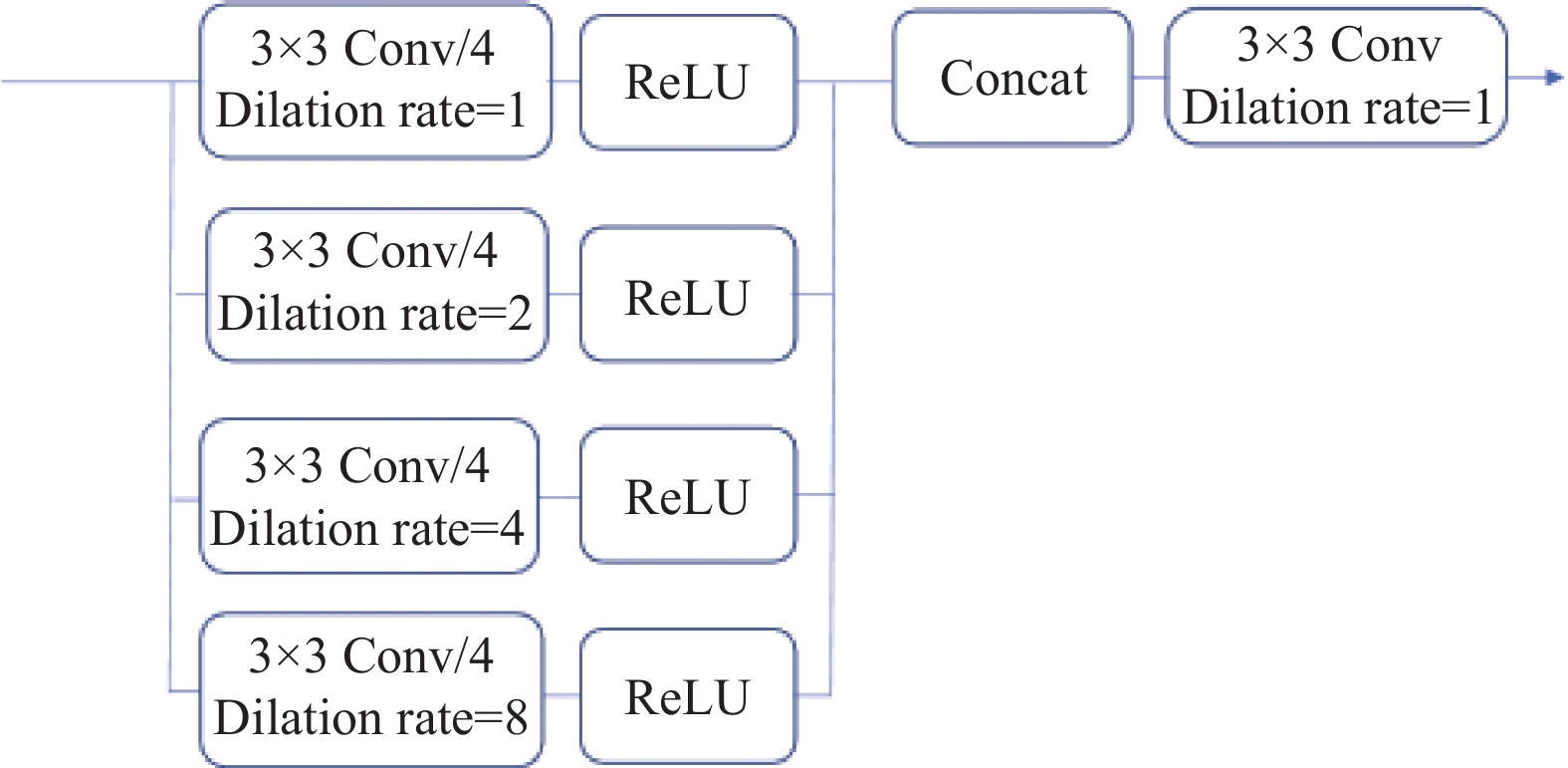
2.2 多尺度卷积核融合模块MSFM模块采用多尺度特征融合机制, 如图3所示. 为了减少参数, 本模块在其4个分支流中引进膨胀率分别为1, 2, 4, 8的4个空洞卷积. 再将空洞卷积处理后得到的特征分别以输入特征通道数的1/4输出. 接着, 在通道维度上将以上特征进行拼接. 紧接着, 利用一个3×3卷积对拼接后的特征图进行普通卷积操作, 以整合多尺度特征的信息. 模块中较大膨胀率的空洞卷积负责获得更广域的上下文信息, 而其较小膨胀率的空洞卷积负责获得更小范围的上下文信息. 多尺度卷积结合缺失区域远端与近端的像素信息, 帮助网络整合多层次的特征, 以提升补全图像的精细度.
|
图 3 MSFM模块示意图 |
2.3 基于快速傅里叶变换的选择性注意力模块
如图4, 基于快速傅里叶变换的选择性注意力(FSKAM)模块先利用卷积核大小为3×3的卷积提取特征, 再对该特征进行批量归一化以及激活处理. 接着, 对处理后的特征进行实数快速傅里叶变换. 不同于快速傅里叶变换(FFT), 实数快速傅里叶变换(Real FFT)仅使用频谱的一半, 并保留一半的实数值[22], 表示如下:
| RealFFT2d:RH×W×C→CH×W2×C |
再将张量的实部和虚部进行融合, 最终转化为实数, 该过程表示如下:
| Complex To Real:CH×W2×2C→RH×W2×2C |
接着, 将上述操作获得的特征输入到ASKNET (改进后的SKNET)中, ASKNET根据不同卷积核的贡献赋予它们不同的权重, 实现感受野的动态调整. 该过程涉及的具体操作将在第2.4节详细介绍. 该模块将帮助FSKAM模块保留更多细节信息.
接着, FSKAM在频域处理实数特征, 该过程表示如下:
| ReLU∘BN∘Conv 1×1:RH×W2×2C→RH×W2×2C |
其中,
最后, 我们对所得的实数特征进行实数反向快速傅里叶变换(real inverse fast Fourier transform, Real IFFT), 进而将该特征修复回一个空间结构:
| {Real To Complex:RH×W2×2C→RH×W2×2CInverse Real FFT2d:CH×W2×C→RH×W×C |

|
图 4 FSKAM模块示意图 |
2.4 聚合型的选择性卷积核网络
实际应用中, 图像补全任务面临着复杂背景以及掩膜扰动带来的诸多挑战. 针对此类问题, 本文在网络中添加了选择性卷积核网络(SKNET). 选择性卷积核网络采用动态学习的方式分配各个尺度的权重, 以提升整体模型的精度与鲁棒性. 此外, 该模块空洞率各异的卷积核能够捕获输入特征的多尺度信息, 帮助网络保留输入特征的各类结构信息与细节信息.
考虑到图像补全的任务特性, 本文对SKNET进行适应性改进, 提出一种新的注意力模块, 并将其命名为聚合型的选择性卷积核网络(ASKNET). 首先, 为了丰富网络的特征层次, 本文在SKNET的基础上将其卷积核分支拓展到4路, 并将这4个卷积核的大小分别设置为[1, 3, 5, 7] .
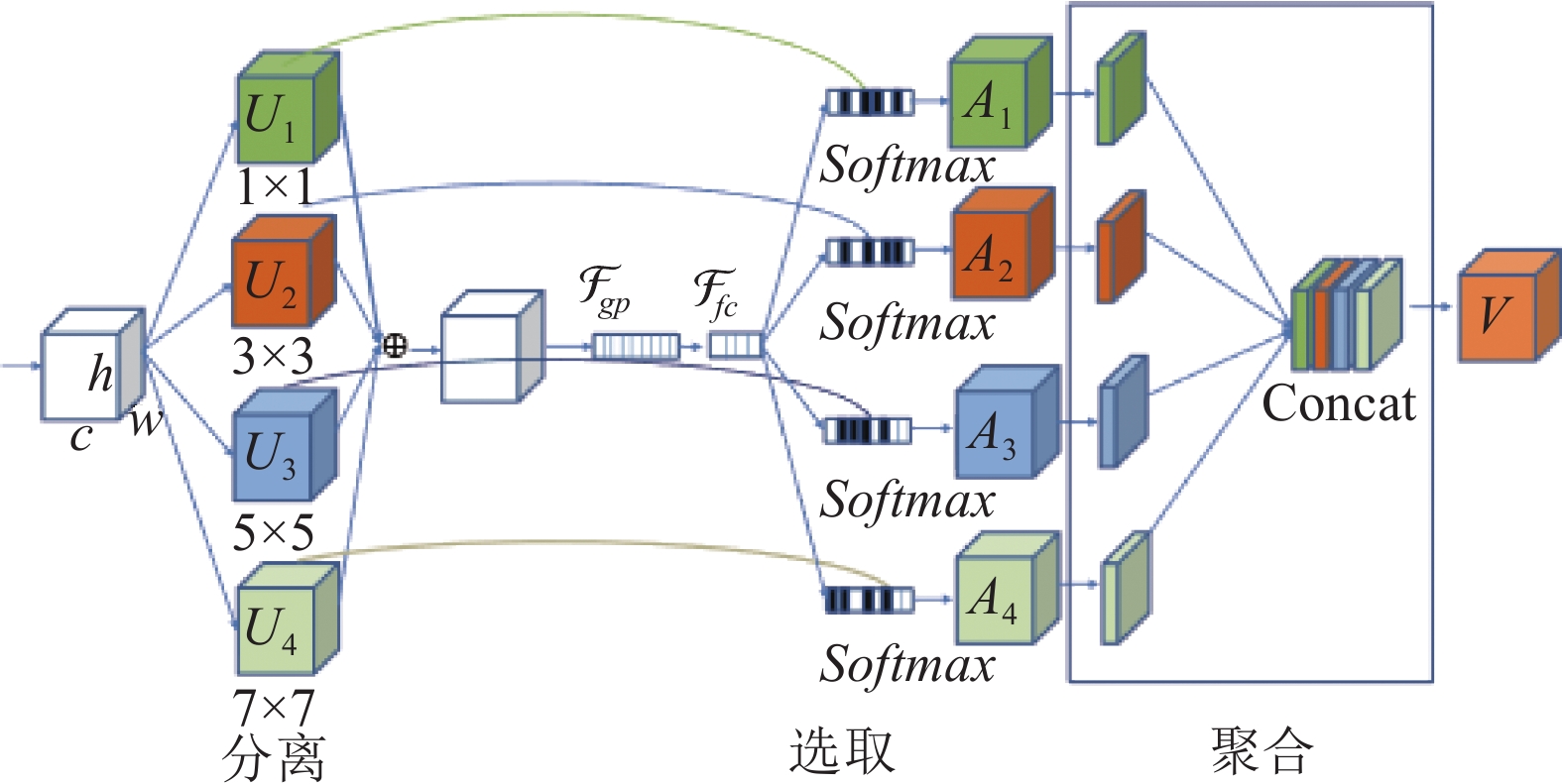
大量实验证明, 多尺度、多层次的特征融合操作有利于网络保留更多轮廓、边缘等结构信息. 此外, SKNET模块针对不同图像选取相应的感受野组合, 帮助网络适应输入图像以及图像中目标的尺度变化. 需要特别提到, 本网络将原始SKNET模块的多尺度特征融合操作替换为特征聚合操作. 如图5, 该聚合过程先利用一个1×1的卷积将不同尺度特征图降维. 通道数压缩为原来的1/4. 模型将所获多个特征图以通道维度进行拼接, 再利用一个1×1的卷积对拼接后的特征进行聚合. 相比于直接相加, 该设计能保留更多的细节信息, 同时获得更高的参数效率.
|
图 5 ASKNET模块示意图 |
2.5 目标函数
本文采用经典的损失函数限制生成图片与真实图片的误差, 具体包括对抗损失、感知损失以及风格损失.
对抗损失表达式如下:
| Ladv=EIgt(logD(Igt))+EIinp(logD(1−D(Iinp)) | (6) |
其中,
绝对值损失
| L1=E(∥Iinp−Igt∥ 1) | (7) |
其中,
感知损失
| Lper=N∑i1CiHiWi‖ϕi(Iinp)−ϕi(Igt)‖ 1 | (8) |
其中,
最后本文还采用了风格损失
| Lsty=∑Ni||Gφi(Iinp)−Gφi(Igt)||1 | (9) |
其中,
在求得上述损失函数后, 本文提出一种联合损失函数, 最终将该损失函数设置如下:
| Lfin=λl1L1+λperLper+λstyLsty+λTvLTv+λadvLadv | (10) |
式(10)中, 我们赋予模型涉及的损失函数相应正则化参数再对其加和以获得联合损失, 其中
Celeb-A数据集: 该数据集, 可以有效检验模型补全效果, 因此在图像修复领域较为常用. 该数据集由10177位名人的人脸组成, 其人物年龄跨度大、五官差异明显, 这给补全模型带来了一定的挑战.
Place2 数据集: 该数据集共含1000万张图片, 包括 400种场景, 场景频次接近现实世界. 而每一场景又包含5 000到30 000张图片. 该数据集的多样性能够很好地检验模型性能.
3.2 实验设置 3.2.1 数据集准备本次实验采用Celeb-A和Place2数据集验证模型有效性. 我们先在Celeb-A数据集选取20 000张图片作为模型训练集, 选取5000张图片作为模型测试集. 此外, 我们还在Place2数据集随机筛选800万张图片作为训练集, 再另外选取2万张图片作为测试集. 最后, 本文参考GC模型[14]的掩膜生成方法, 获得5000张不规则掩膜用以训练和测试模型.
3.2.2 对比方法PEN[24]: 提出了一种金字塔式的上下文编码网络, 利用注意力机制计算高层特征图受损区域内外的区域相似度, 进而指导下一层的低层特征补全.
GC[14]: 在部分卷积的基础上进行改进, 采用马尔科夫判别器解决部分卷积迭代过程的权重变化缓慢问题, 加快网络收敛, 进而提高模型精度.
AOT GAN[16]: 聚合多尺度特征, 增强网络对远距离信息的利用, 结合上下文信息, 生成细粒度纹理.
TFill[7]: 利用Transformer模块建立图像像素的长距离依赖, 充分利用缺失区域外的远端信息, 生成全局契合的补全结果.
Co-Mod[25]: 通过将条件输入与风格表征进行协同调制, 结合条件和无条件图像生成, 实现任意带有不规则缺失的精细图像补全.
3.2.3 评价指标本文选用SSIM和PSNR作为实验的评价指标, 其中SSIM的计算方式如下:
| SSIM(Iout,Igt)=(2μIoutμIgt+c1)(2σIoutσIgt+c2)(μ2Iout+μ2Igt+c1)(σ2Ioutσ2Igt+c2) | (11) |
其中,
另一个重要的指标峰值信噪比(PSNR)用以衡量修复质量. 其计算方式如下:
| MSE=1HWH−1∑i=0W−1∑i=0[Iinp(i,j)−Igt(i,j)] 2 | (12) |
| PSNR=10⋅lg((28−1)2MSE) | (13) |
其中,
本文实验的运行框架为通用的PyTorch, 运行环境是搭载了6张NVIDIA Tesla P100 GPU的服务器. 实验训练批次选定为12, epoch设置为100次. 此外, 我们选取Adam优化器优化网络模型, 并按照经验将训练和验证阶段的学习率定为
本文选取不同损坏程度的图像作为模型输入, 从定性和定量两方面出发, 比较多个补全方案的修复质量. 实验表明本文模型在多个指标上超越其他对比方法, 且在视觉效果上更接近真实图像. 本次实验选用的TFill方法作为对比方法仅应用于Place2数据集, 以探究建立长距离依赖后, 选择性卷积核网络对本方案处理复杂背景图像能力的影响. 此外, Co-Mod方法作为对比方法仅应用于Celeb-A数据集, 以探究本方法补全受损区域不规则图像的能力.
3.3.1 定性比较图6展示了PEN模型、GC模型、AOT GAN模型、Co-Mod模型以及本文模型应用于Celeb-A数据集的生成结果. GC模型和PEN模型的修复结果表明, 这两个模型倾向于生成模糊的纹理和带有色差的细节, 其中PEN存在比较明显的修复痕迹. 相较上述方案, AOT GAN模型的修复内容更为清晰, 但其生成的部分人物五官存在真实性偏差. 例如, 图6第2行人物生成的右眼与真实的人眼偏差较大. Co-Mod模型生成了生动真实的图像, 但局部区域出现偏差. 例如, 图6中其对男性人物嘴角的修复结果偏差较大. 本模型相较其他方法针对不规则缺失孔洞有更优的修复表现.

|
图 6 不同方法在Celeb-A数据集上的修复性能比较 |
图7展示了本文方法以及其他对比方法应用于Place2数据集的补全结果. GC与PEN模型生成了模糊的纹理以及明显的伪影, 输入图像的不规则缺损给这两个模型的修复能力带来了可观的扰动. 虽然AOT GAN模型生成结果的清晰度有所提升, 但色彩还原度不及本文模型. TFill方法生成了一定的伪影, 并且其生成图像存在些许补全痕迹. 相比之下, 本文方法补全结果, 具有个更高的契合度和精细度. 实验证明, 模型通过建立像素间的长距离依赖, 引进多尺度融合机制, 有助于模型生成细节纹理提升补全图像契合度.

|
图 7 不同方法在Place2数据集上的修复性能比较 |
3.3.2 定量比较
本文采用相对损失
表1显示, 本文方法在Place2数据集的各项指标相比其他对比方法具有综合性优势. 当遮挡比例为20%–30%时, 模型生成图片的SSIM值比PEN高出11.2%. 当遮挡比例达到40%–50%时, 本模型相比于GC方法具有2.82 dB的PSNR优势, 并且降低了1.32%的
表2显示, 相较其他方法, 本文方法在Celeb-A数据集的各项指标具有更好的表现.当图像遮挡率达到30%–40%时, 本模型的PSNR值相较GC模型高出3.75 dB, 并降低了2.48%的
| 表 1 在Place2数据集上的结果指标 |
| 表 2 在Celeb-A数据集上的结果指标 |
3.4 消融实验
本文模型在Celeb-A数据集上实施消融实验. 该实验将针对性地去除模型中的关键模块, 并比较模块去除前后网络的PSNR值和
| 表 3 在Celeb-A数据集上的消融实验结果 |
3.5 大面积缺失实验
为了验证本模型修复大面积孔洞的能力, 本文在Celeb-A数据集上进行大面积受损图像的补全实验. 我们设置一种图像可见信息极少的情况, 具体做法是将图像的遮挡率提升到70%–90%这种极限程度的比例.
图8表明, 当图像的受损面积占比达到70%–90% 时, 本文模型生成了更多的合理细节. 不难看出本模型对邻近像素信息的依赖较少. 如图8中第3行图像所示, 在处理缺失面积占比大于80%的图像时, 本文模型的生成能力没有受到太大的影响, 其生成图像甚至仍然保持着局部的语义连贯以及全局的结构契合. 而其他方法则过度依赖邻近像素的有效信息导致缺失区域出现大面积的伪影和纹理断层, 在处理可见信息极少的图像时表现不佳.

|
图 8 大面积损毁后图像复原效果对比 |
4 结束语
本文提出了一种以编解码器为主体框架的图像补全模型. 为了提高补全效率以及充分利用图像中的远端像素信息, 本文在网络的生成阶段加入快速傅里叶变换模块. 此外, 考虑到输入变化给模型带来的干扰, 本文在快速傅里叶变换模块引进增强型选择性卷积核网络. 该模块能够有效地聚合不同尺度的特征, 帮助网络获得适应性调整能力, 同时实现模型的精度提升. Place2和Celeb-A数据集上的实验证实, 本方案能够生成视觉真实的结果, 保留更多的细节信息. 此外, 该模型的联想能力十分突出, 能够应对大面积缺失带来的挑战. 本模型处理遮挡比例达到80%的图像时, 仍能保证生成结果的真实性. 目前, 本方法仅针对正脸, 对侧脸类型图片的补全效果一般. 后续工作将针对多视角人脸的修复问题展开研究.
| [1] |
Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Transactions on Graphics, 2009, 28(3): 24. |
| [2] |
Nazeri K, Ng E, Joseph T, et al. EdgeConnect: Generative image inpainting with adversarial edge learning. arXiv:1901.00212, 2019.
|
| [3] |
Patel H, Kulkarni A, Sahni S, et al. Image inpainting using partial convolution. arXiv:2108.08791, 2021.
|
| [4] |
Yu JH, Lin Z, Yang JM, et al. Generative image inpainting with contextual attention. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 5505–5514.
|
| [5] |
Liu WR, Cao CR, Liu J, et al. Fine-grained image inpainting with scale-enhanced generative adversarial network. Pattern Recognition Letters, 2021, 143: 81-87. DOI:10.1016/j.patrec.2020.12.008 |
| [6] |
Li CT, Siu WC, Liu ZS, et al. DeepGIN: Deep generative inpainting network for extreme image inpainting. Proceedings of the 2020 Workshops on Computer Vision. Glasgow: Springer, 2020. 5–22.
|
| [7] |
Zheng CX, Cham TJ, Cai JF, et al. Bridging global context interactions for high-fidelity image completion. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 11502–11512.
|
| [8] |
Elliott DF. Fast Fourier transforms. Handbook of Digital Signal Processing. Amsterdam: Elsevier, 1987. 527–631.
|
| [9] |
Li ZY, Hu F, Wang CL, et al. Selective kernel networks for weakly supervised relation extraction. CAAI Transactions on Intelligence Technology, 2021, 6(2): 224-234. DOI:10.1049/cit2.12008 |
| [10] |
Weickert J. Theoretical foundations of anisotropic diffusion in image processing. In: Kropatsch W, Klette R, Solina F, et al., eds. Theoretical Foundations of Computer Vision. Vienna: Springer, 1996. 221–236.
|
| [11] |
Liang L, Liu C, Xu YQ, et al. Real-time texture synthesis by patch-based sampling. ACM Transactions on Graphics, 2001, 20(3): 127-150. DOI:10.1145/501786.501787 |
| [12] |
Xu ZB, Sun J. Image inpainting by patch propagation using patch sparsity. IEEE Transactions on Image Processing, 2010, 19(5): 1153-1165. DOI:10.1109/TIP.2010.2042098 |
| [13] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2672–2680.
|
| [14] |
Yu JH, Lin Z, Yang JM, et al. Free-form image inpainting with gated convolution. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4470–4479.
|
| [15] |
Iizuka S, Simo-Serra E, Ishikawa H. Globally and locally consistent image completion. ACM Transactions on Graphics, 2017, 36(4): 107. |
| [16] |
Zeng YH, Fu JL, Chao HY, et al. Aggregated contextual transformations for high-resolution image inpainting. IEEE Transactions on Visualization and Computer Graphics, 2023, 29(7): 3266-3280. DOI:10.1109/TVCG.2022.3156949 |
| [17] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [18] |
Liu HY, Jiang B, Xiao Y, et al. Coherent semantic attention for image inpainting. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4169–4178.
|
| [19] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
|
| [20] |
Johnsson SL, Krawitz RL. Cooley-Tukey FFT on the connection machine. Parallel Computing, 1992, 18(11): 1201-1221. DOI:10.1016/0167-8191(92)90066-G |
| [21] |
Isola P, Zhu JY, Zhou TH, et al. Image-to-image translation with conditional adversarial networks. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 5967–5976.
|
| [22] |
Suvorov R, Logacheva E, Mashikhin A, et al. Resolution-robust large mask inpainting with Fourier convolutions. Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision. Waikoloa: IEEE, 2022. 3172–3182.
|
| [23] |
Gatys LA, Ecker AS, Bethge M. Image style transfer using convolutional neural networks. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2414–2423.
|
| [24] |
Zeng YH, Fu JL, Chao HY, et al. Learning pyramid-context encoder network for high-quality image inpainting. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 1486–1494.
|
| [25] |
Zhao SY, Cui J, Sheng YL, et al. Large scale image completion via co-modulated generative adversarial networks. Proceedings of the 9th International Conference on Learning Representations. ICLR, 2021.
|
 2023, Vol. 32
2023, Vol. 32



