移动互联网的不断迭代升级推动了大量新型服务和业务的涌现, 使得用户移动数据流量呈爆炸式增长, 网络带宽无法满足数据流量快速增加的需求, 某些物联网设备的存储和计算能力受物理限制无法提供高速稳定的数据传输和计算能力. 因此, 物联网技术的发展必须考虑如何解决计算能力和带宽压力的问题[1].
MEC是一种面向物联网设备的新型计算范式, 旨在提供云端计算服务并降低用户设备(user equipment, UE)的时延和能耗, 提高数据处理效率[2]. MEC将边缘云服务器部署在小型基站或无线接入点上可以为UE提供计算卸载服务以有效降低时延, 但这种部署方式使得UE与基站之间的有效通信距离受到限制. UAV因具有机动性高、易灵活部署等优点使其成为一种备受关注的新型移动边缘计算接入方式. 相较于传统的单层UAV辅助MEC系统, 双层UAV辅助的MEC系统具有高可靠性、低延迟、高效能、灵活性和多任务协同等优势, 为数据处理和通信任务提供了高效的解决方案. 但在双层UAV辅助的MEC系统中, 需要对任务进行调度和分配. 这个调度过程可能会引入一定的延迟, 尤其是在任务规模较大或系统资源有限的情况下, 可能需要更长的时间来完成任务调度, 从而增加了整体系统的延迟. 因此, 为了克服双层UAV辅助的MEC系统在延迟方面存在的局限性, 需要综合考虑系统的设计、资源分配、任务调度以及UAV的移动策略, 以降低延迟并提高系统的性能和可靠性.
深度强化学习(deep reinforcement learning, DRL)算法近年来在MEC中已经得到了广泛应用. DRL可以用于决策何时、何地、如何将计算任务从边缘设备卸载到边缘服务器或云端. 它可以学习从环境状态和任务需求中提取特征, 并根据奖励信息来优化卸载策略. 边缘计算资源的分配和调度的优化问题可以利用DRL来最大化计算任务的执行效率和系统性能. 它可以学习在不同的资源约束和环境条件下, 如何动态地分配计算资源以满足任务需求. 为此, 本文将研究如何将DRL方法应用到双层UAV辅助的MEC系统中以更好地提升系统性能问题.
1.2 相关工作近年来, 许多学者开始研究基于UAV的通信系统. 虽然大量的传统优化算法都已经应用于解决UAV辅助MEC系统的计算卸载问题, 但对于传统优化模型来说, UAV辅助的MEC系统环境不利于优化模型, 制定复杂的MEC环境具有挑战性. 传统的优化算法无法根据不断变化的环境实时调整策略以实现长期效果. 此外, 标准优化方法的计算成本也随着参数的增加而呈指数级增长.
DRL使用深度神经网络(deep neural network, DNN)来捕获UAV辅助MEC的复杂状态, 并通过强化学习(reinforcement learning, RL)进行决策. 将DRL运用到UAV辅助MEC系统的计算卸载问题中, 可以使其更智能化, 从而减少卸载过程中的能耗, 降低时延, 能够解决传统计算卸载方案不适用于大规模MEC系统的情况. 目前, 已经有很多学者使用DRL中不同的算法来解决MEC中的各种问题. Kiran等人研究了无线MEC中的任务卸载和资源分配问题[3], 提出了一种基于Q-learning的优化框架, 旨在同时最小化延迟和节省用户设备电池功率. 尽管该方法在某些特定场景下表现出了良好的卸载效果, 但在面对状态和动作空间过于庞大且高维连续的优化问题时, 需要存储的Q值内存空间会呈指数级增长. 同时, 搜索最优计算卸载决策也会带来巨大的时间开销. 文献[4–7]采用将UAV飞行方向进行离散化的方法以简化UAV飞行模式, 并将其建模为马尔可夫决策过程(Markov decision process, MDP), 再使用基于值函数的DRL算法进行求解. 但这种方法与UAV实际飞行模式具有较大差异. 虽然在UAV辅助的MEC决策中引入了DRL方法能够实现系统的高性能, 但其并未考虑到部分卸载, 即计算任务只在本地设备或UAV上进行处理. Liu等人[8]将double DQN (double deep Q network)与dueling DQN (dueling deep Q network)相结合, 来解决UAV辅助MEC系统中的计算卸载问题. 该算法虽然在能耗和延迟上取得了较好的效果, 但该方法的UAV动作空间过于简化, 其将UAV的动作空间分解为UAV的水平方向和UAV水平飞行距离等, 并未考虑到部分卸载以及UAV电量不够的情况. Qi等人[9]提出了一种DRL方法联合优化UAV轨迹和用户调度以最大化计算效率. 但该方法基于PPO算法, 适用于离散动作空间, 在一些复杂环境中, 与确定性策略算法相比, PPO算法显然并不那么适用.
尽管已经有了广泛的研究和应用, 但在需要高质量通信的高密场景中, 如何构建UAV辅助的MEC系统, 如何提供低时延高性能的计算服务, 以及如何在存在环境障碍的情况下动态选择合适的通信链路在UAV辅助的MEC系统中尤为重要.
1.3 研究目标及创新点基于上述分析, 本文主要贡献如下.
(1)建立了由一个搭载边缘服务器的T-UAV和多个B-UAV组成的双层UAV辅助MEC系统. T-UAV为B-UAV提供通信和计算卸载服务, 并建立了相应的通信模型和计算模型. 在存在环境障碍的场景下, 构建了动态信道下任务卸载问题模型.
(2)通过联合优化B-UAV调度、T-UAV机动性和资源分配求解以最小化最大处理时延. 考虑到系统状态空间的复杂性, 本文提出了一种DDPG-CPER的卸载算法来解决UAV辅助MEC系统中的卸载决策问题. 相较于传统的DDPG经验回放机制采用的随机采样方式, 该方法综合考虑了TD-error值高的经验和立即回报值高的经验两种评估指标, 采用复合优先级的抽样机制来更高效地利用经验样本. 这种算法设计能够加快训练收敛速度, 更好地降低系统的处理时延.
(3)仿真实验结果表明, 在不同参数和通信条件下, 本文所提出的DDPG-CPER卸载算法可有效应对存在障碍的复杂环境场景下的任务卸载问题, 在处理延迟方面比DDPG等基线算法表现得更加出色.
2 系统模型如图1所示, 我们考虑的是在三维笛卡尔坐标系中, 由单个T-UAV和K个B-UAV组成的MEC系统. 将B-UAV视为采集信息的底层终端, 配有MEC服务器的UAV作为T-UAV, 部署在B-UAV上方, 为B-UAV提供通信和计算服务. 由于T-UAV所搭载的MEC服务器比B-UAV具有更大的计算能力, 因此, B-UAV可以将其计算密集型和延迟敏感型的任务卸载给T-UAV, 以便B-UAV能降低能耗成本, 获得较低的延迟.
2.1 通信模型假设B-UAV与T-UAV的通信过程采用等时隙划分, 每个时隙有且只有一个B-UAV与T-UAV保持通信[10]. 在高度H的二维平面区域范围内, T-UAV可以自由飞行移动. 系统将通信周期T平均划分为I个时隙,
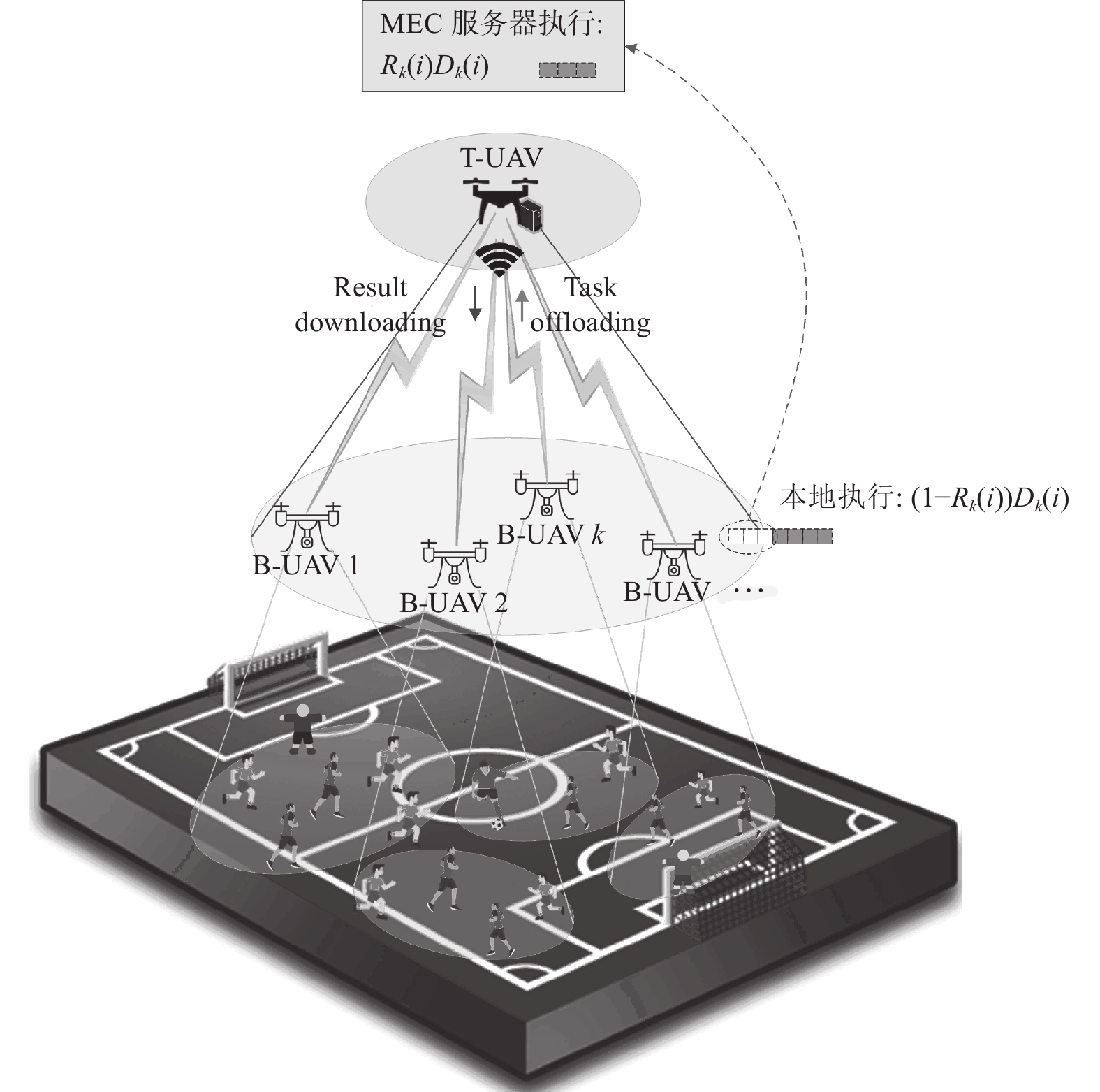
|
图 1 双层UAV辅助的MEC系统模型 |
在UAV辅助的网络中, 由于T-UAV高度远高于B-UAV高度, UAV通信链路的视距信道比其他信道受到的损伤更小, 因此LoS (line-of-sight)信道为T-UAV和B-UAV之间的所有无线信道选择[11]. T-UAV与B-UAV k在时隙i的视距链路下的信道增益可表示为:
| gk(i)=α0d−2k(i)=α0‖q(i+1)−pk(i)‖2+H2 | (1) |
其中,
在研究中, 由于T-UAV的飞行周期被平均分为I个时隙, 并且每个时隙之间的间隔非常短, 因此, 我们可以假设在每个时隙中T-UAV保持悬停状态, 而B-UAV则以相对较低的速度移动. B-UAV和T-UAV通过时分多址接入方式接入, 保证每个时隙的B-UAV都能获得全部的计算资源和通信带宽. 由于无线传输速率可能受障碍物遮挡影响, 因此可用式(2)表示:
| rk(i)=Blog2(1+Pupgk(i)σ2+fk(i)PNLoS) | (2) |
其中,
在UAV辅助的MEC系统里面, 部分卸载策略用于在每个时隙中B-UAV的任务. 设在第i个时隙, B-UAV k将一部分任务卸载到MEC服务器上, 这部分卸载任务占B-UAV总任务量的比例表示为
| tlocal,k(i)=(1−Rk(i))Dk(i)sfB-UAV | (3) |
假设T-UAV的质量为
| Efly(i)=ϕ‖v(i)‖2 | (4) |
由于MEC服务器所提供的计算结果一般来说非常小, 因此, 在进行下行链路传输时, 其对传输时延和能耗的影响可忽略不计[12]. MEC服务器的处理延迟由两部分组成, 其中一部分为传输时延, 计算方法如下:
| ttr,k(i)=Rk(i)Dk(i)rk(i) | (5) |
另一部分是在MEC服务器上计算卸载任务的时延, 假设挂载在T-UAV上的MEC服务器的CPU计算能力用
| tT-UAV,k(i)=Rk(i)Dk(i)sfT-UAV | (6) |
同样, 在第i时隙将任务卸载到服务器所消耗的能量包括来自传输计算任务的能耗和MEC服务器执行卸载任务的能耗这两部分. 在MEC服务器上执行计算时的功率为:
| pT-UAV,k(i)=kf3T-UAV | (7) |
故, MEC服务器在第i时隙的计算能耗表示如下:
| ET-UAV,k(i)=PT-UAV,k(i)tT-UAV,k(i)=kf2T-UAVRK(i)Dk(i)s | (8) |
基于上述构建的双层UAV协助MEC系统模型, 我们得出了研究的优化目标. 为了确保有效利用在B-UAV和T-UAV上的计算资源, 考虑到T-UAV和B-UAV的移动性, 通过联合优化B-UAV调度、T-UAV移动性和资源分配以尽可能地提高B-UAV在所有时隙内的最小处理时延. 优化目标表述如下:
| Tsum=K∑k=1tk=min{αk(i),q(i+1),Rk(i)}I∑i=1K∑k=1αk(i)Tmax | (9) |
| s.t.αk(i)∈{0,1},∀i∈{1,2,⋯,K} | (10) |
| Tmax=max{tlocal,k(i),tT-UAV,k(i)+ttr,k(i)} | (11) |
| K∑k=1αk(i)=1,∀i | (12) |
| 0⩽ | (13) |
| q\left( i \right) \in \left\{ {x\left( i \right), y\left( i \right)|x\left( i \right) \in \left[ {0, L} \right], y\left( i \right) \in \left[ {0, W} \right]} \right\}, \forall i | (14) |
| p\left( i \right) \in \left\{ {{x_k}\left( i \right), {y_k}\left( i \right)|{x_k}\left( i \right) \in \left[ {0, L} \right], {y_k}\left( i \right) \in \left[ {0, W} \right]} \right\}, \forall i, k | (15) |
| {f_k}\left( i \right) \in \left\{ {0, 1} \right\} , \forall i, k | (16) |
| \sum\limits_{i = 1}^I {\left( {{E_{{\rm{fly}}, k}}\left( i \right) + {E_{{\rm{T}} {\text{-}} {\rm{UAV}}, k}}\left( i \right)} \right) \leqslant {E_b}} , \forall k | (17) |
| \sum\limits_{i = 1}^I {\sum\limits_{k = 1}^K {{\alpha _k}\left( i \right){D_k}\left( i \right)} } = D | (18) |
| {t_k} \leqslant t_k^{\max }, \forall k | (19) |
其中, 式(10)–式(12)限制T-UAV在每个时隙只能向一个B-UAV提供计算卸载服务决策. 式(13)限制计算任务卸载比的取值必须在规定范围内. 式(14)和式(15)规定B-UAV和T-UAV只能在规定区域内移动. 式(16)表示T-UAV和B-UAV之间的遮挡情况. 采用式(17)确保T-UAV在所有时隙的能耗不会超过最大电池容量. 式(18)表示在整个通信周期内所有B-UAV需要完成的任务大小. 式(19)表示每个B-UAV的计算延迟必须小于最大容忍延迟.
3 DDPG-CPER卸载算法 3.1 DDPG-CPER算法DDPG算法的经验回放机制为随机采样[13], 这种采样方式忽视了经验样本重要性的差异对agent学习的影响, 未能高效利用高重要性的经验样本以促进网络训练效率. 已有的优先经验回放机制虽然提高了样本的采样效率[14], 但要计算样本集中所有样本的TD-error并进行排序, 增加了算法的复杂度. 且该方法没有考虑到立即回报值较高的经验, 其重要性也高于其他经验样本, 同样应该被高效利用. 因此, 本文提出了一种名为DDPG-CPER的算法, 该算法综合考虑了TD-error值高的经验和立即回报值高的经验两种评估指标, 采用复合优先级抽样机制. 与传统的DDPG算法和基于优先经验回放的DDPG算法相比, 能明显提高经验样本的利用率, 并加快网络的收敛速度. 通过综合考虑这两种评估指标, 能够更好地联合优化B-UAV调度、T-UAV移动性和资源分配, 最终实现系统时延的最小化. 图2为DDPG-CPER算法架构图.
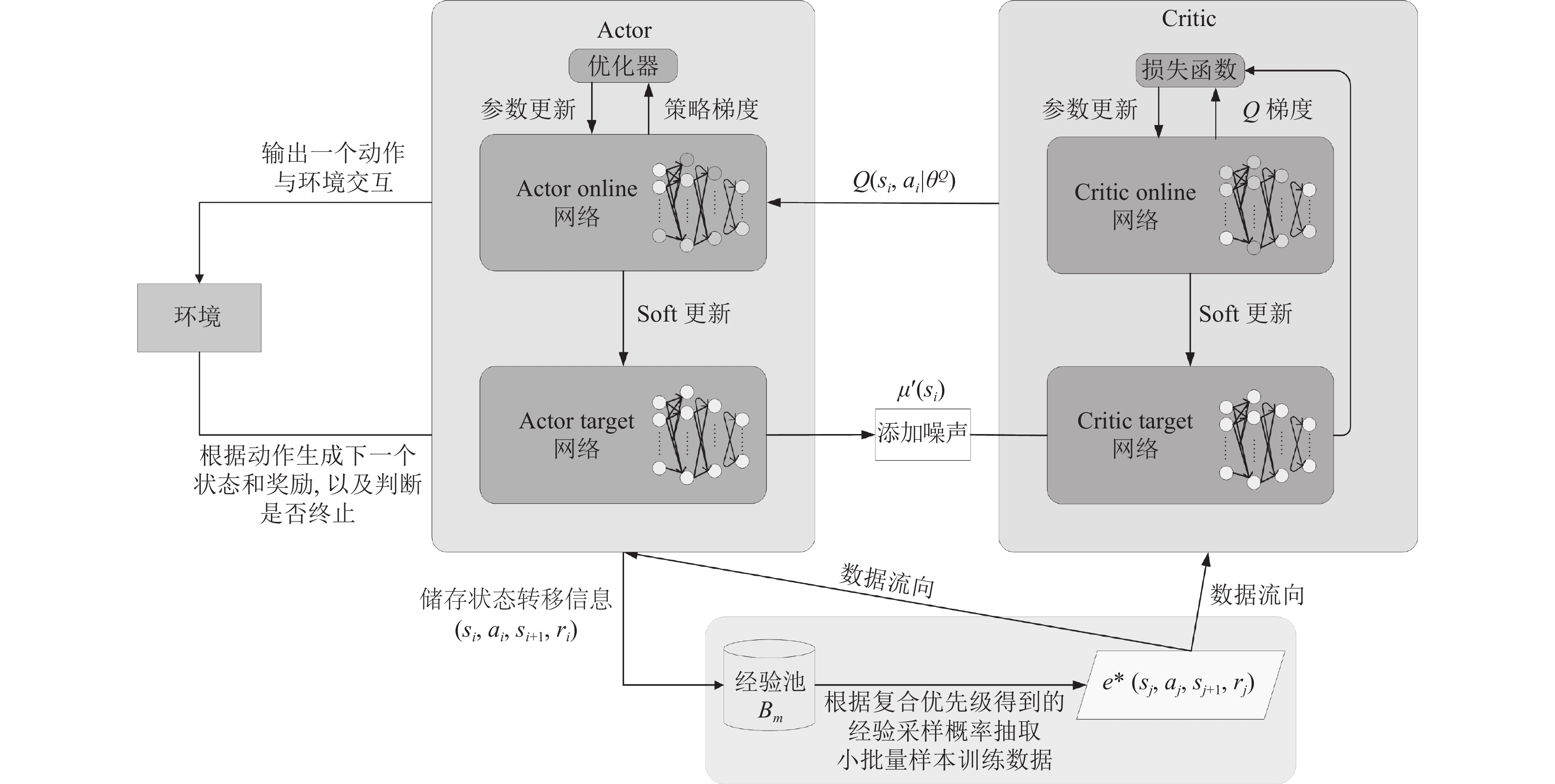
|
图 2 DDPG-CPER算法框架 |
DDPG-CPER算法的具体流程如下.
(1)计算agent在当前状态下的TD-error:
| {\delta _t} = {r_{t + 1}} + \gamma {Q_\pi }\left( {{s_{t + 1}}, {a_{t + 1}}} \right) - {Q_\pi }\left( {{s_t}, {a_t}} \right) | (20) |
其中,
| {Q_\pi }\left( {{s_t}, {a_t}} \right) = {E_\pi }\left[ {{r_{t + 1}} + \gamma {Q_\pi }\left( {{s_{t + 1}}, {a_{t + 1}}} \right)|{s_t} = s, {a_t} = a} \right] | (21) |
(2)定义经验样本在立即回报标准中的优先级和TD-error标准中的优先级:
| \left\{\begin{gathered} {Y_i} = {r_t} + \varepsilon \\ {Y_j} = \left| {{\delta _t}} \right| + \varepsilon \\ \end{gathered} \right. | (22) |
其中,
(3)将经验样本分别按照在立即回报标准中的优先级
| u\left( k \right) = \frac{{rank\left( i \right) + rank\left( j \right)}}{2} | (23) |
(4)计算复合的优先级:
| {Y_k} = {\left( {\frac{1}{{u\left( k \right)}}} \right)^\alpha } | (24) |
其中, 参数
(5)定义采样经验的概率为:
| {P_k} = \frac{{{Y_k}}}{{\displaystyle\sum\nolimits_n {{Y_n}} }} | (25) |
其中, n为经验的数量.
3.2 DDPG-CPER卸载算法在UAV辅助的MEC场景中, 对B-UAV调度、T-UAV的移动性和计算任务分配进行了联合优化, 采用RL对系统状态进行预测, 状态空间可表示为:
| \begin{split} {s_i} =& ({E_{{\rm{battery}}}}(i), q(i), {p_1}(i), \cdots, {p_k}(i), \\ & {D_1}(i), \cdots, {D_k}(i), {f_1}(i), \cdots{f_k}(i)) \end{split} | (26) |
其中,
Agent根据当前状态和观察到的环境选择动作, 动作空间可以表示为:
| {a_i} = \left( {k\left( i \right), \beta \left( i \right), v\left( i \right), {R_k}\left( i \right)} \right) | (27) |
其中,
根据优化目标(10)可以假设奖励函数如下:
| {r_i} = r\left( {{s_i}, {a_i}} \right) = - {\tau _{{\rm{delay}}}}(i) | (28) |
其中,
为了更有效地训练DNN, 使用状态归一化算法对观察到的状态进行预处理, 然后将其馈送到DDPG-CPER卸载算法中. DDPG-CPER卸载算法流程如算法1所示.
算法1. DDPG-CPER卸载算法
1) Require: 总训练Episode数E; 训练样本数据长度I; Critic网络学习率
2)分别随机初始化Actor网络
3)初始化Actor目标网络的权重:
4)初始化经验池
5) for
6) 初始化T-UAV辅助的MEC系统仿真参数, 获得初始观测状态
7) for
8) 根据现有的策略和探索的干扰, 状态
9) 为Actor网络输出的动作添加高斯噪声:
10) agent执行动作
11) 下一时刻的状态
12) if经验池存储空间剩余then
13) 存储元组
14) 把经验按照经验优先级
15) 把经验按照优先级
16) 对经验进行复合平均排序并得到
17) else
18) 以概率
19) end if
20) 从经验池
21) 计算预测Q值:
22) 通过最小化损失函数更新Critic网络参数:
23) 策略梯度更新Actor网络
24) 软更新Actor网络和Critic网络
25) end for
26) end for
4 仿真实验和分析 4.1 仿真设置在UAV辅助的MEC系统中, 设定T-UAV服务的作业场地大小为
| 表 1 仿真参数设置 |
4.2 仿真结果分析
本文首先对算法中一些重要的超参数进行了分析验证. 图3展示了DDPG-CPER卸载算法在不同学习率下的收敛表现. 分别用
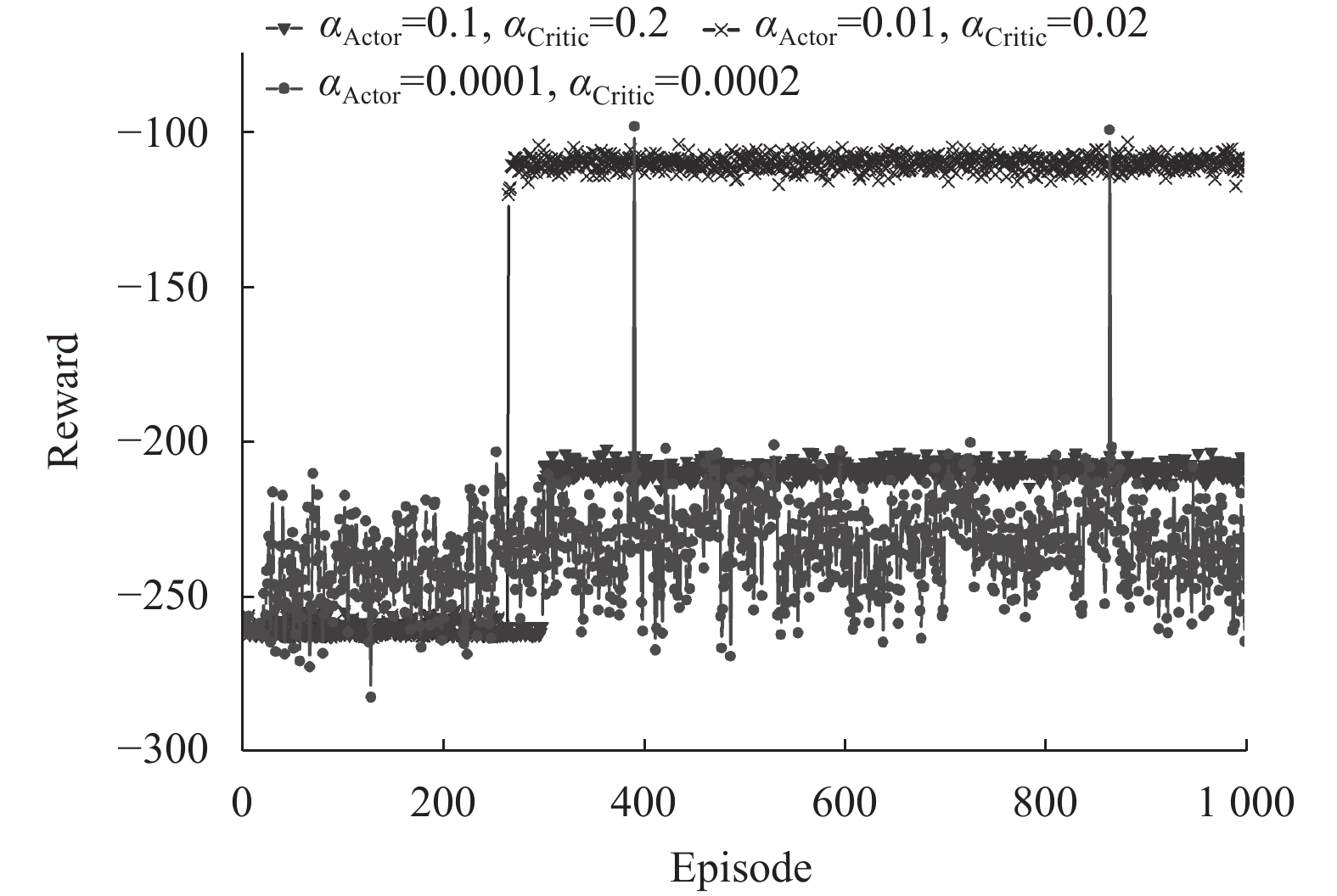
|
图 3 不同学习率下DDPG-CPER卸载算法的收敛表现 |
根据图4的实验结果可以看出, 折扣因子
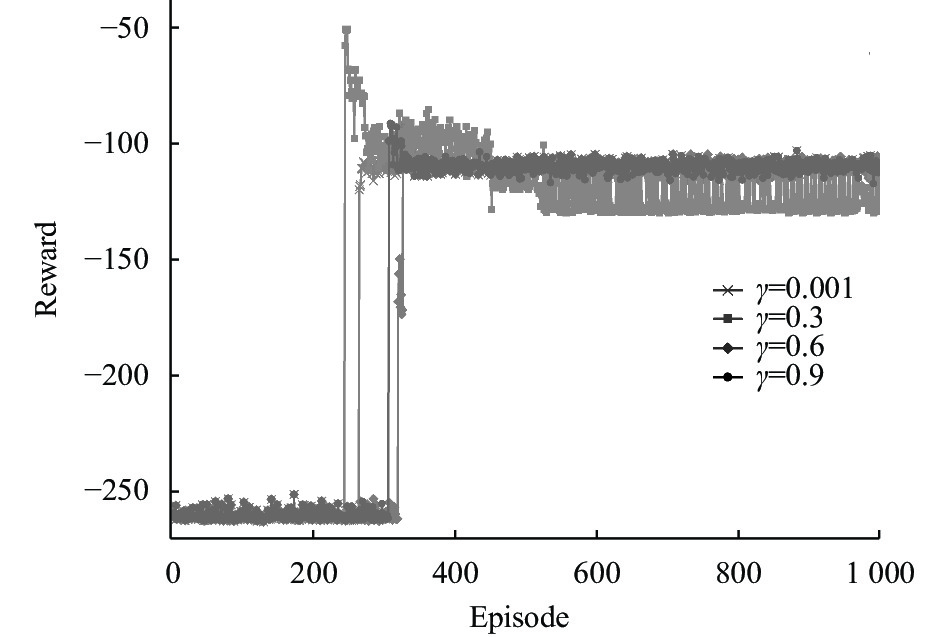
|
图 4 不同折扣因子对DDPG-CPER收敛性能的影响 |
通过图5可以看出, 较高的探索率

|
图 5 不同探索参数设置对DDPG-CPER收敛性能的影响 |
4.3 性能比较
为了进一步验证本文所提出的DDPG-CPER卸载算法的优越性, 采用5种基准方法进行比较, 它们分别描述如下.
(1)完全卸载算法(offloading-only): 将B-UAV的所有任务卸载到T-UAV上的MEC服务器进行计算.
(2)完全本地算法(local-only): 所有计算任务都由B-UAV在本地执行, T-UAV不参与任务处理.
(3)基于连续动作空间的Actor-Critic[17]卸载算法(AC): 为了消除状态变化带来的干扰, 对AC卸载算法进行了状态归一化的操作, 以保证与DDPG-CPER卸载算法比较的公平性.
(4)基于DDPG[18]的卸载算法(DDPG): 将传统的DDPG卸载算法同样采用状态归一化进行预处理以进行公平性比较.
(5)基于离散动作空间的DQN的卸载算法(DQN): 在agent选择动作时, 等分割所选动作取值区间. 为了公平地与DDPG-CPER卸载算法、DDPG卸载算法、AC卸载算法进行比较, DQN卸载算法也对获取的状态进行了预处理.
根据图6可以看出不同算法之间的性能差异, AC卸载算法在迭代次数增加时未能达到收敛状态, 而DQN卸载算法、DDPG卸载算法、DDPG-CPER卸载算法都能够收敛. 原因是AC算法的Actor网络和Critic网络存在依赖关系, 而Critic网络的难以收敛则会导致AC算法不收敛. 与此相比, DQN卸载算法, DDPG卸载算法和DDPG-CPER卸载算法的双重网络结构则可以找到最佳卸载策略.
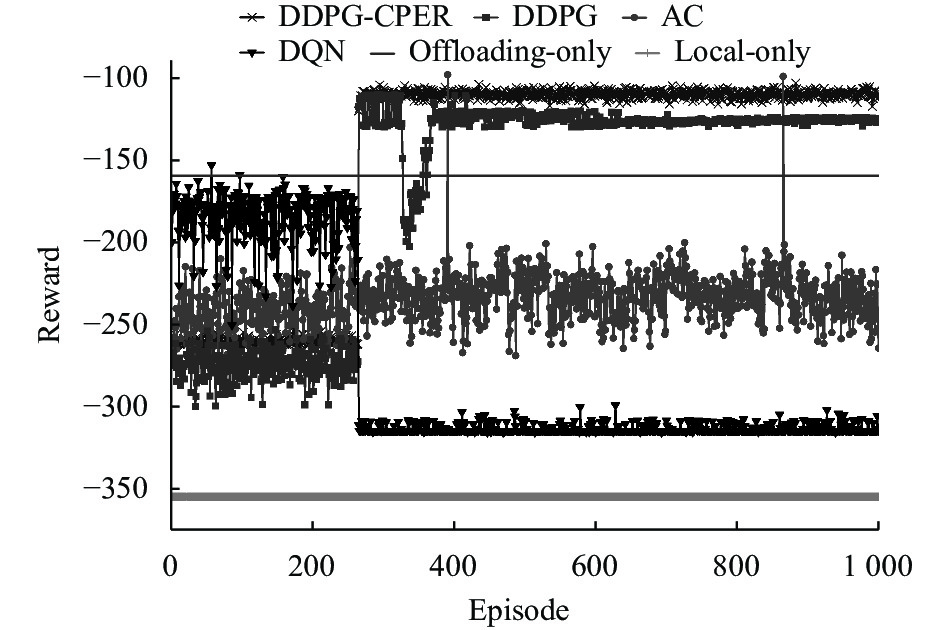
|
图 6 DDPG-CPER与基线算法性能对比 |
图7展示了DDPG-CPER卸载算法在不同任务规模下的性能总是优于其他几种基准算法. 由于DQN卸载算法的动作空间是离散的, 因此无法完全探索动作空间, 从而导致难以找到最优卸载策略. 相比之下, DDPG-CPER卸载算法和DDPG卸载算法能够探索整个连续动作空间并采取更精准的动作, 从而得出最优策略. 相较于传统的DDPG卸载算法, DDPG-CPER卸载算法能够显著地提高奖励值并加快训练速度, 从而大大减少处理时延. Offloading-only算法和local-only算法无法有效地利用系统的计算资源, 因此, 对于相同的任务规模, DDPG-CPER卸载算法具有更低的处理延迟.
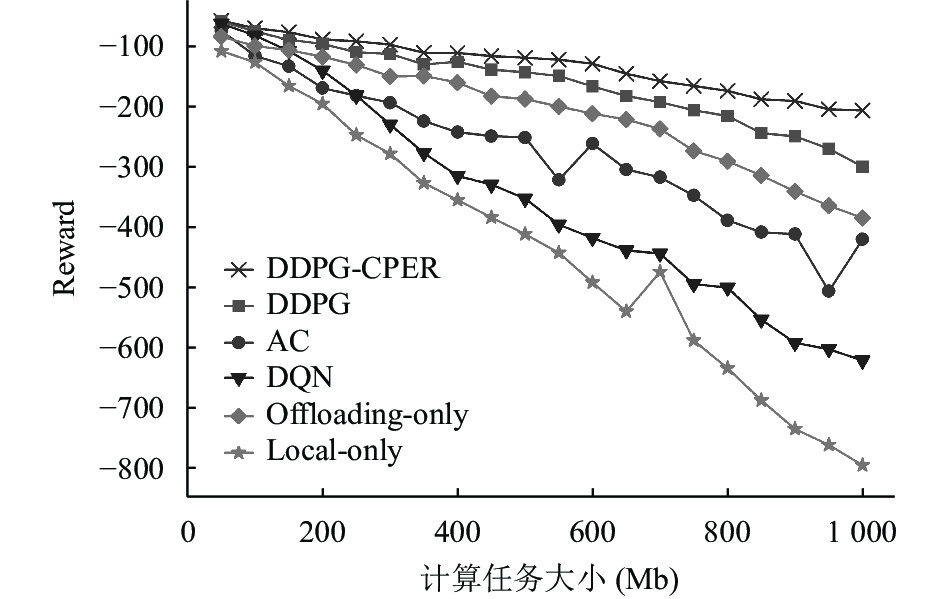
|
图 7 不同任务大小情况下算法性能对比 |
图8展示了不同B-UAV数量下算法之间的性能差异. 可以看出, 因为离散动作空间的值函数对于不同B-UAV数量的场景下有很大变化, 所以DQN卸载算法波动很大. 而DDPG-CPER卸载算法和DDPG卸载算法可以输出多维的连续动作, 保证了DDPG-CPER卸载算法和DDPG卸载算法的收敛性和稳定性. 此外, 在传统的DDPG卸载算法基础上进行了优化的DDPG-CPER卸载算法实现了最大的Reward, 即最小的处理时延. 这是因为DDPG-CPER卸载算法平衡了立即回报值和TD-error两种评价指标, 提高了样本利用率, 加快网络收敛速度, 从而更快地得到最优控制策略.
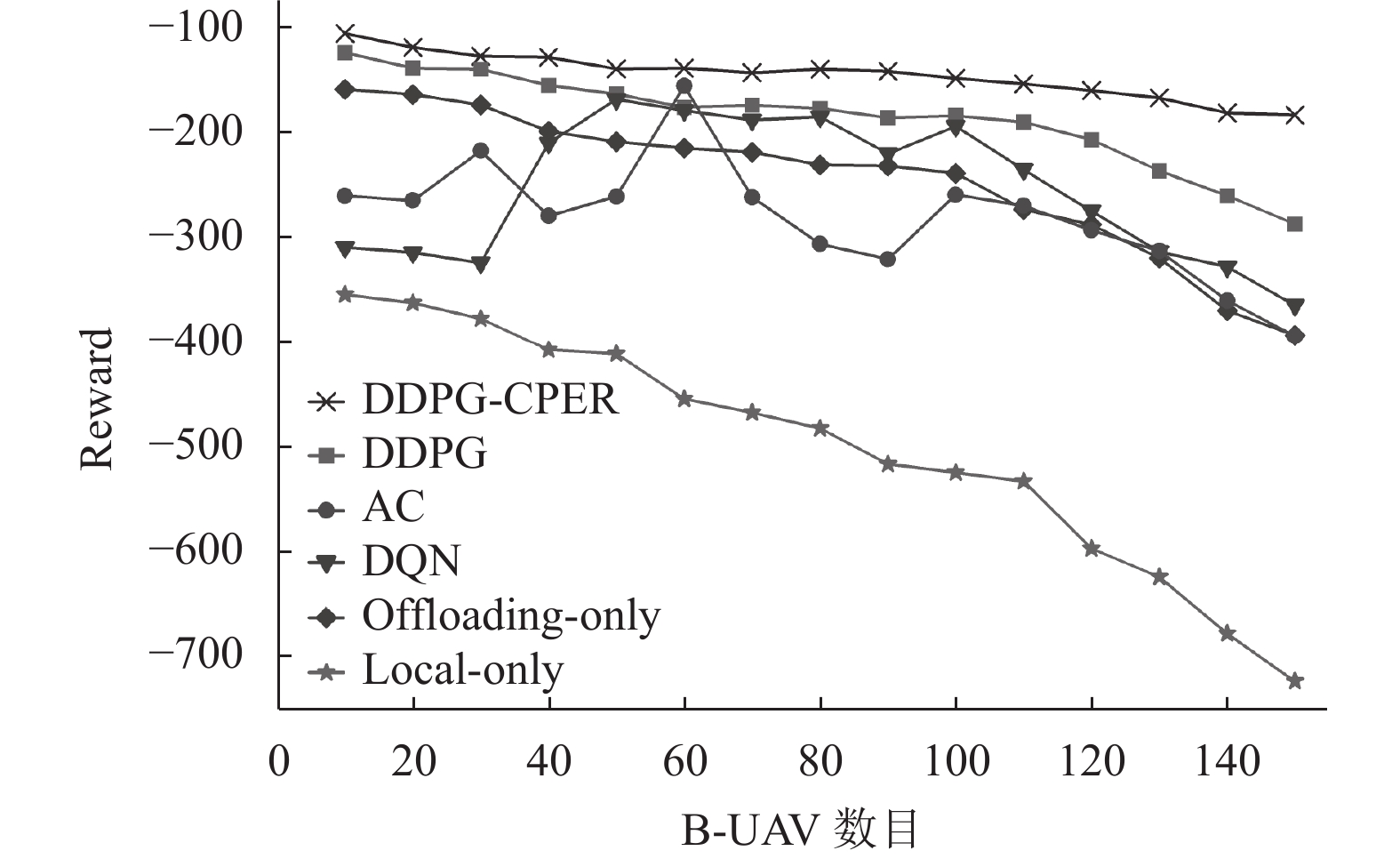
|
图 8 不同B-UAV数量下算法性能对比 |
5 结论与展望
本文研究了双层UAV辅助的MEC系统中的计算卸载问题. 通过协同优化B-UAV调度、任务卸载率、T-UAV移动策略以最小化计算时延. 本文将该优化问题转化为MDP, 提出了DDPG-CPER算法提升样本利用率, 加快网络收敛速度. 通过仿真实验, 我们对DDPG-CPER卸载算法的卸载性能进行了比较分析, 探究了不同参数对其性能的影响. 仿真结果表明本文提出的算法在处理延迟方面表现更优, 相较于基线算法有着显著的性能提升. 尽管UAV辅助的MEC卸载技术已经得到了广泛的关注和研究, 但该领域仍存在一些亟待解决的问题. 比如, 在多UAV辅助的MEC系统中, 多UAV之间的干扰, 多UAV与多UE之间的卸载选择以及MEC卸载的安全性问题. 针对安全与隐私问题, 可以运用区块链等技术使卸载更具安全性和可靠性. 在今后的工作中, 我们考虑将区块链技术与MEC结合以提高用户信息传输的安全性.
| [1] |
Qiu T, Chi JC, Zhou XB, et al. Edge computing in industrial Internet of Things: Architecture, advances and challenges. IEEE Communications Surveys & Tutorials, 2020, 22(4): 2462-2488. |
| [2] |
Hu YC, Patel M, Sabella D. Mobile edge computing—A key technology towards 5G. Sophia Antipolis CEDEX: ETSI, 2015. 1–16.
|
| [3] |
Kiran N, Pan CY, Wang SH, et al. Joint resource allocation and computation offloading in mobile edge computing for SDN based wireless networks. Journal of Communications and Networks, 2020, 22(1): 1-11. |
| [4] |
Li RX, Fu L, Wang LL, et al. Improved Q-learning based route planning method for UAVs in unknown environment. Proceedings of the 15th IEEE International Conference on Control and Automation (ICCA). Edinburgh: IEEE, 2019. 118–123.
|
| [5] |
Yan C, Xiang XJ. A path planning algorithm for UAV based on improved Q-learning. Proceedings of the 2nd International Conference on Robotics and Automation Sciences (ICRAS). Wuhan: IEEE, 2018. 1–5.
|
| [6] |
Zhao YJ, Zheng Z, Zhang XY, et al. Q-learning algorithm based UAV path learning and obstacle avoidence approach. Proceedings of the 36th Chinese Control Conference (CCC). Dalian: IEEE, 2017. 3397–3402.
|
| [7] |
Zhang TZ, Huo X, Chen SL, et al. Hybrid path planning of a quadrotor UAV based on Q-learning algorithm. Proceedings of the 37th Chinese Control Conference (CCC). Wuhan: IEEE, 2018. 5415–5419.
|
| [8] |
Liu X, Chai ZY, Li YL, et al. Multi-objective deep reinforcement learning for computation offloading in UAV-assisted multi-access edge computing. Information Sciences, 2023, 642: 119154. DOI:10.1016/j.ins.2023.119154 |
| [9] |
Qi HM, Zhou Z. Computation offloading and trajectory control for UAV-assisted edge computing using deep reinforcement learning. Applied Sciences, 2022, 12(24): 12870. DOI:10.3390/app122412870 |
| [10] |
Chen Z, Wang XD. Decentralized computation offloading for multi-user mobile edge computing: A deep reinforcement learning approach. EURASIP Journal on Wireless Communications and Networking, 2020, 2020(1): 188. DOI:10.1186/s13638-020-01801-6 |
| [11] |
Jin RX, Yang LY, Zhang HT. Performance analysis of temporal correlation in finite-area UAV networks with LoS/NLoS. Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC). Seoul: IEEE, 2020. 1–6.
|
| [12] |
Hu QY, Cai YL, Yu GD, et al. Joint offloading and trajectory design for UAV-enabled mobile edge computing systems. IEEE Internet of Things Journal, 2019, 6(2): 1879-1892. DOI:10.1109/JIOT.2018.2878876 |
| [13] |
Rizvi SAA, Lin ZL. Experience replay-based output feedback Q-learning scheme for optimal output tracking control of discrete-time linear systems. International Journal of Adaptive Control and Signal Processing, 2019, 33(12): 1825-1842. DOI:10.1002/acs.2981 |
| [14] |
Hou YN, Liu LF, Wei Q, et al. A novel DDPG method with prioritized experience replay. Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Banff: IEEE, 2017. 316–321.
|
| [15] |
Diao XB, Zheng JC, Cai YM, et al. Fair data allocation and trajectory optimization for UAV-assisted mobile edge computing. IEEE Communications Letters, 2019, 23(12): 2357-2361. DOI:10.1109/LCOMM.2019.2943461 |
| [16] |
Ren T, Niu JW, Dai B, et al. Enabling efficient scheduling in large-scale UAV-assisted mobile-edge computing via hierarchical reinforcement learning. IEEE Internet of Things Journal, 2022, 9(10): 7095-7109. DOI:10.1109/JIOT.2021.3071531 |
| [17] |
Cheng N, Lyu F, Quan W, et al. Space/aerial-assisted computing offloading for IoT applications: A learning-based approach. IEEE Journal on Selected Areas in Communications, 2019, 37(5): 1117-1129. DOI:10.1109/JSAC.2019.2906789 |
| [18] |
Wang YP, Fang WW, Ding Y, et al. Computation offloading optimization for UAV-assisted mobile edge computing: A deep deterministic policy gradient approach. Wireless Networks, 2021, 27(4): 2991-3006. DOI:10.1007/s11276-021-02632-z |
 2023, Vol. 32
2023, Vol. 32



