随着定位技术和移动通信技术的快速发展和应用普及, 轨迹数据的获取变得越发容易, 已经在不同的领域突显出重要的研究价值^[1]. 然而, 较高的采样频率会产生大量的轨迹记录, 从而导致轨迹数据规模的爆炸式增长. 对于一线城市而言, 仅是出租车的轨迹数据量, 一天就已经能够达到TB级以上^[2]. 这将严重影响数据存储、管理与查询分析效率, 给服务器带来极大的压力, 为进一步的数据挖掘工作带来巨大的挑战, 且轨迹中往往包含大量的冗余数据, 导致了不必要的存储空间浪费. 为减少轨迹数据存储空间和简化轨迹数据分析, 轨迹数据的压缩存储成为加速轨迹模式挖掘的一种方式和研究热点^[3]. 然而, 轨迹数据同时具有时序特征和空间特征, 常规的时序数据压缩算法并不能简单适用于轨迹数据压缩的场景, 需要充分考虑轨迹的特殊性, 设计更有效的轨迹压缩算法以满足海量轨迹数据管理的需求.

常见的轨迹压缩算法可以分为以下几类^[4]: 基于路网约束的轨迹压缩, 此类算法考虑到车辆受限于道路的特点, 仅适用于车辆轨迹的压缩工作^{[5, 6]}; 基于相似度量的轨迹压缩, 此类算法通过度量轨迹间的相似性, 将相似的轨迹进行统一的压缩, 适用于存在较多相似轨迹的压缩场景^[7]; 基于语义信息的轨迹压缩, 此类算法一般通过提取轨迹中的语义信息进行压缩, 具有较好的可读性, 但是将导致轨迹空间信息的丢失^{[8, 9]}; 基于特征点提取的轨迹压缩, 此类算法限制条件较少, 适用于大多数轨迹压缩场景, 本文将主要研究此类压缩算法.

基于特征点提取的轨迹压缩关键在于如何寻找到轨迹中具有代表性的特征点, 轨迹中的特征点通常具有丰富的信息能够很好地反映出轨迹的形状以及运动规律. 根据选择特征点方式的不同, 轨迹压缩算法分为基于全局特征的轨迹压缩以及基于局部特征的轨迹压缩^[1]. 道格拉斯-普客算法(Douglas-Peucker, DP)^[10]是最为经典的基于全局特征的轨迹压缩算法, 它以一种从上到下的思想, 逐步对轨迹进行迭代划分, 并使用垂直欧氏距离度量轨迹的压缩误差. Meratnia等^[11]在DP算法的基础上考虑了轨迹的时空特征, 使用时间同步欧氏距离(synchronous Euclidean distance, SED)代替垂直欧氏距离进行轨迹迭代划分, 提出了从上到下的时间比压缩算法(top down time ratio, TD-TR). DP和TD-TR算法作为经典的全局压缩算法, 能够很好地保留轨迹的整体形状, 但是由于其递归的特性, 算法时间复杂度为 ${\rm{O}}\left({n}^{2}\right)$ . 与上述两种考虑位置的压缩算法不同, SP算法^[12]是保留方向的轨迹压缩算法, 算法基于一个给定的方向误差构建轨迹与误差阈值的图结构, 通过找到图中的最短路径, 得到保留方向信息的轨迹. 由于选择合适的方向误差阈值对于不同的应用具有挑战性, 作者又提出了Error-Search算法^[13], 该算法能够搜索在一定压缩率下方向误差最低的压缩轨迹. 同样这两个算法的时间复杂度也较高, 因此不适合处理大型轨迹数据集.

基于局部特征的轨迹压缩算法相比而言有着更快的执行效率, 其时间复杂度一般为 ${\rm{O}}\left(n\right)$ , 对于需要实时在线的轨迹压缩需求, 基于局部特征的压缩算法较为合适. 垂距限值法和角度限值法是其中比较有代表性的方法: 通过依次遍历轨迹中的三元组, 每一步进行垂距(或角度)的判断决定是否保留轨迹点. 李升宏等^[14]借鉴垂距限值法和角度限值法的思想, 提出了余弦垂距判别算法(cosine vertical distance discrimination, CVDD), 压缩效果要优于DP算法. 邬群勇等^[15]对轨迹进行开放角计算, 去除了轨迹中方向变化较小的中间点. Yuan等^[16]考虑了轨迹的方向运动特征, 提出了一种基于轨迹转角的拐点提取方法. 上述方法拥有较高的执行效率, 但是难以识别出局部变化小而累积变化大的时空弯曲现象, 因此很有可能会遗漏某些重要的轨迹特征点. 田智慧等^[17]对基于轨迹转角的方法^[16]进行改进, 在角度阈值的基础上增加了累积变向角阈值, 一定程度上减少了关键特征点的丢失, 同时考虑速度特性, 使算法能识别出相对完整的特征点. 相对而言, 基于窗口的轨迹压缩算法将更能满足实时压缩的需求. STTrace算法^[18]是一种基于SED进行度量的在线轨迹压缩算法, 该算法依赖于一个固定大小的缓冲区, 通过每次删除缓冲区中SED误差最小的轨迹点进行压缩工作.

有学者考虑将聚类算法与轨迹压缩算法相结合, 在进行压缩之前, 通过对轨迹的特征进行聚类以获取到潜在的轨迹特征点. Lin等^[19]提出了保留轨迹速度特性的自适应轨迹压缩算法(adaptive trajectory simplification, ATS), 该算法首先从全局的角度对轨迹的速度特征进行聚类, 确定出合理的速度间隔区间, 并基于基尼系数对轨迹进行递归切分, 切分后的子轨迹再应用自适应的DP算法. 张甜等^[20]在ATS算法的基础上进行改进, 使用轮廓系数(silhouette coefficient, SC)^[21]确定聚类簇数, 且使用TD-TR算法替代DP算法, 考虑了轨迹的时间特性. 杨家轩等^[22]同时对轨迹的方向特征和速度特征进行聚类, 在得到潜在的轨迹特征点后, 使用信息熵对轨迹进行切分, 切分后应用TD-TR算法实现二次压缩. 上述方法的优势在于能够较好地保留轨迹的运动特征, 但是实现较为复杂, 且在对轨迹划分后又应用了DP或TD-TR算法, 因此也具有较高的时间复杂度.

文献[12]已证明保留轨迹方向的压缩(direction-preserving trajectory simplification, DPTS)比起保留轨迹位置的压缩(position-preserving trajectory simplification, PPTS)而言一般有着更好的压缩效果. 使用DPTS算法进行轨迹压缩, 将保证压缩后轨迹在方向上的误差较小, 同时在位置上的误差也能被控制在一定范围内. 相反, PPTS却无法保证方向误差. 因此, 本文所设计的轨迹压缩算法将考虑对轨迹方向信息的保留, 也属于一种DPTS算法.

针对目前大多数轨迹压缩算法存在的需要人为选择阈值的问题, 本文从轨迹的全局方向特征和局部方向特征出发考虑, 提出一种自适应的轨迹拐点提取压缩算法, 在避免人为选择参数的同时, 实现高精度的自适应轨迹拐点提取.

1 轨迹相关定义

轨迹压缩问题定义如下: 给定一条轨迹TR, 描述为TR $ = \{ {p_1}, {p_2}, \cdots, {p_i}, \cdots, {p_n}\} \; (1 \leqslant i \leqslant n) $ , 其中 ${p_i}$ 为轨迹点, 描述为一个三元组 $ {p_i} = \left\langle {lo{n_i}, la{t_i}, {t_i}} \right\rangle $ $ ( {t_1} < {t_2} < \cdots < {t_i} < {t_n} ) $ , 包括轨迹点的经度、纬度和采样时间戳, 一条轨迹的总采样点数则描述为 $\left| {{{TR}}} \right|$ . 推导出一条压缩轨迹 ${{{TR}}_{{\rm{sim}}}} = \left\{ {{p_1}, {p_{{s_1}}}, {p_{{s_2}}}, \cdots, {p_{{s_m}}}, {p_n}} \right\}$ $ (1 < {s_1} < {s_2} < {s_m} < n) $ , 其中轨迹起始点 ${p_1}$ 和 ${p_n}$ 必定被保留在轨迹中, ${p_{{s_i}}}\left( {1 \leqslant i \leqslant m} \right)$ 则代表压缩后保留的轨迹的特征点.

在轨迹TR中, 按序列顺序取任意两个轨迹点 ${p_i}$ 和 ${p_j} \; (1 \leqslant i < j \leqslant n)$ 之间的轨迹点组成的新轨迹, 称为子轨迹, 描述为STR $ = \left\{ {{p_i}, {p_{i + 1}}, \cdots, {p_j}} \right\}\left( {j > i + 1} \right)$ . 其中 ${p_i}$ 和 ${p_j}$ 为子轨迹的边界轨迹点, ${\text{TR}}{{\text{S}}_i} = \overline {{p_i}{p_{i + 1}}} $ 和 ${\text{TR}}{{\text{S}}_{j - 1}} = \overline {{p_{j - 1}}{p_j}} $ 为子轨迹的边界轨迹段.

依次计算轨迹TR中2个相邻轨迹点的方向向量, 得到一条长度为n–1的方向向量序列 $\left\{ {\overrightarrow {{\text{TR}}{{\text{S}}_1}} , } \right.\overrightarrow {{\text{TR}}{{\text{S}}_{\text{2}}}} , \cdots, $ $\left. {\overrightarrow {{\text{TR}}{{\text{S}}_{n - 1}}} } \right\}$ , 其中每一项为轨迹段方向, 描述为 ${\overrightarrow {{\text{TRS}}} _i} = \left( {{p_{i + 1}}\cdot lon - } \right.{p_i} \cdot lon, \left. {{p_{i + 1}}\cdot lat - {p_i} \cdot lat} \right)$ .

2 自适应轨迹拐点提取压缩算法

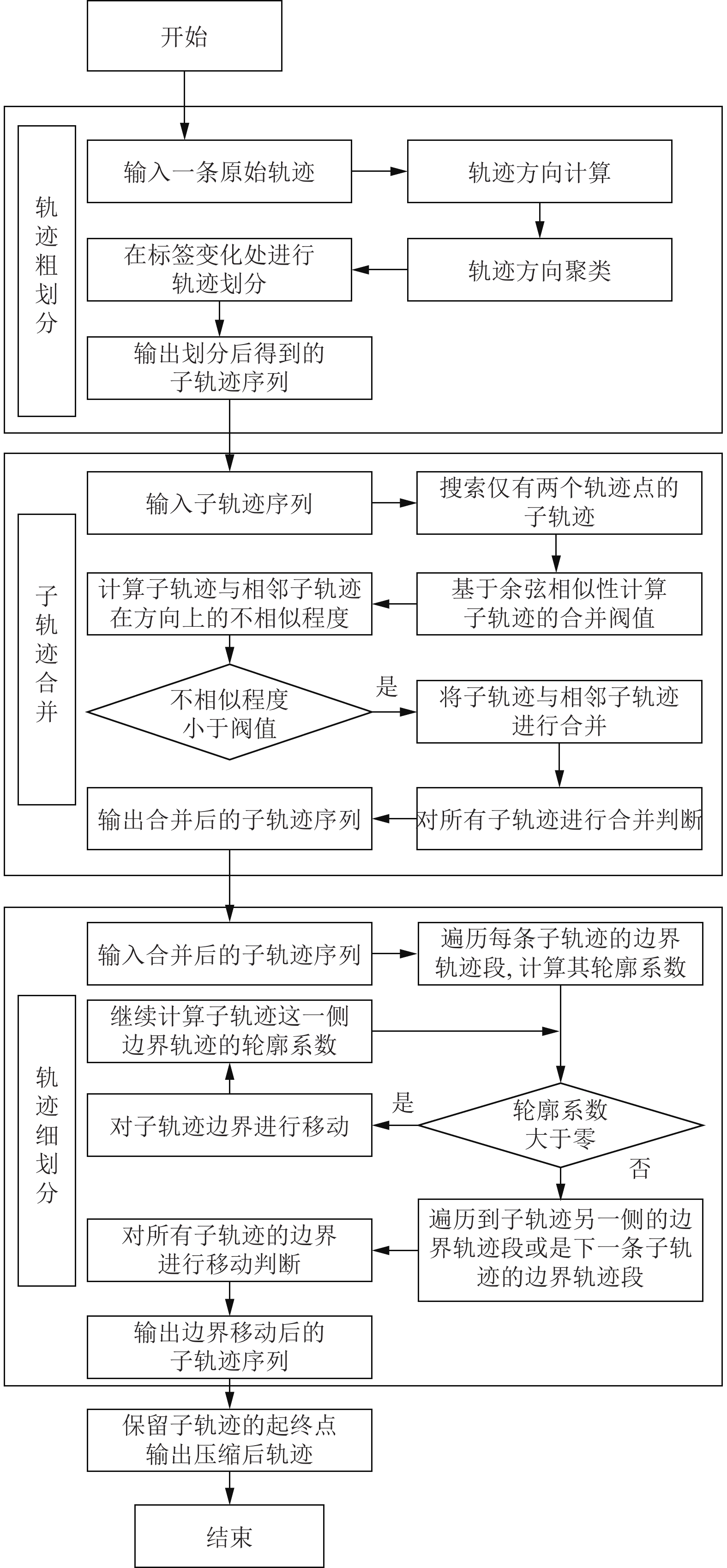
综合轨迹特征聚类的思想^[20]和无监督的序列划分方法^[23]提出一种自适应的轨迹拐点提取压缩算法, 算法流程如图1所示. 首先, 从轨迹的全局方向特征进行考虑, 通过计算得到轨迹的方向向量序列; 再确定合适的类簇数, 使用聚类算法以方向向量序列中的每一项为基本单元进行聚类, 将轨迹映射成一条类簇标签序列, 在标签变化处进行轨迹划分得到了粗划分下的子轨迹序列; 其次, 遍历子轨迹序列, 搜索到仅有两个轨迹点的子轨迹作为待合并子轨迹, 通过判断基于余弦相似性的子轨迹合并条件来决定是否将其与相邻子轨迹进行合并, 完成对所有子轨迹的判断后得到合并后的子轨迹序列; 之后, 对于每一条子轨迹的边界轨迹段, 计算其轮廓系数以决定是否对子轨迹的边界进行移动, 完成对所有子轨迹的判断后得到边界移动后的子轨迹序列. 相邻的子轨迹间共享一个边界轨迹点, 提取此类轨迹点即为轨迹的拐点. 最后保留轨迹的起点、拐点和终点, 其轨迹序列为压缩后轨迹.

2.1 基于轨迹方向特征聚类的轨迹粗划分

本文使用K-means对轨迹的方向向量进行聚类, 以获得具有代表性的方向间隔. 聚类要求输入一个k值以表示数据分类簇, 一般可以根据先验知识或肘部法^[19]得出. 本文将轨迹的行驶方向划分为8个核心方向, 方位角依次为0, 45°,…, 315°. 以核心方向作为区间中心, 8个核心方向恰好将行驶方向划分为8个区间, 分别为[337.5°, 360°] $ \cup $ [0, 22.5°), [22.5°, 67.5°), …, [292.5°, 337.5°). 据此, 给出了确定k值的方法: 对于一条轨迹TR的方向向量序列, 计算每一个向量的方位角, 记录每一个向量方位角所属的方位角区间, 最后统计向量所属的方位角区间总个数, 将其作为K-means聚类的k值.

聚类算法中的核心步骤在于针对数据集中的每一个向量, 计算它到k个聚类中心的距离并将其分配到距离最小的聚类中心所对应的类中, 通常使用欧氏距离度量向量与聚类中心的距离. 针对轨迹方向向量进行聚类, 倾向于计算向量之间的方向相似性, 因此本文使用余弦距离进行距离度量, 计算公式如式(1)所示. 余弦距离的取值范围为 $ \left[\mathrm{0, 2}\right] $ , 越趋近于0, 表示向量之间的方向更加吻合.

$ cosineDistance\left( {x, y} \right) = 1 - \frac{{\displaystyle\sum\nolimits_{i = 1}^n {{x_i}{y_i}} }}{{\sqrt {\displaystyle\sum\nolimits_{i = 1}^n {{x_i}^2} } \sqrt {\displaystyle\sum\nolimits_{i = 1}^n {{y_i}^2} } }} $

(1)

其中, x和y为两个向量, $ {x}_{i} $ 和 $ {y}_{i} $ 分别描述向量x和y中的每一个分量.

基于余弦距离对轨迹的方向向量序列进行聚类后, 每一个方向向量被分配了一个标签以标识其所属的类别, 一条轨迹映射为一条标签序列, 在标签变化处进行轨迹划分实现轨迹的粗划分.

对轨迹粗划分的时间复杂度进行分析. 这部分的算法时间复杂度基本由K-means算法决定, 为 ${\rm{O}}\left( {lnk} \right)$ , 其中l为迭代次数, n为轨迹段数, k为类簇数.

2.2 基于余弦相似性的子轨迹合并

通过分析发现, 粗划分后的子轨迹序列中的部分子轨迹仅包含两个轨迹点, 对于这种情况, 需要考虑将该子轨迹与其相邻的子轨迹进行合并. 对轨迹方向特征聚类后会得到一系列的类簇划分边界, 如果某一向量距离划分边界越近, 则说明该向量距离其相邻的类簇也越近, 认为该向量与其相邻的类簇中的部分向量在一定条件下也是相似的, 称之是可匹配的. 本文定义一个阈值以判断向量是否是可匹配的, 阈值将根据不同的向量进行自适应计算, 如式(2)所示:

$ \begin{split} & {\mathit{mergeThreshold}}(x) = {{\rm{max}} _{{x^i} \in cluste{r_x}}}\{ {\mathit{cosineDistance}}(x, {x^i})\} \end{split} $

(2)

其中, x为某一向量, ${x^i}$ 为与x属于同一类簇 $cluste{r_x}$ 的向量, 向量间的相似性度量使用余弦距离.

根据向量在所属类簇中的位置自适应计算合适的子轨迹合并阈值, 如果向量靠近类簇的划分边界, 那么将会得到较大的阈值; 反之, 则会得到较小的阈值. 计算待合并子轨迹与其相邻子轨迹方向的不相似程度, 将计算的结果与阈值进行对比, 若小于阈值, 则进行合并, 否则不进行合并. 越大的阈值将表现出越强的子轨迹合并倾向, 而越小的阈值将表现出越弱的子轨迹合并倾向. 通过考虑子轨迹间的局部方向相似情况, 对子轨迹进行适当的合并, 能够有效地减少某些潜在错误的轨迹划分结果, 一定程度上提高了轨迹划分的准确性. 子轨迹合并的伪代码如算法1所示.

算法1. 子轨迹合并算法

输入: 子轨迹序列 $\scriptstyle {\textit{STRS = }}\left[ {\left\{ {{p_1}, \cdots, {p_i}} \right\}, \left\{ {{p_i}, \cdots, {p_j}} \right\}, \cdots, \left\{ {{p_m}, \cdots, {p_n}} \right\}} \right] ( 1 < i < j < \cdots < \scriptstyle m < n ) $

输出: 原地得到合并处理后的子轨迹序列STRS

1) For STR from $\scriptstyle \left\{ {{p_1}, \cdots, {p_i}} \right\}$ to $\scriptstyle \left\{ {{p_m}, \cdots, {p_n}} \right\}:$ /*遍历每一条子轨迹*/

2) 　 $\scriptstyle {\text{If}} \; \left| {{\textit{STR}}} \right| \; {\text{ = = }}2:$ /*如果当前子轨迹仅有两个轨迹点(一个轨迹段), 需要判断合并条件*/

3) 　　 计算STR中唯一轨迹段方向向量 $\scriptstyle \overrightarrow {{\text{TRS}}} $ 的合并阈值 $\scriptstyle {\textit{mergeThreshold}} \scriptstyle (\overrightarrow{{\text{TRS}}} )$

4) 　　计算STR与其相邻子轨迹 $\scriptstyle {\textit{STR}}{{}_{{\rm{pre}}}}$ 和 $\scriptstyle {\textit{STR}}{{}_{{\rm{next}}}}$ 在方向上的不相似程度(分别计算 $\scriptstyle \overrightarrow {{\text{TRS}}} $ 与 $\scriptstyle {\textit{STR}}{{}_{{\rm{pre}}}}$ 及 $\scriptstyle {\textit{STR}}{{}_{{\rm{next}}}}$ 中所有轨迹段方向的余弦距离的均值), 并取二者中的最小值minSim

5) 　　If $\scriptstyle {\text{minSim}} \leqslant mergeThreshold{\text{(}}\overrightarrow {{\text{TRS}}} {\text{)}}$ :

6) 　　　将STR与 $\scriptstyle {\textit{STR}}{{{}}_{{\rm{pre}}}}$ 和 $\scriptstyle {\textit{STR}}{{}_{{\rm{next}}}}$ 中方向更相近的那条子轨迹进行合并

7)　 　Else:

8) 　　　不对STR进行合并处理

9) 　Else:

10)　 　Continue

对子轨迹合并的时间复杂度进行分析. 该部分的时间复杂度将主要由计算子轨迹合并阈值以及计算当前子轨迹与相邻子轨迹的不相似程度决定. 计算合并阈值的时间复杂度为 ${\rm{O}}\left( c \right)$ , 计算当前子轨迹与相邻子轨迹的不相似程度的时间复杂度为 ${\rm{O}}\left( {p + q} \right)$ , 总时间复杂度为 ${\rm{O}}\left( {n(c + p + q)} \right)$ , 其中n为子轨迹数, c为与当前待合并子轨迹内唯一方向向量属于同一类的向量数, p和q分别为与当前待合并子轨迹相邻的两条子轨迹中的轨迹段数.

2.3 基于轮廓系数的轨迹细划分

子轨迹合并之后, 将对每一条子轨迹的边界进行调整移动以进一步提高轨迹划分的准确性. 轨迹细划分上主要考虑两点^[24], 一是如何衡量子轨迹内的同质性(即同一子轨迹内的轨迹点(或轨迹段)具有较为相似的特征); 二是如何衡量相邻子轨迹之间的异质性(即相邻子轨迹之间具有不相似的运动行为). 轮廓系数^[21]通过考虑数据向量的内聚度和分离度来评价聚类效果的好坏. 本文将使用轮廓系数来评价轨迹基于方向特征的划分效果, 计算如式(3)所示:

$ S(\overrightarrow {{\text{TR}}{{\text{S}}_i}} ) = \frac{{b\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right) - a\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right)}}{{\max \left\{ {a\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right), b\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right)} \right\}}} $

(3)

其中,

$ \begin{gathered} a\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right) = \frac{1}{{\left| {{\textit{STR}}} \right| - 1}}\sum\limits_{j = 1}^{\left| {{\textit{STR}}} \right| - 1} {{\textit{cosineDistance}}} (\overrightarrow {{\text{TR}}{{\text{S}}_i}} , \overrightarrow {{\text{TR}}{{\text{S}}_j}} ) \end{gathered} $

$ \begin{gathered} b\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right) = \\ \frac{1}{{\left| {{\textit{STR}}{{{}}_{{\rm{nearest}}}}} \right| - 1}}\sum\limits_{j = 1}^{\left| {{\textit{STR}}{{{}}_{{\rm{nearest}}}}} \right| - 1} {{\textit{cosineDistance}}} (\overrightarrow {{\text{TR}}{{\text{S}}_i}} , \overrightarrow {{\text{TR}}{{\text{S}}_j}} ) \\ \end{gathered} $

其中, 轮廓系数 $S(\overrightarrow {{\text{TR}}{{\text{S}}_i}} )$ 的值介于[−1, 1], $S(\overrightarrow {{\text{TR}}{{\text{S}}_i}} )$ 越趋近于1代表轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_i}} $ 的内聚度和分离度都相对较优; 反之, 则代表轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_i}} $ 的内聚度和分离度都相对较差. $ a\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right) $ 是计算轨迹段方向的内聚度(同质性), 即描述为当前轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_i}} $ 与同一子轨迹内其他轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_j}} $ 的不相似程度的平均值; $ b\left( {\overrightarrow {{\text{TR}}{{\text{S}}_i}} } \right) $ 是计算当前轨迹段方向的外离度(异质性), 描述为当前轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_i}} $ 与其直接相邻子轨迹内的所有轨迹段方向 $\overrightarrow {{\text{TR}}{{\text{S}}_j}} $ 的不相似程度的平均值. 其中相似性的度量使用余弦距离(即式(1))计算.

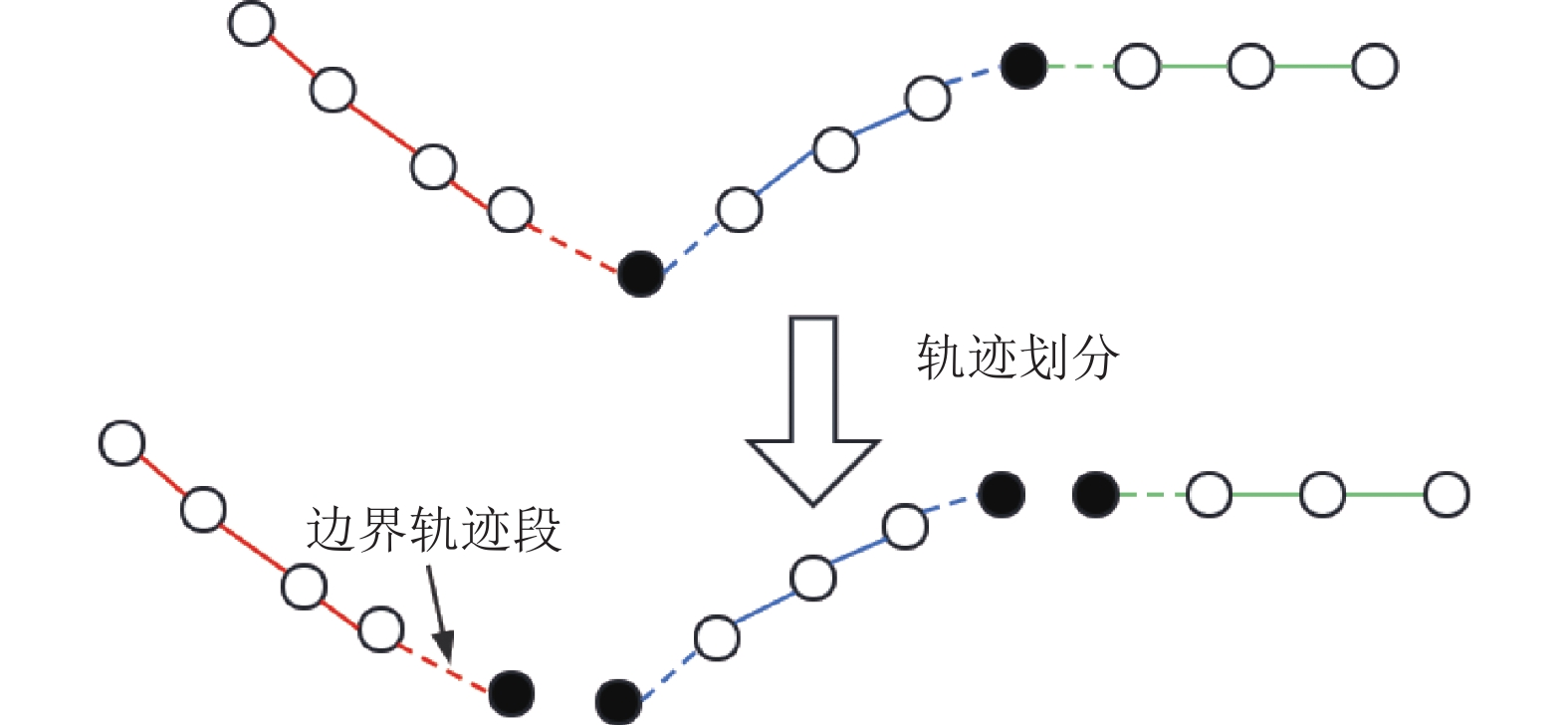
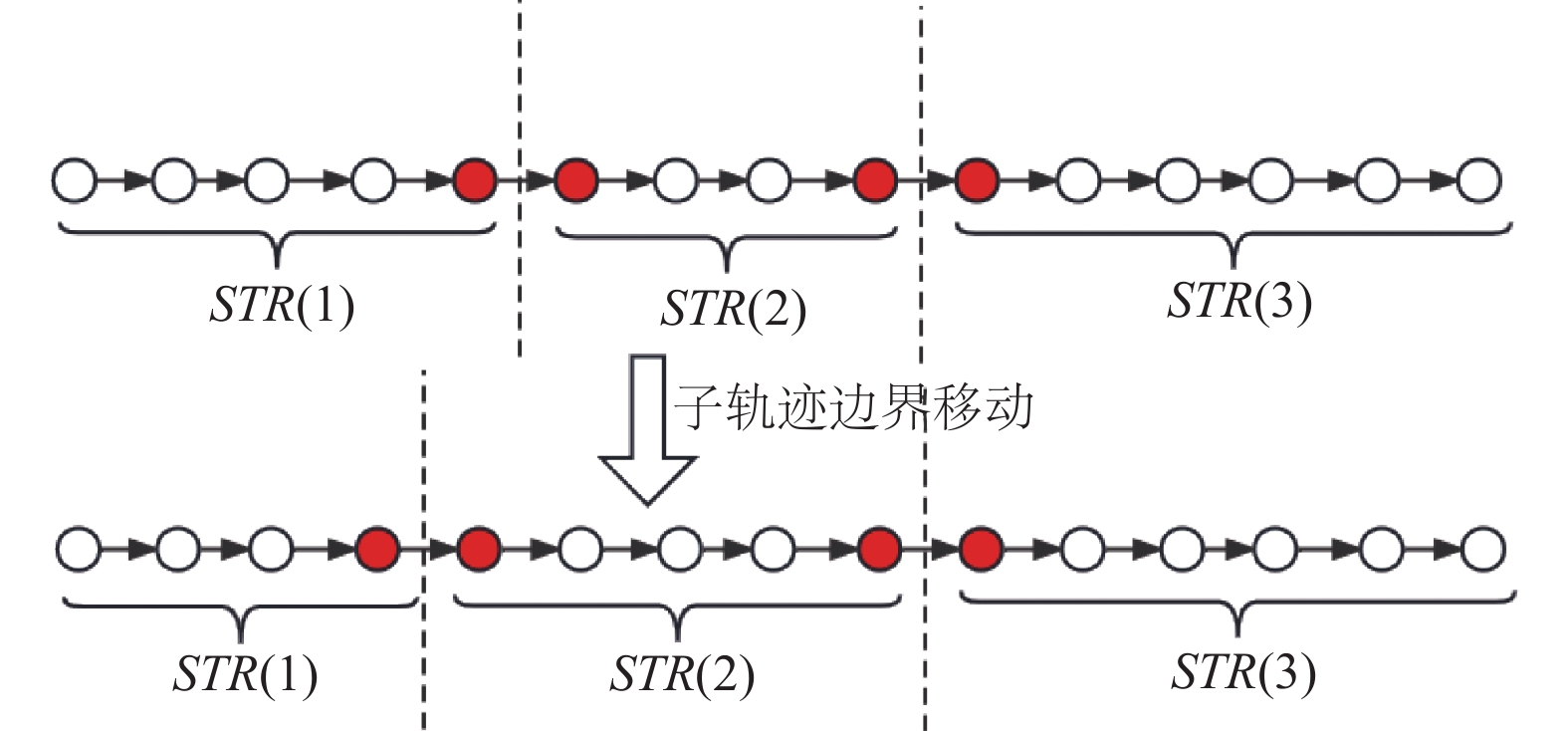
轨迹属于一种时间序列数据, 一条轨迹的轨迹点(或轨迹段)之间有着严格的先后顺序, 因此轨迹的划分边界只能进行线性的移动, 且边界移动时, 只需优先考虑位于子轨迹边界附近的轨迹点(或轨迹段). 因此, 本文在进行轮廓系数计算时, 沿着线性方向逐个移动优先对子轨迹的边界轨迹段进行计算判断. 如图2所示, 一条轨迹被划分为了3条子轨迹, 每条子轨迹的边界轨迹点被标为深色而边界轨迹段则被标为虚线, 在进行子轨迹的边界移动时, 将对边界轨迹段(即图中虚线部分)先进行判断. 值得关注的是, 第1条子轨迹和最后一条子轨迹都只有一个边界轨迹点和一个边界轨迹段. 如图3所示为抽象的子轨迹边界移动示意图, 图上轨迹被划分为3个子轨迹STR(1)、STR(2)和STR(3), 子轨迹上的每一个轨迹段抽象为图中的一个点, 且边界轨迹段被标记为深色, 子轨迹边界则用虚线表示. 子轨迹划分边界移动调整的伪代码如算法2所示.

算法2. 子轨迹边界移动算法

输入: 子轨迹序列 $\scriptstyle {\text{STRS = }}\left[ {\left\{ {{p_1}, \cdots, {p_i}} \right\}, \left\{ {{p_i}, \cdots, {p_j}} \right\}, \cdots, \left\{ {{p_m}, \cdots, {p_n}} \right\}} \right] ( 1 < i < j < \cdots \scriptstyle < m < n ) $

输出: 原地得到边界移动后的子轨迹序列STRS

1)初始化一个变量Flag用以标识前一子轨迹是否移动了相邻边界

2) For STR from $\scriptstyle \left\{ {{p_1}, \cdots, {p_i}} \right\}$ to $\scriptstyle \left\{ {{p_m}, \cdots, {p_n}} \right\}$ : /*遍历每一条子轨迹*/

3)　 $\scriptstyle {\text{If}} \; \left| {{\textit{STR}}} \right|{\text{ = = }}2:$ /*子轨迹中仅有两个轨迹点(一个轨迹段), 不进行划分边界调整*/

4)　　 Continue

5) 　If STR不是第一条子轨迹且Flag==False:

6) 　　While True:

7) 　　　 $\scriptstyle {\text{If}} \; \left| {{\textit{STR}}} \right|{\text{ = = }}2:$ /*经过边界调整后, 当前子轨迹中仅有两个轨迹点(一个轨迹段)*/

8) 　　　　根据算法1判断STR的合并条件

9) 　　　　Break

10) 　　 得到STR中的第1个轨迹段 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{first}}}}$ 以及其方向 $\scriptstyle \overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{first}}}}}$

11) 　　 计算 $\scriptstyle \overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{first}}}}}$ 的轮廓系数 $\scriptstyle S(\overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{first}}}}} )$

12) 　　 If $\scriptstyle S(\overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{first}}}}} ) \geqslant 0:$ /*如果轮廓系数为正, 边界不移动*/

13)　　　　 Break

14) 　　 Else: //如果轮廓系数为负, 边界右移

15) 　　　　将 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{first}}}}$ 插入到前一条子轨迹 $\scriptstyle {\textit{STR}}{{{}}_{{\rm{pre}}}}$ 的末尾

16) 　　　　将 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{first}}}}$ 从STR的开头移除

17) 　Flag=False

18) 　If STR不是最后一条子轨迹:

19) 　　While True:

20) 　　　 $\scriptstyle {\text{If}} \; \left| {{\textit{STR}}} \right|{\text{ = = }}2:$ /*经过边界调整后, 当前子轨迹中仅有两个轨迹点(一个轨迹段)*/

21) 　　　　根据算法1判断STR的合并条件

22)　　　　 Break

23) 　　　得到STR中的最后一个轨迹段 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{last}}}}$ 以及其方向 $\scriptstyle \overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{last}}}}}$

24) 　　　计算 $\scriptstyle \overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{last}}}}}$ 的轮廓系数 $\scriptstyle S(\overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{last}}}}} )$

25)　　　 If $\scriptstyle S(\overrightarrow {{\text{TR}}{{\text{S}}_{{\rm{last}}}}} ) \geqslant 0:$ /*如果轮廓系数为正, 边界不移动*/

26)　　　　 Break

27) 　　　Else: //如果轮廓系数为负, 边界左移

28) 　　　　Flag=True //边界移动, 更新Flag

29) 　　　　将 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{last}}}}$ 插入到后一条子轨迹 $\scriptstyle {\textit{STR}}{{{}}_{{\rm{next}}}}$ 的开头

30) 　　　　将 $\scriptstyle {\text{TR}}{{\text{S}}_{{\rm{last}}}}$ 从STR的末尾移除

对轨迹细划分的时间复杂度进行分析. 该部分的时间复杂度将主要由子轨迹边界移动的次数以及轮廓系数的计算决定. 判断子轨迹边界移动条件的总次数为 $2m\left( {n - 1} \right)$ , 计算一个轨迹段方向的轮廓系数的时间复杂度为 ${\rm{O}}\left(i+j\right)$ , 总的时间复杂度为 ${\rm{O}}(2m(n - 1)(i + j))$ , 其中n为子轨迹数, m为待移动边界子轨迹某一侧边界移动的次数, i为待移动边界子轨迹内的轨迹段数, j为与当前子轨迹的边界轨迹段直接相邻的子轨迹内的轨迹段数.

3 轨迹压缩算法性能评估 3.1 实验配置及数据集

实验配置具体如下: 处理器为Intel(R) Core(TM) i7-10700K CPU @ 3.80 GHz 16 GB RAM; 实验环境为Windows 10操作系统和Anaconda3开发环境, 并基于Python 3.8实现.

为验证本文算法针对不同规模轨迹数据的方向特征提取及压缩效果, 实验数据使用(Microsoft Research Asia) Geolife项目^[25–27]中收集的由182名用户在5年多(2007年4月–2012年8月)的时间内产生的GPS轨迹. 该数据集中的GPS轨迹由一系列采样时间点表示, 每个点包含纬度、经度和海拔的信息, 轨迹具有较高的采样率, 91.5%的轨迹采样密度较高.

对数据集进行简单预处理后, 提取部分轨迹作为最终的实验数据集, 并根据轨迹的点数将轨迹集分为4个等级, 分别为短轨迹(10–300个点)、中长轨迹(300–1000个点)、长轨迹(1000–2000个点)和超长轨迹集(>2000个点), 数据集详细信息如表1所示.

本文主要考虑将角度的压缩算法^[15–17] 、融合聚类的压缩算法^[19–20,22]和SP算法^[12]这3类算法作为实验的对比算法. 其中基于角度的压缩算法拥有简单高效的优势, 在轨迹预处理工作中较为常见, 本文选择文献[17]中的算法(不考虑速度特征)作为代表此类的对比算法; 融合聚类的压缩算法与本文算法的实现思路有一定的相似之处, 都采用聚类的手段先对轨迹特征进行聚类以发现潜在的轨迹特征点, 本文选择文献[22]中的方法(不考虑速度特征, 且不对划分后的轨迹进行二次压缩)作为代表此类的对比算法; SP算法属于该领域较为经典的算法, 文献[12]中首次证明了保留方向信息的压缩算法能够在保持方向误差的同时限制空间距离误差, 因此本文选择文献[12]中SP算法作为对比算法.

3.2 性能度量指标

本文选取运行时间、压缩率以及平均方向误差3个指标来评估所提出算法的性能. 运行时间通常用来衡量一个算法的执行效率; 压缩率通过计算压缩后的轨迹点数与原始轨迹点数的差距来评价压缩程度; 平均方向误差用来评价轨迹压缩前后在方向这一运动特征上的损失程度, 同时也可以很好地衡量轨迹拐点提取的精度.

本文定义压缩率的计算如式(4)所示:

$ \begin{gathered} {\textit{compressionRatio}}({\textit{TR}}, {\textit{TR}}{{{}}_{{\rm{sim}}}}) = \left(1 - \frac{{\left| {{{T}}{{{R}}_{{\rm{sim}}}}} \right| - 2}}{{\left| {{{TR}}} \right| - 2}}\right) \times 100{\text{%}} \end{gathered} $

(4)

其中, TR与 ${\textit{TR}}{_{{\rm{sim}}}}$ 分别代表原始轨迹和压缩后轨迹, $\left| {{\textit{TR}}} \right|$ 与 $\left| {{\textit{TR}}{{{}}_{{\rm{sim}}}}} \right|$ 则分别代表压缩前后轨迹中所包含的点数. 压缩率越高表示压缩后轨迹中所包含的点数越少, 从而压缩程度也越深.

本文定义平均方向误差的计算如式(5)所示:

$ \begin{split} aveDi{r_{{\rm{error}}}} & \left( {{\textit{TR}}, {\textit{TR}}{{{}}_{{\rm{sim}}}}} \right) \\ & = \frac{1}{{\left| {{\textit{TR}}} \right| - 1}}\sum\limits_{i = 1}^{\left| {{\textit{TR}}{{{}}_{{\rm{sim}}}}} \right| - 1} {\sum\nolimits_{j = 1}^m {\theta (\overrightarrow {{{\rm{TRS}}_j}} , \overrightarrow {{{\rm{TRS}}_{{{\rm{sim}}_i}}}} )} } \end{split} $

(5)

其中, $\left| {{\textit{TR}}} \right| - 1$ 与 $\left| {{\textit{TR}}{{{}}_{{\rm{sim}}}}} \right| - 1$ 分别代表轨迹压缩前后所包含的轨迹段数, m代表原始轨迹TR在压缩轨迹 ${\textit{TR}}{{{}}_{{\rm{sim}}}}$ 第i个轨迹段上的冗余轨迹段数, $\theta (\overrightarrow {{{\rm{TRS}}_j}} , \overrightarrow {{{\rm{TRS}}_{{{\rm{sim}}_i}}}} )$ 描述 $\overrightarrow {{{\rm{TRS}}_j}}$ 和 $\overrightarrow {{{\rm{TRS}}_{{{\rm{sim}}_i}}}}$ 的向量夹角.

3.3 算法性能指标对比分析

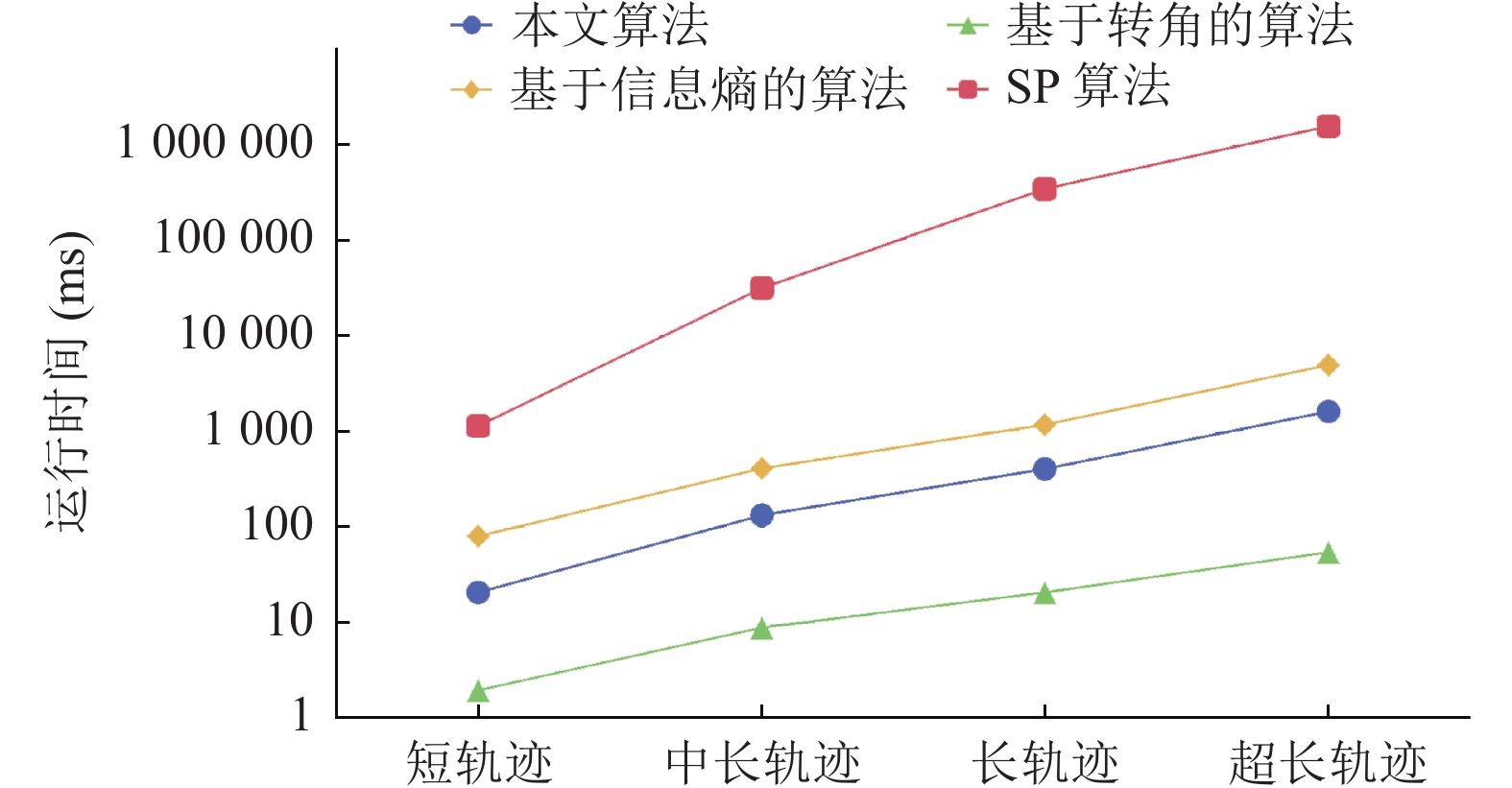
如图4所示, 对4种算法在同一压缩率水平下的运行时间进行了对比. 整体来看, 4种算法的运行时间都随着轨迹规模的增大而提高. 其中, 基于转角的算法的运行时间变化幅度较小, 最高耗时不超过100 ms, 因此, 该算法有着最高的运行效率; 相对而言, SP算法在运行时间上变化幅度较大, 随着轨迹规模的增大, 与其余3种算法的差距逐渐明显, 说明SP算法并不适用于规模较大的轨迹压缩工作; 本文算法介于中间, 比起基于信息熵的算法和SP算法耗时较低.

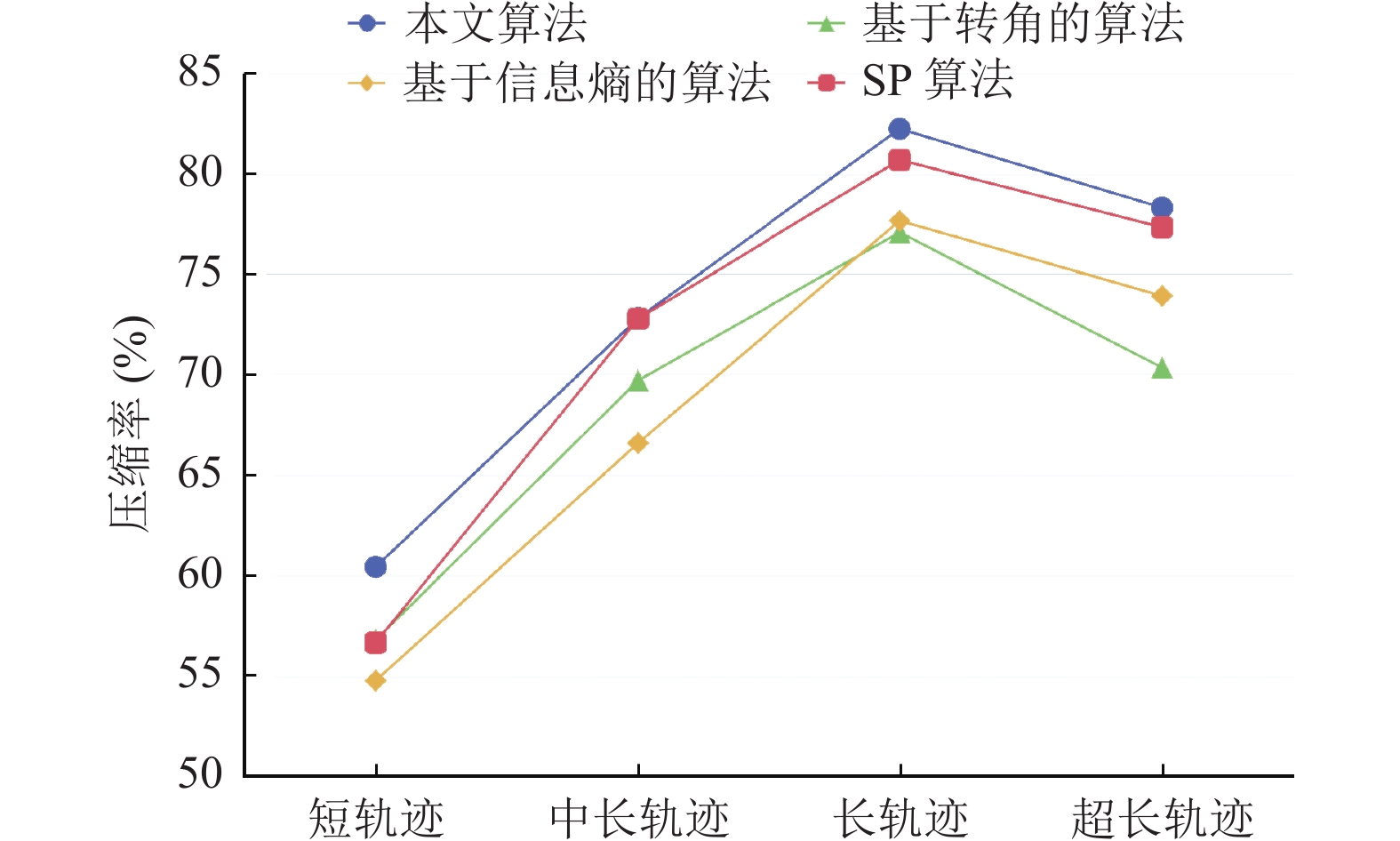
如图5所示, 对4种算法在同一方向误差水平下的压缩率进行了对比. 整体来看, 4种算法的压缩率都随着轨迹规模的增大而提高. 其中, SP算法与本文算法的压缩率较为相近, 最高都超过了80%, 本文算法的压缩率仅略高于SP算法. 另外, 随着轨迹规模的增大与其余两种算法的差距也越来越大. 使用本文算法进行压缩的压缩率在任何的轨迹规模下都基本高于另外3种算法, 说明本文算法所提取的轨迹拐点精度较高, 能用更少的轨迹点保留相当的轨迹方向信息.

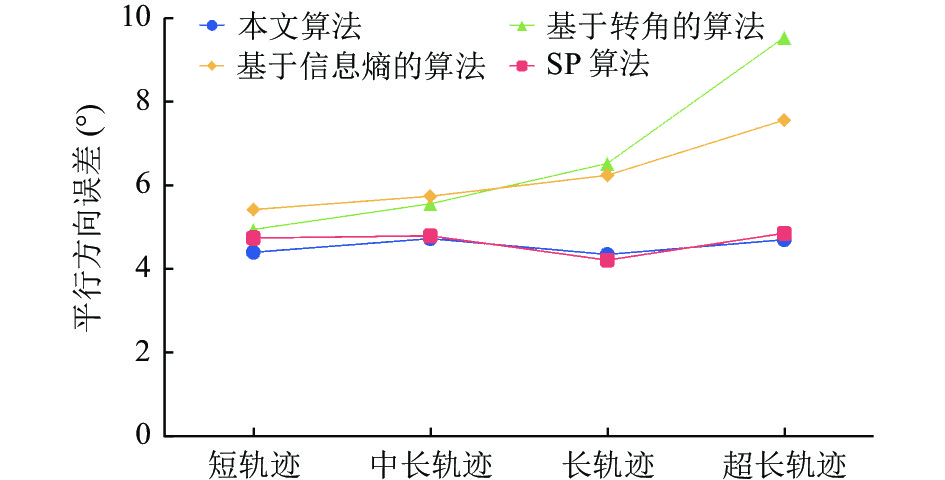
如图6所示, 对4种算法在同一压缩率水平下的方向误差进行了对比. 整体来看, 基于转角的算法和基于信息熵的算法所产生的方向误差都随着轨迹规模的增大而提高; 而SP算法和本文算法产生的方向误差变化较为稳定, 基本能保持在5°以下, 也与另外两种算法的差距随着轨迹规模的增大而逐渐明显. 使用本文算法进行压缩产生的方向误差在任何轨迹规模下都基本低于另外3种算法, 这再一次说明本文算法提取的轨迹拐点精度较高, 能用相当的轨迹点保留更多的轨迹方向信息.

综上, 基于转角的算法有着较高的执行效率, 但是压缩效果一般, 因此可应用于对压缩性能要求不高的场景; SP算法在压缩效果上较好, 但是由于其高昂的运行耗时, 仅适用于短轨迹集或中长轨迹集; 基于信息熵的算法在本文的实验中表现不突出, 随着数据集规模的增大, 压缩效果逐渐超过基于转角的算法; 本文算法在压缩效果上基本与SP算法持平, 然而在算法耗时上却比SP算法有着明显优势, 且本文算法无需额外的输入参数, 能够根据轨迹自身的特点自适应识别轨迹拐点并压缩, 因此适用于更多的轨迹压缩场景.

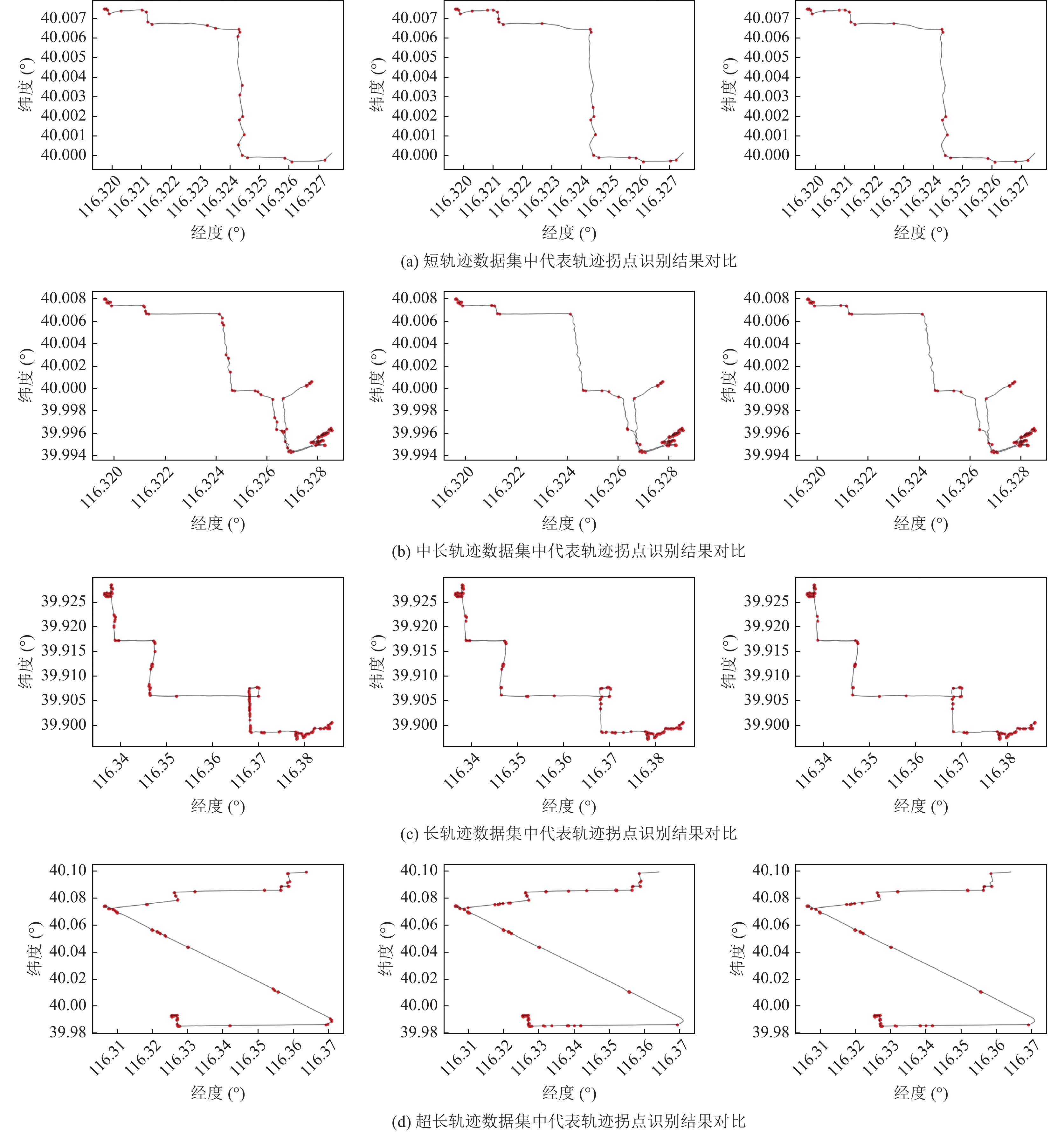
3.4 自适应的轨迹拐点识别结果分析

为证明本文所提算法对于轨迹方向特征点识别的有效性, 分别可视化呈现了短轨迹数据集、中长轨迹数据集、长轨迹数据集和超长轨迹数据集中的一条代表轨迹的拐点识别结果, 每条轨迹的点数分别为77、494、1283和2619, 并再一次将文献[17]中使用的基于轨迹转角的方向特征提取算法(不考虑速度特征)作为对比算法进行实验分析, 该算法需要两个参数分别为转角阈值和累积转角阈值, 结果如图7所示, 每一行为一条代表轨迹, 从左到右依次为本文算法、基于转角的算法(取较小阈值)和基于转角的算法(取较大阈值)对应的结果; 算法的有关度量指标如表2所示.

综合分析图7和表2所示的结果, 以短轨迹数据集中的一条代表轨迹为例, 使用本文算法可以在保证平均方向误差为3.9°的同时, 达到64.0%的压缩率; 使用基于转角的算法(取较小阈值)得到了更低的压缩率, 保留了更多的轨迹点, 但是产生的平均方向误差却高于本文算法的结果, 为5.2°, 说明算法识别出的轨迹拐点有部分是冗余的, 且同时存在遗漏部分重要拐点的情况; 使用基于转角的算法(取较大阈值)得到了更高的压缩率, 不存在明显的冗余拐点识别, 却也遗漏了轨迹中部分重要的轨迹拐点, 因此平均方向误差也相对较高, 为5.3°. 通过分析, 对于基于转角的算法而言, 继续调小阈值能够将方向误差降至与本文算法相当, 但却会导致更低的压缩率, 减少压缩的程度. 所以, 这也能再次说明本文算法识别轨迹拐点的准确性.

本文算法能够识别出较为准确的轨迹拐点, 没有明显的拐点遗漏或是识别过多冗余拐点的情况, 能够在保持较高压缩率的同时产生较少的方向误差. 而文献[17]方法的拐点识别结果受阈值影响较大, 对于同一条轨迹而言, 取不同的阈值可能会出现遗漏某些关键拐点或是识别出许多不具有代表性的拐点的情况, 从而导致不准确的拐点提取结果. 且对于不同的轨迹, 需要选择不同的阈值才能分别实现较好的拐点识别效果, 在实际应用中, 由于轨迹数据集海量的特点, 几乎不可能以人为的方式为不同的轨迹设置不同的参数阈值, 通常只能为完整的轨迹数据集确定一个相对不错的阈值, 这也将导致部分轨迹的压缩效果较好而另一部分轨迹的压缩效果较差的情况.

大多需要进行人为干预选择参数的轨迹压缩算法都存在上述类似问题, 而本文所提出的自适应轨迹拐点提取压缩算法却很好地解决了这个问题, 能够根据轨迹自身的特点, 自适应地在合适的位置识别出轨迹拐点, 且识别的结果较准确, 得到了较好的压缩效果.

4 结束语

本文针对基于方向特征的移动对象原始轨迹压缩问题, 融合特征聚类和轨迹划分的思想研发了一种自适应的轨迹拐点提取压缩算法. 算法从每条轨迹的全局方向特征和局部方向特征出发, 能够根据每条轨迹不同的方向变化情况, 进行自适应的拐点识别, 多数情况轨迹拐点识别的效果也较为准确. 本文算法具有自适应和高精度拐点识别的优势, 在其他轨迹压缩场景之下仍有着较高的参考价值, 本文算法也可应用于轨迹划分工作.