2. 成都西图科技有限公司, 成都 610024
2. Chengdu Xitu Technology Co. Ltd., Chengdu 610024, China
目前地质科研人员主要根据岩石薄片显微图像[1]对岩石的岩性[2]进行判断, 但在利用显微镜对岩石薄片进行成像的过程中, 视野大小和物镜倍数成反比, 利用显微镜只能观察到岩石图像的微小区域, 不利于研究人员对岩石整体性能的探究. 所以将多张单视域的岩石显微图像拼接成一张全幅面的岩石显微图像尤为重要, 能够帮助研究人员从更宏观的角度对整张薄片进行研究和保存, 极大地推进了标本薄片的数字化进程[3].
特征提取是图像拼接的关键组成部分, 从1977年至今一系列特征点提取算法相继被提出, 例如1977年著名的Moravec角点检测算法[4]问世, 之后尺度不变特征变换(scale invariant feature transform, SIFT)[5]和加速稳健特征(speeded up robust features, SURF)[6]被提出, 但是SIFT算法在提取特征点时速度慢并且鲁棒性差, 在构建线性空间时丢失了大量的图像细节[7], 陈敏等[8]对SIFT和SURF特征提取算法进行了对比, 发现针对待匹配图像之间旋转变形不大的情况, SURF算法的配准准确度更高, 所以针对图像之间旋转角度不大的图像, 通常采用SURF算法进行特征点的提取.
图像拼接技术研究多见于无人机影像[9]和遥感图像领域[10]. 曹南等[11]利用SURF算法进行遥感影像配准, 并利用GPU对SURF算法进行优化, 实现准确匹配并且提高了匹配速度. 张二磊等[12]将改进的SURF算法应用到遥感图像的配准中, 在原描述算子中加入特征点色彩信息, 提高了配准的准确性和稳定性. 王森等[13]利用SURF算法对现场概貌进行配准, 通过随机抽样一致(random sample consensus, RANSAC)算法筛选出正确匹配点, 提高配准准确率, 获取到完整的现场概貌图. 徐全飞等[14]利用SURF算法和矩阵乘法完成超大规模的遥感全景图像拼接, 在宏观视野图像中应用良好, 不适用于精度级别高的显微图像, 柴政等[15] 改进SURF算法对显微图像进行拼接, 拼接效果较好, 但是当拼接图像数量较多时, 会产生累计误差, 使得拼接错位.
利用SURF算法进行岩石显微图像的全幅面图像拼接时, 由于大部分岩石图像内容丰富并且包含大量的相似易混淆区域, 使得错误匹配点较多, 拼接不准确, 并且有些薄片的边缘图像内容稀疏, 使用此方式无法完成全幅面图像的配准. 针对此问题提出基于SR-SURF算法的岩石显微图像拼接方法, 利用此方法在进行全幅面图像的拼接时, 拼接准确率高, 耗时较短, 能解决多幅图像拼接时产生的错位现象, 在工程中能得到较好的拼接结果.
1 岩石显微图像采集通过分析显微镜的特性得出先验知识: 岩石显微图像的拼接方法与显微镜采集图像的方式有密切的关系, 显微镜载物台的移动方式决定了采集顺序, 在岩石薄片全幅面显微图像采集过程中, 载物台的移动路径为S形路径, 如图1所示, 从岩石薄片的起点运动到岩石薄片的终点, 载物台的移动方向只存在水平方向和垂直方向, 并且得到的每幅图像存在空间上的重叠, 由此得出拼接路径.

|
图 1 扫描方式 |
在采集过程中, 理想情况下相邻岩石显微图像之间只存在水平方向或者垂直方向偏移. 但在实际采集过程中, 由于相机和载物台之间不可能绝对平行, 当载物台移动时显微镜采集的每幅图像都会产生x和y方向的偏移, 如图2所示, 其中d表示显微镜载物台水平方向的移动距离, h表示显微镜载物台垂直方向的移动距离.
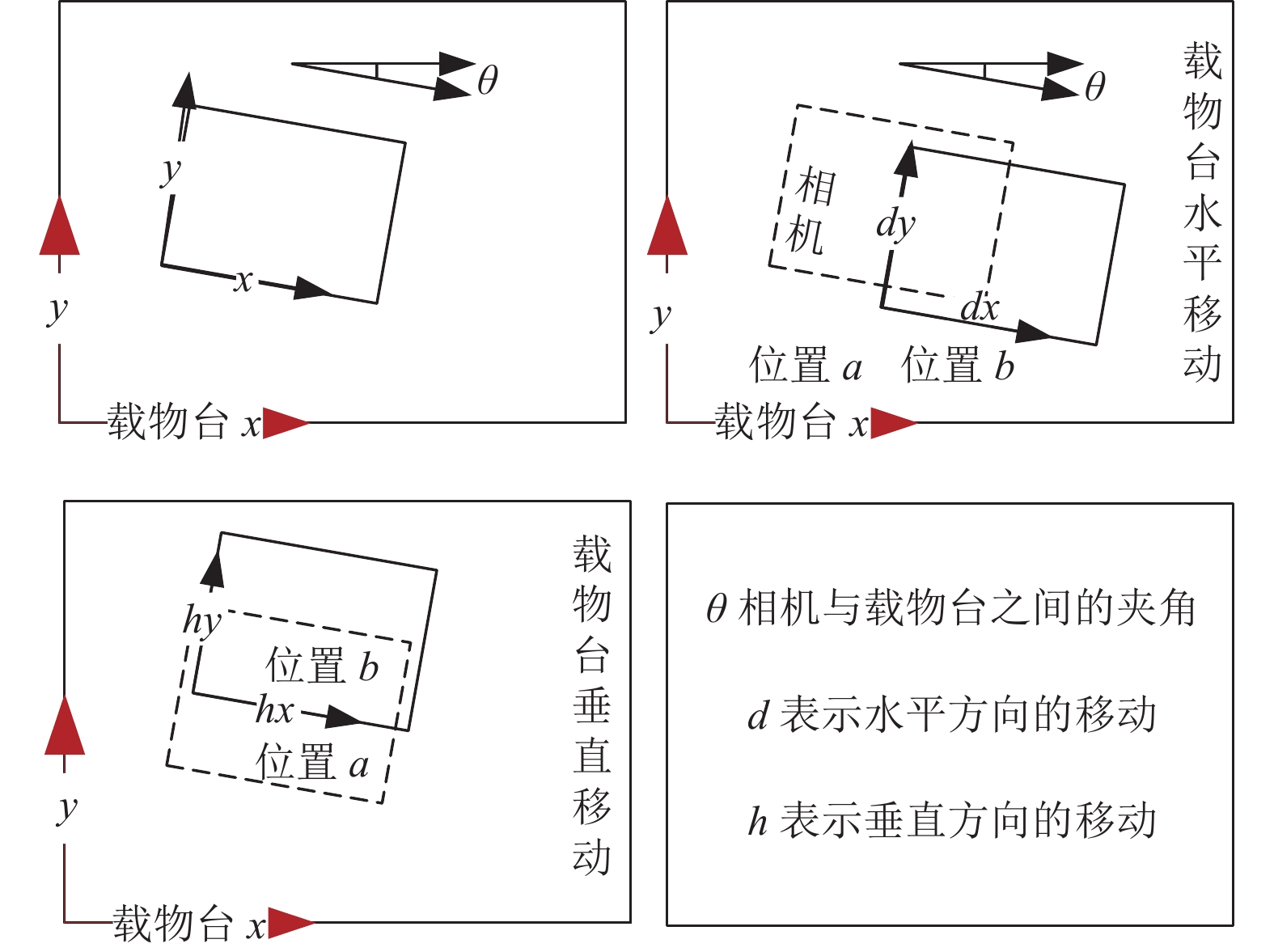
|
图 2 载物台与相机坐标系 |
地质科研人员需要在高倍镜下观察岩石图像, 显微镜载物台在移动过程中, 由于电机齿轮转动等原因会产生机械误差, 相邻视域的位移量并不固定值, 存在偏差.
载物台
x的距离偏差会在
| D(dx,vx)={x|dx−vx<x<dx+vx} | (1) |
y的距离偏差会在
| D(dy,vy)={y|dy−vy<y<dy+vy} | (2) |
其中,
本文提出的岩石显微图像拼接流程如图3所示, 输入图像为利用显微镜采集一张岩石薄片得到的序列图像, 首先对图像进行等宽度定步长分割, 利用哈希指纹提取相似区域, 提高特征点提取速度和匹配准确率、减少多幅图像拼接时计算机的资源消耗, 然后使用改进的RANSAC算法剔除错误匹配点, 针对错误匹配图像引入最佳模板进行纠正, 再然后利用最小二乘法消除单应性矩阵累计相乘产生的累计误差, 最后利用渐入渐出法对图像进行融合.
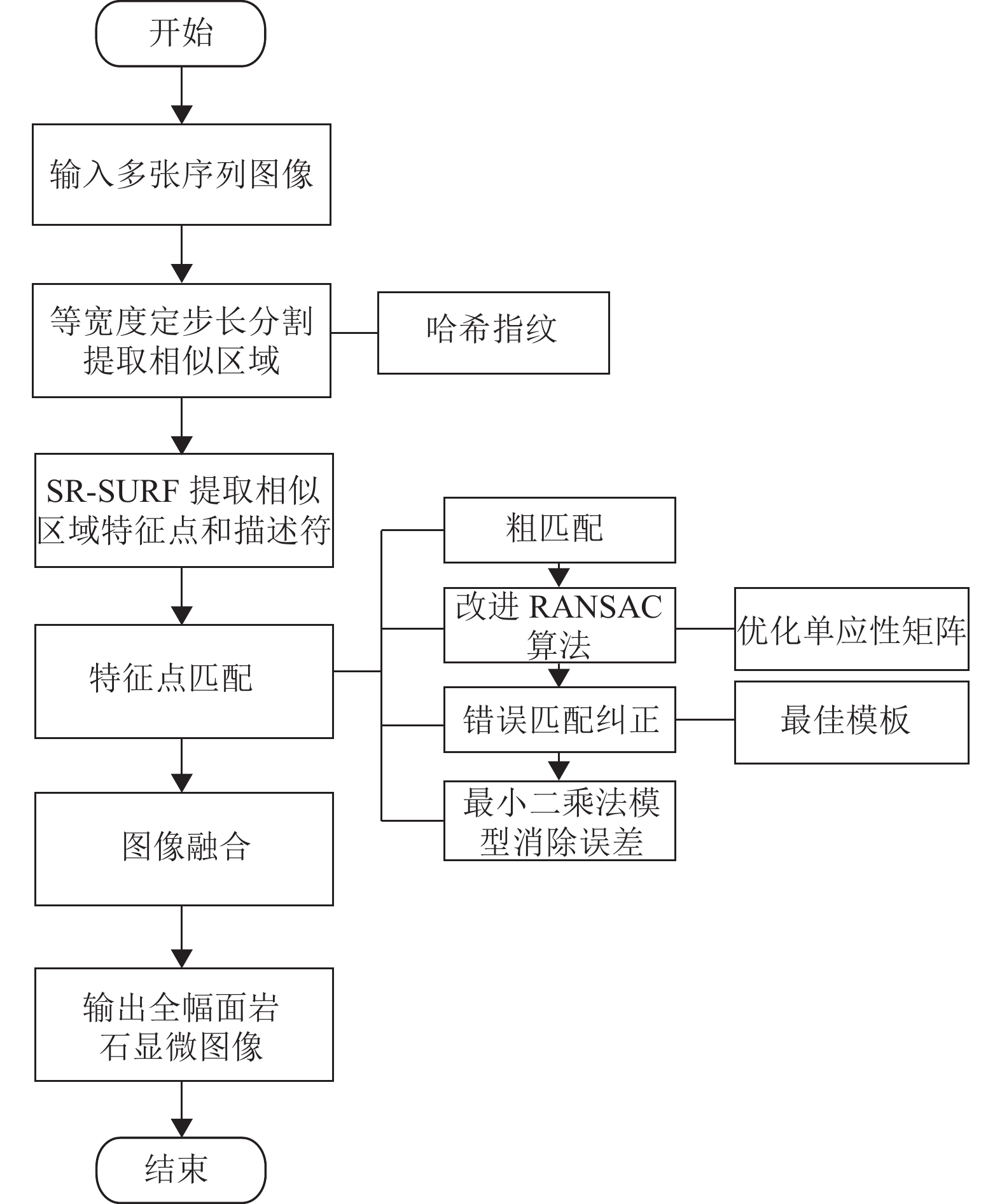
|
图 3 岩石显微图像拼接流程图 |
2.1 SR-SURF算法提取特征点
在图像的拼接中, 拼接图像的大小会影响匹配特征性能, 所以本文选择寻找最佳相似区域, 利用该区域进行特征提取可以提高有效特征点的数量, 为本文提高匹配点的正确匹配率奠定了基础, 本文是对多幅岩石显微图像进行拼接, 耗费大量的计算机资源, 仅利用相似区域进行特征点的提取与匹配, 减少了资源的消耗. 本文选用哈希算法[16]对岩石显微图像进行编码生成哈希指纹, 从而提取岩石显微图像的相似区域.
基准图像为左侧(上侧)图像, 待匹配图像为右侧(下侧)图像, 通过等宽度定步长移位来获取两张图像的相似区域, 如图4所示, 左侧的目标相似区域初始宽度为n, 其中n为图像宽度的1/4; 待匹配图像的目标相似区域则选择左侧的n区域; W为图像的大致相似区域, 当左侧的n区域到达W时, 随着移位的不断增加, 两侧n区域的相似度将降低, 通过该规律来获取最佳相似区域. 将左侧图像以n为区域宽度, 步长为1/32不断对左侧图像进行等宽度定步长分割, 生成左侧图像目标n区域的哈希指纹, 计算此指纹和待匹配图像相似区域的哈希指纹之间的汉明距离, 找到距离的极小值时, 此区域即为匹配图像的相似区域.
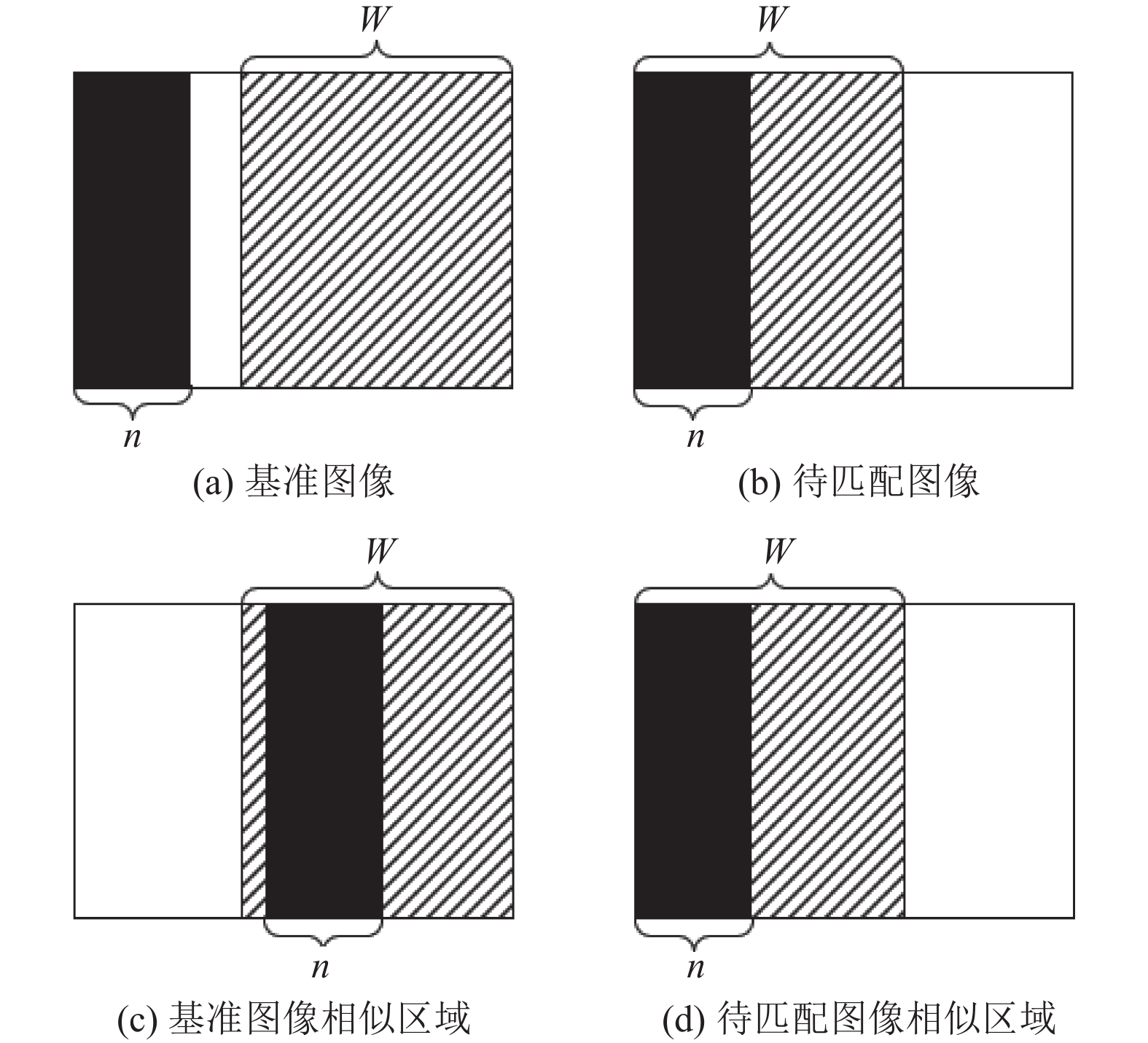
|
图 4 相似区域 |
SURF算法是对整个图像进行特征点的提取, 而本文的SR-SURF则利用等宽度定步长分割方法, 并且引入哈希指纹提取最佳相似区域, 对此区域进行特征点提取, 提高了匹配准确率和匹配速度、解决了多幅图像拼接时, 计算机资源受限的问题.
2.2 RASNSAC算法改进RANSAC算法的主要思想是从给定的数据集合中, 找出最佳的符合数据集合的模型, 其中将内点定义为符合模型的数据, 将外点定义为不符合模型的数据. 计算步骤如下: 首先随机选取4组数据, 代入公式求得符合此数据的参数模型Q, 在给定的数据集中求得数据与参数模型Q的误差, 如果误差小于所设定的阈值, 则认为此数据为内点, 否则此数据被认为外点, 内点数量最多的模型就是最佳模型.
由于RANSAC算法是通过随机抽取样本点进行不断的迭代求得的单应性矩阵H, 如式(3)所示, 该矩阵由8个参数和一个常数组成.
| [ˆxˆy1]=[m0m1m2m3m4m5m6m71][xy1]=H[xy1] | (3) |
其中,
求解该单应性矩阵, 需要随机抽取4对匹配点进行计算, 由先验知识可知, 图像仅存在x, y方向的平移变换, 为减少模型的参数量, 对
| [ˆxˆy]=[tx00ty][xy]=Ht[xy] | (4) |
其中,
在对岩石薄片的整张图像进行拼接时, 由于有些图像缺少有效内容, 在该图像上提取不到有效特征点, 会导致匹配失败. 在进行全幅面岩石显微图像拼接时, 如果提取的特征点较少, 可能会存在错误匹配情况, 需要对错误匹配进行纠正, 否则将影响最终的拼接结果以及后续的融合, 所以本文提出利用最佳模板[17]对错误匹配进行纠正.
首先在水平方向和垂直方法分别找到拥有最多内点集的岩石显微图像的下标h和v, 水平方向的最佳匹配模板定义为
| n∑i=1|Wi−Wh|+|Wi−Wv|>δ | (5) |
其中,
最后利用
由于单应性矩阵的累计相乘, 在转换过程中会产生累计误差, 在对大量的图像进行拼接时, 会产生错位现象, 本文引入非线性最小二乘法[18]消除累计误差, 根据特征点匹配对的内点, 定义匹配初始向量V1与待匹配结果向量V2, 如式(6)所示:
| V=(m1,n1,m2,n2,⋅⋅⋅,nl,nl) | (6) |
其中, m与n分别是内点的横纵坐标, l是内点的总数量.
定义约束向量V, 如式(7)所示:
| V=V1F−V2 | (7) |
其中, V1为匹配初始向量, V2为待匹配结果向量, 利用非线性最小二乘法更新迭代F, 使得约束向量V足够小, 得到
实验环境如下: Intel(R) Core(TM) i7-4790K CPU @ 4 GHz、32 GB内存, 开发环境为 Visual Studio 2015. 多幅图像拼接时利用多线程进行图像拼接.
3.1 实验结果分析利用显微镜对10张岩石薄片进行图像采集, 共获得3965张图像, 从中随机选取100张岩石显微图像分别使用SIFT算法, SURF算法和本文提出的SR-SURF算法进行特征点的提取与匹配, 从表1中可知针对岩石显微图像的特征提取与匹配, SURF算法比SIFT算法的正确匹配率高并且耗时较少. 利用SR-SURF算法对岩石显微图像进行匹配, 正确匹配率达到了92%, 比SURF算法的正确匹配率提高9%.
| 表 1 算法性能对比 |
在岩石显微图像拼接中, 拼接错位会影响研究人员对岩石薄片的进一步分析研究, 因此拼接后的图像在视觉上的效果是否良好显得尤为重要. 由于部分图像提取不到有效特征点, 所以本文提出利用最佳模板对图像进行匹配纠正; 由于单应性矩阵累积相乘, 会产生累计误差, 会使拼接结果产生不同程度的错位现象, 所以本文通过改进的RANSAC算法求得单应性矩阵之后, 利用模板匹配对错误匹配图像进行纠正, 最后利用最小二乘法消除累计误差. 在未纠正前, 存在错误匹配和误差累积导致拼接后的全幅面岩石显微图像出现大量的错位现象, 如图5(a)和(e)所示, 该结果会影响地质科研人员对岩石类型的分析. 为进一步分析未纠正前的拼接结果存在明显的错位现象, 将全幅面岩石显微图像拼接结果图进行放大, 如图5(c), (d), (g), (h)所示, 从标注区域可以看出SURF拼接方法存在特别明显的错位现象, 而本文方法得到的拼接图像没有发生错位. 由此得出本文的拼接算法匹配准确率高, 拼接后的全幅面岩石显微图像不仅无错位现象, 而且保留了完整的结果图.

|
图 5 拼接结果图像 |
本文选择在不同样本下利用SURF方法以及本文方法对配准错误率和拼接时间进行分析, 配准错误的图片通过最佳模板匹配进行纠正, 如表2所示, 分析了4种样本的实验数据, 每种样本拥有不同的图像数量. 在进行全幅面岩石显微图像拼接时, 在拼接耗时方面, 本文方法耗时较少. 在配准准确率方面, 本文方法在进行全幅面图像拼接时配准错误率远低于SURF算法. 样本1的最终拼接结果图如图5所示, 可以看出本文方法在进行全幅面岩石显微图像拼接时不仅配准准确率高、视觉效果良好而且速度快. 在对上千幅图像进行拼接时, 拼接速度较慢, 采用多线程方式对图片进行特征提取、匹配、融合, 极大地提高了拼接速率, 提高了工程的适用性.
| 表 2 不同样本实验数据对比 |
3.2 工程应用
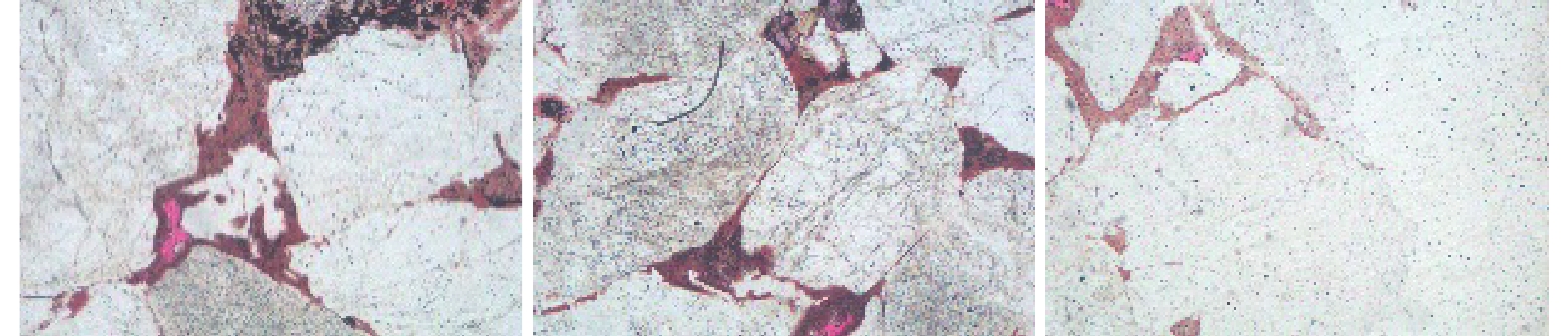
通过显微镜采集得到的岩石显微图像是单视域图像, 只能展现岩石薄片的局部特征, 无法满足地址科研人员的需求. 所以在实际的应用中需要将多张的单幅岩石显微图像拼接成全幅面岩石显微图像. 图6是由180张单视域图像利用SR-SURF算法拼接而成的全幅面岩石显微图像, 尺寸大小为27802×21762. 该图像由15行12列单视域岩石显微图像组成如图7所示, 图7是利用显微镜采集得到的3幅岩石显微单视域图像, 尺寸大小为2736×1824. 实验结果证明本文算法不仅能在实际工程应用中得到较好的结果, 而且仅仅利用相似区域提取特征点, 减少了计算机资源消耗, 提高了拼接速率, 实现了岩石薄片的资源共享, 提高了工程的适用范围.
4 结论与展望针对岩石显微图像拼接存在配准准确率低, 速度慢等问题, 提出拼接多张岩石显微图像的拼接方法, 该方法能快速拼接出能够展示细节的高分辨率的全幅面图像. 创新之处在于利用SR-SURF算法提取特征点, 耗时较少, 减少了计算机资源的消耗; 之后通过改进的RANSAC算法筛选出正确匹配点, 利用最佳模板纠正错误匹配图像, 并且引入最小二乘法消除累计误差, 提高拼接准确率. 试验结果表明: 本文方法的拼接结果图像质量较好, 准确率高, 拼接速度快, 能够有效帮助地质科研人员对岩石的探索, 推动了岩石显微图像的数字化进程, 目前已在部分地质部门生产应用, 效果较好. 针对多张岩石显微图像的拼接, 拼接速度尤为重要, 在进行多幅图像拼接时, 可以利用GPU提取图像特征点进一步加快拼接速度.
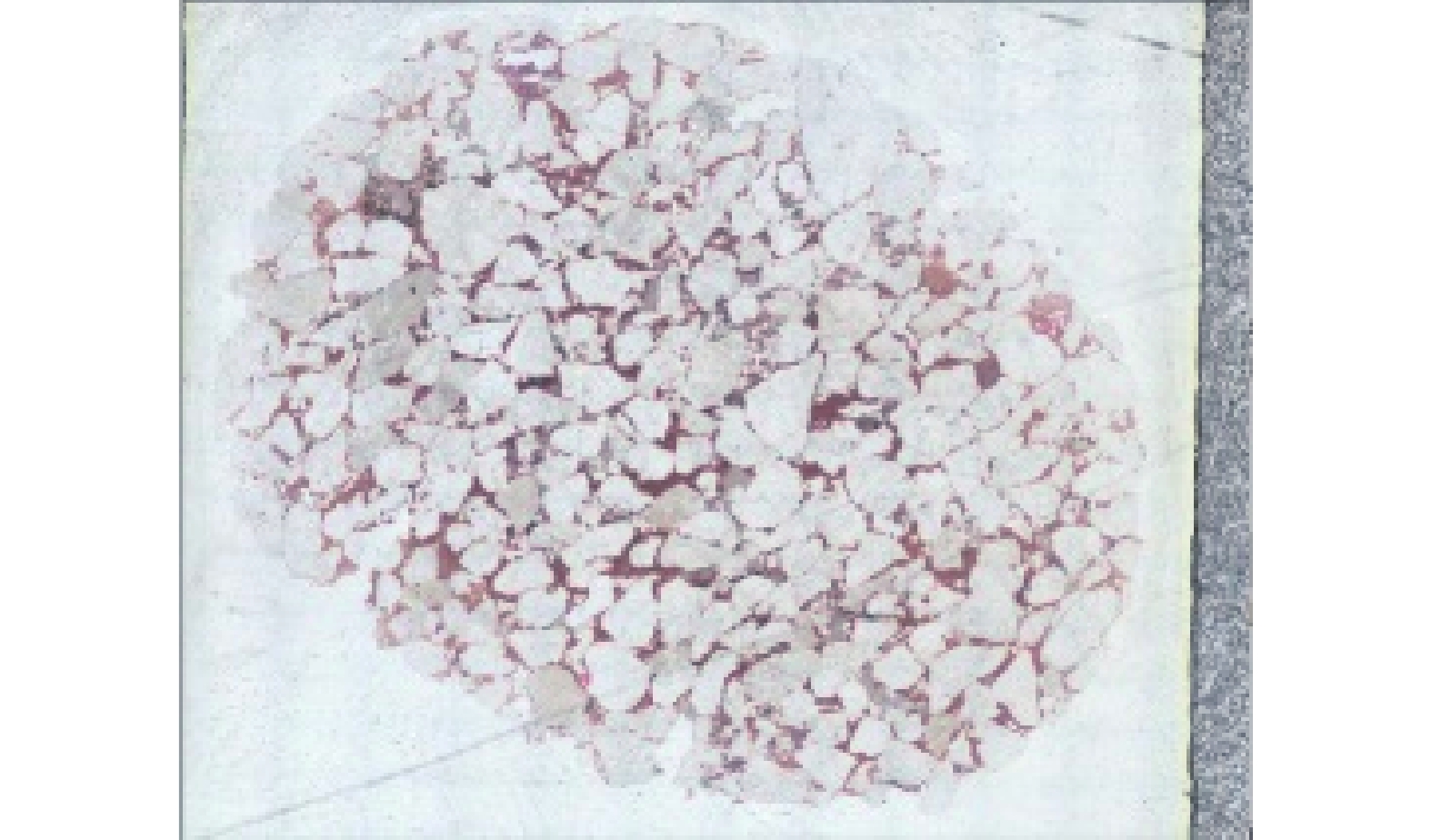
|
图 6 全幅面岩石显微图像 |
|
图 7 单幅岩石显微图像 |
| [1] |
苏程, 朱孔阳. 岩石薄片图像智能分析研究进展. 矿物岩石地球化学通报, 2023, 42(1): 13-25. |
| [2] |
王琼, 杨杰, 霍凤财, 等. 基于MobileViT的岩石薄片图像岩性识别方法研究. 地质通报, 2023, 23(2): 1-11. |
| [3] |
刘向东, 王增祥. 关于新时代实物地质资料科普发展的思考——以自然资源实物地质资料中心为例. 地质论评, 2021, 67(1): 180-184. |
| [4] |
Lowe DG. Object recognition from local scale-invariant features. Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra: IEEE, 1999. 1150–1157.
|
| [5] |
Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [6] |
Bay H, Tuytelaars T, van Gool L. SURF: Speeded up robust features. Proceedings of the 9th European Conference on Computer Vision. Graz: Springer, 2006. 404–417.
|
| [7] |
Li Y, Wang JL, Yao KN. Modified phase correlation algorithm for image registration based on pyramid. Alexandria Engineering Journal, 2022, 61(1): 709-718. DOI:10.1016/j.aej.2021.05.004 |
| [8] |
陈敏, 汤晓安. SIFT与SURF特征提取算法在图像匹配中的应用对比研究. 现代电子技术, 2018, 41(7): 41-44. |
| [9] |
江智, 江德港, 黄子杰, 等. 基于IB-SURF算法的无人机图像拼接技术研究. 计算机工程与应用, 2023, 23(2): 1-10. |
| [10] |
Gao XQ, Yang F, Fan HR, et al. Remote sensing image S-type fusion/stitching via low-error matching strategy. Laser & Optoelectronics Progress, 2019, 56(21): 211005. |
| [11] |
曹南, 蔡扬扬, 李旭洋, 等. 高分辨率遥感影像特征点自动化匹配方法研究. 地理空间信息, 2022, 20(11): 9-13. |
| [12] |
张二磊, 马骏, 王晓田. 一种改进的SURF彩色遥感图像配准算法. 液晶与显示, 2017, 32(2): 144-152. |
| [13] |
王森, 李俊瑶, 肖洋洋, 等. 基于SURF算法的现场概貌图像拼接技术分析. 电子技术, 2022, 51(5): 36-37. |
| [14] |
徐全飞, 冯旗. 基于SURF和矩阵乘法的超大规模遥感图像亚像素配准算法研究. 红外技术, 2017, 39(1): 44-52. |
| [15] |
柴政, 刘任任, 梁光明. 基于机械扫描与改进SURF的显微图像拼接算法. 计算机技术与发展, 2019, 29(11): 97-101. |
| [16] |
霍德璐, 袁超, 李佳龙. 基于特征点相对位置的指纹图像感知哈希算法. 工业控制计算机, 2022, 35(3): 52-53, 85. |
| [17] |
张鹏宇, 申亮, 黄晓涛, 等. 基于对称结构特征的探地雷达图像模板匹配算法. 地球物理学进展, 2022, 37(6): 2657-2666. |
| [18] |
兰猗令, 康传利, 王宁, 等. 附加增值条件的移动最小二乘法的点云孔洞修补. 红外与激光工程, 2023, 52(2): 20220390. |
 2023, Vol. 32
2023, Vol. 32



