2. 上海海事大学 物流工程学院, 上海 201306
2. Logistics Engineering College, Shanghai Maritime University, Shanghai 201306, China
教与学优化算法(teaching-learning-based optimization, TLBO)[1,2]是一种简单且高效的新型智能优化算法. 该算法是根据班级中教师传递知识给学生以及学生间学习来进行模拟的. 由于该算法有比较容易实现、控制参数少等优点, 已经吸引了诸多学者去进行更深入的研究. 该算法也已经被应用解决了很多实际的问题. 比如求解非合作博弈纳什均衡问题[3]、定向过流继电器的调度优化问题[4]、拥堵管理的实际发电问题[5]、变压器故障诊断准确性优化问题[6]等.
对于智能优化算法来讲, 大的种群规模可以使其具有好的种群多样性; 但对硬件有一定的要求. 针对该问题, 部分学者提出诸多基于微种群的进化算法. 比如, Ren等[7]提出一种基于小种群的差分进化算法. 该算法提出了改进的变异策略; 根据进化情况, 自适应的调整扰动的强度, 实现了对局部开发和全局探索的平衡. 实验结果对比表明, 在减少种群规模的情况下, 所提算法依然能保持种群的多样性, 且比差分进化算法有更好的寻优能力. Cabrera等[8]提出了一种基于小种群的多目标粒子群优化算法, 该算法通过重新初始化和使用两个外部存档信息来保持种群的多样性, 另外加入了变异算子来提高算法的探索能力. 实验结果表明, 与 NSGA-II相比, 该算法能够提供更好的解. Olguin-Carbajal等[9]提出了光线搜索的微差分进化算法. 该算法将线性搜索方法用到小种群的差分进化算法中, 用来解决一组新的复杂函数, 结果表明, 所提算法在解决复杂函数时能够获得比线性进化策略更好的性能. 范勤勤等[10]提出了基于反向学习的微种群教与优化算法. 该算法利用了小种群优势, 同时还在“教”阶段加入反向学习生成新的个体来引导种群进化, 提高算法的全局探索能力. 实验表明, 所提算法具有较快的收敛速度和较好的寻优能力. 王筱薇等[11]提出一种基于基因水平多样性的微种群教与学优化算法. 利用基因层面上对种群多样性测量结果, 选择合适的扰动策略以增加种群的多样性, 仿真结果表明, 所提算法与其他8种智能优化算法相比, 其整体的性能更优.
对于微种群进化算法的种群多样性容易变差的问题, 虽提出诸多性能优良的算法, 但很多是从个体层面的多样性研究. 此外, 每个决策变量(即基因水平)在种群中的多样性表现是不一样的. 即, 个体水平的多样性并不能反映整个种群的多样性. 其主要理由是若存在决策变量过早收敛, 会对个体进化产生不利[11]. 因此, 对于微种群进化算法必须考虑基因水平的多样性. 基于文献[11], 本文提出一种基于多源基因学习的微种群教与学优化算法 (micro-population teaching-learning-based optimization based on multi-source gene learning, MTLBO-MGL). 在所提算法中, 首先对教与学优化算法进行改进, 提出了随机选择“教”或“学”阶段的策略, 并在随机选择“教”或“学”阶段之后使用改进的交叉策略. 然后, 从基因层面对多样性检测和使用稀疏谱聚类方法对种群的每个决策变量进行聚类; 并根据多样性检测和聚类结果, 选择不同的进化策略来提高搜索性能. 最后, 在CEC2013标准测试集上, 将所提的算法与其他4种优化算法作比较, 证明了所提算法的有效性.
1 预备知识 1.1 标准教与学优化算法标准的教与学优化算法[1,2]主要包括老师教学的阶段和学生班级内交流学习的阶段, 算法详细过程如下.
1.1.1 教学过程在该阶段, 算法把最好个体作为教师; 使学生向老师的水平靠近. 更新公式如下[1,2]:
| Xnew=Xold+r×(XT−TF×XM) | (1) |
其中, r是[0, 1]范围内的均匀随机数, XT (即教师)是种群中适应度值最好的个体, TF = round(1+r(0, 1))是教学因子, 它的取值为1或2, XM是所有个体的平均值. 若Xnew优于其父代个体, 则选择Xnew; 反之, 保留父代个体.
1.1.2 学习过程学习阶段主要是学生课下与同学相互学习来提高自己. 该阶段个体具体的更新公式如下[1, 2]:
| Xnew={Xold+r×(Xold−Xl),iff(Xold)<f(Xl)Xold+r×(Xl−Xold),else | (2) |
其中, old≠l, old,l∈(1, 2, …, NP). 若Xnew优于其父代个体, 则选择Xnew; 反之, 保留父代个体.
1.1.3 TLBO算法实现步骤TLBO算法的主要步骤如下.
1) 初始化种群, 设置种群大小NP和最大迭代次数.
2) 教学阶段: 由式(1)对每个个体更新, 之后对个体选择.
3) 学习阶段: 由式(2)对每个个体更新, 之后对个体选择.
4) 判定程序是否达到终止条件, 若没有达到, 则转至步骤2); 否则, 输出结果.
1.2 稀疏谱聚类算法谱聚类[12]是由图论的知识所演化出的聚类方法, 它利用样本数据的拉普拉斯矩阵的特征向量对其聚类. 由于它实现简单, 对数据的分布适应性更强, 所以其聚类效果往往比传统聚类方法(比如K-means算法[13])好. 稀疏谱聚类算法的步骤描述如算法1所示[14].
算法1. 稀疏谱聚类算法
输入: n个样本点X={x1, x2, …, xn}和聚类簇数K.
输出: 聚类簇C1, C2, …, Ck.
(1)计算由Sab组成的n×n的相似矩阵W, Sab由式(3)可得:
| Sab=exp{−‖xa−xb‖22σ2} | (3) |
其中,
(2)计算标准化拉普拉斯矩阵L, 如式(4)所示:
| L=D−12LD−12 | (4) |
其中, D是对角矩阵:
| Daa=∑nb=1Wab | (5) |
(3)计算标准化拉普拉斯矩阵的特征值, 取其前k个最小值, 并计算其对应的特征向量v1, v2, …, vk.
(4)将各自对应的特征向量v组成矩阵, 最终组成n×k维的特征矩阵V;
(5) V中的每一行是一个k维的样本, 使用K-means算法将这个n样本聚类成簇C1, C2, …, Ck;
(6)输出簇C1, C2, …, Ck;
2 基于多源基因学习的微种群教与学优化算法小的种群规模容易使得优化算法出现“早熟收敛”情况, 因此, 如何保持种群多样性对于MTLBO算法来讲显得十分重要. 现有大多研究是从个体水平进行的, 但根据文献[11]的研究, 提出一种MTLBO-MGL算法. 此外, 根据文献[15], 采用了随机选择“教”或“学”阶段的策略, 并在随机选择“教”或“学”阶段之后引入了改进的交叉机制.
2.1 改进的教与学优化算法根据文献[15], 首先, 在MTLBO-MGL算法中提出“教”和“学”随机选择的策略. 每代只能选择一个过程发挥对应的搜索功能. 并在随机选择“教”或者“学”阶段之后, 引入一种改进的交叉策略.
2.1.1 教阶段在原始TLBO算法的教阶段, 由于所有个体被引导向最优个体收敛, 为了避免算法陷入局部最优. 在基因水平上, 引进一种改进的交叉策略, 将“教”过程好的局部搜索能力与差分进化算法好的全局搜索能力相结合. 该方法确保了算法的收敛能力, 同时还维持了种群多样性. 如式(6)所示:
| Xnew,j={Xold,j+r×(XT,j−TF×XM,j),ifrand⩽0.5Xr1,j+r×(Xbest,j−Xold,j)+r×(Xr2,j−Xr3,j),else | (6) |
其中, Xbest是种群中适应度值最小的个体, r1≠r2≠r3≠old∈(1, 2, …, NP).
2.1.2 学阶段在教与学优化算法的学阶段, 每个个体只能在班级中任意选择一个同学课下彼此交流学习, 并没有充分利用其他个体的信息. 通过上述改进的交叉策略, 混合部分基因来保持种群的多样性. 具体过程如式(7)所示:
| Xnew,j={Fnew,j,ifrand⩽0.5Xri,j+r×(Xbest,j−Xold,j)+r×(Xr2,j−Xr3,j),else | (7) |
其中,
| Xnew,j={Xold,j+r×(Xold,j−Xl,j),iff(Xold)⩽f(Xl)Xold,j+r×(Xl,j−Xold,j),else | (8) |
鉴于文献[16]的研究, 利用方差来监测种群基因水平的多样性, 具体公式如下:
| md,G=1NP∑NPi=1(xGi,d) | (9) |
| sdd,G=√1NP∑NPi=1(xGi,d−mGd) | (10) |
其中, md,G和sdd,G分别表示第G代种群第d维度的均值和标准差.
一般来说, 元启发式算法在进化过程中种群多样性会逐渐减少. 如果当某个变量的标准差为0时, 那么说明这个变量的多样性已完全丢失. 此外, 研究表明: 标准差降为0需要很长的时间[17]. 由式(11)可知, Οd,G会逐渐变小, 因此用Οd,G来识别种群中基因水平的多样性情况, 并设Οd,G的最小值为10−5. 采取每5代进行1次多样性检测.
| Od,G=(1−D×FESMaxFES)×zGd | (11) |
其中,
| zGd=max | (12) |
根据文献[17], 基于随机游走的拉普拉斯矩阵的谱聚类方法对每个决策变量进行聚类. 根据基因水平的多样性监测结果, 当决策变量的多样性好时, 利用同类的基因可以加快算法的收敛速度; 当决策变量的多样性差时, 利用邻近类或者存档中的外部基因可以提高种群的多样性. 具体操作如下.
(1)若sdd,G<Οd,G, 则认为第d个决策变量多样性差. 采用DE中“DE/rand/1”的变异策略(如式(13))来对每个基因进行进化操作. 不同于原有的变异策略, 所提算法使用类外基因来进行扰动.
(2)若sdd,G≥Οd,G, 则认为其对应的第d个变量多样性较好. 同样采用式(13)的策略, 从相同类的基因中随机选择基因来进行更新. 当同类的基因少于3个时, 则从其对应的整个变量中选取部分基因进行更新. 以加速算法收敛, 同时能够维持种群的多样性, 提高解的质量.
| X_{ {new }}=X_{ {old }}+r \times \left(X_{s 1}-X_{s 2}\right) | (13) |
其中, s1≠s2≠s3≠old
1)初始化种群: 设置种群大小NP、最大评价次数、聚类数K、参数σ.
2)如果rand1≤rand2, 选择教阶段, 根据式(6)对个体进行更新, 并对个体进行选择; 否则, 选择学阶段, 根据式(7)对个体进行更新, 并对个体进行选择.
3)每隔5代, 根据式(10)对种群基于基因水平进行多样性检测, 并利用稀疏谱聚类对种群的每个决策变量聚类.
4)根据式(11)计算第d个变量的Οd,G值, 然后根据其标准差与Οd,G的大小进行以下扰动.
a)若sdd,G<Οd,G, 则认为该变量的多样性较差, 则采用式(13), 从与其不同类中的基因中随机选择部分基因进行更新. 当不同类的基因少于3个时, 则从不同类和存档个体中随机选取部分基因来进行更新, 如果新生成的维度超出预设范围, 则重新生成.
b)反之, 则认为该变量的多样性较好, 同样采用式(13)的策略, 从相同类的基因中随机选择部分基因来进行更新. 当同类的基因少于3个时, 则从其对应的整个变量中随机选取部分基因进行更新.
5)对个体进行选择.
6)判断算法是否满足终止条件, 如果没有达到终止条件, 则跳至步骤2); 如果达到了终止条件, 则输出结果.
3 实验结果与分析为了验证所提算法的有效性, 本实验选取文献[18]中的CEC2013标准测试集. 其中, f1–f5为单模态函数, f6–f20为多模态函数, f21–f28为复合函数.
将所提算法分别与MDEVM[19]、MDE[20]、μJADE[21]及MTLBO-GLD[11]这4种微种群算法对比. 5种算法均独立运行30次. 实验结果利用Friedman[22], Bonferroni-Dunn[23], Holm 和 Hochberg[24]检验深入分析, 验证所提算法的可靠性. 显著性水平设为5%.
3.1 与微种群算法的比较将所提算法与4种微种群算法对比. MDEVM、MDE算法的种群大小是5, 其他算法的种群大小是8. 其他参数设置均与文献[25]相同. 即函数结果精度为1.0E–08, 最大适应度函数评价次数为30000. 所有比较微种群算法所得实验结果见表1. 得到最好平均值用加粗表示.
| 表 1 所有比较微种群算法所得实验结果 |
由表1可知, 与MDEVM算法相比, 所提算法在25个测试函数上优于MDEVM算法. 但在求解f2、f21、f26时, MDEVM的寻优能力要略好于MTLBO-MGL. 与MDE算法相比, 在求解f4、f8、f15、f23时, MDE的寻优能力要略好于MTLBO-MGL. 与μJADE算法相比, 在求解f14、f22时, MTLBO-MGL算法的寻优性能要略差于μJADE算法. 针对以上3个算法, 在求解特定问题时, MTLBO-MGL的寻优能力略差的主要原因可能是: 所提算法虽然对原始教与学算法, 采取了改进的交叉策略, 平衡了算法的全局与局部搜索能力; 根据基于基因水平的多样性监测结果以及聚类结果进行扰动, 可以更好地掌握每个变量的分布情况, 采取更精准的扰动策略来提高种群的多样性, 但DE算法的全局探索能力要优于教与学优化算法. 与MTLBO-GLD算法相比, MTLBO-MGL在求解28个测试函数时, MTLBO-MGL的寻优能力均优于MTLBO-GLD算法. 其主要原因是所提算法首先对原始教与学算法进行了改进, 与基础TLBO算法相比, 平衡了算法的全局与局部搜索能力; 其次, 将基于基因水平的多样性监测结果以及聚类结果从相同类、邻近类或者存档中选择基因并利用变异策略“DE/rand/1”生成新的决策变量. 该部分利用了邻近类以及历史个体信息来提供进化方向的信息.
从以上比较结果可以看出, 所提算法不仅具有良好寻优性能, 而且能够保持种群多样性以提供进化动力.
本文使用Friedman测试方法对几种算法的结果展开进一步分析, 对实验结果的可靠性进行验证. 统计分析结果如表2、表3所示. 由表2可得, MTLBO-MGL算法的整体寻优能力要优于其他几种微种群算法. 由表3可得, 所提算法的寻优能力明显比MDE、μJADE、MTLBO-GLD算法好, 未显著优于MDEVM, 但根据表2可以证明, 所提算法整体寻优能力优于MDEVM.
| 表 2 Friedman 测试在微种群算法上所得排序 |
| 表 3 Friedman 测试在微种群算法上所得排序Bonferroni-Dunn、Holm 和 Hochberg 在微种群算法上所得p值 |
3.2 实验分析 3.2.1 与随机选择的微种群教与学优化的比较
为证明所提算法的有效性, 将其与随机选择的微种群教与学优化(randomly selected micro-population teaching -learning-based optimization algorithm, RSMTLBO)算法(没有对维度聚类)进行性能比较. 参数设置同第3.1节, 结果见表4.
| 表 4 MTLBO-MGL与RSMTLBO算法的实验结果 |
由表4可得, 所提算法在23个测试函数上的寻优结果要优于RSMTLBO算法; 故MTLBO-MGL算法的性能要好于RSMTLBO算法. 其主要原因是MTLBO-MGL算法在基因水平上对种群多样性进行检测, 并使用稀疏谱聚类算法对每个决策变量进行聚类, 可以提高种群多样性. 另外, 使用非参数统计分析对两个算法的均值进行了深入的分析, 统计结果见表5, 由表5可得, 所提MTLBO-MGL算法具有更好的性能. 通过以上分析可以证明, 基于基因水平的多样性检测以及聚类措施可以有效地提高微种群TLBO算法的性能.
| 表 5 Friedman 测试在MTLBO-MGL与RSMTLBO算法上的排序结果 |
3.2.2 间隔代数值敏感性分析
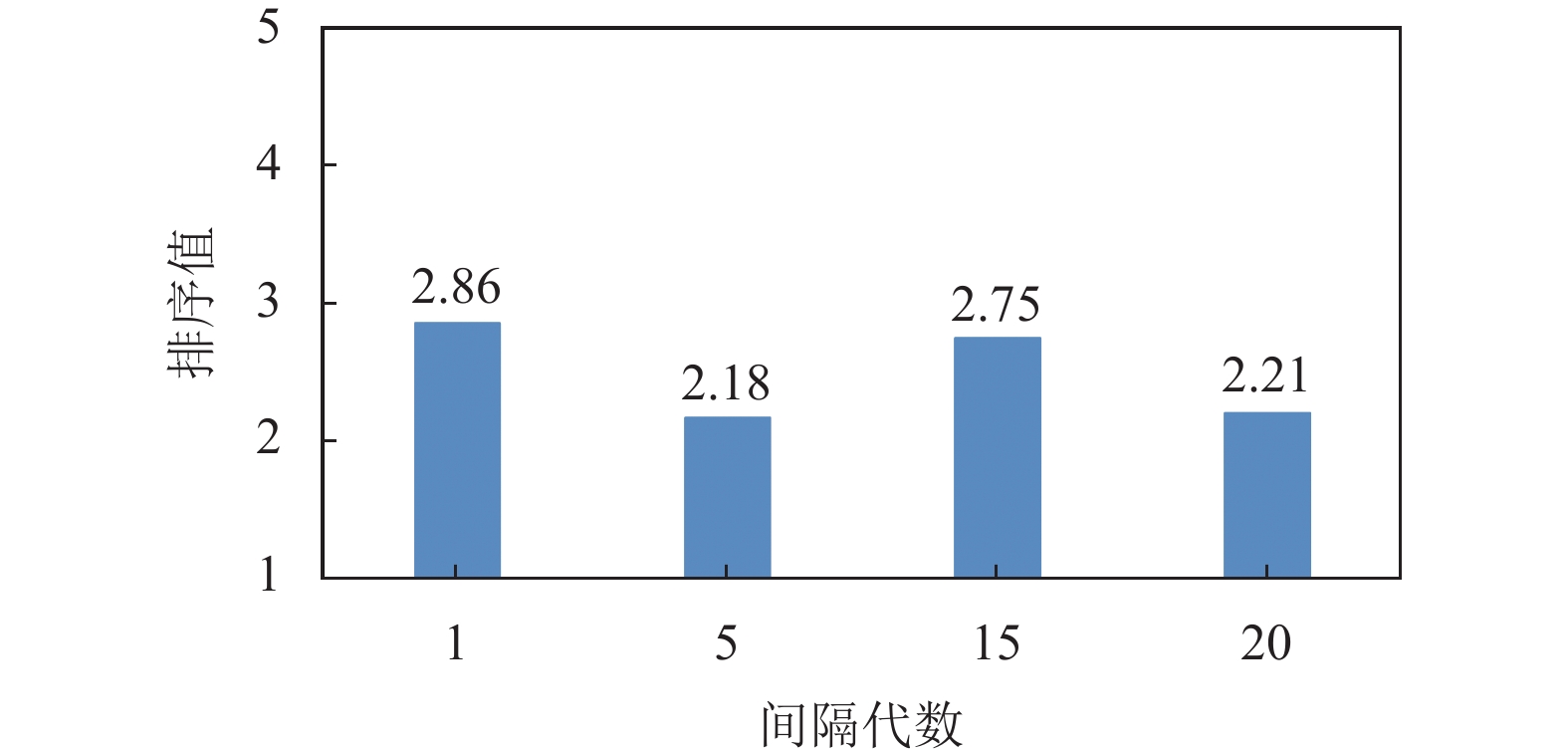
本部分主要是进行间隔代数值敏感度分析. 相关参数设置如下: 种群数量大小是8, 最大迭代次数是30000次, 在CEC2013标准测试集中独立运行30次. 对间隔代数分别在1、5、15、20进行测试, 对比均值的非参数统计分析结果见图1. 由图1可得, 所提算法的整体性能在间隔代数为5时表现最好. 因此, 该算法间隔代数设置为5.
|
图 1 Friedman测试在不同代数间隔下的排序结果 |
3.2.3 聚类数K敏感性分析
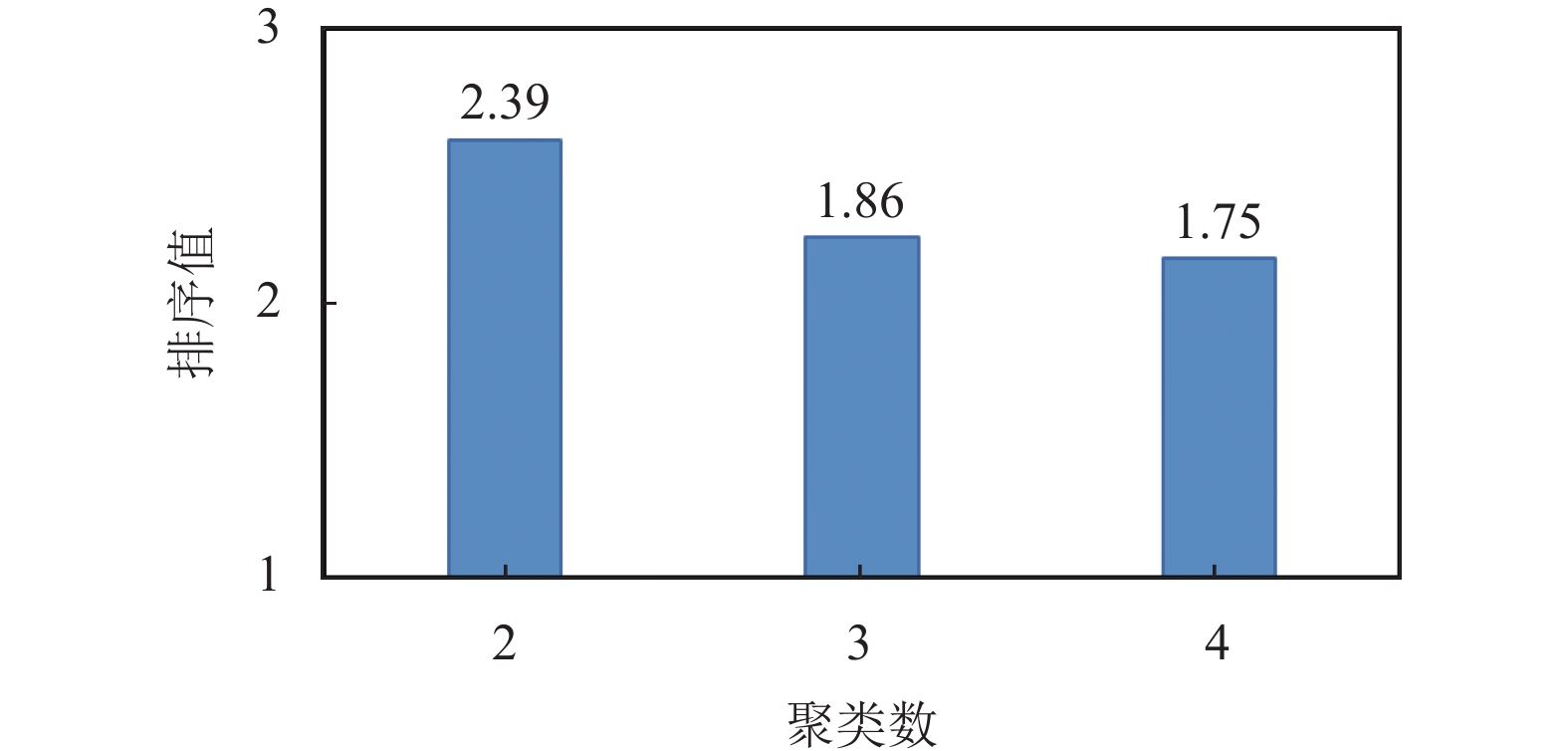
本部分主要是进行聚类数K敏感性分析, 实验参数设置同第3.2.2节. 对聚类数K分别在2、3、4进行测试, 并利用其均值的非参数统计进行分析, 结果见图2. 由图2可知, 聚类数为4时, 所提算法的整体性能表现最好. 因此, 该算法的聚类数设置为4.
|
图 2 Friedman 测试在不同K值的排序结果 |
3.2.4 参数σ敏感性分析
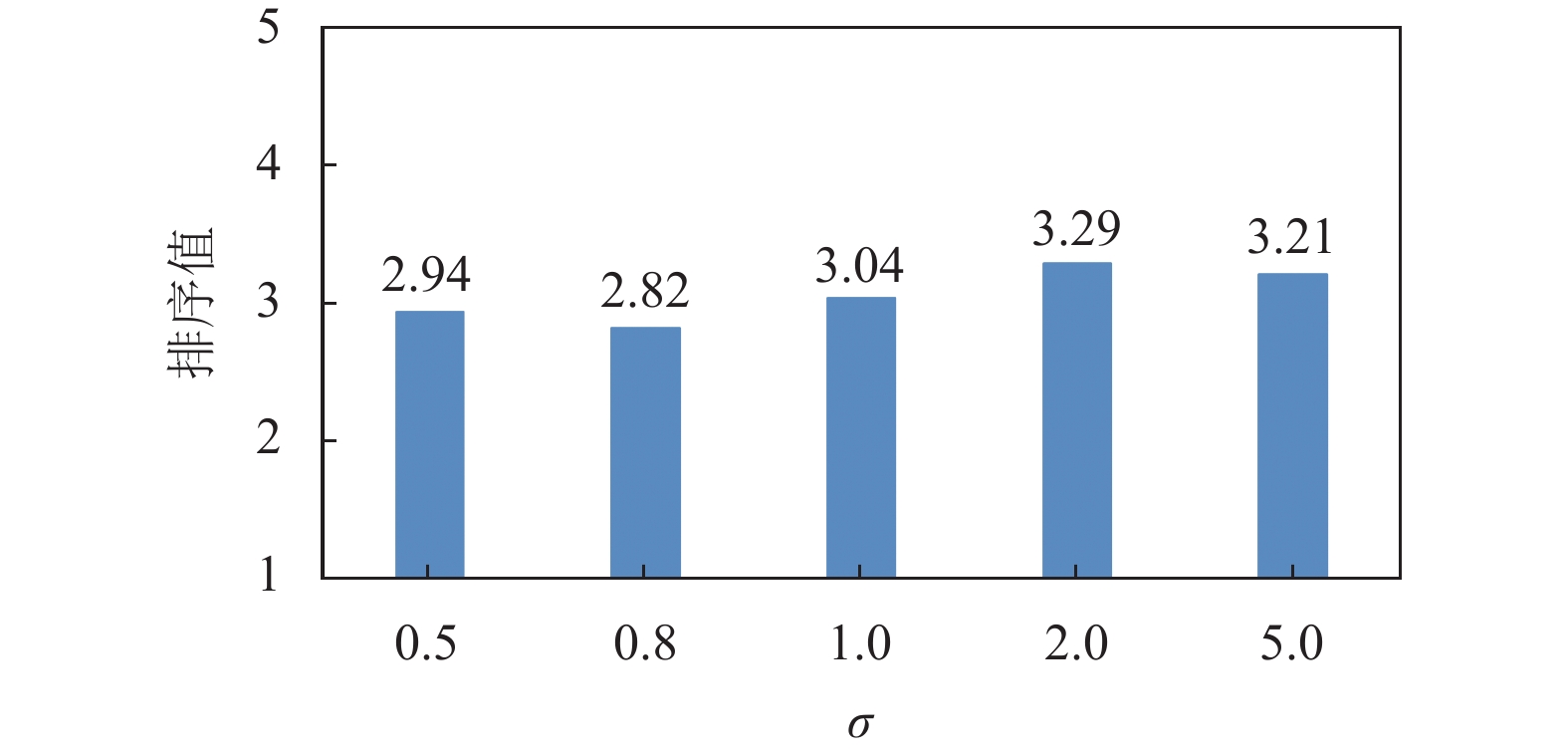
σ是变量间相似度量中重要的控制参数. 本节主要是进行参数σ敏感性分析, 实验参数设置同第3.2.2节. 对参数分别取0.5、0.8、1、2、5进行测试, 并利用其均值的非参数统计进行分析, 结果见图3. 由图3可得, 当参数大小为0.8时, 所提算法的整体性能表现最好. 因此, 该算法的σ值设置为0.8.
|
图 3 Friedman测试在不同σ值的排序结果 |
3.2.5 Οd,G值敏感性分析
Οd,G会随着迭代次数的累加逐渐变小, 种群多样性也是随着迭代次数的增加而变差. 因此用Οd,G识别基因层面的种群多样性. 本部分是对Οd,G的下限值选择进行分析, 实验参数设置同第3.2.2节. 对Οd,G分别取10−1、10−2、10−3、10−4、10−5进行测试, 并对其均值做进一步分析, 结果见图4. 由图4可得, 当Οd,G的下限值为10−3时, 所提算法的整体性能表现最好. 因此, 该算法Οd,G的下限值设置为10−3.

|
图 4 Friedman 测试在Οd,G取不同下限值时的排序结果 |
4 MTLBO-MGL在无人机三维路径规划问题中的应用
随着无人机技术的发展, 军事和民用等领域得到广泛应用[26,27]. 但是, 规划是无人机能否有效完成任务的一个重要环节. 因此, 学者对无人机三维路径规划问题进行了研究[28–31]. 本文将使用所提算法来对三维环境下的无人机进行路径规划, 其与其他算法进行比较.
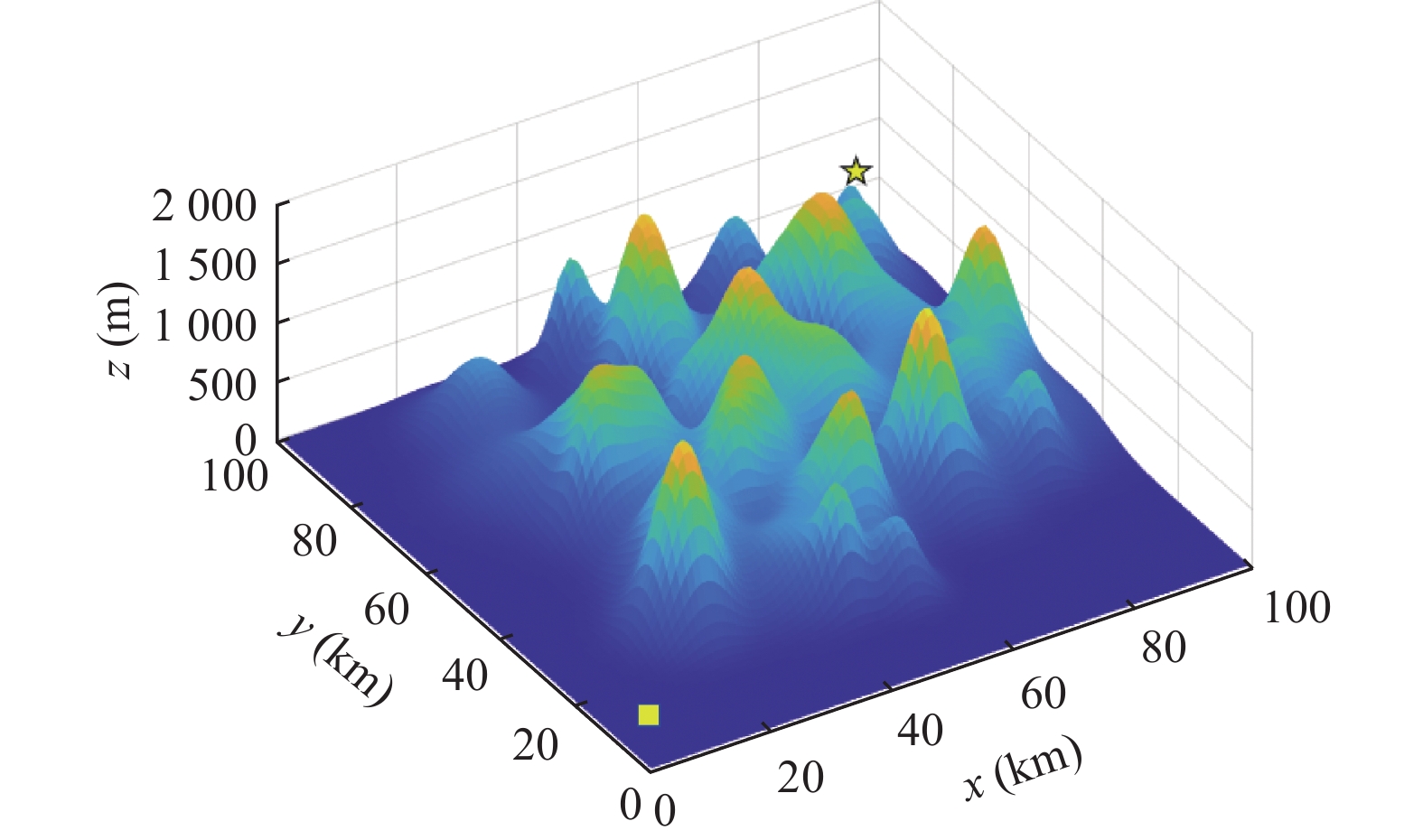
4.1 三维环境建模首先对无人机飞行环境进行建模. 本节采用三维立体的环境建模方法, 在100 km×100 km×2 km的立体区域内进行可行性仿真实验. 起点坐标为(0, 0, 0.5), 终点坐标为(90, 90, 1). 三维地形环境如图5所示.
|
图 5 三维地形环境 |
4.2 无人机三维路径规划模型
无人机三维路径规划模型可由式(14)表示.
| \left\{ \begin{split} & J=\min \sum_{i=1}^{N-1} \sqrt{\left(x_{i+1}-x_i\right)^2+\left(y_{i+1}-y_i\right)^2+\left({\textit{z}}_{i+1}-{\textit{z}}_i\right)^2} \\ &\text { s.t. }\left\{\begin{array}{l} h\left(x_i, y_i\right)+Z_{\min }<Z_i<Z_{\max } \\ \displaystyle\sum_{i=1}^n L_i \leqslant L_{\max }, \; i=1, 2, \cdots, n \\ \theta_i \leqslant \theta_{\max }, \; i=1, 2, \cdots, n \end{array}\right. \end{split} \right. | (14) |
其中, J为目标向量, 该问题为带有约束的最小化单目标优化问题. N为无人机经过所有点的个数. 本文将路径长度作为优化目标. h(xi, yi)表示二维坐标对应的山峰高度. Zmin和Zmax表示无人机的最小飞行高度和最大飞行高度. 本文还考虑了最大航迹长度[32]和最大拐弯角[33]的无人机性能约束. Li为第i个航迹段的长度, Lmax为最大航迹长度. θi为第i个航迹点的拐弯角度, θmax为最大拐弯角度.
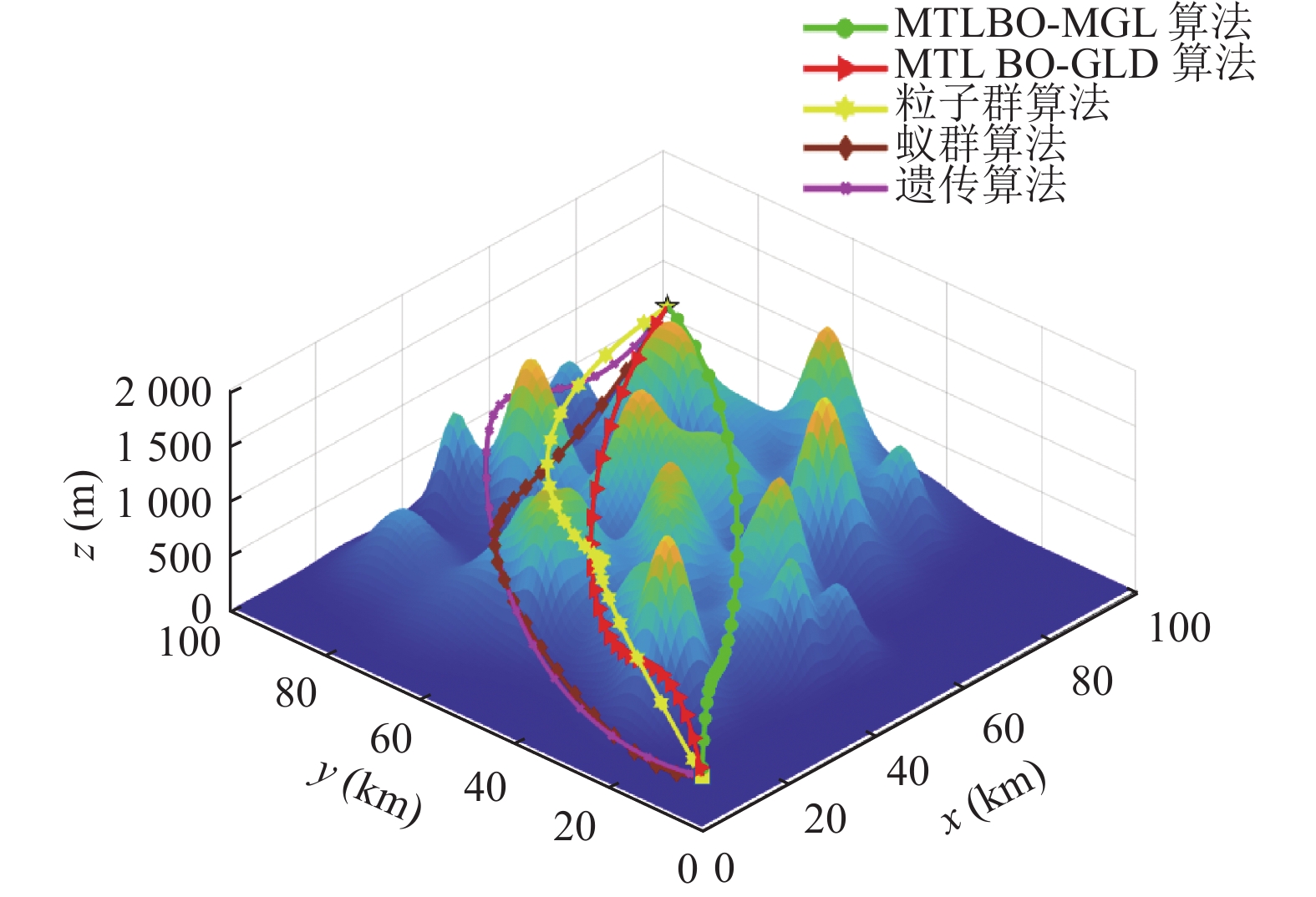
4.3 实验结果为验证所提算法在无人机三维路径规划问题上的性能, 本实验将MTLBO-MGL算法与粒子群算法[34]、蚁群算法[35]、遗传算法[36]以及微种群MTLBO-GLD算法[11]进行比较. 对于各个比较算法, 它们的种群规模和迭代代数见表6, 并且独立运行20次.
| 表 6 比较算法的参数设置 |
从表6中可以看出, 所有对比算法的函数评价次数都设置为3000. 各算法所得的实验结果见表7. 从表7可以看出, 在无人机三维路径规划问题上, MTLBO-MGL算法无论在平均值, 还是在最佳值上都要好于其他比较算法. 这表明, 相比于常规种群规模的非微种群算法和微种群算法, 所提算法能够在有限计算资源下找到更短飞行路径. 此外, 各个算法得到的航迹见图6. 从图6可以看出, MTLBO-MGL算法能够从复杂的三维飞行环境中找到一条最短路径以减少飞行时间和能耗.
| 表 7 比较算法的实验结果 |
|
图 6 路径规划结果 |
5 结束语
为了提高MTLBO算法的种群多样性, 提出了MTLBO-MGL算法. 在所提算法中, 首先在“教”和“学”阶段, 根据随机选择策略来对个体进行基因水平的进化操作; 然后从基因层面对种群多样性进行检测, 并使用稀疏谱聚类方法对种群的每个决策变量进行聚类; 最后, 根据多样性检测和聚类结果, 选择不同的进化策略来提高所提算法的搜索性能. 将所提算法与4种微种群算法进行对比. 仿真结果表明, 所提算法的整体性能要好于对比的4种算法, 证明了所提算法的有效性. 此外, 本文还将所提算法用于求解无人机三维路径规划问题, 实验结果表明, 所提算法能够在复杂飞行环境下找到更短路径.
| [1] |
Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: An optimization method for continuous non-linear large scale problems. Information Sciences, 2012, 183(1): 1-15. DOI:10.1016/j.ins.2011.08.006 |
| [2] |
Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-aided Design, 2011, 43(3): 303-315. DOI:10.1016/j.cad.2010.12.015 |
| [3] |
柳缔西子, 范勤勤, 胡志华. 基于混沌搜索和权重学习的教与学优化算法及其应用. 智能系统学报, 2018, 13(5): 818-828. |
| [4] |
Singh M, Panigrahi BK, Abhyankar AR. Optimal coordination of directional over-current relays using teaching learning-based optimization (TLBO) algorithm. International Journal of Electrical Power & Energy Systems, 2013, 50: 33-41. |
| [5] |
Verma S, Saha S, Mukherjee V. Optimal rescheduling of real power generation for congestion management using teaching-learning-based optimization algorithm. Journal of Electrical Systems and Information Technology, 2018, 5(3): 889-907. DOI:10.1016/j.jesit.2016.12.008 |
| [6] |
Ghoneim SSM, Mahmoud K, Lehtonen M, et al. Enhancing diagnostic accuracy of transformer faults using teaching-learning-based optimization. IEEE Access, 2021, 9: 30817-30832. DOI:10.1109/ACCESS.2021.3060288 |
| [7] |
Ren X, Chen ZZ, Ma Z. Differential evolution using smaller population. Proceedings of the 2nd International Conference on Machine Learning and Computing. Bangalore: IEEE, 2010. 76–80.
|
| [8] |
Cabrera JCF, Coello CAC. Micro-MOPSO: A multi-objective particle swarm optimizer that uses a very small population size. Multi-objective Swarm Intelligent Systems. Berlin: Springer, 2010. 83–104.
|
| [9] |
Olguín-Carbajal M, Herrera-Lozada JC, Sandoval-Gutierrez J, et al. A micro-differential evolution algorithm for continuous complex functions. IEEE Access, 2019, 7: 172783-172795. DOI:10.1109/ACCESS.2019.2954296 |
| [10] |
范勤勤, 柳缔西子, 王筱薇, 等. 基于反向学习的微种群教与学优化算法及其应用. 郑州大学学报(工学版), 2020, 41(4): 59-67. |
| [11] |
王筱薇, 范勤勤, 王维莉. 基于基因水平多样性的微种群教与学优化算法. 计算机应用研究, 2021, 38(4): 1097-1101. |
| [12] |
Von Luxburg U. A tutorial on spectral clustering. Statistics and Computing, 2007, 17(4): 395-416. DOI:10.1007/s11222-007-9033-z |
| [13] |
Hartigan JA, Wong MA. Algorithm AS 136: A K-means clustering algorithm. Applied Statistics, 1979, 28(1): 100-108. DOI:10.2307/2346830 |
| [14] |
Lu CY, Yan SC, Lin ZC. Convex sparse spectral clustering: Single-view to multi-view. IEEE Transactions on Image Processing, 2016, 25(6): 2833-2843. DOI:10.1109/TIP.2016.2553459 |
| [15] |
Ramírez M, Castellanos R, Calderón JG. Modified teaching-learning based optimization algorithm and damping of inter-area oscillations through VSC-HVDC. Proceedings of the 19th International Conference on Intelligent System Application to Power Systems (ISAP). San Antonio: IEEE, 2017. 1–6.
|
| [16] |
Yang M, Li CH, Cai ZH, et al. Differential evolution with auto-enhanced population diversity. IEEE Transactions on Cybernetics, 2015, 45(2): 302-315. DOI:10.1109/TCYB.2014.2339495 |
| [17] |
Verma D, Meilă M. A comparison of spectral clustering algorithms. Washington: Technical Report, 2003.
|
| [18] |
Liang JJ, Qu BY, Suganthan PN, et al. Problem definitions and evaluation criteria for the CEC 2013 special session on real-parameter optimization. Singapore: Technical Report, 2013.
|
| [19] |
Salehinejad H, Rahnamayan S, Tizhoosh HR. Micro-differential evolution: Diversity enhancement and a comparative study. Applied Soft Computing, 2017, 52: 812-833. DOI:10.1016/j.asoc.2016.09.042 |
| [20] |
Salehinejad H, Rahnamayan S, Tizhoosh HR, et al. Micro-differential evolution with vectorized random mutation factor. Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014. 2055–2062.
|
| [21] |
Brown C, Jin YC, Leach M, et al. μJADE: Adaptive differential evolution with a small population. Soft Computing, 2016, 20(10): 4111-4120. DOI:10.1007/s00500-015-1746-x |
| [22] |
Friedman M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 1937, 32(200): 675-701. DOI:10.1080/01621459.1937.10503522 |
| [23] |
Dunn OJ. Multiple comparisons among means. Journal of the American Statistical Association, 1961, 56(293): 52-64. DOI:10.1080/01621459.1961.10482090 |
| [24] |
García S, Molina D, Lozano M, et al. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC 2005 special session on real parameter optimization. Journal of Heuristics, 2009, 15(6): 617-644. DOI:10.1007/s10732-008-9080-4 |
| [25] |
Suganthan PN, Hansen N, Liang JJ, et al. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. Natural Computing, 2005: 1–50.
|
| [26] |
Ahn N, Kim S. Optimal and heuristic algorithms for the multi-objective vehicle routing problem with drones for military surveillance operations. Journal of Industrial and Management Optimization, 2022, 18(3): 1651-1663. DOI:10.3934/jimo.2021037 |
| [27] |
Sanchez-Fernandez AJ, Romero LF, Bandera G, et al. VPP: Visibility-based path planning heuristic for monitoring large regions of complex terrain using a UAV onboard Camera. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 15: 944-955. DOI:10.1109/JSTARS.2021.3134948 |
| [28] |
褚宏悦, 易军凯. 无人机安全路径规划的混沌粒子群优化研究. 控制工程, 2022: 1–8. https://doi.org/10.14107/j.cnki.kzgc.20220231. (2022-07-01).
|
| [29] |
Yu Z, Sun FC, Lu X, et al. Overview of research on 3D path planning methods for rotor UAV. Proceedings of the 2021 International Conference on Electronics, Circuits and Information Engineering (ECIE). Zhengzhou: IEEE, 2021. 368–371.
|
| [30] |
Du NT, Zhou YQ, Deng W, et al. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimedia Tools and Applications, 2022, 81(19): 27397-27422. DOI:10.1007/s11042-022-12882-4 |
| [31] |
Huang C. A novel three-dimensional path planning method for fixed-wing UAV using improved particle swarm optimization algorithm. International Journal of Aerospace Engineering, 2021, 2021: 7667173. |
| [32] |
Bai H, Fan T, Niu Y, et al. Multi-UAV cooperative trajectory planning based on many-objective evolutionary algorithm. Complex System Modeling and Simulation, 2022, 2(2): 130-141. DOI:10.23919/CSMS.2022.0006 |
| [33] |
Yu XB, Li CL, Yen GG. A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management. Applied Soft Computing, 2021, 98: 106857. DOI:10.1016/j.asoc.2020.106857 |
| [34] |
杨维, 李歧强. 粒子群优化算法综述. 中国工程科学, 2004, 6(5): 87-94. |
| [35] |
李成凤, 邵俊倩, 张阳伟. 基于蚁群算法的群集系统协同分群控制方法. 控制工程, 2021, 28(11): 2215-2222. |
| [36] |
Cao Y, Wei WY, Bai Y, et al. Multi-base multi-UAV cooperative reconnaissance path planning with genetic algorithm. Cluster Computing, 2019, 22(3): 5175-5184. |
 2023, Vol. 32
2023, Vol. 32



