2. 南京邮电大学 通信与信息工程学院, 南京 210003
2. School of Communication and Information Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
图像作为一种直观易懂的信息载体, 已经成为人们交流的重要形式之一. 然而, 图像在采集、保存以及传递过程中易受环境、设备和技术影响[1] , 容易出现信息缺失的现象. 图像修复是指给定一张部分像素缺失的图像, 根据图像中的已知信息对缺失的区域进行像素级填充, 从而使填充后的图像达到人类视觉满意的效果. 图像修复作为计算机视觉领域一项基本内容, 也是许多图像处理任务的重要组成部分, 研究图像修复的技术并将其应用到实际生活中具有重要意义.
传统的图像修复算法主要分为基于扩散和基于块匹配两类, 通常是根据图像样本相似性或者结构纹理方面的信息, 推理缺失区域, 传统方法对图像纹理和分辨率具有较高的鲁棒性, 但是计算代价非常昂贵, 并且它无法有效提取并利用图像的语义信息, 往往不适用于具有复杂结构或缺失区域占比较大的图像. 基于深度学习的图像修复方式通过训练深度神经网络, 挖掘图像深层语义特征, 弥补了传统图像修复技术的不足.
基于深度学习的图像修复方式按照网络结构层次分为单阶段和多阶段图像修复. 单阶段图像修复算法通常利用编解码或者U-Net结构, 在多个损失函数联合约束下, 直接恢复缺失图像. 典型算法如Pathak等人提出的上下文编码器CE[2], Liu等人提出的基于特征均衡的互编解码网络MED[3]. 多阶段图像修复算法按照技术路线大致分为两类, 第1类以第1阶段重构的信息作为先验指导后续纹理合成任务, 如Liao等人[4]采用多尺度联合优化, 首先对语义和纹理的联合先验进行建模. 第2类采用由粗到细渐进恢复图像缺失区域的方式. 如Yang等人[5]提出的多尺度神经网络合成, 首先将512×512大小的测试图像以步长为2进行两次下采样, 创建3层金字塔结构图像作为输入, 然后执行由粗到细的图像修复. Zamir等人[6]将输入图像分为不重叠的块, 第1阶段分为4块, 第2阶段分为2块, 为保留更多的空间细节, 最后一阶段在原始图像上进行操作. Lamba等人[7]将原图分辨率分别降为1/32, 1/8以及1/2再通过级联操作依次恢复.
考虑到渐进式图像修复算法在下采样过程中会丢失大量信息, 且相较于图像色彩的细微差异, 人们往往对图像整体结构一致性更为敏感, 故本文提出一种新的基于色彩聚类的图像修复算法. 这与Wang等人[8]为解决图像修复过程中可能会出现的色彩渗透问题, 提出的将图像修复工作分为外部结构重建以及内部色彩引导修复两个阶段想法相类似. Wang等人在结构重建阶段将三通道彩色图片转化为单通道黑白图片, 接着在单色空间中重建缺失的结构和细节, 色彩引导阶段利用渐进学习策略实现内部颜色传播与恢复. 本文同样采用了色彩量化情形下的结构重建思想, 不同的是, 本文用K-means聚类算法对图像色彩进行处理, 处理后的图像保留了一定量级(≥2)的色彩信息和更加完整的结构信息; 并且为满足细粒度图像恢复质量需求, 采用渐进式图像恢复结构, 将K-means聚类处理后的生成图像作为输入, 结合K值较小的图像恢复结果, 由粗到细来恢复色彩损失, 优化修复结果. 主流图像修复方式常采用上下文注意力机制提取远距离图像信息, 这会带来大量的计算开销. 为降低计算成本, 本文在最后一层修复网络中引入交叉注意力机制, 从水平和垂直两个维度建模全局依赖性, 增强逐像素表征能力. 同时, 为修复任意位置、任意形状缺失的图像, 采用门控卷积在每个空间位置为每个通道提供可学习的动态特征选择机制.
我们在Paris StreetView和Places2数据集上进行了大量实验以评估模型性能, 结果表明, 我们提出的图像修复方法与经典修复方式EC[9]、MED[3]、CA[10]、GC[11]相比, 修复图片更加清晰, 边缘伪影明显减少, 且峰值信噪比(peak signal to noise ratio, PSNR)与结构相似度(structural similarity, SSIM)均有提升. 相较于其他方法, 本文主要解决了如下两个方面的问题.
(1) 提出了一种基于色彩聚类的图像修复算法, 该算法将对全分辨率图像进行色彩聚类处理的结果作为输入, 为后续修复任务保留了更多的结构和色彩细节, 也为渐进式图像修复网络的输入提供了新的思路.
(2) 引入交叉注意力机制, 从水平和垂直两个维度建模全局依赖性, 增强逐像素表征能力, 可以有效减少网络参数, 降低计算开销.
1 相关工作 1.1 基于深度学习的图像修复算法基于深度学习的图像修复算法利用卷积神经网络提取图像的语义信息, 填充图像的缺失区域. 然而, 这些方式生成的图像通常会存在边缘伪影以及与已知区域结构纹理信息不一致的现象. 为此, Iizuka等人[12]引入全局和局部上下文鉴别器, 分别从整体和局部确保生成图像的上下文一致, Yu等人[11]提出门控卷积, 与用户输入兼容, 根据当前位置是否被遮挡自动学习掩码, 同时融合上下文注意力机制, 优化已知区域与未知区域之间的纹理相似性. Liu等人[3]提出交互编解码网络, 由图像浅层特征提取纹理信息, 深层特征提取结构信息, 并采用双边传播激活函数均衡图像结构和纹理特征, 有效去除了缺失区域周围的模糊和伪影. Zeng等人[13]在U-Net架构中引入了多尺度编码器, 使用注意力转移网络由深到浅逐层修复. Wang等人[14]在U-Net编码器中采用分层金字塔卷积和动态归一化机制获取不同感受野的图像特征图, 解码器部分使用金字塔注意力机制以学习更加精细的特征信息. Li等人[15]设计了一个即插即用的循环特征推理模块, 利用部分卷积多次循环由外向内逐步完善修复图像.
1.2 注意力机制在图像修复任务中引入注意力机制可以使图像信息得到充分利用, 注意力机制在背景区域中搜索可能的纹理信息, 替换生成的部分, 从而生成纹理一致的结果. 如Yu等人[10]为利用图像远距离已经区域信息, 提出上下文注意力机制, 通过卷积计算前景与背景区域的余弦相似性, 接着在相似性图上作通道维度的 , 选取 值最大的背景块进行反卷积. Shin等人[16]基于两向量之间角度的考虑, 提出使用欧式距离代替余弦相似性得分. Liu等人[17]认为生成图像块之间的相似性同样重要, 提出利用图像已知区域与未知区域之间的相似性保证图像的全局语义一致性, 利用未知区域内部相邻块之间的相似性进行迭代优化保证图像局部特征一致性.
2 基于K-means聚类的图像修复算法本文所提出的图像修复算法网络结构如图1所示, 由色彩聚类图像生成、图像结构分层重建以及光谱归一化马尔可夫鉴别器3部分组成, 首先, 为降低计算成本, 选用K-means算法对图像进行聚类处理, 处理后图像的结构信息可以得到更好的保留. 在图像结构分层重建中引入交叉注意力机制和门控卷积, 前者有利于减少网络的参数量, 降低计算成本, 后者用于处理任意位置形状的缺失区域图像修复. 鉴别器模块采用结合SN-GAN和PatchGAN的光谱归一化马尔可夫鉴别器SN-PatchGAN[11], 以提高训练的稳定性.
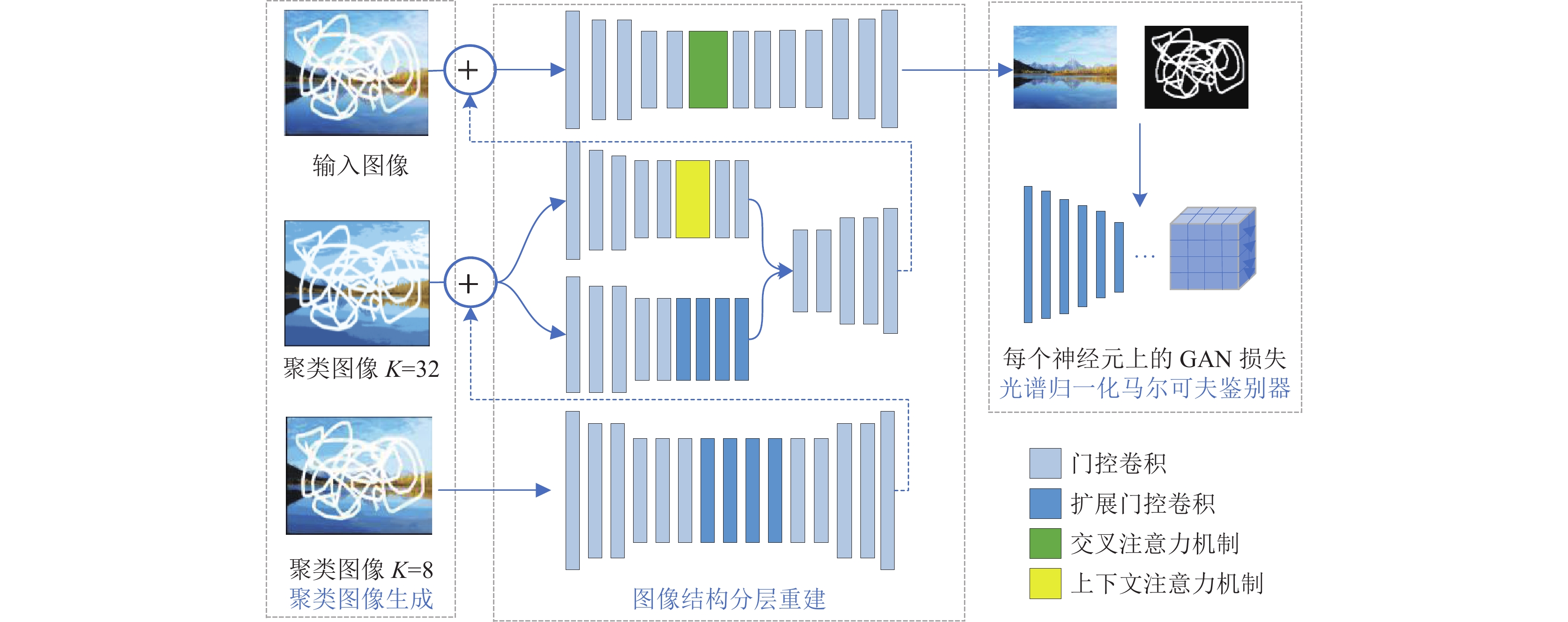
|
图 1 网络结构模型图 |
2.1 K-means聚类图像生成
图像可以看作是若干像素点的集合, 对图像进行聚类就是将构成图像的像素点进行分组, 一个聚类就是一组像素点的集合, 聚类的最终目标是使同一集合中的元素具有较高的相似度, 不同集合间差别尽可能大. 给定一张图像, 根据K-means算法[18], 首先随机初始化K个不同颜色分量作为聚类中心, 将图像中的每个像素根据颜色距离最短的原则分配到相应的簇, 颜色距离公式如(1)所示:
| Distance=√(R−R′)2+((G−G′)2+((B−B′)2 | (1) |
其中,
当所有像素对象划分完成后, 重新计算每个簇的颜色分量的均值, 将均值作为新的聚类中心重新划分簇, 算法运行停止准则为中心点颜色分量不再发生变化.
考虑到人们对细微颜色差异并不敏感和推理速度的要求以及计算可行性, 我们跳过会带来大量计算开销和延迟的较低尺度, 仅在K=8、K=32以及原输入图像上进行操作. 如图2所示, 聚类生成图像更为完整保留了图像的结构信息, 作为分层修复网络的输入, 更有利于后续的修复任务进行.

|
图 2 聚类图像生成示例 |
2.2 图像结构分层重建
相较于图像细微颜色的差异, 人们观察图像时更加注重整体结构的观感. 为使生成图像结构合理以及保持上下文语义的一致性, 我们采用图像结构分层重建逐层细化修复结果. 网络采用编解码结构, 首先, 以K=8时的聚类图像作为编码器输入, 并且在编解码结构中引入扩展卷积, 其在标准卷积的基础上引入了扩展率的参数, 如图3所示图3(a)为普通卷积, 图3(b)为扩展卷积, 扩展率为2. 即扩展卷积通过向卷积核各参数之间引入间隔, 可以在保持网络参数量不变的前提下增加卷积核的感受野, 使得卷积核的输出能够包含较大范围的信息, 再由解码器恢复出粗略修复结果. 将第一层粗略恢复的图像生成部分与K=32时的聚类图像结合, 作为第2层的输入, 第2层采用融合上下文注意力机制和扩展卷积两条路径的编解码结构进行图像修复, 再将修复的结果送入原始输入图像中进行更细粒度的修复.
考虑到上下文注意力机制的计算复杂度, 为降低计算成本, 在最后一层修复网络中引入可以简化计算的交叉注意力机制[19], 同时, 为修复任意位置、任意形状缺失的图像, 采用门控卷积[11]代替普通卷积.
2.2.1 交叉注意力机制交叉注意力机制从水平和垂直两个维度建模图像全局依赖, 增强逐像素表征能力. 模型结构如图4所示. 交叉注意力模块首先使用两个带有1×1滤波器的卷积层对输入局部特征图
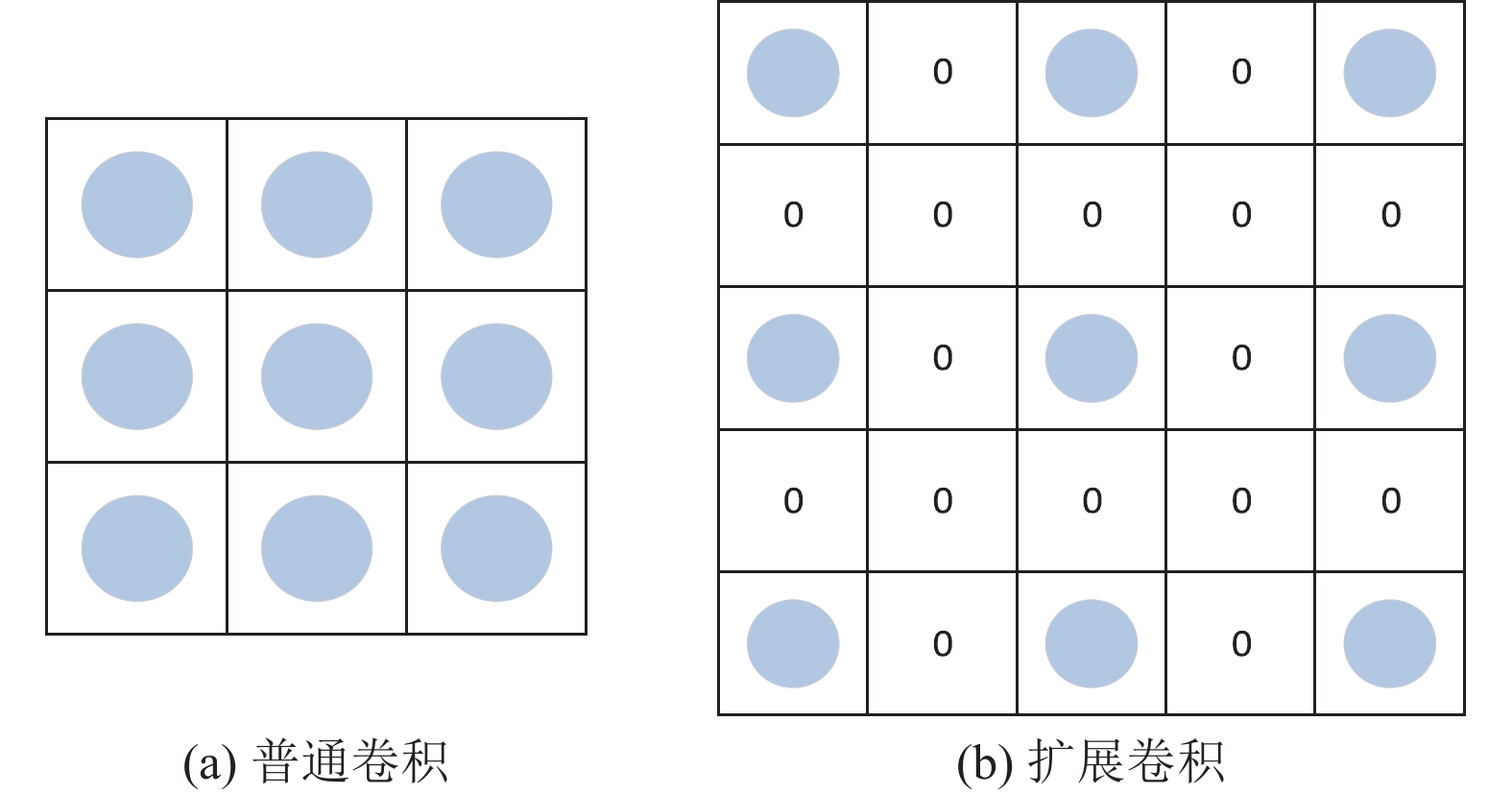
|
图 3 扩展卷积模块结构图 |
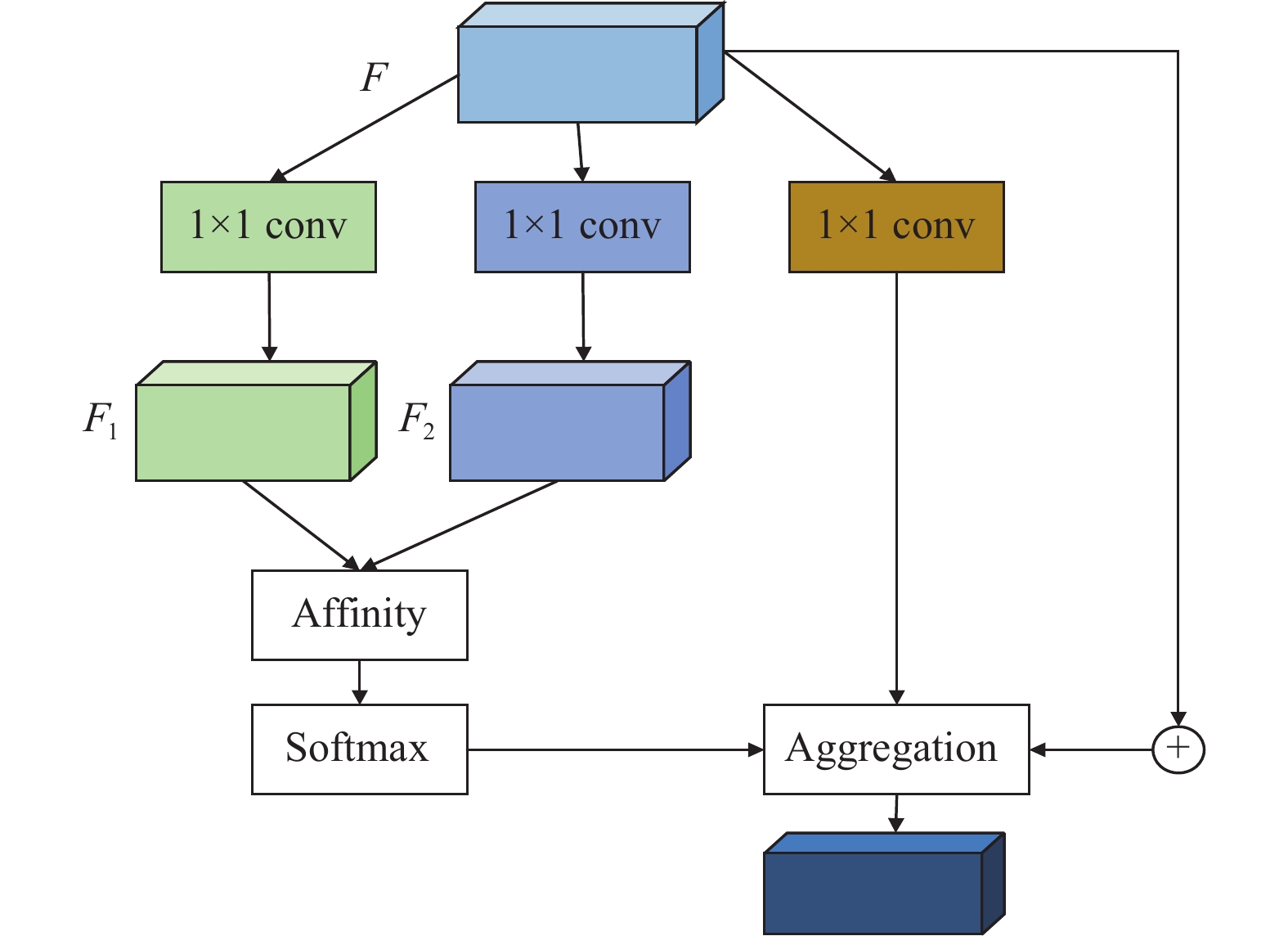
|
图 4 交叉注意力模块结构图 |
交叉注意力模块中单个像素与其非同行或同列的像素之间不存在联系, 为充分利用上下文信息, 采用双层交叉注意力模块, 在第1次注意力传播过程中, 像素点A的信息传递至其同行同列, B点接收不到A的信息, 在第2次传播过程中, B通过其所在行列与A所在行列的交叉点获取像素点A的信息, A点注意力传播过程如图5所示, 所以通过双层交叉注意力模块的堆叠, 任意像素点能够收集图像中所有像素的上下文信息.
非局部注意力机制首先生成每个位置的注意力图, 并将输入特征图转化为每个位置注意力图的加权和, 需要
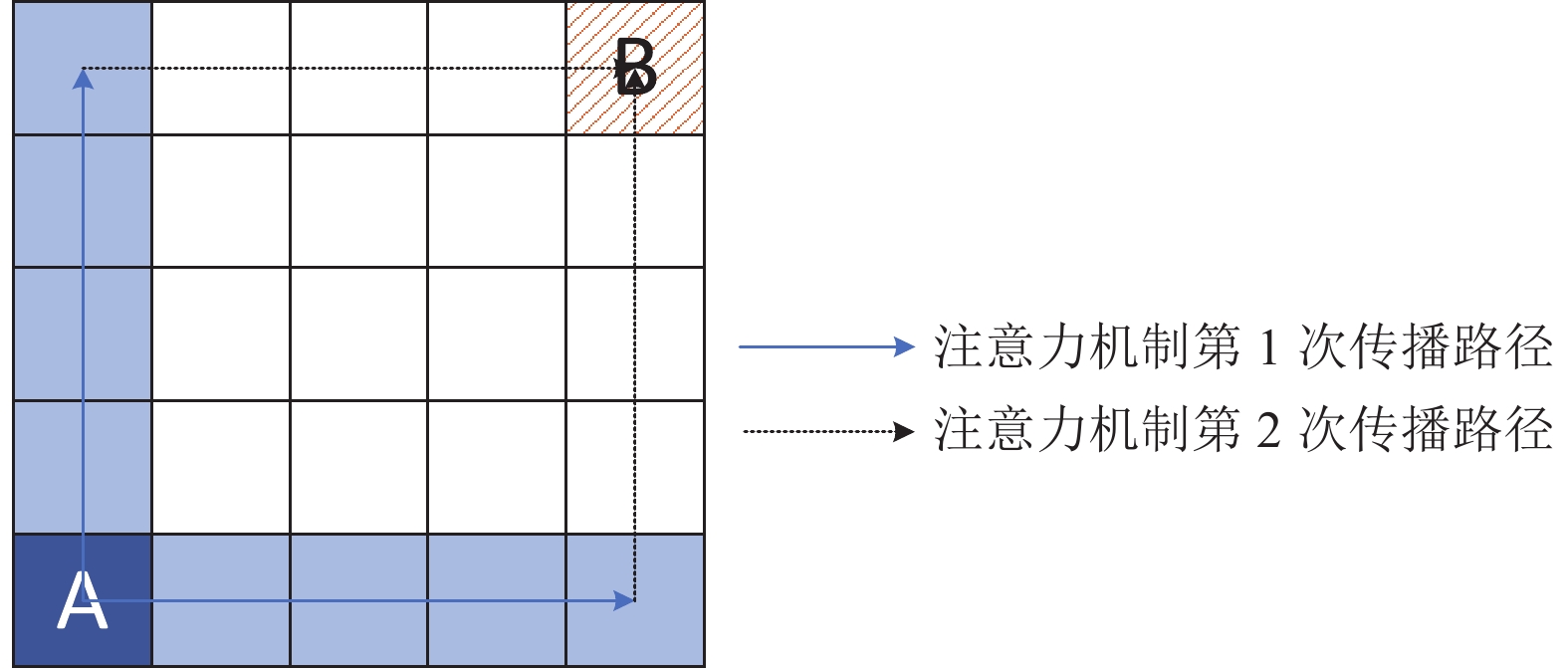
|
图 5 双层交叉注意力模块示意图 |
2.2.2 门控卷积
普通卷积中将所有像素视作有效像素, 采用同样处理方式, 容易造成图像缺失区域边缘模糊, 门控卷积采用动态特征选择机制, 可以动态学习不同通道和空间特征, 获取缺失区域与已知区域的关联特征, 门控卷积
| Gatingy,x=∑∑Wg⋅I | (2) |
| Featurey,x=∑∑Wf⋅I | (3) |
| Oy,x=ϕ(Featurey,x)⊙σ(Gatingy,x) | (4) |
其中,
为提高训练的稳定性, 鉴别器模块采用结合SN-GAN和PatchGAN的光谱归一化马尔可夫鉴别器SN-PatchGAN[11], SN-PatchGAN由堆叠的卷积层构成. 鉴别器的输入是图片和掩码, 输出为
为得到结构一致且视觉满意的图像修复结果, 本文采用重构损失和SN-PatchGAN损失提高所有尺度下的像素重建精度, 默认损失平衡超参数为1:1.
SN-PatchGAN损失由生成器损失函数和鉴别器损失函数两部分组成, 公式分别为:
| LG=−Ez∼Pz(z)[Dsn(G(z))]) | (5) |
| LDsn=Ez∼Pdata(x)[ReLU(1−Dsn(x))]+Ez∼Pz(z)[ReLU(1+Dsn(G(z)))] | (6) |
其中,
重建损失函数要保证修复图像真实感和清晰度, 对于像素级的重建过程, 算法选用
| L1=‖ | (7) |
本文在巴黎街景和Places2数据集上展开实验, 验证模型的性能, 在巴黎街景数据集中随机抽取500幅图像作为测试集, 其余为训练集, 在Places2数据集中选取6种类型图片, 再从中随机抽取500张作为测试集, 其余为训练集. 硬件配置环境为Intel(R) Core(TM) i7-10875H CPU @ 2.30 GHz. 我们使用Adam优化器对模型进行训练, 设置batch_size为4, 初始阶段学习率设置为1×10–4, 最后使用1×10–5进行微调. 训练过程中所有图片和掩码均被调整至256×256大小, 本文中所有实验结果都是由训练好的模型直接输出, 没有任何后续处理.
3.2 对比模型为验证图像恢复质量, 本文将提出的K-means聚类的图像修复方式与图像修复的经典算法进行对比, 通过定性和定量实验, 验证本文所提出的模型的性能.
定性比较: 图6分别展示了本文所提出方法与对比方法在Paris StreetView和Places2数据集中心区域缺失情形下的恢复效果. 如图, 在巴黎街道数据集上, EC[9]、MED[3]恢复出的图像缺失区域有明显的伪影, 存在修复区域边缘模糊问题, 而本文所提出的方法能够有效推理出缺失区域的信息, 恢复出与输入图像结构更为一致协调的结果. 在Places2数据集上, 本文提出的修复算法相比于CA[10]、GC[11]也能推理出与上下文更为一致的合理结构, 测试效果如图7所示.
图8展示了本文所提出的方法与EC方法在Paris StreetView数据集上不同比例不规则缺失情形下的恢复效果. 当缺失区域占比较小时, 对比方法和本文提出的方法都能在复杂的场景中得出合理的恢复结果, 而随着缺失区域占比逐渐增加, EC恢复出来的图像恢复结果则更为模糊. 在多数情况下, 我们的方法可以恢复出更加合理准确的图像结构.

|
图 6 Paris StreetView掩码为中心为失时恢复效果对比 |

|
图 7 Places2图像使用中心缺失掩码恢复效果对比 |
定量比较: 为衡量图像修复质量, 我们采用SSIM、PSNR指标来客观展示对比各种模型性能. SSIM用来反映生成图像与原始图像之间的结构相似性, SSIM值越高表示越相似, PSNR用来反映恢复图像质量的高低, 公式如下, PSNR值越高表明恢复图像质量越高. 具体数值如表1所示.
| {\textit{PSNR}}=20\mathrm{lg}\left({\frac{(MA{X}_{i})}{\sqrt{{\textit{MSE}}}}}^{2}\right) | (8) |
其中,
| {\textit{SSIM}} = \frac{{(2{\mu _x}{\mu _y} + {c_1})(2{\delta _x}_y + {c_2})}}{{(\mu _x^2 + \mu _y^2 + {c_1})(\delta _x^2 + \delta _y^2 + {c_2})}} | (9) |
其中,
通过对本文提出的模型进行定性定量分析可以看出, 可以看出, 本文提出的方法可以恢复出更加合理一致的图像结构, 更适合用于复杂场景较大面积缺失图像恢复中.
3.3 消融实验为验证本文所提出的基于K-means图像修复算法的有效性, 在Paris StreetView数据集上展开了消融实验. 实验结果如图9所示, 其中, 图9(a)为原始输入图像, 图9(b)为采用单张原始图像作为输入生成图像, 图9(c)为去掉交叉注意力层所生成的图像.

|
图 8 使用不规则缺失掩码恢复效果对比 |
| 表 1 巴黎街景数据集模型指标对比 |

|
图 9 消融实验对比图 |
通过对比可以看出, 采用单张图片作为输入时, 会明显出现图像结构模糊, 而采用本文提出的基于色彩聚类的图像输入可以更好地保留图像的结构信息, 生成更加自然的图像; 并且添加了交叉注意力机制可以进一步减小无效特征信息对图像修复的干扰, 保持缺失区域与周围像素的一致性. 本文提出的基于色彩聚类的图像修复相较于采用单张图片作为输入, 不添加交叉注意力机制的原始模型, PSNR和SSIM分别提升了5.31%和2.36%.
4 结论为解决现有图像修复方法容易引起的修复边缘模糊的问题, 本文提出了一种基于色彩聚类的图像修复方式. 首先采用K-means算法对图像进行聚类处理, 为渐进式图像修复方式输入提供了新的思路, 也可以保存更多的图像结构信息, 同时为降低传统注意力机制的计算复杂度, 引入了交叉注意力机制, 从水平和垂直两个维度建模图像全局依赖性, 有效减少了计算量. 大量实验表明, 对比经典主流的修复方式, 我们提出的方法更有利于复杂场景的结构重建, 能有效减少修复边缘模糊的现象. 但是本文仅在注意力模块降低了计算量, 如何从整个网络的角度减小参数量和计算量将是接下来主要的研究方向.
| [1] |
陈东岳, 朱晓明, 马腾, 等. 双尺度顺序填充的深度图像修复. 中国图象图形学报, 2022, 27(8): 2344-2355. |
| [2] |
Pathak D, Krähenbühl P, Donahue J, et al. Context encoders: Feature learning by inpainting. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2536–2544.
|
| [3] |
Liu HY, Jiang B, Song YB, et al. Rethinking image inpainting via a mutual encoder-decoder with feature equalizations. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 725–741.
|
| [4] |
Liao L, Xiao J, Wang Z, et al. Image inpainting guided by coherence priors of semantics and textures. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 6535–6544.
|
| [5] |
Yang C, Lu X, Lin Z, et al. High-resolution image inpainting using multi-scale neural patch synthesis. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 4076–4084.
|
| [6] |
Zamir SW, Arora A, Khan S, et al. Multi-stage progressive image restoration. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 14816–14826.
|
| [7] |
Lamba M, Mitra K. Restoring extremely dark images in real time. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 3486–3496.
|
| [8] |
Wang TF, Ouyang H, Chen QF. Image inpainting with external-internal learning and monochromic bottleneck. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 5116–5125.
|
| [9] |
Nazeri K, Ng E, Joseph T, et al. EdgeConnect: Generative image inpainting with adversarial edge learning. arXiv:1901.00212, 2019.
|
| [10] |
Yu JH, Lin Z, Yang JM, et al. Generative image inpainting with contextual attention. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 5505–5514.
|
| [11] |
Yu JH, Lin Z, Yang JM, et al. Free-form image inpainting with gated convolution. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4470–4479.
|
| [12] |
Iizuka S, Simo-Serra E, Ishikawa H. Globally and locally consistent image completion. ACM Transactions on Graphics, 2017, 36(4): 107. |
| [13] |
Zeng YH, Fu JL, Chao HY, et al. Learning pyramid-context encoder network for high-quality image inpainting. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 1486–1494.
|
| [14] |
Wang C, Shao MW, Meng DY, et al. Dual-pyramidal image inpainting with dynamic normalization. IEEE Transactions on Circuits and Systems for Video Technology, 2022, 32(9): 5975-5988. DOI:10.1109/TCSVT.2022.3165587 |
| [15] |
Li JY, Wang N, Zhang LF, et al. Recurrent feature reasoning for image inpainting. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 7757–7765.
|
| [16] |
Shin YG, Sagong MC, Yeo YJ, et al. Pepsi++: Fast and lightweight network for image inpainting. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 252-265. DOI:10.1109/TNNLS.2020.2978501 |
| [17] |
Liu HY, Jiang B, Xiao Y, et al. Coherent semantic attention for image inpainting. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4169–4178.
|
| [18] |
任恒怡, 贺松, 陈文亮. 一种改进的K-means聚类算法在图像分割中的应用. 通信技术, 2017, 50(12): 2704-2707. |
| [19] |
Huang ZL, Wang XG, Huang LC, et al. CCNet: Criss-cross attention for semantic segmentation. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 603–612.
|
 2023, Vol. 32
2023, Vol. 32



