时间序列是由一组在时间轴上按照时间点顺序记录的数据所构成的序列.每个数据代表了特定时间点的观测值或测量值. 时间序列预测指通过对给定的时间序列建模, 对模型输入未来一段时间点预测未来一段时间点上的取值或概率分布[1], 这是诸如工业、金融、医疗、交通、能源、气象以及电商等各领域进行管理和决策的关键方法. 例如工业用电有着庞大的历史用电数据, 对这些数据做分析, 可以预测未来几天、几月的电量需求情况, 用于用电规划、电价调补等, 有利于电力系统的经济运行与安全运行管理[2]. 在以往的研究落地应用中侧重于传统统计学方法. 传统时序预测基于统计学理论与方法[3,4], 通过对数据进行加权平均来平滑数据, 这种方法具有高可解释性, 理论基础稳固, 但如今数据的多样性、复杂性和大规模, 使得传统数据分析方法在应对各领域数据上显得非常吃力. 机器学习是当前研究中的主流方法之一, 它通过对数据进行预处理、自动学习数据特征、根据特征选择模型以及对模型进行训练和优化来预测数据. 机器学习因其能自学习特征, 改善了传统统计学方法的手动学习特征带来的高人力物力需求弊端[5], 能够处理大规模数据, 也在一定程度上提高了预测准确率, 但其同时需要设计更复杂的计算模型以及更长的训练时间. 因此, 深度学习方法在近年成为时间序列预测方法的热门研究方法之一, 它通过构建多层神经网络模型来实现对数据的自动特征提取和学习, 弥补了传统预测方法需要高计算高人力的弊端, 用自动学习特征工程代替了手动设计特征工程[6,7]. 但仅使用深度学习的预测方法所作结构假设较少, 通常需要较高的计算资源以及大量的数据来学习得到准确的模型, 并且由于其缺乏可解释性, 实际落地方案也是比较少, 很难真正应用到实际场景中. 结合已有研究经验, 研究者们又提出了“分解”“重构”的预测框架, 实验证明了融合多模型的时序预测模型效果往往会更好[8]. 其中, “分解”方法通常采用传统统计学方法如小波变换[9]等, 预测部分可以使用传统统计方法、机器学习方法或深度学习方法. 现有的“分解”“重构”框架, “分解”部分没有考虑到时序数据的全局特点, 无法跨领域应用[9]; 预测部分采用模型也各不相同. 因此, 研究出能跨领域应用, 且能保证精确度的预测模型仍然是研究时序预测方向研究者们的一个研究热点, 也是需要进行时序预测的各领域翘首以盼的“得力助手”.
综上所述, 时间序列预测的应用前景广泛, 但目前的预测技术仍然无法更好地满足当下的需求, 因此, 对时间序列预测的方法还需更深入的研究.
2 相关研究对时序预测的方法目前存在3种主流方法, 分别是传统时序预测方法、机器学习预测方法、深度学习预测. 近年来研究者们提出了一种“分解”“重构”的预测框架, 该方法取不同方法的优点结合起来, 效果比单一预测模型更好. 传统时序预测方法状态转移模型如ARIMA模型[10,11], 由状态方程和观察值方程组成, 但其预测过程具有较强的假设限制, 无法在相同数据集上推出共享模式. 机器学习方法[12,13]如决策树、随机森林改善了传统统计学方法难以迁移学习的问题, 但其在建立过多节点的情况下存在过拟合问题. 此外, 机器学习还需要做大量的特征工程来提高模型的准确率. 而深度学习方法在时序预测方面的应用, 改善了传统预测方法忽略数据自相关性以及需要大量人力算力等弊端, 改善了机器学习手动设计特征工程[14–18]. 但仅使用深度学习的预测方法所作的结构假设较少, 通常需要更大的训练数据集来学习得到准确的模型. 现阶段, 将传统高鲁棒性数据预处理技术结合现有高准确度预测模型的混合预测方法被广泛应用于时间序列预测中[19,20]. 与此同时, 研究者提出的“分解”“重构”的预测框架, 有效提高了预测精度, 其主要思想是先分析时间序列数据, 用时序分解法分析数据特征, 根据不同特征用不同预测方法分别预测, 最后将分支结果加和作为最终预测结果[21,22]. 其中, 小波分解法[23]被广泛应用于分解部分对时序数据进行分析, 文献[24]就先通过小波分解来分析时序数据, 再使用人工神经网络对分解后的数据进行预测, 最后对预测结果进行“重构”. 但是小波分解法无法处理非线性时序数据. 经验模态分解(empirical mode decomposition, EMD)法[25]是一种基于数据的局部自适应方法, 能较好地处理非线性时序序列. 文献[26]先用EMD分解出各个IMF, 对各IMF与特征分量进行相关性分析, 再利用最小二乘支持向量机算法对获得的最优特征矩阵进行预测. 林昱等人[27]通过利用经验模态分解对传统技术因子进行分解去噪, 得到高频和低频的特征序列, 然后将这些具有明显趋势特征的序列映射到新的表示空间中, 结合预测模型实现了对股票涨跌的预测, 但仅使用经验模态分解得到的数据缺少可解释性. 为了考虑时间序列分解的全局性, 在对时间序列做预测的过程中, 往往会将时间序列定义为由周期、季节及残差组成的序列, 如经典的移动平均法分解方法[3], 首先估计周期长度, 以一周期为区间对以周期为单位的数据取均值, 得出趋势. 通过原数据减去趋势, 再对以周期为单位的数据求均值, 得出周期序列, 原数据减去趋势和周期得到残差. 但移动平均法无法预测趋势变化明显的时序数据. X11[28]在传统分解法的基础上提出了一种复杂的方法来处理交易日、假期及一些其他已知的影响因素的影响. 但其在处理非常规和异常数据时能力不足. STL (seasonal and trend decomposition using LOESS)[29]是一种多功能、鲁棒性的方法, 与X11不同, STL可以分解任意定义的具有季节性特征的数据, 而不局限于按月度或季度划分的数据, 季节部分可以随时间变化, 变化率及趋势周期的平滑度可以由用户控制. STL序列分解在早期多用于金融领域[30], 近年来被越来越多地应用到了电力、环境和交通等领域. 如在电力领域, STL分解用于分析短期负荷预测[31,32]. 郭利进等人通过时序分解改进算法进行水质预测[33]. 赵建东等人通过结合时序分解和门控循环的单元来预测地铁换乘流量[34]. 后续也有学者提出了STL类模型的改进: 如基于STL-LSTM-TCN的模型[32]和改进的序列分解预测模型(SEGS)[35]等. 这些改进模型增强了STL在多项式拟合、去噪和预测等方面的性能, 可以更好地适应不同领域的数据.
基于以上研究存在的问题, 本文将提出采用“分解”“重构”预测框架, 并采用融合t检验的EMD经验模态将序列分为高频分量和低频分量, 对高频分量采用先分解后进行Prophet预测以及低频分量直接进行Prophet预测的方法, 高频分解方法通过鲁棒性更强且能跨领域应用的STL序列分解方法做进一步分解, 把分解出的季节和趋势作为预测模型输入特征, 尝试以此提高预测的精确度以及保证预测的全局性.
3 理论基础 3.1 EMD分解方法EMD分解方法是以傅里叶变换为基础的线性和稳态频谱分析的序列分解方法, 该方法根据数据自身局部的时间点特征来进行序列分解, 无需借助先验性的谐波基函数和小波基函数. 与傅里叶分解与小波分解方法具有本质性的差别. 理论上, EMD方法可以用来分析具有任何特征的序列数据, 更适合于分析非线性、非平稳数据. EMD的基本思想是将一个复杂信号分解成一系列的局部的震荡模式, 每个模式中都包含一个明显的共振频率和对应的振幅. 在实际应用中, EMD可以用于提取时间序列中的趋势性或周期性变化. EMD通过算法将序列按定义分解为中间信号, 满足条件的为本征模态函数(intrinsic mode function, IMF), 基于IMF进行下一次分解, 每个IMF为在不同时间点上的序列特征, IMF需满足以下两个条件.
1) 在整个数据序列中, 极值点的个数等于零点的个数或两者相差不超过1.
2) 任意时刻, 上包络线和下包络线的平均值为零. 其中上包络线由局部极大值点形成, 下包络线由局部极小值点形成.
3.2 STL序列分解STL序列分解是一种常见的时间序列与预处理方法. 具有高鲁棒性和高可适用性. 该方法将时间序列分解为季节性、趋势性和残差3个部分, 用于减少时间序列预测的噪声和调整模型的偏差. STL序列分解使用LOESS (locally weighted regression), 局部加权回归[36]算法来平滑季节和趋势. LOESS是一种局部平滑回归方法, 它会针对每个数据点进行拟合, 根据它周围的数据点来估计一个平滑的函数. 在STL序列分解中, LOESS用于平滑趋势和季节分量. 具体来说, LOESS用于将趋势分解为慢变和快变两个部分, 同时也用于将季节分解为周期性和非周期性两个部分, 从而实现对原始时间序列的分解.
4 模型算法 4.1 Prophet预测模型算法Prophet模型算法是由Facebook团队在2017年提出的一种时间序列建模方法[37,38], 该方法将时间序列看作是关于t的一个函数, 用拟合函数曲线的方法进行预测, 与传统的时间序列模型有本质上的区别, 更倾向于机器学习的建模方式. Prophet目的是为非专业用户提供一种简单易用、高效准确的时间序列预测工具. Prophet提供了丰富的统计信息和可视化工具, 具备高可解释性. 适用于各种行业和场景下的数据预测任务. 杨贵军等人提出的Prophet-X-12-ARIMA组合模型[39]的半年度和年度预测效果明显优于Prophet模型、X-12-ARIMA模型及ARIMA模型, 并发现当原始序列趋势变化剧烈时, Prophet-X-12-ARIMA组合模型的预测效果更优.
Prophet算法充分考虑到了时间序列常见的4个影响因素, 算法模型如下:
| y(t)=g(t)+s(t)+h(t)+εt | (1) |
其中,
g(t)模型函数有两个函数, 一个是基于逻辑回归函数, 另一个是基于分段线性函数, 常用的是基于逻辑回归函数.
逻辑回归函数:
| f(x)=C1+e−k(x+m) | (2) |
分段线性函数:
| f(x)=kt+m | (3) |
其中, C=C(t)为曲线的最大渐近值, k=k(t)表示曲线的增长率, m=m(t)表示曲线的中点.
4.2 改进Prophet模型算法 4.2.1 EMD算法1) 通过算出原始序列X(t)的上下极值点, 用插值函数来拟合原数据, 分别画出上、下包络线, 插值函数可选三次样条插值.
2) 求上、下包络线的均值ml, 画出均值包络线.
3)原始序列减均值包络线, 得到中间序列hl=X(t)–ml.
4) 判断中间序列是否满足作为IMF的条件, 若满足, 该序列就为原序列的一个IMF分量; 若不满足, 则迭代步骤1)–4), 直到满足为止.
根据上述步骤获得第1个IMF分量, 即IMF1, 作为得到下一个IMF的原始序列分解, 迭代执行步骤1)–4), 得到IMF2, 以此类推, 直到达到预设的IMF分量数量完成EMD分解.
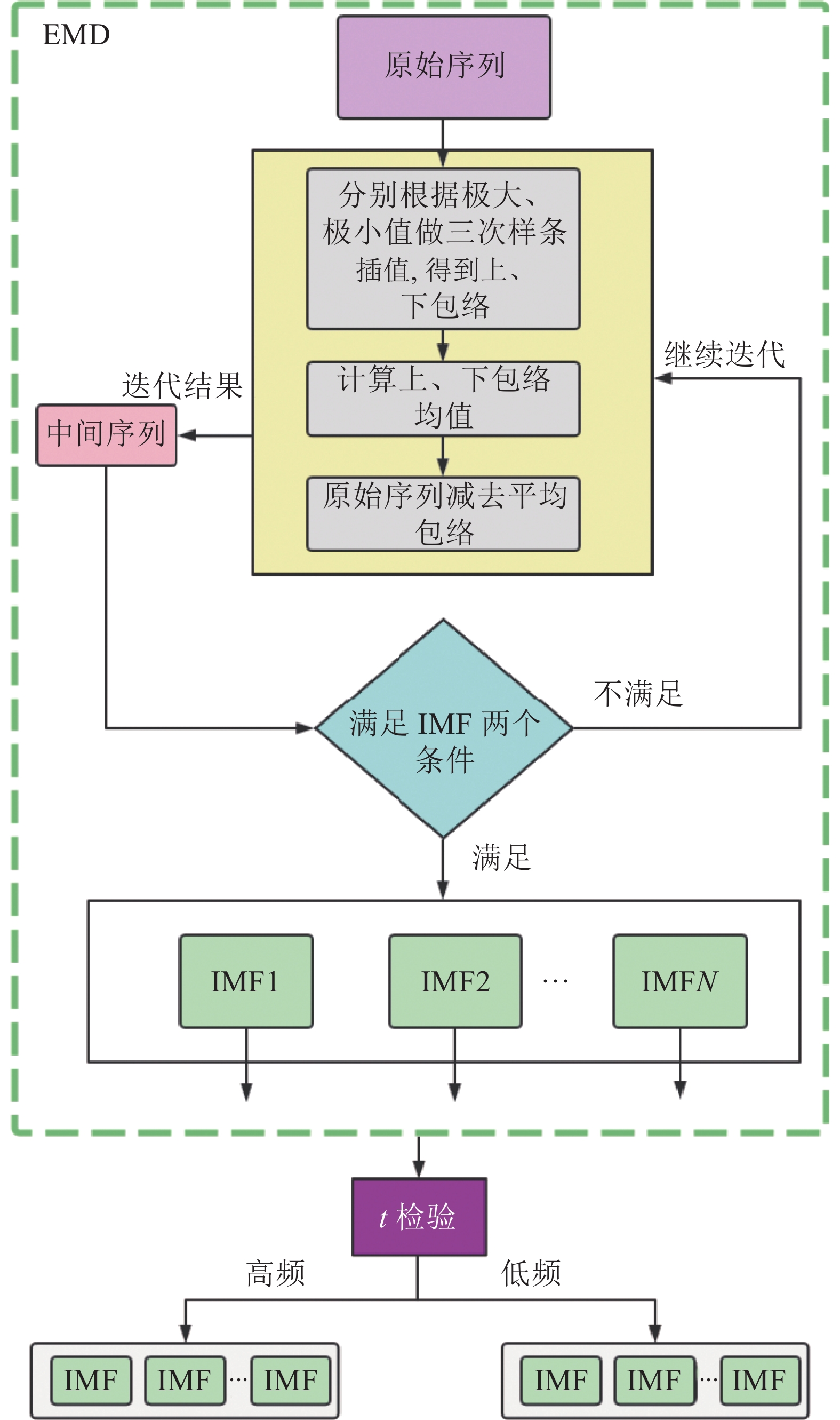
4.2.2 融合t检验的EMD算法融合t检验的EMD算法, 如图1所示, 在EMD的基础上增加了t检验, 该步骤进一步将得到的IMF划分为高低频IMF. 首先将时序数据做EMD处理, 得到IMF分量, 每个IMF的周期各不相同, 因此本文根据重构算法将分解得到的IMF进行高低频区分. 该方法[40]将得到的m个IMF进行前项累加和, 各累加和分别记作指标i(
| t=(ˉXi−0)/σi√n−1 | (4) |
其中,
|
图 1 融合t检验的EMD模型 |
4.2.3 ES-Prophet模型算法
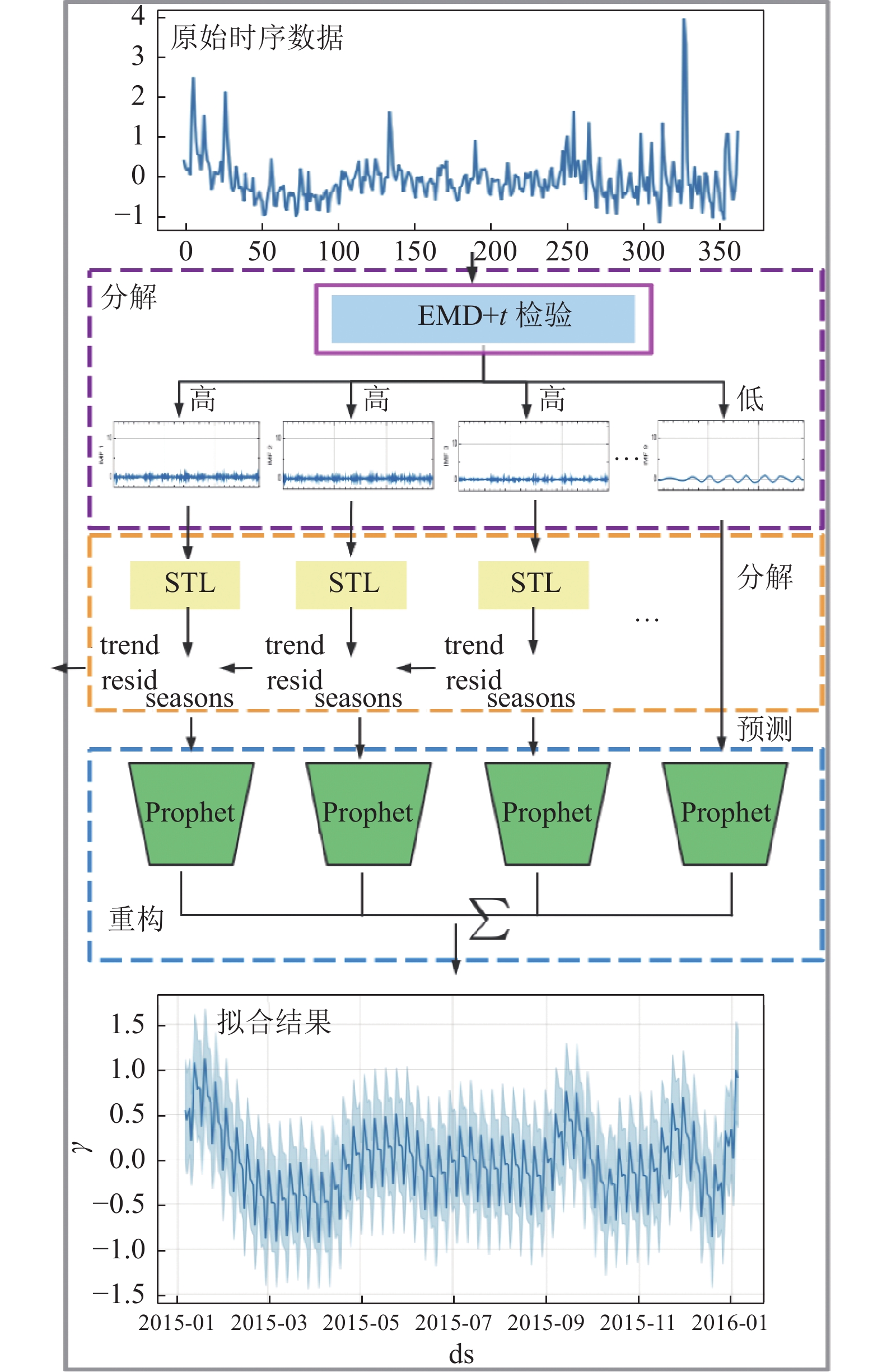
本研究将融合t检验的EMD和STL与预测模型Prophet融合得到ES-Prophet模型(如图2所示), 其中, ds为时间序列中dates列, y为values列. ES-Prophet模型算法比单一Prophet算法增加了融合了t检验的EMD, 融合t检验的EMD分解首先将时序数据做EMD处理, 得到IMF分量, 每个IMF的周期各不相同, 根据t检验将分解得到的IMF进行高低频区分. 这样能区别对待高低频数据, 对高频数据做进一步信息挖掘, 对高频分量做STL分解, 得到seasons、trend和resid分量, 去除resid分量, 将trend和seasons输入到Prophet进行预测, 而对低频分量直接做Prophet预测, 将各分量的预测结果进行累和, 得到最总预测结果. 相较于传统的LSTM以及Prophet预测模型, 经过STL序列分解后的周期数据能够提升模型的整体预测精确度, 而且融合EMD经验模态的Prophet模型较明显地提升了训练效率. 算法步骤如下.
|
图 2 ES-Prophet模型结构图 |
1) 首先将数据集进行EMD分解获得n个IMF分量, 观察分量特征, 通过t检验, 将IMF分为高频分量和低频分量.
2) 将分好的低频分量输入到Prophet模型中训练得到低频分量预测结果.
3) 将高频分量通过STL分解后输入Prophet模型预测得到高频分量预测结果.
4) 分别将高频、低频预测结果相加, 得到最终预测结果.
5 实验与分析 5.1 实验数据实验中使用的时间序列数据是佩顿·曼宁(Peyton Manning)的维基百科主页每日访问量[34], 数据年限从2007/12/10 到2016/01/20, 时间细粒度为天, 共计2903条数据. 佩顿·曼宁的维基百科主页每日访问量数据特征如下: 1)季节性: 佩顿·曼宁的维基百科主页每年都会出现季节性的波动, 通常在橄榄球赛季期间(9月–2月), 访问量较高. 2) 突发性: 佩顿·曼宁的某些重要事件或消息, 如退役、入选名人堂等, 会引发突发性的访问量增加. 3) 容易受到外部因素的影响: 佩顿·曼宁的维基百科主页的日访问量容易受到橄榄球比赛、相关新闻报道等外部因素的影响. 4) 长期趋势: 经过观察, 佩顿·曼宁的维基百科主页的日访问量呈现出长期稳定的趋势, 整体呈现增长态势. 5) 周期性: 除了季节性的波动之外, 每个月的访问量也会有周期性的变化, 通常在月初和月中访问量较高, 在月末则略有下降. 本研究选取数据集中2015/01/05–2016/01/05共365条数据作为建模数据, 预测2016/01/06–2016/01/20共15天数据.
5.2 评价指标本文通过均方根误差(root mean square error, RMSE), 绝对平均误差百分比(mean absolute percentage error, MAPE)以及拟合优度R2来评价ES-Prophet时序预测模型准确性的指标. ERMSE是预测值与实际值之差的平方再均值的平方根, 其值越小代表预测的性能越稳定, 计算公式如式(5), EMAPE是绝对平均误差百分比, 计算预测值和实际值的绝对平均误差, 其值越小说明模型预测精度更好, 公式如式(6), R2是拟合优度值, 值越大越好, 公式如式(7).
| ERMSE=√1nn∑i=1(ˆxi−xi)2 | (5) |
| EMAPE=100%nn∑i=1|ˆxi−xixi| | (6) |
| R2=1−n∑i=1(ˆxi−xi)2n∑i=1(ˉx−xi)2 | (7) |
其中,n为测试样本数,
本研究运行环境为Python 3.8, 采用的深度学习框架是PyTorch 1.13.1. 实验硬件配置为AMD Ryzen 5 4600U with Radeon Graphics.
实验中LSTM模型的参数设置如下.
输入维度inp_dim为1, 输出维度out_dim为1, 网络宽度mid_dim为16, 全连接层mid_layer为2, 迭代epoch设置为1000, 损失函数采用MSE损失, 优化器采用adma.
实验中ARIMA模型的参数设置采用默认值.
实验中Prophet模型的参数设置如下.
增长模型采用线性模型, changepoints变点数量设置为25, daily_seasonality和yearly_seasonality设置为true. 周期periods设置为1, freq为天. 其余为默认值.
实验中ES-Prophet模型的参数设置如下.
EMD的imf分量设置最大为6, STL的周期长度90, 时间窗口长度为30, Prophet增长模型采用线性模型, changepoints变点数量设置为25, daily_seasonality和yearly_seasonality设置为true. 周期periods设置为1, freq为天. 其余与Prophet保持一致.
5.4 对比实验分别选取Prophet、LSTM和ARIMA 共3个单一预测模型作为比较基准, 利用测试集的预测结果做预测准确率的评价.
表1所示本文所提算法与传统单一算法对比结果, ES-Prophet模型在ERMSE、EMAPE及R2上的结果分别是0.53、0.02%、0.82, 与Prophet模型对比, 指标ERMSE下降了22%, EMAPE下降了50%, R2提高了22%, 与LSTM模型对比, 指标ERMSE下降了61%,EMAPE下降了84%, R2提高了50%, 与ARIMA模型对比, 指标ERMSE下降了90%, EMAPE下降了89%, R2提高了58%, 综上所述, 本文提出的融合STL、EMD与Prophet的模型预测算法相对于其他单一算法有更高的预测精度.
| 表 1 对比实验结果 |
5.5 消融实验
为了验证本文提出的ES-Prophet预测模型的有效性. 本文通过删除实验因素EMD和STL来研究其对实验结果的影响. 通过消融实验, 验证本文所提出的理论或假设的有效性. 消融实验分别为融合EMD和Prophet模型预测实验、融合STL和Prophet模型预测实验以及ES-Prophet模型预测实验. 融合STL的模型预测先将数据通过STL分解出趋势项、季节项、残差, 分别将趋势项、季节项、残差进行Prophet预测, 再对各项预测结果进行加和. 融合EMD的模型预测先将数据通过EMD分解出6个IMF分量以及残差部分. 将数据的IMF分量求和, 分别对求和后的IMF分量以及残差部分做Prophet预测.
表2所示为本研究消融实验结果, Prophet模型与EMD-Prophet、STL-Prophet在ERMSE、EMAPE及R2上的对比结果, EMD-Prophet模型指标ERMSE比Prophet降低了35.4%, EMAPE降低了25%, R2提高了16%, STL-Prophet模型指标ERMSE比Prophet降低了46%, EMAPE降低了25%, R2提高了20%, 综上所述, EMD-Prophet模型以及STL-Prophet都对基准模型Prophet有了一定的改进.
| 表 2 消融实验结果 |
6 结论与展望
本文提出了融合序列分解及Prophet的预测模型, 即ES-Prophet预测模型, 本研究在佩顿·曼宁的维基百科主页每日访问量的时间序列数据集上进行了预测实验, 实验结果表明ES-Prophet预测模型比单一使用Prophet、LSTM及ARIMA预测模型效果更好. 本实验得出如下结论.
1) 融合EMD的预测模型降低了原始时序数据的非平稳性, 提高了时序数据质量.
2) t检验将IMF分为高、低频分量, 对高频分量用STL分解进行Prophet预测, 低频分量直接用Prophet预测, 比仅使用Prophet或LSTM的误差要小, 考虑到了数据的全局性.
3) 改进的时序预测模型效果更好.
本文提出的融合模型具有一定的实际意义: 与传统单一算法相比本文算法提高了预测的准确度; 与其他模型相比该算法在保证准确度的同时提高了训练效率; 该算法使用不同领域、不同特征的时序数据, 迁移效果较好. 尽管在准确度和效率上都有明显提高, 但该算法对极端值的处理并没有达到理想水平, 原因是突变点偏离常规数据的水平无法准确估计, 通过设置Prophet的变点并不能完全覆盖, 后续将研究如何更好捕获数据的变点.
| [1] |
Kuznetsov V, Mohri M. Theory and algorithms for forecasting time series. arXiv:1803.05814, 2018.
|
| [2] |
Li YL, Yu NP, Wang W. Machine learning-driven virtual bidding with electricity market efficiency analysis. IEEE Transactions on Power Systems, 2022, 37(1): 354-364. DOI:10.1109/TPWRS.2021.3096469 |
| [3] |
De Livera AM, Hyndman RJ, Snyder RD. Forecasting time series with complex seasonal patterns using exponential smoothing. Journal of the American Statistical Association, 2011, 106(496): 1513-1527. DOI:10.1198/jasa.2011.tm09771 |
| [4] |
Gelper S, Fried R, Croux C. Robust forecasting with exponential and Holt-Winters smoothing. Journal of Forecasting, 2010, 29(3): 285-300. DOI:10.1002/for.1125 |
| [5] |
Ahmed NK, Atiya AF, El Gayar N, et al. An empirical comparison of machine learning models for time series forecasting. Econometric Reviews, 2010, 29(5–6): 594–621.
|
| [6] |
Lim B, Zohren S. Time-series forecasting with deep learning: A survey. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2021, 379(2194): 20200209. DOI:10.1098/rsta.2020.0209 |
| [7] |
Zhao Z, Chen WH, Wu XM, et al. LSTM network: A deep learning approach for short-term traffic forecast. IET Intelligent Transport Systems, 2017, 11(2): 68-75. DOI:10.1049/iet-its.2016.0208 |
| [8] |
Li BW, Zhang J, He Y, et al. Short-term load-forecasting method based on wavelet decomposition with second-order gray neural network model combined with ADF test. IEEE Access, 2017, 5: 16324-16331. DOI:10.1109/ACCESS.2017.2738029 |
| [9] |
Zhang GW, Ren T, Yang YF. A new unified deep learning approach with decomposition-reconstruction-ensemble framework for time series forecasting. arXiv:2002.09695, 2020.
|
| [10] |
赵婷婷, 韩雅杰, 杨梦楠, 等. 基于机器学习的时序数据预测方法研究综述. 天津科技大学学报, 2021, 36(5): 1-9. DOI:10.13364/j.issn.1672-6510.20200203 |
| [11] |
Li CG, Yang B, Li M. Forecasting analysis of shanghai stock index based on ARIMA model. MATEC Web of Conferences, 2017, 100: 02029. DOI:10.1051/matecconf/201710002029 |
| [12] |
Domingos P. The Master Algorithm: How the Quest for the Ultimate Learning Machine will Remake Our World. Basic Books, 2015.
|
| [13] |
Franklin J. The elements of statistical learning: Data mining, inference and prediction. The Mathematical Intelligencer, 2005, 27(2): 83-85. |
| [14] |
Goodfellow J, Bengio Y, Courville A. Deep learning. Genetic Programming and Evolvable Machines, 2018, 19(1): 305-307. |
| [15] |
Wang JS, Chen XH, Zhang F, et al. Building load forecasting using deep neural network with efficient feature fusion. Journal of Modern Power Systems and Clean Energy, 2021, 9(1): 160-169. DOI:10.35833/MPCE.2020.000321 |
| [16] |
庞传军, 张波, 余建明. 基于LSTM循环神经网络的短期电力负荷预测. 电力工程技术, 2021, 40(1): 175-180, 194. |
| [17] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [18] |
魏健, 赵红涛, 刘敦楠, 等. 基于注意力机制的CNN-LSTM短期电力负荷预测方法. 华北电力大学学报, 2021, 48(1): 42-47. |
| [19] |
陈振宇, 刘金波, 李晨, 等. 基于LSTM与XGBoost组合模型的超短期电力负荷预测. 电网技术, 2020, 44(2): 614-620. DOI:10.13335/j.1000-3673.pst.2019.1566 |
| [20] |
彭湃, 刘敏. 基于Prophet-LSTM组合模型的短期负荷预测方法. 电力系统及其自动化学报, 2021, 33(11): 15-20. DOI:10.19635/j.cnki.csu-epsa.000705 |
| [21] |
Huan J, Cao WJ, Qin YL. Prediction of dissolved oxygen in aquaculture based on EEMD and LSSVM optimized by the Bayesian evidence framework. Computers and Electronics in Agriculture, 2018, 150: 257-265. DOI:10.1016/j.compag.2018.04.022 |
| [22] |
Zhou YR, Li TY, Shi JY, et al. A CEEMDAN and XGBoost-based approach to forecast crude oil prices. Complexity, 2019, 2019: 4392785. |
| [23] |
Percival DB, Walden AT. Spectral Analysis for Uunivariate Time Series. Cambridge: Cambridge University Press, 2000. 491.
|
| [24] |
Bento PMR, Pombo JAN, Calado MRA, et al. Optimization of neural network with wavelet transform and improved data selection using bat algorithm for short-term load forecasting. Neurocomputing, 2019, 358: 53-71. DOI:10.1016/j.neucom.2019.05.030 |
| [25] |
Fan CD, Ding CK, Zheng JH, et al. Empirical mode decomposition based multi-objective deep belief network for short-term power load forecasting. Neurocomputing, 2020, 388: 110-123. DOI:10.1016/j.neucom.2020.01.031 |
| [26] |
孔祥玉, 李闯, 郑锋, 等. 基于经验模态分解与特征相关分析的短期负荷预测方法. 电力系统自动化, 2019, 43(5): 46-52. |
| [27] |
林昱, 常晋源, 黄雁勇. 融合经验模态分解与深度时序模型的股价预测. 系统工程理论与实践, 2022, 42(6): 1663-1677. |
| [28] |
许江雯, 杨航. 基于X11过程的陕西省月度快递量预测分析. 轻工科技, 2021, 37(11): 102-104. |
| [29] |
Sun TH, Zhang TY, Teng Y, et al. Monthly electricity consumption forecasting method based on X12 and STL decomposition model in an integrated energy system. Mathematical Problems in Engineering, 2019, 2019: 9012543. |
| [30] |
Zhang G, Patuwo BE, Hu MY. Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting, 1998, 14(1): 35–62.
|
| [31] |
张子森, 徐晓钟. 基于分解和多分量集成学习的负荷预测方法. 计算机与现代化, 2023(3): 96-101, 106. |
| [32] |
李飞宏, 肖迎群. 基于STL-LSTM-TCN模型的短期负荷预测方法. 电子设计工程, 2023, 31(7): 47-51, 56. |
| [33] |
郭利进, 许瑞伟. 时序分解下改进果蝇算法的LSTM在水质预测的应用. 长江科学院院报. http://kns.cnki.net/kcms/detail/42.1171.TV.20221223.1013.003.html. (2022-12-26).
|
| [34] |
赵建东, 朱丹, 刘佳欣. 基于时间序列分解与门控循环单元的地铁换乘客流预测. 华南理工大学学报(自然科学版), 2022, 50(5): 22-31. |
| [35] |
林海飞, 刘时豪, 周捷, 等. 基于STL-EEMD-GA-SVR的采煤工作面瓦斯涌出量预测方法及应用. 煤田地质与勘探, 2022, 50(12): 131–141.
|
| [36] |
Cleveland WS, Devlin SJ. Locally weighted regression: An approach to regression analysis by local fitting. Journal of the American Statistical Association, 1988, 83(403): 569-610. |
| [37] |
Taylor SJ, Letham B. Forecasting at scale. The American Statistician, 2018, 72(1): 37-45. DOI:10.1080/00031305.2017.1380080 |
| [38] |
Li SS, Shen Z, Xiong G. A K-nearest neighbor locally weighted regression method for short-term traffic flow forecasting. Proceedings of the 15th International IEEE Conference on Intelligent Transportation Systems. Anchorage: IEEE, 2012. 1596–1601.
|
| [39] |
杨贵军, 李晓霞, 孙玲莉. Prophet-X-12-ARIMA组合模型及交通运输量预测. 统计与决策, 2023, 39(4): 29-34. DOI:10.13546/j.cnki.tjyjc.2023.04.005 |
| [40] |
齐绍洲, 赵鑫, 谭秀杰. 基于EEMD模型的中国碳市场价格形成机制研究. 武汉大学学报(哲学社会科学版), 2015, 68(4): 56-65. DOI:10.14086/j.cnki.wujss.2015.04.008 |
 2023, Vol. 32
2023, Vol. 32



