自动制造系统(automated manufacturing systems, AMSs)用一组有限的资源同时处理多种零件. 因此不适当的资源分配将导致系统出现循环等待, 带来巨大的经济损失^[1–4]. AMSs中可能出现故障的资源称为不可靠资源. 当不可靠资源故障时, 需要故障资源的零件无法继续加工. 此外, 资源故障可能造成系统阻塞, 导致不需要故障资源的零件也无法进行加工. 因此, 需要为AMSs开发有效的死锁控制策略, 以阻止系统出现死锁和阻塞状态^[5–11].

目前广泛使用的死锁控制策略之一是死锁预防, 其主要应用以下两种技术预防死锁. 一种是可达性分析^[12–14], 该方式可以使系统达到最大许可性. 然而, 它存在状态爆炸的问题. 另一种是结构分析^[15–19], 分为以下两种方法. 基于虹吸的方法通过预防标记不足的虹吸解决死锁问题^[15,16]. 基于资源回路的方法通过阻止回路饱和解决死锁问题^[17–19]. 对于各类复杂的AMSs, 研究人员分别通过最大完美资源变迁(maximal perfect resource transition, MPRT)回路^[18,19], 最大完美控制变迁(maximal perfect control transition, MPCT)回路^[20], 最大关键资源变迁(maximal critical resource transition, MCRT)回路^[21], 完美活动(perfect activity, PA)回路^[22,23]等解决死锁问题.

Li等基于资源回路的概念划分Petri网(Petri nets, PNs), 通过为划分后的子网设计管理器合成整个PNs的活性增强管理器. 这种分治策略相比以往方法可以降低复杂度, 但复杂度仍为指数级^[17]. Liu等对于具有资源的简单序列进程系统(systems of simple sequential processes with resources, S³PRs), 仅为有效变迁覆盖中的MPRT回路添加控制器以预防死锁. 这种添加方法可以降低外部控制器的结构, 但会拒绝一些可达标记^[19]. Liu等通过为MPRT回路添加控制器预防系统死锁, 并为MPCT回路添加控制器预防二次死锁, 解决具有关键资源的S³PRs的死锁. 该策略考虑了造成死锁的一种特殊标记, 称为无死锁不安全标记, 但其控制器添加方式会拒绝一些可达标记^[20]. Feng等将S³PRs的活性条件推广到具有共享资源的顺序系统(systems of sequential systems with shared resources, S⁴PRs), 通过饱和的PA回路表征S⁴PRs中的死锁. 该方法考虑具有多资源获取的系统, 但控制器结构较为复杂^[22]. 为此, Feng等在文献[22]的基础上将可饱和PA回路分为独立和依赖两类, 通过为独立可饱和回路添加控制器预防死锁. 该方法已经取得突破性的进展, 但其没有考虑造成死锁的无死锁不安全标记^[23]. 对于多数量资源获取的系统, Feng等将死锁用饱和的PRT回路表征, 得到系统的变迁覆盖. 该方法复杂度较低, 但会拒绝一些可达标记, 且该方法可适用的系统较少^[24].

上面提到的死锁控制方法没有考虑到资源故障的情况, 但现实生活中, 资源故障是不可避免的. 对于具有不可靠资源的AMSs, 需要应用有效的控制策略预防系统死锁. Feng等研究了具有一种不可靠资源, 且一次最多有一个不可靠资源故障的S³PRs, 并在变迁覆盖^[17]的基础上提出强变迁覆盖. 该方法确保即使资源故障, 系统也可以无限地处理所有类型的零件. 但他们没有考虑具有多种不可靠资源的系统^[18]. Du等对于具有多种不可靠资源的S³PRs, 通过线性约束控制死锁标记下的MCRT回路. 该控制器考虑了需要MCRT回路中不可靠资源的活动库所, 保证资源故障时进程的连续操作. 该方法考虑了多种资源故障的情况, 但S³PRs中没有同时需要可靠和不可靠资源的阶段, 其不能解决这种阶段下资源故障造成的阻塞^[21].

面向进程Petri网(process-oriented Petri nets, POPNs)可以直观地描述AMSs, 但其模型结构复杂度较高, 且不易寻找造成死锁的回路. 为此, 人们提出面向资源Petri网(resource-oriented Petri nets, ROPNs)的建模方式. Zhao等使用饱和的生产进程回路(production process circuit, PPC)描述死锁, 通过在线监督管理器, 前瞻预测托肯的前进. 该策略通过控制变迁的触发解决死锁问题. 但其复杂度较高^[25]. 对于具有加权资源分配的简单顺序进程系统(weighted S³PRs, WS³PRs), Liu等定义其对应的ROPN模型, 提出一种基于结构分析的不需要外部监督的死锁预防方法. 该方法主要借助回路中弧线的权值合理分配资源, 其主要关注资源的利用率, 没有考虑可达标记的问题^[26]. Chen等定义S³PRs对应的ROPN模型, 通过对其进行可达性分析揭示不良标记与强连通子网之间的关系. 他们仅为每个强连通子网添加一个死锁控制器, 因此控制器的结构较为简单. 但是这种借助可达分析的方法复杂度较高^[27]. Chen等对具有权重的AMSs, 通过控制一些特定变迁的触发, 避免受控系统出现死锁. 该方法具有多项式复杂度, 但会拒绝一些可达标记^[28].

通过分析发现, 现有死锁预防策略的问题集中体现在计算复杂度较高、拒绝一些可达标记、外部控制器的结构复杂、资源故障导致阻塞等多个方面. 由于ROPN模型的结构特征, 其更方便寻找造成死锁的可饱和回路. 然而现有的ROPN模型较为简单, 它们大多仅为具有灵活路径的AMSs建模. 基于这些前提, 本文研究一类具有多种不可靠资源的复杂AMSs的死锁问题, 其主要贡献总结如下.

(1) 通过建立POPNs与ROPNs的联系, 提出一种将POPNs转化为ROPNs的算法. 与现有ROPN模型相比, 本文的模型可以表示具有多类型资源获取、装配操作和灵活路径的AMSs.

(2) 提出一种新的死锁监督控制器. 与现有控制器相比, 该控制器具有控制开关, 通过实时改变控制库所的容量, 系统可以接受更多的安全标记.

(3) 提出危险库所的概念, 并为它们添加资源缓冲子网. 使得即使不可靠资源故障, 不需要故障资源的零件仍然可以持续加工.

1 使用ROPNs建模

本节首先介绍了ROPNs的基本符号, 然后提出一种新的算法建立一类复杂AMSs的ROPN模型. 与文献[25–28]使用的模型不同, 本文的模型可以表示具有多类型资源获取、装配操作和灵活路径的AMSs, 且其考虑了同时需要可靠和不可靠资源的特殊阶段.

1.1 ROPNs

在AMSs中, 零件在每个阶段获取不同的资源进行加工处理. ROPNs使用资源库所表示AMSs中零件加工所需资源, 用变迁表示零件的加工阶段. 通过使用变迁将资源库所与零件存储中心相连接, 可以描述一种零件的加工过程. 由于一个AMS中具有多种不同的零件, 在ROPNs中引入颜色, 使用有色变迁区分不同零件的加工阶段. 此外, 库所中的有色托肯只能触发具有相同颜色的变迁. 通过这种触发方式, ROPNs可以完整的描述AMSs中所有零件的加工进程.

在ROPNs中, K表示资源库所的容量. 资源库所中的托肯表示当前状态下已经被占用的资源空间, 托肯的移动表示零件的加工过程. 此外, P表示库所集, T表示变迁集, I表示输入函数, O表示输出函数, M表示当前标记.

定义1. $\forall $ p∈P, p的输入变迁为: •p = {t: t∈T, O(p, t) > 0}, p的输出变迁为: p• = {t: t∈T, I(p, t) > 0}. 与 p类似, $\forall $ t∈T, t的输入库所为: •t = {p: p∈P, I(p, t) > 0}, t的输出库所为: t• = {p: p∈P, O(p, t) > 0}.

在ROPNs中, 每个变迁t_id只有一个独特的颜色c_id, 用来区分不同的零件阶段. 一个库所p_l可能包含多种颜色的托肯, 且不同库所中可能有相同颜色的托肯, 用(p_l, c_i)表示p_l中c_i颜色的托肯. M(p_l)表示标记M下p_l中所有颜色的托肯数量, M(p_l, c_id)表示标记M下p_l中c_id颜色的托肯数量.

定义2. 给定可达标记M∈R(N, M₀), 当同时满足式(1)和式(2)时, 称变迁t_id是使能的.

$ M(p_{l}, c_{id}) ≥ I(p_{l}, t_{id}) $

(1)

$ K(p_{l}) ≥ M(p_{l}) − I(p_{l}, t_{id}) \cdot (c_{id}) + O(p_{l}, t_{id}) \cdot (c_{id}) $

(2)

当仅满足式(1)时, 表明t_id的输入库所中都有足够的c_id颜色的托肯, 此时t_id为进程使能. 当仅满足式(2)时, 表明t_id的输出库所都有足够的资源空间, 此时t_id为资源使能. 用T_EN表示标记M下的使能变迁集.

定义3. 给定可达标记M∈R(N, M₀), 如果触发使能变迁t_id后M变为M', 用符号表示为M [t_id 〉 M'.

$ M'(p_{l}) = M(p_{l}) − I(p_{l}, t_{id}) \cdot (c_{id}) + O(p_{l}, t_{id}) \cdot (c_{id})　　 $

(3)

1.2 SRMGs

多类型资源获取阶段可以表示同时需要可靠和不可靠资源的零件阶段, 装配操作可以提高零件的生产效率, 灵活路径可以增强零件加工的灵活性, 这些结构都具有很重要的现实意义. 但是现有的POPNs不能为同时具有这些结构的AMSs建模. 因此本节建立POPNs与ROPNs的联系, 提出一种新的ROPN模型, 称为特殊资源标记图(special resource marked graphs, SRMGs).

定义4. 一个SRMG表示为一个八元组N = (P, T, C, X, I, O, M, K), 其结构为:

(1) P = P₀∪P_R, P₀为零件存储中心. P_R = P_Rr∪P_Ru 是一组有限的资源库所集, 其中P_Rr是一组可靠资源库所集, P_Ru是一组不可靠资源库所集. $ \forall $ p_a, p_b∈P, |p_a•| ≥ 1且|•p_b| ≥ 1, 表示系统可以具有灵活路径.

(2) T = ∪T_i, T_i表示第i种零件加工过程中的变迁. $\forall $ t_c, t_d∈T_i, |t_c•| ≥ 1且|•t_d| ≥ 1. 若t_c• = •t_d, 表示多类型资源获取阶段. 若t_c• ≠ •t_d, 表示装配操作. P∪T ≠ $\varnothing $ 且P∩T = $\varnothing$ .

(3) C: C(p_l)和C(t_id)分别代表p_l中托肯的颜色和t_id的颜色.

(4) X = ∪X_i, i∈ $\mathbb{N}_{{n}}^ +$ = ${\mathbb{N}_n}$ \ {0} = {1, …, n}是零件类型集, X_i表示第i种零件.

(5) I: P×T→ $\mathbb{N}$ = {0, 1, 2, …}, 表示从库所到变迁的有向弧.

(6) O: P×T→ $\mathbb{N}$ , 表示从变迁到库所的有向弧.

(7) M: P→ $\mathbb{N}$ , 表示库所中托肯的数量, M₀为初始标记.

(8) K: P→ ${\mathbb{N}^ + }$ = $\mathbb{N}$ \ {0} = {1, 2, …}, K(p_l)表示p_l一次可以具有的最大托肯数, K(P₀) = ∞.

假设AMSs中没有零件会连续使用同一资源, 如果有, 将这些连续操作视为一个加工阶段. $\forall $ p_l∈P_R, p_l有多个输入变迁表示零件对p_l的资源空间的竞争, 多个输出变迁表示p_l可选择的加工零件.

下面使用算法1建立ROPN模型, 其主要借助AMSs的POPN模型, 通过删减活动库所以及更改部分弧线, 在已有POPN模型的基础上生成其对应的ROPN模型. 对于可以描述多类型资源获取、装配操作和灵活路径的ROPN模型, 称它们为SRMGs.

算法1. 基于ROPNs建立的模型

输入: AMSs的POPN模型

输出: 对应的ROPN模型

1) 删除POPN模型中的P_B和P_A, 以及连接这些库所的弧;

2) 删除为资源库所标记的容量, 并将r_l转化为对应的p_l, 其中K(p_l) = M₀(r_l);

3) 将剩余网中弧的方向反转;

4) 添加零件存储中心P₀;

5) 在P₀与没有输入库所的变迁t_i之间添加I(P₀, t_i), 在P₀与没有输出库所的变迁t_j之间添加O(P₀, t_j);

6) 为变迁赋予颜色, C(t_id) = c_id;

对于一个没有资源循环等待的标记M, 其是一个无死锁标记. 如果M中所有使能变迁触发后都会到达死锁标记, 称该标记为无死锁不安全标记.

定义5. 给定可达标记M∈R(N, M₀), 如果M为死锁或无死锁不安全标记, 称M为不安全标记. 否则, 称M为安全标记.

将触发后不会导致不安全标记的使能变迁称为活性变迁, 用T_RL表示标记M下的活性变迁集. 下面, 介绍本文的死锁预防策略, 其通过计算活性变迁, 阻止系统到达不安全标记.

2 死锁预防策略

本文的目标是解决AMSs的死锁问题, 因此需要破坏死锁的循环等待条件. 在方法的选取上, 采用死锁预防的思想. 其通过分析模型找到造成死锁的特殊结构, 然后添加控制器阻止这些特殊结构饱和达到预防死锁的目的. 基于这一思想, 本文借助SRMGs的结构特征, 找到造成死锁的可饱和回路, 通过离线方式为这些回路设计控制器. 控制器通过限制变迁的触发阻止系统到达不安全标记. 考虑到资源故障问题, 为危险库所添加资源缓冲子网. 这种子网起到缓冲区的作用, 使得资源故障不会影响系统的正常运行.

2.1 基本控制器

对于触发后导致回路没有剩余资源空间的变迁, 现有死锁控制器阻止它们的触发. 这导致控制策略会拒绝一些可达安全标记. 针对这一问题, 本节设计一种具有开关的控制器. 该方法可以使系统接受更多的可达安全标记. 针对控制器的结构复杂性问题, 基于简化策略仅为基本资源等待回路添加基本控制器, 在降低外部结构的基础上预防系统到达死锁标记.

定义6. 在SRMGs中, 将每个库所(变迁)视为一个节点. 一条路径是有序的节点序列, 表示为<x₁, x₂, …, x_n >. 其中(1) { x₁, x₂, …, x_n} $ \subseteq $ P∪T; (2) x_i+1∈x_i•. 对于一条路径, 如果x₁ = x_n, 称该路径为回路. 如果一个回路不包含P₀, 称该回路为资源等待回路(RWC).

定义7. 在SRMGs中, 如果回路R_l中的所有资源库所都是回路R_k的资源库所, 称R_k包含R_l. 如果一个RWC不包含任何其他的RWC, 称其为基本资源等待回路(BRWC). 用R_i表示一个BRWC, R_I表示R_i集.

定义8. 如果t不在R_i中, t的输入(输出)库所在R_i中, 且t的输出(输入)库所不在R_i中, 称t为R_i的输出(输入)变迁. T_I(R_i)(T_O(R_i))表示R_i的输入(输出)变迁集.

根据定义8可知, 变迁t不可能同时为一个回路的输入和输出变迁.

定义9. 对于变迁t_id, 用R_Iid表示输入变迁是t_id的BRWC集, R_Oid表示输出变迁是t_id的BRWC集.

定义10. 具有多个输出库所的变迁称为多资源获取变迁, 用t_ma表示, T_ma表示t_ma集. 具有多个输入库所的变迁称为多资源释放变迁, 用t_mr表示, T_mr表示t_mr集. t_ma的输出库所用P_Oma表示, t_mr的输入库所用P_Imr表示, 如果P_Oma = P_Imr, 称t_ma和t_mr是相对应的变迁.

由于t_ma具有多个输出库所, 如果t_ma为R_i的输入变迁, 其触发后可能占用R_i的多个资源空间. 当然, t_ma的输出库所不一定都位于R_i中.

定义11. R_i(P) = {p₁, …, p_r}表示R_i中的库所集, R_i(T) = {t₁, …, t_r}表示R_i中的变迁集.

事实上, 回路中的库所数一定等于变迁数.

定义12. 在标记M下, 对于R_i中的某个托肯, 如果其触发R_i的活性输出变迁后仍在R_i中, 称该托肯为标记M下R_i的循环托肯. 否则, 称该托肯为标记M下R_i的可离开托肯.

定义13. 给定标记M, 如果回路R_i同时满足以下条件, 称其为饱和回路: (1) M(R_i) = K(R_i) = ∑K(p_l); (2) 在标记M下, R_i中没有可离开托肯.

为了控制BRWC中托肯的数量, 算法2为R_I添加具有开关的基本控制器. R_i的基本控制器定义如下: R_ci = {p_ci, s_ci, I(p_ci), O(p_ci), W(p_ci), K(p_ci)}. p_ci表示基本控制库所, 其分为基本可用空间p_ci1和基本缓冲空间p_ci2. s_ci表示基本控制开关. I(p_ci)表示p_ci的输入弧, O(p_ci)表示p_ci的输出弧. W(p_ci)表示p_ci的弧的权重, 意味着变迁的触发会占用或释放p_ci的多个资源空间. K(p_ci) = K(p_ci1)⊕K(p_ci2)表示p_ci的容量, 其是根据开关状态动态变化的. 初始时, M₀(s_ci) = off, K(p_ci) = K(p_ci1). 当s_ci = on时, K(p_ci) = K(p_ci1) + K(p_ci2). 由于触发t_ma可能会占用R_i的多个资源空间, 用|O(R_i(P), t_a)|表示t_a指向R_i中库所的弧的数量, 则W(O(p_ci, t_a))表示触发t_a占用的p_ci的资源空间数. 触发t_mr可能会释放R_i的多个资源空间, |I(R_i(P), t_b)|表示R_i中库所指向t_b的弧的数量, W(I(p_ci, t_b))表示触发t_b释放的p_ci的资源空间数.

算法2. 基本控制器的添加方法

输入: R_I

输出: R_CI

1) for(i = 1; i ≤ |R_I |; i++)

2) 　 R_i = R_i∪p_ci∪s_ci;

3) 　 M₀(s_ci) = off;

4) 　 K(p_ci1) = ∑K(p_l) − 1;

4)　 K(p_ci2) = 1; K(p_ci) = K(p_ci1)♁K(p_ci2); // $\forall $ p_l∈R_i

5) 　 for(a = 1; a ≤ |T_I(R_i)|; a++)

6) 　　 R_i = R_i∪O(p_ci, t_a); // $\forall $ t_a∈T_I(R_i), W(O(p_ci, t_a)) = |O(R_i(P), t_a)|

7) 　 for(b = 1; b ≤ |T_O(R_i)|; b++)

8)　　 R_i = R_i∪I(p_ci, t_b); // $\forall $ t_b∈T_O(R_i), W(I(p_ci, t_b)) = |I(R_i(P), t_b)|

定义14. 给定标记M, $\forall $ p_l∈R_i, p_ci的剩余资源空间为Re(M(p_ci)) = ∑Re(M(p_l)), 其中Re(M(p_l)) = K(p_l) − M(p_l). p_ci的可用资源空间为Ra(M(p_ci)) = Re(M(p_ci)) − K(p_ci2). 如果 $\exists $ t_il∈T_RL∩T_O(R_i), M [t_il 〉M₁, p_ci的潜在资源空间为Rp(M(p_ci)) = Re(M'(p_ci)). 否则, Rp(M(p_ci)) = Re(M(p_ci)).

当Re(M(p_ci)) > 0时, R_i至少有一个未被占用的资源空间. 根据定义13可知, R_i不是饱和的. 即使Re(M(p_ci)) = 0, 只要标记M下R_i有活性输出变迁, Rp(M(p_ci)) > 0. 此时 R_i具有可离开托肯, 该托肯离开R_i后可以释放占用的资源空间, R_i不是饱和的. 当Re(M(p_ci)) = 0, 且R_i没有活性输出变迁时, Rp(M(p_ci)) = 0. 此时R_i没有可离开托肯, R_i是饱和的.

引理1^[22]. 对于S⁴PR, 其死锁等价于系统中存在饱和的PA回路.

定理1. 对于SRMGs, 其死锁等价于系统中存在饱和的RWC.

证明: 根据引理1可知, 系统死锁时部分资源库所没有剩余资源空间, 且这些资源库所之间存在循环等待. 在SRMGs中, 这些资源库所构成饱和的回路. 此外, 由于K(P₀) = ∞, 包含P₀的回路永远不会饱和. 因此, 当AMSs出现死锁时, SRMGs中存在饱和的RWC. 同理, 当某个回路饱和时, 该回路一定是RWC. 由于该回路是饱和的, 回路中一定没有剩余资源空间, 且其输出变迁不能触发. 此时回路中的托肯相互等待其他托肯占用的资源空间, 因此需要这些资源的零件永远无法完成加工, 系统出现死锁.

定理2. 如果R_k包含R_l, 只要R_l不饱和, R_k也不会饱和.

证明: 根据定义13和定义14, 对于R_l, 以下两种情况下它不会饱和: 1) Re(M(p_cl)) ≠ 0, 此时不满足定义13的条件1. 由于R_k包含R_l, R_l中具有剩余资源空间的库所也一定在R_k中, 因此Re(M(p_ck)) ≠ 0; 2) Re(M(p_cl)) = 0, 且R_l有活性输出变迁, 表明R_l有可离开托肯, 此时不满足定义13的条件2. 由于R_k包含R_l, R_l的活性输出变迁一定是R_k的输出变迁, 因此R_k不会饱和. 综上所述, 只要R_l不饱和, R_k也不会饱和.

R_CI = {p_CI, s_CI, I(p_CI), O(p_CI), W(p_CI), K(p_CI)}表示R_I的基本控制器. (N_CI, M_0CI) = (N, M₀) $ \otimes $ R_CI表示为一个SRMG添加基本控制器, 在控制开关状态不变的情况下, M(R_i) = M(p_ci) ≤ K(R_i) − 1. 根据定理2可知, 此时所有回路都不会饱和.

2.2 总控制器

现有的死锁预防策略很少考虑无死锁不安全标记. 由于这种特殊标记一定会导致死锁, 因此有必要阻止系统到达这些标记. 前文通过添加基本控制器的方式仅能预防回路饱和, 不能阻止系统到达无死锁不安全标记. 为此, 本节引入总控制器.

定义15. 由n (n ≥ 2)个BRWC组成的回路称为交互式基本资源等待回路(IBC), B_j表示一个IBC.

与BRWC中的定义类似, T_I(B_j)(T_O(B_j))表示B_j的输入(输出)变迁集. B_Iid表示输入变迁是t_id的IBC集, B_Oid表示输出变迁是t_id的IBC集. B_j(P)表示B_j中的库所集, B_j(T)表示B_j中的变迁集.

为了控制IBC中托肯的数量, 算法3为部分回路添加总控制器, 其中B_J表示需要添加总控制器的所有回路. 与基本控制器类似, B_j的总控制器定义如下: B_cj = {P_cj, S_cj, I(P_cj), O(P_cj), W(P_cj), K(P_cj)}. 假设B_j由n_j个BRWC组成, 将S_cj(P_cj2)分成n_j份, 每一份用 $S_{{{cj}}}^i$ ( $P_{{{cj2}}}^i$ )表示, 对应于组成B_j的回路R_i的s_ci(p_ci2). K(P_cj) = K(P_cj1)⊕K(P_cj2), 其中K( $P_{{{cj2}}}^i$ ) = 1, K(P_cj2) = ∑K( $P_{{{cj2}}}^i$ ) = n_j. 子开关 $S_{{{cj}}}^i$ 与s_ci具有相同的状态, 用于控制子缓冲空间 $P_{{{cj2}}}^i$ 的资源空间. 初始时, 所有子开关处于关闭状态, M₀(S_cj) = off, K(P_cj) = K(P_cj1). 当s_ci = on时, 其对应的子开关 $S_{{{cj}}}^i$ = on, K(P_cj) = K(P_cj1) + K( $P_{{{cj2}}}^i$ ).

算法3. 系统中总控制器的添加方法

输入: B_J

输出: B_CJ

1) for(j = 1; j ≤ |B_J|; j++)

2) 　 B_j = B_j∪P_cj∪S_cj;

3) 　 M₀(S_cj) = off;

4) 　 K(P_cj1) = ∑K(p_ȴ) − n_j; K( $\scriptstyle P_{{{cj2}}}^i$ ) = 1; K(P_cj) = K(P_cj1)⊕K( $\scriptstyle P_{{{cj2}}}^1$ )⊕···⊕K( $\scriptstyle P_{{{cj2}}}^{{n_j}}$ ); // $\scriptstyle \forall $ p_ȴ∈B_j

5)　 for(c = 1; c ≤ |T_I(B_j)|; c++)

6) 　　 B_j = B_j∪O(P_cj, t_c); // $\scriptstyle \forall $ t_c∈T_I(B_j), W(O(P_cj, t_c)) = |O(B_j(P), t_c)|

7) 　 for(d = 1; d ≤ |T_O(B_j)|; d++)

8) 　　 B_j = B_j∪I(P_cj, t_d); // $\scriptstyle \forall $ t_d∈T_O(B_j), W(I(P_cj, t_d)) = |I(B_j(P), t_d)|

定义16. 给定标记M, $\forall $ p_ȴ∈B_j, P_cj的剩余资源空间为Re(M(P_cj)) = ∑Re(M(p_ȴ)), P_cj的可用资源空间为Ra(M(P_cj)) = Re(M(P_cj)) − K(P_cj2). 如果 $\exists $ t_il∈T_RL∩ T_O(B_j), M [t_il 〉 M₁, P_cj的潜在资源空间为Rp(M(P_cj)) = Re(M'(P_cj)). 否则, Rp(M(P_cj)) = Re(M(P_cj)).

定理3. 给定无死锁标记M, 对于n_j (n_j > 1)个BRWC组成的 B_j, 当且仅当B_j中的剩余资源空间小于n_j, 且这n_j个回路都没有活性输出变迁时, M为无死锁不安全标记.

证明: 充分性: 由于M是无死锁标记, 此时系统中没有饱和的回路. 若B_j中的剩余资源空间小于n_j, 表明只有多个BRWC共享的资源库所具有剩余资源空间. 此时任一BRWC的使能输入变迁触发后都会造成该回路饱和, 且已知回路没有活性输出变迁, 因此回路的使能变迁都不能触发, M为无死锁不安全标记.

必要性: 当M为无死锁不安全标记时, 回路的使能变迁触发后都会到达死锁标记, 因此回路没有活性输出变迁. 对于由n_j个BRWC组成的B_j, 由于多个BRWC具有共享的资源库所, Re(M(P_cj)) < ∑ Re(M(p_ci)). 由于M是无死锁标记, 且回路没有活性输出变迁, 因此每个BRWC都至少有一个剩余资源空间, 即 ∑Re(M(p_ci)) $\leqslant$ n_j. 因此Re(M(P_cj)) < n_j.

定理4. 如果B_k和B_l由相同的资源库所组成, 且组成B_k的BRWC的数量小于等于组成B_l的. 假设已经为B_l添加总控制器, 则不需要为B_k添加总控制器.

证明: 假设B_k、B_l的控制器分别为P_ck、P_cl, 由于B_k和B_l具有相同的资源库所, 那么P_ck、P_cl的剩余资源空间是相同的. 若组成B_k的BRWC的数量小于等于组成B_l的, 那么P_ck的可用资源空间大于等于P_cl的. 因此添加P_cl后, 无需添加P_ck就能控制B_k中允许存在的最大托肯数.

对于由n_j个BRWC组成的B_j, 主要有以下4种构成方式: (1) 组成B_j的多个回路具有同一个t_ma和t_ma相对应的变迁t_mr, 但这些BRWC中t_ma的输出库所(t_mr的输入库所)不同; (2) 组成B_j的n_j个BRWC共享一个或多个资源库所; (3) 组成B_j的n_j个BRWC两两之间具有共享的一个或多个资源库所. (4) 组成B_j的n_j1个BRWC共享一个或多个资源库所, 且组成B_j的n_j2个BRWC两两之间具有共享的一个或多个资源库所.

根据定理3可知, 只要每个BRWC都至少有一个仅属于自己的剩余资源空间, 或者某些没有剩余资源空间的BRWC具有活性输出变迁, 系统就不会到达无死锁不安全标记. 为实现这一目标, 下面将结合B_j的4种构成方式, 分别介绍总控制器的添加规则.

总控制器的添加规则: 对于第1种情况, 由于t_mr是组成B_j的多个BRWC的输出变迁, 其触发会释放B_j的多个资源空间. 因此即使不添加额外的总控制器, 也能保证系统不会出现无死锁不安全标记. 对于第2种情况, 由于n_j个BRWC具有相同的共享资源库所, 仅需为组成B_j的所有BRWC两两之间构成的IBC添加总控制器. 对于第3种情况, 一个BRWC会与相邻的两个BRWC分别具有不同的共享资源库所. 因此, 需要分别为组成B_j的所有2, 3, …, n_j个BRWC构成的IBC添加总控制器. 对于第4种情况, 结合第2种和第3种情况下的控制器添加方式即可. 最后, 根据定理4删减冗余的控制器.

B_CJ = {P_CJ, S_CJ, I(P_CJ), O(P_CJ), W(P_CJ), K(P_CJ)}表示B_J的总控制器. (N_CIJ, M_0CIJ) = (N, M₀) $ \otimes $ R_CI $ \otimes $ B_CJ = (N_CI, M_0CI) $ \otimes $ B_CJ表示为(N_CI, M_0CI)添加总控制器. 在控制开关状态不变的情况下, M(B_j) = M(P_cj) $ \leqslant $ K(B_j) − n_j, 且每个组成B_j的R_i都满足M(R_i) = M(p_ci) $ \leqslant $ K(R_i) − 1, 因此构成IBC的每个BRWC至少具有一个属于自己的剩余资源空间, 保证系统不会出现无死锁不安全标记.

2.3 变迁控制

为回路添加控制器后, 回路的输入变迁触发后同时会占用控制库所的资源空间. 通过控制库所的容量限制可以控制回路中的托肯数. 以此可以判断使能变迁是否为活性变迁, 从而实现变迁的控制, 预防系统到达不安全标记.

对于使能变迁t_id, 如果它不是任何回路的输入变迁, 那么触发t_id只会释放回路中库所的资源空间, 因此t_id一定是活性变迁. 给定无死锁标记M, M [t_id 〉 M', 算法4可以确定以t_id为输出变迁的回路在M'下的状态. (1)假设t_id是R_i的输出变迁, 由于t_id可能属于T_mr, 则t_id触发后可能释放p_ci的多个资源空间. 若Re(M'(p_ci)) $ \geqslant $ 1, 表明M'下R_i具有足够的可用资源空间, 因此无需借助基本缓冲空间p_ci2, M'(s_ci)= off. (2)假设t_id同时也是B_j的输出变迁, 若Re(M'(P_cj)) $ \geqslant $ K(P_cj2), 同理需要关闭s_ci对应的子开关 $S_{{{cj}}}^i$ , M'( $S_{{{cj}}}^i$ ) = off.

算法4. R_i的输出变迁t_id触发后控制器的状态

输入: 一个可达标记M∈R(N, M₀), R_i的输出变迁t_id

输出: M'

1) 初始化: M'(p_ci) = M(p_ci), M'(P_cj) = M(P_cj);

2) if(R_Oid ≠ $\scriptstyle \varnothing$ )

3) 　 for(i = 1; i $ \leqslant $ |R_Oid|; i++) // $\scriptstyle \forall $ R_i∈R_Oid

4)　　 M'(p_ci) = M(p_ci) − W(I(p_ci, t_id));

5)　　 if(M(s_ci) = on且 $\scriptstyle \nexists S_{{{cj}}}^i$ )

6)　　　 if(Re(M'(p_ci)) $ \geqslant $ 1)

7) 　　　　 M'(s_ci) = off;

8) 　 if(B_Oid ≠ $\varnothing$ )

9)　　 for(j = 1; j $ \leqslant $ |B_Oid|; j++) // $\forall $ B_j∈B_Oid

10) 　　　 M'(P_cj) = M(P_cj) − W(I(P_cj, t_id));

11) 　　　 if(M(s_ci) = on且M( $\scriptstyle S_{{{cj}}}^i$ ) = on)

12) 　　　　 if(Re(M'(p_ci)) $ \geqslant $ 1且Re(M'(P_cj)) $ \geqslant $ K(P_cj2))

13)　　　　　 M'(s_ci) = off; M'( $\scriptstyle S_{{{cj}}}^i$ ) = off;

14) M'(p_l) = M(p_l) − I(p_l, t_id) + O(p_l, t_id);

算法5将输出库所是P₀的变迁t称为结束变迁t_f, 并用T_F表示结束变迁集. 用M(R)表示Ra(M(p_ci)) < W(O(p_ci, t_id))的R_i集, M(B)表示Ra(M(P_cj)) < W(O(P_cj, t_id))的B_j集. 需要依次检查标记M'下M(R)与M(B)中的回路是否会饱和. 当所有的Rp(M(p_ci)) $ \geqslant $ W(O(p_ci, t_id))且Rp(M(P_cj)) $ \geqslant $ W(O(P_cj, t_id))时, 表明标记M下回路具有活性输出变迁t_il. 由于t_id是回路的输入变迁, 触发t_id后占用的资源空间一定不是t_il需要的, 因此标记M'下t_il仍是回路的活性输出变迁. 这意味着标记M'下回路具有可离开托肯, M'是安全标记, 因此t_id是活性变迁.

算法5. 判断使能变迁t_id是否为活性变迁

输入: 一个可达标记M∈R(N, M₀), 使能变迁t_id

输出: M'(p_ci), M'(P_cj), M'(s_ci), M'( $\scriptstyle S_{{{cj}}}^i$ ), Fl; //Fl = true表示t_id是活性变迁

1) 初始化: Fl = true;

2) if(B_Iid∩M(B) = $\scriptstyle \varnothing$ 且R_Iid∩M(R) = $\scriptstyle \varnothing$ )

3) 　 M' = 算法4(M, t_id);

4) if(R_Iid∩M(R) ≠ $\scriptstyle \varnothing$ )

5) 　 if(t_id••∈T_F)

6) 　　 M'(s_ci) = on; M'( $\scriptstyle S_{{{cj}}}^i$ ) = M'(s_ci);

7) 　 else

8) 　　 for(i = 1; i ≤ |R_Iid∩M(R)|; i++)// $\scriptstyle \forall $ R_i∈B_j∩R_Iid∩M(R)

9)　　　 if(Rp(M(p_ci)) < W(O(p_ci, t_id)))

10 ) 　　　　 Fl = false; break;

11)　　　 if(Rp(M(p_ci)) ≥ W(O(p_ci, t_id)))

12) 　　　　 M'(s_ci) = on; M'( $\scriptstyle S_{{{cj}}}^i$ ) = M'(s_ci);

13) if(B_Iid∩M(B) ≠ $\scriptstyle \varnothing$ )

14)　 if(t_id∈T_F)

15) 　　 M'(s_ci) = on; M'( $\scriptstyle S_{{{cj}}}^i$ ) = M'(s_ci);

16)　 else

17) 　　 for(j = 1; j ≤ |B_Iid∩M(B)|; j++) // $\scriptstyle \forall $ B_j∈B_Iid∩M(B)

18) 　　　 if(Rp(M(P_cj)) < W(O(P_cj, t_id)))

19)　　　　 Fl = false; break;

20)　　　 if(Rp(M(P_cj)) ≥ W(O(P_cj, t_id)))

21)　　　　 M'( $\scriptstyle S_{{{cj}}}^i$ ) = on; M'(s_ci) = M'( $\scriptstyle S_{{{cj}}}^i$ );

22) if(Fl = true)

23) 　 M'(p_ci) = M(p_ci) + W(O(p_ci, t_id));

24) 　 M'(P_cj) = M(P_cj) + W(O(P_cj, t_id));

25) 　 M'(p_l) = M(p_l) − I(p_l, t_id) + O(p_l, t_id);

在算法5中: (1)由于K(P₀) = ∞, 如果使能变迁t_id是结束变迁, 其一定是活性变迁. (2)如果t_id••是结束变迁, 由于结束变迁的前集库所中的托肯一定是可离开托肯, 因此触发t_id不会使回路饱和, t_id一定是活性变迁. 若此时回路的可用资源空间不足, 只需打开控制开关, 回路一定具有充足的剩余资源空间. (3)如果t_id是某些回路的输入变迁, 其触发后会占用回路中库所的资源空间, 可能导致回路饱和.

定理5. 算法5得到的活性变迁触发后不会到达不安全标记.

证明: 算法2为所有BRWC添加基本控制器. 对于算法5求得的任意一个活性变迁t_id, M [t_id 〉M'. 对于 $\forall $ R_Iid, 当Ra(M(p_ci)) $ \geqslant $ W(O(p_ci, t_id))时, 由于Ra(M(p_ci)) = Re(M(p_ci)) − 1, 即Re(M(p_ci)) − 1 $ \geqslant $ W(O(p_ci, t_id)), Re(M'(p_ci)) = Re(M(p_ci)) − W(O(p_ci, t_id)) $ \geqslant $ 1, 因此触发t_id不会导致R_i饱和. 当Ra(M(p_ci)) < W(O(p_ci, t_id))时, Rp(M(p_ci)) $ \geqslant $ W(O(p_ci, t_id))表明R_i具有活性输出变迁, 根据定义13和定义14可知, 标记M'下R_i不是饱和的. 若Rp(M(p_ci)) < W(O(p_ci, t_id)), 表明p_ci的潜在资源空间不足. 算法5不允许这样的变迁t_id触发, t_id不是活性变迁. 算法5可以通过限制基本控制库所中的托肯阻止BRWC饱和, 使所有回路有剩余资源空间或可离开托肯, 因此触发t_id不会导致系统到达死锁标记.

算法3为B_J添加总控制器. 对于B_J中的任意一个B_j, 与R_i类似, 当Ra(M(P_cj)) $ \geqslant $ W(O(P_cj, t_id))时, 由于Re(M(P_cj)) − n_j $ \geqslant $ W(O(P_cj, t_id)), Ra(M(P_cj)) = Re(M(P_cj)) − n_j, Re(M'(P_cj)) = Re(M(P_cj)) − W(O(P_cj, t_id)) ≥ n_j. 此时每个回路都有属于自己的一个剩余资源空间, M'不是无死锁不安全标记. 当Ra(M(P_cj)) < W(O(P_cj, t_id))且Rp(M(P_cj)) $ \geqslant $ W(O(P_cj, t_id))时, 表明B_j具有活性输出变迁. 标记M'下托肯可以存放在P_cj的总缓冲空间, 此时组成B_j的每个BRWC都至少有一个仅属于自己的资源空间, 因此M'不是无死锁不安全标记. 当Ra(M(P_cj)) < W(O(P_cj, t_id))且Rp(M(P_cj)) < W(O(p_ci, t_id))时, P_cj的潜在资源空间不足. 此时算法5不允许t_id触发, t_id不是活性变迁. 算法5可以限制总控制库所中的托肯, 因此触发t_id不会导致系统到达无死锁不安全标记.

由于t_id是在T_RL中任意选取的一个变迁, 因此对于算法5求得的任一活性变迁, 其触发后到达的M'一定是安全标记.

由于算法5得到的活性变迁触发后不会到达不安全标记, 因此本文的控制策略允许这些变迁触发. 该策略在系统具有未完成加工的零件时, 允许处理新的零件, 这可以提高零件的生产效率.

2.4 资源缓冲子网

本节考虑资源故障造成的阻塞问题. 现有的死锁预防策略通常没有考虑同时需要可靠和不可靠资源的阶段. 针对具有这种复杂结构的AMSs, 本节提出危险库所的概念, 通过为这些库所添加资源缓冲子网, 确保资源故障时系统不会出现阻塞.

定义17. 给定t_ik∈T_ma∩T_i, 如果 $\exists $ t_ir∈T_mr∩T_i, 且t_ik• = •t_ir, 称t_ik为危险变迁, t_ir为修复变迁. p_k = t_ik•∩P_Rr, p_u = t_ik•∩P_Ru. 称p_k为危险库所, p_k和p_u为相对t_ir的相关库所. 用P_K表示危险库所集.

下面通过算法6为P_K添加资源缓冲子网, 使得即使不可靠资源故障, 托肯也能及时释放占用的危险库所的资源空间.

算法6. 为SRMGs添加资源缓冲子网

输入: SRMG(N, M₀)

输出: SRMG(N_q, M_0q) //添加资源缓冲子网后的SRMG

1 for(k = 1; k ≤ |P_K|; k++)

2 　 if(p_k∈•t_ir∩P_Rr) // $\scriptstyle \forall $ p_k∈P_K

3 　　 N = N∪q_k∪t_fir∪t_rir;

4 　　 N = N∪I(p_k, t_fir)∪I(q_k, t_rir)∪O(q_k, t_fir)∪O(p_k, t_rir);

5　　 if(p_u∈•t_ir∩P_Ru)

6　　　 K(q_k) = min{K(p_u), K(p_k)};

算法6为每个危险库所p_k添加资源缓冲子网, 其包含资源故障变迁t_fir, 资源恢复变迁t_rir, 恢复库所q_k, 以及输入弧和输出弧. 其中K(q_k) = min{K(p_u), K(p_k)}用来保证q_k具有足够的资源空间放置(p_k, c_ir).

对于本文的死锁预防策略: (1)如果托肯的剩余路径中不需要故障资源, 那么只需根据算法5确定该托肯能否前进. (2)否则, 在算法5的基础上, 仅允许托肯前进到故障资源库所. (3)当p_u故障时, 其输出变迁t_ir无法触发. 1)如果该阶段托肯没有占据可靠资源的资源空间, 只需等待故障资源修复, 系统就可以回到正常运行状态. 2)如果该阶段托肯同时占据危险库所p_k的资源空间, 令p_k触发资源缓冲子网中的资源故障变迁t_fir. 此时(p_k, c_ir)前进到恢复库所q_k并释放p_k的资源空间, Re(M(p_k)) = K(p_k) − M(p_k) − M(q_k). 同理可以计算出含有p_k的回路的剩余资源空间、可用资源空间和潜在资源空间. 当Re(M(q_k)) = K(q_k) − M(q_k) = 0时, 不允许托肯触发危险变迁t_ik. (4) p_u修复后, 如果p_k具有剩余资源空间, 允许q_k中的托肯可以触发t_rir回到p_k, 系统回到正常运行状态.

综上所述, 算法5可以与资源缓冲子网结合, 求得任何状态下系统的活性变迁. 使得p_u的故障不会影响需要p_k的零件的生产, 且故障资源修复后系统仍能持续的加工所有零件.

3 例子

本文使用CPN tools进行仿真分析. 首先通过弧线连接库所与变迁, 为库所设置容量. 然后为库所中不同颜色的托肯赋予不同的类型描述它们的颜色. 此外, 通过赋值也可以描述变迁的颜色. 最终建立一个完整的ROPN模型. 在未限制变迁的触发时, 使能变迁的触发可能导致系统死锁, 此时系统无法继续运行. 通过在现有ROPN模型上加入控制器限制变迁的触发, 可以使系统正常运行, 系统不会出现死锁.

示例1: 给定一个AMS, 其零件所需资源为: X₁: r₃→r₁∪r₅→r₂, X₂: r₂→(r₃→r₁→r₅)∪(r₄→r₆→r₇)→r₈, X₃: r₂→(r₃→r₆→r₄) | (r₈→r₁→r₇)→r₅, X₄: r₃→r₄→r₆. $\forall $ i∈ $\mathbb{N}_8^ + $ \1, M₀(r_i) = 2, M₀(r₁) = 3, r₁和r₈可能出现故障.

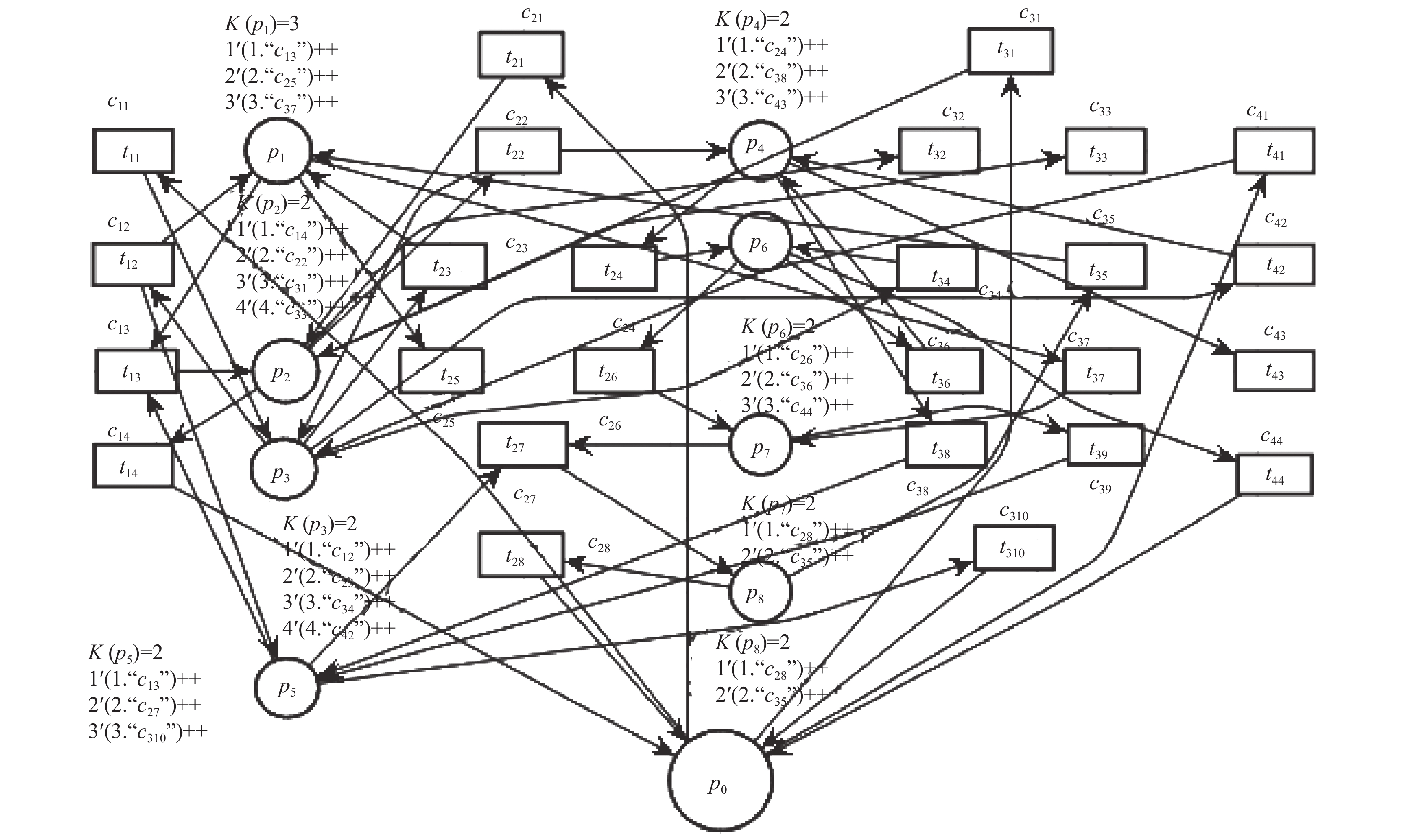
示例1中r₁和r₅之间的“∪”表示某个零件阶段同时需要r₂和r₃. (r₃→r₁→r₅)和(r₄→r₆→r₇)之间的“∪”用来区分并行加工的多个子零件分别需要的资源. “ | ”表示某零件具有多条灵活子路径. 对于该AMS, 通过算法1可以得到其对应的SRMG, 使用CPN tools对该AMS进行仿真如图1.

对于示例1中AMS对应的SRMG, R_I = {R₁, R₂, R₃, R₄, R₅}, 其中R₁ = < p₄, t₂₄, p₆, t₃₆, p₄ >, R₂ = < p₂, t₂₂, p₃, t₁₂, p₁, t₁₃, p₂ >, R₃ = < p₂, t₂₂, p₃, t₁₂, p₅, t₁₃, p₂ >, R₄ = < p₁, t₂₅, p₅, t₂₇, p₈, t₃₅, p₁ >, R₅ = < p₇, t₂₇, p₈, t₃₅, p₁, t₃₇, p₇ >. 通过算法2为 R_I添加的基本控制器如表1所示.

t₁₂是R₄的输入变迁, t₁₃是R₄的输出变迁, t₁₂• = •t₁₃ = {r₁, r₅}. 由于触发t₁₂会同时占用r₁和r₅的资源空间, 且R₄中同时具有r₁和r₅, 因此触发t₁₂会占用p_c4的两个资源空间. 同理, 触发t₁₃会释放p_c4的两个资源空间. 因此W(O(p_c4, t₁₂)) = 2, W(I(p_c4, t₁₃)) = 2. p_ci的其他输入、输出弧的权值都是1.

对于由R₂、R₃、R₄和R₅组成的B_j, 由于R₂和R₃组成的回路属于构成IBC的第1种情况, 不需要为其添加总控制器. 对于由R₂、R₄和R₅组成的B_j, 其是构成IBC的第2种情况, 因此需要分别为R₂和R₄, R₂和R₅, R₄和R₅组成的回路添加总控制器. 对于R₃、R₄和R₅组成的B_j, 其是构成IBC的第3种情况, 需要分别为R₃和R₄, R₄和R₅, R₃、R₄和R₅组成的回路添加总控制器. 由于R₃和R₄组成的回路与R₂和R₄组成回路的资源库所相同, 且构成IBC的BRWC的数量相同, 根据定理4, 不需要额外为R₃和R₄组成的回路添加总控制器. 因此需要添加总控制器的B_J = {B₁, B₂, B₃, B₄}, 其中B₁ = < p₂, t₂₂, p₃, t₁₂, p₁, t₂₅, p₅, t₂₇, p₈, t₃₅, p₁, t₁₃, p₂ >, B₂ = < p₂, t₂₂, p₃, t₁₂, p₁, t₃₇, p₇, t₂₇, p₈, t₃₅, p₁, t₁₃, p₂ >, B₃ = < p₁, t₂₅, p₅, t₂₇, p₈, t₃₅, p₁, t₃₇, p₇, t₂₇, p₈, t₃₅, p₁ >, B₄ = < p₂, t₂₂, p₃, t₁₂, p₅, t₂₇, p₈, t₃₅, p₁, t₃₇, p₇, t₂₇, p₈, t₃₅, p₁, t₂₅, p₅, t₁₃, p₂ >. 通过算法3为 B_J添加的总控制器如表2所示.

与R₄添加的基本控制器的弧权重计算方式类似, 由于t₁₂是B₃的输入变迁, t₁₃是B₃的输出变迁, 且B₃中同时具有r₁和r₅. 因此触发t₁₂会占用P_c3的两个资源空间, 触发t₁₃会释放P_c3的两个资源空间. W(O(P_c3, t₁₂)) = 2, W(I(P_c3, t₁₃)) = 2. P_cj的其他输入、输出弧的权值都是1.

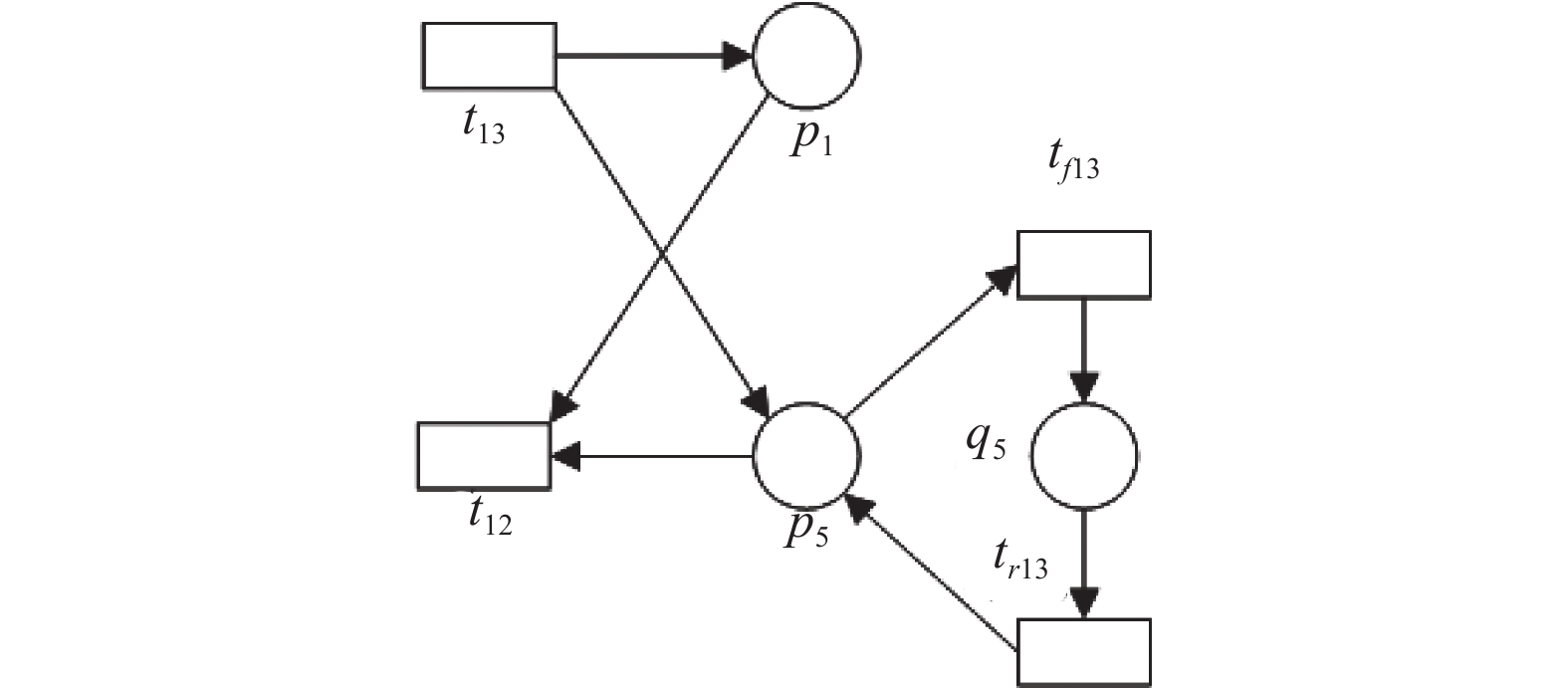
对于示例1中的AMS, P_K = {p₅}. 通过算法6为p₅添加资源缓冲子网如图2. 其中K(q₅) = min{K(p₁), K(p₅)} = K(p₅) = 2.

对于示例1中的AMS, 给定安全标记M, M(p₁, c₁₃) = M(p₁, c₃₇) = 1, M(p₂, c₂₂) = M(p₂, c₃₂/c₃₃) = 1, M(p₃, c₁₂) = M(p₃, c₂₃) = 1, M(p₄, c₄₃) = 1, M(p₅, c₁₃) = M(p₅, c₂₇) = 1, M(p₆, c₂₆) = M(p₆, c₃₆) = 1, M(p₇, c₂₇) = M(p₇, c₃₉) = 1, M(p₈, c₃₅) = 1. M(p_c1) = 0♁1, M(p_c2) = 0♁1, M(p_c3) = 0♁0, M(p_c4) = 1♁1, M(p_c5) = 1♁1. M(P_c1) = 0♁1♁1, M(P_c2) = 0♁1♁1, M(P_c3) = 0♁1♁1, M(P_c4) = 0♁0♁1♁1. M(s_c3) = on, M( $S_{{{c}}4}^3$ ) = on. 使能变迁集T_EN = {t₂₃, t₂₇, t₃₃, t₃₅, t₃₆}. 其中M(p₂, c₃₂\c₃₃)表示p₂中的托肯根据当前标记决定触发哪个变迁.

下面, 通过本文的控制策略, 进行以下分析: 1) 没有资源故障时, 根据算法5判断使能变迁是否为活性变迁; 2) 不可靠资源故障时, 结合危险库所的资源缓冲子网, 根据算法5判断使能变迁是否为活性变迁.

t₂₃是R₄、R₅和B₃的输入变迁, 且Ra(M(P_c3)) = 0 < 1. 由于标记 M下B₃没有使能输出变迁, Rp(M(P_c3)) = 0 < 1. 对于 M [t₂₃〉M₁, M₁不是安全标记, t₂₃ $\notin $ T_RL.

t₂₇不是任何回路的输入变迁, 因此t₂₇∈T_RL. 由于t₂₇是R₃的输出变迁, M(s_c3) = on, M( $S_{{{c}}4}^3$ ) = on. 假设M [t₂₇〉 M₂, 由于Re(M₂(p_c3)) = 1, Re(M₂(P_c4)) = K(P_c42) = 3, 根据算法4, M₂(s_c3) = off, M₂( $S_{{{c}}4}^3$ ) = off.

与t₂₃类似, t₃₃是R₄、R₅和B₃的输入变迁, 且Ra(M(P_c3)) = 0 < 1. 由于标记 M下B₃没有使能输出变迁, Rp(M(P_c3)) = 0 < 1. 对于 M [t₃₃〉 M₃, M₃不是安全标记, t₃₃ $\notin $ T_RL.

t₃₅是R₂的输入变迁, 且Ra(M(p_c2)) = 0 < 1. R₂仅具有使能输出变迁t₃₃, 由于t₃₃ $\notin $ T_RL, R₂没有活性输出变迁, Rp(M(p_c2)) = 0 < 1. 对于 M [t₃₅〉 M₄, M₄不是安全标记, t₃₅ $\notin $ T_RL.

t₃₆不是任何回路的输入变迁, 因此t₃₆∈T_RL. 由于t₃₆是R₁的输出变迁, 且M(s_c1) = off, s_c1的状态不变.

因此根据以上分析, T_RL = {t₂₇, t₃₆}.

在标记M, 触发t₂₇会分别释放p₅和p₇的一个资源空间到达M'. M'(p₁, c₁₃) = M'(p₁, c₃₇) = 1, M'(p₂, c₂₂) = M'(p₂, c₃₂/c₃₃) = 1, M'(p₃, c₁₂) = M'(p₃, c₂₃) = 1, M'(p₄, c₄₃) = 1, M'(p₅, c₁₃) = 1, M'(p₆, c₂₆) = M'(p₆, c₃₆) = 1, M'(p₇, c₃₉) = 1, M'(p₈, c₂₈) = M'(p₈, c₃₅) = 1. M'(p_c1) = 0♁1, M'(p_c2) = 0♁1, M'(p_c3) = 0♁1, M'(p_c4) = 1♁1, M'(p_c5) = 1♁1. M'(P_c1) = 0♁1♁1, M'(P_c2) = 0♁1♁1, M'(P_c3) = 1♁1♁1, M'(P_c4) = 0♁1♁1♁1.

在M', 如果p₁和p₈同时故障. 在p₁未修复之前, p₁的输出变迁t₁₃、t₂₅和t₃₇暂时不能触发. 在p₈未修复之前, p₈的输出变迁t₂₈和t₃₅暂时不能触发. 使能变迁集T'_EN = {t₁₂, t₂₃, t₂₆, t₃₆, t₃₉}. 此时, 危险库所p₅可以触发t_f13前进到q₅, 并释放p₅的一个资源空间, 使需要p₅的零件不会因为p₁的故障出现阻塞.

t₁₂是R₄和R₅的输入变迁, 由于W(O(p_c4, t₁₂)) = 2, Ra(M'(p_c4)) = 1 < 2. 在 p₁和p₈的故障修复之前, t₂₈和t₃₇暂时不能触发, 标记M'下R₄没有使能输出变迁, Rp(M'(p_c4)) = 1 < 2. 对于 M' [t₁₂〉M'₁, M'₁不是安全标记, t₁₂ $\notin $ T'_RL

对于t₂₃, 由于Ra(M'(p_c4)) = Ra(M'(p_c5)) = Ra(M'(P_c3)) = 1 ≥ 1, 则t₂₃∈T'_RL. 此外, 由于t₂₃是R₃的输出变迁, 且M'(s_c3) = off, s_c3的状态不变.

t₂₆是R₅、B₂、B₃和B₄的输入变迁, 且Ra(M'(P_c2)) = Ra(M'(P_c4)) = 0 < 1. B₂有使能输出变迁t₃₉, 但B₄没有使能输出变迁, Rp(M'(P_c4)) = 0 < 1. 对于 M' [t₂₆〉M'₃, M'₃不是安全标记, t₂₆ $\notin $ T'_RL.

t₃₆不是任何回路的输入变迁, 因此t₃₆∈T'_RL.

t₃₉是R₃、R₄和B₁的输入变迁, 且t₃₉•• = t₃₁₀∈T_F. 由于Ra(M'(p_c3)) = Ra(M'(P_c1)) = 0 < 1, 此时 p_c3和P_c1的可用资源空间不足, 因此开启控制器的开关. 对于M' [t₃₉〉M'₄, M'₄(s_c3) = on, M'₄( $S_{{\text{c}}1}^3$ ) = on, M'₄是安全标记, t₃₉∈T'_RL.

因此根据以上分析, T'_RL = {t₂₃, t₃₆, t₃₉}. 通过不断的迭代这一过程寻找不同标记下的活性变迁, 使得无论是否出现资源故障, 系统都不会到达不安全标记.

4 对比

在本节中, 简要的对比本文与现有的死锁预防策略, 结果如表3^{[1-4,13-16,18,21,23,25,28-30]}所示. 其中第2列表示系统中是否具有灵活路径, “Y”表示“是”, “N”表示“否”. 第3列表示系统中是否具有装配操作. 第4列表示系统中是否具有多类型资源获取阶段. 第5列表示死锁控制方法的计算复杂度, “E”表示指数复杂度, “P”表示多项式复杂度. 第6列表示使用的建模方式. 第7列表示系统中是否存在不可靠资源, 如果存在, 是仅有一种不可靠资源, 还是具有多种不可靠资源. 第8列表示如果系统具有不可靠资源, 一次最多允许多少不可靠资源故障, “—”表示不存在这种情况. 第9列表示系统中是否存在同时需要可靠和不可靠资源的零件阶段.

从表3可以看出, 大多数死锁预防方法是指数级复杂度. 为此, 研究人员提出各种策略降低计算复杂度, 以解决大规模AMSs的死锁问题. 对于具有不同结构的AMSs, 研究人员先后提出多种不同的回路进行死锁控制. 此外, 他们通过减少控制器的添加数量不断优化控制策略. 后来, 人们发现借助ROPNs的结构特征, 可以很容易找到造成系统死锁的回路, 通过为这些回路添加控制器, 在阻止回路饱和的基础上可以预防死锁. 然而, 尽管基于ROPNs的建模方式复杂度较低, 但其很少考虑具有装配操作或多类型资源获取的复杂AMSs. 另外, 人们在ROPNs的建模过程中, 很少考虑资源故障的问题.

本文在现有的ROPN模型的基础上, 提出一种新的算法, 得到一类复杂AMSs的ROPN模型. 与文献[13–16]等不同, 本文的死锁预防方法是多项式复杂度的, 更加适用于大规模的系统. SRMGs同时考虑了具有多类型资源获取、装配操作和灵活路径的一类复杂AMSs, 而文献[1,3,25,29,30]等没有考虑具有多类型资源获取的系统, 文献[2–4,16,18,21,29]等没有考虑具有装配操作的系统, 文献[1,13,16,18]等没有考虑具有灵活路径的系统. 此外, 本文的监督控制器具有控制开关. 通过借助控制库所额外的缓冲空间, 受控系统允许更多的安全标记发生.

对一类同时需要可靠和不可靠资源, 且允许多种不可靠资源同时故障的系统, 本文通过为危险库所添加资源缓冲子网, 避免系统出现死锁和阻塞. 而文献[1,13,25,27]等没有考虑具有不可靠资源的系统, 文献[2,14,16,18]仅考虑了具有一种不可靠资源的系统. 文献[3,4]虽然考虑了多种不可靠资源同时故障的情况, 但系统中没有多类型资源获取阶段. 因此以上论文中的策略无法应用于同时需要可靠和不可靠资源的AMSs.

综上所述, 本文使用的SRMGs不仅可以表示复杂的AMSs, 而且具有更简单的结构. 本文的死锁预防策略考虑了资源故障的问题, 与现有控制策略相比, 其在计算复杂度、许可性和实用性等方面都较好.

5 结论与展望

本文主要研究了一类具有多类型资源获取、装配操作和灵活路径的AMSs, 然后使用一种新的算法建立这类AMSs对应的ROPN模型. 称这类模型为SRMGs, 其用不可靠资源库所来表示可能出现故障的资源. 为解决资源竞争造成的死锁问题, 首先建立死锁与饱和回路之间的关系. 通过为一些特殊回路添加控制器, 使得没有资源故障时, 系统不会出现不安全标记. 然后, 为每个危险库所添加资源缓冲子网, 使得即使不可靠资源故障, 不使用故障资源的零件仍然可以持续生产. 与现有的死锁控制器不同, 本文添加的监督控制器具有控制开关, 因此控制策略可以接受更多的安全标记. 此外, 本文的死锁预防策略是多项式复杂度的, 适用于具有装配操作的大规模AMSs. 在未来, 可以考虑将本文的方法扩展到结构更复杂的AMSs. 另外, 可以进一步优化监督控制器的结构, 通过减少添加的控制器数量设计最优的监督控制器.