2. 哈尔滨理工大学 自动化学院, 哈尔滨 150080
2. School of Automation, Harbin University of Science and Technology, Harbin 150080, China
手写签名认证是一种以手势行为特征为基础的生物特征认证技术, 该技术以其方便快捷、实时响应、难以伪造和独立性等特点, 已广泛应用于电子商务、电子合同、金融、司法等领域的身份认证过程[1]. 然而, 手写签名存在误判率高、不具备安全保障以及隐私泄露等问题, 需要通过各类技术手段加强安全措施来保障认证的可靠性[2]. 因此, 深入研究并实现一个安全、可靠、便捷的签名认证系统对身份验证技术的发展具有重要意义.
根据签名样本的获取方式不同, 手写签名可分为在线签名和离线签名两种. 相较于传统的手写签名认证, 在线手写签名认证是通过电子设备采集用户书写的动态信息, 然后使用动态特征进行认证的技术, 准确率高, 不易模仿[3]. 虽然在线签名认证技术具有广泛的应用前景, 但是面临较大的研究难题和不同应用环境下的定制化需求. 首先, 电子签名技术、公钥基础设施、个人专属签名以及在线环境下的服务安全技术等, 都是该领域需要解决的技术难题. 另外, 不同应用对系统有不同要求. 譬如, 电子政务追求低成本和大规模验证, 电子商务要求高安全性和准确识别, 网络文件传输要求签名认证的合法性, 在线办公要求良好的用户体验等.
为此, 本文设计并实现了一种非触摸式在线签名认证系统, 旨在解决签名特征获取的设备依赖性和特征匹配的可靠性问题, 以提升手写签名认证性能. 该系统以MediaPipe[4]人手检测模型为基础框架, 通过视频计算获取人手在屏幕前的二维签名轨迹, 从时域和频域两个方面生成联合时序特征描述子, 进而采用加权概率匹配策略构建签名认证模型, 最后利用PyQt开发一套交互式UI界面, 实现非触摸式在线签名系统认证.
1 相关工作自Plamondon等[5]对签名认证技术做系统的总结后, 出现了很多有效的在线签名认证算法, 其中最具代表性的有: 动态时间规划(dynamic time warping, DTW)[6], 隐马尔可夫模型(hidden Markov models, HMM)[7], 支持向量机(support vector machine, SVM)[8], 神经网络[9], 以及多种算法的结合[10–16]. 譬如, 邹杰等[10]提出了一种基于段匹配差异观察值的HMM在线签名认证方法, 结合DTW提取签名的局部细微差异性和HMM模型对时间序列的鲁棒性, 有效地提升了认证的准确率. Sharma等[13]使用向量量化策略构建了一组编码向量, 结合规整路径中的对齐对评分, 改善DTW单一决策规则不足的问题. 汤升庆等[14]提出基于模板聚类的两级签名认证方法, 有效提升了认证效率. 李相然[15]构建了一个基于神经网络的写者独立的在线手写签名认证模型, 增强了用户认证的交互性. 何彤童[16]提出了基于毫米波雷达的非接触式用户手写签名认证系统, 有效提升了在新增用户时的识别准确率. 这类方法本质上都是以模板匹配为基本思想, 在匹配算法上进行优化改进, 虽然取得了不错的性能, 但存在较大的安全性和鲁棒性问题.
随着深度学习在各个领域的应用, 近年来涌现了不少基于深度学习的在线签名技术. Lai等[17]将签名认证表述为序列建模问题, 提出一种新的称为长度归一化路径签名度量方式来表示真伪签名之间的距离, 并通过训练循环神经网络对其进行学习以提升认证性能. Vorugunti等[18]将人工提取的在线签名特征与AE提取的在线签名特征进行融合, 首次将深度可分离卷积神经网络应用于在线签名认证任务中. 卞浩等[19]提出了基于特征选择和一维幻象残差网络, 解决了从有限的签名样本中提取稳定的签名特征以及模型参数量大的问题. 以上学习方法均是基于单任务对网络参数进行更新的, 认证性能有限. 为此, 沈奇等[20]提出了一种基于多任务学习的注意力机制双向门循环单元模型来实现在线签名的认证, 进一步提高了在线手写签名认证的准确率. 王乐乐等[21]提出了一种基于DTW的注意力机制双向长短期记忆网络(BLSTM)在线手写签名认证方法, 将以笔段特征为输入的BLSTM与稳定笔段相结合, 从而提高了认证精度, 验证了其方法的有效性. 基于深度学习的方法虽然在认证精度上得到了很大的提升, 但学习过程需要相对庞大的训练集和计算量, 甚至还需要负样本来提升训练性能, 而在实际应用中并不易获取.
以上两类认证方法虽然已经基本成熟, 但大都需要借助平板、手机屏等电子设备来获取签名特征, 因而对设备具有较大的依赖性. 为此, 空中签名认证作为一种新兴的技术手段, 在生物识别技术领域应运而生, 并得到了快速发展[22]. Fang等[23]提出了基于视频的空中签名T-DTW-FFT层级融合认证算法, 有效降低了加速度传感器带来的噪声影响和对设备的依赖程度. 任妍等[24]提出了基于三轴加速度传感器的序列极值点分段空中签名身份认证方法, 提升了认证效率和精度. 陆鑫益[25]改进了DTW算法, 在一定程度上提升了准确度. 这类方法虽然解决了设备依赖问题, 并且在某种程度上提升了认证性能. 然而, 由于用户每次签名会存在较大差异, 不易形成固定的签名特征, 从而导致生成的特征模板失效或部分特征缺失等问题. 因此, 这类方法需要在签名特征获取和认证算法上进行再优化.
2 系统设计 2.1 系统架构本系统设计了3个功能模块, 如图1所示, 分别为视频数据采集模块、签名特征提取模块和签名认证决策模块. 总体来说, 系统先采集签名视频, 然后从视频中提取特征描述子, 最后采用加权概率匹配的方式进行认证决策. 视频数据采集模块负责采集手写签名视频数据, 通过采集用户签名过程中的视频, 并传输给签名特征提取模块进行特征提取. 签名特征提取模块负责生成适用于认证的签名轨迹特征描述子, 通过分析签名视频, 提取空间坐标特征、速度特征、加速度特征等描述子, 用于表征一个签名的整体特征及动态信息, 是实现签名认证的基础. 签名认证决策模块负责生成签名特征模板, 进而采用加权概率匹配策略, 实现认证决策, 最终将解析结果可视化传输至客户端. 下面将分别介绍系统各个模块的功能和流程.
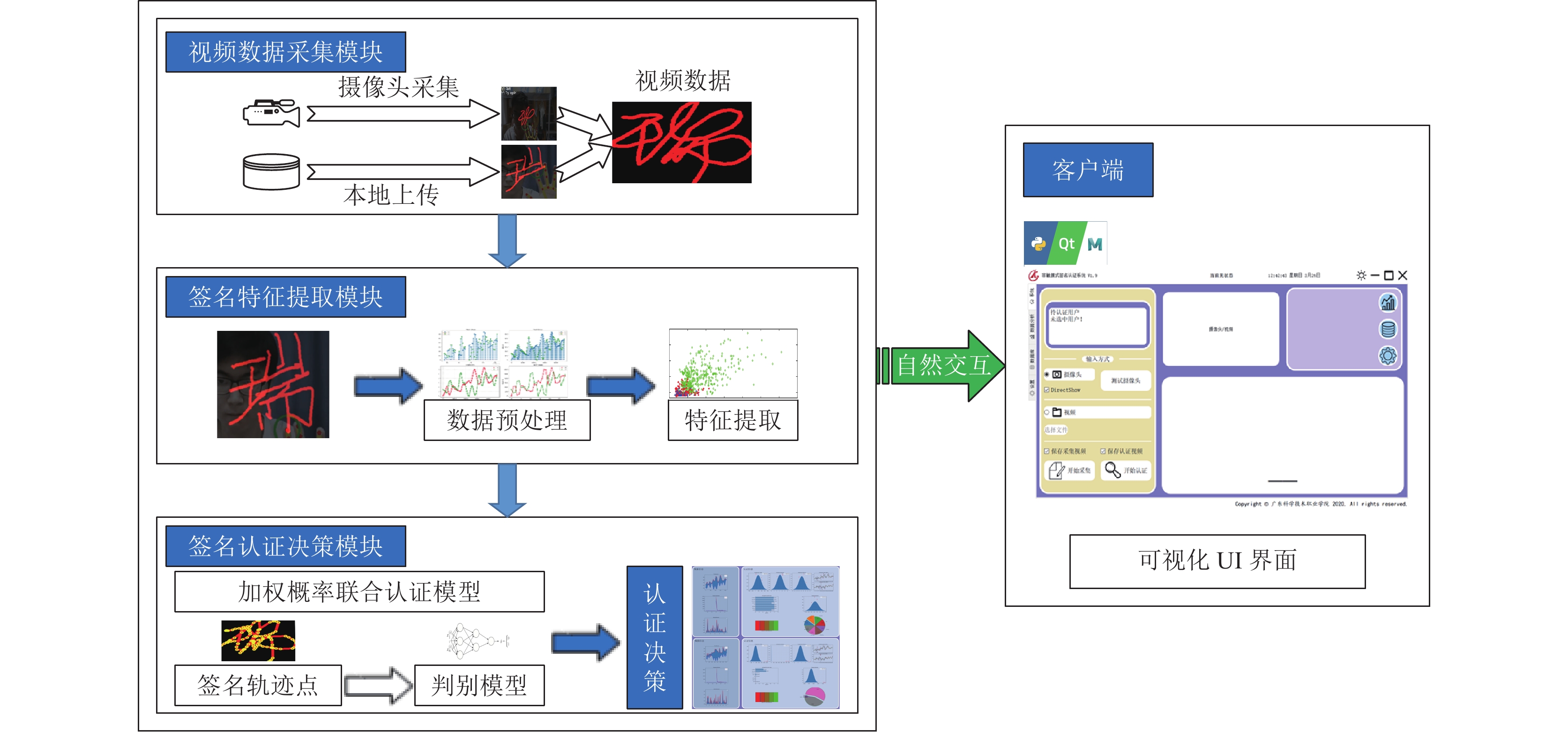
|
图 1 系统架构图 |
2.2 视频数据采集模块
视频数据采集设置两种方式, 分别是摄像头采集和本地视频文件上传. 图2为视频数据采集的具体流程.
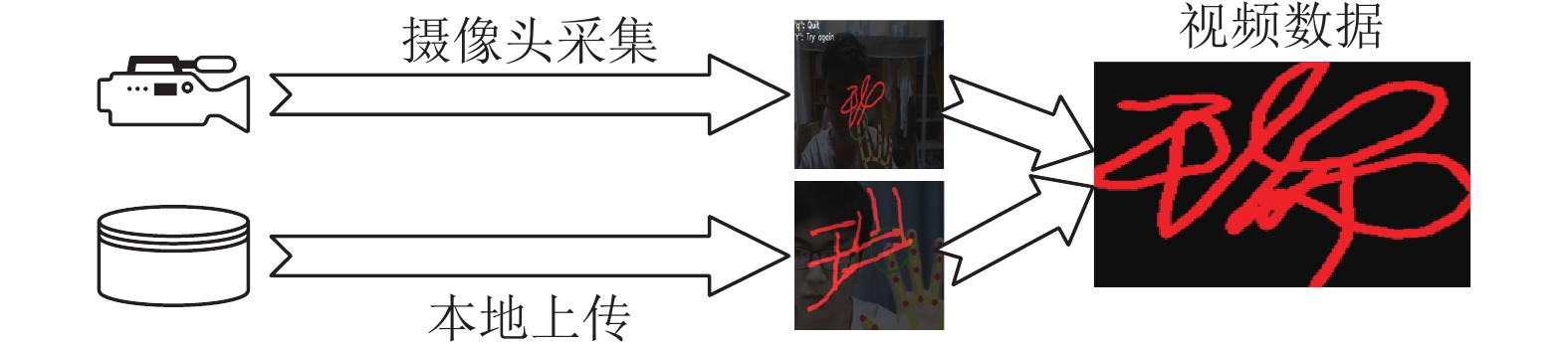
|
图 2 视频数据采集流程图 |
对于摄像头采集方式, 利用MediaPipe手部姿态估计模型获取人物手部关键点坐标信息, 对签名轨迹进行实时追踪. 采集签名时, 将手掌限定在采集框内, 利用手指在空中勾画签名, 系统将实时记录用户的签名轨迹, 并将当前采集的数据写入数据库, 用于调取认证.
对于本地视频上传方式, 系统会将本地上传的视频文件自动完成签名采集, 并在采集完成后自动写入数据库.
2.3 签名特征提取模块签名特征提取模块分为数据预处理和特征描述子生成两个部分. 该模块的具体思路为: 首先, 将收集到的视频数据利用粒子淘汰、重采样线性插值以及GSA极值点提取方法进行预处理; 然后, 通过ELCS、HMM、fastDTW和FFT方法, 分别提取时域特征和频域特征; 最后, 将提取的时域特征和频域特征进行融合, 生成联合时序特征. 图3为签名特征提取的具体流程.
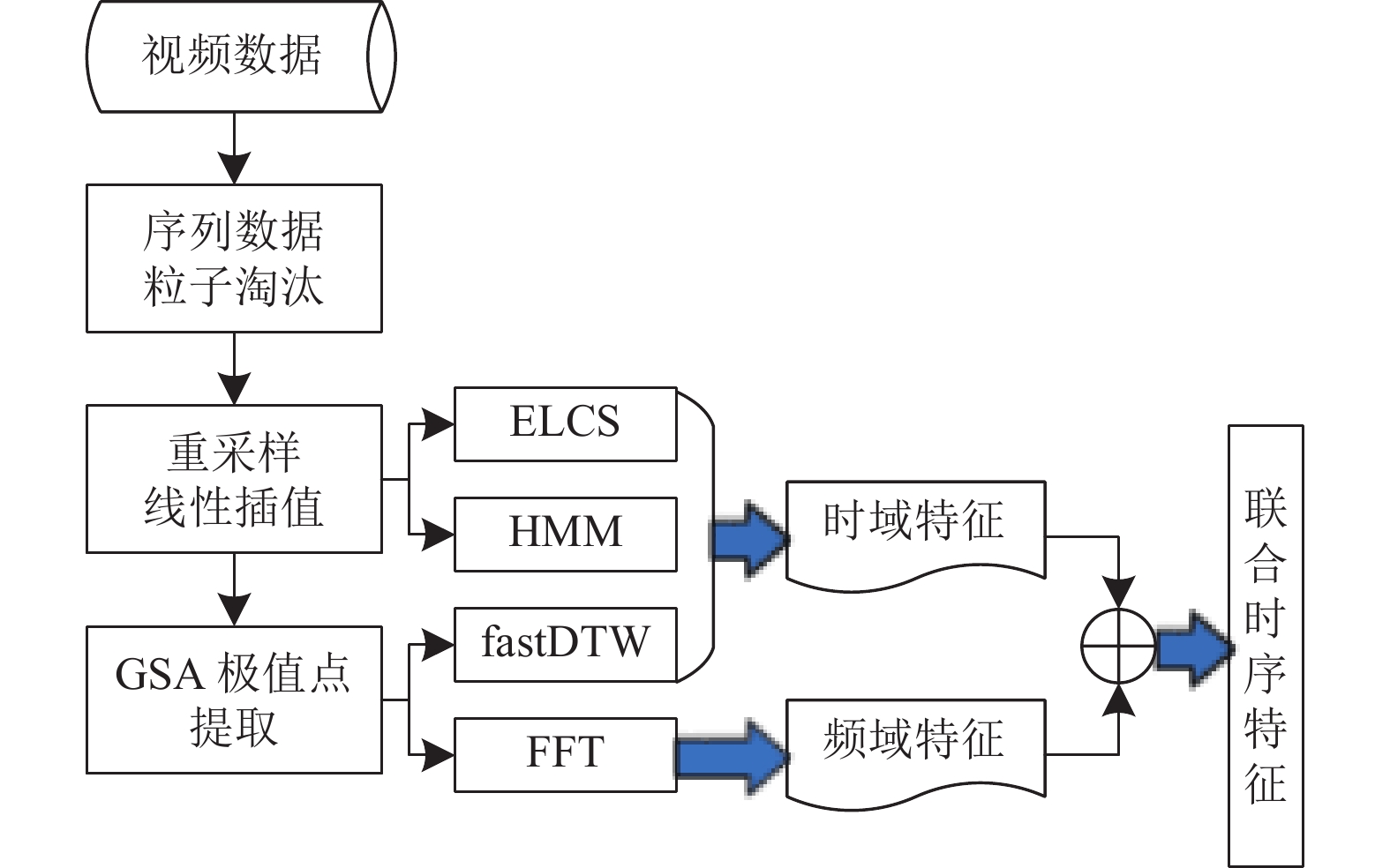
|
图 3 签名特征提取流程图 |
2.3.1 数据预处理
为了消除数据冗余和提高计算速度, 本系统结合数据粒子淘汰、数据重采样和极值点提取3种方法对数据进行预处理和优化. 具体过程如下.
首先, 进行数据粒子淘汰处理. 对采集数据计算轨迹点间的平均距离, 记作mean_dist, 则轨迹点序列Pi (0 ≤ i ≤ n) 的淘汰阈值Thrpe定义为:
| Thrpe=σpe×mean_dist(P0,P1,⋯,Pn) | (1) |
其中,
其次, 进行数据重采样. 采用线性插值法将数据重采样为平均长度的等长样本序列. 对于数据样本序列Li (1 ≤ i ≤ n), 其平均长度Lmean定义为:
| Lmean=n∑i=1Lin | (2) |
最后, 进行极值点提取. 利用全局序列对齐算法(global sequence alignment, GSA)[26]对上述处理后的轨迹点序列保留最显著极值点作为序列特征点.
2.3.2 特征提取与融合本系统分别从时域和频域两个方面提取轨迹序列特征, 通过融合将两者在坐标系下形成联合时序特征描述子, 用于描述在线签名轨迹.
首先, 对于时域特征, 系统分别采用fastDTW算法[13], 具有最长公共子序列的编辑距离(edit distance with longest common subsequence, ELCS)[23]和基于隐马尔科夫模型(HMM)[10]的观察状态概率3种方式提取时域特征. 具体过程如下.
步骤1: 计算参考模板中样本序列间的平方欧氏距离, 得到距离矩阵dmDTW, 定义为:
| dmDTW=[0dl(s1,s2)⋯dl(s1,sn)dl(s2,s1)0⋯dl(s2,sn)⋮⋮⋱⋮dl(sn,s1)dl(sn,s2)⋯0] | (3) |
其中, dl(si, sj) (i, j=1, 2, …, n)表示序列si和sj之间的平方欧氏距离, 计算公式为:
| dl(si,sj)=(si−sj)2 | (4) |
步骤2: 计算参考模板中样本序列间的ELCS距离, 得到距离矩阵dmELCS, 定义为:
| dmELCS=[0el(s1,s2)⋯el(s1,sn)el(s2,s1)0⋯el(s2,sn)⋮⋮⋱⋮el(sn,s1)el(sn,s2)⋯0] | (5) |
其中, el(si, sj) (i, j=1, 2, …, n)表示序列si和sj之间的ELCS距离, 计算公式为:
| el(si,sj)=n∑k=1{w|dist(s(k)i,s(k)j)<Threlcs} | (6) |
其中,
| {Threlcs=[AVG(k,l|dist(s(k)1,s(l)1)AVG(k,l|dist(s(k)2,s(l)2)⋮AVG(k,l|dist(s(k)n,s(l)n))]1⩽k,l⩽mk≠l | (7) |
其中, AVG(·)为求平均值函数.
步骤3: 计算模板样本序列各轨迹点在每个状态的发生概率, 得到观察状态概率矩阵PM, 定义为:
| PM=[s(1)xs(2)x⋯s(n)xs(1)ys(2)y⋯s(n)y] | (8) |
其中,
| {s(i)x=δ(i)xλxs(i)y=δ(i)yλy,1⩽i⩽n | (9) |
其中,
| {δ(i)x=1mm−1∑j=1m∑k=j+1|x(i)j−x(i)k|δ(i)y=1mm−1∑j=1m∑k=j+1|y(i)j−y(i)k| | (10) |
其中,
其次, 对于频域特征, 系统通过对重采样线性插值后的时序信号执行快速傅里叶变换(fast Fourier transform, FFT), 转成频域信号, 输出相关频谱幅值. 根据余弦定理, 特征向量a与b之间的向量夹角余弦值cosθ定义为:
| cosθ=n∑i=1aibi√n∑i=1a2i×n∑i=1b2i | (11) |
如果对时域x(t)和y(t)分别计算夹角余弦值, 可得到cosxθ和cosyθ. 对于参考序列S和待测序列T, 两者之间的FFT距离distFFT(S, T)定义为:
| distFFT(S,T)=1−(αcosxθ+βcosyθ) | (12) |
其中, α和β分别为cosxθ和cosyθ的权重系数, 且α + β = 1.
计算所有样本序列之间的FFT距离矩阵dmFFT, 其定义为:
| dmFFT=[0d(s1,s2)⋯d(s1,sn)d(s2,s1)0⋯d(s1,s2)⋮⋮⋱⋮d(sn,s1)d(sn,s2)⋯0] | (13) |
其中, d(si, sj) (i, j=1, 2, …, n)表示序列si和sj之间的FFT距离.
最后, 将以上的时域特征和频域特征进行融合, 将所有样本对应的匹配距离在二者构成的坐标系下形成联合时序特征描述子, 记作jfDES, 则有:
| jfDES(S)=Φ(sk:dmDTW∘dmELCS∘PM∘dmFFT,1⩽k⩽n) | (14) |
其中,
本系统采用加权概率联合策略, 利用平均加权法计算联合概率, 最终输出认证结果. 具体过程描述如下.
步骤1: 计算序列样本数量, 利用特征矩阵dmDTW、dmFFT和dmELCS分别生成对应的高斯概率模型
步骤2: 计算样本高斯分布的匹配概率. 令x是一个d维样本向量, 则关于x的高斯匹配概率
| pl(x)={exp(−12(x−μl)TΣl−1(x−μl))(2π)d/2|Σl|1/2,x>μl0.9999,x⩽μl | (15) |
其中,
步骤3: 根据观测状态概率和待匹配数据特征向量, 计算相似度概率
| pPM=p(x)PM+p(y)PMn−1∑i=1s(i)x+s(i)y | (16) |
其中,
| {p(x)PM=n−1∑i=1s(i)x,−δ(i)x<¯s(i)x−t(i)x<δ(i)xp(y)PM=n−1∑i=1s(i)y,−δ(i)y<¯s(i)y−t(i)y<δ(i)y | (17) |
其中,
步骤4: 计算加权平均匹配概率. 令avgPj为序列S的第j个轨迹点的加权平均匹配概率, 则:
| avgPj=4∑i=1wip(i)j4∑i=1wi | (18) |
其中,
| wi=1mm∑j=1p(i)j | (19) |
其中, m是序列数据点个数.
步骤5: 计算待测数据序列的加权平均匹配概率, 输出认证结果. 对于待测序列T, 其加权平均匹配概率
| avgP=m∑j=1avgPjm | (20) |
其中, m为序列数据点个数.
决策规则为: 如果
本系统采用PyQt5来实现前端可视化应用交互, 支持PC、平板等多种客户端设备, 用户可自行选择进行体验. 系统主界面如图4所示. 整体界面包含了系统导航栏、视频采集、视频信息分析、认证结果展示、数据库以及系统设置等功能部件.
如图4所示, 主界面左边区域是待认证用户信息和输入方式的选择, 以及采集与认证的选择; 中上区域是摄像头或视频获取的签名轨迹预览窗口, 右上区域分别是数据分析、数据库、设置的跳转按钮; 右下区域是认证结果的各项信息. 各功能部件的具体描述如下.
(1) 系统导航栏. 包括[系统]、[数据分析]、[数据库]以及[设置] 4个功能导航. 其中, [系统]显示主界面, [数据分析]显示数据分析子界面, [数据库]显示数据库信息子界面, [设置]显示系统参数设置子界面, 同时在主界面的右上区域设置了各个子界面的快捷跳转按钮.
(2) 视频采集区. 提供视频信息输入方式的选择, 以及是否保存采集数据的选择. 同时在[摄像头/视频]区域可以预览签名轨迹的生成过程.
(3) 视频信息分析区. 提供待认证用户信息, 包括用户编号, 用户样本数和备注信息.
(4) 认证结果展示区. 位于主界面的右下区域, 将当前认证结果的各项数据信息可视化展示.
图5展示了系统各子模块界面图. 其中, 图5(a)为视频采集界面, 图5(b)为数据库信息界面, 图5(c)为数据分析界面, 图5(d)为系统设置界面.
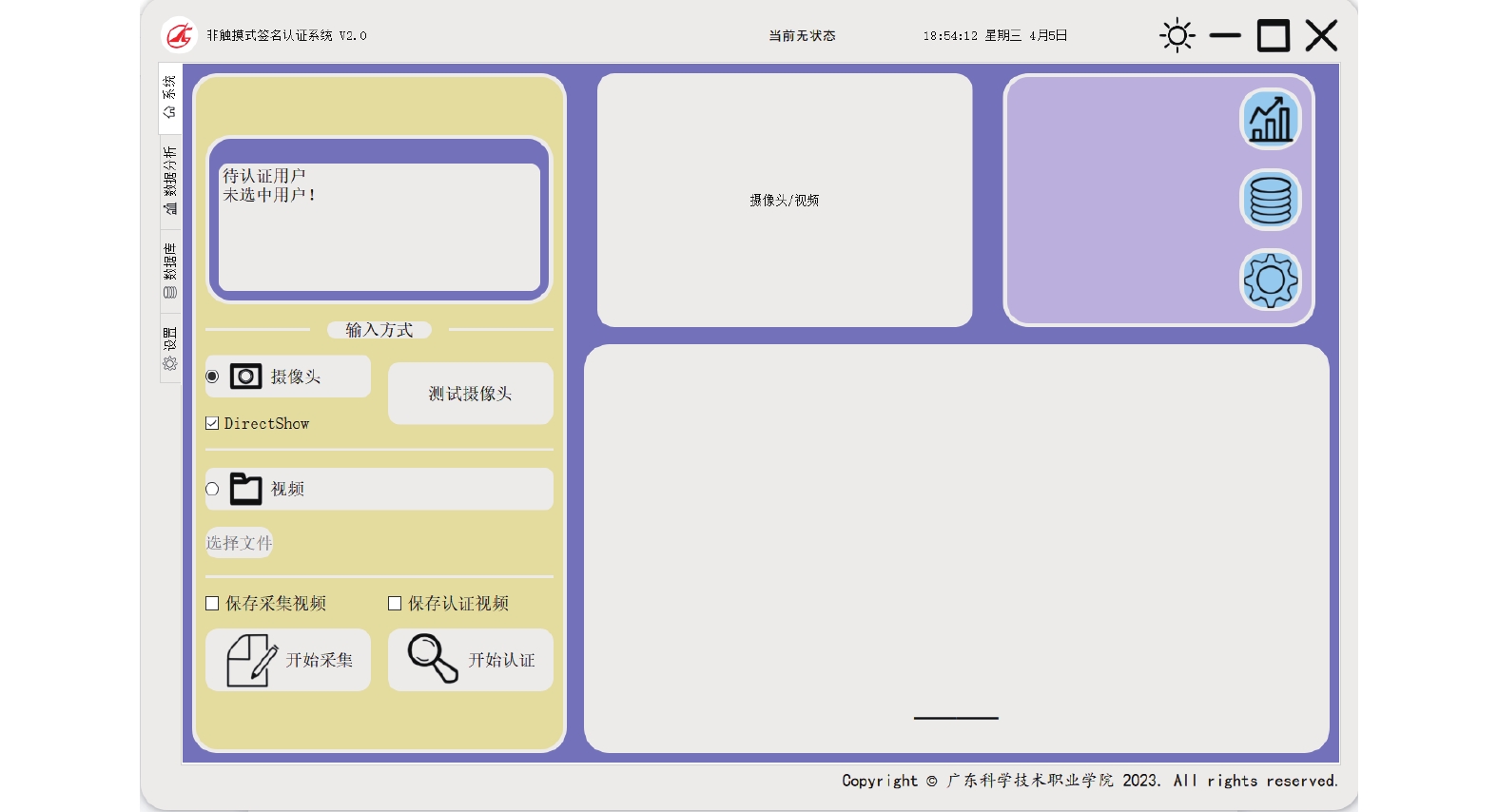
|
图 4 系统主界面 |

|
图 5 系统子模块界面 |
4 系统测试
为了验证系统的可用性和有效性, 提供良好的用户体验和模型性能, 我们进行了系统功能性测试和模型性能测试.
4.1 功能性测试系统采用PC作为可视化交互设备, 操作系统为Windows 10, 安装应用所需依赖环境, 系统功能性测试流程如下.
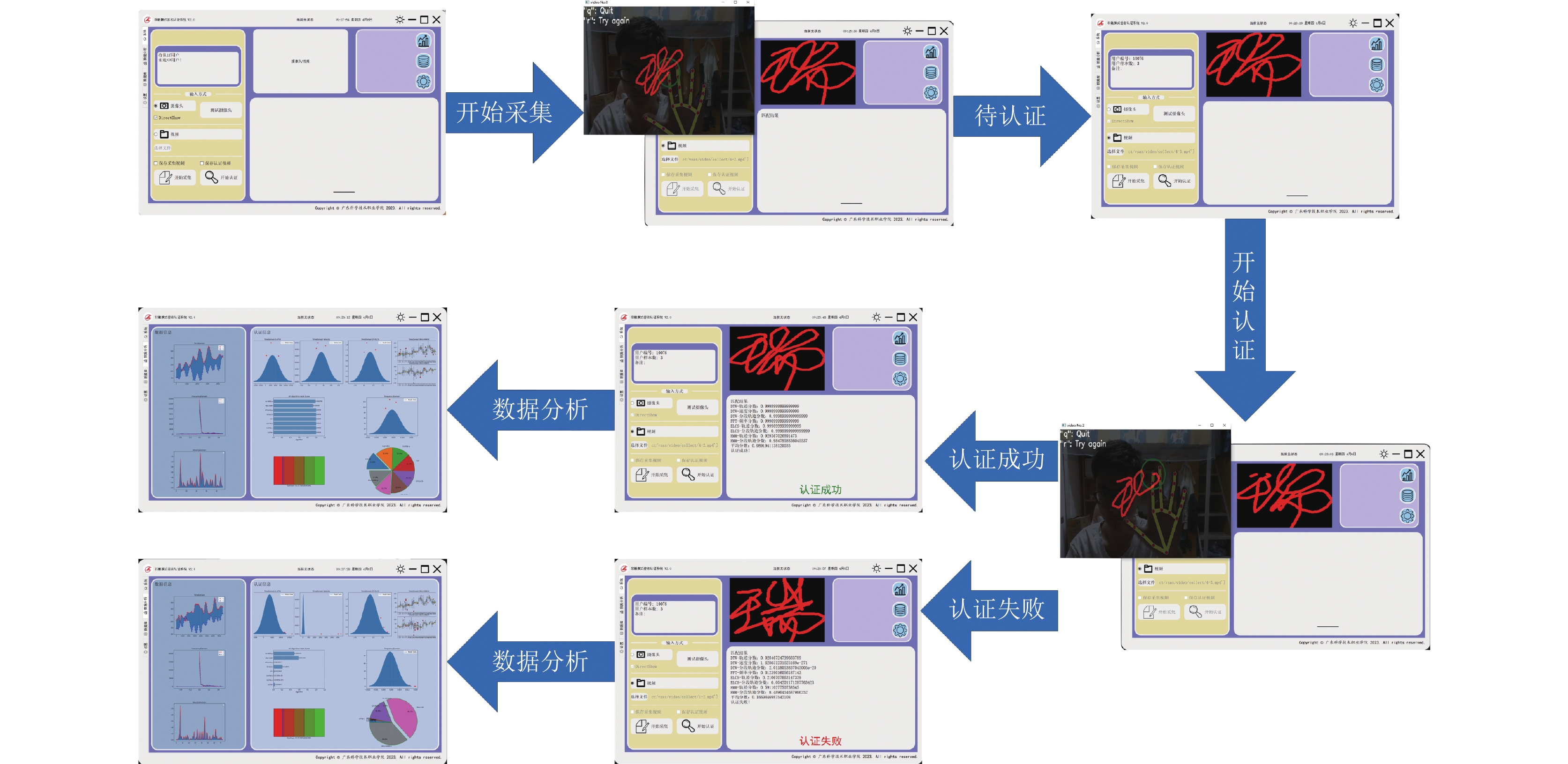
(1) 启动应用程序, 设置采集模式, 选择摄像头或视频, 并保存采集视频.
(2) 开始认证, 保存认证视频, 输出认证结果, 并生成认证文件.
(3) 数据分析, 输出采集数据的时域信息、频域信息、速度信息等分析可视化结果.
(4) 数据库信息调取, 查看用户特征模板、用户样本数据以及计算安全分数等信息.
(5) 系统参数设置, 设置画面缩放倍率、认证阈值、采集样本、数书写检测系数、断点续连阈值以及优化方式等信息.
经过测试, 整个系统运行流畅, 达到了实时性的要求. 整个测试过程如图6所示.
4.2 模型性能测试 4.2.1 测试数据集系统采用两个公开数据集SVC2004 (task2)[27]和SCUT-MMSIG[28], 以及自建数据集NT-Sign (下载地址: https://gitee.com/tofu1207/nt-sign-database)进行模型性能测试. 表1给出了各个数据集的详细参数.
|
图 6 系统功能性测试过程 |
| 表 1 各个数据集的参数 |
表1中, 自建数据集的签名模态为基于视频的非触摸式签名, 收集了32名用户共320组数据, 真伪签名比例为1:1, 采样间隔为一周, 采样频率为50 Hz. 与其他两个公开数据集不一样的是, 自建数据集的数据分为3批, 签名的长度分别为1、2和3个字, 可以更好地检验算法模型的鲁棒性.
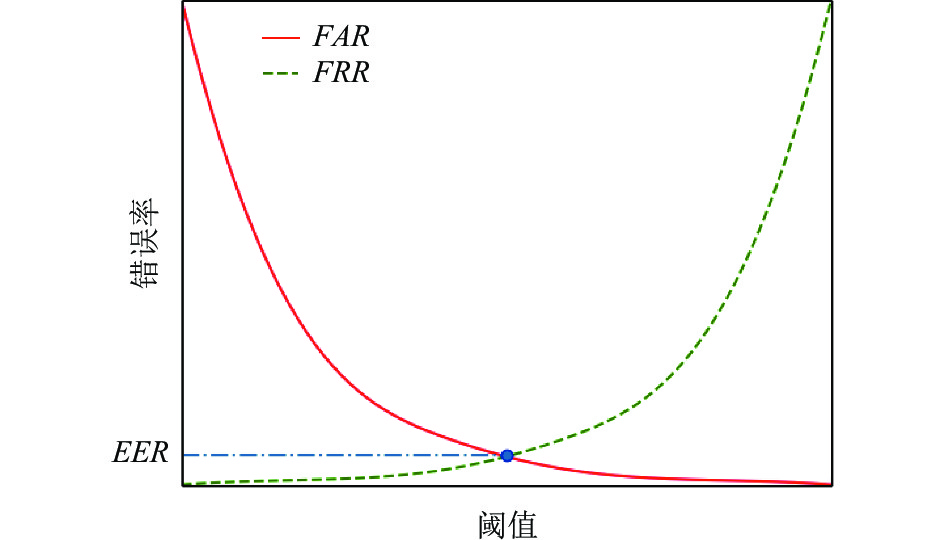
4.2.2 性能评价指标系统采用等误率(equal error rate, EER)[29]作为模型性能的评价指标. 该指标值是当错误接受率(false accept rate, FAR)和错误拒绝率(false reject rate, FRR)相等时的系统安全阈值. EER值越小, 模型性能越好. 它们之间的关系如图7所示.
图7中, 错误接受率FAR是指伪造签名错判为真实签名而被系统接受的错误率, 而错误拒绝率FRR是指真实签名误判为伪造签名而被系统拒识的错误率, 具体的计算公式分别为:
| FAR=FPFP+TN×100% | (21) |
| FRR=FNTP+FN×100% | (22) |
其中, TP, FP, TN, FN分别表示真阳性、假阳性、真阴性和假阴性的样本数.
|
图 7 FAR、FRR和EER之间的关系图 |
4.2.3 消融实验结果与分析
为了验证系统的有效性, 我们对模型算法进行了消融实验. 表2给出了系统的认证模型在不同数据集下的消融结果.
| 表 2 不同数据集下系统的EER值 (%) |
从表2可知, 在不同数据集上, 本文融合算法的性能均为最佳, EER值分别为3.78%和3.75%和1.6%, 3个数据集的平均EER为3.04%. 另外, 融合算法在真实数据样本数量较少的情况下性能较佳, 但在样本数量较多时, 算法性能有所下降. 从实验结果可以看出, 单一的特征很难满足认证精度要求, 时域特征和频域特征确实具有互补性, 融合后可以大大提高系统性能.
4.2.4 与其他算法的性能比较为了验证本系统作为一种潜在签名认证方式的有效性和可行性, 我们对本文算法与其他算法作了比较. 表3给出了本文算法与其他常见算法在公开数据集上的性能比较结果.
| 表 3 不同算法的EER认证性能比较 (%) |
从表3可知, 在公开数据集上, 本文算法在不同真实数据样本的情况下都表现出了最佳的认证性能. 在SVC2004 (task2)数据集上, 本文算法针对20个真实数据和10个真实数据, 训练多的模板反而效果变差了, 这是由于真实数据是间隔时间段采集的, 产生了误差导致. 不过总体而言, 本文算法的表现优于其他算法, 证明了本系统有较高的可靠度.
5 结论与展望本文设计了一个基于实时视频感知的非触摸式在线签名认证系统. 该系统利用MediaPipe的手部姿态估计模型采集人体手部关键点坐标信息, 引入加权联合概率策略, 提出基于融合时序特征的轨迹点匹配方法, 实现在线签名认证. 用户界面采用PyQt设计的可视化交互界面来呈现. 通过系统功能性测试和性能测试表明, 我们的系统不仅开放性强, 而且具有更低的设备依赖性和更高的认证可靠性.
同时, 本系统也存有不足, 如签名特征较少、签名对象较单一等, 后续会提取更多的签名特征, 以及采集更丰富的签名对象来增加认证可靠性. 此外, 目前用户界面设计较为初级, 后期会继续优化界面, 进一步提升用户的交互体验.
最后, 为了更好地与众多研究者交流, 促进该领域的发展, 本文提出的系统测试代码公开在 Gitee: https://gitee.com/tofu1207/vsas-test.
| [1] |
田启川, 张润生. 生物特征识别综述. 计算机应用研究, 2009, 26(12): 4401-4406, 4410. |
| [2] |
张淑婧. 手写签名认证技术研究发展概述. 电脑知识与技术, 2020, 16(10): 277-278. |
| [3] |
Paudel N, Querini M, Italiano GF. Online handwritten signature verification for low-end devices. Proceedings of the 2nd International Conference on Information Systems Security and Privacy. Rome: Springer, 2017. 25–43.
|
| [4] |
Lugaresi C, Tang JQ, Nash H, et al. MediaPipe: A framework for building perception pipelines. arXiv:1906.08172, 2019.
|
| [5] |
Plamondon R, Lorette G. Automatic signature verification and writer identification—The state of the art. Pattern Recog-nition, 1989, 22(2): 107-131. DOI:10.1016/0031-3203(89)90059-9 |
| [6] |
Muramatsu D, Yagi Y. Attacks using random forgery against DTW-based online signature verification algorithm. Proceedings of the 2012 IEEE International Conference on Systems, Man, and Cybernetics. Seoul: IEEE, 2012. 1303–1308.
|
| [7] |
Van BL, Garcia-Salicetti S, Dorizzi B. On using the Viterbi path along with HMM likelihood information for online signature verification. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(5): 1237-1247. DOI:10.1109/TSMCB.2007.895323 |
| [8] |
徐莎莎, 魏金成, 邱晓初. 基于改进的支持向量机的脱机中文签名验证. 电子设计工程, 2012, 20(2): 17-19. |
| [9] |
O-Khalifa O, Alam K, Abdalla AH. An evaluation on offline signature verification using artificial neural network approach. Proceedings of the 2013 International Conference on Computing, Electrical and Electronic Engineering. Khartoum: IEEE, 2013. 368–371.
|
| [10] |
邹杰, 吴仲城. 基于段匹配差异观察值的HMM在线签名认证方法研究. 模式识别与人工智能, 2011, 24(4): 555-560. |
| [11] |
Ansari AQ, Hanmandlu M, Kour J, et al. Online signature verification using segment-level fuzzy modelling. IET Biometrics, 2014, 3(3): 113-127. DOI:10.1049/iet-bmt.2012.0048 |
| [12] |
Liu YS, Yang ZH, Yang LH. Online signature verification based on DCT and sparse representation. IEEE Transactions on Cybernetics, 2015, 45(11): 2498-2511. DOI:10.1109/TCYB.2014.2375959 |
| [13] |
Sharma A, Sundaram S. On the exploration of information from the DTW cost matrix for online signature verification. IEEE Transactions on Cybernetics, 2018, 48(2): 611-624. DOI:10.1109/TCYB.2017.2647826 |
| [14] |
汤升庆, 胡华成. 基于模板聚类的在线签名认证方法. 荆楚理工学院学报, 2020, 35(5): 60-67. |
| [15] |
李相然. 在线手写签名认证技术的研究与实现[硕士学位论文]. 北京: 中国电子科技集团公司电子科学研究院, 2021.
|
| [16] |
何彤童. 基于毫米波雷达的非接触式用户手写签名认证[硕士学位论文]. 秦皇岛: 燕山大学, 2022.
|
| [17] |
Lai SX, Jin LW, Yang WX. Online signature verification using recurrent neural network and length-normalized path signature descriptor. Proceedings of the 14th IAPR International Conference on Document Analysis and Recognition. Kyoto: IEEE, 2017. 400–405.
|
| [18] |
Vorugunti CS, Pulabaigari V, Gorthi RKSS, et al. OSVFuseNet: Online signature verification by feature fusion and depth-wise separable convolution based deep learning. Neurocomputing, 2020, 409: 157-172. DOI:10.1016/j.neucom.2020.05.072 |
| [19] |
卞浩, 栾方军, 袁帅. 基于特征选择和幻象残差网络的在线手写签名认证. 计算机科学与应用, 2023, 13(3): 635-646. |
| [20] |
沈奇, 栾方军, 袁帅. 基于多任务学习的注意力机制双向GRU用于在线手写签名认证. 计算机科学与应用, 2022, 12(2): 473-485. |
| [21] |
王乐乐, 栾方军, 师金钢, 等. 基于DTW的注意力机制BLSTM在线手写签名认证. 小型微型计算机系统, http://kns.cnki.net/kcms/detail/21.1106.TP.20221114.1711.008.html. (2022-11-15).
|
| [22] |
袁红. 空中签名身份认证研究[硕士学位论文]. 武汉: 武汉理工大学, 2016.
|
| [23] |
Fang YX, Kang WX, Wu QX, et al. A novel video-based system for in-air signature verification. Computers & Electrical Engineering, 2017, 57: 1-14. |
| [24] |
任妍, 汪阳, 郑建彬, 等. 基于序列极值点分段的空中签名身份认证. 计算机应用研究, 2019, 36(2): 511-514. |
| [25] |
陆鑫益. 在线签名认证算法研究[硕士学位论文]. 广州: 华南理工大学, 2020.
|
| [26] |
Smith TF, Waterman MS. Identification of common molecular subsequences. Journal of Molecular Biology, 1981, 147(1): 195-197. DOI:10.1016/0022-2836(81)90087-5 |
| [27] |
Yeung DY, Chang H, Xiong YM, et al. SVC2004: First international signature verification competition. Proceedings of the 1st International Conference on Biometric Authentication. Hong Kong: Springer, 2004. 16–22.
|
| [28] |
Kholmatov A, Yanikoglu B. SUSIG: An on-line signature database, associated protocols and benchmark results. Pattern Analysis and Applications, 2009, 12(3): 227-236. DOI:10.1007/s10044-008-0118-x |
| [29] |
Schuckers ME. Receiver operating characteristic curve and equal error rate. Computational Methods in Biometric Authentication. London: Springer, 2010. 155–204.
|
 2023, Vol. 32
2023, Vol. 32



