1 引言

智能体是环境中的实体, 可以执行对环境产生影响的行为. 多智能体系统是多个智能体组成的集合, 其目标是将大而复杂的系统建设成小而彼此互相通信协调的易于管理的系统^[1]. 多智能体系统具有自主性、分布性、协调性, 并具有自组织能力、学习能力和推理能力, 较单智能体而言具有很强的鲁棒性和可靠性^[2]. 多智能体系统广泛应用于自动驾驶^[3]、智能电网优化调度^[4,5]、网络数据传输路由优化^[6]、多无人系统协同任务^[7,8]等领域中.

深度强化学习的兴起解决了由于计算设备性能的提高而产生的海量数据问题, 强化学习中的智能体通过与环境进行交互得到相应的奖励值, 进一步获得最优策略, 但在多个智能体环境中, 每个智能体为了自身的利益, 不断学习优化自身策略, 从而导致每个智能体在训练过程中的状态空间不断变化, 无法找出最优策略^[9]. 在以上问题的基础上, 许多研究人员开始将深度强化学习(deep reinforcement learning, DRL)与多智能体系统结合起来, 多智能体深度强化学习(multi-agent DRL)方法应运而生, OpenAI Five、AlphaStar、“绝悟”等游戏 AI 都能够达到甚至超越人类顶尖玩家的水平, 为 MADRL 在无人控制系统、智能决策等诸多领域的应用前景提供了广阔想象空间^[10].

基于以上研究, 提出了基于CoP-MADDPG算法的多无人机辅助移动边缘计算系统, 本文主要贡献如下.

(1)构建了一个由多架无人机组成的移动边缘计算系统模型. 采用三维动力学模型为在三维空间中随机移动的无人机和地面移动终端进行建模. 无人机与地面移动终端之间的信道模型为莱斯信道.

(2)使用部分可观察马尔可夫决策过程对系统模型进行建模, 并提出了CoP-MADDPG算法实现无人机飞行轨迹和任务卸载的联合优化. 考虑到传统的数据抽取方式容易导致训练效率低, 收敛速度慢, 故在抽样过程中使用了复合优先级, 复合优先级由基于立即回报的优先级和基于TD-error的优先级组成.

(3)构建了一个面向多无人机的飞行轨迹和任务卸载联合优化的仿真实验. 不同参数下的仿真实验表明, 当Actor网络和Critic网络的学习率均为0.01, 折扣因子为0.95时总奖励可以在最短时间内收敛到最大值. 不同算法下的仿真实验表明, 本文算法的总奖励收敛速度和收敛值均优于其他基准算法; 在地理公平性方面, 本文算法可以较为均匀的覆盖整个区域, 且为90%左右的地面移动终端提供服务.

2 相关工作

Jiang等人^[11]提出了一种基于MADRL的协同优化策略, 以解决5G超密集异构网络中的计算卸载和资源分配问题. Wu等人^[12]提出了一个基于排队理论的时延和能耗联合约束优化模型, 并使用MADRL获得动态和随机多用户卸载环境中的最优卸载策略. Seid等人^[13]提出了一种基于MADRL的方法, 以最大限度地降低整体网络计算成本, 同时确保物联网网络中物联网设备或UE的服务质量(QoS)要求. Zhou等人^[14]提出了一个分层的多智能体深度强化学习(H-MADRL)框架来解决混合计算卸载问题, 高级代理驻留在AP中并优化波束成形策略, 低级用户代理学习并调整个人的卸载策略. Seid等人^[15]提出了一个区块链和MADRL集成框架, 用于在多无人机辅助物联网网络中与EH进行计算卸载. Xue等人^[16]考虑了UE卸载成本和MEC服务器的定价, 提出了一种MADRL算法, 通过联合优化功率控制、资源分配和UE关联来最小化系统能耗, 从而在保证系统性能的前提下, 有效提高无人机的整体收益. Li等人^[17]研究了一种空间/空中辅助边缘计算网络架构, 提出了一种基于MADRL的方案, 以获得考虑动态计算请求和随机时变信道条件的最优任务卸载策略, 同时确保服务质量要求. Cheng等人^[18]使用MASAC算法对无人机辅助和能量约束智能边缘网络下的联合任务和能量卸载问题进行了研究. Zhao等人^[19]考虑无人机距离、碰撞和通信等因素, 构建了复杂环境下多无人机协同任务分配模型, 并提出了一种求解该模型的MASAC算法. Dai等人^[20]在多智能体系统中引入了联邦学习框架, 通过无人机之间共享用户的非私有数据, 生成相应的全局模型, 从而生成无人机网络的全局最优决策.

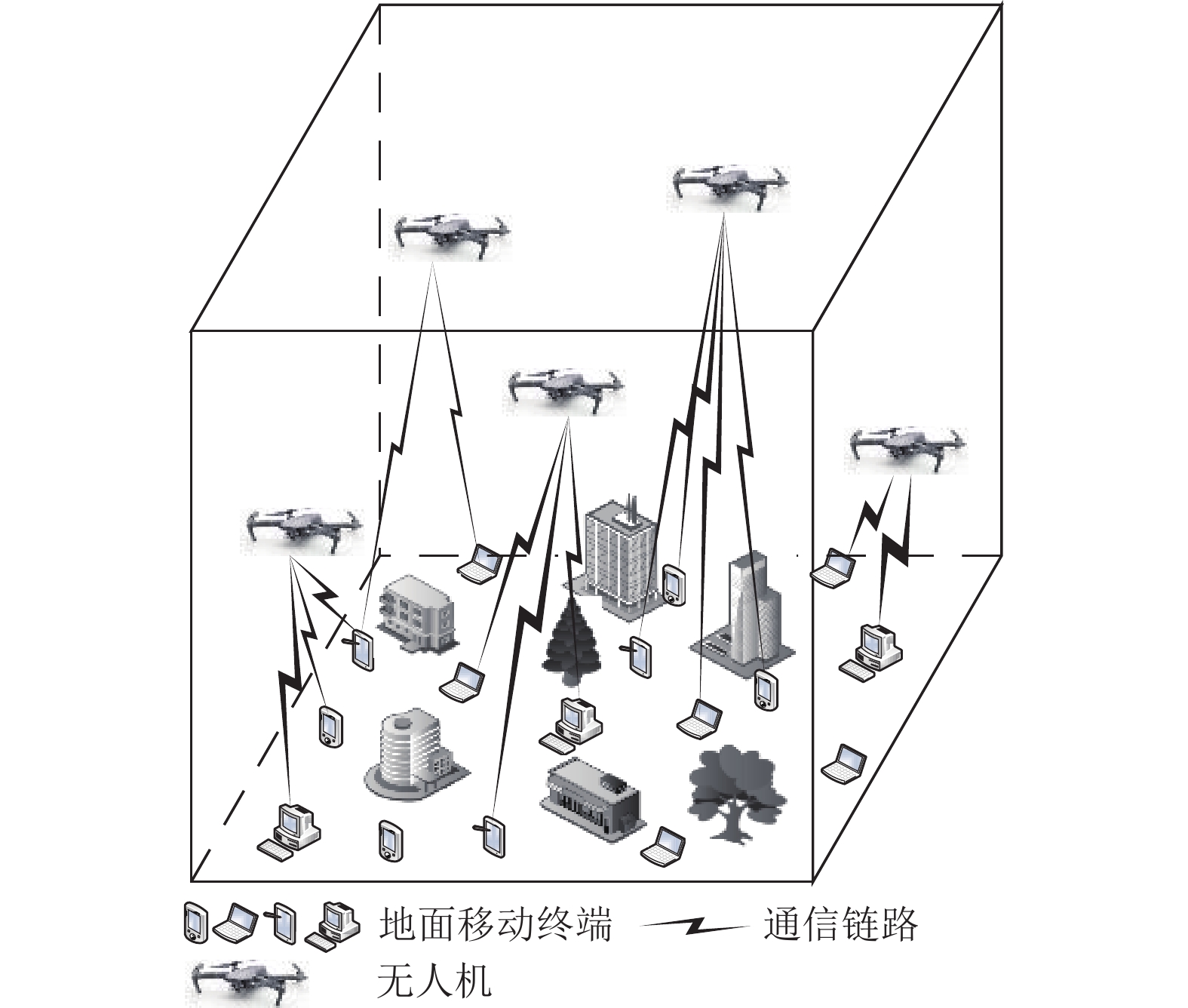
3 网络模型 3.1 系统模型

如图1所示, 本文在环境中部署了 $ O $ 个障碍物、 $ M $ 个地面移动终端和 $ K $ 架搭载MEC服务器的无人机, 无人机的整个飞行周期 $ T $ 被分为 $ t $ 个时隙, 设定无人机和地面移动终端的位置在每一时隙均不发生变化, 且无人机只在悬停时处理由地面移动终端卸载的部分任务. ${{pos}}_t^k = \{ x_t^k, y_t^k, {\textit{z}}_t^k\}$ 表示 $ t \in \{ 1, 2, 3, \cdots, T\} $ 时隙第 $k \in \{ 1, 2, 3, \cdots, K\}$ 架无人机的位置, ${{pos}}_{}^m = \{ x_{}^m, y_{}^m\}$ 表示地面移动终端 $ m \in \{ 1, 2, 3, \cdots, M\} $ 的位置, ${{pos}}_{}^o = \{ x_{}^o, y_{}^o, {\textit{z}}_{}^o\}$ 表示障碍物 $ o \in \{ 1, 2, 3, \cdots, O\} $ 的位置, 无人机 $ k $ 的CPU频率用 $ {f^k} $ 表示, 地面移动终端 $ m $ 的CPU频率用 $ {f^m} $ 表示, $ R_t^k $ 表示 $ t $ 时隙无人机 $ k $ 的覆盖范围, 可以根据波束宽度进行计算.

传统的概率Los信道模型往往不能适应农村、城市及森林等复杂环境^[21]. 故本文引入了莱斯衰弱信道模型^[22–24]. 无人机与地面移动终端之间的信道增益可以表示为:

$ {{{h}}_k} = \sqrt {{\beta _k}} {g_k} $

(1)

其中, $ \;{\beta _k} = {\beta _0}{({d_k})^{ - {\alpha _0}}} $ 是大尺度平均信道功率增益, $ \;{\beta _0} $ 是参考距离为1 m时的信道增益, $ {d_k} $ 是地面移动终端与无人机 $ k $ 之间的距离, $ {\alpha _0} $ 是路径损耗指数. $ {g_k} $ 表示小尺度衰减系数, 可以定义为:

$ {g_k} = \sqrt {\frac{{R{F_k}}}{{R{F_k} + 1}}} g + \sqrt {\frac{1}{{R{F_k} + 1}}} \widetilde g $

(2)

$ {\theta _k} = \arcsin\left(\frac{{{{\textit{z}}_k}}}{{{d_k}}}\right) $

(3)

其中, $R{F_k} = {A_1}{{\rm{e}}^{{A_2}{\theta _{{k}}}}}$ , $ g $ 对应可视距链路分量, $ \widetilde g $ 对应散射分量, $ R{F_k} $ 表示莱斯因子, $ {A_1} $ , $ {A_2} $ 是由环境决定的常数, $ {\theta _k} $ 表示无人机 $ k $ 与地面移动终端之间的仰角.

无人机 $ k $ 最大传输速率可以定义为:

$ {{{r}}_k}{{ = B}}{{\text{log}}_2}\left(1{\text{ + }}\frac{{{\text{|}}{{{h}}_{{{k|}}}}^2p_k^{{\text{up}}}}}{{{{\sigma}^2}\omega }}\right) $

(4)

其中, $ \sigma $ 为无人机接收处的噪声功率, $ \omega $ 为信噪比差值, $ B $ 表示信道带宽, $ p_k^{{\text{up}}} $ 为无人机 $ k $ 的上行链路传输功率.

3.2 计算模型

由于地面移动终端有限的计算能力, 无法处理计算密集型任务, 故需要将部分任务卸载到无人机进行处理, $ o(t) $ 表示任务的卸载比率, $ D_t^k $ 表示 $ t $ 时隙地面移动终端 $ m $ 产生的总任务量, $ C $ 表示处理单位字节所需的CPU周期数, 通过式(5)–式(7)可以计算出 $ t $ 时隙的本地执行时延和卸载计算时延, 其中卸载计算时延为传输时延和计算时延的累加和, 即 $T_t^{{\rm{off}}} + T_t^{{\rm{up}}}$ .

$ T_t^{{\rm{local}}} = \frac{{(1 - o(t))D_t^kC}}{{{f^m}}} $

(5)

$ T_t^{{\rm{up}}} = \frac{{o(t)D_t^k}}{{r{}_k}} $

(6)

$ T_t^{{\rm{off}}} = \frac{{o(t)D_t^kC}}{{{f^k}}} $

(7)

能耗与无人机和地面移动终端的芯片结构有关, 可以通过式(8)–式(10)进行计算, 其中卸载能耗为传输能耗和计算能耗的累加和, 即 $E_t^{{\rm{up}}} + E_t^{{\rm{off}}}$ .

$ E_t^{{\rm{local}}} = {\rho _l}{k_l}{({f^m})^3} $

(8)

$ E_t^{{\rm{up}}} = p_k^{{\text{up}}} \cdot T_t^{{\rm{up}}} $

(9)

$ E_t^{{\rm{off}}} = {\rho _o}{k_o}{({f^k})^3} $

(10)

其中, $\; {\rho _l} $ , $ \;{\rho _o} $ 分别是取决于地面移动终端芯片结构和无人机芯片结构的系数. $ {k_l} $ 和 $ {k_o} $ 为有效开关系数, 取决于地面移动终端的芯片结构和无人机的芯片结构.

3.3 无人机运动模型

无人机需要在避开障碍物的同时为地面移动终端提供服务, 故本文使用了三维动力学模型为无人机进行建模. 无人机的位置由飞行速度、角度和时延决定, 角度包括与XOY面的夹角和与Z轴的夹角, 时延包括无人机的飞行时延和处理上传任务的时延. 由式(11)–式(13)可以计算出无人机 $ k $ 在 $ t + 1 $ 时隙的位置:

$ x_{t + 1}^k{\text{ = }}x_t^k{\text{ + }}distanc{e_{{\rm{fly}}}}{\times}\cos\theta {\times}\sin\beta $

(11)

$ y_{t + 1}^k{{ = y}}_t^k + distanc{e_{{\rm{fly}}}}{\times}\sin\theta {\times}\sin\beta $

(12)

$ {\textit{z}}_{t + 1}^k{\text{ = }}{\textit{z}}_t^k + distanc{e_{{\rm{fly}}}}{\times}\cos\beta $

(13)

其中, $ \theta $ 是无人机飞行过程中与XOY面的夹角, $ \;\beta $ 是无人机飞行过程中与 $ Z $ 轴的夹角, ${{distanc}}{{{e}}_{{{{\rm{fly}}}}}}{{ = }} {{{v}}_{{{\max}}}}{{\times}}({{{t}}_{{{{\rm{fly}}}}}}{{ + }} {{{t}}_{{{{\rm{delay}}}}}}){{\times}} {{{v}}_{{{{\rm{weight}}}}}}$ , ${{{v}}_{{\text{max}}}}$ 表示无人机的最大飞行速度, ${{{v}}_{{\text{weight}}}}$ 表示无人机的速度分量, ${{{t}}_{{\text{delay}}}}$ 表示无人机处理上传任务的时延.

3.4 问题描述

本文采用了一种联合优化的策略, 将任务卸载比率、无人机飞行轨迹和无人机覆盖率3个方面作为优化目标, 旨在寻找一种平衡的解决方案, 使得整个系统的性能得到最优提升. 具体而言, 任务卸载比率的优化旨在保证整个系统任务处理的高效性和负载均衡性, 无人机飞行轨迹的优化则能够最小化整个时间段内的最大处理时延和能耗, 并确保无人机之间不会发生碰撞, 无人机覆盖率的优化则能够最大化地面移动终端的服务范围和服务质量, 使得整个网络系统的性能得到最大化提升. 本文的优化问题可以表示为:

$ \mathop {\min }\limits_{\{ {\text{collision}}_t^{ko}, r_t^k, {cov} \} } \sum\limits_{t = 1}^T {\sum\limits_{k = 1}^K {\max\left\{ {E_t^k + T_t^k} \right\}} } $

(14)

$\tag{14a} {\rm{s.t.}}\;0 \leqslant r_t^k \leqslant 1 $

(14a)

$\tag{14b} {cov} \in {\text{\{}}0, 1{\text{\} }} $

(14b)

$\tag{14c} {{pos}}_t^k = \left\{ {(x_t^k, y_t^k, {\textit{z}}_t^k)|x_t^k \in [0, L], y_t^k \in [0, W], {\textit{z}}_t^k \in [0, H]} \right\} $

(14c)

$\tag{14d} 0 \leqslant {\textit{Task}}(t) \leqslant sum\_{\textit{Task }}$

(14d)

$\tag{14e} 0 \leqslant R_t^k \leqslant {{{R}}_{{\text{max}}}} $

(14e)

$\tag{14f} 0 \leqslant {v_k} \leqslant {v_{\max}} $

(14f)

其中, 式(14)中的 $ {\text{collision}}_t^{ko} $ 表示在 $ t $ 时隙无人机 $ k $ 和障碍物 $ o $ 之间是否存在障碍, 若存在则 $ {\text{collision}}_t^{ko} = 1 $ , 否则 $ {\text{collision}}_t^{ko} = 0 $ . 式(14a)表示计算任务卸载比率 $ r_t^k $ 的取值范围. 式(14b)表示无人机覆盖率 $ {cov} $ 的取值范围. 式(14c)表示无人机的移动范围. 式(14d)表示剩余任务量的范围, $sum\_{\textit{Task}}$ 表示总任务量. 式(14e) 表示 $ t $ 时隙无人机 $ k $ 的覆盖范围 $ R_t^k $ 应小于等于无人机的最大覆盖范围 ${{{R}}_{{\text{max}}}}$ . 式(14f)表示无人机 $ k $ 在飞行过程中的速度 $ {v_k} $ 不能超过无人机的最大飞行速度 ${v_{\max}}$ .

4 CoP-MADDPG算法 4.1 MADDPG算法

DDPG算法在单智能体领域得到了广泛的应用, 将其进行扩展便得到了多智能体领域的MADDPG算法^[25], 如图2所示, 该算法引入了其他智能体的动作作为额外信息以获得Q值函数. MADDPG算法在集中训练过程中不需要知道环境的动力学模型以及特殊的通信需求, 每个智能体根据其他智能体的行为评估当前动作的价值. 分散执行是指当每个智能体都训练充分后, 每个Actor网络就可以自己根据状态采取合适的动作, 此时是不需要其他智能体的状态或者动作的.

传统强化学习算法在学习和应用时都必须使用相同的数据信息, 而MADDPG算法允许在学习时使用一些额外的信息, 即全局信息, 但是在应用决策的时候只使用局部信息. 因此, 该算法不仅可以用于合作环境, 也可以用于竞争环境. MADDPG算法在保证精度的基础上, 能够解决因多智能体输出的动作维度太大而导致的算法收敛问题^[26], 但传统的MADDPG算法从经验回放缓冲区中随机抽取数据, 而不考虑数据质量, 导致训练效果差, 收敛速度慢, 容易陷入局部最优. 因此, 本文使用复合优先级抽样方法对MADDPG算法进行了改进, 从而对任务卸载比率、无人机飞行轨迹和无人机覆盖率进行联合优化.

4.2 构建POMDP

本文的联合状态空间可以表示为 $state = \{ {{pos}}_t^k, {{pos}}_{}^o, {{pos}}_{}^m, task_t^m, block_t^k, {{ele}}_t^k\}$ , $ task_t^k $ 表示地面移动终端 $ m $ 在 $ t $ 时隙产生的任务量. $ block_t^k $ 表示在 $ t $ 时隙无人机 $ k $ 与地面移动终端之间是否存在遮挡, 若存在遮挡, 则 $ block_t^k = 1 $ , 否则 $ block_t^k = 0 $ . ${{ele}}_t^k$ 表示 $ t $ 时隙无人机 $ k $ 的电量.

本文的联合动作空间可以表示为 $a = [R_t^k, {v_k}, {\varphi _k}, {\theta _k}, {\textit{offloading}}]$ , $ {\varphi _k} $ 和 $ {\theta _k} $ 表示无人机 $ k $ 的飞行角度, ${\textit{offloading}}$ 表示卸载比率.

奖励函数会影响神经网络的收敛情况, 故它的设置是非常重要的, 本文的奖励函数设置为时延能耗、无人机覆盖率、碰撞因子和边界因子的加权和, 由于时延和能耗不是一个数量级, 故需要对其进行归一化, 无人机覆盖不同的区域应得到正向奖励鼓励对区域的探索, 碰撞因子与无人机和障碍物之间的距离有关, 边界因子可以避免无人机飞出边界.

4.3 CoP-MADDPG算法

经验回放机制随机重复地抽取过去的经验以提高神经网络的稳定性, 但未考虑到数据的质量, 导致训练效率低, 收敛速度慢, 故本文在抽样过程中使用了复合优先级, 其中, 复合优先级包括基于立即回报的优先级和基于TD-error的优先级. 复合优先经验回放采样方法的具体步骤如下所示.

(1)使用Q值计算TD-error.

(2)利用式(15)分别定义基于立即汇报的优先级和基于TD-error的优先级, $ {r_t} $ 表示经验的立即汇报, $ \varepsilon $ 表示一个正常数, $ {\delta _t} $ 表示TD-error:

$ {Y_i} = {r_t} + \varepsilon {; } \;{Y_f} = \left| {{\delta _t}} \right|{\text{ + }}\varepsilon $

(15)

(3)把经验池中的经验分别按步骤(2)中得到的优先级从大到小进行排列得到序列 $ ran{k_i} $ 和 $ ran{k_f} $ , 通过式(16)计算出每个经验的复合优先级, $ \alpha $ 表示算法使用优先级的程度, 当 $ \alpha = 0 $ 时表示均匀采样.

$ {{{u}}_k} = \frac{{ran{k_i} + ran{k_f}}}{2} {; }\; {Y_k} = {\left(\frac{1}{{{u_k}}}\right)^\alpha } $

(16)

(4)定义采样经验的概率 $ {P_k} = \left(\dfrac{{{Y_k}}}{{\displaystyle\sum\nolimits_n {{Y_n}} }}\right) $ , 其中 $ n $ 表示经验的数量.

算法1. MADDPG算法

输入: 使用参数随机初始化Actor和Critic网络; 初始化经验池 $\scriptstyle D $ , 最小取样数量 $\scriptstyle S $ , 回合数 $\scriptstyle N $ .

输出: 奖励值.

for episode=1: $\scriptstyle N $ do

　　初始化初始状态 $\scriptstyle s $

　　for t=1: $\scriptstyle T $ do

　　　对于每个智能体 $\scriptstyle i $ , 选择动作 $\scriptstyle {a_i} = {\mu _{{\theta _i}}}({o_i}) + {N_t} $ 并执行动作 $\scriptstyle a = ({a_1}, \cdots, {a_N}) $ 得到奖励值和下一时刻状态 $\scriptstyle s' $ 并计算TD-error;

　　　将经验 $\scriptstyle (s, a, r, s', {y_i}, {y_f}) $ 存储到经验池 $\scriptstyle D $ , 首先将经验按优先级 $\scriptstyle {Y_i} $ 和 $\scriptstyle {Y_f} $ 从大到小进行排序, 得到 $\scriptstyle ran{k_i} $ 和 $\scriptstyle ran{k_f} $ , 其次对经验做复合平均排序得到 $\scriptstyle {{{u}}_k}$ 并计算经验的复合优先级 $\scriptstyle {Y_k} $ , 最后通过 $\scriptstyle {Y_k} $ 计算经验采样概率 $\scriptstyle {P_k} $ ;

　　　for agent $\scriptstyle i $ =1:M do

　　　　从经验池 $\scriptstyle D $ 中根据经验采样概率抽取 $\scriptstyle S $ 个样本进行训练;

　　　　设置:

　　　　　 $\scriptstyle {y^j} = {r_i}^j + \gamma {Q_i}^{\mu '}(s{'^j}, a_1', \cdots, a_N'){|_{{a_k'} = {\mu _k'}(o_k^j)}}$

　　　　　使用Loss值更新Critic网络:

　　　　 $\scriptstyle L({\theta _i}) = \frac{1}{s}\sum\nolimits_j {{{({y^j} - Q_i^\mu ({s^j}, a_1^j, \cdots, a_N^j))}^2}}$

　　　　使用梯度下降方法更新Actor网络:

　 $\scriptstyle {\nabla _{{\theta _i}}}J \approx \frac{1}{s}\sum\nolimits_j {{\nabla _{{\theta _i}}}{\mu _i}(o_i^j){\nabla _{{a_i}}}Q_i^\mu ({s^j}, a_1^j, \cdots, a_i^j, \cdots,a_N^j)} {|_{{a_i} = {\mu _i}(o_i^j)}}$

　　　end for

　更新目标网络:

　　 $\scriptstyle {\theta ^{Q'}} \leftarrow \tau {\theta ^Q} + (1 - \tau ){\theta ^{Q'}} $ ; $\scriptstyle {\theta ^{\mu '}} \leftarrow \tau {\theta ^\mu } + (1 - \tau ){\theta ^{\mu '}} $

　　end for

end for

5 仿真实验

在进行仿真实验时, 通过比较不同学习率和折扣因子下的平均奖励值可以获得最佳学习率和折扣因子, 通过与基准算法进行对比, 验证了本文算法的可用性和先进性. 本文的基准算法为: MADDPG、MAA3C、MAPPO、MAAC.

5.1 参数设置

在模拟过程中, 使用的编程语言是Python 3.8和TensorFlow 2.5. 使用了一台配备Intel酷睿 i7-1165G7 CPU的PC, 最高频率2.80 GHz. 本文环境参数设置如表1所示.

5.2 仿真结果 5.2.1 无人机分布示意图

二维坐标系中黑色实心小圆表示地面移动终端, 深灰色实心圆表示障碍物, 浅灰色实心圆表示无人机的覆盖范围, 5种不同的线条分别表示5架无人机的飞行轨迹.

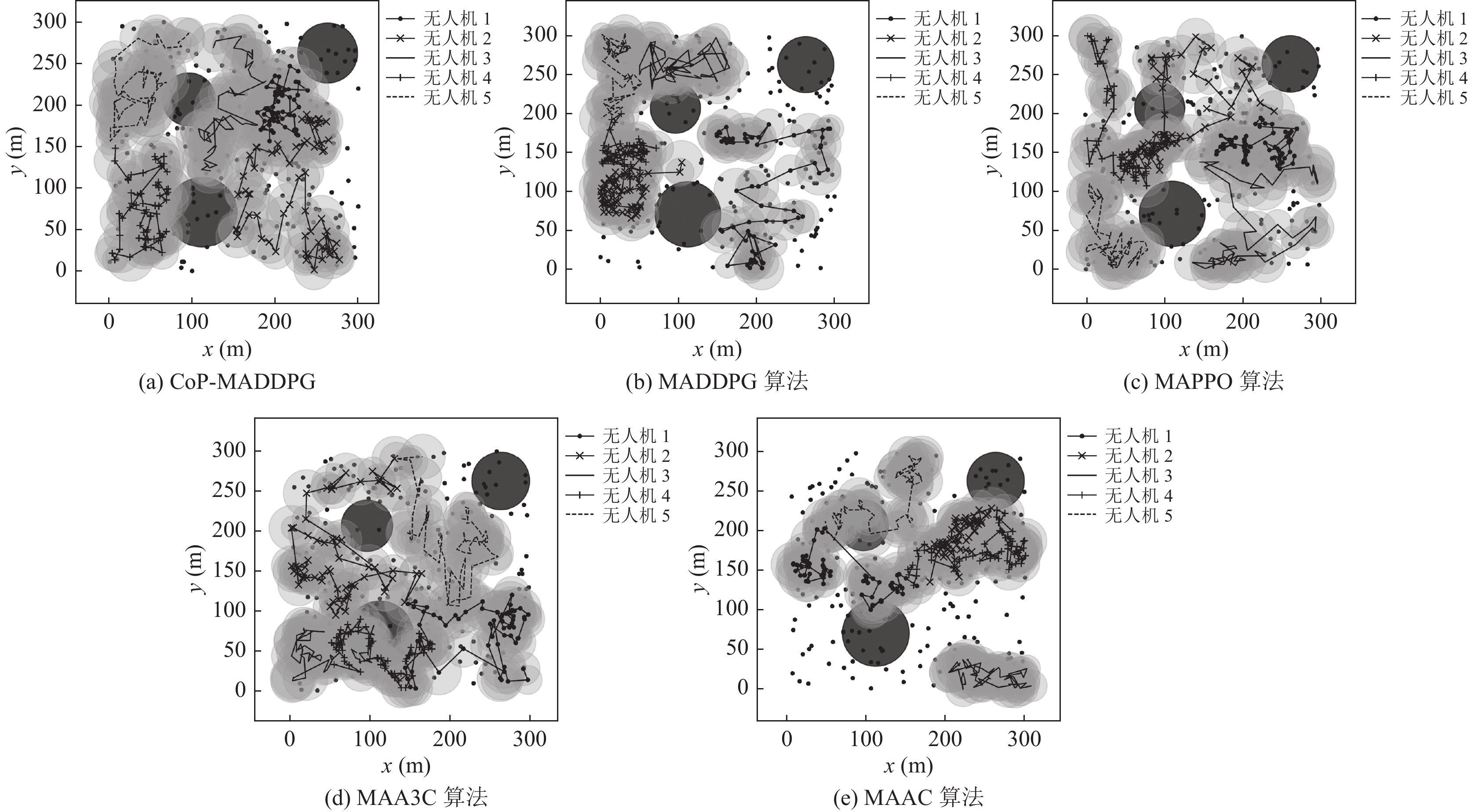
不同算法下的无人机飞行轨迹如图3所示. 图3(a)是基于本文算法的无人机飞行轨迹, 可以看出无人机能够完全避开障碍物和避免无人机之间的碰撞, 5架无人机在飞行过程中轨迹分布较为均匀, 基本实现了区域全覆盖, 通过深灰色实心圆中黑色实心圆的个数可以看出, 无人机在飞行过程中为90%左右的地面移动终端提供了服务, 实现了服务用户公平性, 提高了服务效率. 图3(b)是基于MADDPG算法的无人机飞行轨迹, 可以看出无人机能够完全避开障碍物和避免无人机之间的碰撞, 但为了避免碰撞, 大多数无人机陷入了局部最优, 只在一块较小的区域内移动, 导致该算法不能很好地覆盖整个区域, 从图中可以看出, 4架无人机覆盖的总面积仅占整体区域的1/4左右, 且几乎一半的地面移动终端不能得到服务. 图3(c)是基于MAPPO算法的无人机飞行轨迹, 可以看出无人机可以较好地为地面移动终端提供服务且能够在飞行过程中避免无人机之间发生碰撞, 但无法完全避开障碍物, 该算法解决了MADDPG算法陷入局部最优的问题, 稳定性相较于MADDPG也得到了提升, 但最终训练效果较差. 图3(d)是基于MAA3C算法的无人机飞行轨迹, 可以看出无人机基本实现了地理公平性和服务用户公平性, 但由于A3C算法未使用经验回放机制, 导致采样速度变慢, 训练十分不稳定, 因此, 无人机在飞行过程中不能避免任何一种情况的碰撞. 图3(e)是基于MAAC算法的无人机飞行轨迹, 从图中可以看出除了无人机之间发生了碰撞之外, 还未能避免无人机与障碍物之间的碰撞, 在训练过程中无人机无法很好地对环境进行探索, 导致无人机分布较为集中, 且单架无人机覆盖区域较小, 因此, 无法全面覆盖整个区域且只为一半左右的地面移动终端提供了服务.

5.2.2 基于不同学习率的奖励曲线图

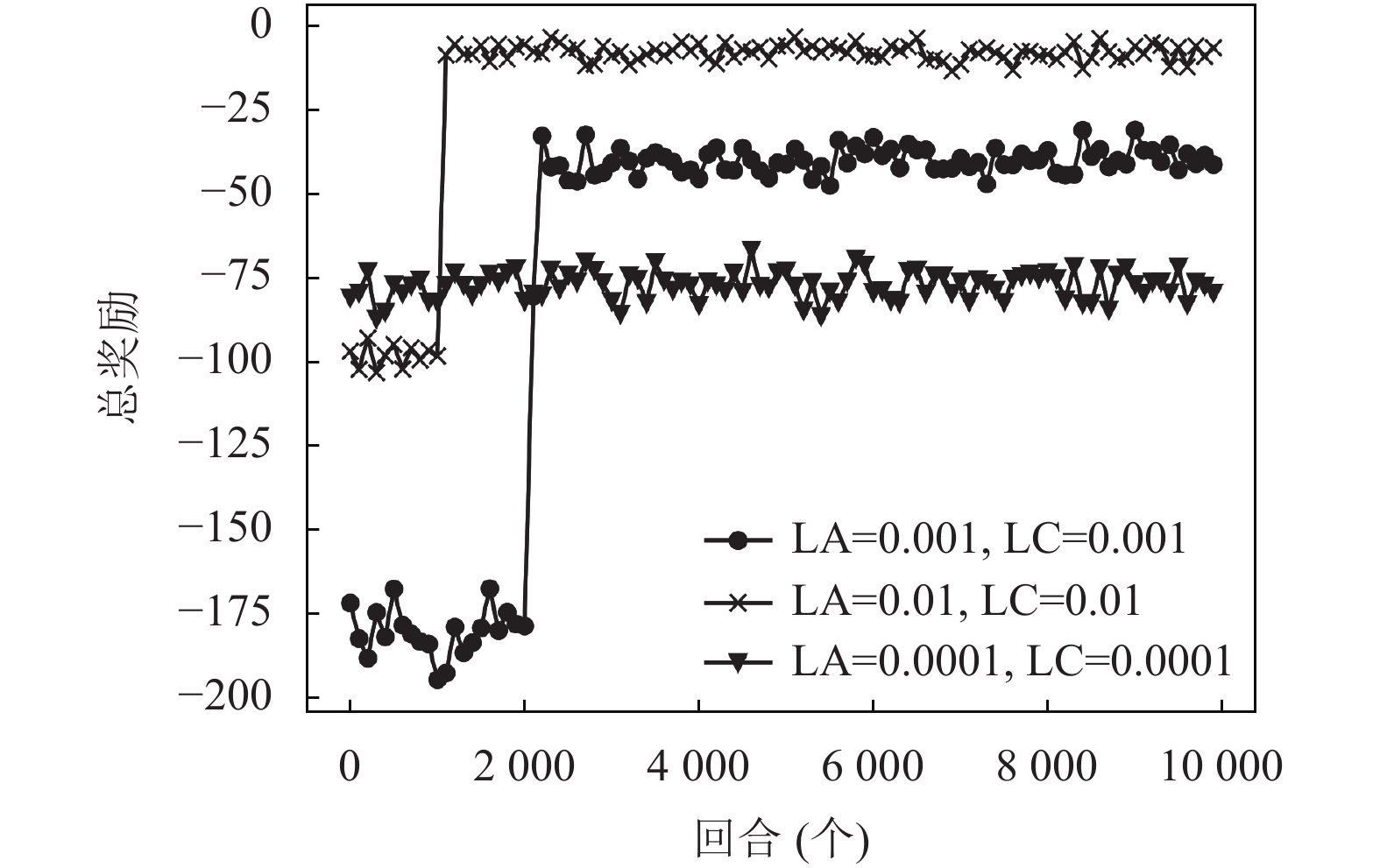
目标函数是否收敛以及何时收敛由学习率控制, 图4是不同学习率下的奖励曲线图, 其中LA表示Actor网络学习率, LC表示Critic网络学习率. 从图中可以看出, 当Actor网络的学习率和Critic网络的学习率均为0.0001时, 奖励值在−80附近震荡, 无法收敛. 当Actor网络的学习率和Critic网络的学习率均为0.001时, 奖励值在2 000回合左右开始收敛, 最终收敛到−30左右. 当Actor网络的学习率和Critic网络的学习率均为0.01时, 奖励值在1000回合附近开始收敛, 最终收敛到−10附近. 通过对图4的分析, 可以得出结论: 当Actor网络的学习率和Critic网络的学习率均为0.01时, 可以获得较好的收敛速度和收敛值.

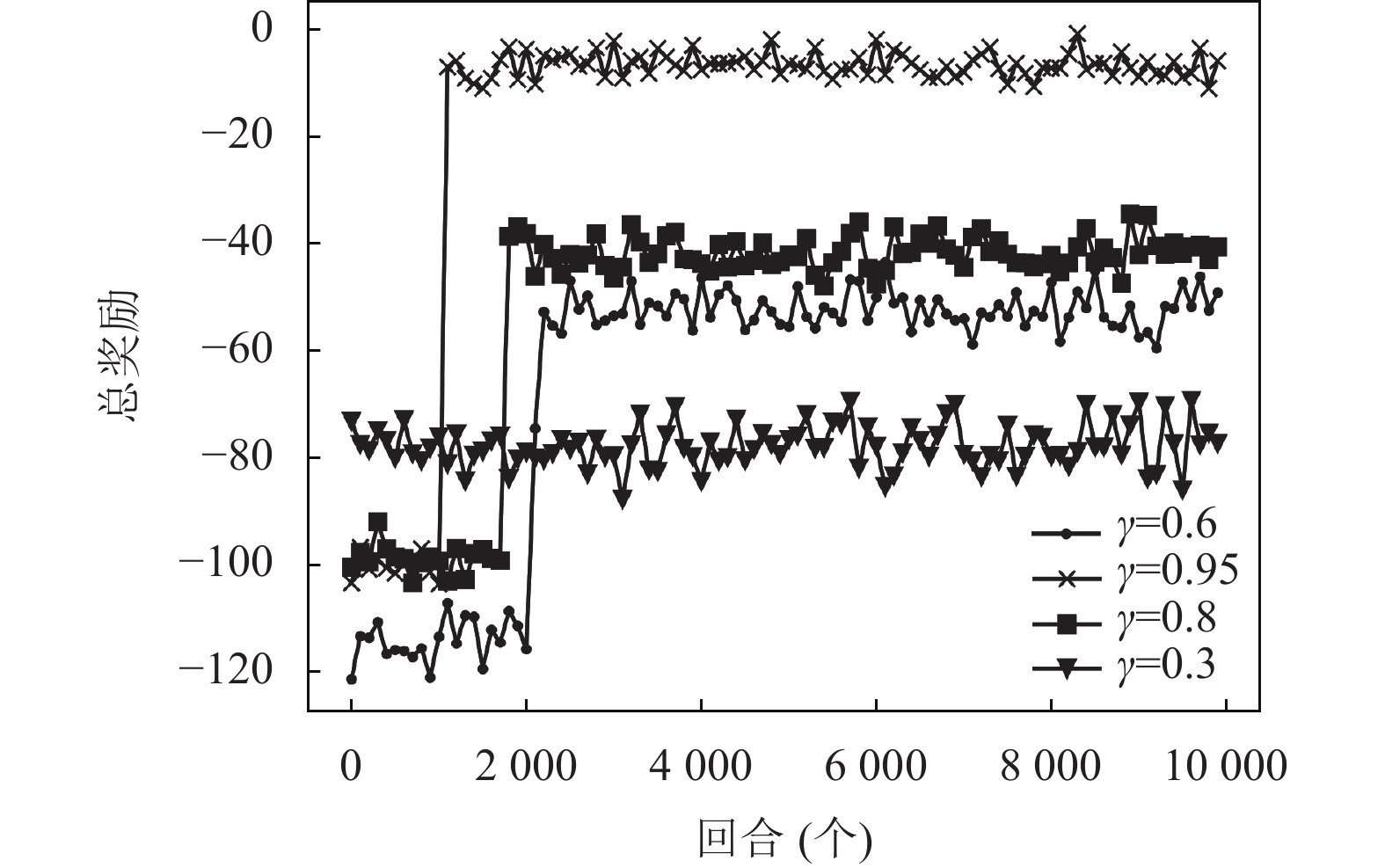
5.2.3 基于不同折扣因子的平均奖励曲线图

折扣因子 $ \gamma $ 用来调节未来奖励对当前奖励值的影响, 它的选取原则是: 在算法能够收敛的前提下尽可能的大. 图5是不同折扣因子下的奖励曲线图, 当 $ \gamma = 0.3 $ 时, 奖励值在−80左右震荡不收敛, 当 $ \gamma = 0.6 $ 时, 奖励值在2 000回合左右收敛, 最终收敛到−50左右, 当 $ \gamma = 0.8 $ 时, 奖励值在1800回合左右开始收敛, 最终收敛到−40左右, 当 $ \gamma = 0.95 $ 时, 奖励值在1 000回合左右开始收敛, 最终收敛到−10左右. 通过分析不同折扣因子下奖励值的收敛速度和收敛值, 可以得出结论: 当 $ \gamma = 0.95 $ 时的收敛速度是最快的, 收敛值是最高的.

5.2.4 本文算法与基准算法平均奖励和概率对比图

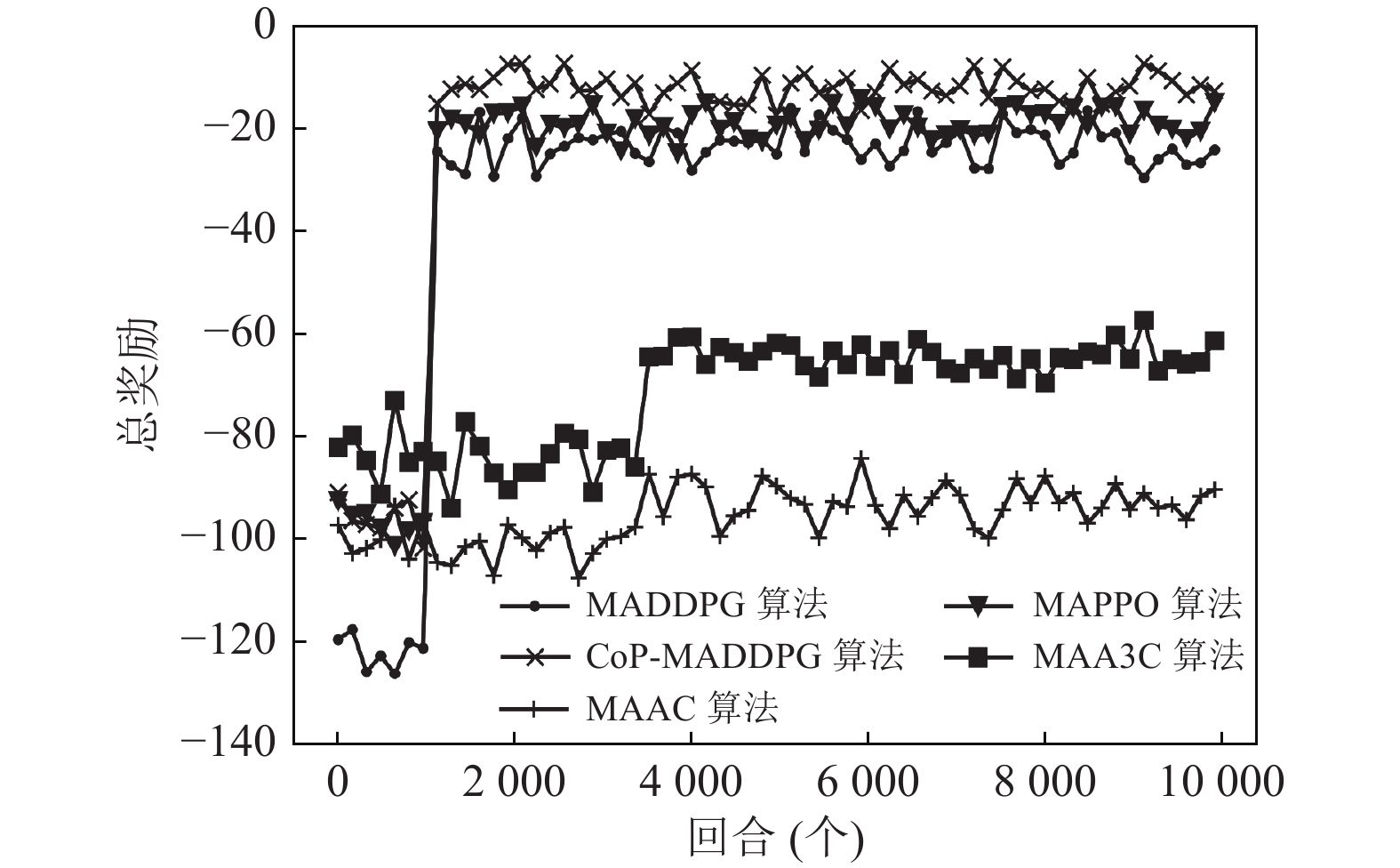
图6是本文算法与基准算法的奖励值对比, 从图中可以看出5种算法均有收敛趋势, MAA3C和MAAC算法收敛速度慢, 收敛幅度小, MAPPO, MADDPG算法和本文算法相比, 3个算法都在1000回合左右收敛, 但是本文算法的收敛值略高于其他两个算法且收敛幅度较大. 通过对图6中数据的分析比较, 验证了本文算法的可用性与有效性.

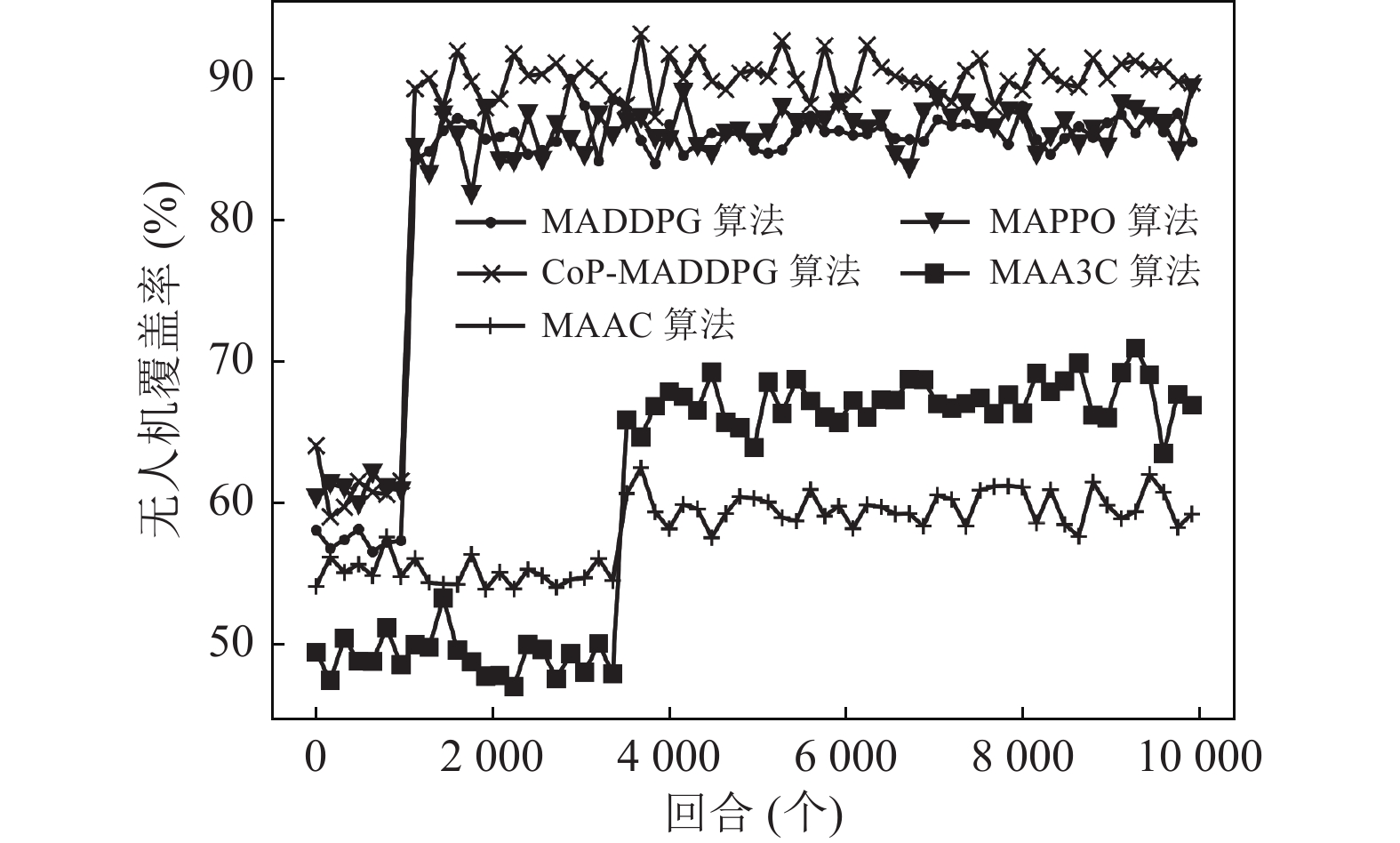
图7是本文算法与基准算法的无人机覆盖率对比图, 从图中可以看出MAAC算法在训练过程中无人机覆盖率从55%左右增加到了60%左右. MAA3C算法在训练过程中无人机覆盖率从50%左右增加到了65%左右. MADDPG算法在训练过程中无人机覆盖率从58%增加到85%左右. MAPPO算法在训练过程中无人机覆盖率从62%增加到85%左右. 本文算法在训练过程中无人机覆盖率从60%左右增加到了90%左右, 并最终在90%左右震荡收敛. 通过对图7进行分析, 可以得出结论: 本文算法在训练过程中无人机可为90%左右的地面终端提供服务, 基本实现了地理公平性.

5.2.5 性能分析

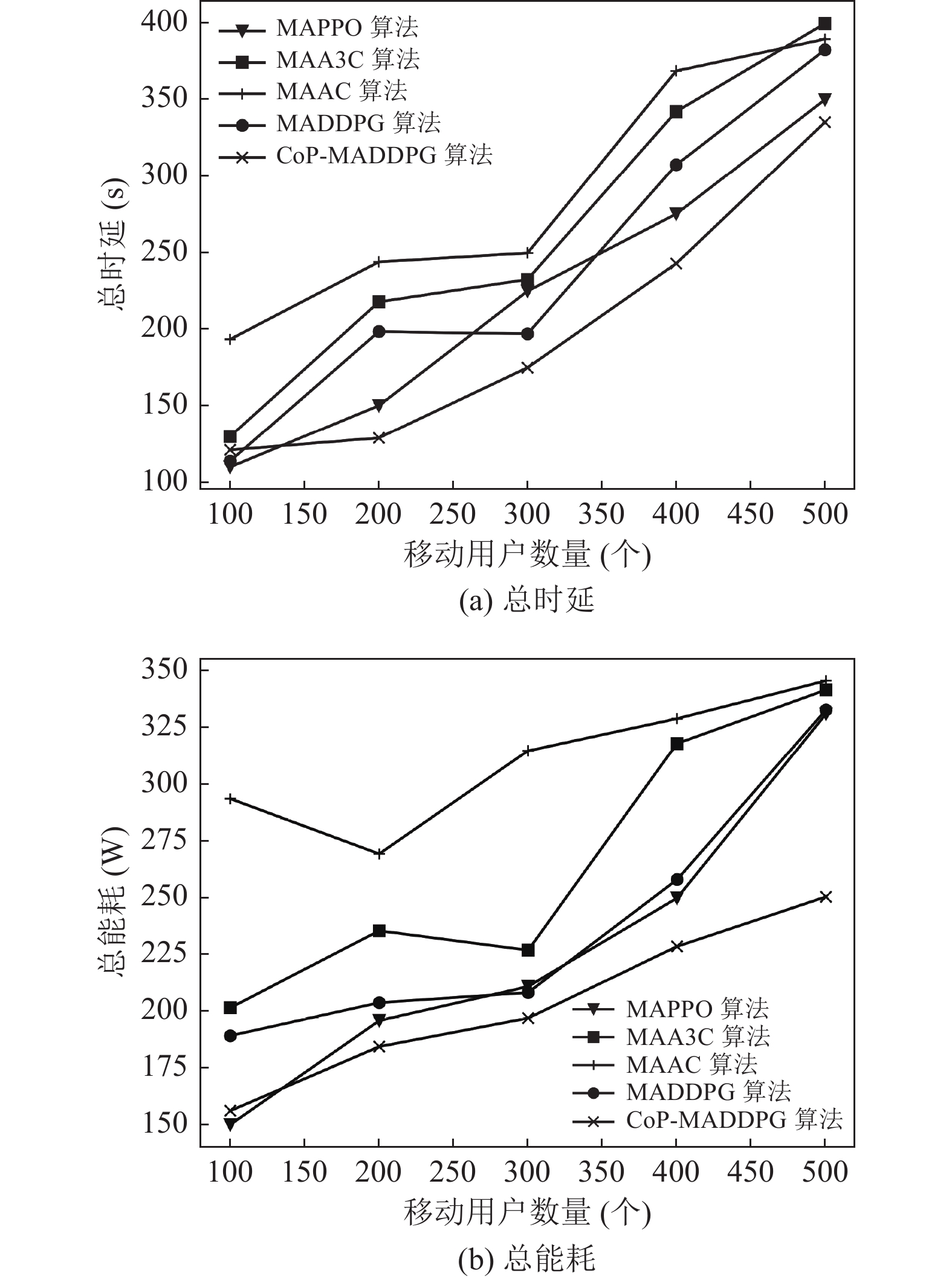
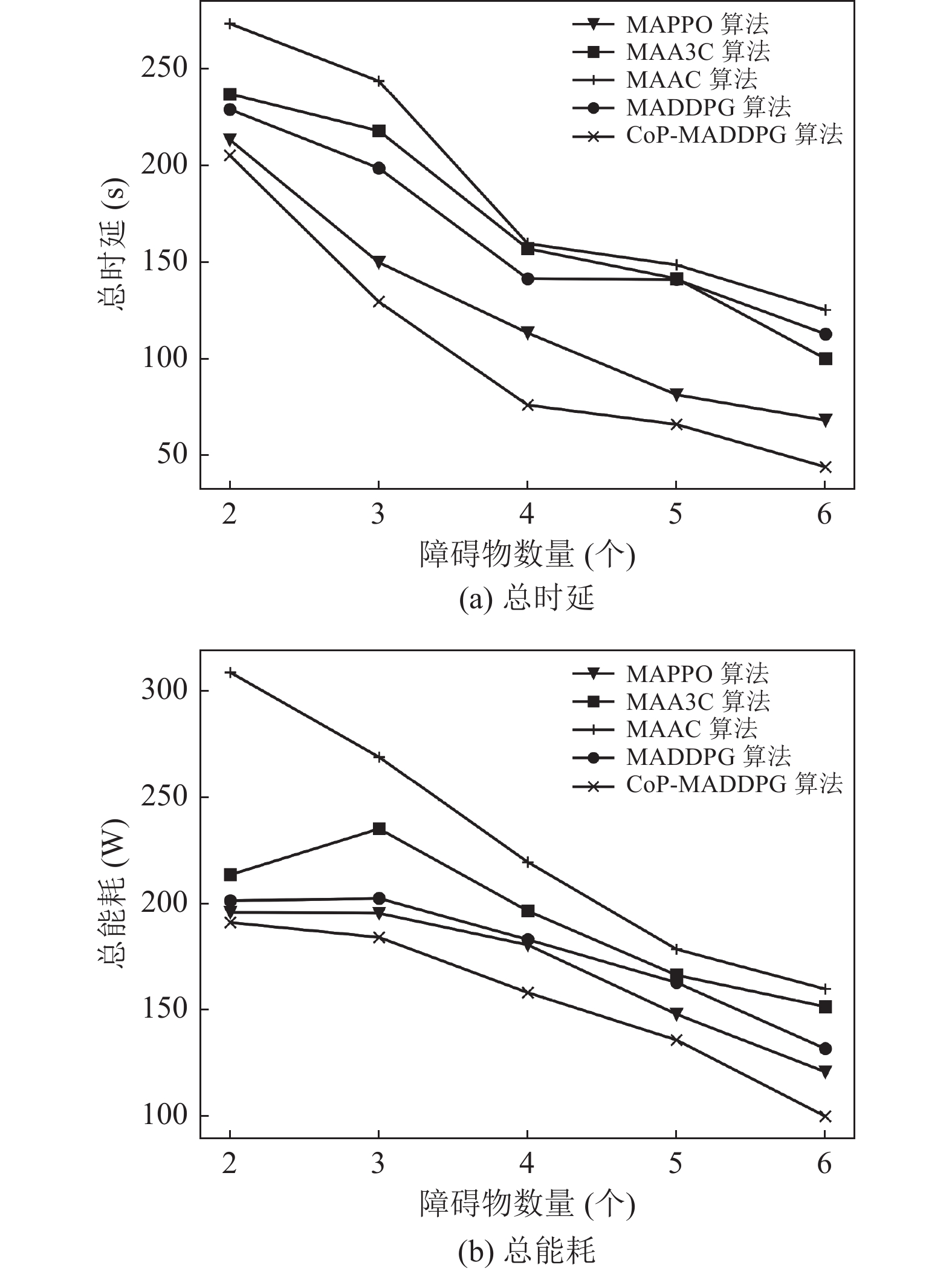
地面移动终端和障碍物的数量在实际场景中可能并不固定. 因此, 本文算法必须适应真实场景的复杂性和可变性. 图8比较了5种算法在不同移动终端数量下的性能. 图8中显示, 延迟和能耗与移动终端数量成正比, 这是因为数据的传输速度和无人机的处理速度都会随着地面终端数量的增加而下降. 图9比较了5种算法在不同障碍物数量下的性能. 图9中折线呈现下降趋势, 因为随着障碍物的增加, 无人机为了更好地避开所有障碍物, 其机动性会随之下降, 因此, 能耗和时延也会减少. 通过图9中数据趋势可以看出: 本文所提出的算法使得无人机在飞行过程中使用了最少的时延和能耗, 验证了本文算法的有效性. MAAC算法具有最高的延迟和能耗, 因为AC算法存在空间复杂度高, 构建时间长的问题. 在延时和能耗方面; MAA3C算法优于MAAC算法, A3C算法中未使用较大存储空间存储历史经验, 大大加速了采样速度, 但训练十分不稳定, 网络难以收敛; MAPPO算法和MADDPG算法性能相近且优于MAA3C算法, DDPG算法探索环境的方式太过复杂, 且简单地从经验池中抽取数据的方法导致训练较慢且不稳定, PPO算法在稳定性方面得到了提升, 但算法的时间复杂度较大, 因此, 这两种算法均会导致较高的延时和能耗. 本文算法在MADDPG算法的基础上使用复合优先级的方法从经验池中抽取数据, 以获得更加有用的经验, 使得训练速度和稳定性得到了一定的提升, 因此, 本文算法和所有基准算法相比, 具有最低的延迟和能耗.

6 总结

本文针对灾区场景建立了多无人机辅助的移动边缘计算系统模型. 地面移动终端将部分任务卸载到对应的无人机进行处理, 配备MEC服务器的无人机在避免碰撞的情况下, 使用最小的时延和能耗为所有地面移动终端提供服务. 本文采用部分可观察马尔可夫决策过程对系统模型进行建模, 并采用CoP-MADDPG算法求解目标问题的最优解, 考虑到经验池的状态, 本文在抽样过程中使用了复合优先级, 其中, 复合优先级包括基于立即回报的优先级和基于TD-error的优先级. 仿真结果表明, 本文算法的奖励值和无人机覆盖率均优于其他基准算法, 在进行飞行轨迹和任务卸载联合优化时具有更好的性能.