1 引言

随着大数据、人工智能等新兴领域的快速发展, 用户的数据量已开始呈指数型增长. 存储系统作为数据存在和发挥价值的基础平台需要保证大容量数据存储的可靠性^[1-3]. 目前, 存储系统通常以块为单位对数据进行存储和处理. 为了保证这些数据块不会因为系统故障而丢失, 存储系统通常会额外存储着一定的冗余数据, 并通过对应的修复机制来保证当系统发生节点或服务器故障等突发情况时, 数据仍然能够被修复, 这被称为存储系统的冗余容错机制. 冗余容错大致分为多副本技术和纠删码技术两类. 多副本技术通过将原始数据拷贝多份并分别存储来保证数据的可靠性. 纠删码技术(erasure coding, EC)作为另一种被广泛应用的存储系统容错策略^[2], 相对于多副本而言能够使用更低的存储开销提供更高的存储可靠性^[4]. 然而, 由于纠删码需要额外的编解码计算以及更为复杂的数据条带化的逻辑, 纠删码会导致更高的计算、元数据等开销, 例如在数据读写、降级读以及故障修复等过程中, 纠删码存储系统需要对数据进行大量的编解码计算. 在当前RDMA等技术相继出现, 数据传输速度不断提升的背景下, 修复数据带来的计算开销对于纠删码存储系统的性能影响不断增大, 在许多场景下会成为其正常读写工作以及数据修复的性能瓶颈.

RS码(Reed-Solomon codes, RS codes)^[5]是纠删码中最著名的一类编码. 参数为( $k, m$ )的RS码将一份数据均匀划分为 $k$ 个数据块, 然后将它们编码为 $m$ 个校验块. 系统将这 $k + m$ 个块组织在一起, 成为一个条带. 所有的原始数据都可以从条带里的任意 $k$ 个块中恢复出来, 因此当条带中产生了不超过 $m$ 个并发故障时, 数据仍然可以正常地修复和使用. 这一特性被称为最大距离可分(maximum distance separable, MDS)性. 具有这一性质的编码被称为MDS码, 这类纠删码均具有高容错性. RS码以最小的存储开销实现了MDS特性, 但他们的编码通过在有限域GF( ${2^{{w}}}$ )上的矩阵乘法设计实现, 其编码复杂性很高.

ZD码 (ZigZag-decodable codes, ZD codes)^[6]作为另一种纠删码策略, 整个编码计算都仅通过移位和异或操作实现. 相比于广泛使用的RS码而言, 它通过存储了额外的一部分冗余数据来进行数据校验, 换取了更简单的编解码计算流程, 避免了执行矩阵乘法, 计算的时间复杂度更低, 同时也只使用GF(2)的有限域. 这些使得它的编解码计算过程十分具有优势^[7].

ZD码的解码过程由之字形解码算法设计生成. 经过分析发现, 当前应用在存储系统领域中的之字形解码算法^[6-8]对于编码的信息利用是不完全的, 这导致了系统需要存储更多的冗余数据才能保证编码达到所需要的高容错性. 本文通过对之字形解码算法进行优化, 提高了校验数据中的信息利用率, 从而使得存储系统可以采用存储开销更低的ZD码编码方案, 进而达到降低整个系统的冗余存储开销的目的. 在本文中, 我们设计了一种优化的之字形解码算法, 它继承了原算法的之字形解码思想, 同时更彻底地利用偏移矩阵中包含的信息. 这使我们能够提出更宽松的约束条件来设计更有效的偏移矩阵. 我们提出了一个性质来限制数据块的偏移量, 并进一步推导出一类具有最佳存储开销的新 ZD 码, 可以通过我们新的之字形解码算法对其进行解码. 我们从理论上证明了代码的正确性, 并在现有的EC库中实现了它们. 以下是本文的主要贡献.

(1)我们提出了一种基于之字形解码的新之字形解码算法. 与原有算法相比, 新算法具有更大的适用范围.

(2)我们提出了一个更宽松的偏移矩阵性质, 并证明了这一性质是ZD码具有MDS性质的必要条件. 基于这一性质, 我们可以搜索开销更低的编码方案, 并证明了在保证MDS性质的前提下, 这一编码产生的存储开销达到了理论的最低值.

(3)我们通过数学分析比较了新编码和现有的ZD码产生的存储开销. 与当前ZD码相比, 在常用的编码参数下, 新编码的额外存储开销减少了 33%–67%. 我们实现了新的 ZD 编码方案并对编码性能进行了实验. 与在 Jerasure 中实现的 Cauchy-RS 代码相比, 新编码的编码吞吐量提高了59%. 在多故障修复的场景中, 新编码将解码吞吐量提高了 40%–121%.

目前已有一些工作针对ZD码的额外存储开销进行了研究和优化. Chen等人优化了基于范德蒙矩阵的偏移矩阵设计^[9], 将开销降低了 50%, 但仍然没有达到最优的存储开销. Dai等人设计了一个最优的ZD码编码方案^[10], 但仅是参数 $k = 4,\; m = 4$ 条件下的一个特例, 无法推广到其他参数下. 此外, 还有一些工作^{[6, 11]}为ZD码提出了一些创新的编码方案以获得更好的修复效率, 这对我们未来的工作具有一定的参考意义. 除 ZD 代码外, 多项工作^[12-14]设计了保持MDS性质的同时计算复杂度较低的异或矩阵. 另一些工作^[15-17]则通过设计编码算法来减少异或运算的数量, 从而加速存储系统的编解码过程.

2 背景介绍 2.1 ZD码

ZD码最初在无线网络领域被提出, 用于解决包碰撞的问题^[18]. 以图1作为例子, 这是一个(2, 2) ZD码条带. ${D_1}$ 和 $ {D_2} $ 是两个长为8位(8 bit)的数据块, ${P_1}$ 和 ${P_2}$ 则是由数据块编码生成的两个校验块. 其中, ${P_1}$ 由 ${D_1}$ 和 $ {D_2} $ 直接通过按位异或计算生成, 其大小仍是8位; 而 ${P_2}$ 由 ${D_1}$ 和 $ {D_2} $ 在偏移1位之后异或计算生成, 大小为9位. 可以看到, 由于两个数据块在计算生成校验块 ${P_2}$ 时相对偏移了1位, 校验块 ${P_2}$ 的数据量相比于其他3个块增大了1位. ZD码将这一编码过程推广到任意数量的数据块, 校验块以及数据大小. 我们在这里给出一个存储系统中的ZD码定义.

定义1. 一个l位长的数据块D以多项式:

$ D({\textit{z}}) = {d_0}{{\textit{z}}^0} + {d_1}{{\textit{z}}^1} + {d_2}{{\textit{z}}^2} + \cdots + {d_{l - 1}}{{\textit{z}}^{l - 1}} $

(1)

表示, 其中 $ {d_i} $ 为 $D$ 的第 $i - 1$ 个数据位, $ {\textit{z}} $ 用于表示 $D$ 中每一位的相对偏移量.

定义2. 给出 $k$ 个数据块 ${D_1}, {D_2}, \cdots , {D_k}$ , 其中任意的 ${D_i}\;(1 \leqslant i \leqslant k)$ 由 $l$ 个数据位构成, 并且:

$ {D_i}({\textit{z}}) = {d_{i, 0}}{{\textit{z}}^0} + {d_{i, 1}}{{\textit{z}}^1} + {d_{i, 2}}{{\textit{z}}^2} + \cdots + {d_{i, l - 1}}{{\textit{z}}^{l - 1}} $

(2)

则一个(k, m) ZD码将这 $k$ 个数据块编码生成 $m$ 个校验块 ${P_1}, {P_2}, \cdots , {P_m}$ , 且对于任意的校验块 ${P_j}\;(1 \leqslant j \leqslant m)$ :

$ {P_j}({\textit{z}}) = {{\textit{z}}^{{t_{1, j}}}}{D_1}({\textit{z}}) + {{\textit{z}}^{{t_{2, j}}}}{D_2}({\textit{z}}) + \cdots + {{\textit{z}}^{{t_{k, j}}}}{D_k}({\textit{z}}) $

(3)

以上定义皆在GF(2)的有限域上. 将这 $k + m$ 个块称为一个( $k, m$ ) ZD码条带. 定义2中的 $k + m$ 个块共同构成一个条带. 若任意一个块都可以被同一条带内的其他任意 $k$ 个块重构, 则称其在参数 $k$ 和 $m$ 下具有MDS性质.

式(3)中, 非负整数 ${t_{i, j}}\;(1 \leqslant i \leqslant k, 1 \leqslant j \leqslant m)$ 为数据块 $ {D_i} $ 在校验块 $ {P_j} $ 编码过程中的偏移量. 这样的元素组成的矩阵被称为偏移矩阵, 具体而言, 一个( $k, m$ ) ZD码条带的编解码偏移量组成了如下的偏移矩阵 $ T $ :

$ T = \left[ {\begin{array}{*{20}{c}} {{t_{1, 1}}}&{{t_{1, 2}}}& \cdots &{{t_{1, m}}} \\ {{t_{2, 1}}}&{{t_{2, 2}}}& \cdots &{{t_{2, m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{t_{k, 1}}}&{{t_{k, 2}}}& \cdots &{{t_{k, m}}} \end{array}} \right] $

(4)

在图1的例子中, 只有 $ {D_2} $ 在 ${P_2}$ 的编码过程中有1位偏移, 即 ${t_{1, 1}} = {t_{1, 2}} = {t_{2, 1}} = 0$ , ${t_{2, 2}} = 1$ , 因此对于图1的(2, 2) ZD码条带而言, $T = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&1 \end{array}} \right]$ . 使用式(1)的表示方式, 数据块 $ {D_1} $ 和 $ {D_2} $ 将被表示为 ${D_1}({\textit{z}}) = {{\textit{z}}^2} + {{\textit{z}}^3} + {{\textit{z}}^5} + {{\textit{z}}^6}, {D_2}({\textit{z}}) = {{\textit{z}}^0} + {{\textit{z}}^3} + {{\textit{z}}^6} + {{\textit{z}}^7}$ , 而从偏移矩阵 $ T $ 知, 校验块 $ {P_1}({\textit{z}}) = {{\textit{z}}^0}{D_1}({\textit{z}}) + {{\textit{z}}^0}{D_2}({\textit{z}}) = {{\textit{z}}^0} + {{\textit{z}}^2} + {{\textit{z}}^5} + {{\textit{z}}^7}, $ $ {P_2}({\textit{z}}) = {{\textit{z}}^0} {D_1}({\textit{z}}) + {{\textit{z}}^1}{D_2} ({\textit{z}}) = {{\textit{z}}^1} + {{\textit{z}}^2} + {{\textit{z}}^3} + {{\textit{z}}^4} + {{\textit{z}}^5} +{{\textit{z}}^6} + {{\textit{z}}^7} + {{\textit{z}}^8} $ .

2.2 之字形解码算法

我们接下来再次以图1为例来说明ZD码的解码过程. 当条带中有单个数据块发生故障时, 我们显然可以用剩余的一个数据块与任意一个校验块通过再次进行带有偏移量的异或运算来解码出故障数据. 而当两个数据块同时发生故障时, 我们首先给出该(2, 2) ZD码条带中所有校验位的具体编码:

$\left\{ \begin{split} & {p_{1, i}} = {d_{1, i}} \oplus {d_{2, i}},\quad \;0 \leqslant i \leqslant 7 \\& {p_{2, 0}} = {d_{1, 0}} \\& {p_{2, i}} = {d_{1, i}} \oplus {d_{2, i - 1}},\;\; 1 \leqslant i \leqslant 7 \\& {p_{2, 8}} = {d_{2, 7}} \end{split}\right. $

可以注意到, 由于错位异或, 校验块 ${P_2}$ 中产生了两个特殊的校验位 $ {p_{2, 0}} $ 和 $ {p_{2, 8}} $ , 它们仅由一个数据位编码生成, 事实上等价于该数据位的拷贝. 我们将这样的校验位称为暴露位. 由以上编码我们可以推出:

$ {d_{1, 0}} = {p_{2, 0}} $

(5)

$ {d_{1, i}} = {d_{2, i - 1}} \oplus {p_{2, i}}, \;1 \leqslant i \leqslant 7 $

(6)

$ {d_{2, i}} = {d_{1, i}} \oplus {p_{1, i}},\; 0 \leqslant i \leqslant 7 $

(7)

由于所有的校验位都已知, 又由式(5), 从暴露位 $ {p_{2, 0}} $ 可以直接获得 $ {d_{1, 0}} $ 的值, 则系统可利用式(6)和式(7), 从低位到高位, 通过迭代来修复两个数据块的所有数据位. 在这个例子中, $ {d_{1, 0}} $ 确定后, 更新与之相关的校验位 $ {p_{1, 0}} \leftarrow {p_{1, 0}} \oplus {d_{1, 0}} $ , 由式(7)可知更新后的校验位 $ {p_{1, 0}} $ 成为新的暴露位, 且 ${d_{2, 0}} = {p_{1, 0}}$ , 可直接修复数据位 $ {d_{2, 0}} $ . 而在得到 $ {d_{2, 0}} $ 后, 由式(6)可再次求得一个新的暴露位 $ {p_{2, 1}} \leftarrow {p_{2, 1}} \oplus {d_{2, 0}} $ , 此时直接修复数据位 ${d_{1, 1}} = {p_{2, 1}}$ .

如此循环, 系统每一次通过已有的暴露位修复一个数据位, 并利用已修复的数据位更新校验位来生成新的暴露位, 即可仅靠2个校验块修复所有的数据位. 这一解码过程即是之字形解码算法. 将示例中的情况推广出去, 若对于定义2中的一个( $k, m$ ) ZD码条带, 使用其中任意 $k$ 个块都可以通过之字形解码算法重构出原始的 $k$ 个数据块, 则称这一ZD码条带是之字形可解的. 值得一提的是, 该解码算法产生的计算开销极低, 在上述的例子中, 解码所有16位数据仅需要基于式(6)和式(7)的15次异或运算. 由于图1的(2, 2) ZD码条带中的任意2个块都能重构出数据块 ${D_1}$ 和 $ {D_2} $ , 这个条带是具有MDS性质的.

2.3 额外存储开销

如同上述讨论中的校验块 $ {P_2} $ , ZD码条带中的校验块会出现数据量大于同条带数据块的情况. 在校验块编码时, 参与编码的数据块的最大偏移量将会决定校验块最高位的位置. 由式(3)可知, 具体而言, 对于任意的校验块 ${P_j}\;(1 \leqslant j \leqslant m)$ , 其块大小为:

$ {l_{{p_j}}} = l + \max ({t_{1, j}}, {t_{2, j}}, \cdots , {t_{k, j}}) $

当 $\max ({t_{1, j}}, {t_{2, j}}, \cdots , {t_{k, j}})$ 大于0时, 校验块 $ {P_j} $ 将会比该条带中的数据块更大, 我们将多出的这一部分大小引起的存储开销称为额外存储开销.

在实际的存储系统中, 如果条带里的各个校验块大小都不同会使得系统实现和执行十分的复杂, 因此ZD码的校验块通常被统一按照最大的校验块大小分配存储空间并工作. 这种情况下, 一个( $k, m$ ) ZD码条带的额外存储开销可以更精确地表示为 ${t_{\max }} \times m$ , 其中 ${t_{\max }}$ 是偏移矩阵 $T$ 中的最大元素值, 它将决定最大的校验块的额外存储开销, 而 $m$ 则是条带中的校验块数量.

显然, 这一额外存储开销越大, 系统的性能将会越低. 然而, 从另一方面来说, 之字形解码算法的过程是利用暴露位不断地修复数据位, 同时更新校验位产生新的暴露位并循环迭代直至所有数据被解码. 过少的暴露位会导致一些故障情况下的条带无法按之字形解码恢复数据. 为了保证数据的容错性, ZD码条带必须保证其额外存储的冗余数据足够支持它的MDS性质. 现在的工作最常见的策略是使用基于范德蒙矩阵和汉克尔矩阵来生成偏移矩阵 $T$ . 这两种偏移矩阵已经被证明在任意参数下均能保证对应生成的ZD码条带具有MDS性质, 但它们的额外存储开销都相对较大^[7].

2.4 解码算法的缺陷

我们发现当前使用的之字形解码算法对冗余信息的利用是不完全的. 当前的之字形解码算法只从每个校验块的首位开始寻找暴露位并尝试进行迭代解码. 然而, 由于ZD码的移位特性, 许多校验块的末位也是暴露位. 在第2.2节的示例中, 算法通过使用暴露位 $ {p_{2, 0}} $ 迭代解码出了所有的数据块, 但此例中 $ {p_{2, 8}} $ 同样是一个暴露位, 但 $ {p_{2, 8}} $ 未被选择用于解码. 事实上, 末位的暴露位可以通过类似的逆序形式迭代解码数据. 在这个例子中, 由条带编码我们可以推导出:

$ {d_{2, 7}} = {p_{2, 8}} $

(8)

$ {d_{1, i}} = {d_{2, i}} \oplus {p_{1, i}},\; 0 \leqslant i \leqslant 7 $

(9)

$ {d_{2, i}} = {d_{1, i + 1}} \oplus {p_{2, i + 1}},\; 0 \leqslant i \leqslant 6 $

(10)

通过式(9)和式(10)以及初始的暴露位 $ {p_{2, 8}} $ , 系统可以从高位向低位之字形解码出 ${D_1}$ 和 $ {D_2} $ 两个数据块的所有数据位. 在这个例子中, 现有算法在没有考虑到末位的额外信息的情况下仍然成功地解码了数据. 然而在很多情况下, 缺失了对末位信息的利用将会使得算法对本可以之字形解码修复的数据无法成功解码. 为了弥补这一缺陷, 条带需要存储更多的数据以保证算法可解, 从而保证MDS性质. 表1中给出了3种可用于(3, 3) ZD码条带的偏移矩阵. 其中, 对于存储最优矩阵(表1第2列)对应的(3, 3) ZD码条带, 如果充分利用其末位的暴露位, 理论上可以重构条带中的任意3个块; 但目前的之字形解码算法无法完成解码过程. 现在的存储系统只能使用另外两种 ${t_{\max }}$ 值较大的矩阵. 这意味着当前的之字形解码算法限制了偏移矩阵的选择, 导致了较大的额外存储开销.

3 设计 3.1 新的之字形解码算法

我们提出了一种新的之字形解码算法, 该算法同时利用校验块首部和末尾的额外冗余信息来加速故障块的重建. 新的算法充分利用了校验信息, 使得ZD码能够用更少的存储量保证高容错性, 具体性能见第4.2节.

由于故障的校验块可以在数据块都可用时通过编码修复, 因此我们只考虑如何在发生故障时用之字形解码算法重构所有故障的数据块. 假设一个( $k, m$ ) ZD码条带所对应的偏移矩阵为 $T$ , 故障导致该条带有 $f$ 个数据块需要修复, 则系统需要取出 $k$ 个可用的块进行解码, 其中包括 $f$ 个校验块 ${P_{{i_1}}}, {P_{{i_2}}}, \cdots , {P_{{i_f}}}$ 以及k–f个数据块 ${D_{{j_1}}}, {D_{{j_2}}}, \cdots , {D_{{j_{k - f}}}}$ . 因为 ${D_{{j_1}}}, {D_{{j_2}}}, \cdots , {D_{{j_{k - f}}}}$ 是可用的, 对于 $1 \leqslant t \leqslant f$ , 通过将 ${P_{{i_t}}}$ 与 ${D_{{j_1}}}, {D_{{j_2}}}, \cdots , {D_{{j_{k - f}}}}$ 按照 $T$ 中对应的偏移量进行错位异或, 可将原本的校验块 ${P_{{i_t}}}$ 更新为 ${P'_{{i_t}}}$ . 更新后的校验块 ${P'_{{i_1}}}, {P'_{{i_2}}}, \cdots , {P'_{{i_f}}}$ 将仅与 $f$ 个故障的数据块 $ {D_{{l_1}}}, {D_{{l_2}}}, \cdots , {D_{{l_f}}} $ 有关, 即: ${P'_{{i_1}}}, {P'_{{i_2}}}, \cdots , {P'_{{i_f}}}$ 是由 $ {D_{{l_1}}}, {D_{{l_2}}}, \cdots , {D_{{l_f}}} $ 以 $T$ 的子矩阵 $S$ 作为偏移矩阵编码形成的 $f$ 个校验块. 其中, 子矩阵 $S = {({s_{i, j}})_{f \times f}}$ 由矩阵 $T$ 中与 $f$ 个故障数据块和 $f$ 个更新的校验块所对应的 $f$ 行 $f$ 列数据构成. $S$ 包含了从 ${P'_{{i_1}}}, {P'_{{i_2}}}, \cdots , {P'_{{i_f}}}$ 中解码出 $ {D_{{l_1}}}, {D_{{l_2}}}, \cdots , {D_{{l_f}}} $ 所需的所有偏移量, 因此我们将 $S$ 称为本次解码过程的解码矩阵. 如图2所示, 当使用图1中的 ${D_2}$ 和 ${P_2}$ 解码时, 由于 ${t_{2, 2}} = 1$ , 令 ${p_{2, j + 1}} \leftarrow {p_{2, j + 1}} \oplus {d_{1, j}}, 0 \leqslant $ $ j \leqslant 7 $ , 所得的更新后的校验块 ${P'_2}$ 有 $ {p'_{2, 8}} = 0, {p'_{2, j}} = {d_{2, j}}, 0 \leqslant j \leqslant 7 $ , 不再与 ${D_1}$ 数据相关. 此解码过程变为使用 ${P'_2}$ 以 $1 \times 1$ 的解码矩阵 $S = \left[ {{t_{1, 2}}} \right]$ 重构数据块 ${D_1}$ 的过程. 由于 $f = 1$ , 此时的解码退化为了简单的复制, 即令 $ {d_{2, j}} \leftarrow {p'_{2, j}}, 0 \leqslant j \leqslant 7 $ 即可修复所有数据. 对于一般情况, 我们设计出了新的之字形解码算法(算法1)来重构所有数据.

算法1. 新之字形解码算法

输入: $\scriptstyle f$ 个大小为 $\scriptstyle {l_p}$ 的校验块 $\scriptstyle {P_1}, \;{P_2}, \cdots , \;{P_f}$ , $\scriptstyle f \times f$ 的解码矩阵 $\scriptstyle S = {({s_{i, j}})_{f \times f}}$ .

输出: $\scriptstyle f$ 个大小 $\scriptstyle {l_d}$ 的重构数据块 $\scriptstyle {D_1}, \;{D_2}, \cdots , \;{D_f}$ .

1) 将所有的数据位标记为未修复, 令 $\scriptstyle hea{d_i},\; tai{l_i}$ 分别指向校验块 $\scriptstyle {P_i}$ 的首位和末位, $\scriptstyle 1 \leqslant i \leqslant f$

2) 在所有的校验块首位中寻找1个暴露位 $\scriptstyle {p_{j, hea{d_j}}}$ , 并根据编码确定其对应的未修复数据位 $\scriptstyle {d_{i, hea{d_j} - {s_{i, j}}}}, \;1 \leqslant i, j \leqslant f$

3) 若存在这样的暴露位 $\scriptstyle {p_{j, hea{d_j}}}$ , 令其对应数据位 $\scriptstyle {d_{i, hea{d_j} - {s_{i, j}}}} \leftarrow {p_{j, hea{d_j}}}$ , 并将 $\scriptstyle {d_{i, hea{d_j} - {s_{i, j}}}}$ 标记为已修复; 若不存在 $\scriptstyle {p_{j, hea{d_j}}}$ , 跳转至步骤6)

4) 对所有的 $\scriptstyle 1 \leqslant j' \leqslant f$ , 令:

$\scriptstyle {p_{j', hea{d_j} - {s_{i, j}} + {s_{i, j'}}}} \leftarrow {p_{j', hea{d_j} - {s_{i, j}} + {s_{i, j'}}}} \oplus {d_{i, hea{d_j} - {s_{i, j'}}}}$ 令 $\scriptstyle hea{d_j} \leftarrow hea{d_j} + 1$

5) 若此时所有数据位都标记为已修复, 输出 $\scriptstyle {D_1}, \;{D_1}, \cdots , \;{D_f}$ , 结束算法; 否则跳转至步骤2)

6) 在所有的校验块末位中寻找暴露位 $\scriptstyle {p_{j, tai{l_j}}}$ , 并根据编码确定其对应的未修复数据位 $\scriptstyle {d_{i, tai{l_j} - {s_{i, j}}}},\; 1 \leqslant i, j \leqslant f$

7) 若存在这样的暴露位 $\scriptstyle {p_{j, tai{l_j}}}$ , 令对应数据位 $\scriptstyle {d_{i, tai{l_j} - {s_{i, j}}}} \leftarrow {p_{j, tai{l_j}}}$ , 并将 $\scriptstyle {d_{i, tai{l_j} - {s_{i, j}}}}$ 标记为已修复; 否则退出并报告解码失败

8) 对所有的 $\scriptstyle 1 \leqslant j' \leqslant f$ , 令:

$\scriptstyle {p_{j', tai{l_j} - {s_{i, j}} + {s_{i, j'}}}} \leftarrow {p_{j', tai{l_j} - {s_{i, j}} + {s_{i, j'}}}} \oplus {d_{i, tai{l_j} - {s_{i, j'}}}}$ ;

令 $\scriptstyle tai{l_j} \leftarrow tai{l_j} + 1$

9) 若此时所有数据位都标记为已修复, 输出 $\scriptstyle {D_1}, \;{D_2}, \cdots ,\; {D_f}$ , 结束算法; 否则跳转至步骤6)

算法1将上述的 $f$ 个更新的校验块和解码矩阵 $S$ 作为输入, 并输出重构后的 $f$ 个故障数据块. 在步骤1初始化了所需变量之后, 算法在步骤2)–5)的循环里首先不断地寻找各个校验块首位的暴露位并进行解码. 在步骤2找到了可用的暴露位后, 如第2.2节示例, 步骤3)将进行对应数据位 ${d_{i, hea{d_j} - {s_{i, j}}}}$ 的修复. 通过矩阵 $S$ 可知, 对所有的校验块 ${P_{j'}}, 1 \leqslant j' \leqslant f$ , $ {P_{j'}} $ 中由 ${d_{i, hea{d_j} - {s_{i, j}}}}$ 编码的校验位为 ${p_{j', hea{d_j} - {s_{i, j}} + {s_{i, j'}}}}$ . 步骤4)对这些校验位进行更新, 从而不断生成新的暴露位来继续迭代过程. 若仅通过该循环便成功完成解码, 算法将在步骤5)输出结果, 否则通过步骤3)跳转至步骤6). 步骤6)–9)为第2个循环, 继续利用校验块末位中的暴露位继续之字形解码, 步骤6)会尝试找到一个可用的暴露位, 步骤7)和步骤8)从后向前进行数据位的修复以及校验位的更新. 若从末位解码能够成功完成则算法在步骤9)中输出数据, 否则通过步骤7)报错.

3.2 差异不同性

为了找到ZD码开销的下界, 我们定义了一个新的偏移矩阵性质来描述其元素之间的关系.

定义3. 令 $T = {({t_{i, j}})_{k \times m}}$ 为一个( $k, m$ ) ZD码的偏移矩阵. 若对于任意 $i \ne i'$ , $j \ne j'$ , $1 \leqslant i, i' \leqslant k$ , $1 \leqslant j, j' \leqslant m$ , 有:

$ {t_{i, j'}} - {t_{i, j}} \ne {t_{i', j'}} - {t_{i', j}} $

(11)

则称矩阵T具有差异不同性.

对于图1的(2, 2) ZD码条带, 其偏移矩阵 $T = {({t_{i, j}})_{2 \times 2}}$ 有 ${t_{1, 1}} - {t_{1, 2}} \ne {t_{2, 1}} - {t_{2, 2}}$ , 所以它是一个具有差异不同性的矩阵. 差值 ${t_{i, j'}} - {t_{i, j}}$ 本质上是数据块 ${D_i}$ 在校验块 ${P_j}$ 和 ${P_{j'}}$ 编码中的偏移量之差. 图1的条带具有差异不同性, 意味着校验块 ${P_1}$ 和 ${P_2}$ 的编码里, ${D_1}$ 和 ${D_2}$ 的相对偏移是不同的, 这保证了 ${P_1}$ 和 ${P_2}$ 能够利用编码相对偏移来实现之字形解码.

如果在一个( $k, m$ ) ZD码条带中, 两个不同的数据位 $ {d_{{i_1}, {a_1}}} $ 和 $ {d_{{i_2}, {a_2}}} $ 同时参与了2个不同的校验位 $ {p_{{j_1}, {b_1}}} $ 和 $ {p_{{j_2}, {b_2}}} $ 的编码, 从偏移矩阵的定义中我们可以得出 ${t_{{i_1}, {j_1}}} = {b_1} - {a_1}$ , ${t_{{i_1}, {j_2}}} = {b_2} - {a_1}$ , ${t_{{i_2}, {j_1}}} = {b_1} - {a_2}$ 以及 $ {t_{{i_2}, {j_2}}} = {b_2} - {a_2} $ . 从这4个等式可以推得 $ {t_{{i_1}, {j_1}}} - {t_{{i_1}, {j_2}}} = {t_{{i_2}, {j_1}}} - {t_{{i_2}, {j_2}}} $ . 因此, 如果ZD码条带的偏移矩阵满足差异不同性, 则条带的任何两个数据位将最多同时参与一个校验位的编码. 如果条带不满足该性质, 则条带的数据无法通过特定的解码过程进行重构. 定理1表明偏移矩阵的差异不同性是保证ZD码具有MDS性质的必要条件.

定理1. 如果ZD码是最大距离可分(MDS)的, 则其偏移矩阵满足差异不同性.

证明: 我们使用反证法来证明定理1. 假设一个(k, m) ZD码条带由大小为 ${l_d}$ 的 $k$ 个数据块 ${D_1}, {D_2}, \cdots , {D_k}$ 以及大小为 ${l_p}$ 的 $m$ 个校验块 ${P_1}, {P_2}, \cdots , {P_m}$ 构成, 且其对应的偏移矩阵 $T = {({t_{i, j}})_{k \times m}}$ 不满足差异不同性, 即存在 ${i_1}, {i_2}, {j_1}, {j_2}$ 使得 $ {t_{{i_1}, {j_1}}} - {t_{{i_1}, {j_2}}} = {t_{{i_2}, {j_1}}} - {t_{{i_2}, {j_2}}} $ . 当数据块 ${D_{{i_1}}}$ 和 ${D_{{i_2}}}$ 故障时, 若系统使用除 ${D_{{i_1}}}$ 和 ${D_{{i_2}}}$ 外的 $k - 2$ 个数据块以及 $ {P_{{j_1}}} $ 和 $ {P_{{j_2}}} $ 这2个校验块进行修复, 则其解码过程等价于使用 $ {P'_{{j_1}}} $ 和 $ {P'_{{j_2}}} $ 解码 ${D_{{i_1}}}$ 和 ${D_{{i_2}}}$ 的过程, 其中 $ {P'_{{j_1}}} $ 和 $ {P'_{{j_2}}} $ 为使用已知的 $k - 2$ 个数据块分别更新 $ {P_{{j_1}}} $ 和 $ {P_{{j_2}}} $ 后所得的校验块, 对于 $1 \leqslant h' \leqslant {l_p}$ , ${p'_{{j_1}, h}} = {d_{{i_1}, h - {t_{{i_1}, {j_1}}}}} \oplus {d_{{i_2}, h - {t_{{i_2}, {j_1}}}}}$ , ${p'_{{j_2}, h}} = {d_{{i_1}, h - {t_{{i_1}, {j_2}}}}} \oplus {d_{{i_2}, h - {t_{{i_2}, {j_2}}}}}$ . 不妨假设 $ {t_{{i_1}, {j_1}}} - {t_{{i_1}, {j_2}}} = {t_{{i_2}, {j_1}}} - {t_{{i_2}, {j_2}}} < 0 $ , 则:

$ p'_{{j}_{1}, h}=\left\{ \begin{aligned} & p'_{{j}_{2}, h-{t}_{{i}_{1}, {j}_{2}}+{t}_{{i}_{1}, {j}_{1}}},\; {t}_{{i}_{1}, {j}_{2}}-{t}_{{i}_{1}, {j}_{1}}< h < {l}_{p} \\ & 0\text{, }\qquad\qquad\quad\;\; 其他 \end{aligned}\right. $

(12)

式(12)表示此时 $ {P'_{{j_1}}} $ 所含的编码信息完全包含于 $ {P'_{{j_2}}} $ 中, 即此时的解码过程等价于使用单个校验块 $ {P'_{{j_2}}} $ 解码出两个数据块 ${D_{{i_1}}}$ 和 ${D_{{i_2}}}$ , 而这是不可能做到的. 因为这一组 $k$ 个块无法解码出故障数据, 这个ZD码条带不具有MDS性质.

3.3 存储最优的偏移矩阵

有了差异不同性这一基础之后, 我们便可以求得ZD码的一个额外存储开销的下界. $k = 1$ 时, ZD码的校验块退化为唯一一个数据块的副本冗余; $m = 1$ 时, ZigZag解码退化为普通的异或校验, 此时其最优的额外存储开销都为0. 当 $k \geqslant 2,\; m \geqslant 2$ 时, 偏移矩阵T需要满足差异不同性, 根据抽屉原理, 其元素两两之间至少需要 $\max (k, m)$ 个不同的差值. 由于T所有的元素都为非负整数, 因此其最大元素值 ${t_{\max }}$ 需满足 ${t_{\max }} \times 2 + 1 \geqslant \max (k, m)$ , 即 ${t_{\max }} \geqslant \left\lceil {\dfrac{{\max (k, m) - 1}}{2}} \right\rceil $ . 因此, ZD码的额外存储开销不可能低于 $\left\lceil {\dfrac{{\max (k, m) - 1}}{2}} \right\rceil \times m$ .

在此基础上, 我们通过简单的搜索算法可以对较小的参数( $k \leqslant 10,\; m \leqslant 3$ )找到达到这一理论下界的偏移矩阵, 我们使用计算机验证了这些矩阵对应的ZD码条带能够用任意 $k$ 个块通过我们提出的算法1进行解码修复, 即它们都具有MDS性质. 综上, 使用这些偏移矩阵生成的ZD码将具有最优的额外存储开销, 我们将这一类ZD码命名为OS-ZD (optimal storage-ZD)码. 表2中列举出了(4, 2)和(6, 3)这两个常用的纠删码参数下, 可以使用算法1保证MDS性质的OS-ZD码偏移矩阵. 当前常用的两种ZD码偏移矩阵都是以原本的之字形解码算法为基础, 基于范德蒙矩阵和汉克尔矩阵设计生成. 由于原解码算法对信息的利用不充分, 它们需要更多的额外存储开销来保证解码性质. 相比之下, OS-ZD码由于新解码算法更加充分地利用校验信息, 可以大大地减少额外存储的校验位. 我们将在第4节中展示这一优势.

4 实验与分析 4.1 实验设置

基于上述的编码构造方式和解码算法, 我们成功地在现有的EC库中实现了OS-ZD码. 我们选择广泛使用的EC库Jerasure, 在其中增加了OS-ZD码的编解码方案模块并使其能够正确地运行并执行读、写和修复等功能. Cauchy-RS码是目前最为通用的MDS纠删码, 我们选用Jerasure库中自带的高效Cauchy-RS码模块作为参照, 在服务器上真实地运行这两种纠删码并比较其结果, 来验证OS-ZD码的正确性和工作效率. 由于两种编码都实现在同一个EC库中, 实验避免了底层运算指令等细节对性能测试的影响.

我们在具有512 GB内存, 2 个Intel(R) Xeon(R) E5-2650 v4 CPU, 2 TB SSD, 操作系统为CentOS 7.5.1804 的服务器上运行实验. 我们随机生成一定大小的数据, 并使用 $(k, m)$ Cauchy-RS码和 $(k, m)$ OS-ZD码分别进行编码. 我们分析不同设置下的编码性能, 然后使用各自最快的配置评估编码性能、单节点故障解码性能和多节点故障解码性能. 每个实验进行 1000 次并绘制其平均吞吐量.

由于目前没有其他开源的ZD码库, 我们将OS-ZD码与已有的ZD码在理论层面进行比较, 在同样的参数条件以及配置下, 通过理论计算各ZD编码产生的额外存储开销并作比较, 来体现我们在存储开销上的优化效果.

4.2 存储开销

我们选取了HDFS等分布式存储系统中常见的一些纠删码参数配置, 并根据各个矩阵的生成方式^[7]理论计算了 OS-ZD 码的偏移矩阵与其他两种常用的 ZD 码偏移矩阵在这些配置下的额外存储开销.

表3显示了各个ZD 码偏移矩阵在这些常用参数下产生的具体开销. 第2–4列中的数字表示每个校验块在使用相应的偏移矩阵时额外存储的校验位. 从表3可以看出, OS-ZD 码相比于现有的ZD码总是具有最小的存储开销, 并且存储开销的差距会随着编码参数 $k$ 和 $m$ 的增加而增加. 相较于另外两种偏移矩阵, OS-ZD码矩阵至少降低了33.3%的额外存储开销. 当参数较大时, 降低的幅度会成倍上升. 这是因为在新的解码算法的支持下, OS-ZD码矩阵比其他两种矩阵的限制条件更加宽松, 因此可选择范围更大, 理论的存储开销下限更低; 同时由于OS-ZD码通过差异不同性搜索到了特定编码下的最优偏移矩阵, 成功地达到了上述的理论下限, 使得OS-ZD码在存储开销上达成了最优.

4.3 编码性能

( $k, m$ ) Cauchy-RS码在有限域GF( ${2^w}$ )上进行编码, 其中 ${2^w} \geqslant k + m$ . 因为对于Cauchy-RS码而言, $ w $ 的增大会增加计算的复杂度, 从而导致编解码性能的降低, 因此我们选择了Jerasure库中可选的最小 $ w $ 值来确保Cauchy-RS码达到其最高的编解码吞吐量.

在前面的讨论中, ZD码都是以位为单位进行的异或计算和偏移. 事实上在实现中, 这样的编解码效率是十分低下的, 系统需要以更大的单位来运算以提升效率. 在我们的编码实现中, OS-ZD码和Cauchy-RS码一样, 采用包作为每次运算的最小单位, 数据块将以数据包为单位进行异或和偏移并生成校验数据, 同样的, 校验块最终产生的额外存储开销也从 ${t_{\max }} \times m$ 位放大为了 ${t_{\max }} \times m$ 个包. 为了探究包的大小对编码吞吐量的影响, 我们分别用上述两种纠删码存储12 MB的原始数据. 在 $k = 6, \;m = 3$ 条件下, 我们测试了这两种编码在不同数据包大小设置下的编码吞吐量, 如图3所示.

从图3可以看到, 相同条件下OS-ZD码的编码吞吐量总是比Cauchy-RS码高86.5%–100.1%, 这是因为OS-ZD码的编码计算量远低于Cauchy-RS码, 使得同种条件时OS-ZD码的计算开销优势很明显. 可以注意到包太小或太大时两种编码的吞吐量都较低, 两种编码受到包大小的影响是相似的, 过小的数据包会导致每次计算的粒度太细, 频繁的存取和计算指令减缓了编解码的速度; 而数据包过大会导致一次编码循环中涉及的数据量太多, 超出了缓存的大小而导致数据频繁地换入/换出缓存. 从图3可见, OS-ZD码和Cauchy-RS码都在包大小为16 KB时实现了最大吞吐量, 因此在后续的实验中, 我们都使用16 KB的包大小来比较两种编码各自的编解码速率.

图4展示了使用(6, 3)作为编码参数时两种纠删码的编码吞吐量. 从图4可以看到, OS-ZD码在所有的块大小参数上的表现都优于Cauchy-RS码. 在块大于1 MB时, OS-ZD码的编码吞吐量比Cauchy-RS码高出64.0%–86.8%. 块较小时, OS-ZD码和Cauchy-RS码的性能差距很大, 在块大小为256 KB时, OS-ZD码的编码吞吐量比Cauchy-RS码高出540%. 这是因为Cauchy-RS码需要在包的基础上进一步细分数据才能进行计算. 如果块太小, Cauchy-RS码的计算效率会变得十分低下, 致使编码吞吐量降低, 而OS-ZD码则由大粒度的异或计算完成编码, 所受负面影响更小.

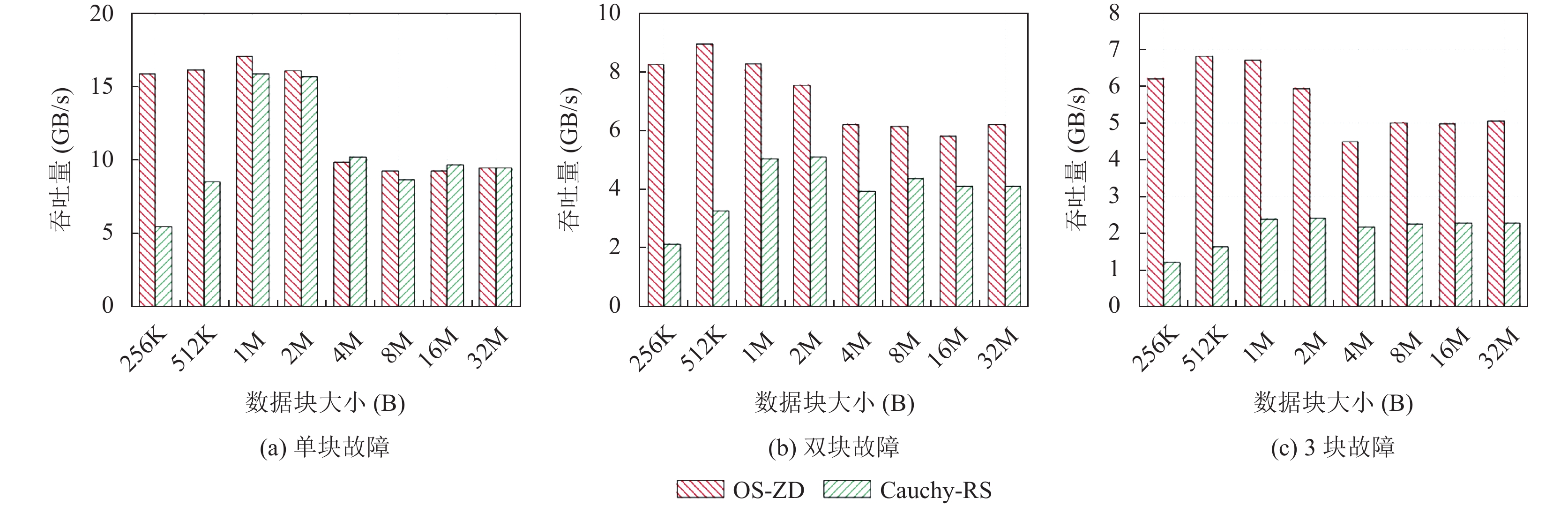
4.4 解码性能

我们测试了两种编码在不同的故障情形下的解码效率, 如图5所示. 图5(a) 展示了发生单个节点故障时的解码吞吐量. 在这种情况下, 两种代码的性能非常接近, 因为Cauchy-RS码条带有一个特殊的校验块 $ {p}_{0} $ , 它可视作由所有的数据块通过异或生成. 当出现单节点故障时, Cauchy-RS码优先使用 $ {p}_{0} $ 校验块进行解码, 此时的解码计算将退化为普通的异或运算, 而不是矩阵乘法. 此时, 两种编码在修复中的计算指令(LOAD、XOR、STORE)的执行时间几乎相等.

在多块故障的情形下, OS-ZD码的解码吞吐量是高于Cauchy-RS码的(如图5(b)和图5(c)). 由于RS码的矩阵乘法逻辑, 随着故障的数据块增多, Cauchy-RS 码执行的解码计算会变得复杂, 即需要执行比OS-ZD码更多的异或指令. 具体而言, 当两节点发生故障和三节点发生故障时, OS-ZD码分别比Cauchy-RS码高出40%–50%和105%–121%的吞吐量, 如图5(b)和图5(c) 所示.

5 总结与展望

本文提出了一种新的基于之字形解码的解码算法, 使ZD码的冗余数据在编解码过程中得到更加充分的利用. 本文还提出偏移矩阵的差异不同性, 并证明了这一性质是ZD码具有MDS性质所需的一个必要条件, 并以此为基础计算出了ZD码存储开销的理论下界, 并提出了OS-ZD码. OS-ZD码以更低的额外存储开销成功地达到了高速编解码的效果.

在目前的工作中, OS-ZD码的编码矩阵暂时还是通过普通的搜索完成的, 这使得该编码无法自由地选取参数; 同时, 现有的解码算法为了寻找暴露位, 需要保存包括各数据位的修复状态在内的许多额外内容, 对内存的占用较大, 并且每次迭代都要通过一次搜索操作来确定所使用的暴露位, 这也增加了不必要的计算开销. 在将来的工作中, 我们会针对这些问题继续展开工作, 不断完善和优化ZD码.