音乐是人类重要的娱乐工具, 由于音乐适用场所氛围不同、各地音乐风俗习惯多样化以及音乐制作人的不断创新等原因, 音乐逐渐衍生成缤纷多彩的流派. 随着数字音乐媒体平台的发展, 在线音乐成为大众音乐消费的主体, 海量的音乐数据引发出用户音乐检索、歌单分类、喜好推荐等个性化需求, 这些个性化需求都离不开对音乐流派的分类, 然而音乐体裁表达的多样性使得音频算法分类成为一项具有挑战性的任务[1], 高效且精确地对音乐流派进行智能分类对音乐平台的发展有着重大意义, 也是音乐信息检索领域亟待解决的难题之一.
音乐流派分类(music genre classification, MGC)已成为目前的研究热点, 目前音乐流派分类步骤大致可分为特征提取和机器学习两个部分[2]. 特征提取在音乐流派分类的过程中占据举足轻重的地位, 其效果和效率很大程度上影响着分类精度. 传统的特征参数有音高、音色、节奏、频谱图、梅尔频谱图、线性预测系数、梅尔倒谱系数(Mel-scale frequency cepstral coefficients, MFCC)、短时特征等. 传统的音乐流派分类模型有K-近邻(K-nearest neighbor, KNN)[3]模型、支持向量机(support vector machine, SVM)[4]模型和高斯混合模型(Gaussian mixture model, GMM)[5]等. 2002年, Tzanetakis等[6]收集音乐数据组成了GTZAN数据集, 它包含10个音乐流派, 共1000首音乐样本, 并将提取出的音高、音色、和节奏3组特征样本分别输入到KNN和GMM进行分类, 分类精度超过了60%, 这是MGC领域的始创性研究之一. 随着机器学习的迅猛发展, 已有不少研究者在MGC领域提出了创新性的特征提取方式和分类模型. Gan[7]用递归神经网络和通道注意力来获取音乐的特征映射应用于音乐流派分类任务中, 在数据集GTZAN中取得了91%的准确率. Gusain等[8]提取数据集的MFCC特征, 并将其作为输入分析比较神经网络和XGBoost算法, 在Kaggle网站搜集的数据集中分别取得90.28%和89.52%的准确率. Ma[9]比较神经网络和传统机器学习算法在音乐类型分类方面的性能和特征提取能力, 用神经网络作为特征提取器并应用简单的传统机器学习模型来训练特征的方法, 通过SVM来训练PCA简化特征可以在GTZAN数据集达到大约83%的分类性能. 郝建林等[10]提出了一种基于用户评论的自动化音乐分类方法, 通过linear CRF进行分词并建立音乐和标签之间的分类模型, 得到了较高的分类精度. Birajdar等[11]分析了色度光谱与视觉特征对音乐流派分类的影响, 用SVM分类器进行的大量实验表明了其优势.
近年来MGC领域出现的创新性方法大多为深度学习神经网络, 由于深度模型带有复杂隐藏层和大量参数, 使得音乐流派分类模型训练耗时, 随着训练的迭代容易出现过拟合问题, 且当训练数据出现增量时无法得到更好的扩展, 训练时间也随着输入数据的增加而变长. Kostrzewa等[12]指出深度神经网络的创建更具有挑战性, 学习过程需要更多的时间, 分类结果表现较差, 因此提出将神经网络组成宽度集合来进行音乐流派的分类, 在FMA-small数据集中取得了65.8%的分类效果.
本文为了解决上述的问题, 设计了一种基于梅尔频谱增强和卷积宽度学习相结合的音乐流派分类方法, 卷积宽度学习(CNNBLS)是一种基于宽度学习(broad learning system, BLS)[13]和卷积神经网络(convolutional neural networks, CNN)[14]的组合算法. 在卷积宽度学习模型中, 通过嵌入到宽度学习特征节点中的卷积层来提取和挖掘音乐流派的特征, 随机生成的权重和偏置将特征节点集合映射成增强节点. 最后将特征节点和增强节点作为扩展的输入数据, 通过伪逆和岭回归运算求出连接输出的权重[15], 进而进行音乐流派的分类. 在卷积层中, 本文使用指数线性单元函数 (exponential linear unit, ELU)[16]替换常用的修正线性单元函数(rectified linear unit, ReLU)[17], 以增强其分类精度. 此外, 当CNNBLS网络遇到新的输入数据时, 它可以增量的方式重新构建, 无需从初始数据重新训练, 训练时间也因此比深度学习的网络少很多. 本文通过谷歌提出SpecAugment方法[18]增强音乐流派的梅尔频谱图, 防止产生过拟合的现象.
1 基本原理 1.1 宽度学习(BLS)宽度学习是由Chen等[13]于2017年提出的, 其整体结构如图1所示. 其中BLS的隐藏层包括特征节点和增强节点两部分. 由输入数据的特征组合成网络的特征节点, 再由特征节点的输出集经过随机加权生成网络的增强节点, 最终输出结果由特征节点和增强节点的输出集进行快速伪逆运算得到.
以下是宽度学习的计算过程:
| $ {Z_i} = {\varphi _i}\left( {X{W_{{e_i}}} + {\beta _{{e_i}, }}} \right), \; i = 1, 2, \cdots, n $ | (1) |
| $ {H_j} = {\xi _j}\left( {{Z^n}{W_{{h_j}}} + {\beta _{{h_j}}}} \right), \; j = 1, 2, \cdots, m $ | (2) |
| $ \begin{split} Y & =\left[ {{Z_1}, {Z_2}, \cdots , {Z_n}|{H_1}, {H_2}, \cdots, {H_m}} \right]{W^m}{\text{}} \\ & =[{Z^n}|{H^m}]{W^m} \end{split} $ | (3) |
其中,
| $ {W^m} \triangleq {\left[ {{Z^n}, {H^m}} \right]^ + }Y $ | (4) |
其中,

|
图 1 宽度学习结构示意图 |
在一些训练数据不断刷新的系统中, 深度模型会使整个训练数据再次建模训练, 而宽度学习是一种增量学习方式, 如果后续加入了新的数据, 无需重新搭载模型, 只需通过更新最新添加的输入样本的权重从而计算加入分量的伪逆即可进行快速的训练. 计算过程如下.
假设
| $ \begin{split} & {A_x} = [\varphi ({X_a}{W_{{e_1}}} + {\beta _{{e_1}}}), \cdots, \varphi ({X_a}{W_{{e_n}}} + {\beta _{{e_n}}})| \\ &\qquad \xi (Z_x^n{W_{{h_1}}} + {\beta _{{h_1}}}), \cdots, \xi (Z_x^n{W_{{h_m}}} + {\beta _{{h_m}}})] \end{split} $ | (5) |
其中,
| $ ^xA_n^m = \left[\begin{array}{*{20}{c}} {A_n^m} \\ {A_x^{\rm{T}}} \end{array}\right] $ | (6) |
相关伪逆更新算法公式如下:
| $ {{(^x}A_n^m)^ + } = [{(A_n^m)^ + } - B{D^{\rm{T}}}|B] $ | (7) |
其中,
| $ {B^{\rm{T}}} = \left\{ {\begin{array}{*{20}{l}} {{C^ + }, {\text{ }}} \\ {{{(1 + {D^{\rm{T}}}D)}^{ - 1}}{{(A_n^m)}^ + }D, } \end{array}} \right.\begin{array}{*{20}{l}} {{\text{ }}{\rm{if}}\;{{ C}} \ne {\text{0}}} \\ {{\text{ }}{\rm{if}}\;{{ C = 0}}} \end{array} $ | (8) |
| $ \begin{split} \\ C = A_X^{\rm{T}} - {D^{\rm{T}}}{A^m} \end{split} $ | (9) |
最终
| $ ^xW_n^m = W_n^m + (Y_a^{\rm{T}} - A_x^{\rm{T}}W_n^m)B $ | (10) |
由于只需计算包含新部分
频谱图是通过傅里叶变换(fast Fourier transform, FFT)得到的可视化表达, 是处理语音信号的关键特征. 音频信号在时域范围内是不稳定的, 为了假定音频信号的稳定性, 要先对音乐原始的音频信号进行分帧和加窗操作[19], 再将FFT变换应用于各窗, 使与之关联的频率分量分布于各信号窗上. 将音乐信号的时间作为横轴, 音乐的频率作为纵轴, 就绘制出了一张能直观表达频率分量在时间上分布情况的二维图像, 随着音乐流派分类领域对特征提取的要求提高, 对于不同流派间差异性区分较弱的频谱图已经不能满足音乐流派分类对特征挖掘的要求, 能增强音乐节奏性和细节表达的梅尔频谱逐渐走进音乐流派分类领域. 梅尔频谱图与原始频谱图的区别在于梅尔频谱图将经过快速傅里叶变换后的音频信号通过梅尔滤波器组, 提取每个信号窗的梅尔频谱分量, 最后将所有的梅尔频谱分量拼接成此音频信号的梅尔频谱图. 图2(a)中展示了GTZAN数据集中Jazz的梅尔频谱图.

|
图 2 梅尔频谱图和屏蔽部分频率信道的梅尔频谱图 |
SpecAugment是Park等[18]在2019年提出的用于增强梅尔频谱的语音增强方法, 该方法类似计算机视觉中cutout[20]的图像处理方法, 能够通过屏蔽或者扭曲梅尔频谱图的局部信息来模拟音频信号的噪声和干扰, 使得模型能够更好地处理此类情况, 降低模型对于局部特征的依赖程度, 使得模型更加注重全局特征, 从而提高网络的鲁棒性并改善过拟合[21-23]. SpecAugment包含时间扭曲、屏蔽频率信道块和屏蔽时间步长块3种方法进行增强, 可以融合使用2种或者3种方法也可以单独使用其中一种方法. 由于本文还需将梅尔频谱图切割处理, 对于时间扭曲和屏蔽时间步长块的超参数不好把控, 所以本文放弃了时间扭曲和屏蔽时间步长块的方法, 仅应用SpecAugment中的屏蔽频率信道的方法对梅尔频谱图进行增强. 沿频域轴方向的
本文将每条音乐数据预处理成随机频率信道屏蔽的梅尔频谱图, 进行切割后再进行特征的挖掘. 基础的BLS模型对于细腻的频谱图特征提取能力较弱, 不能在音乐流派分类上取得很好的效果, 因此本文设计了基于卷积宽度学习(CNNBLS)的模型, 结构如图4所示. 模型主要包括输入数据、特征节点层、增强节点层和输出数据4部分, 其中特征节点嵌入如图5所示的CNN结构, 通过卷积神经网络深度挖掘预处理之后的频谱图, 再将
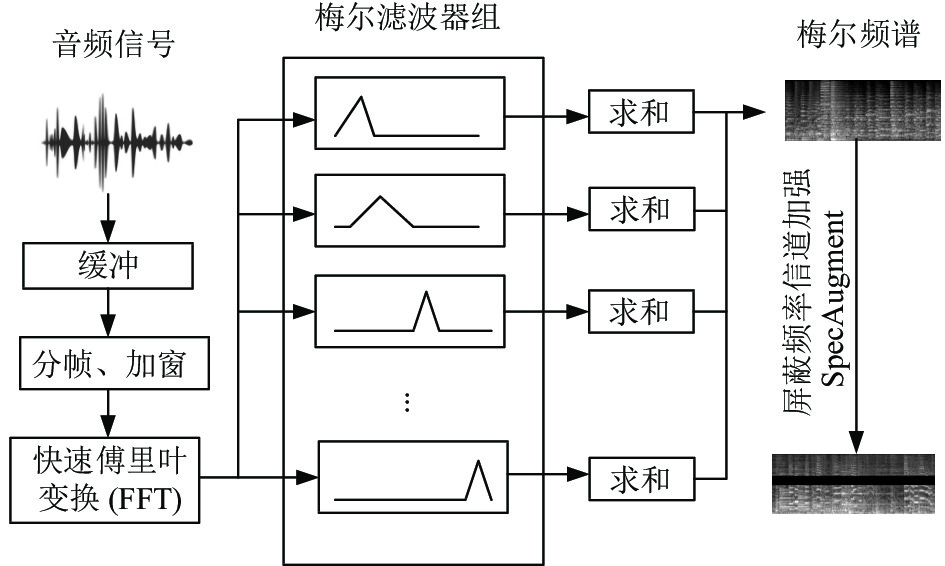
|
图 3 屏蔽频率信道的梅尔频谱图计算过程 |

|
图 4 CNNBLS结构示意图 |
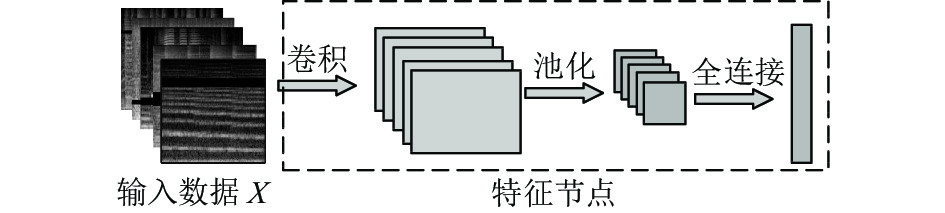
|
图 5 特征节点嵌入CNN示意图 |
经过预处理后的音乐数据
| $ {F^P} = pool\left( {{F^C}} \right) $ | (11) |
同时, 非线性特征
| $ {F^N} = ELU\left( {{F^P}} \right) $ | (12) |
因此, 特征节点
| $ Z = ELU\left( {{F^N}W + \beta } \right) $ | (13) |
其中,
| $ {H_m} = \xi \left( {{Z^n}{W_{{h_1}}} + {\beta _{{h_1}}}} \right) $ | (14) |
因此, CNNBLS模型的输出
| $ \begin{split} Y &= \left[ {{Z_1}, {Z_2}, \cdots, {Z_n}{\text{|}}{H_1}, {H_2}, \cdots, {H_m}} \right]{W^m} \\ & =\left[ {{Z^n}|{H^m}} \right]{W^m}= {\text{A}}{{\text{W}}^m} \end{split} $ | (15) |
其中,
宽度学习是一种可以增加增量的学习方式, 同理, CNNBLS也可以用增量的方式训练新数据, 无需再重建新的模型. 增量学习的卷积层也同样用ELU函数进行激活. Incremental-CNNBLS的增量学习过程如图6所示.

|
图 6 Incremental-CNNBLS增量学习结构图 |
假设输入数据为
| $ {A_x} = \left[ {{Z_{a1}}, \cdots, {Z_{an}}|\xi \left( {Z_x^n{W_{h1}} + {\beta _{h1}}} \right), \cdots, \xi \left( {Z_x^n{W_{hm}} + {\beta _{hm}}} \right)} \right] $ | (16) |
其中,
ELU激活函数是为了弥补ReLU激活函数容易神经元坏死的问题而提出的. 同为避免神经元坏死的而提出的激活函数还有带泄露整流函数 (leaky rectified linear unit, Leaky ReLU)[24]. ELU激活函数表达式为:
| $ f(x) = \left\{ \begin{split} & {x, \qquad\quad\; x > 0} \\ & {\alpha ({{\rm{e}}^x} - 1), {\text{ }}x \leqslant 0} \end{split} \right. $ | (17) |
Leaky ReLU激活函数表达式为:
| $ f(x) = \left\{ \begin{split} &{x, \quad\; x > 0} \\ &{\lambda x,\;\; {\text{ }}x \leqslant 0} \end{split} \right., \; \lambda \in (0, 1) $ | (18) |
ReLU激活函数式为:
| $ f(x) = \left\{ \begin{split} & {x, {\text{ }}x > 0} \\ & {0, {\text{ }}x \leqslant 0} \end{split} \right. $ | (19) |
3种激活函数图像如图7所示, 在正数输入时, 3种激活函数都是线性的, 收敛和计算速度快, 不存在梯度消失的问题. 但当输入为负值的时候, ReLU的梯度为零, 导致神经元坏死不能更新参数, 造成了特征学习的不充分. 而Leaky ReLU和ELU都可以确保模型权重在输入负值时持续更新, 不会出现神经元坏死的情况. 二者区别在于Leaky ReLU在输入负值区添加值微小的斜率, 而ELU在输入负值区是平滑的指数函数. 二者相比, ELU具有左侧软饱和特性, 对于噪声抗干扰能力更强.

|
图 7 3种激活函数图像 |
综上所述, 在分类模型中应用ELU激活函数能够集ReLU和Leaky ReLU的优点, 收敛速度快的同时能够防止神经元坏死, 且其左侧软饱和的特性能够使得CNNBLS模型抵抗干扰和噪声.
3 实验及结果分析 3.1 实验环境及数据集本文实验主要在配置为AMD EPYC 7642 48-Core Processor CPU+RTX 3090 GPU的服务器上进行, 操作系统版本为Ubuntu 18.04, 在PyTorch学习框架下构建CNNBLS实验模型, 并通过音频特征提取工具Librosa[25]进行音频信号到频谱图的转换. 本文采用的是GTZAN数据集[6], 该数据集是MGC领域广泛使用的数据集, 其音乐数据分为10个流派, 每个流派含有100首音乐数据, 分别是Blues、Classical、Country、Disco、Hippop、Jazz、Metal、Pop、Reggae、Rock, 各流派特点见表1.
| 表 1 各音乐流派特点 |
3.2 数据集预处理与划分 3.2.1 数据集预处理
如果要以整张图片输入到模型中将会造成大量的冗余计算, 模型的运算速度会大大降低[26]. 所以本文在声音的预处理方面采用频谱切割的方式, 将音频信号转化为如图8所示的大小为1876×128的部分频率信道屏蔽的梅尔频谱图后, 将一张谱图切割成28张大小为128×128谱图(舍弃最后一张不足128×128的谱图). 同时, 为避免切割时产生信息丢失和突变现象, 相邻的两张频谱切片之间具有50%的重叠比例. 切割后的增强梅尔频谱图如图9所示. 这样不仅使训练样本尺度缩小, 还扩大了训练样本的规模. 音乐流派的最终判定结果, 可以通过该音频所有的频谱切片结果统计后得到, 频谱切割有助于提升流派分类的效果.

|
图 8 未切割前的增强梅尔频谱 |

|
图 9 切割后的增强梅尔频谱图 |
同时, 为了防止数据泄露的情况, 即同一首音乐的不同片段被分别划分到训练集和测试集, 可能存在的重复片段造成评估结果不准确. 所以本文采用先划分训练集和测试集生成频谱后再进行切割的方式进行实验, 使得实验的评估准确严谨.
3.2.2 数据集划分GTZAN数据集共有1000首音乐数据, 本文需要将数据集划分为3组, 分别是用于无增量实验的初始数据训练集、用于增量学习实验的增量数据训练集、用于测试各模型性能的测试集. 为了划分出合理的数据集, 本文选择200首数据作为测试集, 用无增量模型CNNBLS训练不同数量的初始训练数据, 记录测试集的准确率. 绘制出的测试准确率曲线图变化趋势如图10所示. 可以看出当训练集数量为400首时, 为测试准确率曲线的拐点, 接近最高值, 所以选择400首数据作为初始训练集, 200首数据作为测试集, 进行无增量模型CNNBLS的实验, 剩下的400首数据作为增量模型Incremental-CNNBLS增量学习实验的增量数据训练集.

|
图 10 无增量模型的测试准确率随训练集数量变化趋势 |
此外, 本文模型的输入是将音频预处理后的频谱切片, 这在一定程度上扩大了数据集的规模. 一首音乐数据可以分成大小均等的28张频谱切片, 所以GTZAN数据集的频谱切片数据共有1000×28=28000张, 基础数据为400×28=11200张, 增量数据集为400×28=11200张, 测试数据集为200×28=5600张. 400首音乐数据切割生成的11200张频谱数量规模足以支撑本文模型和其他深度学习模型的训练和推理. GTZAN数据集划分情况见表2.
| 表 2 GTZAN数据集划分情况 |
3.3 实验流程
由于传统的音乐流派分类步骤大致可分为特征提取、模型分类两个部分, 所以本文分别在特征提取和分类模型做对比实验. 实验流程图如图11、图12所示. 此外, 为了探索不同的激活函数对于分类模型的影响, 本文分别在有增量数据和无增量数据的CNNBLS模型下进行了激活函数的对比实验. 固定模型参数见表3.
3.4 实验结果分析 3.4.1 特征提取对比实验本文主要对比了原始频谱图、梅尔频谱图和SpecAugment增强后梅尔频谱3种特征提取方法, 为了比较这3种特征提取方式的优良, 本文将GTZAN数据集分别预处理成3个数据集, 分别是切割后的原始频谱图(数据集A)、切割后的梅尔频谱图(数据集B)、切割后的SpecAugment增强梅尔频谱图(数据集C), 由于后续还要进行增量学习的实验, 所以从GTZAN数据集中选出400首数据作为训练集, 200条数据作为测试集, 在参数相同的无增量模型CNNBLS下进行对比实验, 无增量CNNBLS结构如图4所示, 3组数据集准确率见表4.
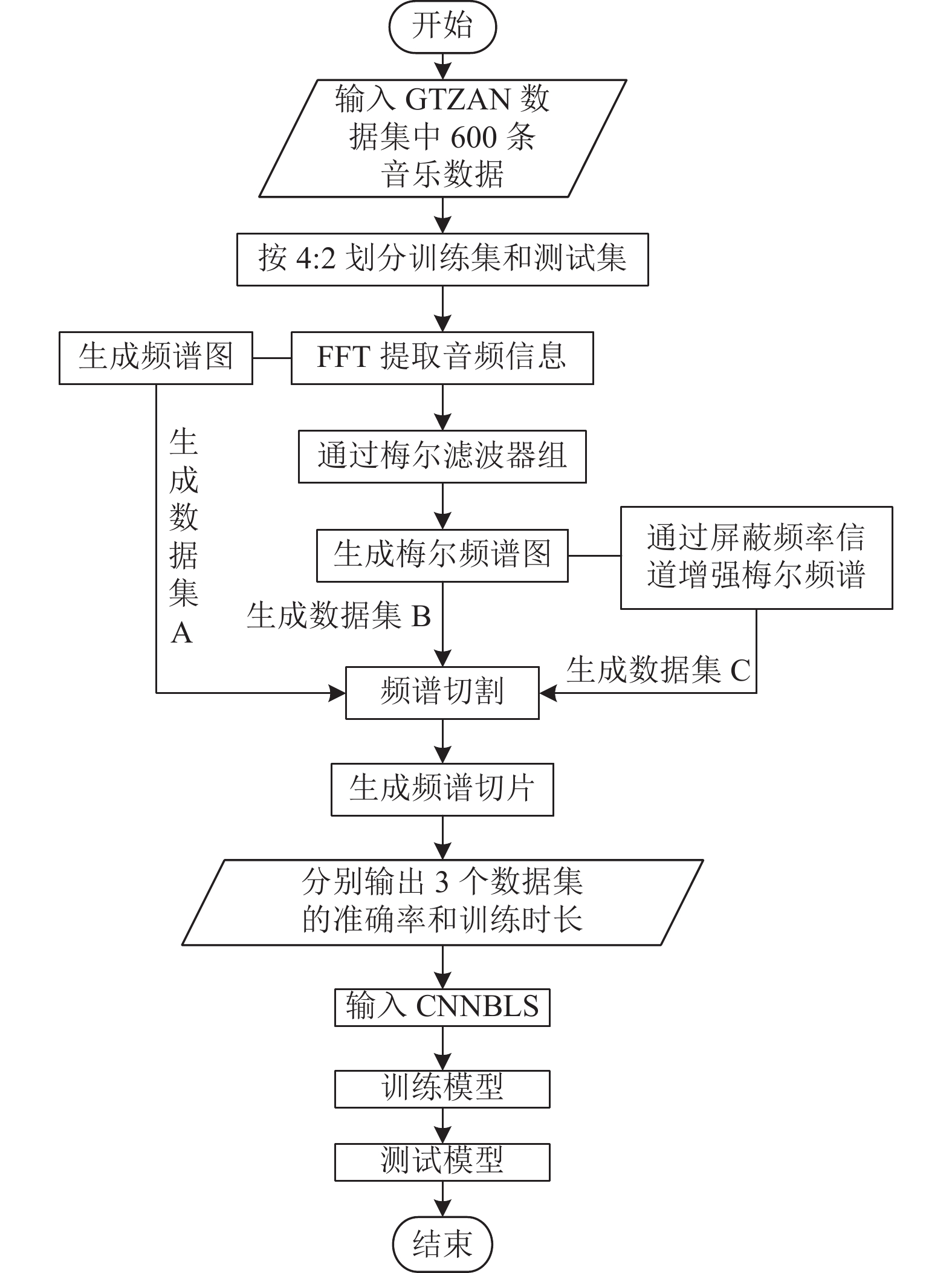
|
图 11 特征提取对比实验流程图 |
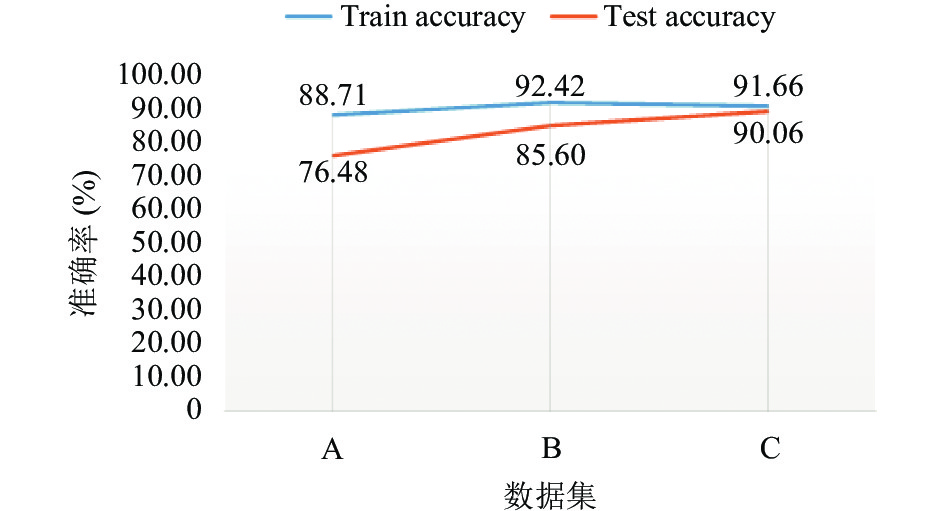
各数据集生成的混淆矩阵如图13所示, 其中x轴和y轴分别表示预测值和真实值, 0–9的标签分别表示流派Blues、Classical、Country、Disco、Hiphop、Jazz、Metal、Pop、Reggae、Rock. 由表4可见: 原始频谱图仅获得76.48%的分类准确率, 挖掘的特征并不能较好的区分各流派的差异性, 且其测试准确率比训练准确率低12.23%, 证明其泛化能力较差. 如图13(a)所示, 几乎每个流派都有大量的数据被分类到其他的流派, 尤其流派9: Rock分类准确率仅有68%. 梅尔频谱图的特征挖掘效率较高, 分类准确率85.60%, 较原始频谱图相比, 已经在特征提取方面取得了较高的准确率, 但其测试准确率比训练准确率低6.82%, 训练模型还是有过拟合的现象, 图13(b)的混淆矩阵可以看出Country、Disco、Reggae和Rock这4个流派分类精度仍然较弱. 本文使用SpecAugment增强后梅尔频谱进行特征挖掘, 在无增量模型CNNBLS下训练后可得90.06%的分类准确率, 图13(c)混淆矩阵也可以看出, SpecAugment增强后梅尔频谱能有效区分各流派的差异性.

|
图 12 分类模型对比实验流程图 |
| 表 3 参数设置 |
为了更好地对比3种特征提取方式的泛化能力, 将表4的数据刻画成如图14所示的曲线图来判断3种特征提取方式的泛化能力和拟合程度, 相比于原始频谱图和梅尔频谱图训练准确率和测试准确率相差较大, 图14中C组的曲线更加趋近拟合, 随机屏蔽部分频率信道的梅尔频谱图的训练准确率和测试准确率仅相差1.6%, 证明了随机屏蔽梅尔频谱图的部分频率信道能够缓解过拟合的问题.
| 表 4 特征提取方式准确率对比 (%) |
这是因为音乐信号通常受到环境噪声、录制设备等因素的影响, 导致信号存在不同程度的变化, 随机屏蔽梅尔频谱图的部分频率信道可以模拟类似上述的噪声和干扰, 从而增加模型的鲁棒性, 使得模型能够更好地处理类似情况. 此外, 随机屏蔽一些频率信道可以降低模型对于局部特征的依赖程度, 使得模型更加注重全局特征, 进一步增强了模型的泛化能力和鲁棒性, 从而缓解过拟合的问题.
3.4.2 无增量模型CNNBLS对比实验分析在无增量模型CNNBLS对比实验中, 用GTZAN数据集中400首音乐数据作为训练集、200条音乐数据作为测试集, 采用频谱分类的准确率和训练时长作为对比实验的性能评价指标. 分别比较了LeNet-5、GoogLeNet、VGG-16、Alexnet等模型和CNNBLS模型的分类准确率和训练时间. 并引用了XGBoost[8]、SVM-PCA[9]和Wide ensemble En10[12]的方法进行对比, 由于这3种方法在工作中没有体现训练时间长短, 所以仅在分类准确率方面与无增量模型CNNBLS作对比, 无增量数据对比结果见表5.
当初始训练数据只有400个时, 无增量模型CNNBLS已经显示出分类的优势, 仅耗时146 s就达到了90.06%的分类准确率, 而其他的训练模型尽管也达到了一定分类效率, 但由于深度学习模型网络架构纵向复杂, 导致训练时长比横向轻量的卷积宽度学习时间长很多. 与其他作者工作对比可以看出: CNNBLS的分类精度分别比XGBoost[8]和SVM-PCA[9]高约0.6%和7%的精度. 本文与Wide ensemble En10[12]都是为了避免深度学习的复杂结构导致训练时间过长而采用了宽度结构, Wide ensemble En10为了用更短的时间得到较好的分类效果, 采用50个基数级分类器的宽度合集En10来进行分类, 其准确率为0.658, 在分类准确率方面, 本文算法比其高出约24%的精度. 此外, CNNBLS还可以在增加增量输入数据的情况下, 较快地进行训练.
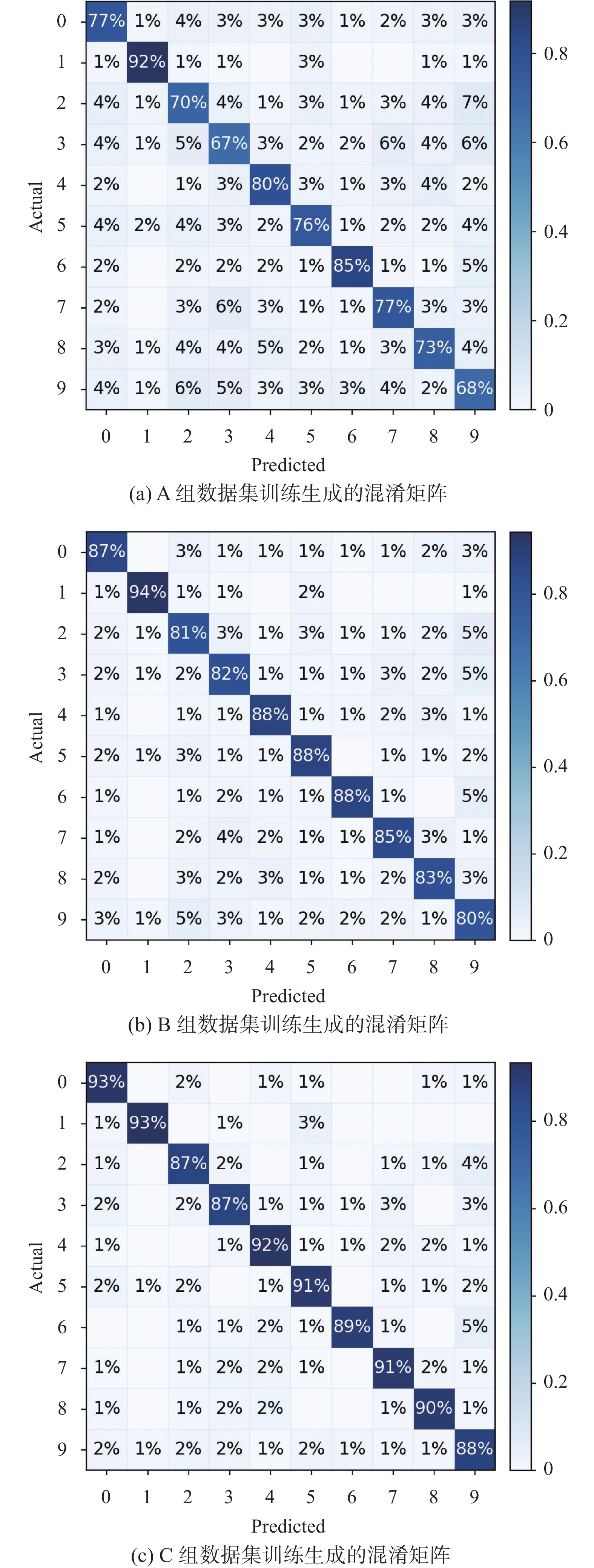
|
图 13 各特征提取数据集生成的混淆矩阵 |
|
图 14 3组数据集准确率对比曲线图 |
| 表 5 无增量数据各模型对比 |
3.4.3 增量模型Incremental-CNNBLS对比实验分析
在增量模型Incremental-CNNBLS的实验中, 将GTZAN中400个数据作为增量训练集加入输入数据中, 剩余200条音乐数据作为测试集, 依旧采用频谱分类的准确率和训练时长作为对比实验的性能评价指标. 加入增量数据各模型分类性能对比结果见表6.
| 表 6 增量数据各模型对比 |
从表6数据可以看出: 加入400个训练数据后, 各模型需要训练一共800首音乐数据, 各模型的准确率和训练时长都有所提高, Incremental-CNNBLS准确率方面获得91.53%的准确率, 图15所示的混淆矩阵可以看出其高效的分类能力, 能够有效对各流派进行区分. 同时Incremental-CNNBLS训练时长上也显示出巨大的优势, 仅用其他网络1/10左右的时间就可获得91.53%的准确率, 这主要与以下几种原因有关.
(1)层数少. CNNBLS网络仅有输入层、特征节点层、增强节点层和输出层4部分, 在特征节点嵌入CNN的层数仅有3层, 而其他深度神经网络少则8层(LeNet), 多则22层(GoogLeNet), 训练时间自然会长.
(2)参数少. 深度学习其数量庞大的待优化参数往往会耗费大量的时间和机器资源[12], 而CNNBLS并没有需要优化的学习率、迭代次数等参数, 随机生成的权重和偏置的数量也比深度网络少, 所以训练会更加快速.
(3)伪逆运算更新权重快. CNNBLS可以从宽度上扩展进行增量学习, 表5、表6训练时间对比可见, 其中除了Incremental-CNNBLS, 其他5个模型在加入1倍的增量数据后训练时间几乎延长了1倍, 因为这4个模型必须重新训练整个网络共800个数据, 而增量Incremental-CNNBLS可以迅速用伪逆计算出新的400个数据分量的权重以进行重建, 无需重新训练800个数据. 这使得它的训练速度比其他模型的训练时间短很多.

|
图 15 增量模型Incremental-CNNBLS生成的混淆矩阵 |
3.4.4 不同激活函数对比实验分析
本文在无增量模型CNNBLS和增量模型Incremental-CNNBLS上分别对比了ELU、ReLU、Leaky ReLU激活函数的影响. 实验结果见表7和表8.
| 表 7 不同激活函数对于无增量CNNBLS的影响 |
| 表 8 不同激活函数对于Incremental-CNNBLS的影响 |
由表7和表8数据可见: 无论是无增量模型还是增量模型, 采用ELU激活函数的分类精度最高, 在无增量模型和有增量模型分别获得了90.06%、91.53%的准确率. 使用ReLU激活函数的模型的分类精度最小. 与ReLU相比, Leaky ReLU和ELU都能解决在输入为负值时神经元坏死的问题, 但ELU具有左侧软饱和特性, 抗干扰和噪声的能力更强. 表7、表8的实验也证明了在卷积层应用ELU激活函数能较好地提高模型的分类效率.
4 结论与展望本文针对频谱图对于音乐特征挖掘较弱、音乐流派深度学习分类模型复杂且训练时间长的问题, 提出了基于梅尔频谱增强和卷积宽度学习的音乐流派分类模型. 一方面通过SpecAugment随机屏蔽频率信道的方法增强梅尔频谱图的特征提取能力, 缓解模型过拟合的问题. 另一方面通过ELU函数对CNNBLS中的卷积层进行加强, 使得模型得到更高的分类准确率. 此外, 少量的参数和轻量的宽度结构也使得网络能迅速的增量学习, 伪逆和岭回归算法动态更新权重使得训练更加快速. 将本文设计的模型与其他机器学习模型在GTZAN数据集上进行对比实验, 实验结果表明, CNNBLS在音乐流派分类问题上具有较高的准确率和较短的训练时间. 无增量模型CNNBLS在数据集GTZAN中耗时146 s获得90.06%的分类准确率, 在比无增量模型增加一倍数据后, 增量模型Incremental-CNNBLS耗时175 s可达91.53%的分类准确率. 基于梅尔频谱增强和卷积宽度学习的音乐流派分类模型还有很大的提升空间, 下一步将充分发挥CNNBLS 的优势以取得更快的训练时间和更高的分类精度.
| [1] |
Łukaszewicz T, Kania D. A music classification approach based on the trajectory of fifths. IEEE Access, 2022, 10: 73494-73502. DOI:10.1109/ACCESS.2022.3190016 |
| [2] |
李伟, 李子晋, 高永伟. 理解数字音乐——音乐信息检索技术综述. 复旦学报(自然科学版), 2018, 57(3): 271-313. |
| [3] |
Wold E, Blum T, Keislar D, et al. Content-based classification, search, and retrieval of audio. IEEE Multimedia, 1996, 3(3): 27-36. DOI:10.1109/93.556537 |
| [4] |
Hearst MA, Dumais ST, Osuna E, et al. Support vector machines. IEEE Intelligent Systems and Their Applications, 1998, 13(4): 18-28. DOI:10.1109/5254.708428 |
| [5] |
Kaur C, Kumar R. Study and analysis of feature based automatic music genre classification using Gaussian mixture model. Proceedings of the 2017 International Conference on Inventive Computing and Informatics (ICICI). Coimbatore: IEEE, 2017. 465–468.
|
| [6] |
Tzanetakis G, Cook P. Musical genre classification of audio signals. IEEE Transactions on Speech and Audio Processing, 2002, 10(5): 293-302. DOI:10.1109/TSA.2002.800560 |
| [7] |
Gan J. Music feature classification based on recurrent neural networks with channel attention mechanism. Mobile Information Systems, 2021, 2021: 7629994. |
| [8] |
Gusain R, Sonker S, Rai SK, et al. Comparison of neural networks and XGBoost algorithm for music genre classification. Proceedings of the 2nd International Conference on Intelligent Technologies (CONIT). Hubli: IEEE, 2022. 1–6.
|
| [9] |
Ma ZZ. Comparison between machine learning models and neural networks on music genre classification. Proceedings of the 3rd International Conference on Computer Vision, Image and Deep Learning & International Conference on Computer Engineering and Applications (CVIDL & ICCEA). Changchun: IEEE, 2022. 189–194.
|
| [10] |
郝建林, 黄章进, 顾乃杰. 基于用户评论的自动化音乐分类方法. 计算机系统应用, 2018, 27(1): 154-161. DOI:10.15888/j.cnki.csa.006155 |
| [11] |
Birajdar GK, Patil MD. Speech/music classification using visual and spectral chromagram features. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(1): 329-347. DOI:10.1007/s12652-019-01303-4 |
| [12] |
Kostrzewa D, Mazur W, Brzeski R. Wide ensembles of neural networks in music genre classification. Proceedings of the 22nd International Conference on Computational Science. London: Springer, 2022. 64–71.
|
| [13] |
Chen CLP, Liu ZL. Broad learning system: An effective and efficient incremental learning system without the need for deep architecture. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 10-24. DOI:10.1109/TNNLS.2017.2716952 |
| [14] |
Li ZW, Liu F, Yang WJ, et al. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(12): 6999-7019. DOI:10.1109/TNNLS.2021.3084827 |
| [15] |
任长娥, 袁超, 孙彦丽, 等. 宽度学习系统研究进展. 计算机应用研究, 2021, 38(8): 2258-2267. |
| [16] |
Djork-Arné C, Unterthiner T, Hochreiter S. Fast and accurate deep network learning by exponential linear units (ELUs). Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2016.
|
| [17] |
Nair V, Hinton GE. Rectified linear units improve restricted Boltzmann machines. Proceedings of the 27th International Conference on Machine Learning (ICML-10). Haifa: ICML, 2010. 807–814.
|
| [18] |
Park DS, Chan W, Zhang Y, et al. SpecAugment: A simple data augmentation method for automatic speech recognition. Proceedings of the 20th Interspeech Annual Conference of the International Speech Communication Association. Graz: ISCA, 2019. 2613–2617.
|
| [19] |
Mannepalli K, Sastry PN, Suman M. MFCC-GMM based accent recognition system for Telugu speech signals. International Journal of Speech Technology, 2016, 19(1): 87-93. DOI:10.1007/s10772-015-9328-y |
| [20] |
DeVries T, Taylor GW: Improved regularization of convolutional neural networks with cutout. arXiv:1708.04552, 2017.
|
| [21] |
杨晓东. 在线藏语语音识别系统的研究[硕士学位论文]. 兰州: 西北师范大学, 2021.
|
| [22] |
赵淼. 基于ASV-Subtools的声纹识别系统设计与鲁棒性优化[硕士学位论文]. 厦门: 厦门大学, 2020.
|
| [23] |
赵宏运. 基于附加间隔Softmax损失函数的CNN-GRU模型说话人识别研究[硕士学位论文]. 哈尔滨: 哈尔滨理工大学, 2021.
|
| [24] |
Xu J, Li ZS, Du BW, et al. Reluplex made more practical: Leaky ReLU. Proceedings of the 2020 IEEE Symposium on Computers and Communications (ISCC). Rennes: IEEE, 2020. 1–7.
|
| [25] |
McFee B, Raffel C, Liang DW, et al. Librosa: Audio and music signal analysis in Python. Proceedings of the 14th Python in Science Conference. Austin: SciPy, 2015. 18–24.
|
| [26] |
王佳铭. 改进DCNN的音乐流派分类研究[硕士学位论文]. 葫芦岛: 辽宁工程技术大学, 2021.
|
 2023, Vol. 32
2023, Vol. 32


