2. 深圳北理莫斯科大学 计算数学与控制联合研究中心, 深圳 518172
2. Joint Research Center for Computational Mathematics and Control, Shenzhen MSU-BIT University, Shenzhen 518172, China
目前, 深度学习在医学图像分析任务上取得很大成功[1, 2], 此类模型的学习效果在很大程度上依赖于专家给出的人工诊断以及大量训练图像的可用性. 半监督学习是利用无标签数据和一部分有标签数据进行训练, PU learning是半监督学习的一个重要分支. 正未标记学习中, 唯一可用的有标签数据是正样本, 它利用无标签数据和正样本进行训练, 学习出一个二分类器. 它不仅符合此类诊断数据的分布特征, 更好地利用无标签数据进行神经网络的训练, 而且能有效解决高质量人工标注难以获得、数量较少的问题. 同时, 近年来对抗性训练被广泛应用在深度学习尤其是半监督学习中. 将对抗性训练思想应用在医学诊断图像的深度学习模型中可以提升模型鲁棒性及稳定性, 所以基于对抗网络的医学图像分类模型也受到广泛关注[3-5].
1 模型相关工作 1.1 正未标记学习模型正未标记学习(PU学习)的研究始于21世纪初. 由于其在生活中的应用广泛, 近年来人们对PU学习的兴趣激增. Denis[6] 对PU学习进行理论分析; Liu 等人[7]对PU 数据集样本的复杂性进行分析. 这些PU学习的早期方法由两步骤组成: 步骤1, 从无标签数据集中查找一些极有可能为负类的样本. 步骤2, 使用正样本和步骤1的可能的负样本作为有标签的数据, 再利用剩余的未标记集来构建单独的分类器. 但是, 此类两步过程容易受到错误的负标签的影响, 因为当用错误的负类样本训练新模型时, 错误会在后续迭代中传播. 以上的PU学习方法都没有像PAN模型一样, 将对抗性思想运用在PU学习中.
1.2 生成式对抗网络生成式对抗网络(generative adversarial networks, GAN)[8]起源于Goodfellow等人在 2014 年研究的噪声对比估计, 它使用与 GAN 相同的损失函数. 对抗性学习思想除了生成建模还有其他用途, 可以应用于神经网络以外的模型. 在控制论中, 基于神经网络的对抗性学习被来训练博弈思想上的鲁棒性控制器, 对抗性学习方法体现在最小化策略(控制器)和最大化策略(干扰)之间的交替迭代. 2017 年, GAN 被用于图像增强领域[9], 其用于提高图像的逼真性而不是清晰度(像素精度), 从而在高放大倍率下产生更高质量的图像. 同年第1批图像被生成了, 并于 2018 年 2 月在大皇宫展出. 在 2019 年, StyleGAN[10]可以更加灵活地生成图像. 2020 年 5 月, Nvidia研究人员研究出了一个 AI 系统(称为“GameGAN”)[11], 它只需通过观看游戏来重现 Pac-Man 游戏.
Hou等人[12]运用GAN生成正类和负类样本, 然后将它们作为有标签数据, 构建单独分类模型, 训练得到最终分类器. Chiaroni等人[13]提出了一种使用GAN生成负样本的方法. 这两篇论文采用的数据类型均为图像. 使用GAN生成文本类型数据和其他形式的数据更困难. 这些基于GAN的分类模型大多单独使用GAN作为数据生成器, 再利用其单独训练一个分类器. 这些模型都没有将对抗性学习思想直接运用在对最终的分类器的训练中, 分类器的训练数据输入也并不是只有正样本和无标签数据集.
1.3 近年来正未标记学习的发展Xu等人[14]都使用传统的基于决策边际(Margin)的方法训练分类器, 但模型结果较差, 尤其在图像分类中; Bekker等人[15]研究PU学习的随机假设; 这些模型的缺点在于, 它们都需要一个先验概率. 研究表明, 如果先验概率的估计值不对, 结果可能会很差. 基于以上分析, Hu等人[16]提出的基于对抗性训练网络的分类模型(PAN), 在该模型中, 作者们将对抗性思想引入PU学习中, 其分类效果较好, 敏感性及鲁棒性较高, 并且不需要先验概率, 可运用在多种类型的数据上.
2 PAN模型背景 2.1 正未标记学习与生成式对抗网络PU learning是半监督学习的一个重要分支. 它利用无标签数据和正样本进行训练, 学习出一个二分类器. GAN是一种深度学习中的无监督学习模型, 因其善于处理复杂分布的数据而广受关注. 此模型框架中含有(至少)两个模块: 生成器(generator)和判别器(discriminator), 以下简称为G和D. 生成器G生成新的样本数据, 鉴别器D评估它们的真实性, 即决定它每个生成的数据样本是否来自有标记的实际训练集. 生成式对抗网络就是通过G和D的互相博弈, 迭代优化模型, 最终学习出一个用于生成图像等数据的一个生成器. 其中, 对抗性神经网络的流程图如图1 所示.
以图像数据为例, 下面具体阐述 GAN 模型的原理. 首先, 本文有一组真实的图片作为训练集中有标签的正样本. 生成器G先接收一组随机噪声Z, 把真实的图片加上这个噪声, 生成假的图片, 记作G(z). 因为本文只向网络输入噪声Z, 而不给它们添加任何标签 (或期望的输出), 所以这种训练过程是无监督学习. D是一个判别网络, 它的输入参数是真实图片x和假数据G(z), 分别输出D(x)和D(G(z)), 代表x和G(z)被D鉴别为正样本的概率. 若概率为1, 就代表100% 是真实的图片, 若输出为0, 就代表不可能是真实的图片.

|
图 1 对抗性神经网络的流程图 |
在 GAN 中, G的功能是产生大量“假图片”来欺骗D, 而D的功能是尽力将生成的假数据(负样本)与真实的有标签的训练数据(正样本)区分开来. 所谓对抗性学习就是一个G和D动态博弈的过程. 最后博弈的结果是: 在最理想的状态下, G可以生成“以假乱真”的图片G(z), 使得D难以判定G生成的图片究竟是不是真实的, 因此D(G(z))=0.5. 通过轮番优化G和D, 从而可得一个生成数据的模型G, 训练的目的就达成了. GAN的目标函数如下:
| $ \begin{split} &{\mathrm{min}}_{G}{\mathrm{max}}_{D} \text{V}(D, G)=\\ &\qquad{\mathbb{E}}_{x\sim{p}_{\text{data }}(x)}[\mathrm{log}D(x)]+{\mathbb{E}}_{{\textit{z}}\sim{P}_{{\textit{z}}}({\textit{z}})}[\mathrm{log}(1-D(G({\textit{z}})))] \end{split} $ | (1) |
首先, 设x代表有标签的训练集样本, 其中z代表传入生成器G的随机噪声.
(1) D的损失函数
D的损失函数可以用常见的二分类器损失函数——二元交叉熵损失函数来定义. 其中k为输入数据. 由于当k为真实数据时y=1, 当k为生成器G生成的数据时y=0, 于是公式简化成:
| $ {D_{{\text{loss }}}} = - \frac{1}{n} \cdot \sum\limits_i^n {\log } \left( {D\left( {{x_i}} \right)} \right) + \log \left( {1 - D(G({\textit{z}}))} \right) $ | (2) |
(2) GAN的目标函数
对D而言, 目的是将损失函数最小化
| $ \begin{split} & {{\rm{max}} _D}V(G, D) = \\ &\qquad {E_{x\sim{p_{{\text{data }}}}(x)}}[\log (D(x))] + {E_{{\textit{z}}\sim{p_{\textit{z}}}({\textit{z}})}}[\log (1 - D(G({\textit{z}})))] \end{split} $ | (3) |
| $ \begin{split} & {{\rm{min}} _G}{{\rm{max}} _D}{\text{V}}(D, G) = \\ &\qquad {{{E}}_{{{x}}\sim{p_{{\text{data }}}}({{x}})}}[\log D({{x}})] + {{\text{E}}_{{{{\textit{z}}}}\sim{P_{{{\textit{z}}}}}({{{\textit{z}}}})}}[\log (1 - D(G({{{\textit{z}}}})))] \end{split} $ | (4) |
本文将对抗性思想直接运用在PU学习中得到的初级的Adapted-GAN (A-GAN). 由第2.1节, PU learning与GAN两者都是利用一部分有标签数据和一部分无标签数据的半监督模型, 且最终都训练出一个二分类器. 将GAN的对抗性思想直接引进正未标记学习里, 这个新型的正未标记学习模型可以理解为: 模型在未标注的数据集里寻找被分为正类的概率大的样本, 去欺骗鉴别器D, 让鉴别器D判别数据是有标签的正样本还是未标注的假样本. 具体对比两者的差别, 不同点是PU learning里面的假数据是从无标签的数据集里面找的; 而GAN的假数据是自身通过生成器生成的.
因此, 将对抗性思想直接运用在正未标记学习中, 可将GAN 中的生成器G换成一个分类器C, 当于将GAN改造成一个对抗性PU学习模型, 这就得到了最初级的Adapted-GAN (A-GAN). 其目标函数如下:
| $ \begin{split} {\mathrm{min}}_{C}{\mathrm{max}}_{D} V(D, C)=&{\mathbb{E}}_{{x}^{p}\sim{P}^{p}\left({x}^{p}\right)}\left[\mathrm{log}D\left({x}^{p}\right)\right]\\ +&{\mathbb{E}}_{{x}^{s}={\mathrm{arg}}_{{x}^{u}\sim{P}^{u}\left({x}^{u}\right)}C\left({x}^{u}\right)=1} \left[\mathrm{log}\left(1 - D\left({x}^{s}\right)\right)\right] \end{split} $ | (5) |
其中,
和GAN模型的公式推导原理相似: 对于D而言, 要尽量把标记的正样本判别为正类, 最大化
值得注意的是, 当本文在训练C时, 相当于保持鉴别器D的各参数不变(固定D的分类标准). 首先, 此时函数中第2项(即鉴别器D将假数据辨认出来的概率)对于固定的无标签数据集U而言, 它的分布与U中数据的分布是有一一映射关系. 而U中的数据分布为离散型, 则函数中第2项的数据分布在训练C时是离散的; 其次, 对于C而言, 第1项是一个固定的无关量, 优化C只与第2项有关. 于是, 对于此离散型的优化函数, 本文采用强化学习中的策略梯度算法来训练C. 在强化学习的训练中, 这一项被视为优化C的奖励. 此种策略梯度算法在后面提出的PAN模型中也有运用.
3 PAN模型本文对Adapted-GAN (A-GAN)模型在对抗性思想上的运用进行改进, 研究了一个更高级的模型——预测性对抗网络(PAN). PAN同样构建PU分类器C替代GAN中生成器G, 但它采用了一种新的方式来运用对抗性学习思想.
3.1 PAN模型提出以上GAN及A-GAN两个模型均用二分类模型的交叉熵函数来定义D的损失函数, 再基于此考虑C的功能, 提出整体优化函数. 这个优化函数本质就是通过迭代更新C和D, 优化鉴别器D分类正确的概率. 而这两个模型的对抗性思想运用在C和D的博弈中, 直接优化鉴别器D分类的总体准确度(ACC). 本文研究的PAN模型则做出以下改进: 它不在D分类的总体准确度上使用对抗性学习思想, 而是在D和C的整体分布上使用对抗性学习思想.
对于单个无标签数据集U中的样本x, 若C选中则
对D而言, D试图区分C选中的负样本与P中的正样本, 也就是增大
PAN模型计算D和C总体概率分布差异, 通过迭代优化D和C进行对抗性训练, 学习出一个二分类器D. 由于PAN以D作为二分类器的模型输出, 它不仅希望C选出的无标签样本很难用鉴别器D来区分, 以达到迷惑鉴别器D的效果, 同时也希望剩余的U中样本点很容易被鉴别器D区分. 于是, C在训练过程中, 不仅要给U中D难以区分的样本赋予高概率, 而且还要给D容易区分的数据赋予低概率.
针对以上目标, C从无标签数据集U中选取假的“正类样本”的原理可以表述如下: C是一个二分类器, 功能是找到一个超平面将数据分成正负两类, 两类样本点的距离就叫做边际(Margin). C的训练过程就是在不断调整这个超平面的参数, 最终训练目标是找到使得Margin最大的超平面. 这与支持向量机(support vector machine, SVM)的二分类原理相同. 总的来说, PAN追求的是C分类整体的精准性, 而不仅只追求把正样本识别出来, 而忽略对负样本输出概率的考虑(后者容易导致高精确度, 低召回率的现象).
3.3 PAN模型中衡量分布差异的函数在PAN中, 本文先利用KL散度度量分类器C和鉴别器D的概率分布差异. 随后研究KL散度的对称化, 得到JS散度作为差异衡量函数.
(1) Kullback-Leibler散度(KL散度)
对连续型概率分布, KL散度的定义如下:
| $ KL(p\Vert q)=-{\displaystyle {\int }_{\mathbb{R}}p}(x)\mathrm{ln}\frac{q(x)}{p(x)}dx $ | (6) |
对离散型概率分布, KL散度的定义如下:
| $ KL(P||Q) = {\Sigma _i}{P_P}\left( {{x_i}} \right)\log \left( {\frac{{{P_P}\left( {{x_i}} \right)}}{{{P_Q}\left( {{x_i}} \right)}}} \right) $ | (7) |
(2) Jensen-Shannon散度(JS散度)
采用KL散度衡量D和C概率分布差异可以最大限度地减少两个概率分布之间的信息损失, 但是KL散度不符合三角不等式及对称性, 所以不符合严格的“距离”的定义. 因此, 我们对KL散度进行对称化, 设
| $ JS(P\Vert Q)=\frac{1}{2}KL(P\Vert M)+\frac{1}{2}KL(Q\Vert M) $ | (8) |
基于KL散度及JS散度的PAN模型的目标函数分别如式(6)和式(7):
| $ \begin{split} {\min _C}{\max _D}{{V}}\left( {D,C} \right)= & \underbrace { - \sum\limits_{i = 1}^n K L\left( {P_i^{pu}\|D_i^{pu}} \right)}_{\rm{I}}\\ & + \lambda \underbrace {\left( {\sum\limits_{i = 1}^{{n_0}} K L\left( {D_i^u\|C_i^u} \right)} \right.}_{{\rm{II}}} - \underbrace {\left. {\sum\limits_{i = 1}^{{n_0}} K L\left( {D_i^u\|\hat C_i^u} \right)} \right)}_{{\rm{III}}} \end{split} $ | (9) |
| $ \begin{split} {{\rm{min}} _C}{{\rm{max}} _D}{{V}}\left( {D,C} \right)= &\underbrace { - \sum\limits_{i = 1}^n {JS} \left( {P_i^{pu}\|D_i^{pu}} \right)}_{\rm{I}} \\+ &\lambda \underbrace {\left( {\sum\limits_{i = 1}^{{n_0}} {JS} \left( {D_i^u\|C_i^u} \right)} \right.}_{{\rm{II}}} - \underbrace {\left. {\sum\limits_{i = 1}^{{n_0}} {JS} \left( {D_i^u\|\hat C_i^u} \right)} \right)}_{{\rm{III}}} \end{split} $ | (10) |
本文规定这个二分类模型中, 正类概率为1, 负类为0, 本文默认无标签数据集中样本全为负类(即U中样本真实标签均为0). 样本通过D和C后输出结果均满足0-1分布. 其中,
目标函数中, 第I项代表PU 数据集中第i个样本的真实概率分布与鉴别器输出结果的概率分布差异, 由于PU数据集中的样本满足0-1分布, 是离散型随机变量, 本文对
(1) 它不需要先验概率, 而很多同类的先进分类器需要先验概率, 但是在实际问题中先验概率是未知的, 所以这是PAN模型对比起同类模型的一大优势.
(2) 应用范围广. 由于PAN没有生成器, 它可以应用在不同类型的数据上, 而不仅限于图像类. 实验得出, 对比起同类的PU模型, 在文本类数据上PAN模型表现优异.
(3) 模型效果好. 将PAN模型 和PU学习的其他高级模型在不同数据集上进行对比. 实验证明, 在给予其他模型准确的先验概率条件下, PAN的精确度、F1-score和鲁棒性都强于所有同类模型. 对结果进行灵敏性分析后, 本文得出如果在未知先验概率的条件下, 其他模型的表现会更差.
4 训练过程本文利用小批量随机梯度下降算法, 对PAN模型进行训练. 设置总训练次数为k, 流程图如图2.
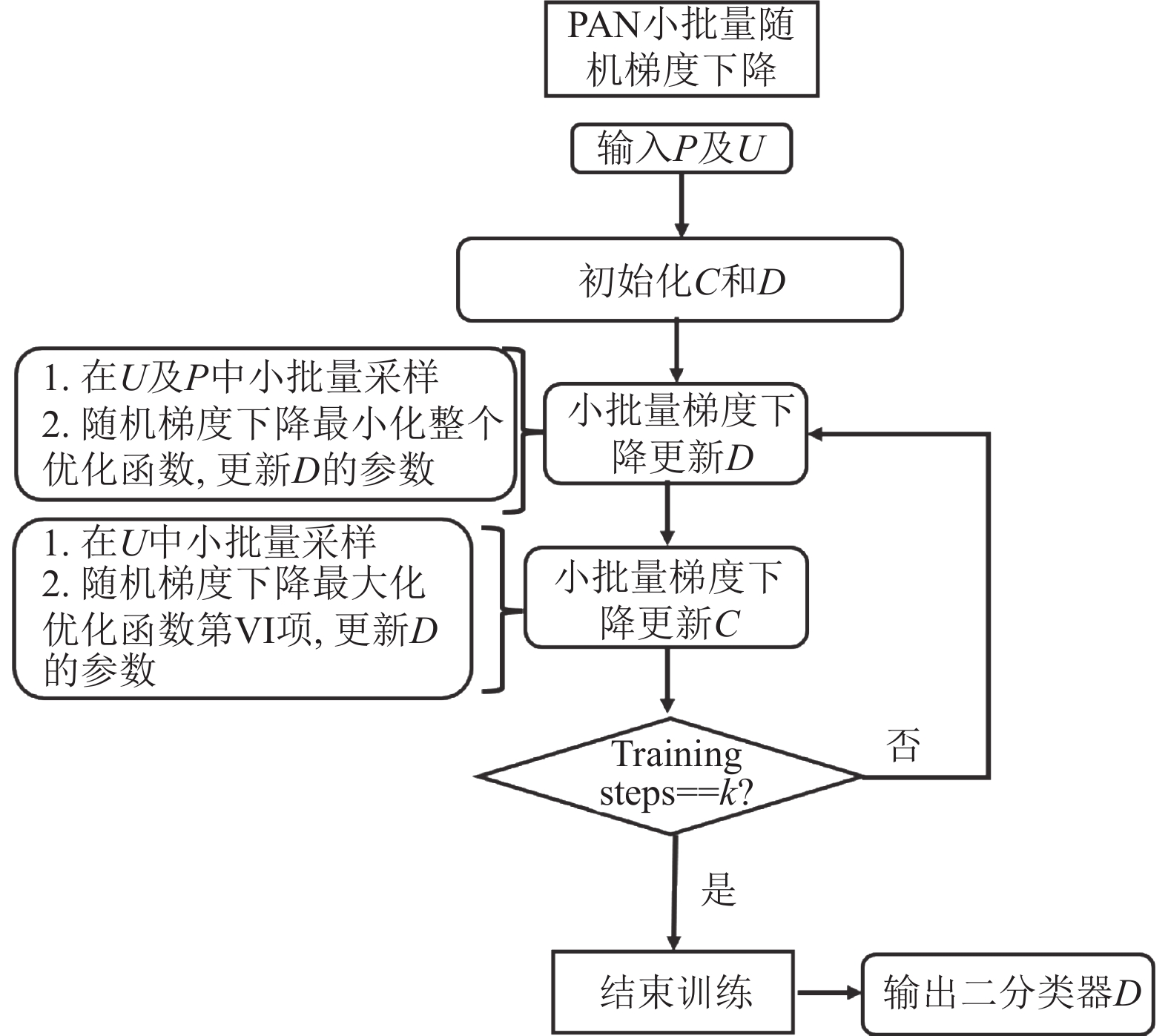
|
图 2 小批量随机梯度下降的流程图 |
5 实验分析
实验分别采用两个普通图像数据集、3个医学图像数据集, 以同类正未标记学习模型, 官网给出的基准模型及原论文的PAN模型结果作为对比, 测试模型的精确度、F1-score指标.
5.1 相关指标定义精确度 (Accuracy, ACC), 也称准确度, 表示的是分类器正确预测占总预测的比例; 召回率(Recall)表示正样本中被预测正确的比例; 误报率表示负样本中预测为正样本的比例; F1-score是精确率和召回率的调和平均数, 最大为1, 最小为0.
对二分类模型而言, 精确度(ACC)及F1-score是重要的衡量指标. 研究者在PU学习中希望通过网络找出所有的正类数据, 从而进行后续分析; 如果模型在找出部分正类数据的同时, 漏掉了很多其他正类样本, 则将大大降低模型的可解释性, 达不到研究目的.
5.2 数据集介绍及准备工作PU数据集有如下特点: 其一, 包含了少量标签数据和大量无标签数据; 其二, 数据集的分类结果只有两类(正类与负类)因此, 我们需要将实验数据集改造成以一定比例的标签数据组成的, 且标签数据只含有正负两类的PU数据集. 本文分别以ratio=0.5, 0.6, 0.7, 0.8, 0.9共5种无标签数据的比例进行实验, 以模拟不同情况下的数据集实验情况. 关于实验采用的3个数据集的示意图如图3. 以下分别介绍本文对每个数据集的二分类标签准备工作.

|
图 3 数据集示意图 |
(1) MNIST[17]
MNIST是一个手写体数字的图片数据集, 标签为0–9的数字, 共10种. 本文将标签为奇数的5类样本作为负类, 偶数的5类样本作为正类, 创建二分类的MNIST数据集.
(2) CIFAR-10[18]
CIFAR-10是一个60万张用于识别普适物体的彩色图片的数据集. 这个数据集一共包含10个不同类别的彩色图像, 图片的尺寸为
(3) Medical-MNIST[19]
Medical- MNIST (简称Med-MNIST)是一个新型开放医疗图像数据集, 提供共十类的医学图像分类数据集. 数据集中的图像分辨率为
首先, 本文在MNIST和CIFAR-10数据集上, 以NNPU[20], UPU[21]和NNPUSB[22]模型为对比的baseline, 设置CPU个数为8, epochs为200, 间隔400个点取样, 实验结果分别为表1及表2. 在 MNIST 数据集上, PAN模型的ACC及F1-score分别为96.35%及96.49%, 均远胜于其他baseline的模型, 这说明PAN模型分类精确、真实可信, 与预期分析一致. 运用对称化KL散度后, 本文得到ACC及F1-score分别为96.68%及96.61%, 分别有了约0.33%及0.12%的效果提升. 在CIFAR-10数据集上, 由表2可见PAN模型的ACC及F1-score都略胜于其他baseline的模型, 说明PAN模型分类效果较好; 运用对称化KL散度后, 本文得到ACC及F1-score分别为89.81%及87.29%, 分别有了约0.40%及0.65%的效果提升. 由于篇幅有限, 本文以基于KL散度的PAN模型在MNIST数据集上的训练数据为代表, 给出损失收敛曲线及精确度曲线随训练轮数epoch的变化图, 如图4所示.
| 表 1 在MNIST[17]数据集上的测试结果 |
| 表 2 在CIFAR-10[18]数据集上的测试结果 |
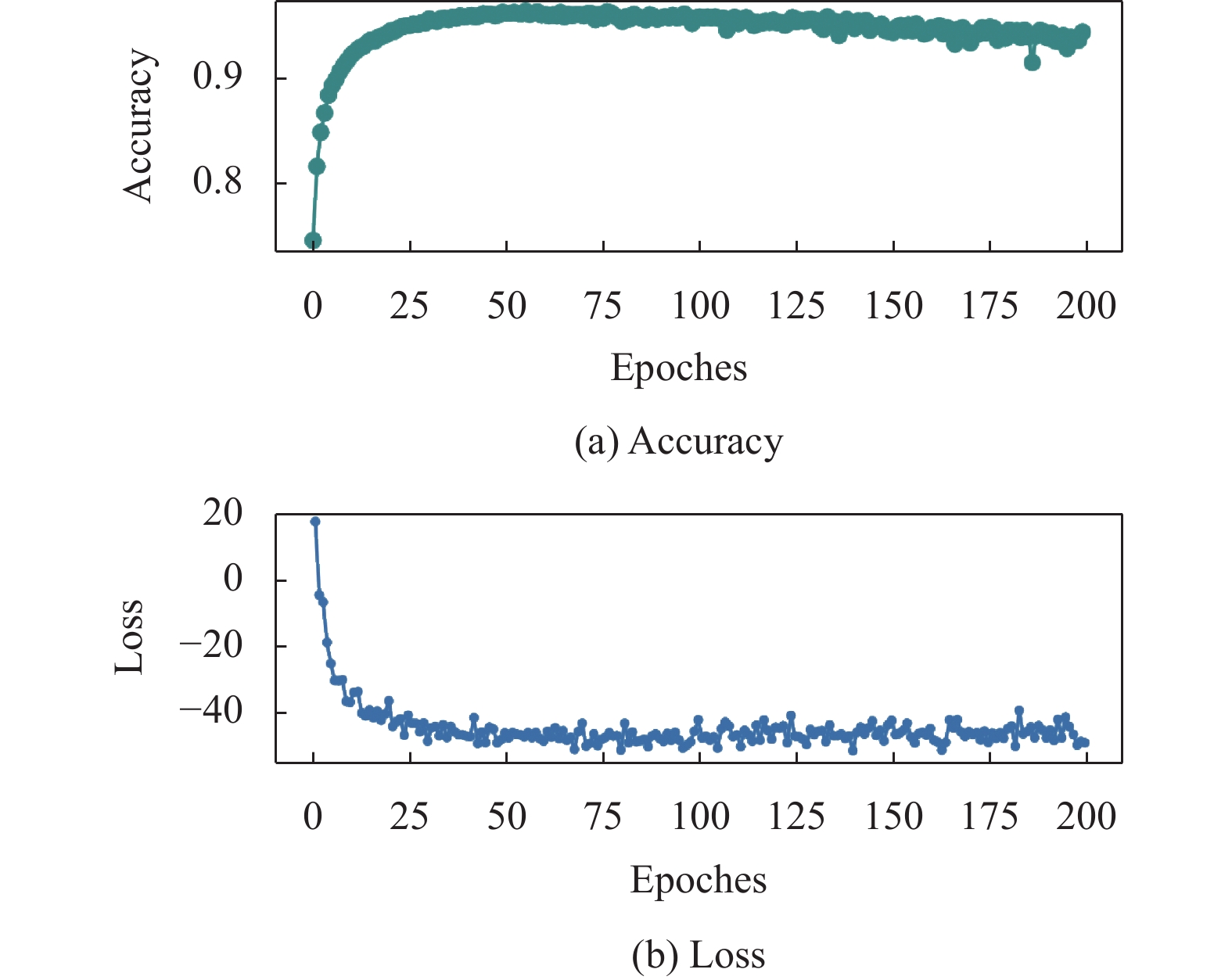
|
图 4 MNIST数据集的精确度及损失收敛曲线 |
最后, 本文在Med-MNIST的3个子数据集Synapse-MNIST3D, Tissue-MNIST, Retina-MNIST上, 实验设置CPU个数为8, epochs为200, 间隔400个点取样, 以Auto-Sklearn[23], ResNet-18 (28)[24], ResNet-50 (28)[25]和AutoKeras[26]模型为对比benchmark, 实验结果如表3. 可以看到, 基于KL散度的PAN模型的ACC都远胜于其他baseline模型, 说明PAN模型在Medical-MNIST医疗图像数据集上分类精确度高, 与预期分析一致; 同时, 对称化改进后的PAN模型也在3个数据集的ACC上有了不同程度的提高, 说明对称化的合理性. 证实了PAN模型在正未标记学习中有出色的二分类表现.
| 表 3 在Med-MNIST[19]的3个子数据集上的精确度 |
6 PAN模型在医疗诊断图像的分类运用
本文着重研究PAN模型在医疗诊断图像数据集上的二分类表现. 以下将从领域特点、实验分析两个角度说明正未标记学习模型PAN在医疗诊断领域图像二分类中有较高的性能.
6.1 领域特点(1)数据集特点
医学诊断领域的数据特点突出. 除了少量确诊病例的各类数据(例如CT图像、MRI和PET等), 医院接收新的病人将有海量未诊断的新数据产生, 未知疾病状况, 没有对应的标签; 同时数据库中较少留存被完全排除疾病可能性的病例样本. 结合以上分析, 医学诊断领域数据集大致满足“包含少量正样本(positive samples)和大量无标签样本点(unlabeled samples)”的特征, 与深度学习中正未标记学习(positive-unlabeled learning, PU learning) 的训练数据条件较为相符. PAN作为正未标记学习的模型, 十分符合医学诊断图像的分类应用背景.
(2) 现状与需求
目前, 深度学习在医学图像分类模型有以下几个局限性: 一方面, 由于诊断费时且只有相关疾病专家才能对数据进行标注, 获取高质量的人工标注进行训练成本高、强度大, 精确标注的训练数据少成为在医学图像上运用深度学习模型的主要障碍; 另一方面, 如何最大化利用无标签的数据进行神经网络的训练是此领域的另一个难题. 最后, 由于有标签的数据少, 训练时需要采取加噪声等措施进一步提升鲁棒性及稳定性, 以避免模型过拟合.
综上, 此领域中获取高质量的数据标记的成本大且耗时长, 模型的学习效果在很大程度上依赖于专家给出的人工诊断以及大量训练图像的可用性. PAN作为正未标记学习模型这种无监督模型之一, 需要的标注数据较少, 可以利用大量无标签数据; 同时PAN的半监督特点又可获得更快、更好的训练效果; 另外, PAN模型中采取的鉴别器与分类器互相对抗的思想, 进一步提升了模型的鲁棒性及稳定性. 因此, 本文研究的PAN模型在医学图像的二分类的任务上具有更高的性能.
6.2 实验分析(1) 模型评价指标
在医疗诊断领域中, 若模型主要用于辅助诊断, 则精确度(ACC)无疑是一个最重要的评价指标——这将关系到患者是否得到准确的疾病信息, 从而接受及时的治疗; 若模型主要用于挑选样本以供医疗工作者研究, 对比起无病样本, 医疗研究者更关注患病样本, 以从中找到疾病相关信息. 这就需要模型尽可能将正类样本全部识别出来, 因此除了ACC外, 召回率(Recall)这一指标也非常重要. 而F1-score作为ACC和Recall两者的调和平均数, 是针对正样本的一个综合衡量性指标, 可以很好地综合代表模型用于医疗领域研究的图像二分类效果. 综上, 在医疗诊断领域中的二分类模型效果主要由ACC和F1-score作为主要衡量指标. 因此我们主要采取这两个指标对PAN模型在CIFAR-10和MNIST两个数据集上的分类效果进行评估, 同时由于Med-MNIST官网没有F1-score数据, 只采取了ACC作为对比指标.
(2) 实验结果对比
在Med-MNIST数据集上, 官网上提供的benchmark模型均为有监督模型, 其分类效果在同等条件下应强于同类半监督模型. 而PAN模型作为半监督模型, 在3个数据集上却获得了更好的精确度(ACC), 这更加证明出PAN模型在医学诊断领域图像的二分类效果出色. 另外, 由于半监督模型数据获取教易, 训练较快等特点, 在医学图像分类中也有更广泛的应用空间.
7 结论与展望本文主要针对半监督学习中的正未标记学习提出了一种基于KL散度及JS散度的预测性对抗网络, 并将其在图像数据集CIFAR-10, MNIST及医学图像数据集Med-MNIST的3个子数据集中进行测试, 得出模型的良好的分类效果及强灵敏度.
PAN模型借鉴了GAN的对抗性学习思想, 通过迭代优化鉴别器D及分类器C, 在两者相互博弈的过程中对网络进行对抗性训练. PAN模型将GAN中的生成器G换成了自身构建的PU分类器C, 它在无标签数据集U里选出可能是正类的样本, 去欺骗鉴别器D, 让D判别数据是否真正是训练集中有标签的正样本; 训练过程中,C尽可能拟合D的数据分布, 以在无标签数据集中选出假数据欺骗D; 而D通过尽可能拉大与C的分布差异, 辨别出C选择的假数据, 以此构成对抗性学习网络; PAN模型将C和D间的总体分布差异作为目标函数, 从而实现对D和C的迭代优化. 本文先研究基于KL散度的PAN模型, 再利用对称化思想创新性提出基于JS散度的PAN模型, 两个模型分别利用KL散度及JS散度作为衡量两个分布的差异函数构建目标函数. 在5个数据集的实验结果表明, PAN模型在精确度、F1-score上优于几乎所有同类模型, 对称化后的JS_PAN模型具有更好的指标, 说明对称思想的合理性及PAN在正未标记学习的出色二分类效果.
由于医疗诊断数据集中含有大量无标签样本及少量正类样本, 适合运用PU学习最大化利用数据信息. PAN模型正是基于这样的数据特征, 是PU学习中的创新模型之一. 对比起同类的PU模型, PAN模型不需要先验概率且不仅仅能运用在图像数据上, 在其他数据类型如文本数据也有较好的分类表现. 经过在Med-MNIST数据集上对比实验, PAN模型作为半监督模型, 其精确度(ACC)明显高于其他benchmark的模型, 说明PAN模型效果好、灵敏度高、应用范围广.
| [1] |
Medley DO, Santiago C, Nascimento JC. CyCoSeg: A cyclic collaborative framework for automated medical image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(10): 8167-8182. |
| [2] |
Lin AL, Chen BZ, Xu JY, et al. DS-TransUNet: Dual swin transformer u-net for medical image segmentation. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 4005615. |
| [3] |
Liu JF, Shen C, Aguilera N, et al. Active cell appearance model induced generative adversarial networks for annotation-efficient cell segmentation and identification on adaptive optics retinal images. IEEE Transactions on Medical Imaging, 2021, 40(10): 2820-2831. DOI:10.1109/TMI.2021.3055483 |
| [4] |
Lei BY, Xia ZM, Jiang F, et al. Skin lesion segmentation via generative adversarial networks with dual discriminators. Medical Image Analysis, 2020, 64: 101716. DOI:10.1016/j.media.2020.101716 |
| [5] |
Yuan WG, Wei J, Wang JB, et al. Unified generative adversarial networks for multimodal segmentation from unpaired 3D medical images. Medical Image Analysis, 2020, 64: 101731. DOI:10.1016/j.media.2020.101731 |
| [6] |
Denis F. PAC learning from positive statistical queries. Proceedings of the 9th International Conference on Algorithmic Learning Theory. Otzenhausen: Springer, 1998. 112–126.
|
| [7] |
Liu B, Lee WS, Yu PS, et al. Partially supervised classification of text documents. Proceedings of the 19th International Conference on Machine Learning. Sydney: Morgan Kaufmann Publishers Inc., 2002. 387–394.
|
| [8] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2672–2680.
|
| [9] |
Sajjadi MSM, Schölkopf B, Hirsch M. EnhanceNet: Single image super-resolution through automated texture synthesis. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 4501–4510.
|
| [10] |
Karras T, Laine S, Aila T. A style-based generator architecture for generative adversarial networks. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019. 4401–4410.
|
| [11] |
Kim SW, Zhou YH, Philion J, et al. Learning to simulate dynamic environments with GameGAN. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 1228–1237.
|
| [12] |
Hou M, Chaib-Draa B, Li C, et al. Generative adversarial positive-unlabelled learning. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: IJCAI, 2018. 2255–2261.
|
| [13] |
Chiaroni F, Rahal MC, Hueber N, et al. Learning with a generative adversarial network from a positive unlabeled dataset for image classification. Proceedings of the 25th IEEE International Conference on Image Processing (ICIP). Athens: IEEE, 2018. 1368–1372.
|
| [14] |
Xu YX, Xu C, Xu C, et al. Multi-positive and unlabeled learning. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: IJCAI, 2017. 3182–3188.
|
| [15] |
Bekker J, Robberechts P, Davis J. Beyond the selected completely at random assumption for learning from positive and unlabeled data. Proceedings of the 2019 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Würzburg: Springer, 2019. 71–85.
|
| [16] |
Hu WP, Le R, Liu B, et al. Predictive adversarial learning from positive and unlabeled data. AAAI, 2021. 7806–7814.
|
| [17] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [18] |
Krizhevsky A. Learning multiple layers of features from tiny images. Technical Report, Toronto: University of Toronto, 2009. 7.
|
| [19] |
Yang JC, Shi R, Wei DL, et al. MedMNIST v2—A large-scale lightweight benchmark for 2D and 3D biomedical image classification. Scientific Data, 2023, 10(1): 41. DOI:10.1038/s41597-022-01721-8 |
| [20] |
du Plessis MC, Niu G, Sugiyama M. Convex formulation for learning from positive and unlabeled data. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille: JMLR.org, 2015. 1386–1394.
|
| [21] |
Kiryo R, Niu G, du Plessis MC, et al. Positive-unlabeled learning with non-negative risk estimator. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 1674–1684.
|
| [22] |
Kato M, Teshima T, Honda J. Learning from positive and unlabeled data with a selection bias. Proceedings of the 7th International Conference on Learning Representations. New Orleans: ICLR, 2019.
|
| [23] |
Feurer M, Eggensperger K, Falkner S, et al. Auto-sklearn 2.0: Hands-free automl via meta-learning. The Journal of Machine Learning Research, 2022, 23(1): 261. |
| [24] |
Odusami M, Maskeliūnas R, Damaševičius R, et al. Analysis of features of Alzheimer’s disease: Detection of early stage from functional brain changes in magnetic resonance images using a finetuned ResNet18 network. Diagnostics, 2021, 11(6): 1071. DOI:10.3390/diagnostics11061071 |
| [25] |
Theckedath D, Sedamkar RR. Detecting affect states using VGG16, ResNet50 and SE-ResNet50 networks. SN Computer Science, 2020, 1(2): 79. DOI:10.1007/s42979-020-0114-9 |
| [26] |
Jin HF, Song QQ, Hu X. Auto-Keras: An efficient neural architecture search system. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. Anchorage: ACM, 2019. 1946–1956.
|
 2023, Vol. 32
2023, Vol. 32


