在医疗研究领域, 疾病风险预测是指预测具有某些特征的人群未来患有某种疾病的概率. 疾病风险预测有助于患者了解自身的发病风险, 并通过早期介入预防干预措施, 以降低疾病的发生率及死亡率[1]. 目前, 基于机器学习的疾病风险预测得到了广泛应用, 对临床疾病的管理与决策起到了积极的辅助作用[2]. 但是, 机器学习算法的性能很大程度上依赖于准确的标注信息. 由于医疗数据通常由医生进行人工标注, 在海量的医疗数据中不可避免地会存在错误的标注信息. 如果数据集标注信息的准确性过低, 机器学习算法的性能将受到严重影响[3].
错误的标注信息会导致机器学习算法的参考标签与真实信息存在偏差, 在模型训练过程中引入标签噪声[4]. 它通常由以下原因导致: (1)标注者偏差, 由于各个医生的诊疗经验不同, 同一条医疗数据的标签可能存在偏差, 相似的医疗数据的标注信息可能存在较大差异; (2)标注(诊断)过程中医学检测信息不够充足, 导致样本特征不足以描述相应标签[5]; (3)待标记样本的可辨识度较低; (4)医疗数据存储中数据编码或通信问题. 使用带有标签噪声的数据训练机器学习模型会导致其出现严重的性能退化, 无法取得理想的性能, 同时也会增加训练所需的样本数量和模型的复杂性[6]. 鉴于此, 许多学者针对标签噪声的处理开展了大量的研究工作, 主要包括基于样本隔离的方法[7-9], 基于损失函数的方法[10-12], 和样本重加权方法[13, 14]. 样本隔离方法从有噪声的样本中筛选干净的样本, 使模型训练过程不受标签噪声的影响. 文献[8]发现在神经网络训练过程中, 网络会优先学习干净样本, 然后再拟合噪声样本, 因此, 研究人员以训练损失为准则, 通过筛选小损失的样本构造干净数据集实现抗标签噪声学习. 文献[9]认为多个网络具有不同的学习能力, 可以过滤不同类型的标签噪声. 因此他们提出一种基于CNN的co-teaching方法, 每个网络都选择一定数目的小损失样本进行学习, 并让他们互相指导对方的训练, 从而具备对标签噪声的鲁棒性. 基于损失函数的方法通过构造对称有界的损失函数提升模型对标签噪声的鲁棒性. 文献[11]提出一种对称的交叉熵损失函数, 通过引入反交叉熵函数构造对称性解决了交叉熵损失函数在有噪声标签数据集中学习不足和过拟合的现象. 文献[12]提出了泰勒交叉熵损失函数, 基于分类交叉熵损失的泰勒级数的阶数对训练标签的拟合程度进行加权, 提高了对标签噪声的鲁棒性. 样本重加权方法在训练过程中对样本分配不同的权重以调节他们的梯度, 通过降低潜在被污染样本的权重以缓和标签噪声对参数优化的影响. 文献[13]采用欧氏距离度量原始数据概率分布的密度以划分不同的区域, 进而根据区域设计相应的检测和过滤规则抑制标签噪声, 可以融合学习任务的先验知识进行局部化设计, 实现具有针对性的标签噪声过滤. 文献[14]通过无约束最小二乘重要性算法估计标签重要性, 结合自训练策略进行半监督训练, 实现样本重加权, 能够有效地抑制标签噪声对参数优化过程的影响, 取得较好的识别准确率. 尽管很多方法在图像识别取得了理想的性能, 但是针对疾病风险预测的标签噪声的相关工作却寥寥无几.
鉴于此, 本文提出了一种标签噪声鲁棒学习算法, 结合鲁棒损失函数和样本重加权方法的优势, 设计了一个非对称的有界损失函数提高对标签噪声的鲁棒性, 并在模型优化过程中动态地评估每个样本的权重, 进一步抑制标签噪声对疾病风险预测模型的影响. 本文的主要贡献如下.
(1) 提出了基于深度神经网络和动态截断损失函数的标签噪声鲁棒学习算法.
(2) 设计了一个动态的非对称有界截断损失函数, 融合了传统交叉熵函数的隐式加权特性和均方差损失函数的标签噪声鲁棒性, 通过限制损失下界增强模型的鲁棒性, 引入与样本相关的权重实现对可疑样本的动态隔离.
(3) 以真实的脑卒中筛查数据集为例, 验证了所提出算法的有效性和可行性.
本文第1节介绍了符号定义及问题描述. 第2节介绍了所用算法. 第3节介绍了实验过程及结果分析. 第4节对本文内容进行了总结.
1 符号定义及问题描述 1.1 符号定义考虑给定数据集
根据标签噪声的统计性质, 可将其分为以下4类.
(1) 随机标签噪声. 受到随机标签噪声影响时, 带噪标签的生成过程是完全随机的, 标签错误与样本特征和真实标签均无关, 常见于人工误差引起的标注错误.
(2) 类相关标签噪声. 受到类相关标签噪声影响时, 标签错误仅与真实标签相关, 与样本特征无关.
(3) 样本相关标签噪声. 受到样本相关标签噪声影响时, 标签错误仅与样本特征相关, 与真实标签无关.
(4) 混合标签噪声. 受到混合标签噪声影响时, 标签错误不仅与样本特征相关, 也与真实标签相关.
由于医院和医疗机构采用统一的行业标准进行数据标注, 人工标注所带来的标签噪声通常可认定为随机的[15]. 因此, 本文针对随机标签噪声开展了相关研究, 带噪标签可表示为真实标签与标签噪声的和.
1.2 问题描述由于不同医生的诊疗经验不同导致的主观性偏差、大量标注工作中的疏忽、数据编码或通信问题导致的标签错误等原因, 医疗数据中可能存在着较多的错误标注信息. 基于带有标签噪声的数据对机器学习模型进行训练和参数优化会使其预测性能急剧下降, 严重阻碍其大范围应用.
给定一个预测模型
| $ \overline{f}\left(x\left(i\right)\right)={E}_{D}\left[f\left(x\left(i\right);D\right)\right] $ | (1) |
定义目标函数为
| $ L={\rm{min}}{E}_{D}\left[{(f\left(x\left(i\right);D\right)-\overline{f}\left(x\left(i\right)\right))}^{2}\right] $ | (2) |
进而, 泛化误差可以由式(3)表示:
| $\begin{split} E\left(f;D\right)=&{\underbrace {{{E}_{D}\left[{\left(f\left(x\left(i\right);D\right)-\overline{f}\left(x\left(i\right)\right)\right)}^{2}\right]}}_{{bias}^{2}\left(x\right(i\left)\right)}}\\ &+{\underbrace {{E}_{D}\left[{\left(\overline{f}\left(x\left(i\right)\right)-\widetilde{y}\left(i\right)+\varepsilon \left(i\right)\right)}^{2}\right]}_{var\left(x\right(i\left)\right)}}\\ &+{\underbrace {{E}_{D}\left({\varepsilon }^{2}\left(i\right)\right)+2{E}_{D}\left[\left(\overline{f}\left(x\left(i\right)\right)-\widetilde{y}\left(i\right)+\varepsilon \left(i\right)\right)\varepsilon (i)\right]}_{{\varepsilon }^{2}\left(i\right)}} \end{split}$ | (3) |
其中,
从式(3)可知, 标签噪声会显著提高方差和噪声, 进而提高模型泛化误差的下界, 导致模型的泛化性能显著下降.
2 标签噪声鲁棒学习算法针对上述问题, 本文提出深度神经网络和动态截断损失函数相结合的标签噪声鲁棒学习算法. 主要策略是设计动态非对称有界的截断损失函数, 结合传统交叉熵函数的隐式加权特性和均方差损失函数的对称特性, 实现了带有标签噪声下的鲁棒性学习; 同时构造了训练损失下界, 并引入了样本动态加权机制有效隔离了带噪样本, 提高了模型对标签噪声的鲁棒性.
第2.1节介绍了模型结构, 第2.2节介绍了动态截断损失函数的相关内容, 第2.3节介绍了模型的实现过程.
2.1 模型结构所提出算法的模型结构图如图1所示. 在模型训练过程中, 神经网络的输入为
| $ f\left(x\right)=\left\{\begin{array}{ll}x, & x\geqslant 0\\ \alpha ({{\rm{e}}}^{x}-1), & x < 0\end{array}\right. $ | (4) |
经过每一层的计算后, 得到最终的输出值. 通过误差反向传播的方式更新参数, 并使用动态截断损失函数实现对带噪标签的鲁棒性, 迭代到一定次数后, 模型训练完毕.
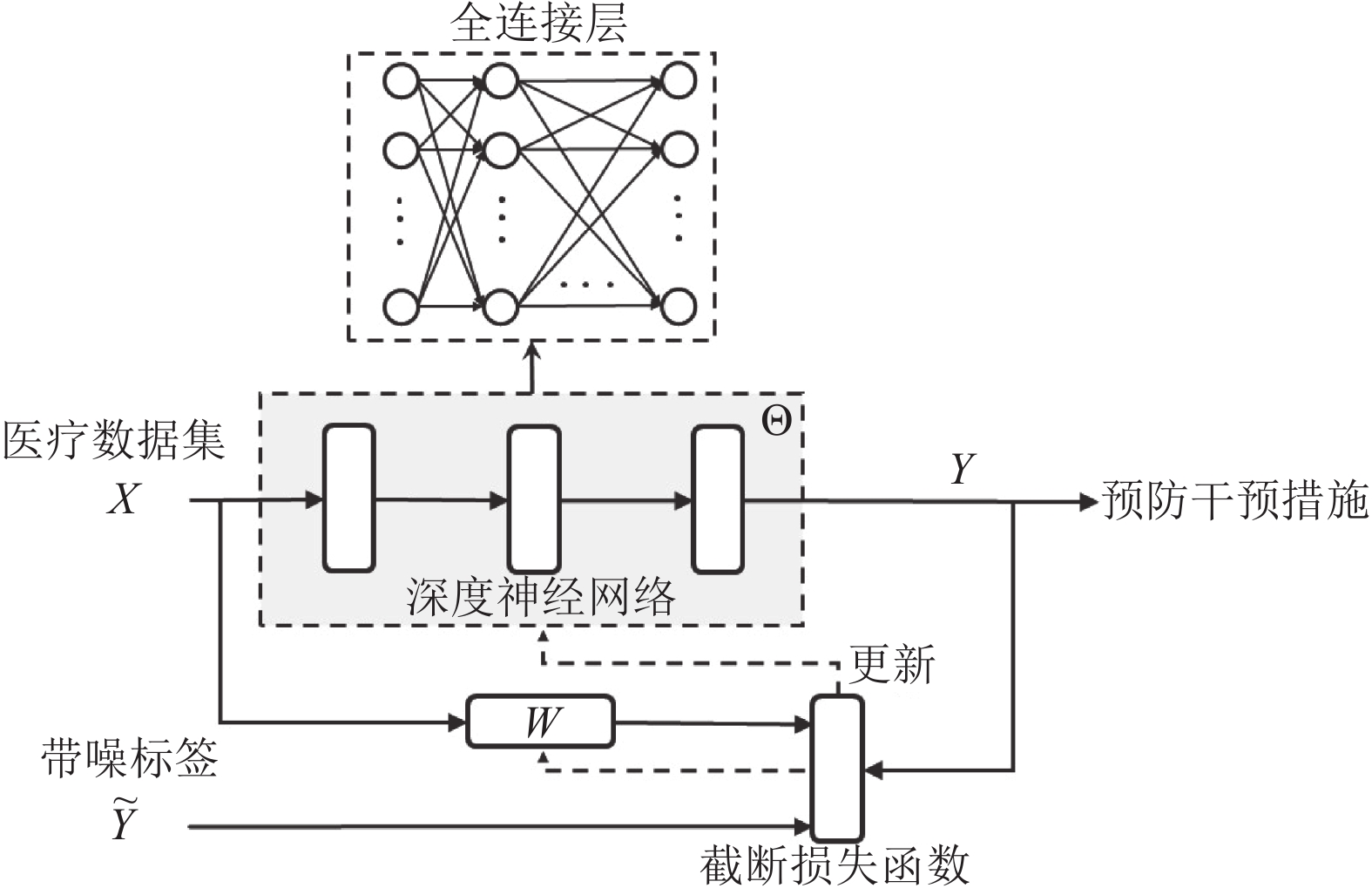
|
图 1 模型结构图 |
2.2 动态截断损失函数
在多分类问题中, 对于任意损失函数
| $ \begin{split} {R}_{L}\left(f\right) = {E}_{D}\left[L\left(f\left(x\left(i\right);\theta \right), y\left(i\right)\right)\right] = - \frac{1}{n}\displaystyle\sum\limits _{i=1}^{n}\displaystyle\sum\limits _{j=1}^{c}{y}_{ij}{\rm{log}}{f}_{j}\left(x\right(i);\theta ) \end{split}$ | (5) |
其中,
进而, 最小化经验风险可以由式(6)表示:
| $ {f}^{*}={\rm{arg \; min}}{R}_{L}\left(f\right) $ | (6) |
其中,
若损失函数满足式(7), 则此损失函数为对称损失函数:
| $ \displaystyle\sum\limits _{j=1}^{c}L\left(f\left(x\left(i\right)\right), j\right)=C, \; \forall x\left(i\right)\in X, \forall f $ | (7) |
其中,
所有的样本都以同样的概率会错标成其他标签的情况, 被称为均匀噪声. 本文所研究的噪声类型属于均匀噪声. 噪声率
| $ p\left(\,{\widetilde{y}}_{i}={c}_{2}|{y}_{i}={{c}}_{1}, x\left(i\right)\right)=p\left(\,{\widetilde{y}}_{i}={c}_{2}|{y}_{i}={{c}}_{1}\right)={\eta }_{{c}_{1}{c}_{2}} $ | (8) |
对于均匀噪声, 若损失函数是对称的且噪声比例满足
传统的交叉熵(cross entropy, CE)损失函数是一类非有界非对称函数, 如式(9)所示:
| $ {L}_{{\rm{CE}}}=-\displaystyle\sum\limits _{i=1}^{n}y\left(i\right) \log \widehat{y}\left(i\right) $ | (9) |
其中,
平均绝对误差(mean absolute error, MAE)损失函数的公式如式(10)所示:
| $ {L}_{{\rm{MAE}}}=\frac{\displaystyle\sum\limits _{i=1}^{n}\left|\widehat{y}\right(i)-y(i\left)\right|}{n} $ | (10) |
其中,
接下来, 将从梯度的角度进一步分析CE和MAE损失函数的标签噪声鲁棒性. 它们的梯度如式(11)所示:
| $\begin{split} &\displaystyle\sum\limits _{i=1}^{n}\frac{\partial L(f\left(x\left(i\right);\theta \right), y(i\left)\right)}{\partial \theta }\\ &\quad =\left\{\begin{array}{l} \displaystyle\sum\limits _{i=1}^{n}-\frac{1}{{f}_{y\left(i\right)}\left(x\left(i\right);\theta \right)}{\nabla }_{\theta }{f}_{y\left(i\right)}\left(x\left(i\right);\theta \right), \;\;{\rm{CE}}\\ \displaystyle\sum\limits_{i=1}^{n}-{\nabla }_{\theta }{f}_{y\left(i\right)}\left(x\left(i\right);\theta \right),\qquad\qquad\quad\;\; {\rm{MAE}}\end{array}\right. \end{split}$ | (11) |
在CE损失函数中, 若某些样本经过Softmax层输出的预测值和给定标签之间存在偏差, 则会导致
在MAE损失函数中, 梯度中并不存在
为了利用MAE提供的噪声鲁棒性和CE的隐式加权方案的优点, 引入了
| $ {L}_{q}\left(f\left(x\left(i\right)\right), {e}_{j}\right)=\frac{{(1-{f}_{j}(x\left(i\right))}^{q})}{q} $ | (12) |
其中,
为了避免
| $\begin{split} &{L}_{{\rm{trunc}}}\left(f\left(x\left(i\right)\right), {e}_{j}\right) =\left\{\begin{array}{l}{L}_{q}\left(k\right),\qquad\quad\;\;\; {f}_{j}\left(x\right(i\left)\right)\leqslant k\\ {L}_{q}(f\left(x\left(i\right)\right), {e}_{j}), {f}_{j}\left(x\right(i\left)\right) > k\end{array}\right. \end{split}$ | (13) |
其中,
引入样本动态加权机制后的动态截断损失函数如式(14)所示:
| $\begin{split} {L}_{{\rm{weight}}}=& \displaystyle\sum\limits _{i=1}^{n}w\left(i\right){L}_{q}\left(f\left(x\left(i\right);\theta \right), y\left(i\right)\right)\\ & -{L}_{q}\left(k\right) \displaystyle\sum\limits _{i=1}^{n}w\left(i\right) \end{split}$ | (14) |
其中,
针对所提出的疾病风险预测任务中的标签噪声鲁棒学习算法, 本节给出模型的具体实现过程, 涉及离线训练和在线预测两个部分. 离线训练方法如算法1所示, 在线预测方法如算法2所示.
算法1. 离线训练方法
输入: 带噪训练集
输出: 最优模型参数
1) 初始化: 对于所有样本,
2) 根据下式更新模型参数
3) 当目前迭代次数小于最大迭代次数
4) 根据下式更新模型参数
5) 输出最优模型参数
离线训练方法首先输入带噪训练集, 对参数进行初始化, 随后对模型进行训练, 最后更新模型参数, 输出最优的模型参数.
算法2. 在线预测方法
输入: 医学数据集的批次数据
输出: 疾病风险等级
1) 数据预处理
2) 计算模型输出
3) 根据预测类别给出预防干预措施
在线预测方法首先输入带噪训练集, 并对数据进行预处理, 然后计算预测类别, 最后根据预测类别给出相应的预防干预措施.
3 实验结果及分析本节以脑卒中筛查数据集为例, 对所提出算法在不同标签噪声比例下的可行性和有效性进行了验证.
3.1 实验设置 3.1.1 实验数据集实验数据集采用中国医学科学院医学信息研究所发布的脑卒中筛查数据集( https://med.ckcest.cn/details.html?id=4054595102525446&classesEn=scientific_data), 数据量总计862424条, 覆盖了国内的6个省份, 41家基地医院, 共有16个属性, 具体如表1所示.
| 表 1 数据集的属性 |
在数据集中, 将脑卒中风险划分为了以下3个等级: 第1级代表低危, 脑卒中风险较低, 低危人群相应的预防干预措施为正常体检. 第2级代表中危, 脑卒中风险较高, 中危人群需定期体检以及控制好相关危险因素. 第3级代表高危, 脑卒中风险极高, 需及时去医院进行进一步检查, 咨询专业医生的建议.
以上3个脑卒中风险等级在数据集中的占比情况如表2所示.
随机标签噪声通过人工注入, 实验中通过随机置换参考标签实现, 即选取一定比例的标签随机替换至其他类别, 噪声的比例范围是5%–40%[17].
| 表 2 数据集的标签分布情况 |
3.1.2 超参数设置
本文中所提出的DNN结合动态截断损失函数算法通过Python中的PyTorch和Scikit-learn实现, 所有实验均在配置Windows 10操作系统的计算机上实现, 具体硬件涉及: Intel i5处理器, 8 GB内存和1024 GB存储空间. 实验相关的超参数设置如表3所示, 其余未提及参数均为默认值.
| 表 3 模型超参数 |
3.1.3 实验对比算法
本节分别开展了无标签噪声下和有标签噪声下脑卒中风险预测的对比实验.
在无标签噪声的脑卒中风险预测实验中, 基准模型包括深度神经网络、决策树、随机森林、LightGBM、XGBoost、CatBoost. 深度神经网络在医疗预测领域有着广泛的应用[18]. 决策树算法在医疗分析与预测领域应用十分广泛[19]. 随机森林是一种高性能的疾病风险预测模型[20]. LightGBM由于其准确率高、模型训练效率高而被广泛用于医疗领域[21]. XGBoost已广泛应用于疾病诊断以及疾病发生风险等方面, 具有较高的效率和准确率[22]. CatBoost不需要复杂的调优就可达到很强的预测效果, 能够较好地应用于医疗诊断领域[23].
在存在标签噪声的脑卒中风险预测实验中, 采用的对比算法有深度神经网络、LightGBM、XGBoost、CatBoost、DNN-Truncated、DNN-mixup. Mixup是一类数据增强方法, 通过平滑特征和带噪标签降低被污染样本的梯度以抑制标签噪声的负面影响.
3.2 无标签噪声下的实验结果及分析在无标签噪声的情况下, 采用决策树、随机森林、LightGBM、XGBoost、CatBoost和深度神经网络进行对比实验. 实验结果如表4所示, 实验的评价指标包括准确率, 加权精确率, 加权召回率, 加权F1分数和Kappa系数. 从表4的实验结果可以看出, 以上算法的准确率都超过了94%, 均已达到实际应用的要求, 其中, 决策树和随机森林的性能指标相对欠佳, LightGBM、XGBoost、CatBoost和DNN的性能指标更为突出, 准确率、加权精确率、加权召回率均超过了98.70%, 加权F1分数超过了0.9870, Kappa系数超过了0.9710, 可以正确识别各类风险等级, 达到了良好的分类效果. 这可能是由于决策树未使用集成学习的方式, 单个树模型的预测能力相对较弱, 可能会受到异常值的影响. 而集成学习方式会参考多个决策树的结果, 降低了异常值带来的影响. 随机森林通过随机采样与随机选择特征构建多个决策树, 而LightGBM、XGBoost、CatBoost都是基于梯度提升的方式进行学习, 沿着梯度下降的方向减小损失函数, 可以得到更精确的模型. 根据以上的实验结果, 可以看出LightGBM、XGBoost、CatBoost和DNN算法都可以实现脑卒中早期预测, 后续将以这几种算法为基准模型开展进一步实验.
| 表 4 无标签噪声下的测试集准确率比较 |
3.3 有标签噪声下的实验结果及分析
本节评估所提出算法和各个基准模型的标签噪声鲁棒性, 在不同噪声比例下的识别准确率如表5所示.
| 表 5 不同噪声比例下的测试集准确率比较 (%) |
从表5的实验结果可以看出, 本文所提出的动态截断损失函数的性能在不同比例的标签噪声影响下均能保持稳定. 随着标签噪声比例的增加, DNN、LightGBM、XGBoost和CatBoost算法的性能出现明显下降; 在40%的标签噪声影响下, 树模型的准确率低于80%, DNN模型的准确率为80.09%, 难以实现准确的脑卒中早期风险预测. 本文所提出算法优于传统算法, 在不同的标签噪声比例下准确率一直保持稳定, 没有受到标签噪声的影响. 与表现最好的树模型相比, 本文算法在10%−40%的噪声比例下分别取得了2.39%、4.93%、7.58%、10.26%、12.67%、15.3%、17.97%的性能提升. 与DNN相比, 本文算法在5%的噪声比例下与其性能接近, 在10%−40%的噪声比例下分别取得了1.95%、4.37%、6.68%、9%、11.42%、13.8%、15.91%的性能提升. 这与
Mixup模型的性能稳定但是效果不理想, 其原因可能是对二元数据进行平滑无法产生可靠的样本, 难以降低标签噪声的影响.
3.4 超参数调节实验为了分析所提出算法对超参数变化的敏感性, 本节进行超参数调节实验, 对
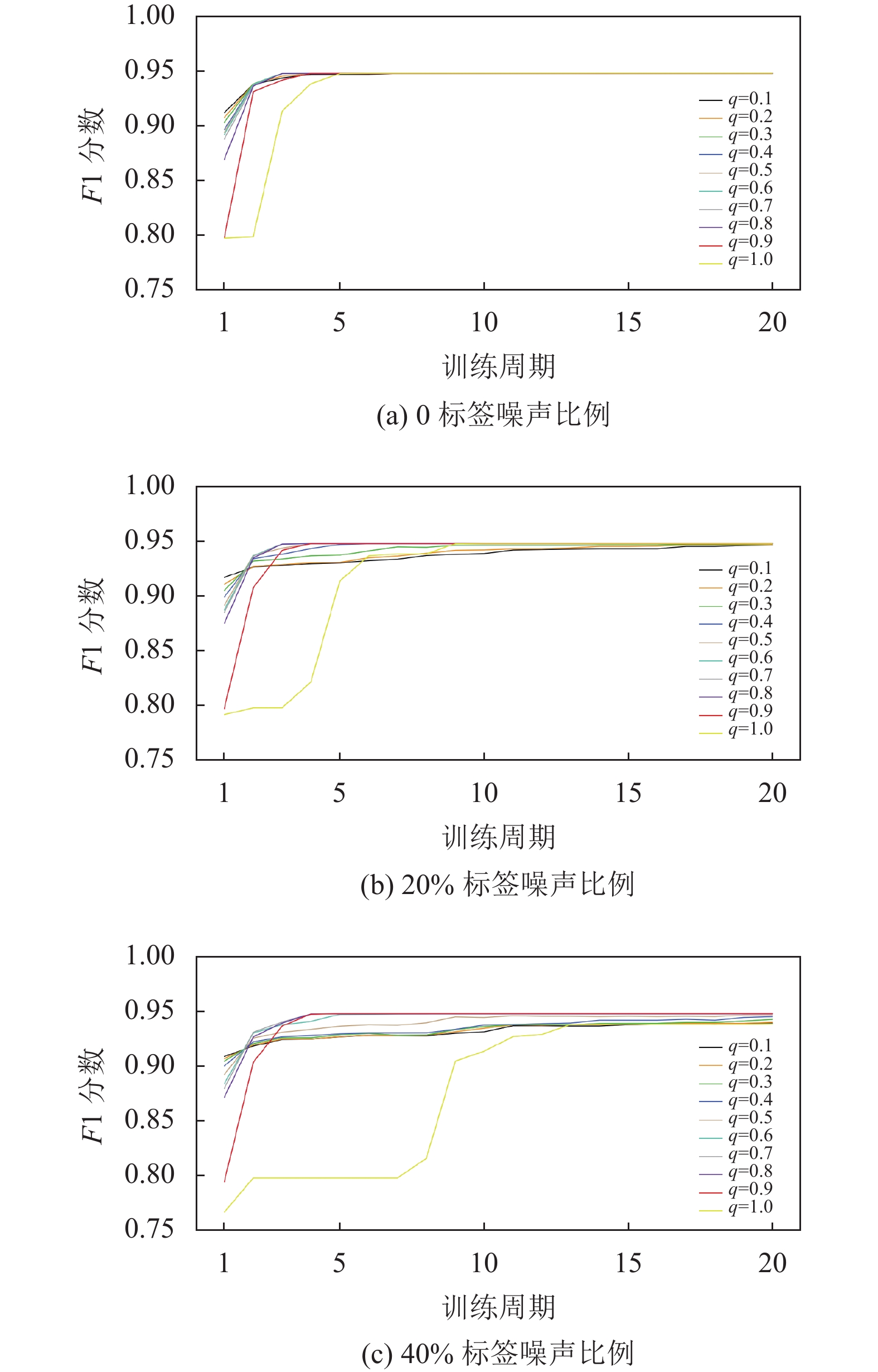
在噪声比例为0、20%和40%下分析了不同的
同时, 从图3可以看出,
|
图 2 不同q值下的F1分数 |

|
图 2 不同q值下的F1分数(续) |
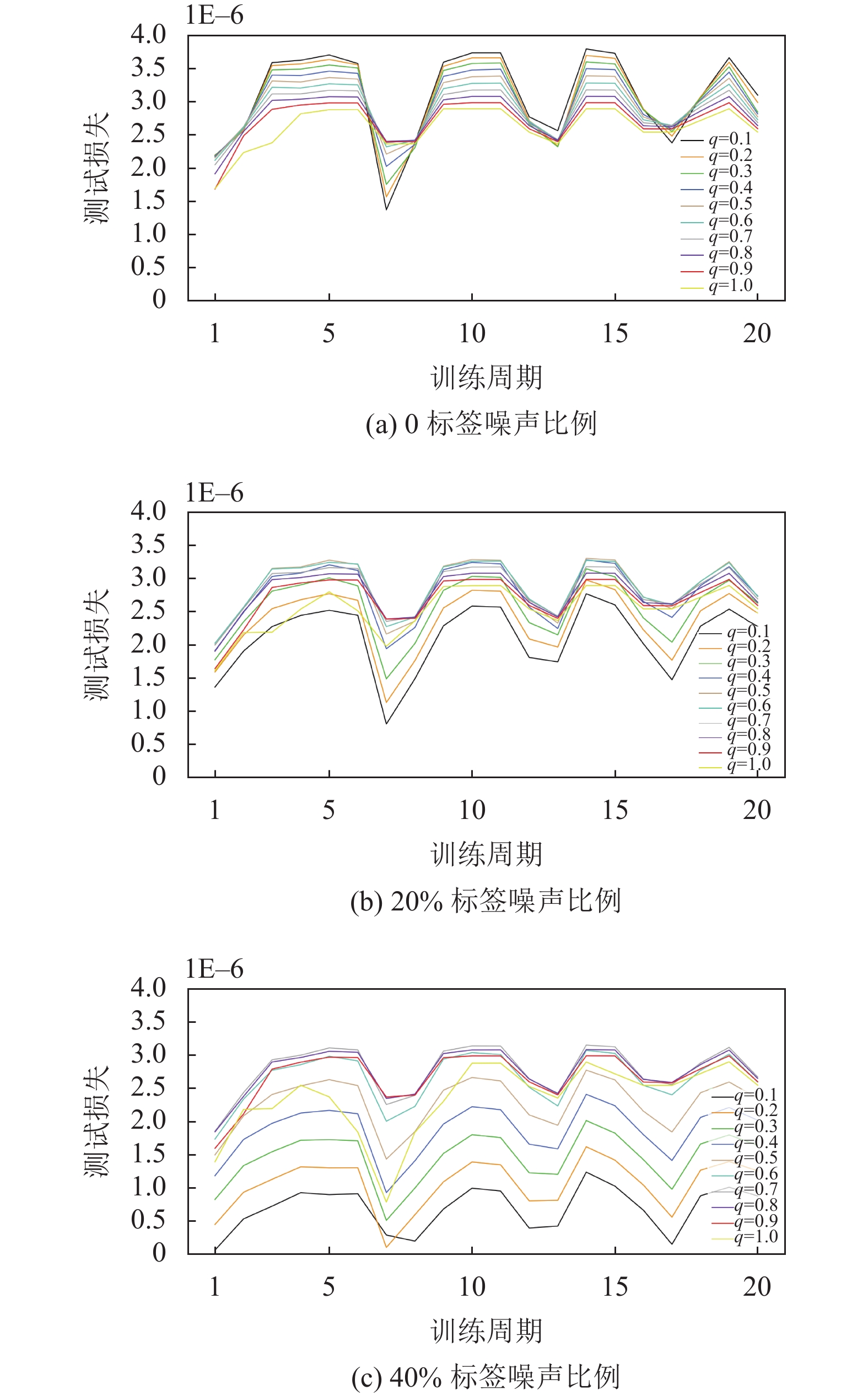
|
图 3 不同
|
4 结论与展望
本文针对疾病风险预测中存在标签噪声的问题, 提出了一种基于深度神经网络和动态截断损失函数的标签噪声鲁棒学习算法. 设计了一个非对称有界的动态截断损失函数, 成功融合了传统交叉熵函数的隐式加权特性和均方差损失函数的对称特性; 构造了训练损失下界, 并引入了样本动态加权机制有效隔离了带噪样本, 提高了模型的标签噪声鲁棒性. 以脑卒中筛查数据集为例, 对本文所提出的算法进行了实验验证. 实验结果表明本文算法在各个噪声比例下都能取得理想性能, 验证了本文算法在存在标签噪声的疾病风险预测任务中的可行性和有效性.
未来将从以下两个方面继续研究: (1)增加更多的医疗数据集进行实验验证. (2)研究其他类型的标签噪声的特点以及处理方法, 提出有效的解决方案.
| [1] |
张蕊, 郑黎强, 潘国伟. 疾病发病风险预测模型的应用与建立. 中国卫生统计, 2015, 32(4): 724-726. |
| [2] |
刘雨安, 杨小文, 李乐之. 机器学习在疾病预测的应用研究进展. 护理学报, 2021, 28(7): 30-34. |
| [3] |
王亚鹏, 李阳, 王家宝, 等. 噪声鲁棒的轻量级深度遥感场景图像分类检索. 中国图象图形学报, 2021, 26(12): 2991-3004. DOI:10.11834/jig.200538 |
| [4] |
佟强, 刁恩虎, 李丹, 等. 分类任务中标签噪声的研究综述. 科学技术与工程, 2022, 22(31): 13626-13635. DOI:10.3969/j.issn.1671-1815.2022.31.003 |
| [5] |
宫辰, 张闯, 王启舟. 标签噪声鲁棒学习算法研究综述. 航空兵器, 2020, 27(3): 20-26. DOI:10.12132/ISSN.1673-5048.2020.0010 |
| [6] |
王晓莉, 薛丽. 标签噪声学习算法综述. 计算机系统应用, 2021, 30(1): 10-18. DOI:10.15888/j.cnki.csa.007776 |
| [7] |
Wu PX, Zheng SZ, Goswami M, et al. A topological filter for learning with label noise. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1795.
|
| [8] |
Arpit D, Jastrzębski S, Ballas N, et al. A closer look at memorization in deep networks. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR.org, 2017. 233–242.
|
| [9] |
Han B, Yao QM, Yu XR, et al. Co-teaching: Robust training of deep neural networks with extremely noisy labels. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 8536–8546.
|
| [10] |
Rusiecki A. Trimmed robust loss function for training deep neural networks with label noise. Proceedings of the 18th International Conference on Artificial Intelligence and Soft Computing. Zakopane: Springer, 2019. 215–222.
|
| [11] |
Wang YS, Ma XJ, Chen ZY, et al. Symmetric cross entropy for robust learning with noisy labels. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 322–330.
|
| [12] |
Feng L, Shu SL, Lin ZY, et al. Can cross entropy loss be robust to label noise? Proceedings of the 29th International Joint Conference on Artificial Intelligence. 2021. 305.
|
| [13] |
陈庆强, 王文剑, 姜高霞. 基于数据分布的标签噪声过滤. 清华大学学报(自然科学版), 2019, 59(4): 262-269. DOI:10.16511/j.cnki.qhdxxb.2018.26.059 |
| [14] |
陈倩, 杨旻, 魏鹏飞. 标签带噪声数据的重加权半监督分类方法. 烟台大学学报(自然科学与工程版), 2019, 32(3): 205-209. DOI:10.13951/j.cnki.37-1213/n.2019.03.001 |
| [15] |
Karimi D, Dou HR, Warfield SK, et al. Deep learning with noisy labels: Exploring techniques and remedies in medical image analysis. Medical Image Analysis, 2020, 65: 101759. DOI:10.1016/j.media.2020.101759 |
| [16] |
Ghosh A, Manwani N, Sastry PS. Making risk minimization tolerant to label noise. Neurocomputing, 2015, 160: 93-107. DOI:10.1016/j.neucom.2014.09.081 |
| [17] |
Yao YY, Wang L, Zhang LM, et al. Learning latent stable patterns for image understanding with weak and noisy labels. IEEE Transactions on Cybernetics, 2019, 49(12): 4243-4252. DOI:10.1109/TCYB.2018.2861419 |
| [18] |
巨荣辉. 基于深度学习和医疗数据的疾病提前诊断和风险预测方法研究[硕士学位论文]. 武汉: 华中科技大学, 2018.
|
| [19] |
王增辉. 决策树方法在医疗诊断及预测中的应用研究[硕士学位论文]. 北京: 华北电力大学(北京), 2019.
|
| [20] |
邰媛媛. 基于随机森林的ICU患者多重耐药菌感染预测模型的研究[硕士学位论文]. 湖州: 湖州师范学院, 2022.
|
| [21] |
覃红键. 基于LightGBM算法的双高疾病风险预测系统设计与实现[硕士学位论文]. 武汉: 中南财经政法大学, 2020.
|
| [22] |
齐巧娜, 刘艳, 陈霁晖, 等. 机器学习XGBoost算法在医学领域的应用研究进展. 分子影像学杂志, 2021, 44(5): 856-862. |
| [23] |
苗丰顺, 李岩, 高岑, 等. 基于CatBoost算法的糖尿病预测方法. 计算机系统应用, 2019, 28(9): 215-218. DOI:10.15888/j.cnki.csa.007054 |
 2023, Vol. 32
2023, Vol. 32


