2. 中山大学 岭南学院, 广州 510275
2. Lingnan College, Sun Yat-sen University, Guangzhou 510275, China
股票指数的多变性、非线性和非平稳性为股指预测带来了非常大的挑战. 探索股指预测工具, 提高股指预测精度一直以来都是金融, 经济统计等领域的研究重点和热点[1]. 传统基于公司财务数据和历史交易数据构建时间序列模型预测股指的方法存在局限性. 首先, 使用基本指标数据忽略了未来价格变动的重要驱动因素, 如在线新闻和政策文件. 其次, 传统时间序列回归模型难以准确地表示影响因子和股票指数之间复杂的时变关系. 因此, 研究如何从选择影响因子和改进预测模型两个方面来提高股指的预测精度是有意义和价值的.
为股指预测选择适当的驱动因素对提高预测准确性至关重要. 以往的研究主要依赖历史交易数据、宏观经济变量或资产价格预测股票指数, 但这些特征所解释的指数变化方差仍然不足. 在这种背景下, Gürkaynak等人[2]指出新闻文章在解释事件窗口内几乎所有收益率曲线变动方面发挥着重要作用. 这为股票指数背后真正的驱动因素提供了更全面的理解. 幸运的是, 计算能力的提高使得分析大量非结构化的数据如文本、音频和视频等数据具有可行性. 因此, 本文聚焦于挖掘新闻文章来预测股票指数.
在金融领域中, 文本分析的应用仍处于萌芽阶段. Foster等人[3]使用主成分回归基于文本数据开发了一个房地产定价模型. Kelly等人[4]和Sert等人[5]指出使用命名实体提取、情感分析和潜狄利克雷分配(latent Dirichlet allocation, LDA)主题建模可以进行合理的股价预测. Bai等人[6]提出了一种基于语义辅助非负矩阵分解的短新闻标题主题指标. 近年来, 随着计算能力的极大提升, 自然语言技术开始被应用于金融市场预测. Ko等人[7]使用基于Transformer[8]的双向编码器表征(bidirectional encoder representation from Transformers, BERT)[9]识别新闻和论坛中的投资者情绪. 这些方法存在一些缺陷. 例如, 主题模型在构建文本模型时没有去除与经济变量不相关的噪声词语, BERT模型不具有可解释性, 且训练需要消耗大量的计算空间和时间.
为了减轻噪声词语对经济变量预测的影响, 并保留模型的可解释性, Taddy[10]提出在有监督生成语言模型——多项逻辑逆回归(multinomial logistic inverse regression, MNIR)上添加Gamma-Lasso惩罚[11]. 生成语言模型假定文档中的词语是通过感兴趣变量确定条件下的词语生成概率定义生成的. 根据感兴趣变量是否可观测, 生成语言模型又可分为有监督生成模型和无监督生成模型. 其中LDA主题模型是无监督生成模型的经典模型. 常见的有监督生成模型包括朴素贝叶斯分类器[12]和 MNIR. 在MNIR中词语生成概率与感兴趣变量之间通过多项逻辑函数建立依赖关系. Taddy[13]详细介绍了 MNIR 在属性预测、治疗效果估计和文档索引等各种应用中的使用. 但MNIR在面临协变量高维情形时同样会出现内存不足, 计算时间长等问题. Taddy[14] 将多项回归转化成多个可并行计算的泊松回归, 使得模型具有计算可伸缩性, 解决了MNIR模型中的计算问题. 该方法称为分布式多项回归(distributed multinomial regression, DMR). 然而, DMR中关于单词计数服从泊松分布的核心假设往往过于严格. 泊松分布具有期望和方差一致的性质, 而实际中文本词频的均值和方差往往并不相同. 例如, 如图1所示, 在《中国证券报》发表的房地产相关新闻报道中, “科技队伍”一词在一篇文章中出现次数的均值和方差分别为5.32和15.46, 两个值显然并不一致. 因此, 本文提出使用条件独立的负二项(negative binomial, NB)回归代替泊松回归来逼近多项回归. 负二项分布中包含能够调整期望与方差之间的数量关系的尺度参数. 当尺度参数趋近于零时, 负二项分布趋近于泊松分布. 所以, 更通用的负二项分布比泊松分布更适合作为词频的假设条件分布, 使用多个条件独立的负二项回归代替泊松回归来逼近多项回归具有重要研究意义.
基于负二项分布的分布式多项回归(DMR-NB)模型可以通过添加惩罚项的方法保留与股票指数相关的词语, 过滤掉噪声词语. 但是, 保留的词语数量仍旧数以千计. 若将这些词语特征不加处理地直接放入预测模型中, 会带来了高维性的挑战. Gürkaynak等人[2]指出可以从新闻中整合出一个解释事件窗口内所有收益率曲线方差的潜在指数. 与Kelly等人[4]一致, 本文基于DMR-NB构建文本词频矩阵在经济变量(即股指)上的低维投影, 并将该投影作为新闻的综合潜在指数代替高维文本作为影响因子添加到预测模型中, 从而克服由文本高维性带来的挑战.
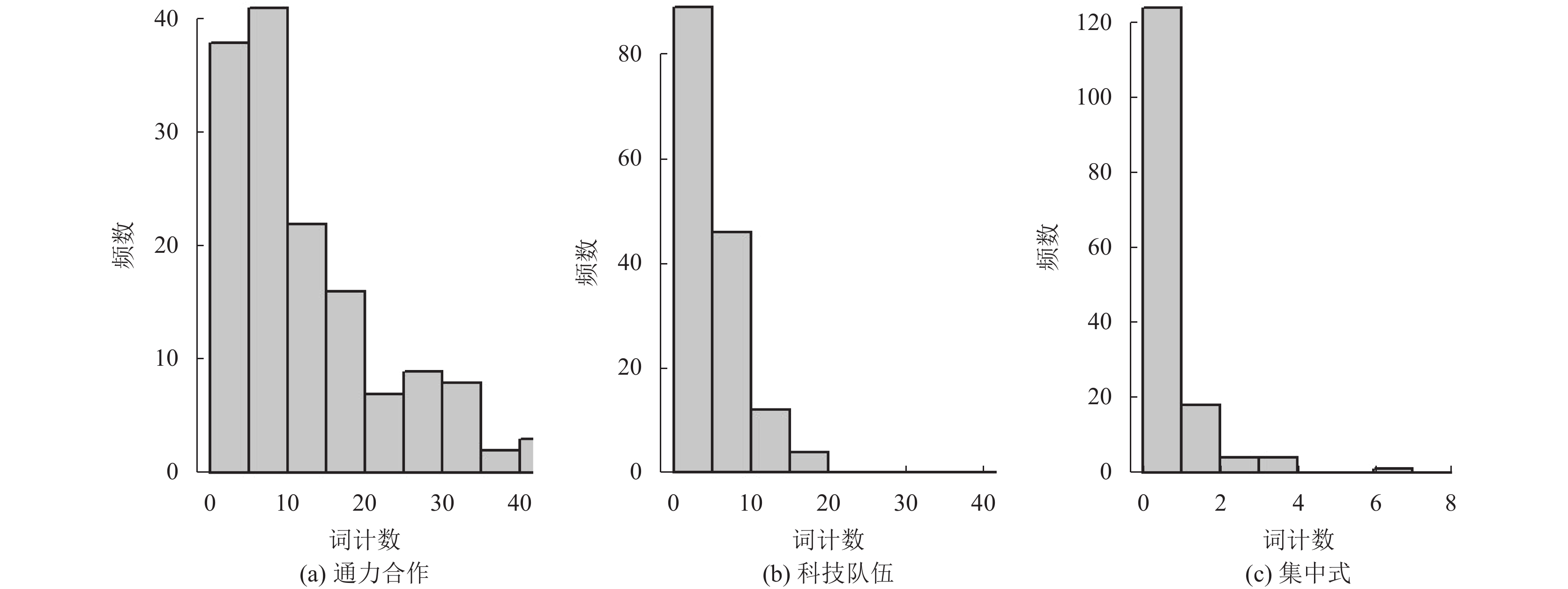
|
图 1 “通力合作”“科技队伍”和“集中式”词计数分布直方图 |
在股指预测问题中, 除影响因子的选择外, 预测模型的选择也是研究的重点和热点. 金融市场预测模型主要可以分为基于统计学和概率论的时间序列方法, 以及基于非统计原理的机器学习, 深度学习等方法. 传统时间序列方法包括差分自回归移动平均(autoregressive integrated moving average model, ARIMA)模型[15]、贝叶斯向量自回归(Bayesian vector autoregressive, BVAR)模型[16, 17]等. 机器学习方法包括长短期记忆网络(long short term memory, LSTM), 支持向量机等[18-20]. 机器学习方法相比于传统时间序列模型虽然可以较大程度地模拟变量的特征, 但是具有无法解释特征的内在影响机制的缺陷. 股市的强烈不稳定性使得传统时间序列模型中参数不随时间变化的假定变得不可靠. 考虑到时变参数(time-varying parameter, TVP)模型[21]可以有效捕捉渐进变动的关键优势, 本文将其作为本文预测框架中的预测模型. 该模型具有与传统时间序列模型类似的经济结构, 且不再假定模型参数是常数. 实证分析结果也验证了TVP模型对可观测股指的拟合几乎与原始股指价值重合.
在TVP模型中, 响应变量的预测依赖于参数状态的预测. Koop等人[22]阐述了两种最常用的状态预测方法: (1)直接使用时刻T的系数状态作为时刻T+1的系数状态的预测值; (2)允许系数在样本外演化, 通过模拟随机游走状态以生成T+1系数状态的预测值. 这两种方法的局限性在于仅考虑了滞后一阶的系数状态, 未考虑滞后多阶的系数状态和特征变量对未来系数状态的影响. 为此, 本文提出使用深度神经网络(deep neural networks, DNNs)作为系数状态预测工具[23, 24]. 与深度学习在金融预测中常用作“黑匣子”预测器不同, 本文基于DNNs预测TVP模型的系数状态而非直接预测响应变量的方式保留了经济模型的可解释性, 具有经济学意义.
总之, 为了同时在影响因子和预测模型两个方面做出改进, 本文搭建了一个基于DMR-NB模型的股指预测框架. 该预测框架具有以下3个贡献.
(1) 本文提出的DMR-NB模型通过分布式计算和正则化方法从超高维和稀疏性的在线新闻数据快速识别和解释词语信息对股指价值波动的影响.
(2) 利用TVP模型对多变的、非线性、非平稳的股指数据进行预测可以揭示影响因素与股指之间的时变关系. 通过高度拟合时变系数状态可以有效提高股指拟合精确度.
(3) 本文提出基于DNNs将学习TVP模型时变系数状态和股指预测损失函数优化结合起来同时进行. 该方法确保深度学习过程遵循基础经济结构, 在利用DNNs卓越的学习能力的同时保留了经济模型的可解释性.
1 基于文本的股指预测框架本文提出的股指预测框架如图2所示, 其涵盖了从收集在线新闻报道到最终评估预测效果的所有阶段. 该框架包含5个不同的步骤: 第1步是收集与股票指数相关的在线新闻文章; 第2步是使用生成语言模型(如, 多项逻辑回归)提取新闻文本中影响股指的所有信息, 去除不相关的信息; 在第3步, 将保留的词语词频矩阵通过投影聚合为一个低维新闻指数; 第4步将得到的聚合指数和历史交易数据应用于预测模型(如, TVP模型)来预测股票指数; 最后使用适当的评估标准评估模型预测性能. 其中第2–4步应用的具体方法与算法将在第1.1–1.5节中详细阐述.

|
图 2 基于在线新闻的股指预测框架 |
1.1 有监督生成语言模型
假设拥有原始的文档数据集, 记为
| {p(ci∣vi,mi)=MN(ci;qi,mi),i=1,⋯,nqij=eηijΛi,Λi=d∑l=1eηil,j=1,⋯,dηij=αj+v⊤iφjmi=d∑j=1cij | (1) |
式(1)即为有监督生成语言模型, 也称为多项逻辑回归模型.
当
| p(ci∣vi,mi)=MN(ci;qi,mi)≈∏jNB(cij;ξj,mieηij)=∏j(1ξj+cij−1cij−1)(11+ξjμij)1ξj(ξjμij1+ξjμij)cij | (2) |
其中,
| l(αj,φj,ξj∣cj,V)=n∑i=1[(1ξj+cij)log(1+ξjmieαj+v⊤iφj)]−n∑i=1[cij(αj+v⊤iφj)] | (3) |
当可观测变量V的维度较高时, 往往存在部分变量只与部分词语相关联. 将所有变量考虑在模型中增加了模型的复杂度. 正则化估计方法往往可以有效降低模型的复杂度. 这种方法通过对系数施加惩罚实现模型性能和复杂性之间的平衡, 从而防止模型过度拟合. 本文为每个词计数的负二项回归应用加权
| {F(αj,φj,ξj)=l(αj,φj,ξj∣cj,V)+nλjp∑k=1ωjk|φjk|ˆαj,ˆφj,ˆξj=argminαj,φj,ξj{F(αj,φj,ξj)}λj,ωjk⩾0 | (4) |
关于权重
| ωtjk=(1+γj|ˆφt−1jk|)−1forγj⩾0 | (5) |
显然, 当
对于模型(2), 我们需要估计的参数包括
在给定
| −H=n∑i=1μij(1+ˆξjcij)(1+ˆξjμij)2viv⊤i=V⊤WV |
而g是基于
| g=n∑i=1vi(cij−μij)1+ˆξjμij=V⊤W(π−ˆηj) |
其中,
| ˆφtj=[V⊤WV]−1V⊤Wπ | (6) |
此时式(6)可以被视为如下加上
| argminαj,φj∈R∑iwi2(αj+v⊤iφj−πi)2+n∑k(1+γj|ˆφt−1jk|)−1λj|φjk| |
本文提出的CD算法具体展示在算法1中. 算法1只有在第1次迭代中才进行所有参数的完整更新, 此后在每次迭代中不会更新非活动
算法1. CD算法
输入: V,
输出:
1) 记whk=
2) while
3) for
4) 定义
5) 定义
6) if
7)
8) end
9) else
10)
11) end
12) 更新
13) end
14) end
为了参数
算法2. DMR-NB模型参数估计流程
1) 初始化
2) 记负二项分布的负对数似然(4)为l;
3) while
4)
5)
6)
7)
8) 给定
9) end
10) 返回
词频在股指上的投影(
| {{{\theta }}_{{{k}}t}} = {{{\theta }}_{k, t - 1}} + {{{\zeta }}_{kt}}, \;\;\;{\kern 1pt} {{{\zeta }}_{kt}}\sim\mathcal{N}\left( {{{0}}, {{{\varOmega }}_k}} \right) | (7) |
| {v}_{{k}t}={x}_{{k}t}^{\top }{\theta }_{kt}+{\epsilon }_{kt}, \;\;\;{\epsilon }_{kt}\sim\mathcal{N}(0, {\sigma }_{k}) | (8) |
其中,
本文使用状态空间模型的非中心参数化来估计时变回归系数
| {{{\theta }}_{{{k}}t}} = {{{\theta }}_{k0}} + \sqrt {{{{\Omega }}_k}}\; {\widetilde {{\theta }}_{kt}} | (9) |
其中,
为了预测下一个时期的股指价值
图3为参数预测结构示意图. 它将MLPs用于倒数第2个“参数层”来学习系数
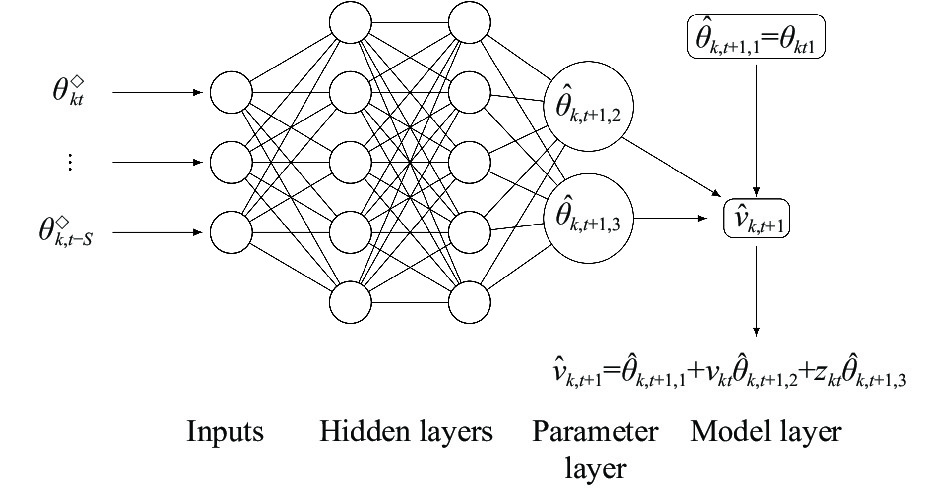
|
图 3 DNNs 预测时变参数结构示意图 |
另外, DNNs输入层中时变参数滞后阶数S的选择会影响到预测结果. 本文利用实证数据将超参数S在[1, 5]范围内搜索选取出最优值. 结果显示当S=4时, DNNs在实证行业股指
本研究主要包含两个数据集, 分别为在线新闻数据和行业股指数据. 其中在线新闻数据来源于在中国领先的证券报纸——《中国证券报》, 该报以其权威性和在金融行业中排名前二的发行量而闻名. 由于《中国证券报》覆盖了上海证券交易所和深圳证券交易所的信息, 因此可以提供较为全面的报道. 在行业股指数据方面, 本文选取农林行业, 制造行业, 水电行业, 批发零售行业, 运输仓储行业以及房地产行业6个代表行业的行业股指在月末的收盘价(CP)对数. 该6个行业的代码分别为399231、399233、399234、399236、399237和399241.
本研究收集的数据时间跨度为2005年1月1日–2017年7月31日. 共计收集到《中国证券报》在此期间发表的259039篇文章. 同期6个行业股指数据可以从网站 http://cn.gtadata.com处获得.
2.2 数据描述图4展示了《中国证券报》平均每月在线新闻发表数量. 图4中显示在1、3、7、8、11和12月发表文章数量增加, 展现了跨年、假期以及季度收益效应对新闻发表数量的影响. 图5提供了《中国证券报》每年发表在线新闻报道的总量. 图中显示, 文章数量在2004–2007年间呈现出一个持续上升的趋势, 然后在2007–2010年期间经历了一个下降期. 这种波动可以归因于一些因素, 包括2005年实施的股票交易改革及其对金融结构市场导向创新的影响, 以及2008年的全球金融危机及其对股市的影响.
为了初步展示6个行业新闻报道的主要信息, 本文绘制了与6个行业相关的新闻报道的词云图, 结果如图6所示. 通过对词云图的视觉分析, 可以发现在6个行业中最普遍的术语是“经济”和“增长”. 这说明了挖掘包含与经济相关的有价值信息的新闻文章的重要性. 另外, 房地产行业的词云图也显示“开发”“贷款”和“需求”这些与房价直接相关的术语也具有相对较高的出现频数.

|
图 4 月平均发布新闻数量统计 |
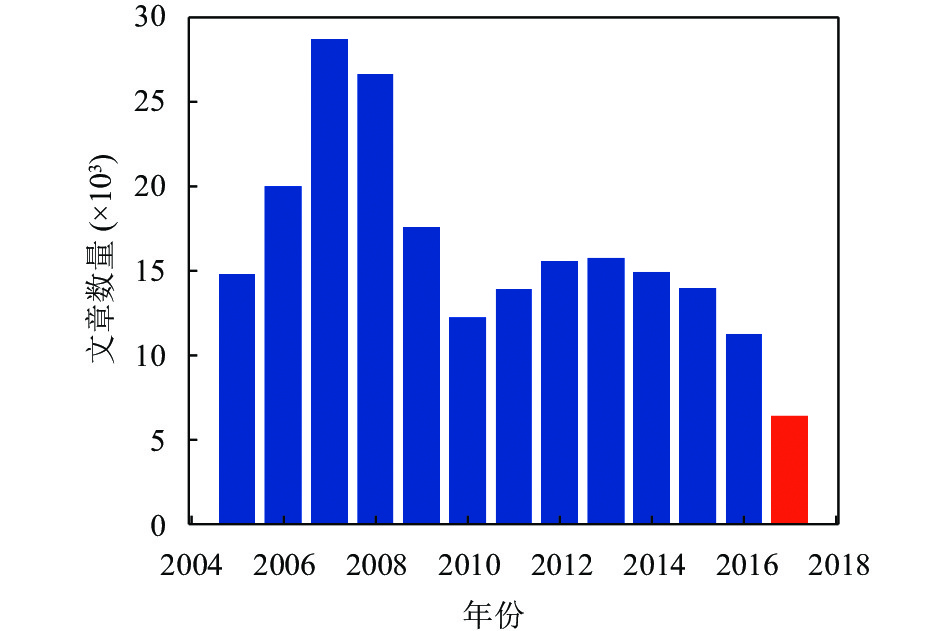
|
图 5 每年发布新闻总量统计 |

|
图 6 6个行业的新闻词云图 |
2.3 数据集划分
本文以月为观测单元, 2005年1月1日–2017年7月31日期间共计151个观测单元. 代表着完整两年时间段的最后24个观测单元作为测试数据集(
实验环境: Windows 10 操作系统 16 GB 内存; 开发工具: R 4.0.5和Python 3.8.3; CPU: AMD R7-4800H @2.90 GHz. 实验是在一台配备有AMD R7-4800H CPU处理器(8个内核, 2.90 GHz, 16 MB). 其中基于R语言实现DMR-NB模型文本特征筛选和TVP模型参数估计; Python 3.8.3实现DNNs时变参数参数预测.
3.2 文本词语特征筛选结果分析基于行业指数及在线新闻报道构建的DMR-NB模型可以通过
为了对比DMR-NB和DMR模型在新闻有效信息提取方面的表现, 本文基于两模型得到的
| \left\{\begin{aligned} {\textit{z}}_{{{k}}, t - 1}^{N{{B}}} = {{{c}}_{{{k}}, t - 1}}{\hat \varphi _{{k}}}^{N{{B}}} \\ {\textit{z}}_{{{k}}, t - 1}^{Po} = {{{c}}_{k, t - 1}}\hat \varphi _k^{Po} \end{aligned}\right. |
其中,
表3展示了6种股指预测框架的组成部分. TVP.z.NB为本文提出的基于DMR-NB模型构建的新闻指数和历史股指结构化数据使用TVP模型预测未来股指价值的股指预测框架. TVP.z.Po为基于DMR模型构建的新闻指数和历史股指结构化数据使用TVP模型预测未来股指价值的股指预测框架. TVP.nonz和LSTM.nonz表示只基于历史股指结构化数据使用TVP模型或者LSTM模型预测未来股指价值. TVP.LDA表示基于LDA模型提取的相关主题和历史股指结构化数据使用TVP模型进行股指预测. BVAR.LDA表示基于LDA模型提取的相关主题和历史股指结构化数据使用BVAR模型进行股指预测.
| 表 1 6个行业指数词语特征筛选结果 |
| 表 2 聚合新闻指数对数与行业指数对数之间的相关系数 |
| 表 3 6种预测框架结构 |
3.4 样本内拟合效果对比
图7展示了测试集中后24期基于6种不同的股指预测框架得到的
在样本外预测中, 本文基于第1.5节所介绍的时变参数预测方法构建了一个包含3层隐藏层, 每个隐藏层有16个隐藏单元, 激活函数都为ReLU函数的DNNs来学习训练集中历史TVP模型时变参数和未来一期参数的之间的联系. 训练过程中的验证集来源于训练集中随机挑选的20%数据. 基于训练完成的DNNs可以使用滑动窗口法预测样本外也即测试集中的24期TVP模型参数. 滑动窗口法以6个时期为一个窗口, 每次滑动一个时期, 在每个窗口内分别以经TVP模型估计完成的前5个时期(
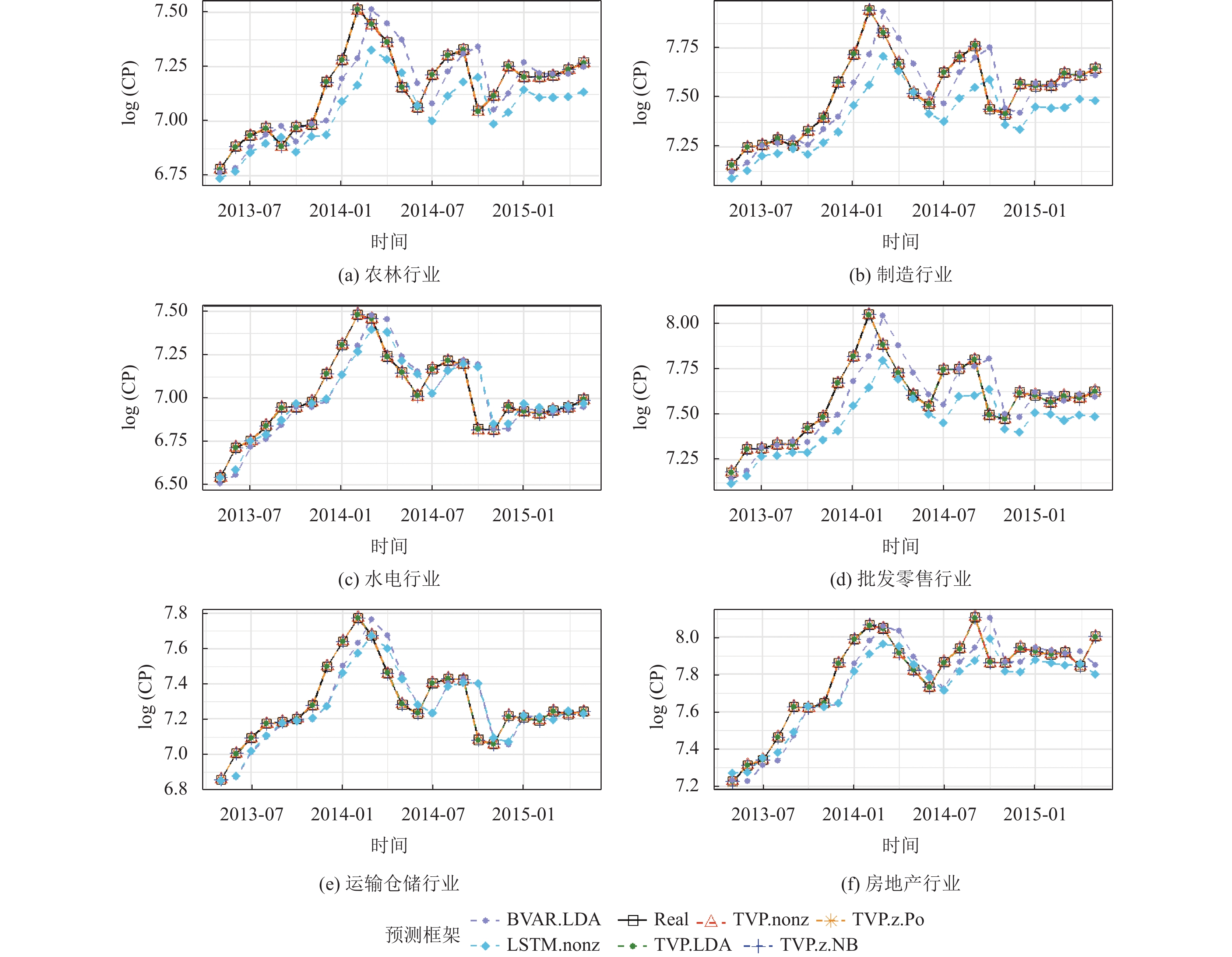
|
图 7 对数行业指数的样本内拟合值和实际值时序图 |
为了评估模型对股指的预测性能, 选择均方误差 (mean square error, MSE)作为评价指标来量化模型的性能. MSE计算公式为
(1) TVP.z vs. TVP.nonz: 相比于TVP.nonz预测框架, 通过TVP.z.NB和TVP.z.Po将在线新闻信息整合到股票指数预测模型中可以降低预测误差. 这一发现支持了考虑新闻驱动因素对提高股票指数预测准确性具有重要价值的观点.
(2) TVP.z.NB vs. TVP.z.Po: 在分析除运输仓储行业外的5个行业的股票指数预测误差时发现TVP.z.NB方法比TVP.z.Po方法具有更小的均方误差. 我们建议有文本数据访问权限的用户使用TVP.z.NB方法进行股票指数预测.
(3) TVP.z.NB vs. TVP.LDA: 在样本外预测方面, TVP.z.NB通常优于TVP.LDA. 这表明在一致的TVP预测模型条件下, 由生成语言模型筛选的新闻信息用于股票指数预测方面比LDA模型聚合的主题更有价值.
(4) TVP.nonz vs. LSTM.nonz: 在4个行业股指中, LSTM.nonz得到的MSE小于TVP.nonz. 说明在结构化时序数据中, TVP模型具有不弱于LSTM模型的预测能力.
(5) 最优模型: 相比于其他5种预测框架TVP.z.NB在性能评估方面具有最好的结果. 本文建议若快速提取新闻文本信息遇到阻碍则可以使用TVP.nonz模型. 否则为了减少股指预测误差, 建议使用TVP.z.NB预测框架.
| 表 4 不同预测框架MSE比较 |
4 总结
本文从影响股指预测的因子选取和预测模型两个方面入手, 提出了一个新的基于在线新闻的股指预测框架. 首先, 在影响因素选择方面将包含了内在驱动金融市场变动的新闻报道纳入考虑, 并基于DMR-NB模型过滤文本中的噪声词语降低文本特征维度, 实现了从在线新闻数据中捕捉与股指变动相关的, 有价值的信息. 相比于自然语言模型, 分布式计算和直观解释词语与股指依赖关系的能力是有监督生成模型的优势. 而实证结果也表明, DMR-NB在捕捉文本特征方面优于DMR和LDA模型. 因此, 若收集文本信息便捷时, 使用DMR-NB模型来挖掘相关文本特征是可行且有效的. 其次, 在预测模型方面, 选择TVP模型作为股指预测模型, 并将深度学习领域的DNNs方法用于时变参数预测. 该方法在保留了TVP经济模型结构的同时利用DNNs的强学习能力. 相比与LSTM和BVAR模型, 本文提出的TVP预测方法在实际股指样本内拟合和样本外预测方面都表现出了它的优势.
本文提出的预测框架使用DMR-NB从新闻中筛选的相关特征, 丰富股指预测模型的驱动因素. 然而DMR-NB模型在文本挖掘中仍旧存在一些不足, 例如没有考虑词语的位置和语境. 相同的词语在不同的语境或者位置有时会表现不同的含义. 这些不足有可能导致DMR-NB模型遗漏或者错会了重要信息. 因此, 考虑将词语的位置信息是有意义的. 虽然自然语言处理是考虑文本位置关系方面的先驱, 但是它不具有生成语言模型的可解释性. 研究如何将文本位置信息和生成语言模型实现融合任重而道远.
| [1] |
Huang JY, Liu JH. Using social media mining technology to improve stock price forecast accuracy. Journal of Forecasting, 2020, 39(1): 104-116. DOI:10.1002/for.2616 |
| [2] |
Gürkaynak RS, Kisacikoğlu B, Wright JH. Missing events in event studies: Identifying the effects of partially measured news surprises. American Economic Review, 2020, 110(12): 3871-3912. DOI:10.1257/aer.20181470 |
| [3] |
Foster DP, Liberman M, Stine RA. Featurizing text: Converting text into predictors for regression analysis. Philadelphia: The Wharton School of the University of Pennsylvania, 2013.
|
| [4] |
Kelly B, Manela A, Moreira A. Text selection. Journal of Business & Economic Statistics, 2021, 39(4): 859-879. DOI:10.1080/07350015.2021.1947843 |
| [5] |
Sert OC, Şahin SD, Özyer D, et al. Analysis and prediction in sparse and high dimensional text data: The case of Dow Jones stock market. Physica A: Statistical Mechanics and its Applications, 2020, 545: 123752. DOI:10.1016/j.physa.2019.123752 |
| [6] |
Bai Y, Li XX, Yu H, et al. Crude oil price forecasting incorporating news text. International Journal of Forecasting, 2022, 38(1): 367-383. DOI:10.1016/j.ijforecast.2021.06.006 |
| [7] |
Ko CR, Chang HT. LSTM-based sentiment analysis for stock price forecast. PeerJ Computer Science, 2021, 7: e408. DOI:10.7717/peerj-cs.408 |
| [8] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2017. 6000–6010.
|
| [9] |
Devlin J, Chang MW, Lee K, et al. BERT: Pre-training of deep bidirectional transformers for language understanding. Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Minneapolis: Association for Computational Linguistics, 2019. 4171–4186
|
| [10] |
Taddy M. Multinomial inverse regression for text analysis. Journal of the American Statistical Association, 2013, 108(503): 755-770. DOI:10.1080/01621459.2012.734168 |
| [11] |
Taddy M. One-step estimator paths for concave regularization. Journal of Computational and Graphical Statistics, 2017, 26(3): 525-536. DOI:10.1080/10618600.2016.1211532 |
| [12] |
Murphy KP. Machine Learning: A Probabilistic Perspective. Cambridge: MIT Press, 2012. 82–95.
|
| [13] |
Taddy M. Document classification by inversion of distributed language representations. Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing. Beijing: Association for Computational Linguistics, 2015. 45–49.
|
| [14] |
Taddy M. Distributed multinomial regression. The Annals of Applied Statistics, 2015, 9(3): 1394-1414. DOI:10.1214/15-AOAS831 |
| [15] |
Mashadihasanli T. Stock market price forecasting using the Arima model: An application to Istanbul, Turkiye. Journal of Economic Policy Researches, 2022, 9(2): 439-454. DOI:10.26650/JEPR1056771 |
| [16] |
Bessler W, Lückoff P. Predicting stock returns with Bayesian vector autoregressive models. Data Analysis, Machine Learning and Applications. Berlin: Springer, 2008. 499–506.
|
| [17] |
Larsen VH, Thorsrud LA. The value of news for economic developments. Journal of Econometrics, 2019, 210(1): 203-218. DOI:10.1016/j.jeconom.2018.11.013 |
| [18] |
Lei BL, Liu ZD, Song YP. On stock volatility forecasting based on text mining and deep learning under high-frequency data. Journal of Forecasting, 2021, 40(8): 1596-1610. DOI:10.1002/for.2794 |
| [19] |
李博, 孟志青, 朱爱花. 时态支持向量机模型在股票操纵模式发现上的研究. 系统科学与数学, 2023, 43(2): 356-378. DOI:10.12341/jssms22213 |
| [20] |
王德广, 马恒锐, 梁叶. 基于ATLG混合模型的股票价格预测. 计算机系统应用, 2023, 32(3): 171-179. DOI:10.15888/j.cnki.csa.008964 |
| [21] |
Hauzenberger N, Pfarrhofer M. Bayesian state-space modeling for analyzing heterogeneous network effects of US monetary policy. The Scandinavian Journal of Economics, 2021, 123(4): 1261-1291. DOI:10.1111/sjoe.12436 |
| [22] |
Koop G, Korobilis D. Large time-varying parameter VARs. Journal of Econometrics, 2013, 177(2): 185-198. DOI:10.1016/j.jeconom.2013.04.007 |
| [23] |
Farrell MH, Liang TY, Misra S. Deep neural networks for estimation and inference. Econometrica, 2021, 89(1): 181-213. DOI:10.3982/ECTA16901 |
| [24] |
Kropotov YA, Proskuryakov AY, Belov AA. Method for forecasting changes in time series parameters in digital information management systems. Computer Optics, 2018, 42(6): 1093-1100. DOI:10.18287/2412-6179-2018-42-6-1093-1100 |
| [25] |
Wright SJ. Coordinate descent algorithms. Mathematical Programming, 2015, 151(1): 3-34. DOI:10.1007/s10107-015-0892-3 |
| [26] |
Frühwirth-Schnatter S, Wagner H. Stochastic model specification search for Gaussian and partial non-Gaussian state space models. Journal of Econometrics, 2010, 154(4): 85-100. DOI:10.1016/j.jeconom.2009.07.003 |
 2023, Vol. 32
2023, Vol. 32



