在面向对象的软件开发中, 统一建模语言 (unified modeling language, UML)已经成为国际标准建模语言^{[1, 2]}. 用例图是在UML中一种重要的模型, 它用于捕获用户的功能需求, 而活动图也是在UML中的一种用于描述系统行为的模型视图, 它既可以用于描述业务过程, 也可以用于描述用例的事件流. 在实际的软件开发中, 活动图描述的业务过程通常对应到用例的事件流. 因此, 在真实的软件开发过程中可以通过业务流程来识别出不同用例的事件流, 从而进一步识别出用例^[3].

用例图通常展示了最初一部分的用例模型, 它刻画了参与者与用例之间的关系, 并描述系统的整体功能需求. UML创始人在他们的著作中提出, 用例是能够向用户提供有价值的结果的系统中的一种功能, 它获取的是功能需求, 所有的用例加在一起组成用例模型, 应当构成目标系统所有的功能^[3].

在面向对象的软件开发过程中, 用例模型还贯穿了软件开发的整个生命周期, 驱动软件开发的整个过程^[3]. 用例模型是否正确直接决定了待开发系统的成败. 然而, 构建用例模型是非常复杂繁琐的工作, 用例模型是对业务流程的分析得出的结果, 它要考虑到参与者的识别、目标系统的行为、用例的粒度大小等多种因素, 一般的开发者难以正确识别出用例模型. 在捕获与识别用例的方面, 大部分开发者往往选择直接从用户的需求描述中根据自己软件开发的经验识别用例. 这样手工获取的用例难以完全表述用户的需要, 常常还会因为用户与开发者的交流不足问题, 产生用户原本不需要或与用户的期望偏差的功能, 导致识别出不正确的用例模型, 使开发出的系统不满足用户的需求.

自从20世纪80年代Jacobson提出用例图的概念以来, 很多研究者对用例图进行了深入的研究, 如用例的描述^[4], 用例的迭代^[5], 以及使用建模工具构造用例的工作^[6], 但是这些工作都是手工完成的, 而没有采取半自动或自动识别用例的方法. 近年来, 一些研究者开始采用自然语言处理与深度学习技术^[7–9]提取需求文档中的需求, 但是, 这些工作都没有涉及到生成用例模型. 而在用例模型相关的研究中^[10-13], 还没有直接从业务流程或业务建模中获取用例的方法. 因此, 本文提出了一种基于UML活动图的半自动用例识别方法. 首先, 通过对活动图进行形式化建模, 从业务流程方面整体描述系统功能; 其次, 识别出活动图中的依赖链, 对依赖链进行分割; 最后, 根据依赖链所对应的活动的执行顺序以及活动与活动所在的泳道之间的关系, 来生成对应的用例以及用例与参与者的关系.

本文描述的方法能够应用于软件开发的早期阶段, 协助建模人员建立用例模型. 由于用例模型来源于需求, 因此构造用例模型一般采用人工构造. 然而正确识别用例并不是一项容易的工作, 直接人工识别用例可能造成需求不明确的问题. 本文的方法通过活动图建模业务流程并分解, 可以快速、准确地识别用例. 本文的方法使用形式化方法对模型进行了建模, 能够保证模型的正确性与一致性, 降低后续维护的成本.

1 用例图与活动图

用例图把系统视为一个黑盒, 从参与者的角度看待系统, 非常适合用来做需求分析^[14]. 需求分析作为软件开发至关重要的阶段, 常需要用例图的支持与驱动. 图1展示了一个简单的用例图.

活动图广泛应用于业务流程建模, 着重表现从一个活动到另一个活动的流程. 在软件开发中, 活动图也用来表示整个业务的业务流程执行顺序. 活动图从需求分析阶段开始, 一直贯穿到软件测试阶段, 在软件开发的各个阶段都起着重要的作用.

图2展示了一个简单的活动图, 它描述了酒店预订业务的业务流程. 在第2节中, 本文将对图2的活动图进行形式化建模, 为之后的用例识别工作提供基础. 为了方便表示, 这里的节点都使用字母进行编号.

2 统一结构

本节给出用于形式化表达UML模型的形式化模型——统一结构(unified structure). 统一结构基于团队先前的依赖结构(dependency structure)模型^[15], 将UML模型进行统一的形式化建模, 从结构层面对UML模型进行分析与表示.

定义1. 统一结构( $ US $ )是一个多元组 $ \langle ME, \prec , \stackrel{1}{\omega }, \cdots , \stackrel{n}{\omega }, \lambda , \stackrel{1}{\tau }, \cdots , \stackrel{m}{\tau }\rangle $ , 其中:

1) $ ME $ 为模型元素的有限集;

2) $ \prec \subseteq ME \times ME $ , 包含关系, 它是一个非自反的偏序;

3) $ \forall i \in \{ 1, \cdots , n\} , \mathop \omega \limits^i \in ME \times ME $ 为依赖关系;

4) $ \lambda \subseteq ME \times ( \prec \cup \mathop \omega \limits^1 \cup \cdots \cup \mathop \omega \limits^n ) $ 为依赖上的限制;

5) $ \forall j \in \{ 1, \cdots , m\} , \mathop \tau \limits^j \in ME $ 为模型元素的类型集, 满足条件: $ \forall e \in ME, \exists \tau \in \{ \mathop \tau \limits^1 , \cdots , \mathop \tau \limits^m \} :e \in \tau $ .

模型元素在此处的概念与UML中的模型元素一致^[5], 它可以根据视点的不同而有不同的类型. 包含关系是非自反的偏序, 用于建模父子关系. 依赖关系的种类与数量会随着模型的不同而变化. 包含与依赖关系都可以根据需要加入额外的限制条件. 显然, 根据定义1, 可以用统一结构对用例图与活动图进行建模. 下面分别介绍如何用统一结构描述用例图与活动图.

图1展示了一个简单的用例图, 它可以用统一结构表示为 $UCD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \mathop \omega \limits^{{\rm{Include}}} , \mathop \omega \limits^{{\rm{Extend}}} , \mathop \omega \limits^{{\rm{Associate}}}$ , $\mathop \omega \limits^{{\rm{Generalize}}}, \lambda , \mathop \tau \limits^{{\rm{UseCase}}} , \mathop \tau \limits^{{\rm{Actor}}} , \mathop \tau \limits^{{\rm{Event}}} \rangle$ , 其中:

1) $ ME = \left\{ {A, B, C, D, Actor1, Actor2} \right\} $

2) $ \prec = \varnothing $

3) $\mathop \omega \limits^{{\rm{Sequence}}} = \varnothing$

4) $\mathop \omega \limits^{{\rm{Include}}} = \{ (A, B), (A, C)\}$

5) $\mathop \omega \limits^{{\rm{Extend}}} = \{ (C, D)\}$

6) $\mathop \omega \limits^{{\rm{Associate}}} = \{ (B, Actor1), (D, Actor2)\}$

7) $\mathop \omega \limits^{{\rm{Genaralize}}} = \varnothing$

8) $ \lambda = \varnothing $

9) $\mathop \tau \limits^{{\rm{UseCase}}} = \{ A, B, C, D\}$

10) $\mathop \tau \limits^{{\rm{Actor}}} = \{ Actor1, Actor2\}$

11) $\mathop \tau \limits^{{\rm{Event}}} = \varnothing$

符号分别有如下含义: $ ME $ 表示模型中所有元素的集合, 如 $ A $ 代表用例 $ A $ , $ Actor1 $ 代表参与者 $ Actor1 $ . $ \prec $ 代表用例与事件的包含关系, 由于例子没有使用事件流, 因此此处为空. $\mathop \omega \limits^{{\rm{Sequence}}}$ 表示事件流的执行顺序, 此处为空. $\mathop \omega \limits^{{\rm{Include}}}$ 表示用例之间的包含关系, 如 $ (A, B) $ 表示 $ B $ 包含 $ A $ . $\mathop \omega \limits^{{\rm{Extend}}}$ 表示用例之间的扩展关系, 如 $ (C, D) $ 表示 $ D $ 扩展 $ C $ . $\mathop \omega \limits^{{\rm{Associate}}}$ 表示用例与参与者之间的关联关系, 如 $ (B, Actor1) $ 表示用例 $ B $ 与参与者 $ Actor1 $ 之间存在关联关系. $\mathop \omega \limits^{{\rm{Generalize}}}$ 表示用例与用例, 或参与者与参与者之间的泛化关系, 此处没有体现, 因此为空. $\mathop \tau \limits^{{\rm{UseCase}}}$ 表示用例集合, $\mathop \tau \limits^{{\rm{Actor}}}$ 是参与者集合, $\mathop \tau \limits^{{\rm{Event}}}$ 表示用例的事件流的集合, 此处没有描述事件流, 因此为空.

图2的活动图用统一结构表示为 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} ,\; \lambda ,\; \mathop \tau \limits^{{\rm{InitialAct}}} ,\; \mathop \tau \limits^{{\rm{FinalAct}}} ,\; \mathop \tau \limits^{{\rm{Activity}}} ,\; \mathop \tau \limits^{{\rm{Fork}}} ,\; \mathop \tau \limits^{{\rm{Join}}} , \mathop \tau \limits^{{\rm{Decision}}} , \mathop \tau \limits^{{\rm{Merge}}}$ , $\mathop \tau \limits^{{\rm{Swimlane}}} \rangle$ , 其中:

1) $ ME = \{ a,\, b,\, c,\, d,\, e,\, g,\, h, j, k, l, m, n, i, {f_1}, {f_2}, t{e_1}, d{n_1}, $ $ m{e_1}\} $

2) $\prec = \{ (i, s{w_1}), (a, s{w_1}), (c, s{w_1}), (e, s{w_1}), (k, s{w_1}), (b, s{w_2}) , (d, s{w_2}), (t{e_1}, s{w_2}), (d{n_1}, s{w_2}), (j, s{w_2}), (h, s{w_2}), ({f_1}, s{w_2}) , $ $(m{e_1}, s{w_2}), (n, s{w_2}), ({f_2}, s{w_2}), (g, s{w_3}), (l, s{w_4}), (m, s{w_4})\} $

3) $\mathop \omega \limits^{{\rm{Sequence}}} = \{ (a, i), (b, a), (c, b), (d, c), (t{e_1}, d), (d{n_1}, t{e_1}), (e, d{n_1}) ,\, (g, e),\, (h, g),\, ({f_1}, h),\, (j, d{n_1}),\, (k, j), (m{e_1}, k), (l, d{n_1}), $ $(m, l), (m{e_1}, m), (n, m{e_1}), ({f_2}, n)\} $

4) $ \lambda = \varnothing $

5) $\mathop \tau \limits^{{\rm{InitialAct}}} = \{ i\}$

6) $\mathop \tau \limits^{{\rm{FinalAct}}} = \{ {f_1}, {f_2}\}$

7) $\mathop \tau \limits^{{\rm{Activity}}} = \{ a, b, c, d, e, g, h, j, k, l, m, n, i, {f_1}, {f_2}, t{e_1}, d{n_1}, m{e_1}\}$

8) $\mathop \tau \limits^{{\rm{Fork}}} = \varnothing$

9) $\mathop \tau \limits^{{\rm{Join}}} = \varnothing$

10) $\mathop \tau \limits^{{\rm{Decision}}} = \{ d{n_1}\}$

11) $\mathop \tau \limits^{{\rm{Merge}}} = \{ m{e_1}\}$

12) $\mathop \tau \limits^{{\rm{Swimlane}}} = \{ s{w_1}, s{w_2}, s{w_3}, s{w_4}\}$

此处解释符号的含义. $ ME $ 表示模型元素中所有元素的集合, 如 $ a $ 表示一个活动节点, $ i $ 表示一个初始化节点; $ \prec $ 表示节点之间的包含关系, 如 $ (i, sw_1) $ 表示节点 $ i $ 归属于节点 $ s{w_1} $ ; $\mathop \omega \limits^{{\rm{Sequence}}}$ 表示节点之间的执行顺序, 如 $ (a, i) $ 表示执行顺序为先 $ i $ 后 $ a $ ; $\mathop \tau \limits^{{\rm{InitialAct}}}$ 表示初始化节点集合; $\mathop \tau \limits^{{\rm{FinalAct}}}$ 表示结束节点集合; $\mathop \tau \limits^{{\rm{Activity}}}$ 表示活动节点集合; $\mathop \tau \limits^{{\rm{Fork}}}$ 表示分支节点集合, 此处没有使用分支节点, 因此集合内没有元素; $\mathop \tau \limits^{{\rm{Join}}}$ 表示汇聚节点集合, 此处没有使用汇聚节点, 因此集合内没有元素; $\mathop \tau \limits^{{\rm{Decision}}}$ 表示决策节点集合; $\mathop \tau \limits^{{\rm{Merge}}}$ 表示合并节点集合; $\mathop \tau \limits^{{\rm{Swimlane}}}$ 表示泳道节点集合.

定义2. 令 $ US=\langle ME, \prec , \stackrel{1}{\omega }, \cdots , \stackrel{n}{\omega }, \lambda , \stackrel{1}{\tau }, \cdots , \stackrel{m}{\tau }\rangle $ 为一个统一结构.

如果序列 $dc = {x_1} \cdots {x_n}$ , $\forall i \in \{ 1, \cdots , n - 1\} ,$ $ {x_i}, {x_{i + 1}} \in ME $ , $({x_i}, {x_{i + 1}}) \in (\mathop \omega \limits^1 \cup \cdots \cup$ $ \mathop \omega \limits^n ) $ , 则称 $ \; dc $ 为 $ US $ 的一个依赖链.

$ \mathop {dc}\limits^ \wedge $ 表示为依赖链 $ dc $ 中的模型元素, 也就是说, $ \mathop {dc}\limits^ \wedge = \{ {x_1} \cdots {x_n}\} $ , $ DC(US) $ 表示 $ US $ 中所有可能的依赖链. $ [dc] $ 表示依赖链 $ dc = {x_1} \cdots {x_n} $ 中模型元素的个数, 也就是说, $ [dc] = n $ .

在图2所示的活动图中, $ iabct{e_1}d{n_1}egh{f_1} $ 是一条依赖链.

性质1. 若 $ US=\langle ME, \prec , \stackrel{1}{\omega }, \cdots , \stackrel{n}{\omega }, \lambda , \stackrel{1}{\tau }, \cdots , \stackrel{m}{\tau }\rangle $ 为一个统一结构, 则 $ ME = \mathop \tau \limits^1 \cup \cdots \cup \mathop \tau \limits^n $ .

证明: 由定义1直接可得.

性质2. 令 $ US=\langle ME, \prec , \stackrel{1}{\omega }, \cdots , \stackrel{n}{\omega }, \lambda , \stackrel{1}{\tau }, \cdots , \stackrel{m}{\tau }\rangle $ 为一个统一结构, 并且 $ dc = {x_1} \cdots {x_n} \in DC(US) $ . 如果 $ \forall i \in \{ 1, \cdots , n - 1\} , $ $ ({x_i}, {x_{i + 1}}) \in \prec $ , 那么在 $ dc $ 中没有环.

证明: 由于依赖链 $ dc $ 中只包含了包含关系, 根据定义1与定义2, 包含关系 $ \prec $ 是一个非自反的偏序, 满足该偏序关系的元素无法关联到自身. 因此 $ dc $ 中不存在环.

性质2说明了只包含了包含关系的依赖链是没有环的.

3 基于活动图的用例的识别

本节介绍使用统一结构建模的活动图进行用例识别的方法.

定义3. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \lambda , \mathop \tau \limits^{{\rm{InitialAct}}} , \mathop \tau \limits^{{\rm{FinalAct}}} ,$ $\mathop \tau \limits^{{\rm{Activity}}} , \mathop \tau \limits^{{\rm{Fork}}} , \mathop \tau \limits^{{\rm{Join}}} , \mathop \tau \limits^{{\rm{Decision}}} , \mathop \tau \limits^{{\rm{Merge}}} , \mathop \tau \limits^{{\rm{Swimlane}}} \rangle$ 为一个活动图, $ DC (AD) $ 是 $ AD $ 中所有可能的依赖链. 如果依赖链 $ dc = $ $ {x_1} \cdots {x_n} \in $ $ DC(AD) $ 且 $ {x_1} \in $ $\mathop \tau \limits^{{\rm{InitialAct}}}$ , $ {x_n} \in $ $\mathop \tau \limits^{{\rm{FinalAct}}}$ , 则称 $ dc $ 是完全的. 这里定义 $ CDC(AD) $ 表示活动图 $ AD $ 所有的完全的依赖链.

在图2的活动图中, 依赖链 $ iabc $ $ t{e_1}d{n_1}egh{f_1} $ . 的首个元素 $ i $ 属于 $\mathop \tau \limits^{{\rm{InitialAct}}}$ , 末尾的元素 $ {f_1} $ 属于 $\mathop \tau \limits^{{\rm{FinalAct}}}$ , 首尾之间的元素全部属于 $ ME $ , 因此它是一个完全的依赖链.

命题1. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \lambda , \mathop \tau \limits^{{\rm{InitialAct}}} , \mathop \tau \limits^{{\rm{FinalAct}}} ,$ $\mathop \tau \limits^{{\rm{Activity}}} , \mathop \tau \limits^{{\rm{Fork}}} , \mathop \tau \limits^{{\rm{Join}}} , \mathop \tau \limits^{{\rm{Decision}}} , \mathop \tau \limits^{{\rm{Merge}}} , \mathop \tau \limits^{{\rm{Swimlane}}} \rangle$ 为一个活动图, $ CDC (AD) $ 是 $ AD $ 中所有可能的完全的依赖链. 如果 $ \forall dc = {x_1} \cdots {x_n} \in CDC $ $ (AD) $ , 则 $ \exists {x_i}, {x_{i + 1}} \in \{ {x_1}, \cdots , {x_n}\} :({x_i}, {x_{i + 1}}) $ $ \in \mathop \omega \limits^{{\rm{Sequence}}}$ .

证明: $ \forall dc = {x_1} \cdots {x_n} \in CDC(AD) $ , 即活动图中所有的依赖链都是完全的依赖链, 每个依赖链中的每两个相邻元素组成的元素对都能在 $\mathop \omega \limits^{{\rm{Sequence}}}$ 中找到, 即 $ \exists {x_i}, {x_{i + 1}} \in \{ {x_1}, $ $\cdots , {x_n}\} :({x_i}, {x_{i + 1}}) \in \mathop \omega \limits^{{\rm{Sequence}}}$ , 命题得证.

命题1表明了一个活动图可以分解为多个独立的依赖链. 图2的活动图能够被分解为依赖链 $ iabct{e_1}d{n_1}egh{f_1} $ 与依赖链 $ iabcdt{e}_{1}d{n}_{1} jkm{e}_{1}n{f}_{2} $ , 分解原始活动图得到的两个依赖链都是完全的依赖链.

定义4. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \lambda , \mathop \tau \limits^{{\rm{InitialAct}}} , \mathop \tau \limits^{{\rm{FinalAct}}} ,$ $\mathop \tau \limits^{\rm{{\rm}{Activity}}} , \mathop \tau \limits^{\rm{Fork}} , \mathop \tau \limits^{\rm{Join}} , \mathop \tau \limits^{\rm{Deci}sion} , \mathop \tau \limits^{\rm{Merg}e} , \mathop \tau \limits^{\rm{Swim}lane} \rangle$ 为一个活动图, 并假定 $\mathop \tau \limits^{{\rm{TimeEvent}}} \subseteq \mathop \tau \limits^{{\rm{Activity}}}$ 是时间事件. 如果一个链 $ dc = {x_1} $ $ \cdots {x_n} $ $ \in CDC(AD) $ , 并且 $\exists x \in \mathop \tau \limits^{{\rm{TimeEvent}}}$ $ \cap \mathop {dc}\limits^ \wedge $ , 则称 $ dc $ 是可分解的.

定义4引入了时间事件的概念. 因为一些业务上的操作需要等待其他业务相关的执行者或用户完成其他操作才能继续进行, 所以将这些等待其他执行者或用户的操作描述为时间事件. 以这一类事件为分界, 将一个完整但较长的业务流程分解成多个独立的业务流程.

满足定义4的依赖链能够被分解为多个依赖链. 如果依赖链的性质不能满足定义4, 说明依赖链所对应的业务流程在实际执行中不需要等待其他业务执行者完成操作, 这样的依赖链能够直接被识别为一个用例.

算法1. 活动图生成已分解的依赖链的集合

输入: 活动图 $\scriptstyle AD = \langle ME, \prec , \mathop \omega \limits^{\rm{Sequence}} , \lambda , \mathop \tau \limits^{\rm{Swimlane}} , \mathop \tau \limits^{\rm{InitialAct}} ,$ $\scriptstyle \mathop \tau \limits^{\rm{FinalAct}} , \mathop \tau \limits^{\rm{Activity}} , \scriptstyle \mathop \tau \limits^{\rm{Fork}} , \mathop \tau \limits^{\rm{Join}} , \mathop \tau \limits^{\rm{Decision}} , \mathop \tau \limits^{\rm{Merge}} , \rangle$

输出: 所有已分解的依赖链的集合DDC

1) $\scriptstyle CDC \leftarrow \varnothing $ //初始化完全的依赖链的集合

2) $\scriptstyle DDC \leftarrow \varnothing $ //初始化已分解的依赖链的集合

3) $\scriptstyle rc \leftarrow \varnothing $ // 初始化依赖链

4) Initialize $\scriptstyle {\textit{pathStack}}$ as a stack //初始化路径栈

5) $\scriptstyle {\textit{InitialNodesSet}}\leftarrow \{e\in ME|\nexists x\in$ $\scriptstyle ME:(x, e) \in \mathop \omega \limits^{{\rm{Sequence}}} \}$ //找出起始节点

6) FOR each i in $\scriptstyle {\textit{InitNodesSet}}$ DO

7)　 pathStack.push(i)

8)　 IF $\scriptstyle \exists x \in ME:(x, i) \in \mathop \omega \limits^{{\rm{Sequence}}}$ THEN

9)　　 DFS(x) //深度优先搜索

10)　 END IF

11) pathStack.pop()

12) END FOR

13) FOR each $\scriptstyle dc $ in $\scriptstyle CDC $ DO

14)　 FOR each $\scriptstyle x $ in $\scriptstyle dc $ DO

15)　 SWITCH the set where x in DO /* 根据x所属的集合做出不同的行为 */

16) 　　 CASE $\scriptstyle \mathop \tau \limits^{{\rm{TimeEvent}}}$

17) 　　　 IF $\scriptstyle \mathop \tau \limits^{{\rm{TimeEvent}}} \subseteq \mathop \tau \limits^{{\rm{Activity}}}$ THEN /* 如果元素表示时间事件, 那么将时间事件之前的链存入DDC中, 之后直接遍历下一个元素. */

18)　　　 $\scriptstyle DDC \leftarrow DDC \cup \{ rc\} $

19)　　　 $\scriptstyle rc \leftarrow \varnothing $ // 清空依赖链, 重新开始记录

20) 　　　 END IF

21) 　　 CASE $\scriptstyle \mathop \tau \limits^{{\rm{FinalAct}}}$ /* 如果元素表示终止节点, 则将依赖链存入DDC中 */

22) 　　　 $\scriptstyle rc \leftarrow rc \cup \{ x\} $

23)　　　 $\scriptstyle DDC \leftarrow DDC \cup \{ rc\} $

24) 　　　 $\scriptstyle rc \leftarrow \varnothing $ // 清空依赖链, 重新开始记录

25) 　　 OTHERWISE $\scriptstyle rc \leftarrow rc \cup \{ x\} $ /* 将元素加入依赖链 */

26) 　　 END

27)　 END FOR

28) END FOR

29) PROCEDURE DFS(x) //深度优先搜索算法

30) 　　 IF $\scriptstyle x \in \mathop \tau \limits^{{\rm{FinalAct}}}$ or $\scriptstyle x = = {\rm{NULL}}$ THEN /*找到终止节点, 或是为NULL的节点 */

31) 　　　　 IF $\scriptstyle x \in \mathop \tau \limits^{{\rm{FinalAct}}}$ pathStack.push(i) /* 只在x不为NULL时将节点入栈*/

32) 　　　　 END IF

33)　　　　 $\scriptstyle CDC \leftarrow CDC \cup {\textit{pathStack}}.path$ /*将完整路径加入路径集合*/

34) 　　　　 IF $\scriptstyle x \in \mathop \tau \limits^{{\rm{FinalAct}}}$ pathStack.pop() /*只在x不为NULL时将节点出栈 */

35) 　　　　 END IF

36)　 　 ELSE //找到其他节点

37) 　　　　 IF !x.isVisited THEN

38)　　　　　 x.isVisited $\scriptstyle \leftarrow $ true //遍历节点

39) 　　　　　 pathStack.push(x)

40) 　　　　　　 IF $\scriptstyle \exists e \in ME:(e, x) \in \mathop \omega \limits^{{\rm{Sequence}}}$ THEN

41) 　　　　　　　 FOR each e in $\scriptstyle \{ e \in ME|(x, e) $ $\scriptstyle \in \mathop \omega \limits^{{\rm{Sequence}}} \}$ $\scriptstyle $

42) 　　　　　　　　 DFS(x) //递归深度优先

43) 　　　　　　　 END FOR

44) 　　　　　　 END IF

45) 　　　　　 pathStack.pop()

46)　　　　 END IF

47) 　　 END IF

48) END PROCEDURE

算法1的设计思路如下: 在构建活动图, 并使用统一结构对它进行描述后, 将这个统一结构作为算法的输入. 遍历整个活动图, 识别出活动图的依赖链. 在识别依赖链后, 对其中含有时间事件的依赖链进行分解, 并将分解的依赖链的集合作为算法的输出. 整个算法基于深度优先搜索, 在此基础上进行扩展.

算法1给出了输出依赖链的详细流程.

1) 输入活动图, 并获得活动图中的所有初始节点, 作为深度优先搜索的起点集合.

2) 将起始节点入栈.

3) 从起始节点开始, 深度优先搜索后继节点.

4) 在深度优先搜索结束之后, 弹出栈顶, 继续从其他起始节点开始搜索, 直到没有起始节点可以搜索.

5) 在搜索完完全的依赖链之后, 遍历所有完全的依赖链, 删除其中的时间事件.

我们修改了一部分深度优先搜索算法来适配需求.

1) 深度优先搜索算法首先接收一个节点作为搜索起点.

2) 如果搜索到了终止节点, 说明这一条路径已经搜索完毕, 将路径存入 $ CDC $ 中.

3) 对其他遍历到的节点, 如果它们没有被遍历过, 就将它们标记为已访问. 如果遍历到一个已经访问过的节点, 就回到分支处继续后续搜索.

在生成 $ CDC $ 之后, 将其中的所有可分解的依赖链 $ dc $ 分解.

1) 遍历依赖链 $ dc $ , 将遍历到的每一个元素都保存在一个链中.

2) 遍历到时间事件时, 将链保存在 $ DDC $ 中, 然后, 不保存时间事件元素, 直接清空链, 从下一个节点继续遍历.

3) 遍历到结束节点时, 保存结束节点元素, 然后将链保存在 $ DDC $ 中, 最后清空链.

通过算法1分解依赖链的操作, 原本的依赖链会被分割成两部分. 将两部分依赖链各自作为独立的元素保存在了集合 $ DDC $ 中. $ DDC $ $ (AD) $ 表示活动图 $ AD $ 中所有完全的依赖链分解之后的依赖链的集合. 如果依赖链没有时间事件, 那么依赖链本身也会存入 $ DDC $ 中.

定义5. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \lambda , \mathop \tau \limits^{{\rm{InitialAct}}} , \mathop \tau \limits^{{\rm{FinalAct}}} ,$ $\mathop \tau \limits^{{\rm{Activity}}} , \mathop \tau \limits^{{\rm{Fork}}} , \mathop \tau \limits^{{\rm{Join}}} , \mathop \tau \limits^{{\rm{Decision}}} , \mathop \tau \limits^{{\rm{Merge}}} , \mathop \tau \limits^{{\rm{Swimlane}}} \rangle$ 为一个活动图. $ \exists dc \in DDC(AD) $ , 对 $ dc = {x_1} \cdots {x_n} $ ,

1) 如果 ${x_1}\not \in \mathop \tau \limits^{{\rm{InitialAct}}}$ , 则称 $ dc $ 是缺首的依赖链.

2) 如果 ${x_n}\not \in \mathop \tau \limits^{{\rm{FinalAct}}}$ , 则称 $ dc $ 是缺尾的依赖链.

3) 如果 ${x_1}\not \in \mathop \tau \limits^{{\rm{InitialAct}}}$ 且 ${x_n}\not \in \mathop \tau \limits^{{\rm{FinalAct}}}$ , 则称 $ dc $ 是缺首尾的依赖链.

所有缺首的依赖链、缺尾的依赖链、缺首尾的依赖链统称为“不完整的依赖链”.

任何满足了定义4的可分解的依赖链都可以在分解之后形成定义5中所述的不完整的依赖链. 不完整的依赖链可以通过补充节点重新恢复成完全的依赖链.

定义6. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{{\rm{Sequence}}} , \lambda , \mathop \tau \limits^{{\rm{InitialAct}}} , \mathop \tau \limits^{{\rm{FinalAct}}} ,$ $\mathop \tau \limits^{\rm{Activity}} , \mathop \tau \limits^{\rm{Fork}} , \mathop \tau \limits^{\rm{Join}} , \mathop \tau \limits^{\rm{Decision}} , \mathop \tau \limits^{\rm{Merge}} , \mathop \tau \limits^{\rm{Swimlane}} \rangle$ 为一个活动图, 并设 $ {x_0}, {x_f} $ 分别是活动图的起始和终止节点. 如果 $ dc = {x_1} \cdots {x_n} \in DDC(AD) $ 且 $ dc $ 是不完整的依赖链. 令 $ rc $ 为修复的依赖链. 根据 $ dc $ 所属的类型,

1) 如果 $ dc $ 是缺首的依赖链, 则 $ rc = {x_0}{x_1} \cdots {x_n} $ .

2) 如果 $ dc $ 是缺尾的依赖链, 则 $ rc = {x_1} \cdots {x_n}{x_f} $ .

3) 如果 $ dc $ 是缺首尾的依赖链, 则 $ rc = {x_0}{x_1} \cdots $ $ {x_n}{x_f} $ .

定义6的操作改变了活动图原本的依赖关系, 因此这个过程是单向不可逆的.

性质3. 设AD是一个活动图, 所有已修复的依赖链 是完全的依赖链, 且不含有时间事件.

证明: 根据定义5, 加入的依赖链中不会再含有时间事件. 根据定义6的操作, 修复的依赖链重新拥有了起始节点与终止节点, 满足定义3中完全的依赖链的性质, 该性质得证.

性质3说明了修复的依赖链具备完全的依赖链的性质, 并且已经无法再分解.

性质4. 设AD是一个活动图, 如果 $ \forall dc \in $ $ DDC (AD) $ , 且 $ dc $ 是完全的, 则 $ DDC(AD) = $ $ CDC(AD) $ .

证明: 该证明可直接得到.

所有满足了性质4的依赖链集合所对应的活动图都不能再分解, 可以直接生成用例.

已经完成修复的依赖链可以描述一个完整的业务流程. 在统一开发过程^[3]中, 一个用例应当只描述系统的某一个功能, 而它的事件流描述了系统与用例相关的参与者之间的交互, 用例的事件流也可以反映为一个活动图. 完全的依赖链与修复的依赖链都具备了与用例相同的性质: 它们都描述了系统的某一个功能, 并且能够通过活动与泳道的关系来进一步描述用例与参与者的关系. 通过一个完整的依赖链能够生成它对应的用例的事件流, 进而描述一个完整的用例.

如果需要从活动图中识别用例, 那么可以采用以下几个步骤.

1) 将活动图建模为统一结构 $ AD $ .

2) 从活动图的每一个起始节点开始, 搜索活动图中的路径, 并在搜索到终止节点时保存对应的路径为完全的依赖链.

3) 在搜索完整个活动图后, 寻找路径中的时间事件, 将时间事件分解为起始节点与终止节点, 并补全依赖关系, 即修复成完全的依赖链.

4) 每个完全的依赖链即为一个用例的事件流, 依赖链中的活动所属的泳道描述为参与者, 最后手动补全用例名与用例描述.

定义7. 令 $AD = \langle ME, \prec , \mathop \omega \limits^{\rm{Sequence}} , \lambda , \mathop \tau \limits^{\rm{InitialAct}} , \mathop \tau \limits^{\rm{FinalAct}} ,$ $\mathop \tau \limits^{\rm{Activity}} , \mathop \tau \limits^{\rm{Fork}} , \mathop \tau \limits^{\rm{Join}} , \mathop \tau \limits^{\rm{Decision}} , \mathop \tau \limits^{\rm{Merge}} , \mathop \tau \limits^{\rm{Swimlane}} \rangle$ 为一个活动图, $UCD = \langle ME', \prec ', {\mathop \omega \limits^{\rm{Sequence}'} }, \mathop \omega \limits^{\rm{Include}} , \mathop \omega \limits^{\rm{Extend}} , \mathop \omega \limits^{\rm{Associate}} , \mathop \omega \limits^{\rm{Generalize}} \lambda '$ , $\mathop \tau \limits^{\rm{UseCase}} , \mathop \tau \limits^{\rm{Actor}} , \mathop \tau \limits^{\rm{Event}} \rangle$ 为一个用例图. 假定在 $ CDC(AD) $ 中有n个完全的依赖链(包括修复的依赖链), 它们的名字分别对应为 $ {N_1}, {N_2}, \cdots , {N_n} $ , 且活动图中所有的依赖链都不能再分解, 那么活动图与用例图有如下关系.

1) $\mathop \tau \limits^{{\rm{Swimlane}}} \cup \mathop \tau \limits^{{\rm{Activity}}} \cup \{ {N_1}, {N_2}, \cdots , {N_n}\} \subseteq ME'$

2) $ \prec ' = \{ (a, b)|a \in b, b \in \{ {N_1}, {N_2}, \cdots , {N_n}\} \} $

3) $ \lambda ' = \lambda $

4) ${\mathop \omega \limits^{{\rm{Sequence}}'} } = \{ (a, b)|a \in \mathop \tau \limits^{{\rm{Activity}}} , b \in \mathop \tau \limits^{{\rm{Activity}}} , (a, b) \in \mathop \omega \limits^{{\rm{Sequence}}} \}$

5) $\mathop \omega \limits^{{\rm{Associate}}} = \{ (a, b)|dc \in CDC(AD), a \in \mathop {dc}\limits^ \wedge , b \in \mathop \tau \limits^{{\rm{Swimlane}}} ,$ $ (a, b) \in \prec \} $

6) $\mathop \tau \limits^{{\rm{UseCase}}} = \{ {N_1}, {N_2}, \cdots , {N_n}\}$

7) $\mathop \tau \limits^{{\rm{Actor}}} = \{ Actor|Actor \in \mathop \tau \limits^{{\rm{Swimlane}}} \}$

8) $\mathop \tau \limits^{{\rm{Event}}} = \{ e|e \in \mathop \tau \limits^{{\rm{Activity}}} \}$

定义7给出了活动图生成用例图时的对应关系. 用例图中所有的元素由泳道对应的参与者与依赖链对应的用例的事件流构成; 用例包含它自己的事件流, 从而形成统一结构上的包含关系, 此关系在活动图中由依赖链及其所属的活动构成; 用例图节点之间的关系对应活动图中泳道与活动的关系; 用例图中的用例对应活动图中的依赖链; 用例图的参与者对应活动图的泳道; 用例的事件对应依赖链所属的活动.

借助定义7中的关系, 图3中的所有依赖链都能够识别出对应的用例. 因为用例描述的是系统功能, 所以将依赖链转为事件流之后, 即可认为已经识别出了对应的用例. 获取事件流后, 根据事件流描述的业务, 手动补充用例名称和事件流描述. 最后, 将系统之外的泳道表示为参与者, 将泳道与活动节点的关系表示为参与者与用例的关联关系, 完成用例的半自动生成.

最终识别并生成的用例图如图4所示. 由于用例图的事件流一般都使用文字叙述, 不直接在图中体现, 因此此处使用文本框简略描述事件流.

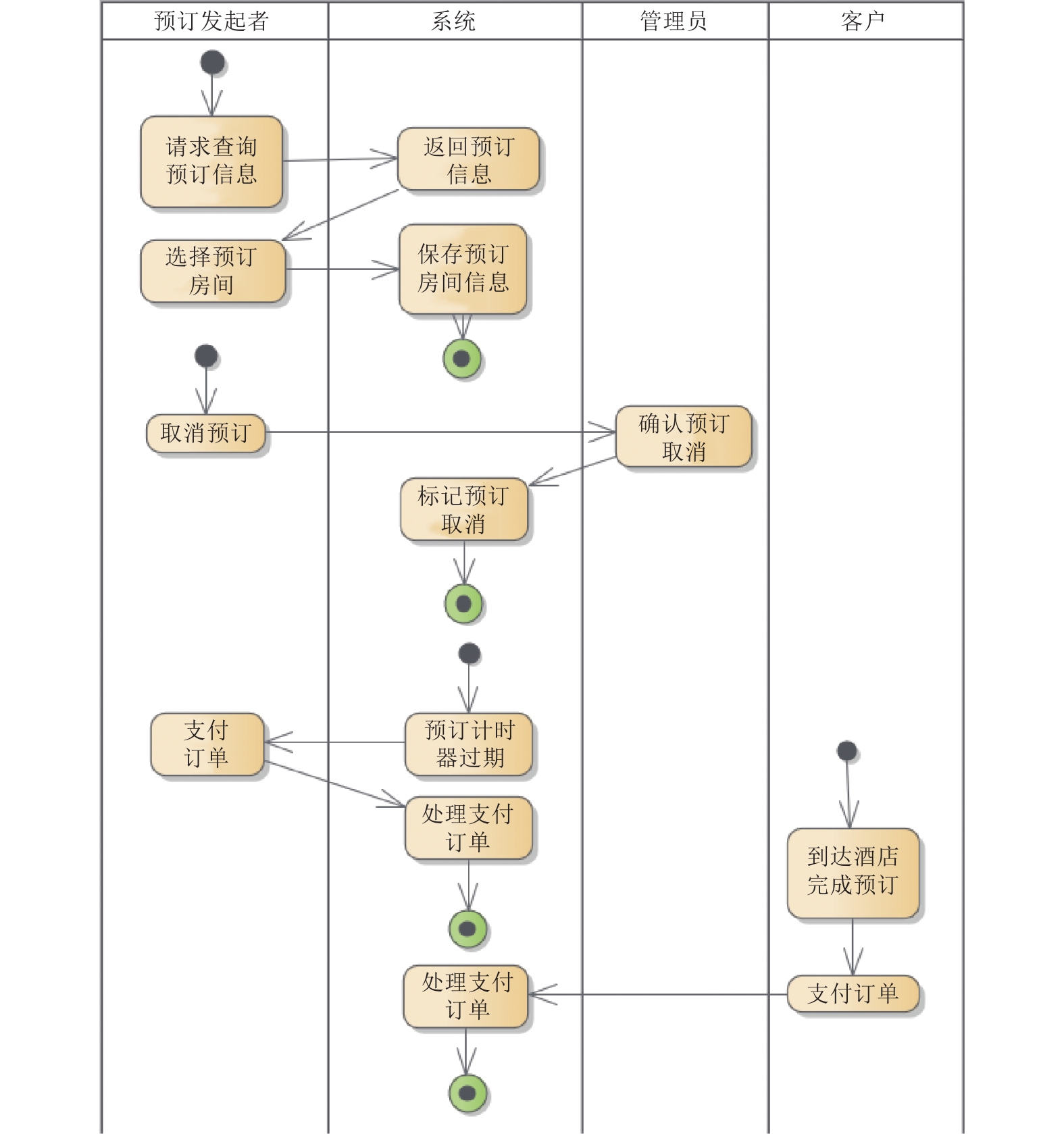
4 案例分析

本节中, 我们将用一个牙科诊所系统的部分业务流程进行案例分析. 描述该系统业务流程的活动图如图5所示. 病人可以在系统上预约诊治, 也可以直接在诊所由医师助手安排安装矫正器.

预约就诊、诊治病人、支付诊治订单的流程由以下步骤组成.

1) 病人首先需要询问诊所接待员预约的日期是否可用, 如果预约的日期有医师能够诊治, 接待员就可以联系病人, 让病人提供信息, 由接待员输入信息之后保存在系统内.

2) 等待病人前来就诊. 在病人就诊完成之后, 医师助手记录病人就诊完成, 并根据病人的就诊情况安排病人是否需要后续诊治.

3) 如果需要安排复诊, 则医师助手在系统上输入诊治安排, 并在病人复诊结束后生成支付订单, 否则系统直接生成支付订单, 等待病人支付.

矫正器定制、矫正器安装的流程由以下步骤组成.

1) 病人来到诊所后, 医师助手安排病人矫正流程, 病人选择自己的矫正器型号. 注意, 病人来到诊所的步骤无需与系统交互, 因此不属于用例的一部分.

2) 在系统确认之后, 等待矫正器制作完成.

3) 助手给病人安装制作完成的矫正器.

4) 在安装完成之后, 系统生成矫正器订单, 等待病人支付.

根据以上步骤, 绘制出图5所示的活动图, 并应用第3节的方法进行用例识别.

首先, 给出活动图的统一结构. 图5的活动图可以用统一结构表示为 $AD = \langle ME, \prec , \mathop \omega \limits^{\rm{Sequence}} , \lambda , \mathop \tau \limits^{\rm{InitialAct}} ,$ $\mathop \tau \limits^{\rm{FinalAct}} , \mathop \tau \limits^{\rm{Activity}} , \mathop \tau \limits^{\rm{Fork}} , \mathop \tau \limits^{\rm{Join}} , \mathop \tau \limits^{\rm{Decision}} , \mathop \tau \limits^{\rm{Merge}} , \mathop \tau \limits^{\rm{Swimlane}} \rangle$ , 其中:

1) $ME = \{ sw_1, sw_2, sw_3, sw_4, {i_1}, a, d{c_1}, b, {f_1}, c, d, e, g, t{e_1}, h, j, d{c_2}$ , $me, k, l, m.n, o, p, {f_2}, {i_2}, q, r, s, t, t{e_3}, u, v, w, x, {f_3} \}$

2) $ \prec = \{ (o, s{w_1}), (s, s{w_1}), (w, s{w_1}), (b, s{w_2}), ({f_1}, s{w_2}), (c, s{w_2})$ , $ (g, s{w_2}), (t{e_1}, s{w_2}), (j, s{w_2}), (d{c_2}, s{w_2}), (l, s{w_2}), (t{e_2}, s{w_2})$ , $ (me, s{w_2}), (n, s{w_2}), (p, s{w_2}), ({f_2}, s{w_2}), (r, s{w_2}), (t, s{w_2}), $ $ (t{e_3}, s{w_2}),\; (v, s{w_2}),\; (x, s{w_2}), ({f_2}, s{w_2}), (h, s{w_3}), (k, s{w_3})$ , $ (m, s{w_3}), ({i_2}, s{w_3}), (q, s{w_3}), (u, s{w_3}), (i, s{w_4}), (d{c_1}, s{w_4}) $ , $ (d, s{w_4}), (e, s{w_4})\} $

3) $\mathop \omega \limits^{{\rm{Sequence}}} = \{ (a, {i_1}), (d{c_1}, a), (b, d{c_1}), ({f_1}, b), (c, d{c_1}), (d, c), (e, d)$ , $ (g, e), \;(t{e_1}, g),\; (h, t{e_1}),\; (j, h), (d{c_2}, j), (k, d{c_2}), (l, k), (t{e_2}, l) $ , $ (me, t{e_2}),\; (me, d{c_2}),\; (m, me),\; (n, m),\; (o, n), (p, o), ({f_2}, p) $ , $ (q, {i_2}), \;(r, q), (s, r), \;(t, s), (t{e_3}, t), (u, t{e_3}), (v, u), (w, v), (x, w), $ $ ({f_3}, x)\} $

4) $ \lambda = \varnothing $

5) $\mathop \tau \limits^{{\rm{InitialAct}}} = \{ {i_1}, {i_2}\}$

6) $\mathop \tau \limits^{{\rm{FinalAct}}} = \{ {f_1}, {f_2}, {f_3}\}$

7) $\mathop \tau \limits^{{\rm{Activity}}} = \{ a, b, c, d, e, g, h, j, k, l, m, n, o, p, q, r, s, t, u,$ $ v, w, x\} $

8) $\mathop \tau \limits^{{\rm{Fork}}} = \varnothing$

9) $\mathop \tau \limits^{{\rm{Join}}} = \varnothing$

10) $\mathop \tau \limits^{{\rm{Decision}}} = \{ d{c_1}, d{c_2}\}$

11) $\mathop \tau \limits^{{\rm{Merge}}} = \{ me\}$

12) $\mathop \tau \limits^{{\rm{Swimlane}}} = \{ s{w_1}, s{w_2}, s{w_3}, s{w_4}\}$

其次, 将活动图的统一结构作为输入, 应用算法1. 算法将识别依赖链, 删除时间事件, 并生成分解的依赖链集合. 图5的活动图能够识别出i₁adc₁bf₁, i₁adc₁cdegte₁hjdc₂klte₂memnopf₂, i₁adc₁cdegte₁hjdc₂memnopf₂, i₂qrstte₃euvwxf₃这4个依赖链. 将它们之中的时间事件删除后, 得到如下7个依赖链i₁adc₁bf₁, i₁adc₁cdeg, hjdc₂kl, hjdc₂memnopf₂, memnopf₂, i₂qrst, uvwxf₃. 其中除i₁adc₁bf₁以外, 剩余6个依赖链都是不完整的依赖链.

随后修复依赖链. 在6个不完整的依赖链中补充起始节点与结束节点, 得到i₁adc₁cdegf, ihjdc₂klf, ihjdc₂memnopf₂, imemnopf₂, i₂qrstf, ieuvwxf₃这6个修复的依赖链.

最后, 根据依赖链生成用例, 根据泳道生成参与者与关联关系, 并补充对应的用例描述, 完成用例识别. 将依赖链对应的活动作为对应用例的事件流, 手动补充用例名, 将泳道与活动的关系转为用例与参与者的关系, 识别用例并生成用例图的整个过程就完成了.

我们使用JavaScript的GOJS图形库结合jQuery开发的原型工具能够重新绘制图5所示的活动图, 工具使用GOJS指定的数据结构描述UML元素, 使用jQuery结合原生JavaScript进行程序逻辑与算法的编写. 图5所示的活动图描述了病人预约就诊的业务、病人就诊之后支付订单的业务与病人安装牙齿矫正器的业务.

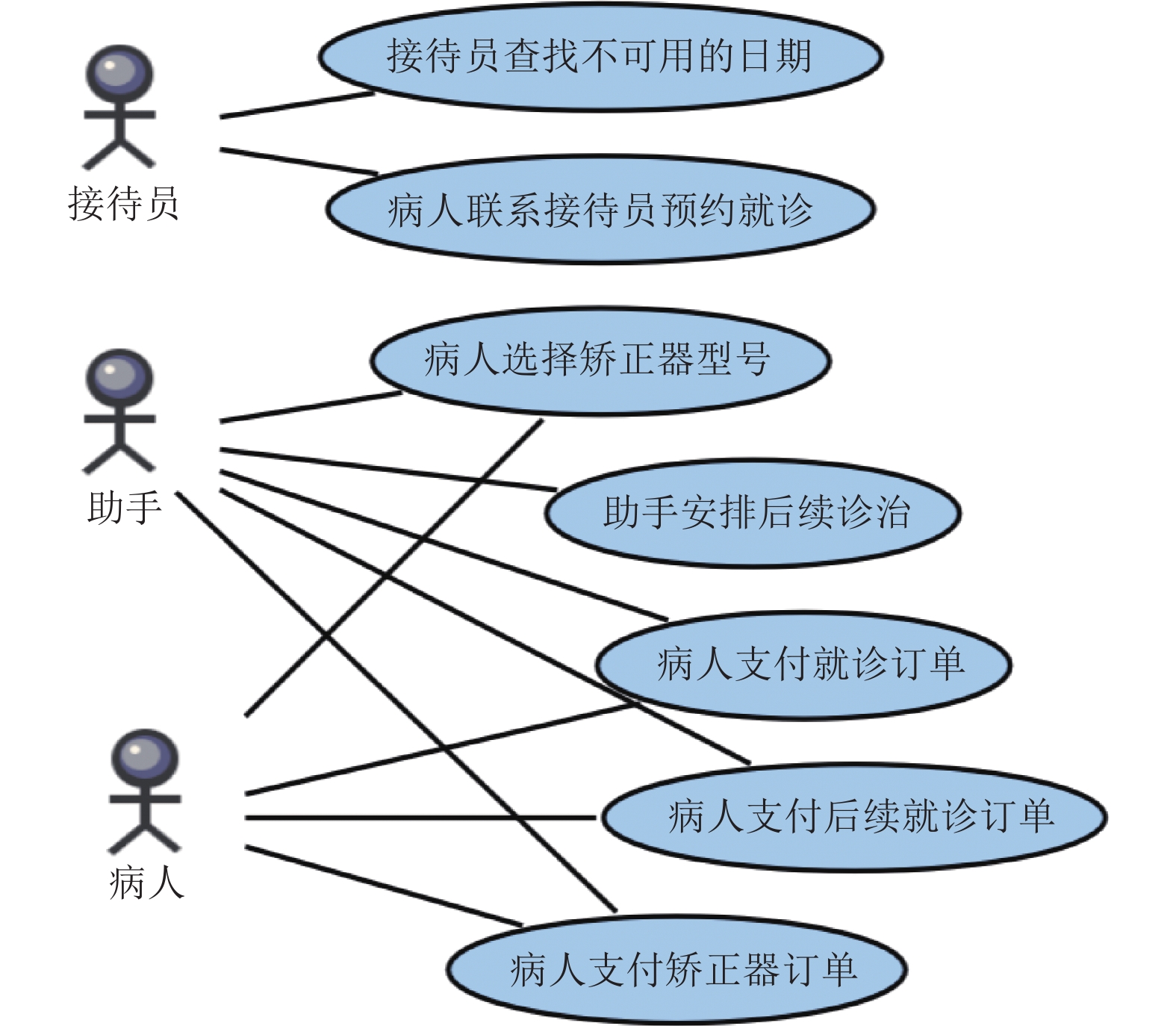
工具可以在绘制活动图后生成它的统一结构, 分解活动图中的时间事件, 并识别活动图中的依赖链, 点击识别出的依赖链则可以高亮显示它, 部分效果如图6所示. 如果有至少一条完全的依赖链被识别, 那么就可以生成依赖链对应的用例, 并根据泳道与活动的关系, 自动生成参与者与关联关系. 对图6的活动图进行识别得到的用例图如图7所示. 此处的用例名需要手动指定. 该案例研究表明, 使用活动图描述业务流程, 将活动图转为形式化模型并进一步识别用例是一个可行的方法.

5 相关工作

用例识别的工作本质上是对需求的进一步解释与挖掘, 是对用户具体需求的完整捕获. 一些早期工作关注于直接从需求文档中捕获需求并识别出用例. Hamza等人^[7]提出了直接使用自然语言处理(natural language processing, NLP)从需求文档中提取需求的方法. 通过对需求文档的内容进行拼写检查、切分、词性标记化、分块、语法模式标记等工作之后, 识别并生成新的用例. Narawita^[8]使用UML Generator配合机器学习来分析需求, 生成XML, 进一步生成用例图与类图. Bajwa等人^[16]使用人工智能技术与LESSA方法来阅读和分析用户提供的场景, 自动生成用例. 这些方法都使用到了NLP与人工智能相关的技术来自动化识别用例, 有着相对较高的生成准确率. 相较于通过NLP方法获取用例, 本文提出的方法直接从业务模型中识别用例, 适合已经进行了业务建模的需求或能够迅速进行业务建模的需求. 本文提出的方法与NLP获取用例的方法存在类似的问题. NLP的识别是一种类似于基于规则的识别方法, 它对对应语言的语法与词性等要求很高, 如果需求文档的编写不规范或者有错误拼写, 那么使用NLP识别出来的用例可能会不完整, 甚至出错. 本文提出的方法也没有对业务流程的来源进行冲突检测工作, 如果业务本身存在冲突或错误描述, 识别的用例描述的系统功能也可能会存在冲突问题. 这一点也是我们后续研究的重点.

此外, 对用例进行识别的工作也与模型之间的可追溯性相关. 能够满足模型之间的可追溯性才能保证整体建模的正确性. Bouzidi等人^[17]设计了一种基于业务流程建模与标注(business process modeling notation, BPMN)与UML用例之间的可追溯性研究, 通过建立一个包含所有BPMN与用例模型元素的元模型, 使用这个元模型定义BPSUC模型(business process supported use cases)之后, 通过BPSUC模型来建立BPMN与用例模型来确保模型之间的一致性. 该方法讨论了业务流程和需求模型之间的可跟踪性, 不过文中使用的用例图案例很简单, 无法验证BPSUC的准确性. Khlif等人^[18]提出了对设计追踪方法的改进和扩展, 以解决设计、需求和代码之间的追踪问题, 该方法给出了一些可追溯性规则, 并基于这些规则评估UML模型之间的一致性. 这些规则都有对应的图解与案例, 但没有验证每一个规则的正确性. Park等人^[19]提出了对UML用例元模型的扩展, 以将抽象用例细化到更细化的用例. 用例的改进允许在不同的抽象级别上跟踪用例, 但是作者没有解释如何建立这些跟踪. 本文的工作可以在一定程度上满足可追溯性. 在需求修改之后, 直接寻找需求对应的依赖链, 再进一步找到通过依赖链识别出的用例, 最后进行版本间的追溯性与一致性分析等工作.

在用例模型本身的研究上, Cockburn^[20]等处于UML早期阶段的研究人员大多根据自己的经验手工描述用例, 这类方法没有采用形式化方法, 无法保证前后建模的一致性, 进而影响到后续的软件开发. 在用例图的形式化研究方面, Kautz 等人^[10]给出了用例图的形式化语义, 并提出了自动识别语义差异的方法. 陈振庆^[11]提出了基于描述逻辑 SHOIN (D)的形式化描述用例图的方法. 李智等人^[12]提出了结合问题框架与模型驱动技术, 将问题模型转换为用例图的方法. 该方法能够根据问题图中需求之间的关系来建立用例之间的扩展或包含关系, 但没有描述用例的事件流. Bensalem等人^[13]提出了一个基于逻辑的形式化方法, 并将其应用在了两个复杂的用例上. 文献[10–13]采用的形式化方法与我们使用的形式化方法都不一样. 相较于之前的工作, 本文提出的识别用例的方法从业务建模中直接获取业务流程信息, 将业务流程通过形式化模型描述为依赖链, 并按时间跨度进行分解, 进一步识别为用例的事件流, 根据泳道与活动的关系自动生成用例与参与者的关联关系, 实现了用例的半自动生成. 这一思路目前还没有在其他工作中体现.

软件需求文档中的信息提取一直是一个备受关注的研究课题. 虽然已经有了需求文档规范化相关的研究^[21], 但是到目前为止, 还没有一种完整的自动化方法能够从软件需求文档的非结构化语言中提取关键信息^[9]. 因此, 我们目前还没有发现任何一种能够直接自动识别用例的方法.

6 结语

本文首先给出了用例模型与活动图的基本概念, 随后使用形式化模型统一结构描述了活动图, 并给出了寻找依赖链的定义与识别方法. 通过原型工具进行案例分析, 说明了本文提出的方法能够识别出完全的依赖链, 并生成对应的用例.

本文提出的方法也有不足之处. 识别依赖链的方法没有考虑活动边的执行条件, 也没有对决策节点的分支做更加细致的处理, 因此只能根据泳道与活动之间的关系识别出用例图的关联关系. 在接下来的工作中, 我们会进一步改进识别用例的功能, 使识别出来的用例能够体现包含与扩展关系, 我们也将验证用例图与其他UML模型之间的一致性与正确性, 并继续完善原型工具, 使之成为可用且高效的CASE工具.