近年来, 随着可穿戴计算设备的快速发展和对沉浸式人机交互环境的需求, 情感计算已经成为全球性的研究热点[1]. 情感计算旨在赋予计算机感知人类情感的能力, 进而做出适当的决策[2]. 在过去的几十年中, 许多基于生理特征的情绪识别方法被提出, 包括面部表情、语音、姿势等[3]. 然而以上的方法均受到被测者主观因素的影响, 难以达到较为理想的检测效果. EEG技术可以直接获取大脑中枢神经系统中的脑电波信号, 不受被测者主观意识的干扰, 同时还具有成本低、便携性强和实时性高的优点, 因此在情绪识别中具有广阔的应用前景[4, 5]. EEG信号的获取一般采用多通道采集的方式, 根据国际10-20系统标准在大脑皮层的32个或62个部位安置传感电极. 尽管多通道EEG信号可以提供丰富的情绪状态变化信息, 但并非所有通道的EEG信号都与情绪变化之间存在相关性. 冗余的通道信息会增加建模的时间和降低模型的鲁棒性, 因此EEG通道的选择在情绪识别中尤为重要. 此外, 原始的EEG信号为连续时间内的时序信号, 很难直接用于识别模型的建立, 因此常采用特征提取的方式表征不同情绪状态的EEG信号[6]. 目前常用的EEG特征主要包括时域特征[7]、频域特征[8]、时频域特征[9]和熵特征[10]. 一方面, 特征提取可以有效降低EEG数据的维度, 减少建模时间, 有助于实际的应用; 另一方面, 特征提取可以增强不同情绪EEG信号之间的差异性, 提高建模的精度和鲁棒性[11, 12]. 王成龙等人[13]提出将IMF能量矩作为脑电情感识别的特征, 对乐趣、高兴、悲伤和糟糕情绪的EEG信号的识别准确率达到了68.59%. Qing等人[14]提取了中性、积极和消极EEG信号的一阶、二级差分特征和微分熵特征, 并建立了决策树、K最邻近算法和随机森林分类模型, 识别精度最高达到了74.85%. Badicu等人[15]提取了EEG信号的功率谱密度 (power spectral density, PSD) 和微分熵 (differential entropy, DE)作为特征, 并建立了长短时记忆神经网络分类模型, 在SEED数据集上的识别精度达到了80%.
由于EEG信号具有低信噪比、非平稳性和被试间差异大等特点, 传统的浅层特征提取方法对多通道EEG信号的全局信息难以取得较为理想的表征性能. 因此, 本研究引入堆叠自动编码器(stacked auto-encoder, SAE)对多通道EEG信号进行深度特征提取, 增强不同情绪EEG信号间的差异性, 然后提出了一种基于广义正态分布优化的支持向量机(generalized normal distribution optimization based support vector machine, GNDO-SVM)分类模型, 并与传统的浅层特征提取方法(PSD和DE), 以及现有的机器学习模型, 包括基于遗传算法(genetic algorithm, GA)[16]、粒子群算法(particle swarm optimization, PSO)[17]和麻雀搜索算法(sparrow search algorithm, SSA)[18]优化的支持向量机模型进行对比, 以验证本文所提出的情感识别方法的有效性.
1 材料与方法本研究的实验步骤如图1所示, 主要包括EEG信号预处理、通道选择、特征提取(浅层与深度特征提取)和情绪识别模型的建立. 具体研究内容如下.
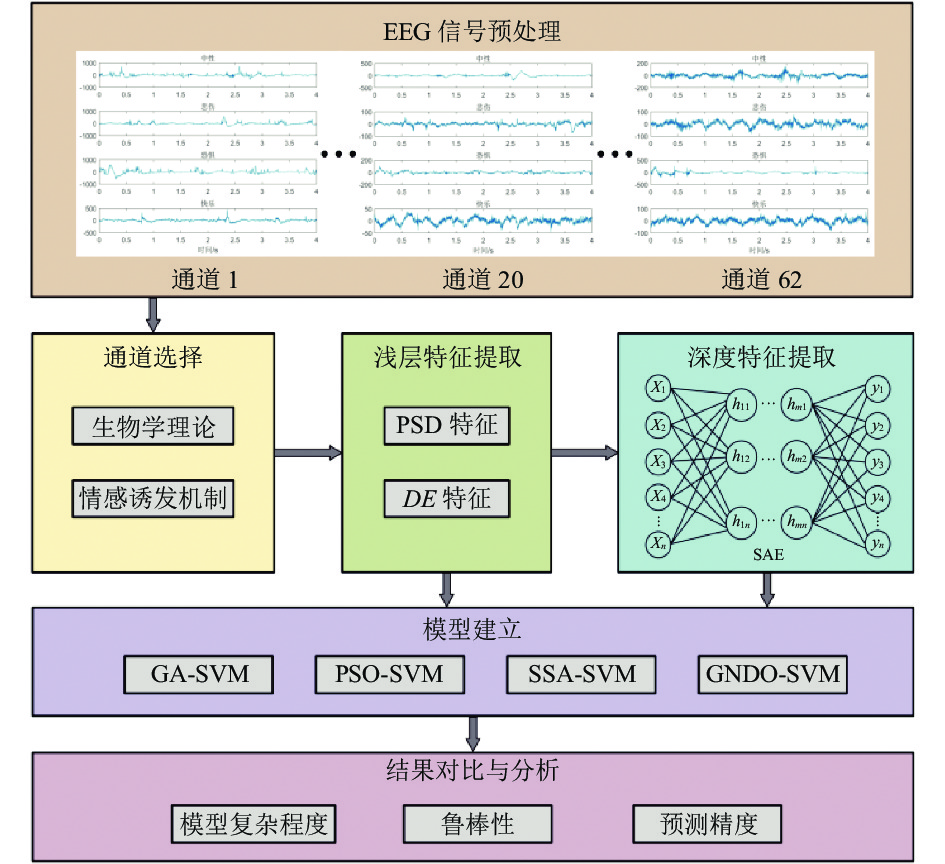
|
图 1 实验流程图 |
(1)对原始EEG信号进行预处理, 获取不同情绪的实验样本.
(2)根据生物学理论和情感诱发机制进行特征通道选择.
(3)提取浅层特征(PSD和DE特征)对不同情绪的EEG信号进行表征, 然后在此基础上, 利用SAE算法提取EEG信号的深度特征, 进一步消除数据中的冗余信息.
(4)基于EEG信号的浅层和深度特征, 分别构建GNDO-SVM情绪识别模型, 并与现有的方法进行对比.
1.1 EEG信号预处理本研究采用的EEG数据由上海交通大学BCMI实验室提供[19], 受试者为15名年龄在20–24岁的大学生(7名男性, 8名女性), 通过62通道ESI NeuroScan系统以1000 Hz采样率进行采集. 在每次实验之前, 参与者都被告知实验的具体流程和目的以及设备的无害性. 通过观看72个带有情感标签的电影片段(快乐、悲伤、恐惧和中性各18个)获得每个受试者的EEG信号. 在每个电影片段观看前都有5 s的开始提示, 观看后有45 s的PANAS量表自我评估[20]以及15 s的休息时间. 将每个电影片段裁剪为多个长度为4 s的非重叠片段, 最终样本集共包括37575个样本, 每个样本都为62个通道下4 s时长的EEG信号.
1.2 通道选择ESI NeuroScan系统可以同时获取人脑62个区域(通道)的EEG信号, 但并非所有通道的EEG信号均与情感的诱发相关. 为了减少建模时间和提高识别精度, 需要对EEG信号的通道进行筛选. 根据生物学脑区功能的划分, 大脑的额叶区主要负责人类的情绪和自我意识等高级功能, 颞叶区(靠近海马体)与人类的记忆、情绪、精神活动高度相关[21]; 由于本研究中的实验是通过观看视频诱发情感, 因此主司视觉感受、观察能力相关信息的枕叶区的激活程度也较高[22]. 因此, 选择了如图2所示的12个区域作为特征通道.
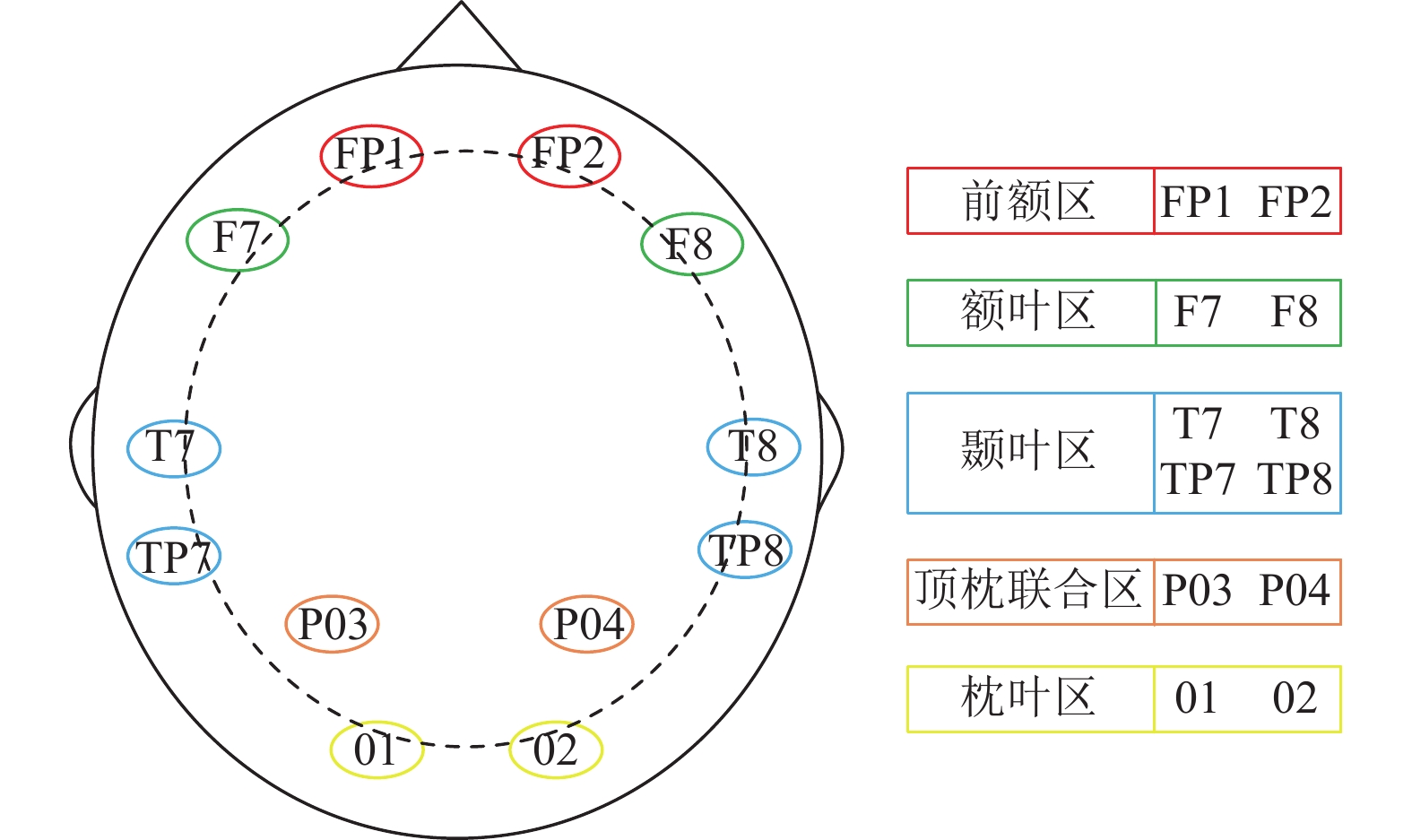
|
图 2 EEG信号特征通道的选择 |
1.3 特征提取 1.3.1 浅层特征提取
原始的EEG信号为连续时间内的时序信号, 数据量较大, 直接用于建模不仅会导致模型的复杂程度增加而且无法保证识别精度. 因此, 需要通过特征提取移除原始EEG数据中的冗余和干扰信息, 降低数据的维度, 从而简化模型和提高分类准确率, 其中PSD和DE是EEG信号分析中常用的和效果较优的两种特征. PSD特征能够量化信号在不同频段上的分布, 可由Welch法[23]计算获得. DE特征可以减小获取EEG高频信号时所产生的滤波误差, 进而提高模型学习效果[19]. DE的定义如下:
| $ DE = - \int_{ - \infty }^\infty {P(x)\ln (P(x))dx} $ | (1) |
其中, P(x)表示随机变量发生的概率. 在固定的频段内, EEG信号可以近似的认为服从高斯分布
| $ \begin{split} DE = & - \int_{ - \infty }^\infty {\frac{1}{{\sqrt {2{\text{π}}\sigma } }}} \exp \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}} \\ & \ln \left(\frac{1}{{\sqrt {2{\text{π}}\sigma } }}\exp \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}\right)dx = \frac{1}{2}\ln (2{\text{π}}{\rm{e}}{\sigma ^2}) \end{split} $ | (2) |
为了过滤EEG信号中的噪声和去除伪影, 将原始信号下采样至200 Hz, 采用1 Hz和75 Hz之间的带通滤波器对原始EEG信号进行预处理. 然后在以下的5个频段中分别提取PSD和DE特征: (1) δ: 1–4 Hz; (2) θ: 4–8 Hz; (3) α: 8–14 Hz; (4) β: 14–31 Hz; (5) γ: 31–50 Hz.
1.3.2 基于SAE的深度特征提取自动编码器(auto-encoders, AE)由3层网络组成, 包括输入层、隐含层和输出层, 结构如图3所示. AE包含了编码和解码两个主要的步骤, 公式分别如下:
| $ h = f({w_h} \times x + {b_h}) $ | (3) |
| $ y = f({w_y} \times h + {b_y}) $ | (4) |
其中, wh为输入层到隐含层的权重矩阵, wy为隐含层到输出层的权重矩阵, bh和by分别为隐含层和输出层的偏置, f (·)代表激活函数, h为特征输出. 训练AE网络的目的是寻找参数θ={wh, wy, bh, by}最小化重构误差, 实现对原始数据的压缩, 达到特征提取的目的.
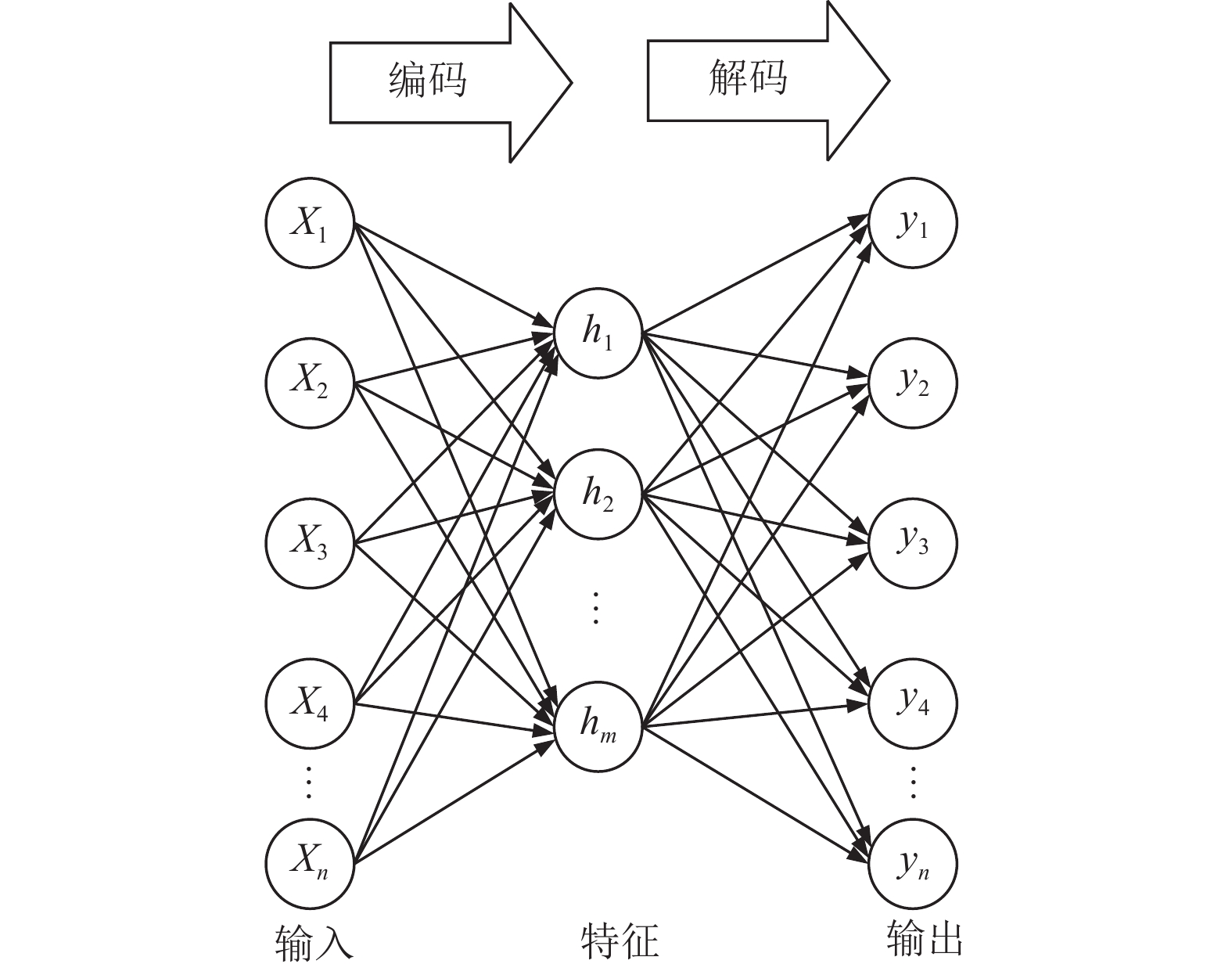
|
图 3 AE网络结构示意图 |
当输入数据的维度较高时, 单个AE的特征提取能力较弱, 为了解决这一问题, SAE被提出. SAE由多个AE逐层堆叠而成, 其结构如图4所示. 对于每个AE, 训练后会得到一个隐含层, 然后将该隐含层作为下一层AE的输入, 通过无监督的方式逐层训练. 最后, 将所有的AE层视为一个整体, 通过有监督的方式对网络的权重和偏差进行微调. 与浅层网络相比, SAE具有更高的非线性运算水平和更强的函数逼近能力, 因此具有更优的特征提取能力. 在传统的浅层特征的基础上, 本研究应用SAE进一步提取EEG数据的有效信息, 降低模型维度, 以期提高预测精度和鲁棒性.
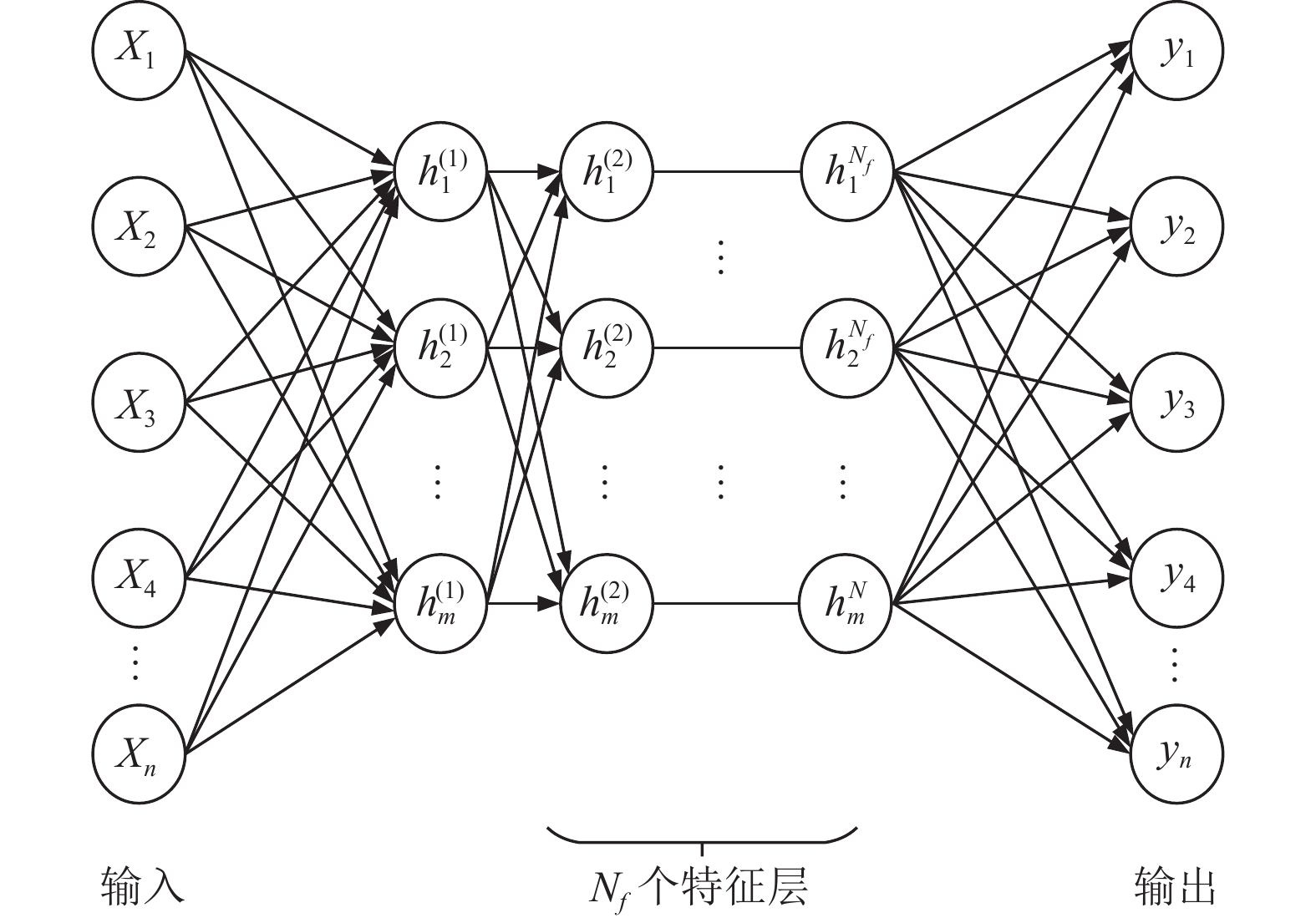
|
图 4 SAE网络结构示意图 |
1.4 情绪识别模型 1.4.1 支持向量机
SVM是一种基于统计学理论中结构风险最小化原则的机器学习算法, 可以用于解决分类和回归问题. SVM的原理是将低维空间中线性不可分的样本通过非线性变换映射到高维空间, 通过构建超平面使不同类别样本之间的边界距离最大化, 从而转换为线性可分问题. 由于其出色的性能, SVM已经被应用到许多实际工程问题中, 如故障诊断[24]、网络入侵检测[25]、语音识别[26]等.
假设给定一个数量为n的样本集合S, S={(xi, yi), i=1, 2, …, n}, y∈{–1, +1}为样本的类别, 其分类超平面的表达式及目标函数分别为:
| $ f(x) = {w^{\rm{T}}}{x_i} + b = 0 $ | (5) |
| $ \left\{\begin{split} &\min \; \dfrac{1}{2}\|w\|^2+c \displaystyle\sum_{i=1}^n \xi_i \\ &\text { s.t. } \; y_i\left[\left(w \cdot x_i\right)+b\right]+\xi_i \geqslant 1, \; \xi_i \geqslant 0, i=1, \cdots, n \end{split}\right. $ | (6) |
其中, w为超平面的法向量; b为截距项. ξi为非负松弛变量, 用来提高模型的泛化能力; c为惩罚参数, 用来权衡分类损失和最大间隔之间的关系.
在SVM中, 样本数据由低维映射到高维空间通过核函数实现, 其中径向基核函数(radial basis function, RBF)的局部性能较好, 不仅能够逼近任何非线性函数, 而且参数较少, 可以有效降低模型的复杂度, 其表达式为:
| $ K({x_i} \cdot {x_j}) = \exp ( - g||{x_i} - {x_j}|{|^2}) $ | (7) |
其中, g为核函数参数, 其大小对支持向量的分布和数量具有影响.
相关的研究表明SVM的分类性能主要受惩罚参数c与核函数参数g的影响, 然而目前尚未有统一的参数选择方法[27]. 因此, 本研究首次引入广义正态分布优化(generalized normal distribution optimization, GNDO)算法来解决SVM的参数优化问题, 以期提高SVM的分类性能.
1.4.2 广义正态分布优化算法GNDO是一种基于正态分布理论的新型元启发式算法, 由Zhang等人[28]于2020年提出. GNDO的结构简单, 优化精度高, 鲁棒性强, 与其他元启发式算法相比其优势在于无控制参数, 因此在解决优化任务时具有一定的优越性.
假设随机变量x服从位置参数μ、尺度参数δ的概率分布, 其概率密度函数可表示为:
| $ f(x) = \frac{1}{{\sqrt {2{\text{π }}\delta } }}{\text{exp}}\left( - \frac{{{{(x{{ - }}\mu )}^2}}}{{2{\delta ^2}}}\right) $ | (8) |
则x可以被称为正态随机变量, 其分布被称为正态分布, 即x~N(μ, δ). 位置参数μ和尺度参数δ分别表示随机变量的均值和标准差.
所有基于群体的优化算法均始于种群初始化, 然后种群中的个体按照一定的规则进行探索和开发向着全局最优解的方向收敛, 最后聚集在全局最优解的附近. GNDO将这个过程视为多个正态分布, 其中每个个体都被视为服从于正态分布的随机变量. GNDO的优化包含了开发和探索两个部分, 分别对应了局部寻优和全局寻优, 数学模型如下.
(1)局部寻优
局部寻优的位置更新方程如下:
| $ v_i^t = {\mu _i} + {\delta _i} \times {\eta _i}, \; i = 1, 2, 3, \cdots, N $ | (9) |
其中,
| $ {\mu }_{i}=\frac{1}{3}({x}_{i}^{t}+{x}_{{\rm{best}}}^{t}+M) $ | (10) |
| $ {\delta }_{i}=\sqrt{\frac{1}{3}\left[({x}_{i}^{t}-\mu {)}^{2}+({x}_{{\rm{best}}}^{t}-\mu {)}^{2}+(M-\mu {)}^{2}\right]} $ | (11) |
| $ \eta = \left\{ {\begin{array}{*{20}{l}} {\sqrt { - \log (\lambda_1)} \times \cos (2{\text{π}}\lambda_2),\quad\;\; \;{\text{if }}a \leqslant b} \\ {\sqrt { - \log (\lambda_1)} \times \cos (2{\text{π}}\lambda_2 + {\text{π}} ), \; {\text{otherwise}}} \end{array}} \right. $ | (12) |
其中, a、b、λ1和λ2为0–1之间的随机数,
(2)全局寻优
全局寻优的位置更新方程如下:
| $ v_i^t = x_i^t + \beta \times (\left| {{\lambda _3}} \right| \times {v_1}) + (1 - \beta ) \times (\left| {{\lambda _4}} \right| \times {v_2}) $ | (13) |
其中, λ3和λ4是受正态分布约束的随机数, β是调整参数, 为0–1之间的随机数, v1和v2为跟踪向量, 定义如下:
| $ v_1=\left\{\begin{array}{l} x_i^t-x_{p 1}^t, \;\;\; \text { if } f\left(x_{{i}}^t\right)< f\left(x_{p 1}^t\right) \\ x_{p 1}^t-x_i^t,\;\;\; \text { otherwise } \end{array}\right. $ | (14) |
| $ v_2=\left\{\begin{array}{l} x_{p 2}^t-x_{p 3}^t, \;\;\; \text { if } f\left(x_{p 2}^t\right)<f\left(x_{p 3}^t\right) \\ x_{p 3}^t-x_{p 2}^t, \;\;\; \text { otherwise } \end{array}\right. $ | (15) |
其中, p1、p2和p3为[1, N]范围内随机生成的3个整数, 且p1 ≠ p2 ≠ p3. 此外, GDNO在迭代过程中还设计了如下的筛选机制:
| $ {x}_{{i}}^{t+1}=\left\{\begin{array}{l}{v}_{{i}}^{t}, \;\;\; \text{if }f({v}_{{i}}^{t})<f({x}_{{i}}^{t})\\ {x}_{{i}}^{t}, \;\;\; \text{otherwise}\end{array} \right.$ | (16) |
GNDO算法的伪代码如算法1所示.
算法1. GNDO算法伪代码
输入: 目标函数
1. 初始化参数
2. for i=1:n
3. 随机产生n个个体{xi | i=1, 2, …, n};
4. 计算每个个体的适应度值;
5. end
6. 记最优个体为xbest
7. while t<最大迭代次数(Tmax)
8. for i=1:n
9. 生成一个随机数rnd∈[0, 1];
10. if rnd>0.5
11. /*局部寻优*/
12. 计算当前种群的平均位置M;
13. 利用式(10)–式(12)计算广义平均位置μ, 广义标准方差δ以及惩罚因子η;
14. 利用式(9)–式(12)和式(16)执行局部寻优;
15. 更新xbest ;
16. else
17. /*全局寻优*/
18. 利用用式(13)–式(16)执行全局寻优;
19. 更新xbest ;
20. end if
21. end for
22. t=t+1;
23. end while
输出: xbest
1.4.3 GNDO-SVM预测模型构建在SVM中, 惩罚参数c影响模型的分类精度, 核函数参数g影响模型的复杂程度和泛化性能. 在以往的研究中, 一些学者已经引入了一些元启发式算法实现对SVM模型参数的自适应优化, 如GA、PSO和 SSA等, 但以往的算法均需要对控制参数进行反复调节才能达到较好的优化效果, 而GNDO无控制参数且优化性能强, 在实际应用中容易实现, 因此具有较强的优势. GNDO优化SVM模型参数的步骤如下.
(1)初始化种群, 包括种群数量、最大迭代次数以及参数c和g的优化范围, 并在搜索空间内随机生成初始种群.
(2)以训练集样本的交叉验证分类准确率作为适应度函数计算每个个体的适应度值, 其中最优的个体记为xbest.
(3)利用GNDO的更新机制更新种群中每个个体的位置.
(4)计算新的种群中每个个体的适应度值, 并更新xbest.
(5)重复步骤(2)–步骤(4)直到达到设定的最大迭代次数.
(6)输出xbest作为SVM模型的最优参数c和g, 并利用训练集样本建立SVM模型, 然后对测试集样本进行预测.
GNDO优化SVM的流程如图5所示.
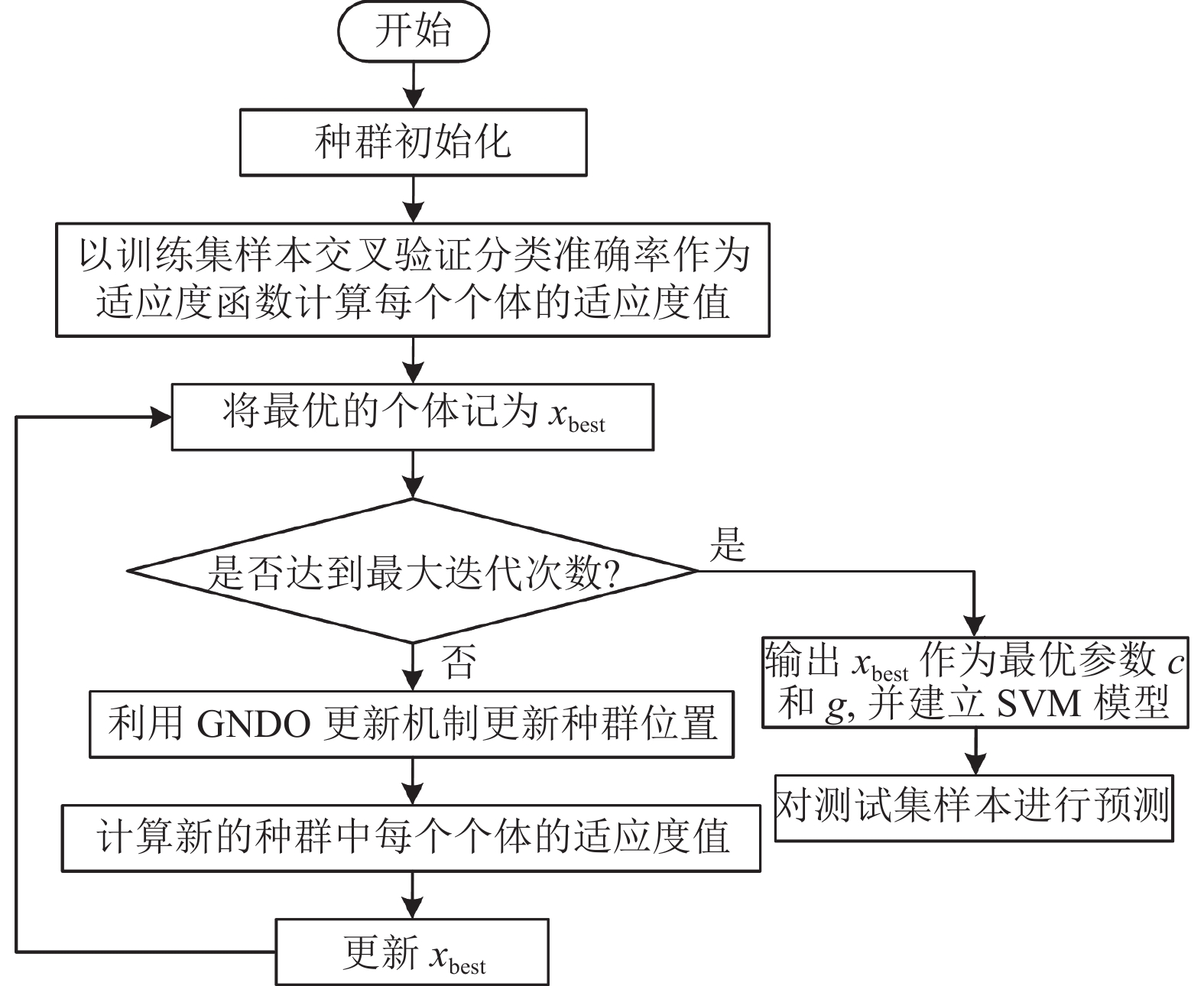
|
图 5 GNDO优化SVM的流程图 |
2 结果与讨论 2.1 基于浅层特征的情绪识别结果
为了消除特征之间的纲量差异, 首先将样本数据进行归一化处理, 然后按3:1比例将所有样本随机划分为训练集和测试集, 则训练集包含28182个样本, 测试集样本包含9393个样本. 利用本研究提出的GNDO-SVM算法建立基于PSD与DE特征的情绪识别模型, 为了对比, GA、PSO和SSA算法也被用于优化SVM的参数. GA-SVM、PSO-SVM、SSA-SVM和GNDO-SVM模型的参数设置如表1所示, 并均采用五折交叉验证分类准确率作为适应度函数.
由于所有元启发式算法均具有一定的随机性, 为了避免结果的偶然性, 所有模型均独立运行30次, 结果如表2所示. 从表2中可以看出, GNDO-SVM模型的方差最小, 表明其具有更强的鲁棒性, 并且平均分类准确率也高于其他3种模型. 采用Wilcoxon检验对GNDO-SVM与其他3种模型的结果进行统计评估, 其中p-value小于0.05表示具有显著性差异. 通过对比可以看出, GNDO-SVM模型的分类性能显著优于GA-SVM和PSO-SVM模型, 略优于SSA-SVM模型, 但在最优结果方面, GNDO-SVM模型的分类精度最高, 测试集分类准确率达到了86.99%. 图6为4个模型的参数寻优过程, 其中红线代表每次迭代中最优个体的适应度值, 蓝线代表种群的平均适应度值. 在收敛速度方面, PSO-SVM的速度最快, 其次是GNDO-SVM, 但由于PSO-SVM可能过早地陷入了局部最优, 导致最终的分类准确率低于GNDO-SVM和SSA-SVM模型. 在迭代的中期, GA-SVM、GNDO-SVM和SSA-SVM模型的最优适应度值仍不断更新, 表明这3种模型具有更强的跳出局部最优的能力. 综合分类精度、鲁棒性和收敛速度3个方面, 易知GNDO-SVM模型具有更强的分类性能. 并且, 由于GNDO无控制参数, 与其他方法相比可以节省参数调节的时间.
| 表 1 模型的参数设置 |
| 表 2 不同模型的建模结果 |
2.2 基于SAE深度特征的情绪识别结果
尽管利用PSD和DE特征结合本研究提出的GNDO-SVM模型对脑电情绪识别已经取得了较好的分类效果, 但仍有一定的提升空间. 首先, 人脑不同部位产生的EEG信号之间存在一定的相关性, 即所选择的12个通道的EEG信号中可能存在一定的冗余信息; 此外, 尚未有研究表明所有频段下的PSD和DE特征均与情绪的诱发之间存在相关性, 因此PSD和DE特征数据中仍可能还存在一定的干扰信息. 为了消除潜在的冗余和干扰信息, 本研究利用SAE对PSD和DE特征数据进一步地进行深度特征提取.
将PSD与DE特征作为SAE网络的输入层, SEA网络的激活函数设置为Sigmoid函数, 学习率设置为0.1, 网络结构设置为[120, 90, 60, h], 其中h代表最后一层隐含层网络的神经元数量, 由分类准确率来决定. 当神经元数量由1逐渐增加到59时, 利用SAE深度特征分别建立GA-SVM、PSO-SVM、SSA-SVM和GNDO-SVM分类模型, 模型的训练集和测试集分类精度变化如图7所示. 当神经元的数量较少时, 所提取的深度特征信息损失较大, 无法对不同类型的EEG信号进行有效的识别; 随着神经元数量的增加, 越来越多的有用信息被保留下来, 使模型的分类精度迅速提高; 当神经元数量大于40时, 各个模型的预测精度均开始降低, 一方面可能是由于所提取的深度特征中包含了一部分相关性较低的信息, 另一方面原因可能是特征数量的增加使建模的难度提高. GA-SVM、PSO-SVM、SSA-SVM和GNDO-SVM的建模结果如表3所示. 其中, 当神经元数量为29, 即网络结构为[120, 90, 60, 29]时, GNDO-SVM模型的预测结果最优, 测试集分类准确率达到了90.94% (8542/9393), 表明此时SAE已经充分提取了EEG信号的关键深度特征. 模型的预测结果以混淆矩阵展示, 如图8所示.
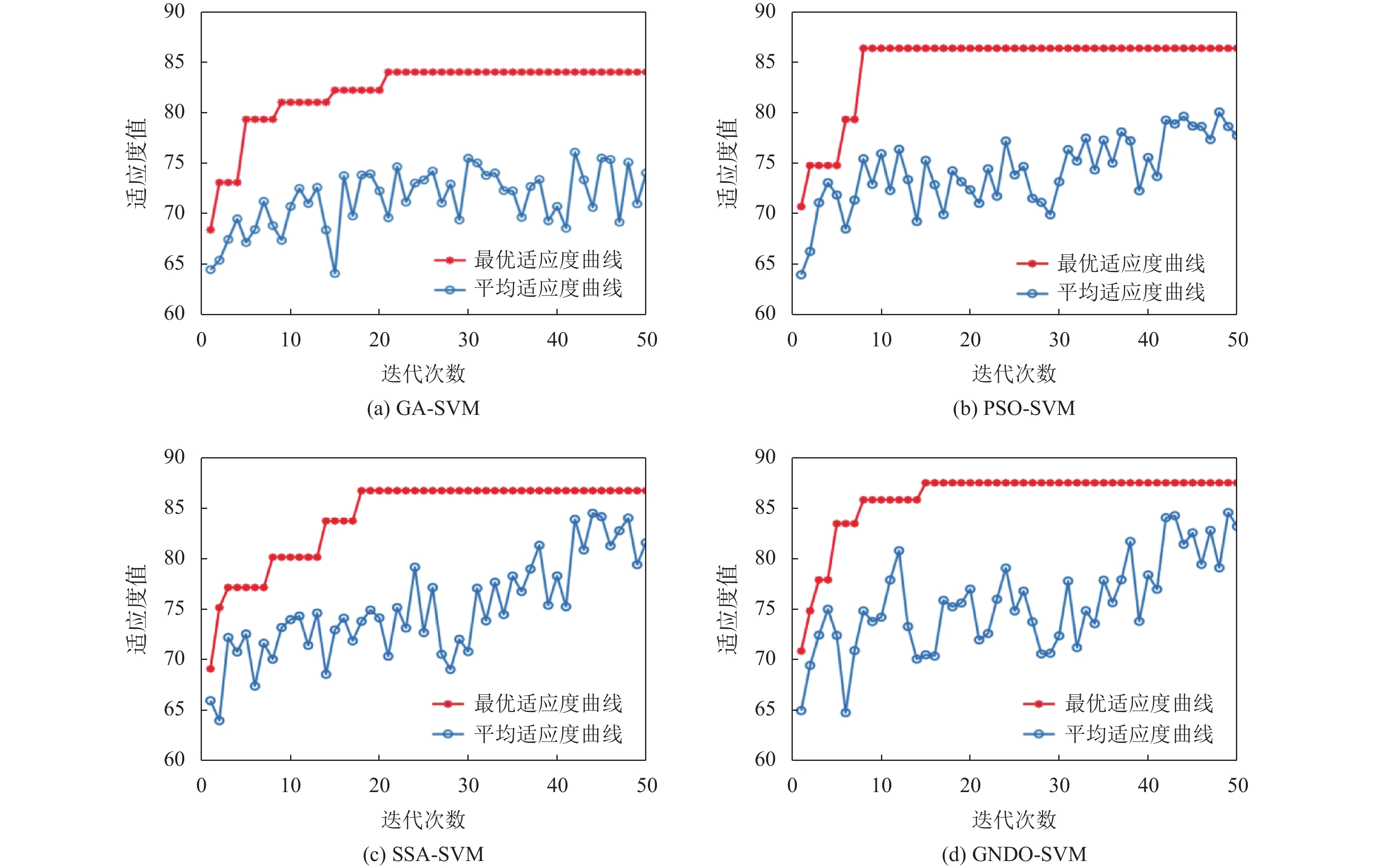
|
图 6 GA-SVM、PSO-SVM、SSA-SVM和GNDO-SVM的优化过程 |
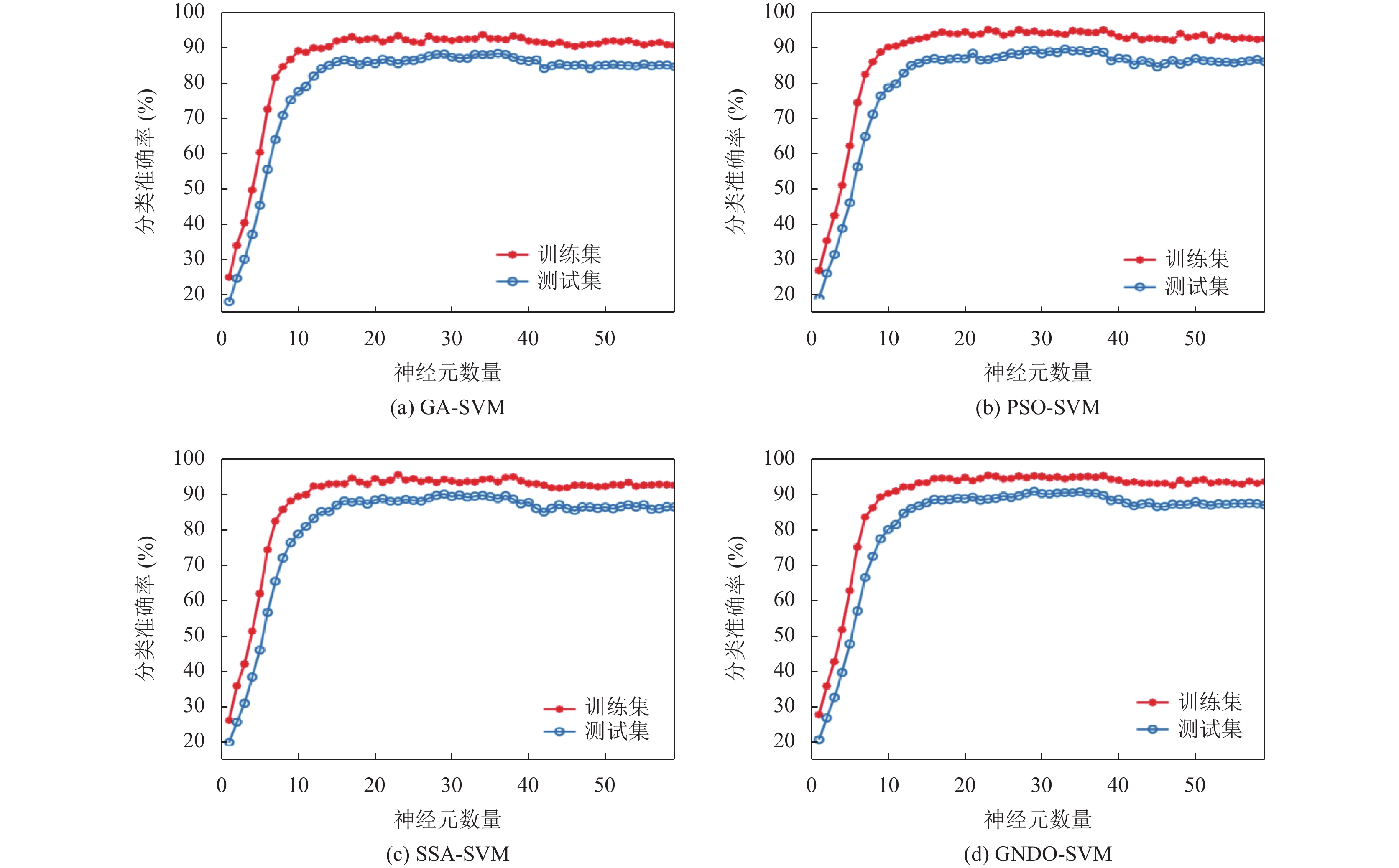
|
图 7 基于不同神经元数量的模型分类结果 |
| 表 3 基于SAE深度特征的建模结果 |
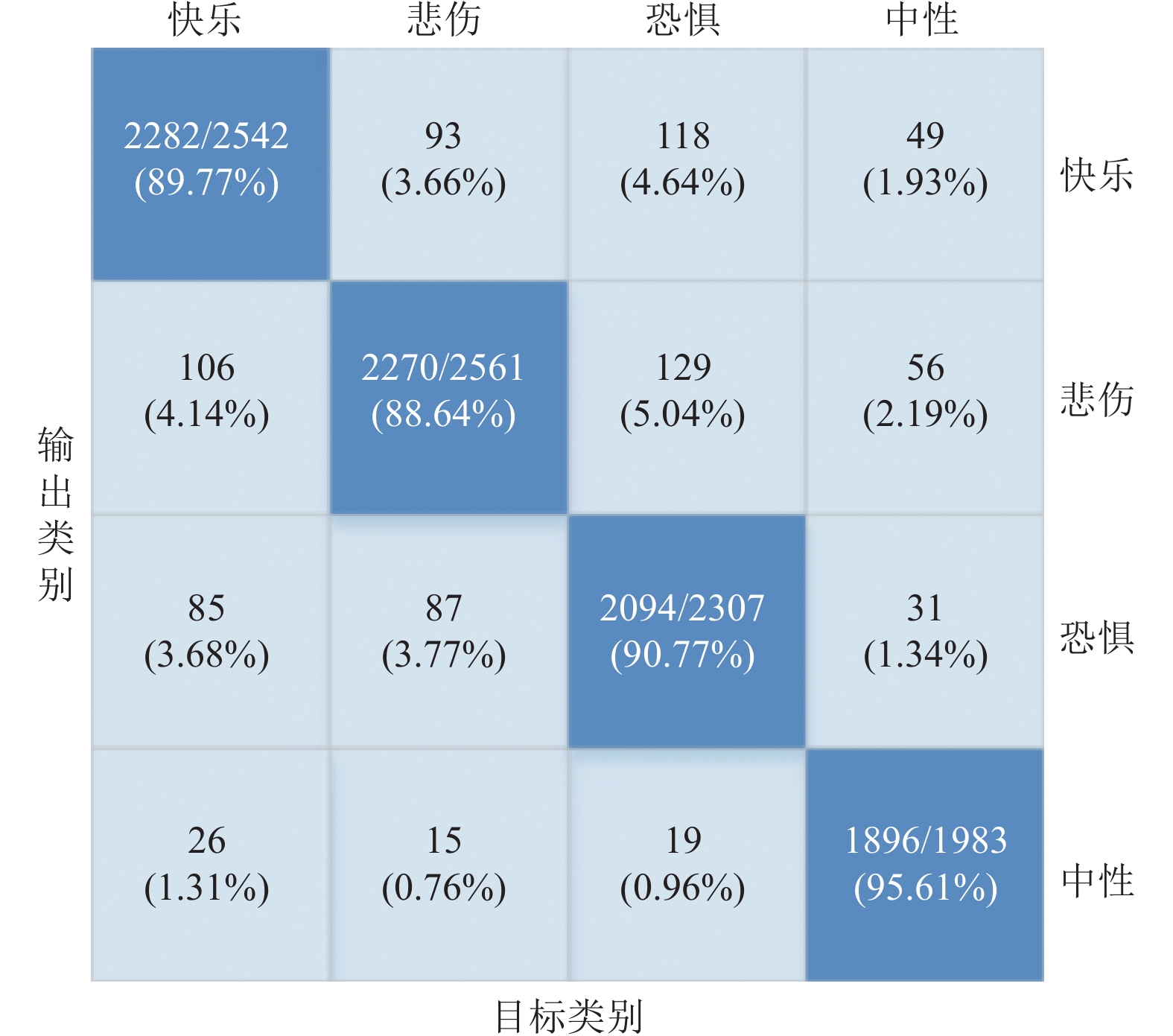
|
图 8 SAE-GNDO-SVM模型的预测集混淆矩阵 |
在建模精度方面, 基于SAE深度特征的模型分类精度明显高于基于PSD和DE特征的模型分类精度; 在模型复杂度方面, SAE有效地简化了模型, 特征的数量显著降低; 并且, 基于SAE深度特征的分类模型具有更高的交叉验证分类准确率, 表明模型的鲁棒性也得到了提升. 综合以上3点可知, SAE具有更强的特征提取性能. 此外, 基于SAE深度特征的GNDO-SVM模型预测结果优于GA-SVM、PSO-SVM和SSA-SVM模型, 再次验证了GNDO算法的有效性. 表4列出了近5年基于EEG信号情绪识别研究的文献, 其中所用数据集与本文相同, 通过对比可以看出, 本文提出的方法具有更高的识别效果. 因此, 利用SAE深度特征结合GNDO-SVM模型可以有效地识别不同情绪的EEG信号.
| 表 4 本文方法与现有方法的对比 |
3 结束语
为了提高EEG信号情绪识别的准确率, 本研究提出了一种基于深度学习和GNDO-SVM的情绪识别模型. 在传统的浅层PSD和DE特征的基础上, 利用SAE从多通道EEG信号中进一步提取深度特征, 降低了特征的维度, 并提高了识别精度. 实验结果表明, 与现有的方法相比, 本研究提出的GNDO-SVM模型具有更高的分类精度和鲁棒性, 对快乐、悲伤、恐惧和中性情绪的EEG信号的识别准确率达到了90.94%. 因此, 利用SAE深度特征提取结合GNDO-SVM分类模型可以有效地实现基于EEG信号的情绪识别.
结合本文研究成果, 本文认为未来可以在以下方面展开进一步研究.
(1)本研究采用单模态的EEG信号实现了情绪识别, 未来可以结合其他生理信号, 如眼电信号, 实现多模态的情绪识别, 以期提高预测效果.
(2)本研究建立的情绪识别模型仅能对常见的快乐、悲伤、恐惧和中性4种情绪进行识别, 后续可加入更多情绪类型的样本, 以提高模型的泛化性能.
| [1] |
Zhang JH, Chen M, Zhao SK, et al. ReliefF-based EEG sensor selection methods for emotion recognition. Sensors, 2016, 16(10): 1558. |
| [2] |
陈景霞, 胡修文, 唐喆喆, 等. 基于卷积联合适应网络的脑电信号情感识别. 数据采集与处理, 2022, 37(4): 814-824. |
| [3] |
晁浩, 刘永利, 连卫芳. EEG情感识别中基于集成深度学习模型的多分析域特征融合. 控制与决策, 2020, 35(7): 1674-1680. DOI:10.13195/j.kzyjc.2018.1667 |
| [4] |
张冠华, 余旻婧, 陈果, 等. 面向情绪识别的脑电特征研究综述. 中国科学: 信息科学, 2019, 49(9): 1097-1118. |
| [5] |
刘宏, 陈玲钰, 韦小平, 等. 基于KIV模型的脑电识别方法. 计算机系统应用, 2022, 31(10): 356-367. DOI:10.15888/j.cnki.csa.008744 |
| [6] |
王晨, 胡景钊, 刘科, 等. 基于脑电通道增强的情绪识别方法. 西北大学学报(自然科学版), 2022, 52(4): 560-570. |
| [7] |
Zhang Q, Lee M. A hierarchical positive and negative emotion understanding system based on integrated analysis of visual and brain signals. Neurocomputing, 2010, 73(16–18): 3264–3272.
|
| [8] |
蔡靖, 袁守国, 李锐, 等. 基于加权KNN算法的脑电信号情绪识别. 电子技术应用, 2022, 48(10): 25-30, 35. |
| [9] |
李明爱, 张圆圆. 基于连续小波变换和符号传递熵的脑功能网络构建方法. 电子学报, 2022, 50(7): 1600-1608. |
| [10] |
聂聃, 王晓韡, 段若男, 等. 基于脑电的情绪识别研究综述. 中国生物医学工程学报, 2012, 31(4): 595-606. |
| [11] |
Wang J, Wang M. Review of the emotional feature extraction and classification using EEG signals. Cognitive Robotics, 2021, 1: 29-40. DOI:10.1016/j.cogr.2021.04.001 |
| [12] |
Nawaz R, Cheah KH, Nisar H, et al. Comparison of different feature extraction methods for EEG-based emotion recognition. Biocybernetics and Biomedical Engineering, 2020, 40(3): 910-926. DOI:10.1016/j.bbe.2020.04.005 |
| [13] |
王成龙, 韦巍, 李天永. 基于IMF能量矩的脑电情绪特征提取研究. 现代电子技术, 2018, 41(20): 10-13. DOI:10.16652/j.issn.1004-373x.2018.20.003 |
| [14] |
Qing CM, Qiao R, Xu XM, et al. Interpretable emotion recognition using EEG signals. IEEE Access, 2019, 7: 94160-94170. DOI:10.1109/ACCESS.2019.2928691 |
| [15] |
Badicu B, Udrea A. Cross-subjects emotions classification from EEG signals using a hierarchical LSTM based classifier. Proceedings of the 2019 E-health and Bioengineering Conference. Iasi: IEEE, 2019. 1–4.
|
| [16] |
路永华. LIBS结合GA-BP神经网络与GA-SVM对塑料分类研究. 激光与红外, 2022, 52(2): 273-279. |
| [17] |
Huang WC, Liu HY, Zhang Y, et al. Railway dangerous goods transportation system risk identification: Comparisons among SVM, PSO-SVM, GA-SVM and GS-SVM. Applied Soft Computing, 2021, 109: 107541. DOI:10.1016/j.asoc.2021.107541 |
| [18] |
Wen FH, Xiao JH, He ZF, et al. Stock price prediction based on SSA and SVM. Procedia Computer Science, 2014, 31: 625-631. DOI:10.1016/j.procs.2014.05.309 |
| [19] |
Zheng WL, Liu W, Lu YF, et al. EmotionMeter: A multimodal framework for recognizing human emotions. IEEE Transactions on Cybernetics, 2019, 49(3): 1110-1122. DOI:10.1109/TCYB.2018.2797176 |
| [20] |
Watson D, Clark LA, Tellegen A. Development and validation of brief measures of positive and negative affect: The PANAS scales. Journal of Personality and Social Psychology, 1988, 54(6): 1063-1070. DOI:10.1037/0022-3514.54.6.1063 |
| [21] |
Wang Q, Wang M, Yang Y, et al. Multi-modal emotion recognition using EEG and speech signals. Computers in Biology and Medicine, 2022, 149: 105907. DOI:10.1016/j.compbiomed.2022.105907 |
| [22] |
何梦渊, 胡松涛, 马浩南, 等. 视觉诱发电位在人体视觉舒适性研究中的应用. 科学技术与工程, 2021, 21(26): 11102-11109. DOI:10.3969/j.issn.1671-1815.2021.26.013 |
| [23] |
段子敬, 赵冰蕾, 李春波, 等. 基于特征融合方法的轻微认知衰退静息态脑电数据自动检测技术研究. 计算机应用研究, 2022, 39(4): 1137-1142, 1167. DOI:10.19734/j.issn.1001-3695.2021.09.0417 |
| [24] |
姚远, 佟佳蓉, 高军, 等. 基于分层分块DLPPCA-SVM的复杂工业过程监测与故障诊断方法. 控制与决策, 2022, 37(5): 1402-1408. |
| [25] |
Mohammadi M, Rashid TA, Karim SHT, et al. A comprehensive survey and taxonomy of the SVM-based intrusion detection systems. Journal of Network and Computer Applications, 2021, 178: 102983. DOI:10.1016/j.jnca.2021.102983 |
| [26] |
Batista GC, Oliveira DL, Saotome O, et al. A low-power asynchronous hardware implementation of a novel SVM classifier, with an application in a speech recognition system. Microelectronics Journal, 2020, 105: 104907. DOI:10.1016/j.mejo.2020.104907 |
| [27] |
Yao KS, Sun J, Zhou X, et al. Nondestructive detection for egg freshness grade based on hyperspectral imaging technology. Journal of Food Process Engineering, 2020, 43(7): e13422. |
| [28] |
Zhang YY, Jin ZG, Mirjalili S. Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models. Energy Conversion and Management, 2020, 224: 113301. DOI:10.1016/j.enconman.2020.113301 |
| [29] |
Zhong PX, Wang D, Miao CY. EEG-based emotion recognition using regularized graph neural networks. IEEE Transactions on Affective Computing, 2022, 13(3): 1290-1301. DOI:10.1109/TAFFC.2020.2994159 |
| [30] |
梁明晶, 王璐, 温昕, 等. 多特征融合的脑电情绪分类. 计算机工程与应用, 2023, 59(5): 155-159. DOI:10.3778/j.issn.1002-8331.2110-0068 |
| [31] |
黄永庆, 周强. 基于CNN-GRU融合网络的情绪脑电信号辨别研究. 传感技术学报, 2021, 34(8): 1109-1116. |
 2023, Vol. 32
2023, Vol. 32


