2. 中国科学技术大学 数学科学学院, 合肥 230026;
3. 中国科学院吴文俊数学重点实验室(中国科学技术大学), 合肥 230026
2. School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China;
3. CAS Key Laboratory of Wu Wen-Tsun Mathematics (University of Science and Technology of China), Hefei 230026, China
在机器学习和数据挖掘领域, 聚类是一种被广泛使用的技术, 其根据数据之间的内在结构和关系将数据点分配至多个子集或类簇, 使得同一子集或类簇中的数据点的相似性高. 聚类技术有助于研究人员更好地理解数据, 并从中提取出有用的信息, 可用来解决图像分割[1]、社交网络[2]、生物信息学[3, 4]等领域的各种问题.
当前常见的聚类算法大致分为5类: 基于层次的方法、基于划分的方法, 这是由Fraley等人[5]给出的分类, 后续Han等人[6]补充增加了基于模型、基于网格以及基于密度的方法. 这些聚类算法被广泛应用于人工智能领域, 并受到许多研究人员的深入研究和探索(可参见相关综述[7, 8]).
最近, Averbuch-Elor等人提出了边界剥离聚类算法(BP), 一种基于密度的聚类方法[9]. 在以往的研究中, 许多基于密度的聚类算法假设可以通过密度推理确定聚类的核心. 然而在实际应用中, 直接定义聚类核心的结构密度非常困难. 与传统的基于密度的方法相比, BP算法通过迭代剥离边界点来揭示聚类的潜在核心, 在许多数据集上表现良好, 并且可在图像分类以及异常值检测等领域进行应用. 但是对于具有复杂空间分布的数据集, BP算法仍需要改进, 首先BP算法采用局部密度函数度量两个数据点之间的相似性, 仅考虑了欧氏距离以及数据点与其第k个最近邻居之间的距离, 使得边界点的判定容易受到异常值的干扰, 并且无法适应相关点的邻域. 其次边界点被剥离后只与固定距离内最近的非边界点相关联, 否则会被标记为异常值, 这种关联策略会导致BP算法在空间分布复杂的数据集上容易进行过度划分, 并且对于一些分布不均匀的数据集容易误判异常值.
针对以上问题, 本文提出了一种基于共享近邻和优化关联策略的边界剥离聚类算法(SOBP), 以缓解现有算法中的一些问题. 该算法主要包含两个方面的贡献: 一是局部密度的改进: 采用一个新的局部密度函数, 该函数基于共享近邻以及数据点与其k个最近邻居之间的平均距离, 不仅考虑了相关点的邻域, 并且可以减少异常值的干扰; 二是关联策略的优化: SOBP 算法改进了连接阈值, 使得每次迭代中边界点不再仅与一个非边界点相关, 而是考虑其非边界点 k 近邻在一个更合理的距离区间内与边界点建立联系, 并通过共享近邻相似性度量来构建边界点之间的联系, 从而有效减少异常值的误判.
1 相关工作数据聚类是一个具有永恒魅力的研究领域. 自聚类算法问世以来, 许多学者提出了各种聚类算法并将其用于解决一些实际问题, 其中基于密度的方法一直是聚类研究的重点.
DBSCAN[10]是最常被引用的基于密度的聚类算法之一, 其原则是: 每个类簇的密度都高于周围的密度, 噪声的密度低于任何类簇的密度, 因此它也可以用于离群点检测. DBSCAN有两个重要参数: eps和minpts, 在聚类过程中, 这两个参数选择不当将会导致聚类质量的下降. HDBSCAN[11]对 DBSCAN进行了扩展, 它使用k最近邻定义密度水平, 将算法参数转换为固定阈值(邻居数k). 很多研究者研究了DBSCAN的参数自适应. BSA-DBSCAN[12]使用鸟群方法的全局搜索能力选择最佳eps参数值. Chen等人通过AP算法生成一个密度列表, 以此列表作为DBSCAN算法的输入, 提出了一种无参数聚类算法APSCAN[13]. 万佳等人[14]利用去噪衰减后的数据生成了eps和minpts参数列表, 并根据去噪的水平获得初始参数值, 提出一种多密度自适应参数确定算法.
2014年, Rodriguez等人[15]提出了DPC算法, 一种非常流行的密度聚类算法. 它使用数据集的密度峰值来找到类簇中心, 可以实现对任意形状数据的高效聚类. 近年来, 许多学者都在努力改进该算法. 例如, SNN-DPC算法[16]引入了共享最近邻来对局部密度进行估计; RDPC-DSS算法[17]使用了新的密度聚类指数(DCI)进行簇中心数的确定; 张清华等人[18]通过构造k近邻密度, 提出了新的局部密度, 并采用了一种加权的k近邻分配策略, 提出了基于代表点与k近邻的密度峰值聚类算法.
BP算法是一种创新的基于密度的算法, 通过迭代确定边界点, 并逐步获得类簇的核心. 最近, Du等人[19]设计了一种新的连接准则, 在剥离的边界点和它们相邻的已剥离边界点之间建立联系, 并使用具有更长尾部的柯西核来衡量数据点之间的相似度, 从而减少算法的运行时间, 提出了鲁棒的基于柯西核的边界剥离聚类算法. 此外, Feng等人[20]提出了基于自然近邻的边界剥离聚类算法(SANBP), 使用自然邻居获得邻域信息作为边界剥离聚类算法的输入, 实现了BP算法的无参化.
2 算法原理及分析 2.1 BP算法基本原理给定数据集
| $ N{N_k}\left( {{x_i}} \right) = \mathop \bigcup \nolimits_{j = 1}^k \left\{ {n{n_j}\left( {{x_i}} \right)} \right\} $ | (1) |
| $ RN{N_k}\left( {{x_i}} \right) = \{ {x_j}|{x_i} \in N{N_k}( {{x_j}} )\} $ | (2) |
对于给定的两个数据点
| $ f\left({x}_{i}, {x}_{j}\right)={\rm{exp}}\left(-\frac{{d}^{2}\left({x}_{i}, {x}_{j}\right)}{{\sigma }_{j}^{2}}\right) $ | (3) |
其中,
在考虑了一个数据点对其邻近点的局部密度的影响后, BP算法定义了一个密度影响值
| $ b_i^{\left( t \right)} = \mathop \sum \limits_{{x_j} \in RNN_k^{\left( t \right)}\left( {{x_i}} \right)} f\left( {{x_i}, {x_j}} \right) $ | (4) |
BP算法的主要思想是迭代剥离边界点, 因此在第t次迭代时, 通过对
| $ {l_i} = \min\left\{ {\frac{C}{k}\mathop \sum \limits_{{x_j} \in N{N_k}_{CB}^{\left( t \right)}\left( {{x_i}} \right)} d\left( {{x_i}, {x_j}} \right), \lambda } \right\} $ | (5) |
其中,
BP算法中经验性地将
最后, 在迭代剥离结束后, 剩余的未剥离点是核心点. 通过迭代过程, 每个剥离点(除了异常值)都与核心点有传递性的关联, BP算法采用简化的DBSCAN版本将核心点分配到类簇中, 并根据剥落的边界点与核心点之间的关联将已剥离数据点分配到类簇中.
2.2 BP算法分析首先, 在BP算法中, 边界点的识别是非常重要的. 只有合理地识别边界点才能够进一步得到有效的聚类核心区域. 边界点是由局部密度函数所定义的密度影响值确定的, 两个数据点
其次, 边界点与非边界点之间的联系与变量阈值

|
图 1 BP算法在Two-circle数据集上的聚类结果 |
同时BP算法对于密度不均匀的数据集很难选择出最优的分区结构. 以图1为例, BP算法在Two-circle数据集上的聚类结果与该数据集的实际分布有着较大差异, BP算法过度分割了该数据集. 这可能是由于每个边界点(除了异常值)只连接到最近的非边界点, 如果同一类簇的两个位于内部的已剥离边界点连接到两个不同的区域, 那么在分配后续的边界点时, 也可能导致连续性的错误, 另外, 如果边界点未能在可变阈值
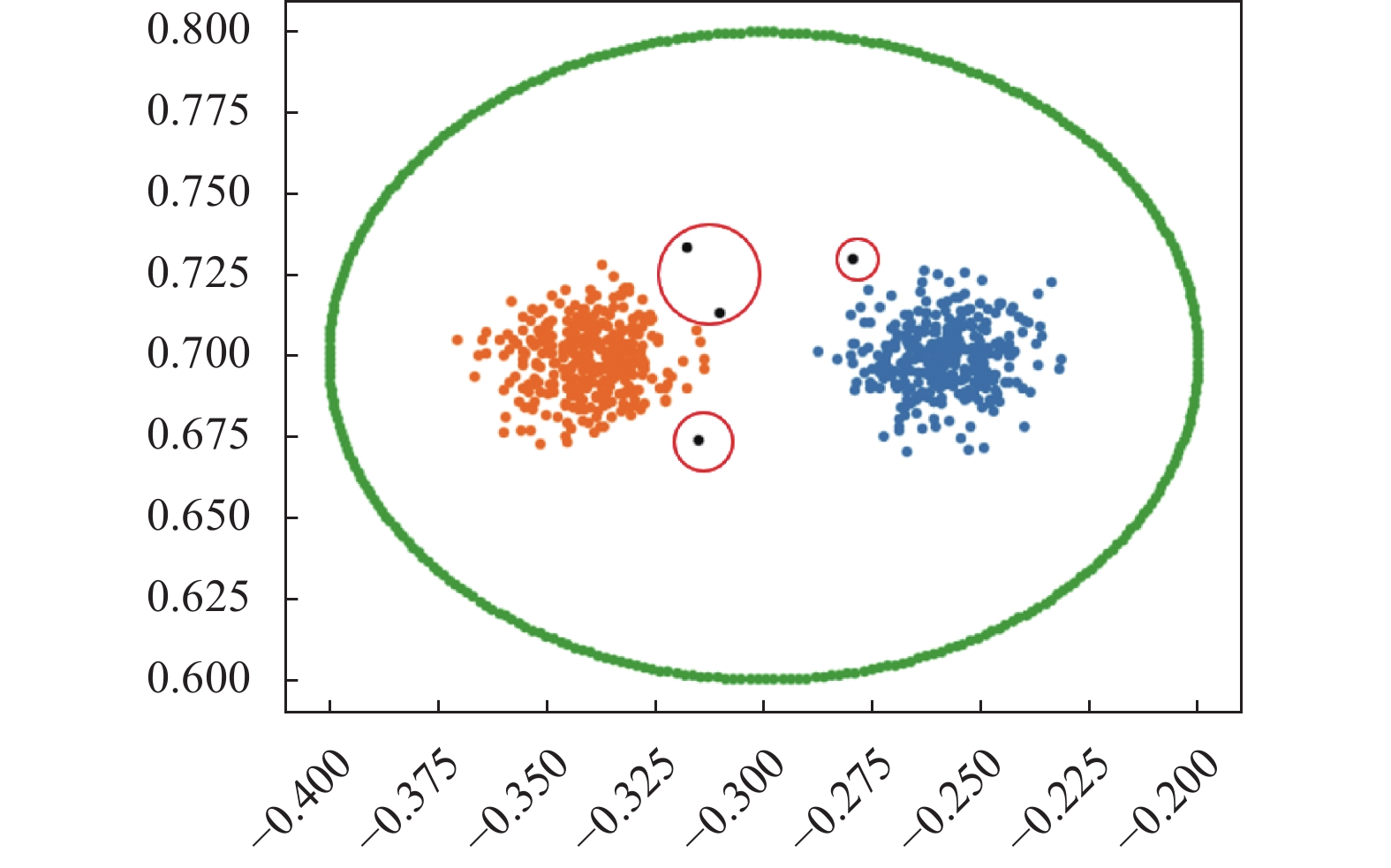
|
图 2 BP算法在Donut3数据集上的聚类结果 |
2.3 改进的BP算法
本节将详细介绍我们提出的改进的BP算法, 即基于共享近邻和优化关联策略的边界剥离聚类算法(SOBP). 首先, 我们将介绍一些重要的概念, 再基于这些概念描述算法的详细流程.
定义1 (共享近邻[21]). 给定数据点
| $ {\textit{SNN}}\left( {{x_i}, {x_j}} \right) = \left\{ {x_r}|{x_r} \in N{N_k}\left( {{x_i}} \right) \cap N{N_k}\left( {{x_j}} \right)\right\} $ | (6) |
为了更好地估计两个数据点之间的相似性, 我们采用了一个基于平均距离和共享近邻的局部密度函数.
定义2 (局部密度函数). 对于任意数据点
| $ f\left( {{x_i}, {x_j}} \right) = {\text{exp}}\left( { - \frac{{{d^2}\left( {{x_i}, {x_j}} \right)}}{{\sigma _j^2\left( {\left| {{\textit{SNN}}^{\left( t \right)}\left( {{x_i}, {x_j}} \right)} \right| + 1} \right)}}} \right) $ | (7) |
其中,
定义3 (密度影响值). 与式(4)中相同, 给定数据点
| $ b_i^{\left( t \right)} = \mathop \sum \limits_{{x_j} \in RNN_k^{\left( t \right)}\left( {{x_i}} \right)} {\rm{exp}}\left( { - \frac{{{d^2}\left( {{x_i}, {x_j}} \right)}}{{\sigma _j^2\left( {\left| {{\textit{SNN}}{^{\left( t \right)}}\left( {{x_i}, {x_j}} \right)} \right| + 1} \right)}}} \right) $ | (8) |
定义4 (边界分类值). 对于数据点
| $ B_i^{\left( t \right)} = \left\{ \begin{array}{*{20}{l}} {1, }&{b_i^{({\text{t}})} \leqslant b_{rnd\left( {10{\text{%}}} \right)}^{\left( t \right)} } \\ {0, }&{{\rm{otherwise}}} \end{array}\right. $ | (9) |
其中,
定义5 (当前剥离点集). 当前剥离点集使用
定义6 (边界点k近邻). 对于数据点
为了建立数据点之间的联系, 并进一步判断噪声点, 算法中提出了新的阈值
定义7 (连接阈值). 连接阈值
| $ {l_i} = \min\left\{ {mean\left( {D_{B, k}^{\left( t \right)}\left( {{x_i}} \right)} \right) + 3std\left( {D_{B, k}^{\left( t \right)}\left( {{x_i}} \right)} \right), \lambda } \right\} $ | (10) |
定义8 (共享近邻相似度[21]). 对于数据点
| $ {\textit{SNS}}\left( {{x_i}, {x_j}} \right) = \left| {{\textit{SNN}}\left( {{x_i}, {x_j}} \right)} \right| $ | (11) |
结合上述连接阈值
定义9 (关联准则(a)). 对于任意边界点
| $ \rho \left( {{x_i}} \right) = \{ {x_j}|{x_j} \in N{N_k}_{NB}^{\left( t \right)}\left( {{x_i}} \right){\text{ and }}d\left( {{x_i}, {x_j}} \right) \leqslant {l_i}\} $ | (12) |
对于
定义10 (关联准则(b)). 考虑边界点与已剥离边界点之间的联系, 对于边界点
| $ \gamma \left( {{x_i}} \right) = \left\{ {x_j}|{x_j} \in NN_{CB, k}^{\left( t \right)}\left( {{x_i}} \right){\text{ }}{\rm{and}}{\text{ }}{\textit{SNS}}\left( {{x_i}, {x_j}} \right) \geqslant \frac{k}{2}\right\} $ | (13) |
对于
当边界点剥离过程停止时, 潜在的核心区域(剩余未被剥离的点)可以被很好地识别, 并且通过简单的DBSCAN可以将它们聚在一起, 根据关联准则(a)以及关联准则(b)分配被剥离点, 改进后的BP算法(SOBP)的具体步骤如算法 1所示.
算法 1. SOBP算法
输入: 数据集
输出: 聚类标签,
计算所有配对点之间的共享近邻相似度及距离
For 迭代次数
For
End for
For
End for
End for
在本节中, 我们将详细介绍实验的参数设置, 并进行实验结果的展示和分析, 以证明改进后的BP算法(SOBP)的有效性.
3.1 实验指标和设置本文选取了6种具有代表性的聚类算法进行比较, 包括BP、K-means[22]、DBSCAN、HDBSCAN、mean-shift (MS)[23, 24]和DPC. 其中BP算法基于作者提供的源代码, DPC算法的代码由其他作者[25]提供, 其他算法均是在sklearn库和其他库的帮助下使用Python实现.
在后续实验中, 我们使用sklearn提供的函数来估计MS中的带宽. 在K-means算法中, 采用正确的聚类数量作为K-means算法的唯一参数. 对于其他算法, 全部的显示结果均是通过网格搜索进行参数调优后的最优结果, 具体搜索范围如下: 对于BP算法和SOBP算法, 我们选择重要的参数k为2到30的值. DBSCAN算法中的重要参数eps从0.1循环到20. HDBSCAN算法要求输入最小的类簇大小, 我们将最小尺寸设置为2到15. 对于传统的DPC算法, 实验中使用高斯核进行密度估计,
在评价指标方面, 本文采用调整兰德指数(ARI)[26]、调整互信息(AMI)[27]和Fowlkes-Mallows指数(FMI)[28]对7个聚类算法的有效性进行评估, 三者的取值上限均为1, 且聚类效果与取值成正比.
3.2 实验结果表1给出了7种聚类算法在不同数据集上的实验指标值, 数据集的详细信息可见表2. 同时, 我们将最高得分的指标以粗体标记, 图3–图8更加直观地展示了人工数据集的聚类结果.
| 表 1 聚类指标对比 |
在图3中, 3-spiral是一个具有3个类别且低密度的数据集, 数据点构成了彼此交叉缠绕的螺旋形曲线. 可以看到BP算法将曲线的尾部识别为异常值, 这可能与关联策略的连接阈值设置有关, 其他基于密度的聚类算法在此数据集上表现良好, 而K-means算法仅考虑数据点之间的距离特性, 无法处理环绕的流线型数据.
Xclara数据集以中心密度高、边界密度低为特征, 该数据集3个类簇边缘数据点彼此交错, 部分数据点无法通过人为划分, 具有一定的难度. 可以看到所有算法在此数据集上的ARI值都高于0.90. 然而, 如图4所示, 其他算法在分类边缘点时不够准确, 只有 SOBP算法在所有情况下都分类正确, 完美地将彼此交错的边缘数据点进行了正确划分.
在图5和图6中, Complex8和Complex9都是具有不均匀密度的复杂结构数据集, 其中Complex8包含8个类别, Complex9包含9个类别, 通过观察两个数据集的原始结构可以发现Complex8相比于Complex9密度更不均匀, 但Complex9的结构更加复杂. 在使用7种聚类算法对它们进行聚类时, DBSCAN在Complex8数据集上具有最佳的聚类结果, 其次是SOBP算法. 对于Complex9数据集, SOBP算法实现了最佳的聚类结果, 而DBSCAN将个别点识别为了离群点, 因此没有获得最佳表现. 与BP算法相比, SOBP算法对于聚类复杂数据集的表现更为优异.
| 表 2 实验数据集 |

|
图 3 3-spiral数据集聚类结果 |

|
图 4 Xclara数据集聚类结果 |
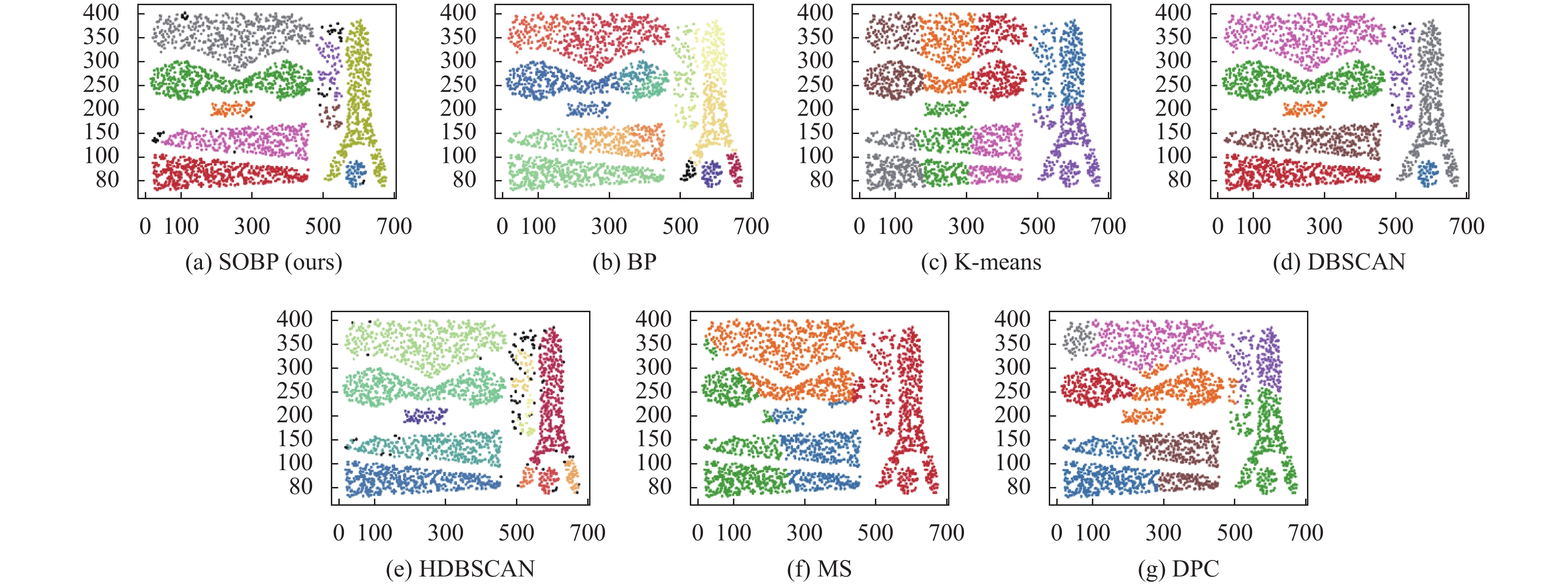
|
图 5 Complex8数据集聚类结果 |

|
图 6 Complex9数据集聚类结果 |
DS1的主体由1个新月形类簇和3个球形类簇组成, 其中新月形类簇包围着球形类簇, 同时含有很多的噪声点, 因此比大多数数据集更具挑战性. 图7展示了7种不同的算法对DS1数据集的聚类结果, 可以看出所有算法的聚类结果都不完美. 相较而言, SOBP 算法在处理DS1数据集时表现较好, 能够大致正确地聚类出数据集中的主体结构, 而其他算法则普遍存在将新月形类簇过度划分的问题.
DS2由不同形状的6个类簇组成, 这些类簇相互包围缠绕, 相对于其他数据集具有较高的密度. 在图8中, BP算法将DS2分成更多的类簇, 远离了数据集的真实分布. DBSCAN以及HDBSCAN在该数据集上表现较好, 它们的3项指标得分都比较高, 但是它们均将类簇的一些边界点判断成了离群点. 只有SOBP算法能够完全识别DS2的真实分布, 获得了最优的聚类效果.
为了验证SOBP算法在实际应用中的有效性, 本文进一步选择了若干个真实数据集进行实验, 这些数据集的样本点数量、数据维数以及聚类的类簇数目各不相同, 相较于人工数据集更加复杂. 为了保证实验的可靠性和准确性, 在实验中我们对于表2所列出的真实数据集进行了预处理, 其中包括数据规范化和降维等, 以消除数据中的噪声和冗余信息. 通过表1中的实验结果可以发现, SOBP算法在真实数据集上的聚类效果总体优于其他6种聚类算法. 因此, 我们认为SOBP算法具有一定的有效性和实用性, 可以在实际应用中发挥作用.

|
图 7 DS1数据集聚类结果 |
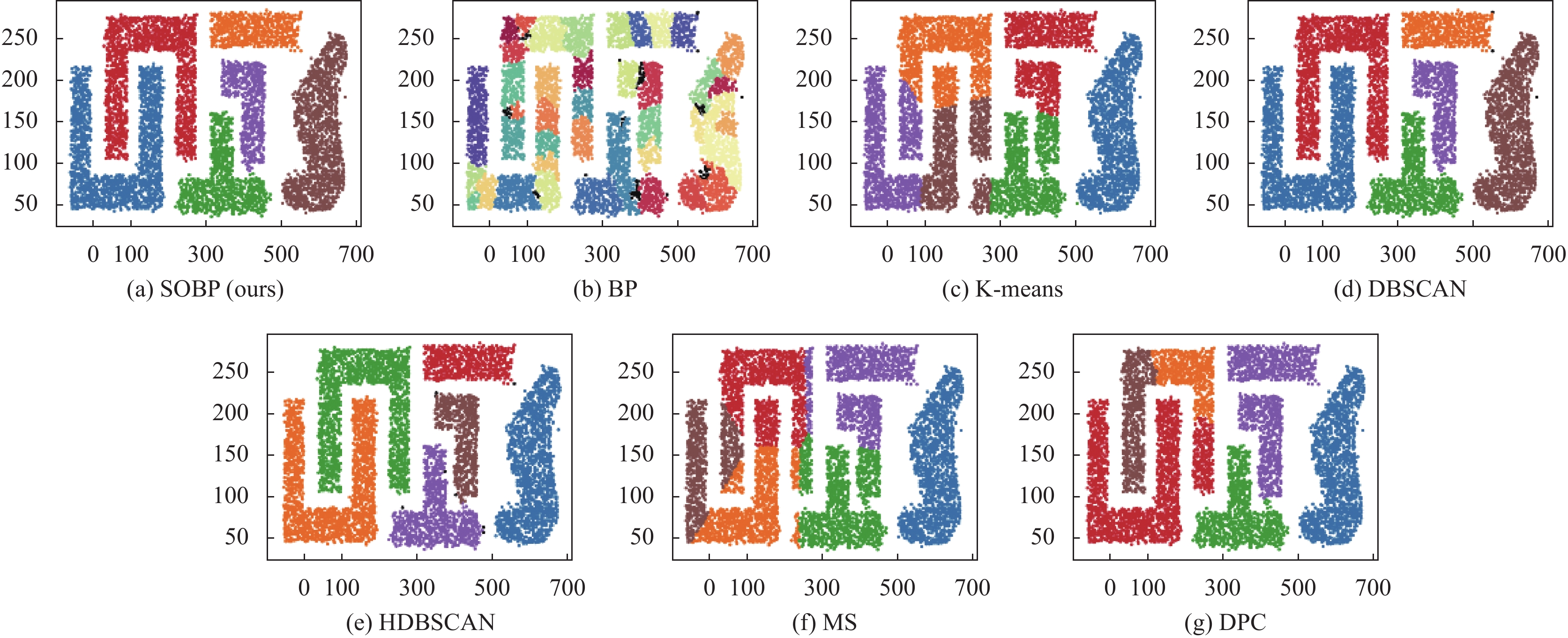
|
图 8 DS2数据集聚类结果 |
4 结论
本文提出了一种基于共享近邻和优化关联策略的边界剥离聚类算法(SOBP), 该算法采用基于共享近邻的局部密度, 考虑了每个数据点的邻域分布, 并减少了异常值对于边界点确定的影响. 针对原始算法在数据集密度不均匀、形状复杂等情况下容易过度分割且误判异常值的问题, 我们改进了关联策略, 大大降低了分配边界点时发生连带错误的概率. 实验结果表明, SOBP算法在人工数据集和真实数据集上都表现出良好的聚类效果, 具有一定的实用价值. 然而, 该算法需要手动输入参数选择, 这对后续研究者在实际问题中应用该算法带来了一定的挑战, 因此, 在后续工作中我们将考虑输入参数的自适应.
| [1] |
Li M, Sha HY, Liu HY. Microfeature segmentation algorithm for biological images using improved density peak clustering. Computational and Mathematical Methods in Medicine, 2022, 2022: 8630449. DOI:10.1155/2022/8630449 |
| [2] |
Niu YY, Kong DT, Liu LG, et al. Overlapping community detection with adaptive density peaks clustering and iterative partition strategy. Expert Systems with Applications, 2023, 213: 119213. DOI:10.1016/j.eswa.2022.119213 |
| [3] |
Petegrosso R, Li ZL, Kuang R. Machine learning and statistical methods for clustering single-cell RNA-sequencing data. Briefings in Bioinformatics, 2020, 21(4): 1209-1223. DOI:10.1093/bib/bbz063 |
| [4] |
Kiselev VY, Andrews TS, Hemberg M. Challenges in unsupervised clustering of single-cell RNA-seq data. Nature Reviews Genetics, 2019, 20(5): 273-282. DOI:10.1038/s41576-018-0088-9 |
| [5] |
Fraley C, Raftery AE. How many clusters? Which clustering method? Answers via model-based cluster analysis. The Computer Journal, 1998, 41(8): 578-588. DOI:10.1093/comjnl/41.8.578 |
| [6] |
Han J, Kamber M. Data Mining: Concepts and Techniques. 2nd ed. San Francisco: Morgan Kaufinann, 2006.
|
| [7] |
Saxena A, Prasad M, Gupta A, et al. A review of clustering techniques and developments. Neurocomputing, 2017, 267: 664-681. DOI:10.1016/j.neucom.2017.06.053 |
| [8] |
Ezugwu AE, Ikotun AM, Oyelade OO, et al. A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects. Engineering Applications of Artificial Intelligence, 2022, 110: 104743. DOI:10.1016/j.engappai.2022.104743 |
| [9] |
Averbuch-Elor H, Bar N, Cohen-Or D. Border-peeling clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(7): 1791-1797. DOI:10.1109/TPAMI.2019.2924953 |
| [10] |
Ester M, Kriegel HP, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise. Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996. 226–231.
|
| [11] |
Campello RJGB, Moulavi D, Sander J. Density-based clustering based on hierarchical density estimates. Proceedings of the 17th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Gold Coast: Springer, 2013. 160–172.
|
| [12] |
Wang LM, Wang HH, Han XM, et al. A novel adaptive density-based spatial clustering of application with noise based on bird swarm optimization algorithm. Computer Communications, 2021, 174: 205-214. DOI:10.1016/j.comcom.2021.03.021 |
| [13] |
Chen XM, Liu WQ, Qiu HN, et al. APSCAN: A parameter free algorithm for clustering. Pattern Recognition Letters, 2011, 32(7): 973-986. DOI:10.1016/j.patrec.2011.02.001 |
| [14] |
万佳, 胡大裟, 蒋玉明. 多密度自适应确定DBSCAN算法参数的算法研究. 计算机工程与应用, 2022, 58(2): 78-85. DOI:10.3778/j.issn.1002-8331.2012-0476 |
| [15] |
Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [16] |
Liu R, Wang H, Yu XM. Shared-nearest-neighbor-based clustering by fast search and find of density peaks. Information Sciences, 2018, 450: 200-226. DOI:10.1016/j.ins.2018.03.031 |
| [17] |
Xu X, Ding SF, Wang LJ, et al. A robust density peaks clustering algorithm with density-sensitive similarity. Knowledge-based Systems, 2020, 200: 106028. DOI:10.1016/j.knosys.2020.106028 |
| [18] |
张清华, 周靖鹏, 代永杨, 等. 基于代表点与K近邻的密度峰值聚类算法. 软件学报, 2023: 1–20.
|
| [19] |
Du MJ, Wang R, Ji R, et al. ROBP: A robust border-peeling clustering using Cauchy kernel. Information Sciences, 2021, 571: 375-400. DOI:10.1016/j.ins.2021.04.089 |
| [20] |
Feng J, Zhang BK, Ran RS, et al. An effective clustering algorithm using adaptive neighborhood and border peeling method. Computational Intelligence and Neuroscience, 2021, 2021: 6785580. DOI:10.1155/2021/6785580 |
| [21] |
Ertöz L, Steinbach M, Kumar V. Finding clusters of different sizes, shapes, and densities in noisy, high dimensional data. Proceedings of the 2003 SIAM International Conference on Data Mining. 2003. 47–58.
|
| [22] |
MacQueen JB. Some methods for classification and analysis of multivariate observations. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press, 1967. 281–297.
|
| [23] |
Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Transactions on Information Theory, 1975, 21(1): 32-40. DOI:10.1109/TIT.1975.1055330 |
| [24] |
Cheng YZ. Mean shift, mode seeking, and clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 790-799. DOI:10.1109/34.400568 |
| [25] |
Zuo WD, Hou XM. An improved probability propagation algorithm for density peak clustering based on natural nearest neighborhood. Array, 2022, 15: 100232. DOI:10.1016/j.array.2022.100232 |
| [26] |
Hubert L, Arabie P. Comparing partitions. Journal of Classification, 1985, 2(1): 193-218. DOI:10.1007/BF01908075 |
| [27] |
Vinh NX, Epps J, Bailey J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. The Journal of Machine Learning Research, 2010, 11: 2837-2854. |
| [28] |
Fowlkes EB, Mallows CL. A method for comparing two hierarchical clusterings. Journal of the American Statistical Association, 1983, 78(383): 553-569. DOI:10.1080/01621459.1983.10478008 |
 2023, Vol. 32
2023, Vol. 32


