棉花从生产者到消费者, 需要经过生产、收购、加工、储存、运输、零售等产业链上的一个或多个环节^[1], 任何一个环节的价格变化都会导致全产业链中产品的价格波动, 而这也使得棉花价格在形成过程中受到多种因素的影响. 然而近几年, 由于全球疫情持续蔓延, 世界经济复苏动力不足, 导致棉花价格持续上升^[2]. 再加上地缘政治冲突、国际贸易摩擦以及极端气候等众多事件的共同作用, 国内棉花供需再次发生变动, 各种因素对棉花的影响变得更加复杂, 价格也一直保持高位波动. 如何通过科学的方法, 基于多种因素对棉花价格进行精准预测, 对于避免价格波动损害棉花产业链中棉农、纺织企业的切身利益, 影响市场稳定运行方面有着重要意义.

1 相关研究

目前, 针对棉花价格有许多研究人员开展了广泛的研究. 在棉花价格影响因素方面. 国家发改委学术委员会办公室课题组^[3]通过1999–2012年棉花价格数据, 详细分析流通体制改革前后棉花价格的波动特点, 指出在流通体制改革后棉花价格持续上涨且波动剧烈, 主要因为供需关系、极端天气变化、国际棉花价格及政府政策调控等因素. 褚志磐等^[4]利用VAR模型分析棉花产量、棉花生产成本、美元汇率及棉花进口数量对棉花价格的影响. 结果表明, 对棉花价格影响最强的因素为汇率, 棉花产量、棉花进口、棉花生产成本次之. 彭新宇等^[5]通过脉冲响应函数、方差分解等方法分析国际原油价格变动对大豆、棉花、花生仁和油菜籽的影响, 结果表明, 国际原油对花生仁、棉花价格波动的贡献率较大. Bodjongo^[6]利用描述性统计技术和VAR模型验证降雨量、温度等气候变化和国际市场棉花价格波动对棉花生产和棉花价格的影响, 最终发现世界棉花价格的上涨和气温的显著变化会对棉花价格造成影响. 此外指数投资、目标政策、货币发行量、居民消费指数、棉花储备量、市场情绪、产业链等^[7-11]因素都对棉花价格具有一定的影响.

在棉花价格预测研究方法方面, 有许多研究人员相继提出多种预测理论与方法. 包括自回归移动平均模型(ARIMA)、马尔科夫链模型、支持向量机(SVM)、基于模糊信息粒化和粒子群优化支持向量回归机(PSO-SVR)^{[2, 12-14]}等. 其中, ARIMA模型应用最为广泛, 部分研究人员将该模型与经验模式分解(EMD)、小波分析、H-P滤波分析、指数自回归条件异方差模型^[15-18]相结合. 这些方法虽然可以很好地对时间序列数据进行预测, 但是这些方法不能很好地处理大规模复杂数据. 因此, 以人工神经网络(ANN)为主的方法逐渐应用于价格预测. 包括反向传播神经网络(BPNN) 、径向基函数网络(RBF)^[9,19]等. 但是人工神经网络对输入数据点进行独立处理, 没有考虑输入数据之间的相关性, 因此在对序列数据建模方面存在一定的局限性.

近些年, 使用深度学习建模方法进行棉花及其他农产品的价格预测研究也得到学者们的广泛关注. 江知航等^[20]引入种植面积、进出口、汇率、气候等因素, 采用双向长短期记忆网络BiLSTM和SWA优化算法对棉花价格进行预测, 使用长短期记忆网络LSTM和 LightGbm 模型进行对比试验, 得到了不错的预测效果. 但是其他深度学习方法在棉花价格领域的应用较少. 事实上, 深度学习模型中的循环神经网络(RNN)及变体模型在农产品价格预测的研究中已经获得了一定进展. Shin等^[21]利用LSTM对大葱、洋葱、西葫芦、大米和菠菜的价格进行了预测, 选择气候数据、油价、产品综合指数、各年度农产品产量等因素作为影响变量, 最后通过RMSE指标验证模型有效性. Gu等^[22]构建双输入注意长短时记忆模型(DIA-LSTM), 利用气象数据、交易量数据等影响农产品价格的变量进行训练, 并通过白菜和萝卜的数据进行价格预测. Li等^[23]根据注意机制开发了异构GRU神经网络(AH-GRU), 引入静态信息对价格波动的影响, 提高了对异构数据的处理能力. 实验结果表明, 该方法对牛羊肉猪肉价格的预测精度、趋势预测和方法收敛性等方面均优于主流的畜产品价格预测方法. 虽然上述方法都取得了很好的预测精度, 但是它们仍然需要大量的时间和计算机内存来训练模型.

2 分析方法及模型构建 2.1 研究思路及分析方法

本文提出了一种基于极限梯度提升(XGBoost)和引入注意力机制的时间卷积网络(TCN)的多因素预测模型.

在特征选择方面, 根据现有的研究, 极端天气变化、国际棉花价格、美元汇率等都对棉花价格有较为显著的影响, 所以本研究将棉花价格的影响因素分为供需关系、宏观经济、国际市场这3类, 其中: 供需关系是导致棉花价格上下波动的主要原因, 并且价格变化也会引起供给和需求的变化, 影响因素包括棉花的种植面积、产量、气候变化等. 国内经济稳定程度、国际收支平衡等整个宏观经济形势对棉花市场运行和价格波动也有着不可忽略的影响, 影响因素包括指数投资、货币发行量、汇率等. 近几年我国积极发展与世界多个国家的贸易合作伙伴关系, 增加贸易往来, 国内市场与国际市场的联动性不断增强, 国际市场变化对国内棉花市场有着很大的影响, 影响因素包括国际棉花价格、原油等.

结合近期时事, 综合从供需关系、国际市场、宏观经济中分别引入如下变量对棉花价格预测. 因为棉花产业链较长, 从生产到产出的过程中产业链里的各参与者会根据自身成本和市场情况来定价, 造成价格的传递^[11], 对棉花的价格波动具有直接影响, 但目前价格预测研究中少有引入该类因素, 因此特选择棉花产业链上游的棉籽和棉粕作为棉花产业链代表数据进行预测.

事实上, 影响因素对价格的影响强度各有不同, 如果利用一些不相关的因素建立预测模型, 模型的性能会因此受到影响. 为此本研究引入了XGBoost算法进行关键特征筛选, 有效地从复杂的原始数据中提取重要的特征信息提高预测性能.

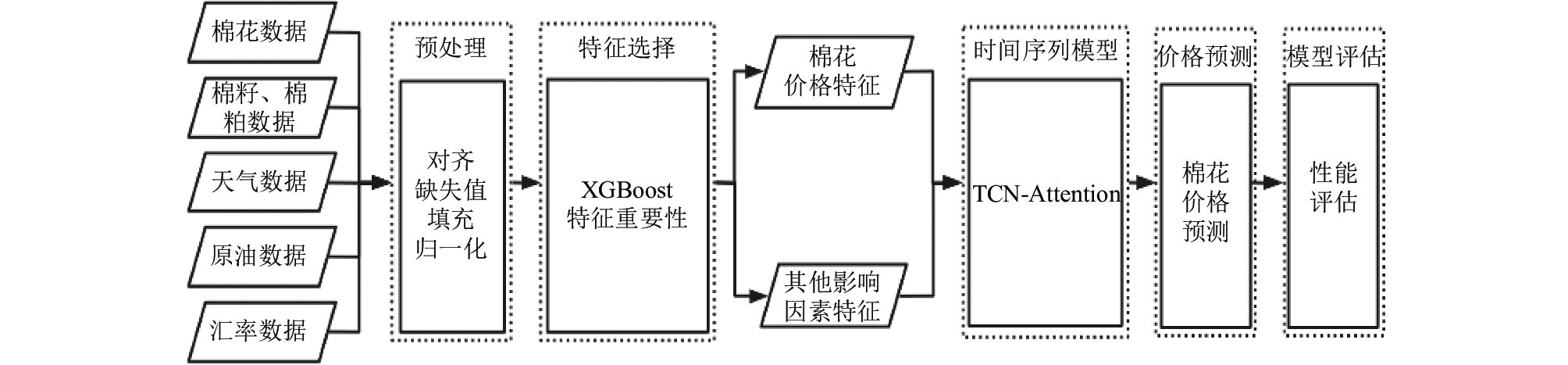
在预测方法方面, Bai等^[24]提出了时间卷积网络(TCN), 它结合了CNN和RNN的优点, 在能源预测、功率预测^{[25, 26]}等领域问题中, 都证明了TCN模型的预测精度和预测效率优于LSTM和GRU模型, 能够有效地利用卷积提取复杂时间序列数据的特征进行预测.因此本文选择使用TCN模型进行棉花价格预测. 同时, 为了增强TCN模型对长时间序列数据学习的能力, 在模型中引入注意力机制, 通过对输入特征赋予不同的权重来缓解重要局部特征随着步长的增加而消失的问题^[27]. 预测流程如图1所示.

2.2 模型构建

本文提出的XGBoost+TCN+Attention (X-TCN-ATT)神经网络模型的结构如图2所示, 分为输入层、特征选择层、TCN网络层、注意力机制层和输出层. 各网络层具体任务如下.

第1层为输入层, 将预处理好的棉花价格数据和其他影响因素数据输入到模型中.

第2层为特征选择层. 使用XGBoost算法计算出每个特征的特征重要性分数, 根据特征重要性排序选择输入特征以降低模型的复杂度.

第3层为TCN网络层. 接受筛选出来的多变量数据, 通过使用卷积网络的变形结构, 在不加深网络深度的情况下捕获长期依赖关系并通过残差模块实现跨层信息传递.

第4层为注意力机制层. 通过计算特征的注意力分数, 为每个特征赋予不同的权重, 忽略对价格影响较低的特征, 提高预测精度.

最后一层为输出6层, 通过全连接层得到价格预测结果.

2.2.1 基于XGBoost的棉花价格特征评估

XGBoost评估特征在特征集中的重要性通常有增益、覆盖度量和频率这3种方式^[28], 其中增益是解释每个特征的相对重要性的最相关属性, 所以本文主要通过枚举所有不同树结构的贪心法求得增益进行特征评估.

对于经过数据预处理之后的棉花数据集 $M= \left\{\left({x}_{i}, {y}_{i}\right)\right\}(i=\mathrm{0, 1}, \cdots, t)$ , 其中 ${x}_{i}=\left({x}_{0}^{i}, {x}_{1}^{i}, \cdots, {x}_{n-1}^{i}, {x}_{n}^{i} \right)$ 表示第i个样本的n维特征向量, 即输入的棉花数据的n个特征值, $ {y}_{i} $ 表示第i个样本的标签值. 将棉花数据集M输入到XGBoost中进行训练得到K棵树, 可以表示为:

$ \widehat{{y}_{i}}=\displaystyle\sum\limits_{k=1}^{K}{f}_{k}\left({x}_{i}\right), \; {f}_{k}\in F $

(1)

$ F=\left\{f\left(x\right)={w}_{q\left(x\right)}\right\} $

(2)

其中, $ \widehat{{y}_{i}} $ 表示第i个样本的预测结果, F是基学习器即K棵树的集合, $ {f}_{k} $ 表示第k棵回归树, $ {w}_{q\left(x\right)} $ 表示叶子节点q的分数. 训练过程中的目标函数为:

$ O=\displaystyle\sum\limits _{i=0}^{t}l({y}_{i}, \widehat{{y}_{i}})+\displaystyle\sum\limits _{k=1}^{K}\Omega \left({f}_{k}\right) $

(3)

其中, l是用于计算预测值和真实值之间的误差的损失函数, $\Omega$ 是表示树的复杂度的函数, 值越小复杂度越低, 泛化能力越强, 其表达式为:

$ \Omega \left({f}_{k}\right)=\gamma N+\frac{1}{2}\lambda {\left\| {w} \right\|}^{2} $

(4)

其中, $ N $ 表示叶子节点的个数, w表示节点的数值. 直观上看, 目标要求预测误差尽量小, 且叶子节点N尽量少, 节点数值w尽量不极端.

通过在梯度方向上不断优化, 目标函数越来越低, 因为预测值 $ \widehat{{y}_{i}} $ 在第T次迭代之后可以由前T−1次迭代输出值总和以及第T次迭代计算得到的树结构值 $ {f}_{T}\left({x}_{i}\right) $ 相加得到, 所以将目标函数O转换成:

$ {O}^{T}=\displaystyle\sum\limits _{i=0}^{t}l({y}_{i}, {\widehat{y}}_{i}\,^{(T-1)}+{f}_{T}({x}_{i}\left)\right)+\Omega \left({f}_{T}\right)+C $

(5)

其中, C为常数. 将式(5)通过二阶泰勒展开可优化为:

$ {O}^{T} = \displaystyle\sum\limits _{i=0}^{t}\left[l({y}_{i}, {\widehat{y}}_{i}\,^{(T-1)})+{g}_{i}{f}_{T}\left({x}_{i}\right)+\frac{1}{2}{h}_{i}{f}_{T}^{2}\left({x}_{i}\right)\right]+\Omega \left({f}_{T}\right) $

(6)

其中, ${g}_{i}={\partial }_{{\widehat{y}}\,^{(T-1)}}l({y}_{i}, {\widehat{y}}\,^{(T-1)})$ 为预测误差对当前模型的一阶导数, ${h}_{i}={\partial }_{{\widehat{y}}\,^{(T-1)}}^{2}l({y}_{i}, {\widehat{y}}\,^{(T-1)})$ 为许多预测误差对当前模型的二阶导数.

由于在第T次迭代时, 第T−1次的模型残差已知, 因此去掉常数项 $l({y}_{i}, {\widehat{y}}_{i}\,^{(T-1)})$ 并对式(6)进行展开, 将目标函数转换成按叶节点累加的形式为:

$\tag{7a}{O}^{T}=\displaystyle\sum\limits _{j=1}^{N}\left[G{w}_{j}+\frac{1}{2}\left(H+\lambda \right){w}_{j}^{2}\right]+\gamma N $

$\tag{7b} G=\displaystyle\sum\limits _{i\in I}{g}_{i} $

$\tag{7c} H=\displaystyle\sum\limits _{i\in I}{h}_{i} $

其中, I表示每个叶子节点上样本的集合, ${I}_{j}= \left\{i\left|q\right({x}_{i})= j\right\}$ ; $ q\left({x}_{i}\right) $ 为树结构函数; $ {w}_{j} $ 表示每棵树叶子节点的输出分数; N表示分裂树的叶子节点个数; $ \lambda $ 和 $ \gamma $ 为权重因子, 用来控制对应部分的比重.

创建好提升决策树后通过计算增益得到每个特征的特征重要性. 与决策树中的信息增益及基尼指数类似, XGBoost算法在每一次尝试对已有的叶子加入一个分割时, 都会计算选取特征的增益Gain:

$ Gain=\frac{1}{2}\left[\frac{{G}_{{\rm{L}}}^{2}}{{H}_{{\rm{L}}}+\lambda }+\frac{{G}_{{\rm{R}}}^{2}}{{H}_{{\rm{R}}}+\lambda }-\frac{{\left({G}_{{\rm{L}}}+{G}_{{\rm{R}}}\right)}^{2}}{{H}_{{\rm{L}}}+{H}_{{\rm{R}}}+\lambda }\right]-\gamma $

(8)

其中, 下标L、R分别表示左子树和右子树; $\dfrac{{G}_{{\rm{L}}}^{2}}{{H}_{{\rm{L}}}+\lambda }$ 表示左子树分数; $\dfrac{{G}_{{\rm{R}}}^{2}}{{H}_{{\rm{R}}}+\lambda }$ 表示右子树分数; $\dfrac{{\left({G}_{{\rm{L}}}+{G}_{{\rm{R}}}\right)}^{2}}{{H}_{{\rm{L}}}+{H}_{{\rm{R}}}+\lambda }$ 表示当前节点不分割的分数.

在单个提升树中通过每个特征分裂点的增益大小来计算特征重要性, 增益越大其权值越大. 特征被越多的提升树所选择, 该特征越重要. 最终将一个特征在所有提升树中的结果进行加权求和后取平均, 得到重要性分数. 按重要性分数从高到低排序后, 通过设置不同的阈值筛选出m (m<n)个影响棉花价格的重要特征.

2.2.2 基于TCN-Attention的棉花价格预测模型

时间卷积网络(TCN)是一种能够处理时间序列问题的网络结构, 其本质上是一种一维卷积网络的变形, 通过扩张因果卷积和残差连接来进行序列建模和预测. 棉花数据集 $M=\left\{\left({x}_{i}, {y}_{i}\right)\right\}(i=\mathrm{0, 1}, \cdots, t)$ 通过XGBoost算法从原始的n个特征中筛选出m个对棉花价格影响较大的特征后, 作为TCN网络的输入, 输入到网络中进行卷积计算提取时序特征, 得到输出向量 ${h}_{i} \; (i= \mathrm{0, 1}, \cdots, t)$ , 其中 ${x}_{i}=({x}_{0}^{i}, {x}_{1}^{i}, \cdots, {x}_{m-1}^{i}, {x}_{m}^{i}) \; (m < n)$ .

(1)因果卷积

因果卷积(causal convolution)使得TCN具有严格的时间约束. 对于输入到网络中的棉花价格序列 $\{{x}_{0}, {x}_{1}, \cdots, {x}_{t-1}, {x}_{t}, \cdots\}$ , t时刻的输出 $ {h}_{t} $ 只能通过当前时刻的输入 $ {x}_{t} $ 和之前时刻的输入 ${x}_{0}, {x}_{1}, \cdots, {x}_{t-1}$ 计算得到, 即当前时刻t的信息只能通过当前时刻t及其之前的信息得到. 为了确保输出张量与输入张量具有相同的长度, 采取在输入张量左侧进行零填充的策略, 这样也满足了因果卷积.

然而, 要想获得较长的历史信息甚至覆盖完整的历史记录则需要特别深的网络, 随着网络深度的增加就会出现梯度消失、计算复杂、拟合效果不好等问题, 所以引入了扩张卷积.

(2)扩张卷积

扩张卷积能够在不增加参数和模型复杂度的情况下, 通过间隔采样指数级增大感受野, 捕获长期依赖关系.

如图3所示是TCN的网络结构, 和传统卷积不同的是, 扩张卷积允许卷积时的输入存在间隔采样, 采样率受扩张因子d控制. 最下面一层d=1表示输入时每个时间点都采样, 隐藏层d=2表示输入时每2个时间点采样一个作为输入. 对于输入的棉花价格序列X=( ${{x}}_{0}, {{x}}_{1}, \cdots, {{x}}_{{t}-1}, {{x}}_{{t}}$ ), 滤波器 $f:\{0, \cdots, k-1\}\to R$ , t时刻的卷积运算F为:

$ F\left({x}_{t}\right)=\displaystyle\sum\limits _{i=0}^{k-1}f\left(i\right)\cdot {x}_{t-d\cdot i} $

(9)

其中, k为卷积核大小, d为扩张因子, $t-d\cdot i$ 表示历史数据. 此时TCN网络的感受野w为:

$ w=1+(k-1)\cdot \frac{{b}^{n}-1}{b-1} $

(10)

其中, n为层数、b为扩张基数(扩张因子 $d={b}^{i}, i=\mathrm{1, 2}, \cdots, n$ ).

可以看到当卷积核大小为3、扩张因子为[1, 2, 4]时t时刻的输出 $ {h}_{t} $ 由输入 ${x}_{0}, {x}_{1}, \cdots, {x}_{t-1}, {x}_{t}$ 共同决定, 即感受野能够覆盖输入序列中的所有值.

(3)残差连接

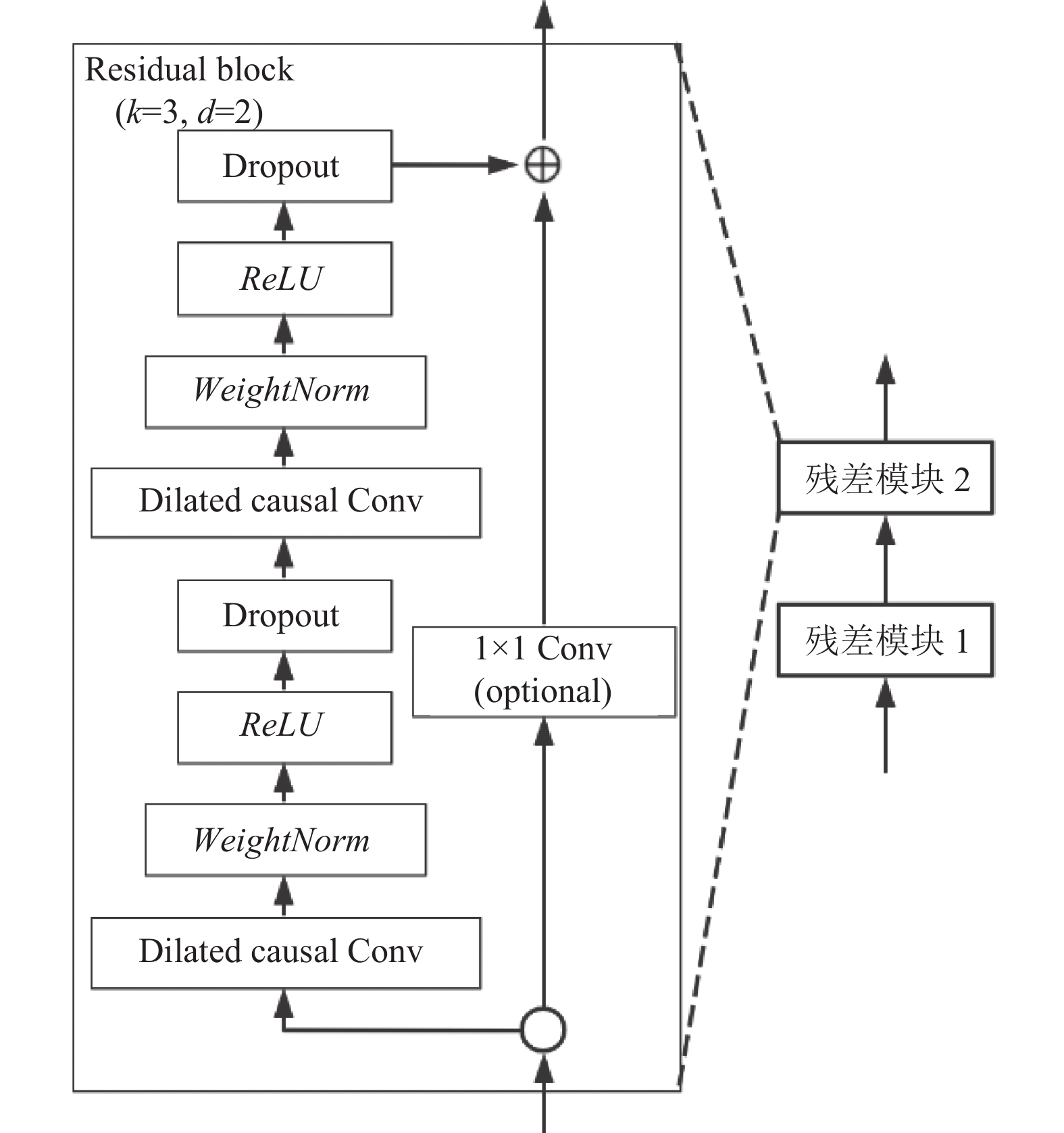
残差连接使得浅层网络可以很容易扩展成深层网络. 本文构建了两个残差模块来代替两层卷积. 残差模块结构如图4所示, 一个残差模块由两层扩张因果卷积和非线性映射构成, 卷积核大小为3.

首先对输入的特征向量进行扩张因果卷积, 之后通过WeightNorm归一化来加速网络训练, 然后使用ReLU激活函数进行非线性计算, 并加入Dropout防止过拟合. 最后将得到的结果与输入求和得到输出向量. 计算过程如下:

$ {S}_{i}=Conv({W}_{i}\times {F}_{j}+{b}_{i}) $

(11)

$ \begin{split} \{{S}_{0}, {S}_{1}, \cdots, {S}_{t-1}, {S}_{t}\}= WeightNorm\left(\right\{{S}_{0}, {S}_{1}, \cdots, {S}_{t-1}, {S}_{t}\left\}\right) \end{split}$

(12)

$\begin{split} \{{S}_{0}, {S}_{1}, \cdots, {S}_{t-1}, {S}_{t}\}= ReLU\left(\right\{{S}_{0}, {S}_{1}, \cdots, {S}_{t-1}, {S}_{t}\left\}\right) \end{split}$

(13)

其中, $ {S}_{i} $ 表示i时刻经过卷积计算得到的特征向量, $ {W}_{i} $ 表示i时刻卷积计算的权重矩阵, $ {F}_{j} $ 表示第j层的卷积核, $ {b}_{i} $ 表示偏置向量; $WeightNorm\left(x\right)=\dfrac{\left\|{{w}_{x}} \right\|}{\left\|{v} \right\|}v$ , $\left\|{{w}_{x}} \right\|$ 表示 $ReLU\left(x\right)={\rm{max}}(0, x)$ 权重w的大小, $\dfrac{v}{\left\| {v} \right\|}$ 表示与w同方向的单位向量; $\{{S}_{0}, {S}_{1}, \cdots, {S}_{t-1}, {S}_{t}\}$ 表示经过第j层完整卷积之后得到的特征图.

(4) 注意力机制

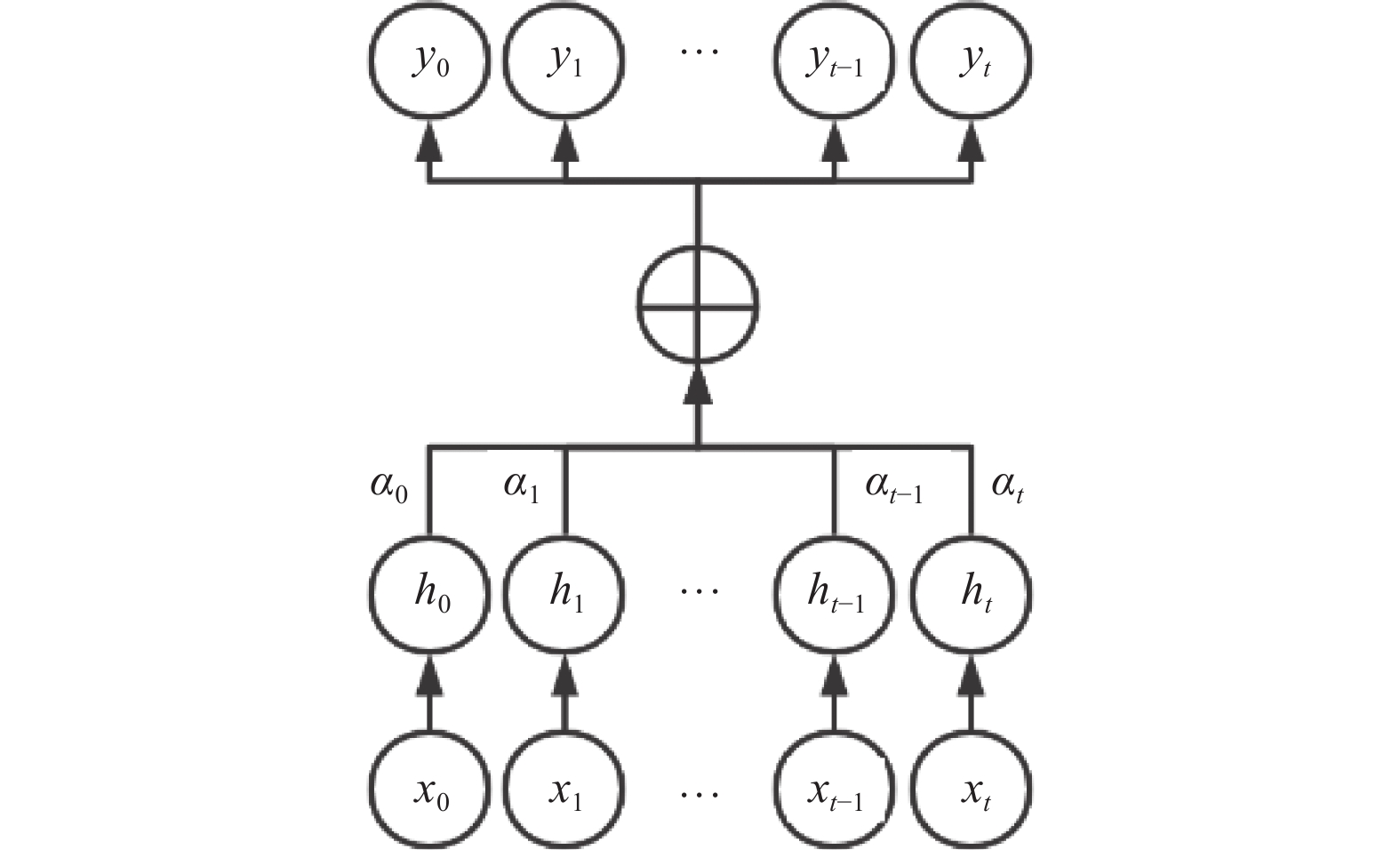
为了更好地从棉花价格时间序列中学习到每个特征的重要程度, 进一步捕捉其中的时序关系, 在模型中加入注意力机制. 注意力机制对由TCN网络输入的特征向量进行加权求和, 通过Softmax函数计算得到注意力分数 $\alpha$ , 将输入特征与注意力分数相乘生成权重矩阵. 注意力机制原理如图5所示.

其中 ${x}_{i} \; (i=\mathrm{0, 1}, \cdots, t)$ 是TCN网络的输入, ${h}_{i} \; (i= \mathrm{0, 1}, \cdots, t)$ 是通过TCN网络输出得到的隐藏层向量, ${\alpha }_{i} \; (i=\mathrm{0, 1}, \cdots, t)$ 是通过对隐藏层输出计算得到的注意力分数, ${y}_{i} \; (i=\mathrm{0, 1}, \cdots, t)$ 是加入注意力机制后的输出向量. 计算公式为:

$ {c}_{i}=u \cdot \tanh\left(w{h}_{i}+b\right) $

(14)

$ {\alpha }_{i}=\frac{{\rm{exp}}\left({c}_{i}\right)}{\displaystyle\sum\limits _{j=0}^{i}{c}_{j}} $

(15)

$ {y}_{i}=\displaystyle\sum\limits _{i=0}^{t}{\alpha }_{i}\cdot {h}_{i} $

(16)

其中, u和w为权重系数, b为偏置系数, 表示第i时刻 TCN 网络输出的隐藏层向量 所确定的注意力权重.

最后将输出向量输入全连接网络, 经过迭代训练得到最终的价格预测值.

3 特征工程 3.1 数据选取及来源

本文的预测对象为新疆棉花现货价格, 数据来源于Wind数据库, 时间周期从2009年5月–2022年5月 (2009/5–2022/5), 价格走势如图6所示. 棉花价格的影响因素从供需关系、宏观经济、国际市场、产业链这4个角度综合选择了平均气温、平均风速、降水量、原油现货价格、汇率、棉粕现货价、棉粕现货平均价. 其中气候数据来源于美国国家信息中心, 其余数据均来源于万德数据库.

3.2 数据预处理

(1)数据清洗

从万德数据库获取到的棉花日现货价格数据均为工作日交易数据, 整体价格数据是真实可靠, 不存在不完整、异常值等脏数据. 因此其他特征数据均按照棉花日现货价格日期进行对齐处理. 针对对齐后部分特征数据存在缺失值情况, 因为考虑到输入数据均为时序序列, 所以选择先以前向填充方法进行填补, 剩余缺失值再以均值填充法处理. 总共包含10个特征指标, 共32540条数据.

(2)数据变换

原始数据集中包含价格、原油、汇率、气候等不同方面的特征数据, 而所有特征数据之间的数量单位和数量级存在差异. 这不可避免会对模型的效果产生不利影响, 因此需要对数据集进行归一化处理, 将所有特征数据映射到[0, 1]之间, 消除不同单位、量级带来的影响. 本文采用Min-Max归一化进行处理, 公式如下所示:

$ {x'}=\frac{x-{x}_{{\rm{min}}}}{{x}_{{\rm{max}}}-{x}_{{\rm{min}}}} $

(17)

其中, $ x $ 、 ${x'}$ 、 ${x}_{{\rm{min}}}$ 和 ${x}_{{\rm{max}}}$ 分别为输入数据、输出数据、输入数据的最小值和输入数据的最大值.

(3)数据划分

数据集时间维度从2009/5/1–2022/5/31. 在使用数据集训练模型之前, 按7:1:2的比重将其划分为训练集、验证集和测试集, 用以增强模型的泛化能力. 其中, 训练集用于更新网络中的权值参数, 寻找最佳参数组合模型. 验证集用于在训练过程中调整模型超参数. 测试集用于评估模型预测性能. 数据划分结果如表1所示.

4 实验与分析 4.1 实验环境

本文的实验环境如表2所示.

4.2 评价指标

本文选择平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)、决定系数R平方( $ {R}^{2} $ )和运行时间(TIME)这5项指标来评估模型的预测性能. 其中, MAE、MAPE、RMSE和 $ {R}^{2} $ 用以评估模型的预测性能. “TIME”反映模型的运行时间, 用以评估模型的复杂性和操作效率, 单位为s. 计算公式如下所示:

$ {\textit{RMSE}}\left(y, \widehat{y}\,\right)=\sqrt{\frac{1}{n}\displaystyle\sum\limits _{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}} $

(18)

$ MAE\left(y, \widehat{y}\,\right)=\frac{1}{n}\displaystyle\sum\limits _{i=1}^{n}|{y}_{i}-{\widehat{y}}_{i}| $

(19)

$ MAPE\left(y, \widehat{y}\,\right)=\frac{1}{n}\displaystyle\sum\limits _{i=1}^{n}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right| \times 100{\text{%}} $

(20)

$ {R}^{2}\left(y, \widehat{y}\,\right)=1-\frac{\displaystyle\sum\limits _{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}{\displaystyle\sum\limits _{i=1}^{n}{({y}_{i}-\bar{y})}^{2}} $

(21)

其中, $ {\widehat{y}}_{i} $ 为预测值; $ {{y}}_{i} $ 为真实值; $ \bar{y} $ 为真实值的平均值; n为总的样本个数.

4.3 特征评估

将特征输入XGBoost模型中对特征进行训练, 通过Fscore指标来衡量各个特征对棉花价格的影响强度, 为特征选择提供参考. 得分如图7所示, 其中各个特征的符号及含义如表3所示.

从图7中不同特征的F score值可以看出, 棉花历史价格对输出几乎有决定性的影响. 这可能是因为棉花价格数据属于时间序列, 未来值会受历史值的影响. 此外, 作为棉花种子的棉籽, 位于产业链的上游与棉花之间存在着纵向价格传递, 对棉花价格具有较强的影响. 而由棉籽加工生产的棉粕对棉花价格影响较小. 同时, 气象条件中温度和风速的变化也会对棉花价格造成影响, 但是风速对输出的影响较小. 此外, 国际原油价格和汇率也具有影响, 其价格波动会导致棉花价格产生变化. 随着特征重要性分数的降低, 特征提供的有效信息逐渐减少. 为了简化输入特征, 同时尽可能保留特征信息, 初步设置阈值大小为40, 选用F score值大于40的前6个特征作为TCN网络的输入进行实验, 分别为棉花现货价、原油现货价、棉籽现货价、平均温度、英国汇率和美国汇率. 其中棉花现货价、原油现货价和棉籽现货价是棉花价格的主要决定因素之一, 与棉花的生产和加工密切相关; 平均温度是影响棉花生产的重要环境因素之一, 对棉花的生长和收成有很大的影响; 英国汇率和美国汇率则是影响棉花进出口贸易的关键因素之一, 因为棉花在国际贸易中往往以美元和英镑计价.

图8是各个特征之间的皮尔逊相关性热力图, 可以看出, 棉籽现货价、原油现货价和美元汇率与棉花现货价之间存在一定的正相关关系, 而英镑汇率与棉花现货价之间存在一定的负相关关系, 天气因素与棉花现货价的相关性较弱.

可以发现相关性分析得到的结果与XGBoost特征评估得到的结果存在一定差异, 这是因为相关系数体现的是特征间的线性相关关系, 而重要性分数F score衡量的是特征在模型中的贡献程度, 它可以帮助我们理解模型中每个特征的重要性, 找出对预测结果最重要的特征. 对于受多种因素影响的棉花价格预测问题, 线性相关仅是其中的一种影响因素, 而且不一定是最重要的影响因素. 这进一步说明了线性相关并不能很好地解决非线性问题. 在实际的数据分析和建模过程中, 我们需要综合运用相关系数和特征重要性评估方法, 以全面了解特征之间的关系和模型中各个特征的重要性, 从而更好地解决复杂的非线性问题.

4.4 参数确定

时间卷积网络中的卷积核大小、卷积核个数、舍弃率以及膨胀系数的设置对模型结果有至关重要的影响. 基于训练样本集对网络进行训练, 经过大量实验确定最佳超参数组合, 如表4所示.

当时间卷积网络(TCN)的结构为2个隐藏层, 每个隐藏层节点数为128, 卷积核大小为3, 个数为128, 丢弃率为0.2, 扩张系数设置为, 损失函数设置为MAE; 优化器为Adam; 迭代次数为100; 学习率初始为0.0005; 每迭代30次学习率会衰减为原来的1/2时, 模型取得了较为出色的预测效果.

4.5 特征选择

根据图7中基于XGBoost的特征评价结果, 选择F score指标前6个特征作为备选项, 分别为f0 (棉花现货价)、f3 (布伦特原油现货价)、f2 (棉籽现货平均价)、f7 (TEMP平均温度)、f6 (USD美元兑人民币汇率)、f5 (GBP英镑兑人民币汇率). 按照F score值的大小, 依次输入不同的特征组合进行实验, 评价结果如表5所示.

当选取f0, f3, f2, f7, f6这5个特征作为输入时预测误差最小, 尽管模型运算时间比选取4个特征时要长, 但是预测问题更需要关注模型的预测误差. 所以当“TIME”指标差异不大时, 预测误差指标更为重要.

4.6 模型对比

(1)消融实验

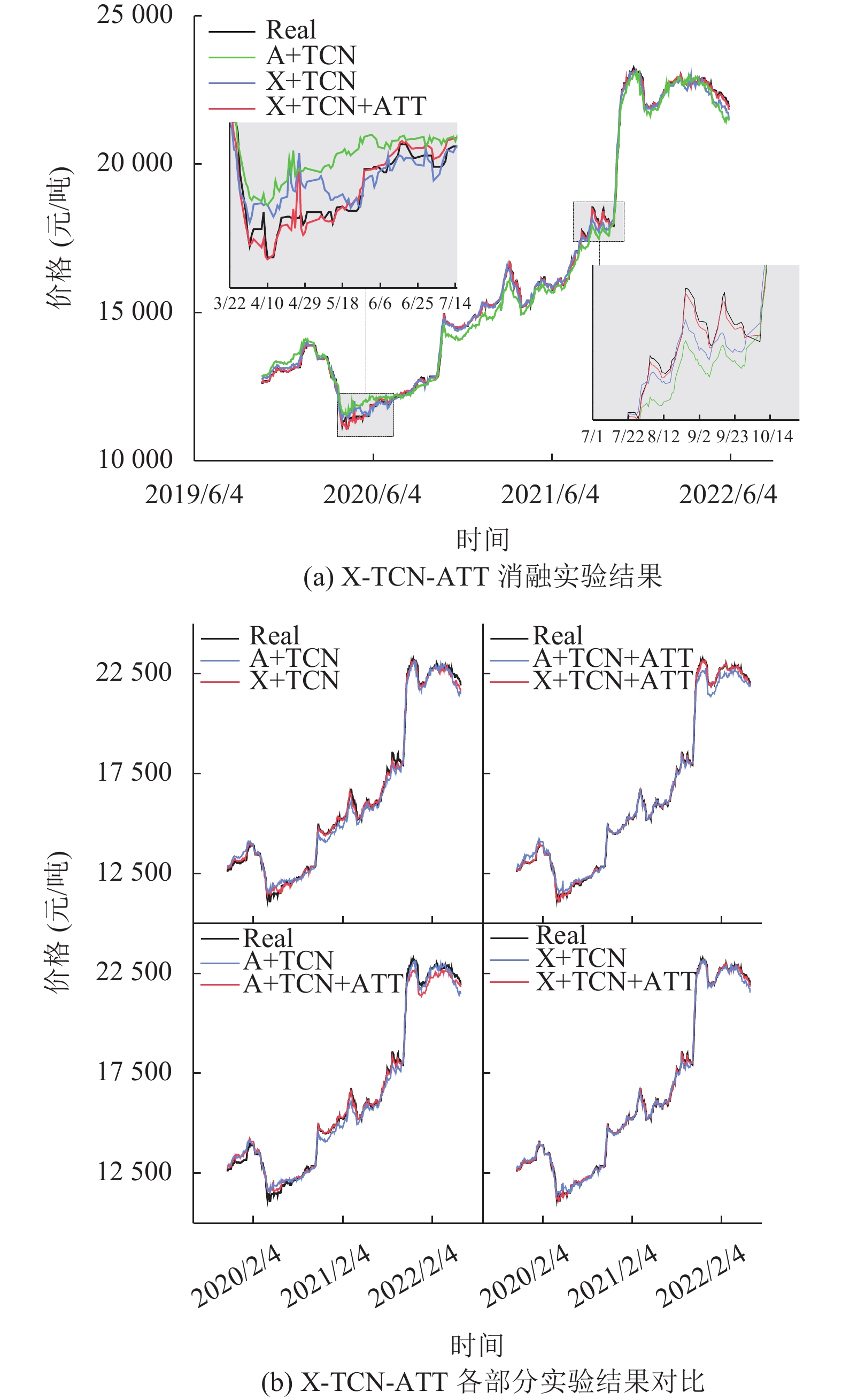
为了验证特征评估和注意力机制的有效性. 使用TCN和引入注意力机制的TCN模型作为预测模型设计了消融实验. 其中, “A+”代表将所有特征都输入模型进行预测, “X+”代表使用经过XGBoost排序筛选后的特征组合来进行预测. “+ATT”代表引入注意力机制的模型. 实验结果如图9和表6所示.

图9中给出消融实验中不同模型的预测曲线, 表6中展示了各模型预测指标. 可以看出:

利用XGBoost进行输入特征的筛选能够有效提高预测精度和模型运算效率. X+TCN与A+TCN相比, MAE、RMSE、MAPE的值分别下降了50.1%、44%、51.8%. X+TCN+ATT与A+TCN+ATT相比, MAE、RMSE、MAPE的值分别下降了77.57%、76.49%、75.18%. 运算时间均有所减少. 证明如果盲目引入其他因素建立预测模型, 会对整个模型的性能造成影响.

同时, 无论以哪种特征组合作为输入, 引入注意力机制的TCN模型的预测效果和模型运算效率都会更好. A+TCN与 A+TCN+ATT相比, MAE、RMSE、MAPE的值分别下降了27%、17.79%、32.76%. X+TCN与X+TCN+ATT相比, MAE、RMSE、MAPE的值分别下降了67.2%、65.48%、65.4%. 运算时间均有所减少. 证明引入注意力机制的预测模型的有效性.

(2)预测模型比较实验

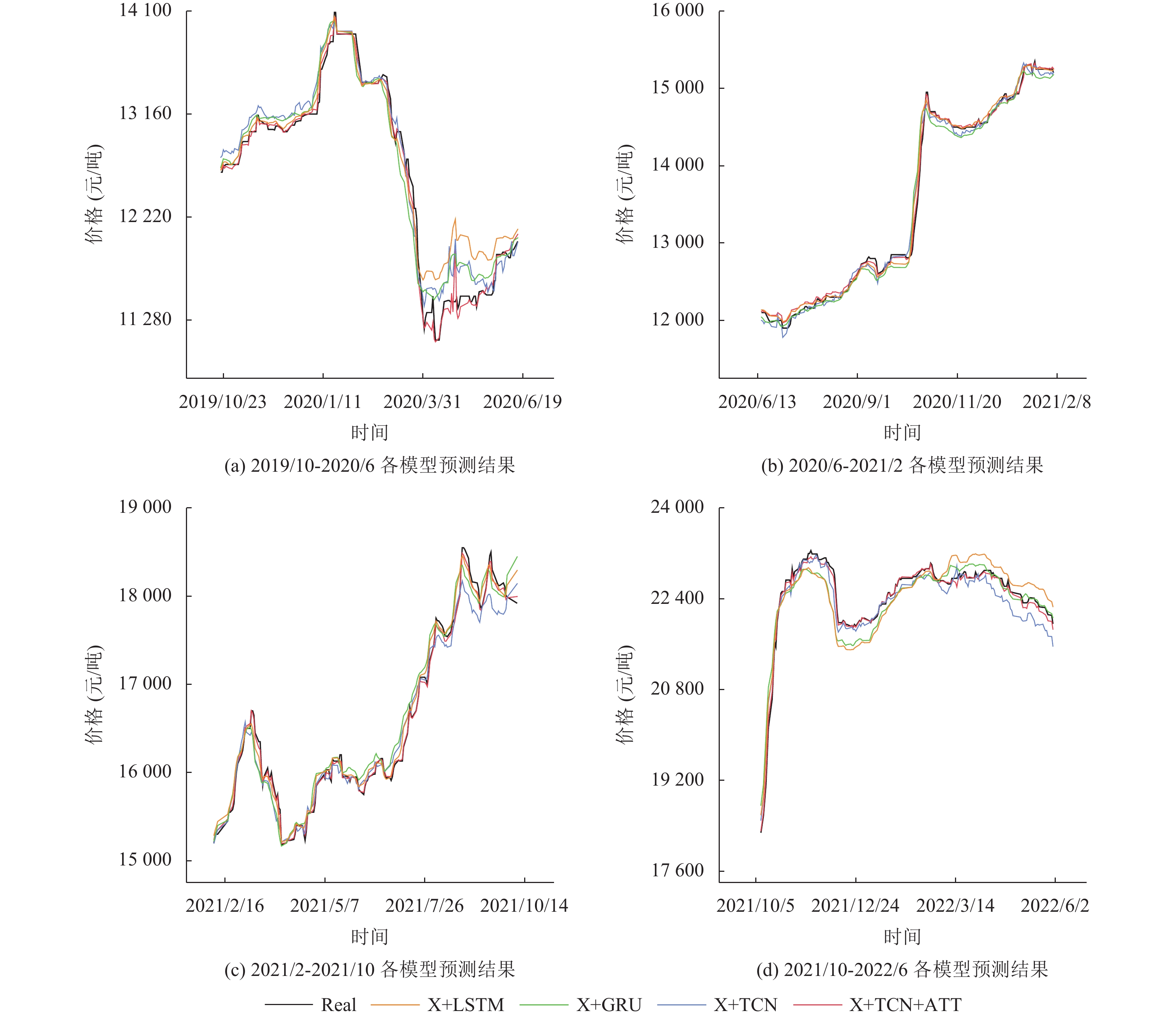
为了验证本文提出的XGBoost+TCN+ATT模型的优越性, 分别建立加入XGBoost算法的X+LSTM、X+GRU和X+TCN这3种组合模型, 并对其进行了对比实验. 实验结果如图10和表7所示. 所有模型的输入数据均由特征选择时选取的5个特征组成, 各比较模型的网络参数如表8所示. 同时, 由于一层TCN网络由两个残差模块组成, 故LSTM和GRU设置两层网络以保证网络层数一致.

图10中给出不同模型的预测曲线. 各个模型的误差如表7所示. 通过实验结果可以看出: 在棉花价格真实值曲线整体波动较大的情况下, 基于极限梯度提升(XGBoost)和引入注意力机制的时间卷积网络(TCN)的模型预测结果最优, 预测值与真实结果拟合状况较好, MAE为41.47, RMSE为58.76, MAPE为0.00273, 在棉花平均价格为16867的基数下, 该误差非常小. 这是因为相比于循环神经网络LSTM和GRU, TCN不需要门控机制, 通过多层卷积和残差连接的方式来建模序列的长期依赖性, 允许并行计算的同时避免了梯度消失或梯度爆炸的问题, 从而可以更加高效地训练模型, 捕捉序列的长期信息. 同时, 在TCN基础上引入注意力机制, 通过学习注意力权重来关注对于预测重要的特征, 可以更加准确地捕捉序列中的重要信息, 从而提高了预测性能和预测结果的可解释性.

5 结论与展望

本文通过对棉花现货价格和其影响因素的分析, 构建了一个基于极限梯度提升(XGBoost)和引入注意力机制的时间卷积网络(TCN)的预测模型. 通过XGBoost算法对所选择的影响因素进行特征评估, 选出影响棉花价格波动的主要因素. 之后将筛选的多特征数据依次组合输入到引入注意力机制的TCN网络模型中进行预测. 最后, 分别通过消融实验和对比实验证明基于XGBoost进行特征评估预测方法比未进行评估的预测方法效果更好, MAE、RMSE、MAPE整体下降了40%以上. 而引入了注意力机制的TCN模型也要比未引入注意力机制的TCN模型、LSTM模型、GRU模型预测精度更高, MAE、RMSE、MAPE整体下降了50%以上. 本文主要贡献如下.

(1)在棉花价格影响因素选择时不仅综合考虑了供需关系、国际市场、宏观经济方面的影响, 同时引入现有的价格预测研究中没有考虑到的棉花产业链因素. 通过特征选择和预测结果证明棉籽、棉粕对棉花价格的影响.

(2)通过XGBoost算法衡量各因素与棉花价格的影响强度, 来对输入影响因素数据进行选择, 通过实验验证特征筛选在价格预测中能够成功降低模型复杂度, 提高模型预测精度和效率.

(3)将引入注意力机制的时间卷积网络(TCN)的预测模型和TCN、LSTM、GRU模型相比, 验证了无论以哪种特征组合作为输入, 引入注意力机制的TCN模型的预测效果和模型运算效率整体更优.

总体来说, 本文所构建的XGBoost-TCN-Attention模型能够选择最少但最有效的特征达到最好的预测效果, 最大提升预测时间, 在棉花现货价格预测中具备可行性和适用性. 同时, 也可以考虑将其应用到不同农产品的价格预测中, 为其他领域的时间序列数据预测提供一定的借鉴. 不过在预测过程中, 存在预测准确度下降点, 之后将对这一情况进行深入研究, 探明其出现的原因, 并采取合适办法解决该问题, 以此提高模型稳定性.