图像修复的应用领域非常广泛, 包括医疗、工业生产、军事、娱乐和卫星通讯等. 但由于在图像的传播扩散或者是保存的过程中, 常有损坏、失真或者受到污染等问题, 从而导致图像信息不完整, 所以, 在图像处理技术当中, 图像修复技术属于一项十分重要的研究工作. 图像修复技术可用于历史文物修复、旧照片修复、刑侦方面等.
与图像去噪、图像去雾、图像去雨以及图像超分等图像处理技术相对比, 图像修复更强调根据图像内容、细节以及特征纹理进行修复, 在对画面损坏或缺失部分进行补充的同时, 还要确保色彩连贯协调以及质感得到适当延伸, 同时, 在图像存在较大面积的破损时, 还要确保修复之后的图像内容与真实图像的一致性以及主观效果, 使得修复后的图像尽可能还原原始图像并且能够符合人类视觉感官.
在图像修复领域, 基于生成对抗网络的深度学习网络模型展现出其独特的优势, 但是在面对较复杂的特征时往往无法实现很好的修复效果, 存在伪影、纹理细节退化等现象, 造成视觉效果上的欠缺问题. 为了解决当前模型对大面积破损图像修复不友好以及修复后的图像存在退化现象等问题, 通过对现有方法进行研究, 改进了图像修复模型.
本文的贡献如下: (1)修复模型采用两阶段修复结构, 使用门控卷积解决部分像素缺失与大尺度损坏情况下的局部特征精确描述的问题, 结合残差思想解决使用Sigmoid函数会出现梯度消失的问题; (2)在精修复阶段引入连贯语义注意机制, 不仅关注已知区域和未知区域之间的联系, 更能通过缺失区域间语义相关性进行建模, 对生成区域像素资源再次分配, 根据语义信息进行引导修复, 提升语义的连贯性.
1 相关工作由于深度学习技术[1]发展迅速, 图像修复也渐渐成为了计算机视觉的热门研究方向. Goodfellow等人[2]在2014年首次提出GANs应用于图像处理方面. Pathak等人[3]提出了Context-Encoder网络, 将编码—解码网络结构与生成对抗网络相结合, 以对抗损失和图像重构损失作为约束条件提高模型的图像修复能力. Iizuka等人[4]提出了全局和局部判别器网络, 引入扩张卷积增大感受野, 通过双判别器来提升网络对全局信息和局部信息的融合利用, 使得图像修复结果不仅符合全局语义, 整体也更加合理. Liu等人[5]提出部分卷积修复方法, 使用U-Net网络结构实现图像修复. Yu等人[6]提出了一种带有内容感知的前馈生成网络, 将注意力机制引入到深度学习图像修复方法中. Yu等人[7]提出了一种基于门控卷积的图像修复算法, 采用两阶段生成结构. 先是在生成器的第1阶段, 提取图像中的语义信息; 然后在生成器第2阶段将粗修复网络的结果作为输入, 细化生成部分的内容, 使生成图像的纹理结构更合理.
2 网络结构 2.1 修复网络体系结构生成器为两阶段修复, 首先, 第1阶段(粗修复阶段)输入被污染的图像以及污染区域的灰度图, 通过网络提取图像中的语义信息; 其次, 第2阶段(精修复阶段)输入第1阶段的生成结果, 引入连贯语义注意机制更好地对被污染区域以及未被污染区域进行关联, 使修复的纹理结构更加合理. 两阶段组成完整的修复流程, 具体修复网络结构如图1所示.
由于门控卷积拥有独特的特征筛选能力, 所以在生成器部分可以将其用于替代普通卷积, 提高图像处理的效率. 为了进一步提升处理效果, 引入扩张卷积层[8], 从而拓展了感受范围, 提供更丰富的特征信息, 促进图像修复, 并在模型设计中引入残差思想[9], 将门控卷积改为残差门控卷积, 防止梯度消失问题. 在生成器第2阶段, 通过使用连贯语义注意力来将局部特征和全局特征相关联, 能够更好地理解图像的整体结构, 提高图像的修复效果, 解决图像修复细节退化、视觉欠缺问题.
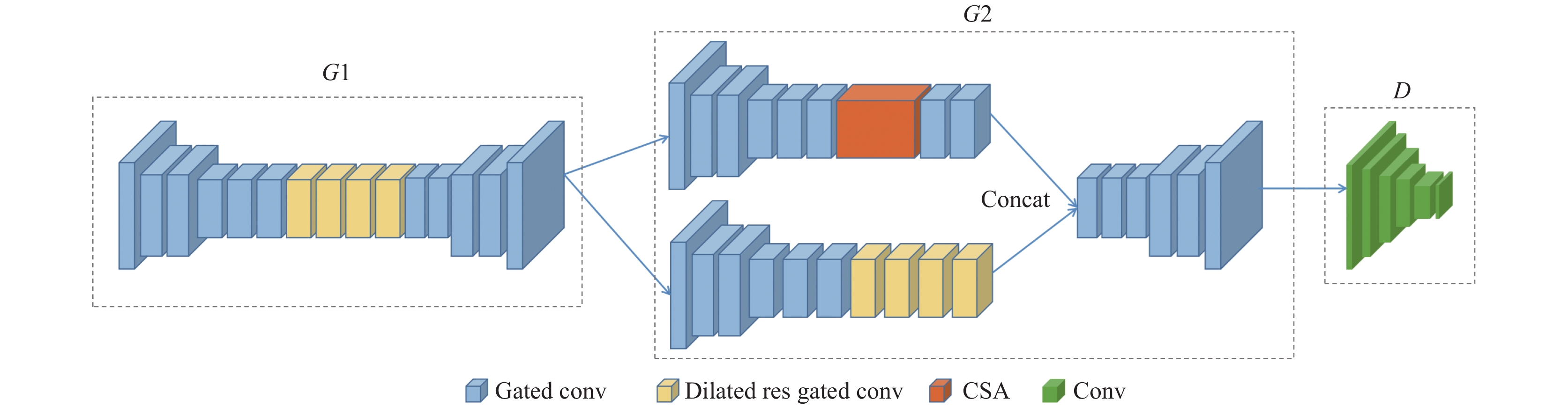
|
图 1 修复网络体系结构 |
2.2 生成器 2.2.1 门控卷积
门控卷积[10]最早出现在NLP的任务中, 取得了良好的结果, Yu等人[7]将其引入到图像修复网络. 门控卷积学习每个通道和每个空间位置的动态特征选择机制, 具体操作的计算公式表达如下:
| Gatingy,x=∑∑Wg⋅I | (1) |
| Featurey,x=∑∑Wf⋅I | (2) |
| Oy,x=Ø(Featurey,x)⊙(Gatingy,x) | (3) |
其中, Sigmoid激活函数用

|
图 2 门控卷积结构图 |
通过在标准卷积后接入Sigmoid激活函数, 使得门控卷积可以实现软门控, 对当前卷积层的输出结果在进入下一个卷积层之前进行加权. 在硬门控中, 使用0或1来进行加权, 但在软门控中, 使用0到1进行加权, 这样更加灵活, 并且这种操作是可学习的. 门控卷积特有的参数动态更新机制, 对缺失区域进行动态学习, 将缺失区域与已知区域进行有效的动态区分, 可以更好地解决局部特征精确描述问题.
2.2.2 扩张卷积Google团队[11]提出的扩张卷积(dilated convolution)也被称为空洞卷积或膨胀卷积, 它是在标准卷积核中注入空洞, 通过拓宽图像的感受野来获取图像中更多的特征信息. 相比普通卷积操作, 扩张卷积多了个扩张率(dilation rate)参数, 扩张率用来定量衡量卷积核超参数的扩张程度. 传统的普通卷积就是扩张率为1的扩张卷积. 图3为卷积核尺寸是3×3, dilation rate是2的扩张卷积示意图.
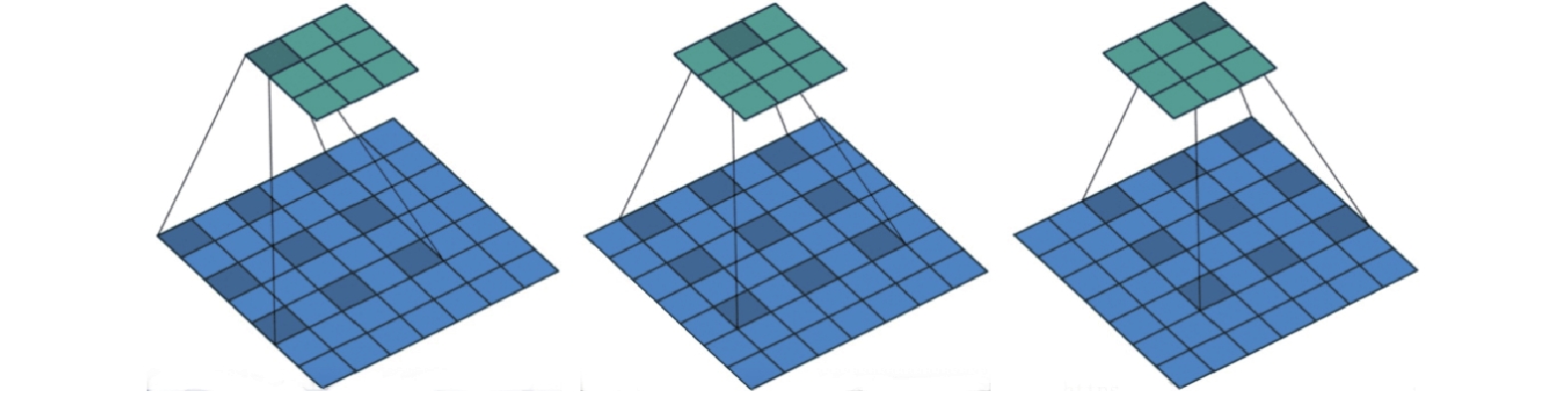
|
图 3 扩张率为2的3×3卷积核的扩张卷积示意图 |
从图3可以看出扩张率为2的3×3卷积核具有与5×5卷积核相同的视野, 而且扩张卷积只使用了9个参数, 也就是说, 在相同的计算成本下, 扩张卷积计算具有更宽的视野, 从而能够捕捉更长的依赖关系.
本文将4层扩张卷积应用于粗修复阶段的中间部分, 扩张卷积层的扩张率自2起随层数递增而翻倍增加, 将扩张率持续变大的扩张卷积层叠加在一起, 以持续增加图像的感受野, 从而加强网络对图像整体特征信息的提取和利用.
2.2.3 残差门控卷积门控卷积的输出门控值通过Sigmoid激活函数, 输出值在 . 基于此, 门控卷积避免了人为设置的更新方法, 通过学习每个通道和每个空间位置的动态特征选择机制, 由每一个通道进行动态特征选择, 让网络自行学习每一个特征值位置.
Sigmoid激活函数值域为(0, 1), 由于Sigmoid函数值趋近于0或1时变化平缓, 如果隐藏层较多梯度接近0时会出现梯度消失问题, 在图像修复中导致一些特征无侧重点, 引入残差思想, 用残差门控卷积替代门控卷积, 图4为以带扩张的门控卷积为例的残差门控卷积结构.

|
图 4 残差门控卷积结构 |
从图4可以看出, 在门控卷积的基础上加上一个1×1的残差块构成残差门控卷积, 对输入的有效特征信息进行卷积, 卷积核大小为1×1, 最后将1×1卷积的输出添加到原门控卷积输出上, 目的是提升对有效像素的使用.
2.2.4 连贯语义注意图像修复任务仅考虑缺失区域与已知区域之间的关系是不够的, 因为其忽略了缺失区域的内容, 为了达到更好的图像修复效果, 将连贯语义注意(coherent semantic attention, CSA)层[12]用于图像修复任务重, 不仅分析了缺失区域特征之间的语义相关性, 而且可以从已知区域提取缺失区域的信息, 通过分析远距离的图像信息、缺失区域之间的关系, 可以保证修复结果的局部连续性.
CSA分为两个阶段实现: 搜索和生成. 图5为CSA的搜索和生成操作. 每张待修复图片中用
| Dmaxi=⟨mi,¯mi⟩‖ | (4) |
| D_{{\rm{ad}}i} = \frac{{\left\langle {{m_i}, {m_{i - 1}}} \right\rangle }}{{\left\| {{m_i}} \right\| \cdot \left\| {{m_{i - 1}}} \right\|}} | (5) |
其中,

|
图 5 CSA层示意图 |
CSA的具体步骤为: 首先, 我们在洞
搜索阶段先提取
生成阶段将
综上所述, 从
| {m_1} = \overline {{m_1}} , \; D_{{\rm{ad}}1} = 0 | (6) |
| \mathop {{m_i}}\limits_{i \in (2 \sim n)} = \frac{{D_{{\rm{ad}}i}}}{{D_{{\rm{ad}}i} + {{D}}_{{{{\rm{max}}}}i}}} \times {m_i} + \frac{{{{D}}_{{{{\rm{max}}}}i}}}{{D_{{\rm{ad}}i} + {{D}}_{{{{\rm{max}}}}i}}} \times \overline {{m_i}} | (7) |
如式(7)所示, 生成操作是一个迭代过程, 每个
算法1. CSA算法流程
输入: 当前批次的特征图集
输出: 重构的特征图
1) 搜索:
2) 将
3) 用式(4)计算
4) 用
5) 结束搜索.
6) 生成:
7) for i=1
8) 用式(5)计算
9) 用式(7)得到
10) end for;
11) 将
12) 重用
13) 结束生成.
14) 返回
马尔可夫判别器(PatchGAN)[13] 一种仅在补丁范围内进行“惩罚”的鉴别器, 如图6所示, PatchGAN在输入上滑动一个N×N的窗口, 并生成一个分数, 输出矩阵的每个值表示对应的图像补丁是真实的还是人为生成的概率.
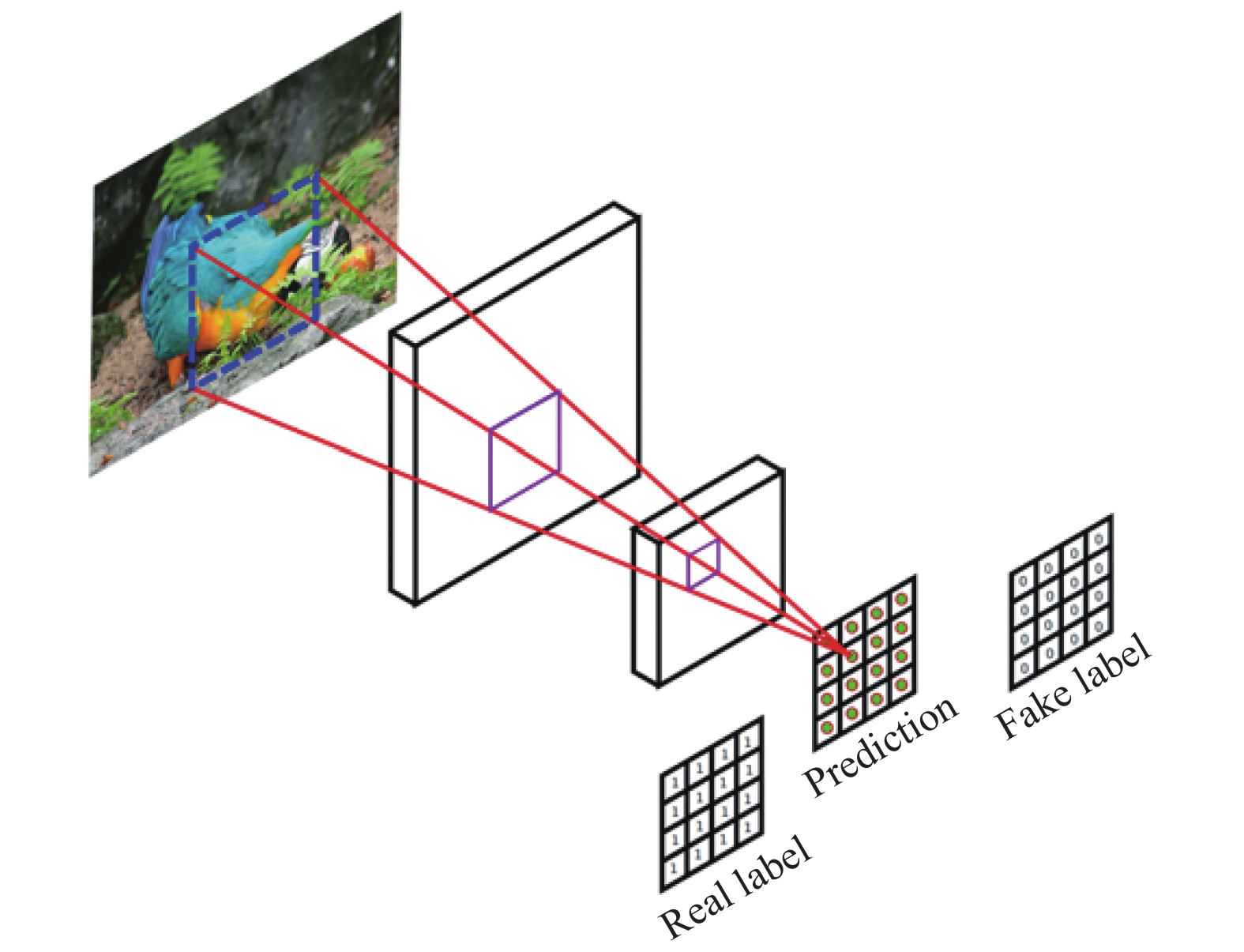
|
图 6 马尔可夫判别器 |
谱归一化马尔可夫判别器(spectral normalized PatchGAN, SN-PatchGAN)用于训练自由形式的图像修复网络, 它直接对卷积判别器的输出特征图中的每个点应用GAN损失, 从而产生高质量的修复效果. 采用光谱归一化马尔可夫判别器作为模型判别器, 通过对图像修复网络特征图进行检验, 将修复后的图像与真实图像进行判别, 并采用谱归一化方法对GANs的训练进行进一步的稳定, 网络通过判别器来进行对抗训练, 进而提升生成器的生成效果.
2.4 损失函数训练模型的损失函数包括像素级L1重建损失以及SN-PatchGAN损失两个损失项, 用来平衡这两个损失项的超参数为1:1. 为了区分输入的真假, 以铰链损失(hinge loss)作为目标函数:
| \begin{split}{L_{{D^{{{s}}n}}}} = &{E_{x \sim {P_{{\rm{data}}}}(x)}}\left[{{ReLU}}(1 - {D^{sn}}(x))\right] \\ & +{E_{{\textit{z}} \sim {P_{\textit{z}}}({\textit{z}})}}\left[{{ReLU}}(1 - {D^{sn}}({\textit{z}}))\right]\end{split} | (8) |
| {L_G} = - {E_{{\textit{z}} \sim {P_{\textit{z}}}({\textit{z}})}}\left[{D^{sn}}(G({\textit{z}}))\right] | (9) |
其中,
由于谱归一化判别器中已经编码了类似的补丁级别信息, 所以这里的损失函数不再使用感知损失.
3 图像质量评价指标文献[6]中提到图像修复缺乏良好的定量评价指标. 本文使用L1、L2损失函数、峰值信噪比(PSNR)以及结构相似度(SSIM)这4种指标来评估图像修复的结果.
L1损失函数被用于最小化误差, 即真实图像与修复图像间全部绝对差的总和.
| L1 = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_{{\rm{true}}}} - {y_{{\rm{predicted}}}}} \right|} | (10) |
L2损失函数用于最小化误差, 该误差是真实图像和修复图像所有平方差的总和.
| L2 = \frac{1}{m}\sum\limits_{i = 1}^m {{{\left( {{y_{{\rm{true}}}} - {y_{{\rm{predicted}}}}} \right)}^2}} | (11) |
峰值信噪比(PSNR)是评价图像质量的一个指标, PSNR值越大, 图像失真越少.
| {\textit{PSNR}} = 10\log_{10} \left(\frac{{{{({2^{bits}} - 1)}^2}}}{{m \cdot L2}}\right) | (12) |
结构相似性(SSIM)是衡量真实图像和生成图像相似度的指标, SSIM值越大代表图像越相似.
| {\textit{SSIM}}(x, y) = \frac{{\left(2{\mu _x}{\mu _y} + {C_1}\right)\left(2{\sigma _{xy}} + {C_2}\right)}}{{\left(\mu _x^2 + \mu _y^2 + {C_1}\right)\left(\sigma _x^2 + \sigma _y^2 + {C_2}\right)}} | (13) |
其中,
实验使用的数据集是Places365数据集[14], 包含数百个实际场景的综合场景, 能够更好地结合各个场景的图像修复, 从中选取30000张图片作为本文实验数据集. 矩形掩码为随机生成破损区域的方式, 随机掩码使用的是文献[7]中提出的.
4.2 实验设置本文模型使用PyTorch深度学习框架. 同时使用CUDA 11.0和CuDNN 8.0加速模型训练, 硬件设备配置表如表1所示. 模型选择Adam优化器, 学习率大小为0.0001, 总计迭代30万次.
| 表 1 硬件设备配置表 |
4.3 实验结果对比与分析
为验证算法的有效性, 将本文提出的算法通过矩形掩码以及不规则掩码在图像质量评价指标上与基线进行对比, 具体结果如表2所示.
由表2可以看出, 当掩码为矩形掩码时, 本文算法在L1指标上提升了0.14%, 在L2指标上提升了0.04%, PSNR提升了0.41 dB, SSIM提升了0.75%; 掩码为不规则掩码时, 本文算法L1提升了0.3%, L2提升了0.05%, PSNR提升了0.55 dB, SSIM提升了1.23%. 可以得出, 本文的算法在各项指标上都优于基线算法.
| 表 2 图像质量评价指标对比 |
除了客观的评价指标, 也能从实际的图像修复结果中反映图像的修复效果, 本文算法的修复结果与基线的对比如图7所示, 从左到右依次为受损图像, 基线模型结果, 本文算法的修复结果以及真实图像. 前2行为矩形掩码, 后3行为随机掩码. 通过对比图6的修复结果可以发现本文算法在图像纹理、边缘细节上的处理都是优于基线的.

|
图 7 修复结果对比 |
5 结论与展望
本文提出了一种基于生成对抗网络的图像修复模型, 在生成器阶段采用门控卷积网络, 使用两阶段修复法, 在第1阶段加入扩张卷积并引入残差思想, 对图像进行粗修复, 在第2阶段引入连贯语义注意对生成区域像素资源再次分配, 根据语义进行引导修复, 从而提升语义的连贯性. 使用谱归一化马尔可夫判别器给生成器提供精细的反馈, 从而提高图像的修复质量. 通过实验表明, 本文提出的图像修复模型修复效果良好, 使修复区域内容更丰富, 纹理更逼真.
本文希望在下一步工作中, 能够对图像缺失部分的关键特征信息进行更好地研究以及得到多重修复结果, 达到更好的修复效果.
| [1] |
赵露露, 沈玲, 洪日昌. 图像修复研究进展综述. 计算机科学, 2021, 48(3): 14-26. DOI:10.11896/jsjkx.210100048 |
| [2] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2672–2680.
|
| [3] |
Pathak D, Krähenbühl P, Donahue J, et al. Context encoders: Feature learning by inpainting. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2536–2544.
|
| [4] |
Iizuka S, Simo-Serra E, Ishikawa H. Globally and locally consistent image completion. ACM Transactions on Graphics, 2017, 36(4): 107. |
| [5] |
Liu GL, Reda FA, Shih KJ, et al. Image inpainting for irregular holes using partial convolutions. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 89–105.
|
| [6] |
Yu JH, Lin Z, Yang JM, et al. Generative image inpainting with contextual attention. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 5505–5514.
|
| [7] |
Yu JH, Lin Z, Yang JM, et al. Free-form image inpainting with gated convolution. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4470–4479.
|
| [8] |
Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions. arXiv:1511.07122, 2015.
|
| [9] |
Yi ZL, Tang Q, Azizi S, et al. Contextual residual aggregation for ultra high-resolution image inpainting. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 7505–7514.
|
| [10] |
Dauphin YN, Fan A, Auli M, et al. Language modeling with gated convolutional networks. Proceedings of the 34th International Conference on Machine Learning. Sydney: PMLR, 2017. 933–941.
|
| [11] |
Chen LC, Papandreou G, Kokkinos I, et al. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/TPAMI.2017.2699184 |
| [12] |
Liu HY, Jiang B, Xiao Y, et al. Coherent semantic attention for image inpainting. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 4169–4178.
|
| [13] |
Demir U, Unal G. Patch-based image inpainting with generative adversarial networks. arXiv:1803.07422, 2018.
|
| [14] |
Zhou BL, Lapedriza A, Khosla A, et al. Places: A 10 million image database for scene recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(6): 1452-1464. DOI:10.1109/TPAMI.2017.2723009 |
 2023, Vol. 32
2023, Vol. 32



