网络数据是复杂系统中个体之间相互关系的一种抽象表示, 网络数据研究的重点议题包括社区发现和链路预测. 社区发现利用高组内连通性和低组间连通性划分网络节点, 划分的节点类被称作社区; 链路预测作为社区发现的下游任务, 探测具有较高互动可能性的个体间的结构, 预测缺失或未来潜在连边. 如在学术合著网络^[1]中, 社区发现探寻作者合著团体与研究方向, 有利于揭示合著产生机制、促进新的合著; 链路预测挖掘潜在的合著可能, 有利于合著关系推荐. 社区发现能揭示网络数据结构形态, 在生物医疗、物流通讯等领域有着广泛的应用场景, 有助于提高人们的工作效率与生活质量. 链路预测可以帮助研究者挖掘网络数据中的潜在关联, 在社交推荐、资源分配等场景发挥重要作用, 为决策分析提供科学依据.

社区发现可被视作网络节点聚类问题, 经典启发式算法包括基于层次聚类的分裂算法(GN)^[2], 贪心算法(FN)^[3]等. 链路预测算法主要以基于网络拓扑结构、基于动力学的算法为主, 如共同邻居算法(CN)^[4]、优先连接算法(PA)^[5]等. 这类启发式算法依赖于现实网络形态的简单假设和离散的优化学习方式, 但难以描述更复杂的网络链路数据^[6]. 在启发式算法的基础上, 生成模型利用具体概率分布对网络进行建模, 将社区发现和链路预测问题转化为统计推断问题.

随机块模型(stochastic blockmodel, SBM)^[7]是网络分析中的经典模型, 能刻画不同类型的网络结构、还原网络生成过程. 此外随机块模型中的区块结构使其在社区发现任务上有天然的优势, 能够挖掘网络隐含结构与潜在联系, 常应用于推荐算法、风控反欺诈、传染病爆发范围预测等领域. 赵学华等^[8]提出精细随机块模型及对应快速学习方法降低时间复杂度. Yu等^[9]提出混合隶属度随机块模型解决动态网络社区发现问题. Liu等^[10]考虑加权随机块模型与块状学习算法分析大规模网络. Noroozi等^[11]提出稀疏随机块模型, 加入惩罚项提高社区发现准确率. Chen等^[12]基于随机块模型讨论多层网络中的社区发现问题. Legramanti等^[13]利用无监督方法同时学习随机块模型中社区个数与节点-社区隶属关系. 然而随机块模型中同一区块内的节点等价, 因此无法描述网络中的传递性与相互性特征, 在链路预测中是粗糙的^[14], 而网络嵌入思想的引入能有效解决这些问题.

网络嵌入(network embedding)将网络结构特征等信息映射为节点向量化表示, 基于此完成聚类、分类、预测等任务, 是网络表征学习的一种方法^[15]. 网络嵌入为网络数据可视化提供一种新的视角, 更直观地展现了节点之间的连接紧密程度与相似程度, 为研究者决策分析、政策规划提供参考与指导. 隐空间模型是一类基于网络嵌入的生成模型, Hoff等^[16]提出两类基于节点隐位置(latent position)的隐空间模型: 距离模型(latent space distance model, LSM)和投影模型(latent space projection model, LPM). Handcock等^[17]基于此提出隐空间聚类模型(latent position cluster model, LPCM)用于社区发现. Chang等^[18]引入节点受欢迎程度, 简化计算步骤. Sewell等^[19]建立动态隐空间模型用于社区发现与链路预测. Zhang等^[20]考虑有向网络中节点的发送、接收模式, 推断社区与节点嵌入表示. Liu等^[21]考虑多个隐空间中的网络嵌入探寻社区. Sosa等^[22]和MacDonald等^[23]讨论多层网络下的隐空间模型与模型选择方法. 遗憾的是, 生物网络、脑网络等数据中常存在异配结构, 异配网络中有差异的节点之间更有可能建立连接, 而这类模型与算法倾向于连接具有相似结构的节点, 在刻画异配网络结构时有一定局限性^[24], 进而影响社区发现的效果.

现有网络模型与算法通常集中在社区发现或链路预测的单一任务中, 仅关注网络区块结构或个体互动传递性的单一层面^[25]. 而现实网络结构复杂, 往往跨越多个研究层面, 当前模型与算法不能完全刻画出现实网络的多样性, 为社区发现与链路预测任务带来挑战. 为了解决上述问题并满足现实需求, 我们在经典随机块模型算法的基础上借助网络嵌入的思想, 通过更具普适性的网络嵌入随机块模型(network embedding stochastic blockmodel, NE-SBM)构建网络, 采用Metropolis Hasting-Gibbs算法和可识别性调整算法得出节点-社区隶属关系完成社区发现任务, 并基于条件概率完成下游链路预测任务, 该方法在这两类任务中均有很好的表现.

本文有如下两方面的创新.

(1)在网络生成方面, 网络建模的方式直接捕获网络结构信息, 还原网络生成过程. 本文将网络嵌入与随机块模型结合, 联合节点隶属社区关系与隐位置投影刻画有向网络连接模式. 本文提出的NE-SBM模型克服了传统随机块模型在链路预测、隐空间模型在社区发现任务中的不足, 可以视作两者的广义形式, 放宽了对网络数据的要求, 更具普适性.

(2)在算法方面, 首先构建贝叶斯框架完成模型参数正则化, 现实网络数据中常存在孤立节点, 传统基于极大似然估计的算法通常失效, 贝叶斯框架使得这些孤立节点具有与其他节点相连的正概率, 有利于链路预测任务; 其次, 利用Metropolis Hasting-Gibbs算法与增补变量法进行参数推断, 规避传统变分推断、EM算法中部分参数无显式迭代表达式的问题; 最后, 利用加权多维尺度变换解决隐位置的可识别性问题. 实验证明了模型框架与算法的有效性. 相比之下, 启发式算法需要依据先验知识指定判断网络结构的准则或评价函数, 先验难以选取且直接影响最终分析结果.

1 网络嵌入随机块模型下的网络构建

本节通过网络嵌入随机块模型(network embedding stochastic blockmodel, NE-SBM)构建网络, 对节点的社区隶属关系的生成、节点嵌入以及边的连接模式做详细说明.

对于包含 $N$ 个节点有向网络 $G = (V, E)$ , V表示节点集合且 $\left| V \right| = N$ , E表示边集合. N维邻接矩阵Y以二维数组的形式描述节点之间的连接关系, ${Y_{ij}} = 0$ 代表节点i和节点j之间没有连边; 反之, ${Y_{ij}} = 1$ 代表存在由节点i发出, 指向节点j的有向边. 不考虑自连接的情形, 邻接矩阵的对角元均为0.

节点-社区隶属关系分配: 假定网络中社区个数为K, 向量 ${{\gamma}}=\left(\gamma_{1}, \cdots, \gamma_{N}\right)$ 表示N个节点的社区隶属关系, 称为社区标签, 每个节点的社区标签相互独立, 服从多项分布, 如式(1)所示:

$ {\gamma _i}|\pi \sim{{{{\rm{Multinomial}}}}} \left( {1;{\pi _1}, \cdots , {\pi _K}} \right), \quad i = 1, \cdots , N $

(1)

网络嵌入下节点隐位置表示: 利用网络嵌入的思想将节点映射到一个d维连续隐空间, 该隐空间能够体现原网络的结构、特征以及其他信息. 记节点对应的隐位置为 ${Z_i}$ , 假定每个节点的隐位置相互独立, 且服从于均值为0的多元正态分布:

$ Z_{i} \sim {{\rm{MVN}}}\left(0, \left(\sigma_{\gamma_i}^{2}\right) I_{d}\right), \quad i=1, \cdots, N $

(2)

社区间随机块模式: 如果节点i和节点j的社区标签不同, 两节点分别隶属于k社区和l社区, 假定产生连边的概率与两节点的社区标签及它们的发送、接收效应有关, 即:

$ \begin{split} & {Y_{ij}}|{\gamma _i} = k, {\gamma _j} = l, {s_i}, {r_j}, k \ne l \sim{{\rm{Bern}}} \left( {{{{{\rm{logit}}} }^{ - 1}}\left( {{\eta _{kl}} + {s_i} + {r_j}} \right)} \right) \end{split} $

(3)

向量 ${s}=\left(s_{1}, \cdots, s_{N}\right)$ 和 ${{{r}}}=\left(r_{1}, \cdots, r_{N}\right)$ 为网络中N个节点的接收、发送效应, $\eta $ 为K维社区间系数矩阵, 其对角元都为0. 定义:

$ {{\theta}}:=\left(\eta_{12}, \cdots, \eta_{1K}, \cdots, \eta_{K, K-1}, s_{1}, \cdots, s_{N}, r_{1}, \cdots, r_{N}\right)^{{\rm{T}}} $

此时, 社区间边连接分布可以简化为:

$ {Y_{ij}}\mid {\gamma _i} = k, {\gamma _j} = l, {s_i}, {r_j}, k \ne l\sim{{{\rm{Bern}}}}({\text{logi}}{{\text{t}}^{ - 1}}(X_{ij}^{\rm{T}}{\boldsymbol{\theta }})) $

(4)

矩阵X是所有块间节点对关于 ${{\theta}}$ 的系数矩阵, 其维数为 $\displaystyle\sum_{i \neq j} I\left(\gamma_{i} \neq \gamma_{j}\right) \times\left(2 N+K^{2}-K\right)$ . $X_{ij}$ 表示节点对 $ (i, j) $ 对应的系数向量. 基于Ng等^[24]工作中有关可识别性的讨论, 我们对应地给出本模型的可识别性条件:

$ \sum_{i:{{\gamma }_{i}}=k} s_{i}=0, \quad \sum_{i:{{\gamma }_{i}}=k} r_{i}=0 $

(5)

社区内网络嵌入模式: 如果节点i和节点j的社区标签相同, 隶属于社区k, 假定产生连边的概率与节点隐位置和社区标签这两个因素有关, 利用节点隐位置投影刻画节点对产生连接的可能性, 连接概率的表达式可以写成如下形式:

$ \operatorname{logit} P\left(Y_{i j}=1 \mid \gamma_{i}=\gamma_{j}=k,Z_{i}, Z_{j}\right)=\beta_{k}+\frac{Z_{i}^{{\rm{T}}} Z_{j}}{\left|Z_{j}\right|} $

(6)

即: $Y_{ij} \mid \gamma_{i}=\gamma_{j}=k, Z_{i}, Z_{j} \sim {{\rm{Bern}}}\left(\operatorname{logit}^{-1}\left(\beta_{k}+\dfrac{Z_{i}^{{\rm{T}}} Z_{j}}{\left|Z_{j}\right|}\right)\right)$ .

随机块模型的区块结构揭示了社区发现结果, 下游的链路预测结果由概率矩阵得到, 但同一区块内节点连接概率相等, 难以刻画网络传递性与相互性, 因此链路预测结果是粗糙的; 隐空间模型结合网络嵌入的思想, 社区发现结果常由隐位置聚类得到, 链路预测结果则是依据节点隐位置间距离、投影等度量计算连接概率得到, 但由于缺少区块结构, 在社区发现任务中适用范围不及随机块模型广泛.

NE-SBM模型的社区内网络嵌入模式克服了随机块模型难以刻画网络传递性和相互性的困难; 社区间随机块模式弥补了隐空间模型在刻画社区结构上的不足. 在不区分社区内与社区间网络连接模式的情况下, 随机块模型和隐空间模型可以视作NE-SBM模型的特殊形式, 因此NE-SBM模型更具普适性, 相比基础模型更加灵活, 平衡了简明性与丰富性, 可以适应于更多类型的网络数据, 在社区发现与链路预测任务中都能有较好的表现.

2 算法实现

本节主要对社区发现与链路预测算法实现做详细说明. 首先构建贝叶斯框架指定先验, 完成模型参数正则化, 之后利用Metropolis Hasting-Gibbs算法进行后验采样得到节点社区标签等参数的估计, 最后利用重新标注算法和加权多维尺度变换分别对节点社区标签与节点隐位置做可识别性调整, 得到社区发现结果, 并计算节点间存在边的条件概率得到链路预测结果.

2.1 贝叶斯框架的构建

针对NE-SBM的模型参数构建贝叶斯框架, 假设模型参数 ${{\pi}}=\left(\pi_{1}, \cdots, \pi_{K}\right)$ , ${{\beta}}=\left(\beta_{1}, \cdots, \beta_{k}\right)$ , ${{\theta}}$ 的先验分布如下:

$ {{\pi}} \sim \text { Dirichlet }(T, \cdots, T) $

(7)

$ \beta_{k} \sim {{{N}}}\left(0, \sigma_{\beta}^{2}\right), \quad k=1, \cdots, K $

(8)

$ {{\theta}} \sim {{\rm{MVN}}}\left(0_{2 N+K^{2}-K}, \sigma_{\theta}^{2} I_{2 N+K^{2}-K}\right) $

(9)

Nowicki等^[7]提出, 选取较小的T会导致推断结果倾向于大小不平衡的社区结构, 本文设定 $ T=10 $ 防止有大小几乎为0的社区产生. 此外, 实验配置与实证分析中我们设定先验分布标准差 $\sigma_{\beta}=5$ , $ \sigma_{\theta}=5 $ , $\sigma_{\textit{z}}=3$ , 此参数设定先验分布下的模型有较好的预测表现.

模型的似然表达式为:

$ P(Y \mid \gamma, Z, \beta, \theta)=\prod_{i=1}^{N} \prod_{j\ne i}^{N} p_{i j}^{Y_{ij}}\left(1-p_{ij}\right)^{1-Y_{ij}} $

(10)

基于上述先验分布的假设, 我们可以得到部分参数的后验条件分布:

$ \begin{split} & P\left( {{\gamma }_{i}}=k|其他参数 \right) \\ & \propto {{\pi }_{k}}\prod\limits_{j\ne i}{\{p_{ij}^{{{Y}_{ij}}}(}1-{{p}_{ij}}{{)}^{1-{{Y}_{ij}}}}\}\{p_{ji}^{{{Y}_{ji}}}{{(1-{{p}_{ji}})}^{1-{{Y}_{ji}}}}\} \\ \end{split} $

(11)

$ {{\pi}} \sim \operatorname{Dirichlet}\left(T+n_{1}, \cdots, T+n_{K}\right) $

(12)

其中, $ n_{k} $ 为社区k中包含的节点数, $ k=1, \cdots, K $ , $p_{ij}$ 由式(6)和式(3)计算得出.

2.2 节点社区标签估计: Metropolis Hasting-Gibbs算法

考虑到传统的EM算法与变分推断算法下, 部分参数不具有显式迭代表达式, 通过数值方法求解耗时较长. 我们采用Metropolis Hasting-Gibbs算法进行逐分量采样求解模型.

隐位置与社区标签的成对更新: 由于节点-社区隶属关系与其隐位置相关, 因此在采样的过程中, 对这两个变量成对更新. 给定节点i, 从当前参数对 $(\gamma _i^t, Z_i^t)$ 采样下一个参数对 $ (\gamma _i^*, Z_i^*) $ 的提议分布形式为:

$ q\left( {\left( {\gamma _i^*, Z_i^*} \right)|\left( {\gamma _i^t, Z_i^t} \right)} \right) = q(\gamma _i^*|\gamma _i^t, Z_i^t)q(Z_i^*|\gamma _i^t, \gamma _i^*, Z_i^t) $

(13)

$ \begin{split} & q(\gamma _i^* = k|\gamma _i^t, Z_i^t) = q(\gamma _i^* = k|Z_i^t) \\ &\qquad \propto {\pi _k}\prod\limits_{j \ne i} \left\{{ p_{ij}^{{Y_{ij}}}(} 1 - {p_{ij}}{)^{1 - {Y_{ij}}}}\right\} \left\{ p_{ji}^{{Y_{ji}}}{(1 - {p_{ji}})^{1 - {Y_{ji}}}}\right\} \end{split} $

(14)

$ \begin{split} &q({Z}_{i}^{*}\mid {\gamma }_{i}^{t}, {\gamma }_{i}^{*}, {Z}_{i}^{t})=\\ &\left\{\begin{aligned} &\text{MVN}({Z}_{i}^{*};{Z}_{i}^{t}, {\delta }_{{\textit{z}}}^{2}{I}_{d}), {\gamma }_{i}^{*}={\gamma }_{i}^{t}\\ &\text{MVN}({Z}_{i}^{*};\overline{{Z}_{{\gamma }_{i}^{*}}}, {\delta }^{2}{I}_{d}), {\gamma }_{i}^{*}\ne {\gamma }_{i}^{t}且{\displaystyle \sum _{j}{I}_{({\gamma }_{j}^{t}={\gamma }_{i}^{*})}} > 0\\ &\text{MVN}({Z}_{i}^{*};{0}_{d}, {\sigma }_{{\textit{z}}}^{2}{I}_{d}), {\gamma }_{i}^{*}\ne {\gamma }_{i}^{t}且{\displaystyle \sum _{j}{I}_{({\gamma }_{j}^{t}={\gamma }_{i}^{*})}}=0\end{aligned}\right.\end{split} $

(15)

其中, $\overline {{Z_{\gamma _i^*}}} $ 表示除去节点i外, 社区标签为 $\gamma _i^*$ 的节点的隐位置均值. 给定节点i, 当前的参数对 $(\gamma _i^t, Z_i^t)$ 转移到 $(\gamma _i^*, Z_i^*)$ 的概率为:

$ \alpha = \frac{{{{P}}\left( {{Y_N}|{{{\gamma }}^*}, {{{Z}}^*}, {{\theta }}, \beta } \right)p(\gamma _i^*|\pi )p(Z_i^*|{\sigma _{\textit{z}}})q\left( {\left( {\gamma _i^t, Z_i^t} \right)|\left( {\gamma _i^*, Z_i^*} \right)} \right)}}{{{{P}}\left( {{Y_N}|{{{\gamma }}^t}, {{{Z}}^t}, {{\theta }}, \beta } \right)p(\gamma _i^t|\pi )p(Z_i^t|{\sigma _{\textit{z}}})q\left( {\left( {\gamma _i^*, Z_i^*} \right)|\left( {\gamma _i^t, Z_i^t} \right)} \right)}} $

(16)

为了保证算法效率, 使得隐位置Z对应的马氏链收敛更快, 在同时更新参数对 $(\gamma _i^t, Z_i^t)$ 之后, 固定 $\gamma _i^t$ 的值对 $Z_i^t$ 再做一次随机游走迭代.

辅助变量下社区间连边参数的更新: 在模型设定和先验分布假设下, 并不能直接得出关于社区间连边参数 ${{\theta }}$ 的后验条件分布表达式, 因此我们利用增补变量法^[26], 引入条件分布为Pólya-Gamma分布的辅助变量 ${{\omega }} = {({\omega _{ij}})_{i \ne j:{\gamma _i} \ne {\gamma _j}}}$ , 以获得 ${{\theta }}$ 的显式条件分布:

$ {\omega }_{ij}|其他参数\sim {\rm{PG}}(1, {X}_{ij}(\gamma {)}^{\prime }{{\theta}} ) $

(17)

定义 $\Omega = {\rm{diag}}({\omega _{ij}})$ , ${u_{ij}} = \left({Y_{ij}} - \dfrac{1}{2}\right)\omega _{ij}^{ - 1}$ , ${{u}} = {({u_{ij}})_{i \ne j}}$ , 此时有:

$ {{\theta }}|{\boldsymbol{\omega }}\sim{{{\rm{MVN}}}}(m, V) $

(18)

其中,

$ m = V{X^{\rm{T}}}\Omega {{u}} $

(19)

$ V = {\left( {{X^{\rm{T}}}\Omega X + {{\left( {{\sigma ^\theta }} \right)}^2}{I_{2N + {K^2} - K}}} \right)^{ - 1}} $

(20)

基于上述推导, NE-SBM模型的Metropolis Hasting-Gibbs后验采样算法如算法1所示. 具体来说, 交替采样更新模型参数, 基于辅助变量更新社区间连边参数, Markov链收敛至平稳分布后可得到后验样本.

算法1. Metropolis Hasting-Gibbs后验采样算法

(1) 对于 $\scriptstyle {\gamma _i}, {Z_i}, \; i = 1, \cdots , N$ :

1) 按照式(13)成对采样 $\scriptstyle (\gamma _i^*, Z_i^*)$ ;

2) 按照式(16)转移概率接受 $\scriptstyle (\gamma _i^{t + 1}, Z_i^{t + 1}) = (\gamma _i^*, Z_i^*)$ , 否则 $\scriptstyle (\gamma _i^{t + 1}, Z_i^{t + 1}) = \scriptstyle(\gamma _i^t, Z_i^t)$ ;

3) 采样 $\scriptstyle Z_i^*\sim{\text{MVN}}\left( {Z_i^{t + 1}, {\delta _{\textit{z}}}^2{I_d}} \right)$ , 以 $\scriptstyle \alpha = \frac{{P\left( {{Y_N}|{\boldsymbol{\gamma }}, {{{Z}}^*}, {{\theta }}, {{\beta }}} \right)p\left( {Z_i^*|{\sigma _{\textit{z}}}} \right)}}{{P\left( {{Y_N}|{{\gamma }}, {{{Z}}^{t + 1}}, {{\theta }}, {{\beta }}} \right)p\left( {Z_i^{t + 1}|{\sigma _{\textit{z}}}} \right)}}$ 的转移概率接受 $\scriptstyle Z_i^{t + 1} = Z_i^*$ , 否则 $\scriptstyle Z_i^{t + 1} = Z_i^t$ .

(2) 对于 $\scriptstyle \;{\beta _k}, \; k = 1, \cdots , K$ :

1) 采样 $\scriptstyle \;\beta _k^*\sim N\left( {\beta _k^t, {\delta _\beta }} \right)$ ;

2) 按照 $\scriptstyle \frac{{P({Y_N}|{\gamma ^*}, {Z^*}, \theta , \beta _k^*)p(\beta _k^*;{\mu ^\beta }, {\sigma _\beta })}}{{P({Y_N}|{\gamma ^*}, {Z^*}, \theta , \beta _k^t)p(\beta _k^t;{\mu ^\beta }, {\sigma _\beta })}}$ 的转移概率接受 $\scriptstyle \;\beta _k^{t + 1} = \beta _k^*$ , 否则 $\scriptstyle \;\beta _k^{t + 1} = \beta _k^t$ .

(3) 按照式(18)采样更新 $\scriptstyle {{\theta }}$ , 做以下变换以保证满足式(5)中可识别性条件成立且式(4)值不变:

η_kl' $\scriptstyle= {\eta _{kl}} + \frac{1}{{{n_k}}}{S_k} + \frac{1}{{{n_l}}}{R_l}, \; {s_{i'}} = {s_i} - \frac{1}{{{n_k}}}{S_k}, \; {r_{i'}} = {r_i} - \frac{1}{{{n_k}}}{R_k}$

(4) 按照式(12)采样更新 $\scriptstyle {{\pi }}$ .

算法1提供了对NE-SBM模型参数进行后验采样的方法, 在得到后验样本之后, 计算后验均值得到模型中的参数估计, 计算后验众数得到节点社区标签估计, 经可识别性调整后即可得到社区发现结果.

2.3 可识别性调整: 重新标注算法与加权多维尺度变换算法

在得到模型参数的估计结果之后, 我们需要考虑节点社区标签的可识别性问题(label switching problem). 事实上, 对节点社区标签做置换变换, 模型的似然值是不变的, 本文借助重新标注算法(relabelling algorithm)^[27]来解决这种可识别性问题, 得到最终的社区发现结果.

此外, 隐位置的可识别性问题同样值得我们注意. 式(10)的值在旋转、反射这两种变换下不发生改变, 因此隐位置不唯一. 我们针对Fosdick等^[25]提出的基于加权多维尺度变换(multidimensional scaling, MDS)的算法加以改进, 将之拓展到有向网络的情形.

设后验样本的样本量为M, 社区k中所有具有非零后验概率的节点集合为 ${S_{k0}}$ , 样本m中社区标签为k的节点集合为 ${S_{km}}$ . 基于算法1中得到的后验样本计算对应权重矩阵与距离矩阵, 利用SMACOF算法^[28]重构最佳相对位置, 依据后验样本中的社区标签利用Procrustes变换^[16]调整节点隐位置. 具体如算法2所示.

算法2. 加权多维尺度变换下的隐位置可识别性调整

(1) 对于社区k, $\scriptstyle 1 \leqslant k \leqslant K$ :

1) 计算权重矩阵 $\scriptstyle {W_{k0}}$ : 对 $\scriptstyle i \ne j \in {S_{k0}}$ , $\scriptstyle {\left( {{W_{k0}}} \right)_{ij}}$ 为后验样本中节点i和节点j社区标签都为k的样本数量;

2) 计算距离矩阵 $\scriptstyle {D_{k0}}$ : 对 $\scriptstyle i \ne j \in {S_{k0}}$ , $\scriptstyle {\left( {{D_{k0}}} \right)_{ij}}$ 为后验样本中节点i和节点j隐位置的平均距离, 若 $\scriptstyle {\left( {{W_{k0}}} \right)_{ij}} = 0$ , 则 $\scriptstyle {\left( {{D_{k0}}} \right)_{ij}}$ 缺失;

3) 基于d维平均距离矩阵 $\scriptstyle {D_{k0}}$ , 利用SMACOF算法^[28]重构最佳相对位置, 得到重构后的隐位置集合 $\scriptstyle {Z_{k0}}$ .

(2) 对每个后验样本m, $\scriptstyle 1 \leqslant m \leqslant M$ :

1) 选取 $\scriptstyle {Z_{k0}}$ 中与集合 $\scriptstyle {S_{km}}$ 标签一致的子集 $\scriptstyle {\tilde Z_{k0m}}$ ;

2) 利用Procrustes变换^[16]得到调整后的节点隐位置 $\scriptstyle {\tilde Z_{km}}$ :

$\scriptstyle {\tilde Z_{km}} =$ arg $\scriptstyle \mathop { \min }\limits_{T{Z_{km}}} \left\{ {{tr} {{\left( {{{\tilde Z}_{k0m}} - T{Z_{km}}} \right)}^{\rm{T}}}\left( {{{\tilde Z}_{k0m}} - T{Z_{km}}} \right)} \right\}$

其中, T代表所有的反射变换、旋转变换.

算法2提供了调整节点隐位置可识别性的方法, 针对算法2中得到的隐位置估计, 结合式(3)和式(4)计算节点之间的连边概率即可得到链路预测结果.

3 实验及结果分析 3.1 实验设置

实验硬件环境为AMD Ryzen 75800H处理器, 运行内存为16 GB, 操作系统为Windows 10, 实验采用的语言是R 4.1.3.

本节旨在验证NE-SBM模型及其算法在社区发现与链路预测任务上, 相比基准模型有更佳的表现效果. 具体地, 参照Ng等^[24]的实验设置, 利用不同参数设定下的NE-SBM模型、隐空间聚类模型(LPCM)^[17]和随机块模型(SBM)^[7]模拟生成3种人工网络数据集. 在每种数据集中, 设定网络节点个数 $ N=100 $ , 社区个数 $ K=3 $ , 隐空间维数 $d = 2$ , 节点隶属于每个社区的概率均等, 重复30次以得到一般性的结论. 3种人工网络数据集的生成方式如下.

数据集1: 由NE-SBM模型生成的网络数据, 考虑社区间概率连接矩阵 $\eta $ 中非对角元 $ \lambda $ 的不同取值.

数据集2: 由LPCM模型生成的网络数据, 考虑隐空间距离参数 $ \;\beta $ 的不同取值^[17].

数据集3: 由SBM模型生成的网络数据, 考虑连接概率矩阵参数 $ \omega $ 的不同取值^[7].

3.2 社区发现实验

本部分评估NE-SBM模型与对应算法在社区发现任务中的表现, 与之对比的基准模型为SBM^[7]和LPCM^[17]模型. 采用的社区发现评价指标为聚类错误率(clustering error)^[20]和标准化互信息(NMI)^[29]. 聚类错误率列举所有节点社区标签的排列, 其计算表达式为:

$ { clust.err }=\frac{2}{N(N-1)} \sum_{i<j} I\left(I\left(\gamma_{i}=\gamma_{j}\right)+I\left(\tilde{\gamma}_{i}=\tilde{\gamma}_{j}\right)=1\right) $

(21)

其中, $\gamma $ 代表节点的真实社区标签, $\tilde \gamma $ 代表节点社区标签的估计值.NMI值从信息论角度衡量不同划分的一致程度, 取值在0和1之间, 越接近1意味着当前聚类结果与真实聚类结果一致性越高, 社区划分越准确. 其定义为:

$ {{NMI}}(\gamma , \tilde \gamma ) = \frac{{\displaystyle\sum\limits_{k = 1}^{\tilde K} {\displaystyle\sum\limits_{l = 1}^K {{N_{kl}}} } \cdot \log \frac{{N \cdot {N_{kl}}}}{{{{\tilde N}_k} \cdot {N_l}}}}}{{\sqrt {\left(\displaystyle\sum\limits_{k = 1}^{\tilde K} {{{\tilde N}_k}} \log \frac{{{{\tilde N}_k}}}{N}\right)\left(\displaystyle\sum\limits_{l = 1}^K {{N_l}} \log \frac{{{N_l}}}{N}\right)} }} $

(22)

其中, 算法得到的社区个数为 $\tilde K$ , ${\tilde N_k}$ 代表算法得到的社区k包含节点的数目; 真实社区个数为K, ${N_l}$ 代表真实分类下社区l包含的节点数目, ${N_{kl}}$ 代表同时属于算法分类下社区k和真实分类下社区l的节点数目.

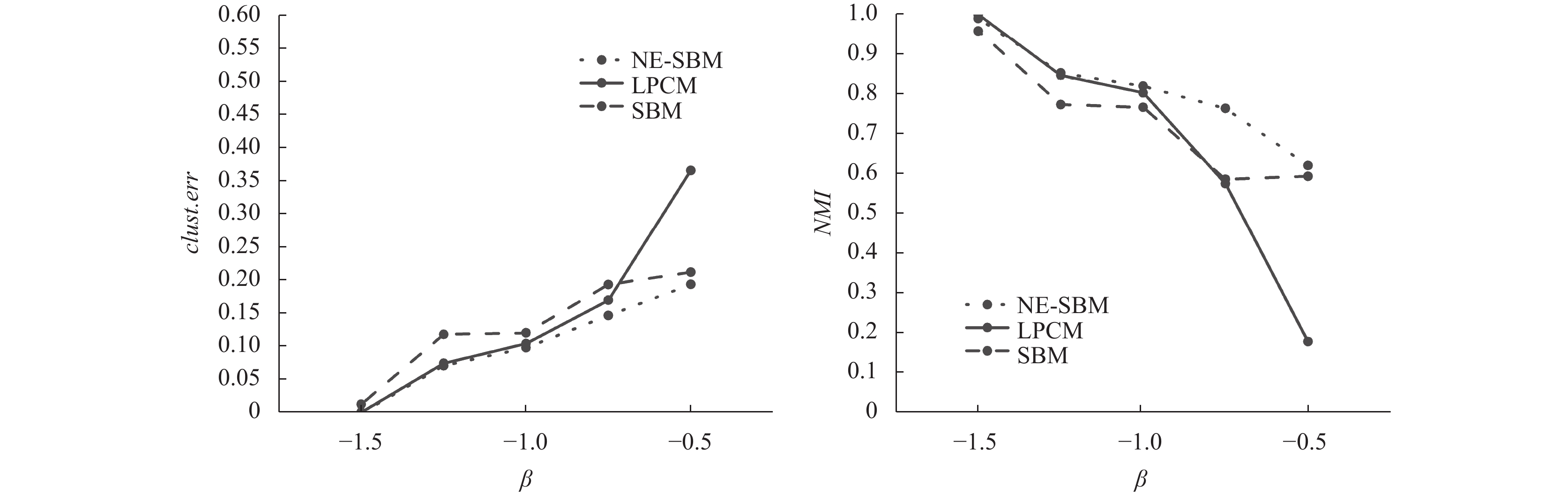
图1–图3展示了NE-SBM, LPCM和SBM模型在不同数据集中社区发现结果的聚类错误率和NMI值. 相对于基准模型, NE-SBM模型及对应算法普遍具有更低的聚类错误率与更高的NMI值, 因此在社区发现上表现更加优越. LPCM模型不包含区块结构, 社区间的随机块模式使得NE-SBM模型具备区块结构, 因此相较于LPCM模型在挖掘社区结构上表现更佳; 此外, SBM模型刻画区块结构的方式单一, 而社区内网络嵌入模式的引入使得NE-SBM模型相较SBM模型应用范围更广, 在不同网络结构中均能有较好的社区发现效果.

值得注意的是, 在数据集1和数据集3中, 横坐标参数的值增大意味着网络结构更加明显, 社区发现的表现随之提升; 在数据集2中, 横坐标参数的值增大意味着网络稠密程度增大, 社区难以区分, 社区发现的表现随之下降.

3.3 链路预测实验

为了评估NE-SBM模型与对应算法在下游链路预测任务中的表现, 我们从3种数据集中随机抽取5%的连边信息设置成缺失值, 利用不同模型拟合带有缺失值的网络数据, 针对缺失的连边信息进行链路预测^[24]. 与NE-SBM模型对比的基准模型为SBM^[7]、LPCM^[17]、LPM^[16]、LSM^[16]模型, 评价指标为AUC, 该值越接近1意味着预测效果越准确.

表1展示了不同数据集中各模型链路预测的AUC均值与标准差. 相对于基准模型, NE-SBM模型及其算法有更低的AUC均值和较小的标准差, 因此在链路预测上有更优越的表现. 在隐空间模型中, 通过隐位置距离度量节点间连接概率的LSM和LPCM模型不能准确地刻画有向网络连接模式, LPM模型不能结合节点隶属社区关系进行链路预测, 因此隐空间模型相较于具有区块结构且利用隐位置投影度量连接概率的NE-SBM模型表现欠佳; SBM模型的同个区块内节点连接概率等同, 难以刻画网络传递性和相互性, 社区内网络嵌入模式的引入使得NE-SBM模型在链路预测中表现更好.

值得注意的是, 链路预测作为社区发现的下游任务, 其表现受到社区发现结果影响, 因此与社区发现的结论有相似之处. 具体地, 数据集1和数据集3中, 链路预测表现会随网络结构的明显而提升; 在数据集2中, 链路预测的表现会随网络稠密程度增加而变差.

4 实际数据分析

为了进一步论证NE-SBM模型及算法的有效性, 我们选取经典的World Trade网络数据集进行分析. 该数据集来自国际贸易组织的贸易方向年鉴, 描述了1994年80个国家之间金属制品的贸易量, 参考文献[19]中的预处理工作, 将国家视作网络中的节点, 国家之间的进口交易视作节点之间的有向连边以分析各国之间的贸易联系, 交易价值低于该国总进口量1%的进口数据被省略^[30]. 我们旨在探索贸易体系的国家构成以及背后的世界分工现象.

我们采取NCV (network cross-validation)方法^[31]来确定该网络中的社区个数, 该方法依据社区划分来切割节点对并进行交叉验证, 得到最优社区个数为5. 从社区划分来看, 5个社区可归纳为: (1)美国-南美洲贸易区, (2)北美洲贸易区, (3)亚洲贸易区, (4)以德国、意大利为中心的欧洲-非洲贸易区, (5)以法国、新西兰为中心的欧洲贸易区. 由此可见, 地理因素在贸易体系的形成中发挥重要作用. 全球分工体系中, 发达的核心国家往往充当中心节点, 从事资本密集型和高科技生产, 从财富落后的外围国家进口原材料与粗加工产品, 将其加工成高科技产品出口至其他国家. 因此核心国家间贸易较多, 而外围国家间贸易较少.

参照Zhang等^[32]的分析思路, 计算各模型聚类结果相对于80个国家所属大洲的分类结果的NMI值, 可以得到NE-SBM, LPCM, SBM模型对应的NMI值分别为0.522 1, 0.100 4, 0.379 4. 验证了社区划分结果与地理位置的相关性, NE-SBM模型对应的NMI值更大, 相对其他模型能更好地刻画这一点.

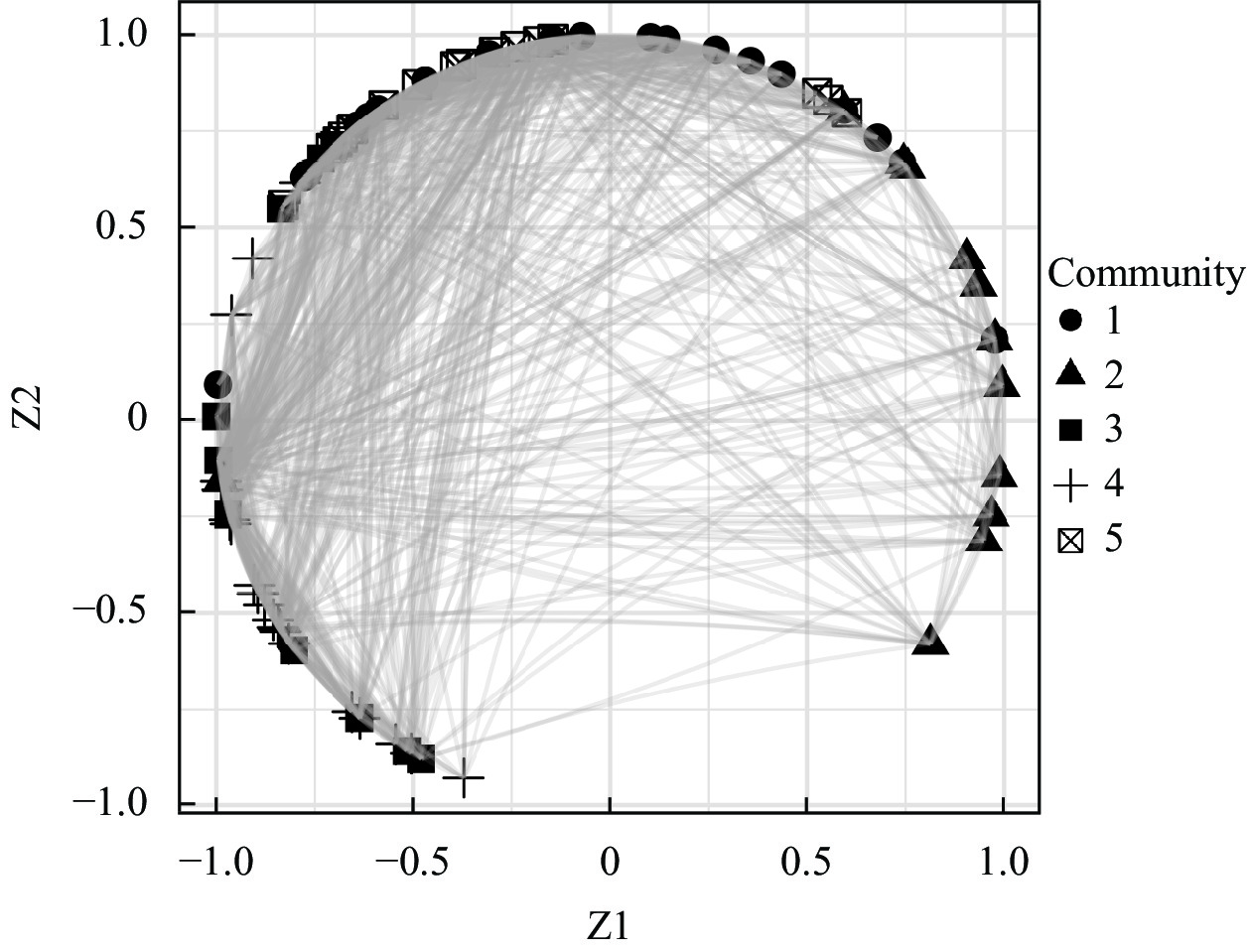
NE-SBM模型中网络嵌入的思想为网络结构可视化提供了一种新思路, 对经过可识别性调整后的节点隐位置的后验估计进行标准化处理, 使其位于单位圆上^[16], 节点隐位置分布以及连边情况如图4所示. 标记为同种形状的节点隶属于同一个社区, 两节点在圆周上距离越近意味着它们与圆心的夹角越小, 即对应隐位置夹角越小, 节点间更有可能产生连边. 具体地, 图4反映出同一社区内节点连接较为稠密, 但也存在一定的异配现象, 如社区5中的节点在圆周上相对分散, 对应子网络密度为0.199 3, 但是社区5与社区1中的节点连接更为紧密, 对应子网络密度为0.251 8. 从实际意义上看, 社区1主要涉及欧洲核心国家, 在1994年进出口贸易频繁. 而社区5涉及少部分欧洲国家以及多数非洲国家, 多数非洲国家作为外围国家内部贸易相对较少. 图4的可视化方式可以清晰地展现网络节点之间的靠近程度与其社区标签的关系, 印证参数估计中体现的异配网络结构, 研究者可利用这些信息进一步分析网络结构, 优化国际贸易政策、促进经济增长和国际合作.

最后, 评估NE-SBM模型在该数据上的链路预测表现. 针对数据进行不同随机数种子下的10折交叉验证, 计算链路预测结果的AUC平均值, 并将NE-SBM模型的预测结果与SBM、LPCM、LPM、LSM模型进行对比, 箱线图结果如图5所示.

NE-SBM模型在链路预测的表现明显优于基准模型, AUC较高并且表现稳定. SBM模型难以刻画网络传递性, 因而表现次之; LPCM和LSM模型由于采用隐位置距离刻画连接概率, 不适用于有向网络, 对应AUC值相对较小; LPM模型在刻画网络异配结构上有所欠缺, 因此表现不如NE-SBM模型. 结合图5可知, NE-SBM模型在链路预测任务中表现优越, 可以帮助研究者在探寻世界贸易体系结构的基础上, 进一步挖掘国家地区之间潜在的贸易关系, 为国家间未来的贸易合作往来提供参考.

5 结论与展望

本文在随机块模型的基础上引入网络嵌入的思想, 提出一种网络嵌入随机块模型下的社区发现与链路预测算法. 一方面, 弥补隐空间模型等基于网络嵌入的传统模型与算法在拟合异配网络结构数据中的不足, 且在社区发现任务上表现更优; 利用节点隐位置投影刻画网络连接模式, 将算法适用范围拓展到有向网络的情形, 弥补随机块模型刻画网络传递性与相互性特征的不足, 在下游链路预测任务中有更好的表现. 另一方面, 建立贝叶斯框架以应对孤立节点的干扰, 引入辅助变量, 利用Metropolis Hasting-Gibbs算法逐分量快速更新参数, 并针对隐位置的可识别性问题给出基于加权多维尺度变换的解决方案. 实验结果和实证分析的可视化展示均验证了该算法的有效性.

本文仍然有许多值得继续研究拓展的地方. NE-SBM模型和对应算法可以拓展到有权网络的情形, 只需要改变节点间的连接概率分布以及相应的联系函数. 其次, 针对大型稀疏网络, 可以参照Raftery等^[33]的思路, 分层抽样不同度的节点, 对似然函数进行近似以降低时间复杂度至 ${\rm{O}}(N)$ . 此外, 网络嵌入中隐空间维数的选择也是一个值得进一步探讨的问题.