医学影像是指通过非侵入方式获得的关于人体或其内部状态的图像[1]. 自从X射线的发现以来, 医学影像就成为了医疗领域之中至关重要的一个工具, 在病情诊断、病灶定位、手术规划之中都起到了关键的作用[2]. 标志点则是医学影像中重要的一个解剖学特征. 医学影像领域中, 标志点的定义是“普遍存在于人体之中, 具有一定特征并在位置和拓扑上有对应关系的点或曲线”[3]. 通过对医学影像中的标志点进行定位和分析, 医生可以把握病人的身体状况并据此判断病情. 因此, 探索高效精确的医学影像标志点定位方法, 对于医疗领域而言有着非常重要的意义.
近年来, 随着人工智能的发展, 深度学习技术进入到医疗领域之中, 而其中绝大部分研究都是和医学影像分析有关[4]. 基于深度学习的医学影像标志点定位算法也随之大量出现, 并展现出了各自优秀的性能. 比起直接通过回归的方式获取标志点的坐标, 研究者们通常更倾向于选择让深度学习模型去预测表示标志点位置概率分布(一般为高斯分布)的热力图, 因为热力图可以更好地建模人类行为[5]: 标注者由于不能每次都完全准确地标注标志点的位置, 对同一标志点进行多次标注时可能会给出不同的结果, 其概率可以用一个分布来表示, 并通过热力图的方式展现出来, 即: 热力图表示了标注过程中存在的不确定性.
然而, 现有的基于热力图的方法并没有充分对这种不确定性进行估计. 在这些方法中, 研究者通常使用预先定义好的热力图作为先验知识, 同时引入了两个假设: (1)所有标志点的位置分布具有相同的方差; (2)标志点的概率在不同方向上具有相同的下降速度. 这两点假设并不符合现实: 首先, 所有标志点的概率分布方差相同意味着所有标志点的定位难度相同, 然而一些较容易定位的标志点(比如在较清晰的边界上)的概率分布应该有着更小的方差, 反之亦然; 其次, 标志点的概率分布具有各向同性意味着该标志点在不同方向上都具有相同的发生误差的概率, 然而处在边缘上的标志点更可能同样被定位在边缘之上, 而不是定位在外侧或内侧, 因此其分布应该具有各向异性. 图1展示了一个下颌角点的样例, 其中图1(a)是目前大多数方法中使用的分布, 然而由于该标志点更可能被定位在下颌边缘上, 图1(b)能更好地表示其位置的真实概率分布.

|
图 1 各向异性概率分布的样例 |
鉴于当前方法在不确定性估计上的不足之处, 本文设计了一种基于不确定性估计的医学影像标志点定位算法. 预测热力图的主干网络为U-Net架构[6], 而为了预测标志点的位置分布, 本文在其中添加了一个协方差预测模块. 协方差预测模块使用注意力机制对主干网络的编码器输出的特征图进行加权, 强化有效特征并从中预测出标志点位置分布的协方差矩阵. 此外, 受启发于关注上下文的金字塔特征提取模块(context-aware pyramid feature extraction, CPFE)[7], 本文使用多分支空洞卷积代替卷积层, 从而捕捉不同尺度的上下文特征.
本文的贡献主要为以下3个方面.
(1) 本文提出了一个基于不确定性估计的医学影像标志点定位算法, 其可以同时预测标志点的位置及其概率分布.
(2) 本文设计了一个协方差预测模块来预测位置分布的协方差矩阵, 从而对标志点的不确定性进行估计. 可视化结果表明本文方法所预测出的分布要比现有其他方法所使用的更符合现实, 能一定程度上表示现实中标志点的标注不确定性.
(3) 在公开数据集上的实验表明, 本文提出的算法整体上提升了标志点定位的性能, 并且在大部分指标上都取得了最优表现, 具有较高的标志点定位能力. 同时本文提出的协方差预测模块可以迁移至其他基于热力图的方法中并进一步提升其定位能力.
1 相关工作 1.1 医学影像标志点定位算法早期的医学影像标志点定位算法通常基于一个简单的分类器, 比如随机森林[8,9]. 而现阶段, 基于深度学习的方法成为了医学影像标志点定位算法中的主要方法. 目前, 根据关注信息和预测原理上的不同, 基于深度学习的医学影像标志点定位算法可以分为以下3种[10]: 通过回归的方式直接预测标志点坐标的基于回归的方法[11]; 利用图表示标志点间的结构从而预测坐标的基于图的方法[10]; 以及基于热力图的方法.
基于热力图的方法是当前方法的主流. 这些方法通过预测出一个热力图的方式来获取标志点在不同位置上的概率, 并由此计算标志点最可能的位置. 部分研究者同时使用偏移图来引入部分空间信息, 从而提升预测的准确度[12]. Zhong等[13]设计了一个两阶段深度学习方法, 首先在全局阶段通过预测热力图的方式获取大致的注意力分布, 并在局部阶段中对切割出的图像块继续回归得到高精度的热力图. Chen等[14]则使用金字塔融合模块, 通过多个空洞卷积获取并融合不同感受野的信息. 他们还使用注意力机制对融合的特征进行加权, 从而进一步突出重要特征的作用. Ao等[15]则将卷积网络和Transformer架构相结合, 利用卷积网络对局部特征的提取能力和Transformer架构对全局特征的挖掘能力, 分别构建两个编码器来提取多尺度的特征并预测出一个热力图. 这些方法都使用了预定义的热力图并通过降低预测的热力图和目标热力图之间的距离来优化模型. 然而, 他们所使用的热力图没有很好地表示真实的标志点位置分布, 从而限制了方法的性能.
1.2 不确定性估计目前有两种不确定性估计的方式: 基于样本的(sampling-based)和无需样本的(sampling-free). 基于样本的方法通过多次预测的方式来估计不确定性, 比如利用贝叶斯网络进行变分推断[16], 或是用蒙特卡洛方法进行随机多次Dropout从而获得不同的预测结果[17], 或者在不同的扩充数据集上进行训练和预测[18]. 而无需样本的方法则是对已有的方法进行优化, 使其具备不确定性估计的功能. 和基于样本的方法不同, 该种方法使用同样的数据集和同样的模型. 比如Ovadia等[19]通过在模型中引入随机变分推断和温度定标的方法来估计不确定性, 而Sensoy等[20]则使用了狄利克雷分布, 通过拟合分布的方式获取不确定性.
2 网络结构与算法原理U-Net架构是医学影像处理中常见的架构. 尽管U-Net具有较为简单的结构, 它却能同时利用底层的结构特征和高层的语义特征, 从而得到不亚于很多其他复杂方法的效果[21]. 鉴于其优秀的性能, 本文同样选择U-Net架构作为主干网络来预测标志点位置. 本文方法整体的网络结构如图2所示.

|
图 2 本文提出的方法 |
2.1 主干U-Net模型
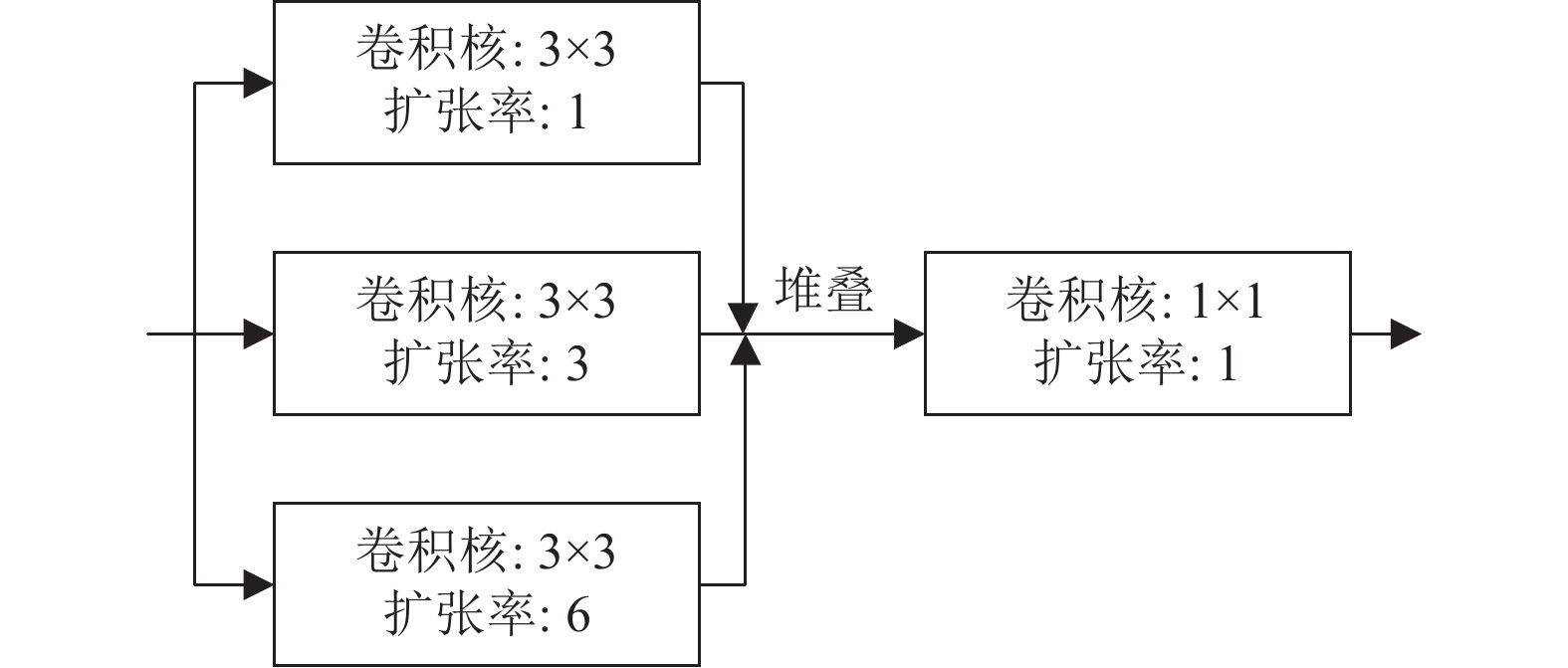
标准的U-Net模型具有一个编码器和一个解码器. 编码器从输入的图像中提取出多尺度的特征, 而解码器则利用这些特征预测出热力图. 编码器和解码器的同层级特征用跳跃连接(skip connection)结合在一起, 从而实现多尺度特征的利用. 本文使用在ImageNet数据集[22]上预训练过的VGG19网络[23]作为模型的编码器, 并在训练过程中对其加以微调. 而在解码器部分, 本文使用多分支空洞卷积替代了原本的卷积块. 多分支空洞卷积的结构如图3所示, 其作用是提取不同尺度的特征并将它们融合起来, 具体而言分为两步: (1)通过多个不同扩张率的空洞卷积[24]提取出不同感受野的特征信息, 用补零的方式保证输入和输出的尺寸一致; (2)由于获取的不同尺度特征的大小相同, 本文将它们直接在通道维度堆叠合并起来, 并使用1×1卷积融合这些特征. 其中堆叠操作是在通道维度堆叠特征进行合并. 由于这些空洞卷积使用相同大小的3×3卷积核, 在增大了模型的感受野的同时, 模型的参数量并没有显著增加.
最后, 对于标志点
| $ {{{\widehat x}}_{{i}}} = \frac{{{\Sigma _{{x}}}\delta \left( {\widehat {{{{H}}_{{i}}}}\left( {{x}} \right)} \right){{x}}}}{{{\Sigma _{{x}}}\delta \left( {\widehat {{{{H}}_{{i}}}}\left( {{x}} \right)} \right)}} $ | (1) |
其中,
|
图 3 多分支空洞卷积 |
2.2 协方差预测模块
协方差预测模块的目标是预测出标志点位置分布的协方差矩阵, 从而对标志点的不确定性进行建模. 本文选择高斯函数来表示标志点的位置分布.
现有的方法往往用如下的二维高斯函数来生成标志点
| $ {{{H}}}_{i}\left(x;{\sigma }_{i}\right)=\frac{\gamma }{2{\text{π}} {\sigma }_{i}^{2}}\mathrm{exp}\left(-\frac{\Vert x-{x}_{i}{\Vert }_{2}^{2}}{2{\sigma }_{i}^{2}}\right) $ | (2) |
其中,
然而, 这个高斯分布是各向同性的, 不能很好地表示真实的标志点位置分布. 因此, 为了更好地对不确定性进行建模, 本文选择如下高斯函数:
| $ {{{H}}_{{i}}}\left( {{{x}};{{{\Sigma }}_{{i}}}} \right) = \frac{{\gamma \cdot {\rm{exp}}\left( { - \dfrac{{{{\left( {{{x}} - {{{x}}_{{i}}}} \right)}^{\rm{T}}}{{{\Sigma }}_{{i}}}^{ - 1}\left( {{{x}} - {{{x}}_{{i}}}} \right)}}{2}} \right)}}{{2{\text{π}} \sqrt {\left| {{{{\Sigma }}_{{i}}}} \right|} }} $ | (3) |
和式(2)不同, 本文使用一个二维的协方差矩阵
| $ det\left( {{{{\Sigma }}_{{i}}}} \right) = cov\left( {{{x}}, {{x}}} \right)cov\left( {{{y}}, {{y}}} \right) - cov{\left( {{{x}}, {{y}}} \right)^2} \geqslant 0 $ | (4) |
而直接输出协方差矩阵各个元素的做法不一定满足式(4). 实际上, 由于
| $ {{{\Sigma }}_{{i}}} = {{{C}}_{{i}}}{{C}}_{i}^{\rm{T}} $ | (5) |
其中,
| $ {{{C}}_{{i}}} = \left[ {\begin{array}{*{20}{c}} {{a_i}}&0 \\ {{b_i}}&{{c_i}} \end{array}} \right] $ | (6) |
为下三角矩阵.
每一个正定矩阵都可以按照式(5)的方式分解. 证明如下: 令
| $ {{\widehat A}} = {{\widehat L}}{{{\widehat L}}^{{{\rm{T}}}}} $ | (7) |
则
| $ {{A}} = \left[ {\begin{array}{*{20}{c}} {{{\widehat A}}}&\alpha \\ {{\alpha ^{\rm{T}}}}&\beta \end{array}} \right] $ | (8) |
令:
| $ {{L}} = \left[ {\begin{array}{*{20}{c}} {{{\widehat L}}}&0 \\ {{\rho ^{\rm{T}}}}&\lambda \end{array}} \right] $ | (9) |
其中,
| $ {{A}} = {{L}}{{{L}}^{{{\rm{T}}}}} $ | (10) |
即
为了方便起见, 本文令预测出的Cholesky分解矩阵中的值均为非负数, 这通过一个ELU函数实现:
| $ f(x) = \left\{ {\begin{array}{*{20}{l}} {x, }&{{\rm{if}} \; x \geqslant 0} \\ {{{\rm{e}}^x}, }&{{\rm{otherwise}}} \end{array}} \right. $ | (11) |
而在矩阵元素均为非负数的情况下, 若:
| $ \left[ {\begin{array}{*{20}{c}} {{a_1}}&0 \\ {{b_1}}&{{c_1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}}&{{b_1}} \\ 0&{{c_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_2}}&0 \\ {{b_2}}&{{c_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_2}}&{{b_2}} \\ 0&{{c_2}} \end{array}} \right] $ | (12) |
则显然有:
| $ {a_1} = {a_2}, \; {b_1} = {b_2}, \; {c_1} = {c_2} $ | (13) |
即此时预测出的Cholesky分解与协方差矩阵有着一一对应的关系, 因此可以通过预测Cholesky分解的方式获得协方差矩阵.
本文利用主干网络提取出的最高层特征来预测协方差矩阵的Cholesky分解. 鉴于自注意力机制[25]在挖掘长距离依赖、强化重要特征等方面的性能, 本文将其应用在协方差预测模块中, 以提升其不确定性估计的能力. 自注意力机制分别将输入
| $ {{Q}} = {{X}}{{{W}}_{{Q}}} $ | (14) |
| $ {{K}} = {{X}}{{{W}}_{{K}}} $ | (15) |
| $ {{V}} = {{X}}{{{W}}_{{V}}} $ | (16) |
其中,
| $ {{S}} = \sigma \left( {\frac{{{{Q}}{{{K}}^{\rm{T}}}}}{{\sqrt d }}} \right){{V}} $ | (17) |
其中,
受启发于负对数似然损失, 本文使用的损失函数和式(3)的负对数似然相似, 具体为:
| $ L = {\left( {{{{{\widehat x}}}_{{i}}} - {{{x}}_{{i}}}} \right)^{\rm{T}}}{{\widehat \Sigma }}_i^{ - 1}\left( {{{{{\widehat x}}}_{{i}}} - {{{x}}_{{i}}}} \right) + \alpha {\rm{ln}} \left| {{{{{\widehat \Sigma }}}_{{i}}}} \right| $ | (18) |
其中,
公式的第1项是预测标志点坐标和真实标志点坐标之间的马氏距离(Mahalanobis distance)的平方, 而第2项则是一个正则项.
本文使用公开数据集进行实验, 首先将本文提出的方法和该领域其他先进方法进行对比, 证明本文方法的优势; 随后进行消融实验, 证明本文提出的协方差预测模块的有效性; 之后将对标志点和协方差矩阵的预测结果进行可视化展示, 并对预测出的不确定性进行分析.
3.1 数据集本文所使用的数据集为IEEE ISBI Challenge 2015中公开的头影测量标志点定位数据集(简称头影数据集)[26]和Digital Hand Atlas数据集(简称左手数据集)[27].
头影数据集含有400张头影测量X光侧位片, 并由两名医生标注19个标志点的位置. 为了和其他方法保持一致, 本文选取两个标注值的平均值作为标志点的真实坐标, 并将全数据集分为150张训练集图片和250张测试集图片. 数据集中图像的分辨率为1935×2400, 每个像素的边长对应到真实空间中是0.1 mm. 图4展示了数据集中的原始影像及其标志点.

|
图 4 头影数据集中的原始图像及标志点[28] |
左手数据集含有895张左手X光片, 并标注了37个标志点, 其平均分辨率为1563×2169. 为了和其他方法保持一致, 本文使用三折交叉验证, 每一折中大致有600张用作训练, 300张用作测试. 图5展示了数据集中的原始影像及其标志点.
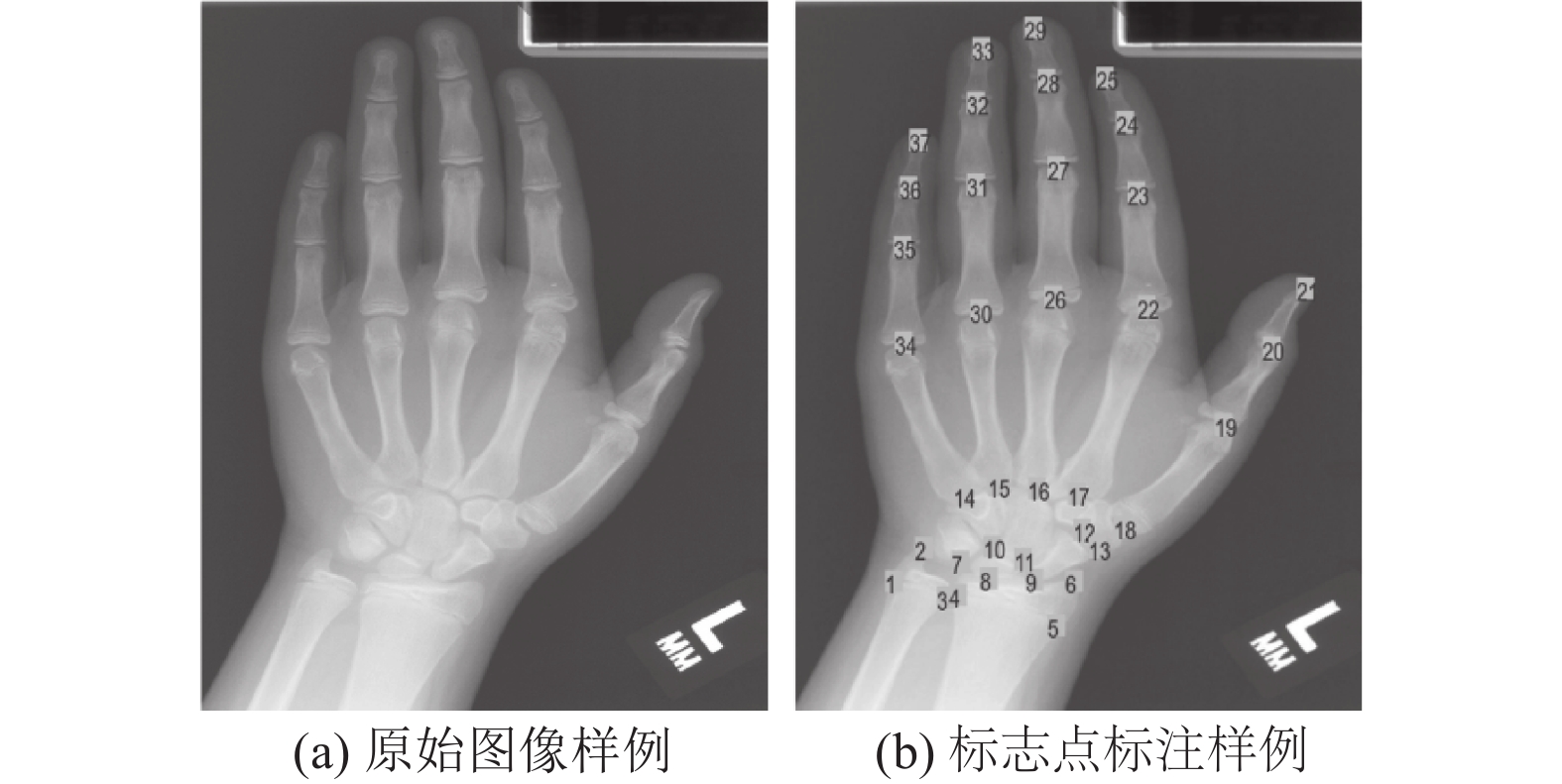
|
图 5 左手数据集中的原始图像及标志点 |
3.2 评价指标
本文采用平均径向误差(mean radial error, MRE)和成功检测率(successful detection rate, SDR)作为算法效果的评价指标.
平均径向误差计算所有标志点的预测坐标和真实坐标之间欧氏距离的平均值, 该指标的值越低, 证明算法的性能越好. 具体计算方式如下:
| $ {{MRE}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\sqrt {\Delta x_i^2 + \Delta y_i^2} } }}{n} $ | (19) |
其中,
成功检测率计算准确预测的标志点在所有标志点中的比例. 从临床角度出发, 如果预测坐标和真实坐标之间的距离对应到现实之中不大于某个阈值, 那么就认为这个标志点是准确预测的. 为了和对比方法保持一致, 本文在头影数据集上选择的阈值为2 mm, 2.5 mm, 3 mm和4 mm, 而在左手数据集上选择的阈值为2 mm, 4 mm和10 mm. 对于某个给定的阈值, 该指标的值越高, 证明算法性能越好. 具体计算方式如下:
| $ {\textit{SDR}} = \frac{{{N_{{\rm{acc}}}}}}{{{N_{{\rm{all}}}}}} \times 100{\text{%}} $ | (20) |
其中,
由于本文使用的两个数据集均具有较高的分辨率, 因此在实验中将图像大小缩小到640×800, 并对其进行标准化. 本文选取Adam[29]作为优化模型的方式, 学习率设置为3E–4, 权重衰减值设置为1E–4.
3.4 对比实验本文将提出的方法和该领域其他方法在头影数据集和左手数据集上进行对比, 以证明本文方法的优越性. 实验结果分别如表1和表2所示, 其中黑体字表示最优结果.
| 表 1 在头影数据集上的对比实验结果 |
| 表 2 在左手数据集上的对比实验结果 |
从实验结果可以看出, 本文所提出的方法无论在头影数据集还是左手数据集上均在MRE指标上达到了最优性能, 并且在大部分SDR指标上也超过了当前主流算法. 这些实验结果表明本文提出的方法在整体而言具有更好的效果, 而这得益于本文算法对于不确定性的利用. 通过预测标志点的位置分布, 本文算法可以提升预测的热力图的质量, 从而可以在一定程度上提高模型定位标志点的能力, 使模型仅依靠热力图就能拥有接近甚至超过同时使用偏移图的方法的性能.
注意到本文算法依旧在部分指标上低于现有主流算法. 但是, 通过在已有方法中添加本文提出的协方差预测模块进行不确定性估计, 已有方法的性能可以得到进一步提升. 鉴于Chen等[14]提出的方法已经有足够优秀的表现, 为了证明不确定性估计对性能的提升作用, 本文将协方差预测模块添加进原模型之中, 并在头影数据集上进行实验, 实验结果如表3所示. 可以看到, 在添加了协方差预测模块之后, 该方法在MRE和大部分SDR指标上的性能都得到了提升, 这表明本文提出的协方差预测模块可以应用在其他基于热力图的方法之中, 进一步提升原有方法的性能.
| 表 3 已有方法添加协方差预测模块的对比实验结果 |
3.5 消融实验
本文将提出的方法和无协方差预测模块的基线模型在头影数据集上的表现进行比较, 以验证协方差预测模块的有效性. 为了进一步验证协方差预测模块的优越性, 本文通过增加卷积层的方式将基线模型加以扩展得到Exp-U-Net, 使其和本文提出的方法具有相近的计算量和参数量, 以确保性能提升不仅是由于参数数量增加所致. 实验结果如表4所示. 实验表明与传统 U-Net 相比, Exp-U-Net 由于参数量的增加而有性能上的提升. 然而, 在增加了协方差预测模块之后, 基线模型的性能得到了全面的提升, 而且本文方法在所有指标上都超过了Exp-U-Net, 这证明本文方法并非只是单纯通过提高参数量的方式来提升效果.
3.6 可视化结果展示本部分将本章方法在头影数据集和左手数据集上的定位效果进行可视化展示, 其结果分别如图6和图7所示, 其中青色的点为真实标志点, 黄色的点为预测标志点, 并用红色数字加以编号. 从图像上可以看出, 尽管不同影像中人体的形态有所不同, 本文算法仍然有着良好的定位效果, 这表明本文算法具有优越的定位性能.
| 表 4 消融实验结果 |

|
图 6 头影数据集上定位效果展示 |

|
图 7 左手数据集上定位效果展示 |
3.7 不确定性分析
本文方法同时获取了标志点位置分布的协方差矩阵, 以此来估计其不确定性. 本文预测的标志点位置分布和现有大多数基于热力图的方法中所使用的分布不同, 其对比如图8所示, 其中上面一行为传统方法使用的分布, 下面一行为本文方法预测的分布, 青色的点为标志点, 黄色的椭圆为分布.
从图8中可以看出, 本文方法可以在一定程度上预测出标志点的分布, 其不仅保证了不同标志点间分布的差异性, 也注意到了标志点分布内部的各向异性. 图上的椭圆长轴方向都在一定程度上和边缘的方向相符, 这符合本文的观点. 而且, 传统方法使用的分布在标志点分布较为密集的地方可能会出现重叠的情况, 这表明重叠部分的像素可能会被同时定位为多个标志点, 而本文方法预测出的分布则大大降低了分布重叠的可能, 这使得标志点分布密集区域的像素更容易区分开, 也因此能够提升模型的性能.
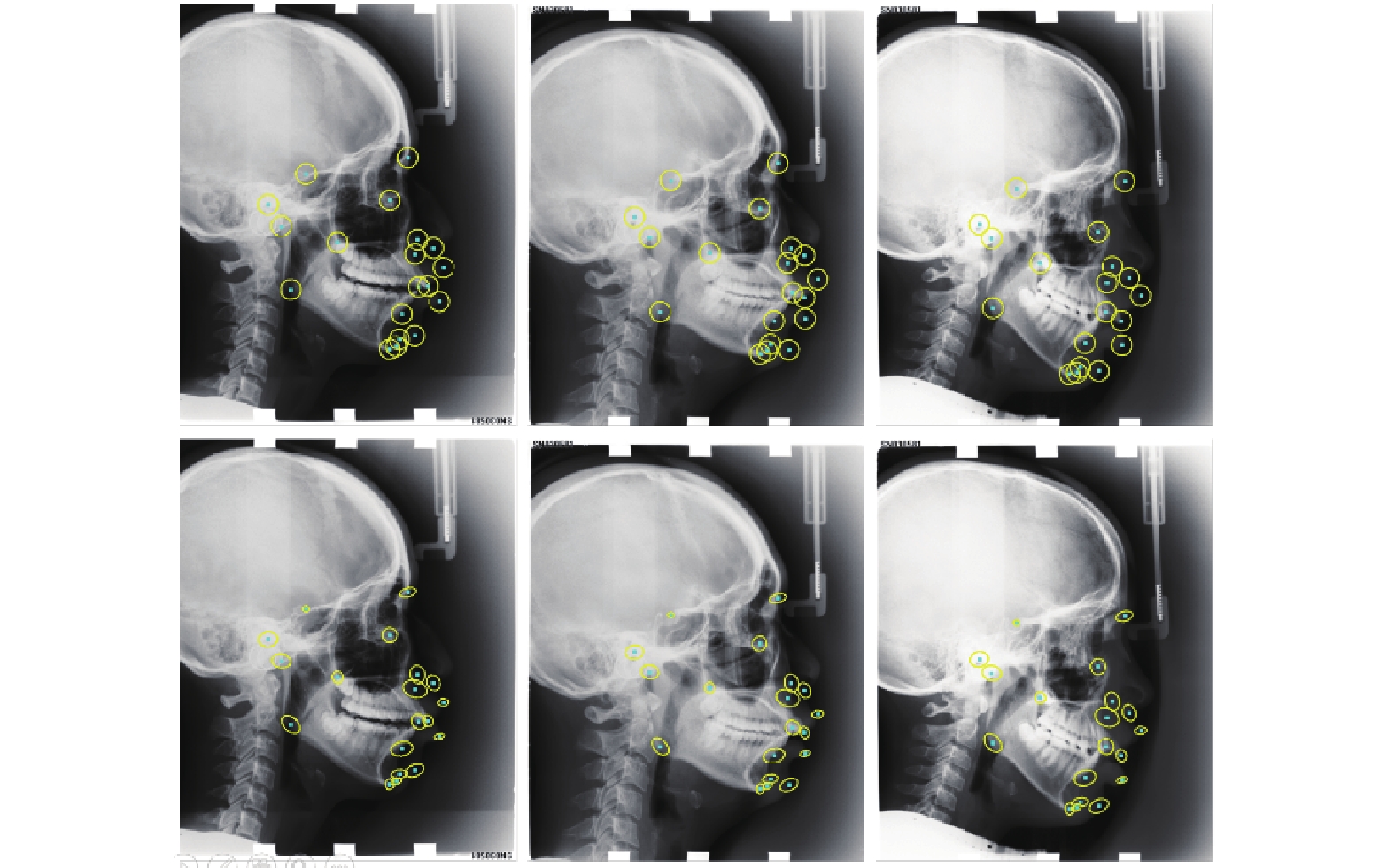
|
图 8 本文预测的分布与传统方法使用的分布的对比 |
同时, 为了进一步验证本文方法在不确定性估计上的有效性, 本文通过可视化偏移标志点的方式来展示标志点的不确定性. 首先, 对于标志点
| $ \Delta X_i^k = \widehat x_i^k - x_i^k $ | (21) |
| $ \Delta Y_i^k = \widehat y_i^k - y_i^k $ | (22) |
其中,
偏移向量能一定程度上代表标注者在标注标志点时的误差状况. 为了观察整体的分布情况, 本文将所有偏移向量集中在一张图片中进行可视化表示, 具体而言, 对于该图片上的标志点
从偏移标志点的分布可以看出, 不同标志点之间的分布范围有所不同, 其分布具有各向异性且基本上沿着边缘, 这和本文的观点相符. 并且图9上不同标志点的分布之间基本没有重叠的情况, 这点表明传统方法使用的分布不能很好地表示真实的分布, 而和传统方法相比, 本文所预测出的分布更为接近偏移标志点的分布, 这表明本文提出的协方差预测模块在不确定性估计上的优越性.

|
图 9 偏移标志点的分布 |
4 总结
针对现有基于热力图的方法没能充分利用标志点的不确定性的情况, 本文从不确定性估计的角度出发提出了一种医学影像标志点定位算法. 该算法在预测标志点位置的同时对其位置的分布加以预测, 以提升预测的热力图的质量, 从而提升模型定位标志点的性能. 在公开数据集上的实验结果表明, 本文算法在整体上提升了标志点定位的性能, 并在大部分指标上都有超过当前主流算法的效果, 且具备一定的可迁移性. 而对预测分布的可视化结果则表明本文方法预测出的分布较现有方法使用的分布有一定优势, 能一定程度上表示现实中标志点的标注不确定性.
| [1] |
Wikipedia. Medical imaging—Wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Medical_imaging.
|
| [2] |
吴毅, 张小勤. 人工智能在医学图像处理中的研究进展与展望. 第三军医大学学报, 2021, 43(18): 1707-1712. DOI:10.16016/j.1000-5404.202106194 |
| [3] |
Hanaoka S, Shimizu A, Nemoto M, et al. Automatic detection of over 100 anatomical landmarks in medical ct images: A framework with independent detectors and combinatorial optimization. Medical Image Analysis, 2017, 35: 192-214. DOI:10.1016/j.media.2016.04.001 |
| [4] |
姚琼, 王觅也, 师庆科, 等. 深度学习在现代医疗领域中的应用. 计算机系统应用, 2022, 31(4): 33-46. DOI:10.15888/j.cnki.csa.008411 |
| [5] |
Kumar A, Marks TK, Mou WX, et al. LUVLi face alignment: Estimating landmarks’ location, uncertainty, and visibility likelihood. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 8236–8246.
|
| [6] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Proceedings of the 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Munich: Springer, 2015. 234–241.
|
| [7] |
Zhao T, Wu XQ. Pyramid feature attention network for saliency detection. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3085–3094.
|
| [8] |
Ibragimov B, Likar B, Pernus F, et al. Computerized cephalometry by game theory with shape- and appearance-based landmark refinement. Proceedings of the 2015 International Symposium on Biomedical Imaging: Automatic Cephalometric X-ray Landmark Detection Challenge. IEEE, 2015. 1–8.
|
| [9] |
Lindner C, Cootes TF. Fully automatic cephalometric evaluation using random forest regression-voting. Proceedings of the 2015 IEEE International Symposium on Biomedical Imaging. Citeseer, 2015. 1–8.
|
| [10] |
Li WJ, Lu YH, Zheng K, et al. Structured landmark detection via topology-adapting deep graph learning. Proceedings of the 16th European Conference. Glasgow: Springer, 2020. 266–283.
|
| [11] |
Noothout JMH, de Vos BD, Wolterink JM, et al. Deep learning-based regression and classification for automatic landmark localization in medical images. IEEE Transactions on Medical Imaging, 2020, 39(12): 4011-4022. DOI:10.1109/TMI.2020.3009002 |
| [12] |
Papandreou G, Zhu T, Kanazawa N, et al. Towards accurate multi-person pose estimation in the wild. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 4903–4911.
|
| [13] |
Zhong ZS, Li J, Zhang ZX, et al. An attention-guided deep regression model for landmark detection in cephalograms. Proceedings of the 22nd International Conference on Medical Image Computing and Computer-assisted Intervention. Shenzhen: Springer, 2019. 540–548.
|
| [14] |
Chen RN, Ma YX, Chen NL, et al. Cephalometric landmark detection by attentive feature pyramid fusion and regression-voting. Proceedings of the 22nd International Conference on Medical Image Computing and Computer-assisted Intervention. Shenzhen: Springer, 2019. 873–881.
|
| [15] |
Ao YY, Wu H. Swin transformer combined with convolutional encoder for cephalometric landmarks detection. Proceedings of the 18th International Computer Conference on Wavelet Active Media Technology and Information Processing. Chengdu: IEEE, 2021. 184–187.
|
| [16] |
Shridhar K, Laumann F, Liwicki M. A comprehensive guide to Bayesian convolutional neural network with variational inference. arXiv:1901.02731, 2019.
|
| [17] |
Gal Y, Ghahramani Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. Proceedings of the 33rd International Conference on Machine Learning. New York: PMLR, 2016. 1050–1059.
|
| [18] |
Ayhan MS, Berens P. Test-time data augmentation for estimation of heteroscedastic aleatoric uncertainty in deep neural networks. Proceedings of the 1st Conference on Medical Imaging with Deep Learning. Amsterdam: OpenReview.net, 2018.
|
| [19] |
Ovadia Y, Fertig E, Ren J, et al. Can you trust your model’s uncertainty? Evaluating predictive uncertainty under dataset shift. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver, 2019. 1254.
|
| [20] |
Sensoy M, Kaplan LM, Kandemir M. Evidential deep learning to quantify classification uncertainty. Proceedings of the 31st Advances in Neural Information Processing Systems. Montréal, 2018. 3183–3193.
|
| [21] |
McCouat J, Voiculescu I. Contour-hugging heatmaps for landmark detection. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 20597–20605.
|
| [22] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe, 2012. 1106–1114.
|
| [23] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. Proceedings of the 3rd International Conference on Learning Representations. San Diego: ICLR, 2015.
|
| [24] |
Chen LC, Papandreou G, Kokkinos I, et al. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/TPAMI.2017.2699184 |
| [25] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [26] |
Wang CW, Huang CT, Lee JH, et al. A benchmark for comparison of dental radiography analysis algorithms. Medical Image Analysis, 2016, 31: 63-76. DOI:10.1016/j.media.2016.02.004 |
| [27] |
Gertych A, Zhang AF, Sayre J, et al. Bone age assessment of children using a digital hand atlas. Computerized Medical Imaging and Graphics, 2007, 31(4–5): 322–331.
|
| [28] |
张灵西. 基于拓扑结构约束和特征增强的医学影像标志点定位算法. 计算机系统应用, 2022, 31(9): 173-182. DOI:10.15888/j.cnki.csa.008700 |
| [29] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations. San Diego, 2015. 1–15.
|
| [30] |
Arik SÖ, Ibragimov B, Xing L. Fully automated quantitative cephalometry using convolutional neural networks. Journal of Medical Imaging, 2017, 4(1): 014501. DOI:10.1117/1.JMI.4.1.014501 |
| [31] |
Qian JH, Cheng M, Tao YB, et al. CephaNet: An improved faster R-CNN for cephalometric landmark detection. Proceedings of the 16th IEEE International Symposium on Biomedical Imaging. Venice: IEEE, 2019. 868–871.
|
| [32] |
Yao QS, He ZC, Han H, et al. Miss the point: Targeted adversarial attack on multiple landmark detection. Proceedings of the 23rd International Conference on Medical Image Computing and Computer-assisted Intervention. Lima: Springer, 2020. 692–702.
|
| [33] |
Lin CZ, Zhu BE, Wang Q, et al. Structure-coherent deep feature learning for robust face alignment. IEEE Transactions on Image Processing, 2021, 30: 5313-5326. DOI:10.1109/TIP.2021.3082319 |
| [34] |
Lindner C, Bromiley PA, Ionita MC, et al. Robust and accurate shape model matching using random forest regression-voting. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1862-1874. DOI:10.1109/TPAMI.2014.2382106 |
| [35] |
Štern D, Ebner T, Urschler M. From local to global random regression forests: Exploring anatomical landmark localization. Proceedings of the 19th International Conference on Medical Image Computing and Computer-assisted Intervention. Athens: Springer, 2016. 221–229.
|
| [36] |
Urschler M, Ebner T, Štern D. Integrating geometric configuration and appearance information into a unified framework for anatomical landmark localization. Medical Image Analysis, 2018, 43: 23-36. DOI:10.1016/j.media.2017.09.003 |
| [37] |
Payer P, Štern D, Bischof H, et al. Integrating spatial configuration into heatmap regression based CNNs for landmark localization. Medical Image Analysis, 2019, 54: 207-219. DOI:10.1016/j.media.2019.03.007 |
| [38] |
Kang J, Oh K, Oh IS. Accurate landmark localization for medical images using perturbations. Applied Sciences, 2021, 11(21): 10277. DOI:10.3390/app112110277 |
 2023, Vol. 32
2023, Vol. 32


