随着Kurs等人[1]提出电磁耦合谐振能量传输技术, 将此技术引入到无线传感器网络中, 形成无线可充电传感器网络(wireless rechargeable sensor network, WRSN)[2], WRSN脱胎于无线传感器网络, 因此WRSN应用领域同样也很广泛, 如家居[3]、军事[4]、交通[5]等. 随着无线可充电传感器网络的深入研究和广泛应用, 而充电的路径规划问题已成为该领域研究的热点. 如何通过一个合理的充电顺序依次为传感器节点充电, 即设计一条合理的充电路径, 对于不同规模的传感器网络中, 充电设备又可以分为单台移动设备[6]或者多台移动设备, 现在常用的充电设备是移动小车(MC)或者无人机, 但由于无人机飞行更便捷, 所遇到障碍物少的特点, 因此研究无人机为WRSN中的节点无线充电时的路径规划非常有意义.
在小规模的传感器网络中, 设计一个无人机补充能量即可满足需求, 但是对于大规模的传感器网络, 就需要采取多个无人机及时为传感器节点补充能量, 此外, 优化算法求解这类问题也有不少突破, 为了找到最优的充电路径同时使得充电设备的能量损耗减少, 吴蕾等人[7]采用遗传算法解决路径问题并且提出了基于半径的聚类算法来减少目标点数目来达到降低路径距离. 雷蕾等人[8]运用萤火虫算法来满足网络中节点的动态能耗需求, 并设置合理的动态充电时隙从而进行有效的及时充电规划. 王茜等人[9]采用改进的鸽群算法和遗传算法混合的方式求解充电路径问题, 并且提出了基于自适应惯性权重的速度更新公式, 以加快全局搜索的收敛速度. Hong等人[10]提出了环形漫游算法和八流算法, 使其平衡多个充电器之间的充电消耗达到节省能量. Mukase等人[11]提出了蜉蝣算法(MA)来降低整体系统能耗和总行驶距离, 同时提高移动充电器设备的休假时间比. Jia等人[12]发明了一种基于计算几何的算法来部署MC停留的多个充电位置为附近的传感器充电. Zhao等人[13]设计了一种改进的蜂群算法来降低充电能耗和路径成本, 从而选出充电效率最高的路径.
上述针对求解充电路径问题, 虽然用了一些启发式算法, 通过减少目标点或者有效部署充电位置、减少充电器休假时间、加快算法的收敛速度和提高算法最优解的能力来减少充电路径上的能耗, 但是在实际充电问题中, 充电设备在传感器节点上花费时间太多会影响到在其他节点, 将等待时间过长, 因此, 不仅要考虑充电设备自身的能量消耗, 还需要对充电时间进行规划, 当多充电设备如果有不同型号, 搭配的问题也不可忽视.
针对上述存在的问题, 本文在建立多个不同类型的无人机可充电的传感器网络场景下, 综合考虑起无人机飞行路径、能量消耗、充电时间成本和无人机分配成本成为目标函数, 同时对海洋捕食者算法[14]进行改进, 加入天牛须算法[15], 并且加入充电模型减少了飞行的停留次数, 用新的算法解决充电路径规划问题.
1 多辆多种无人机的模型与问题描述 1.1 网络模型考虑一种多无人机的可充电传感器网络作为本文研究的网络模型, 如图1所示, 在一个L×L平方的平面区域内随机部署n个传感器节点、基站和多个无人机, 节点之间是通过多跳路由将监测的数据发送给基站, 多个无人机从基站里出发的, 从高空中采取一对多充电的方式为地面的待充节点集进行无线充电, 节点在无人机的充电范围内就可以接收能量, 最后, 所有的无人机返回到基站休息来补充能量.

|
图 1 网络模型 |
1.2 能耗模型
在传感器网络中, 传感器的工作主要是对所检测的数据进行处理. 在接收数据过程中是会消耗能量的, 能量消耗的模型公式如式(1)所示:
| Er=ERX×cm | (1) |
其中,
数据传输消耗能量公式如式(2)所示:
| Et={ETX×dm+Efs×dm×d2,d<d0ETX×dm+Efs×dm×d4,d⩾d0 | (2) |
式(2)指的是, 距离基站越远的节点, 消耗的能量会更多, 其中
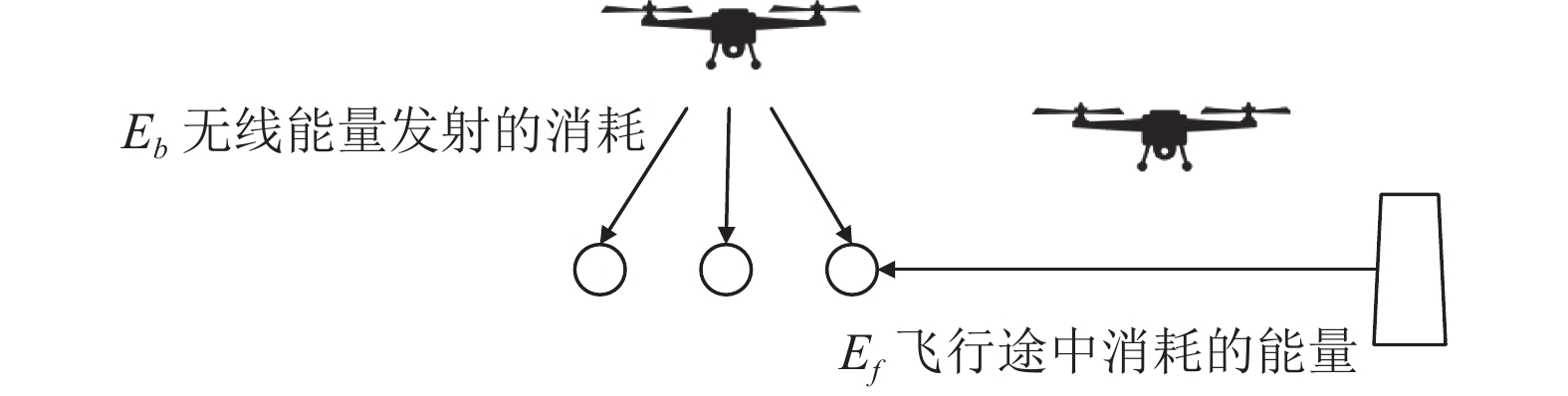
无人机给传感器节点充电中, 主要是分为飞行途中消耗能量和无线能量发射单元消耗(给传感器补充的能量), 如图2所示.
|
图 2 无人机能耗模型 |
无人机总能量消耗公式模型如下:
| Ezong=Ef+Eb | (3) |
| Ef=Pf×Tf=Pf×LV | (4) |
| Eb=Pd×∑ti | (5) |
| ti=Emax−EiPd | (6) |
其中,
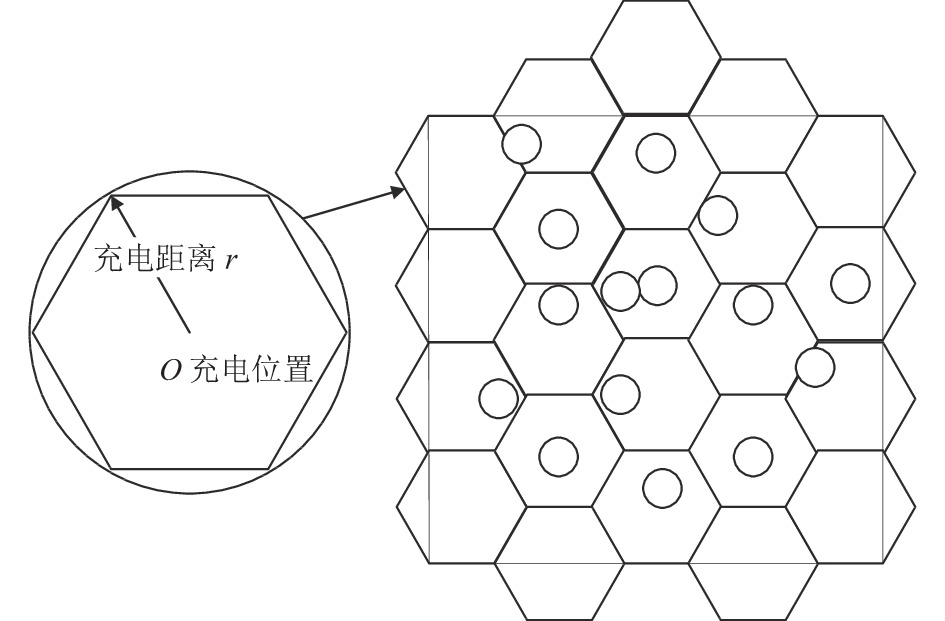
选择正六边形结构的充电簇, 可以覆盖整个网络区域[16], 本文的充电模型如图3所示, 根据在充电半径r内是可以接收无人机的能量进行充电, 假设本文的网络区域中可以按照多个正六边形拼接而成, 那么这就可以把无人机飞行途中的停留点, 也就是把需要到达待充节点的这个位置变为正六边形的正中心的位置点.
1.4 问题描述本文中, 根据参考文献[9]设置了两种不同类型的无人机给传感器节点充电. 在这个过程中, 主要研究的问题是: 在每个无人机所能承受的充电能力没有超过自身的电池容量约束下, 合理分配出无人机的数量, 使其多无人机充电路径规划的成本最小化. 将该问题描述为:
| minF | (7) |
约束条件为:
| max(m)<M | (8) |
| charge(Ci)⩽Euav-max,1⩽i⩽M | (9) |
| N∑iScharge,i⊆V | (10) |
| consume(Si)⩽Emax,1⩽i⩽M | (11) |
| qi⩽ti⩽zi | (12) |
式(8)中的
|
图 3 充电模型 |
式(9)中的
| f1=N∑iM∑m(disi,i+1+dism,0) | (13) |
| f2=N∑iPf×disi,i+1V | (14) |
| f3=N∑iM∑m((ti,m−zi,m)×zcost+(qi,m−ti,m)×qcost) | (15) |
| f4=M1×acost+M2×bcost,0⩽M1+M2⩽M | (16) |
| F=f1+f2+f3+f44 | (17) |
关于
海洋捕食者算法(MPA)主要是模拟海洋生物捕食的行为. 在MPA中, 捕食者与猎物是相对的, MPA的种群个体都以猎物表示, 当一头猎物捕获到它的猎物时, 它就升为捕食者, 其位置为当前的最优解. MPA算法的关键是三段优化和FADs效应.
2.1.1 三段优化三段优化是MPA的重要过程, 主要是为了模拟捕食者和猎物的整个生命周期, 达到从解空间的全局搜索到对解空间的当前最优解位置进行局部搜索过渡, MPA的第1阶段是在迭代初期(当前迭代的次数小于总迭代次数1/3), 通过布朗随机游走更新猎物的位置, 公式如下:
| Stepsizei=Rb×(Elitei−Rb×Preyi),i=1,2,⋯,n | (18) |
| Preyi=Preyi+P×R×Stepsizei | (19) |
其中,
第2阶段是在迭代中期(迭代的次数小于总迭代次数2/3), 种群被分为两部分, 其中猎物是Levy运动, 捕食者是布朗运动, 前者负责在搜索空间内开发, 后者负责在搜索空间内探索. 前一半种群更新公式如式(20), 后一半种群更新公式如式(21).
| Preyi=Preyi+P×R×Rl×(Elitei−Rl×Preyi),i=1,2,⋯,n | (20) |
| Preyi=Elitei+P×CF×Rb×(Rb×Elitei−Preyi),i=1,2,⋯,n | (21) |
| CF=(1−IterMax)(2×IterMax) | (22) |
其中,
最后一个阶段是在迭代后期(迭代的次数发生在最后是总迭代次数的1/3), 该阶段捕食者和猎物速度都慢, 此时捕食者的策略为Levy运动, 公式如式(23):
| Preyi=Elitei+P×CF×Rl×(Rl×Elitei−Preyi),i=1,2,⋯,n | (23) |
FADs效应指的是鱼群喜欢聚集在某个地方, 可以引申为局部最优解, 算法在优化过程中通过设置更长的跳跃可以避免陷入局部最优, 公式如式(24):
| Preyi={Preyi+CF(Xmin+R×(Xmax−Xmin))×U,if r⩽FADsPreyi+(FADs(1−r)+r)×(Preyl1−Preyl2),if r>FADs | (24) |
其中,
移动步长的自适应参数
| CF=cos(π2(1−IterMax))(2×IterMax) | (25) |
海洋捕食者算法虽然在解决一些复杂的优化问题上优势明显[18, 19], 但在解决路径问题上存在收敛速度慢和寻优精度低等问题[20]. 天牛须搜索算法则与其他仿生类算法不同, 天牛须算法是一种单体搜索算法, 天牛觅食时会利用左右触须来感知食物的气味强度, 如果左边触须收到的气味强度大, 它下一步就往气味强度大的左边飞, 否则往右边飞, 天牛所找到位置即为可行解, 且天牛须搜索算法前期收敛性强, 为了进一步增加MPA算法的搜索能力, 本文将天牛须搜索算法(BAS)与改进的MPA算法结合[21]起来解决充电规划的问题.
首先使用天牛须搜索算法在大范围内搜索一组粗略解, 然后以这组粗略的解作为海洋捕食者算法的初始种群, 然后利用MPA算法不断的游走碰到捕食者之后, 将更新好的精英代入BAS算法再进行游走更新, 然后比较MPA更新好的精英个体的目标函数值和BAS更新好的精英个体的目标函数值, 更新公式如下所示:
| dir=rand(1,k)eps+norm(rand(1,k)) | (26) |
| d0=step(i)c | (27) |
| Bright(i)=X(i+1)−dir×d0 | (28) |
| Bleft(i)=X(i+1)+dir×d0 | (29) |
| B(i+1)=X(i+1)−dir×sign(F(Bleft(i))−F(Bright(i))) | (30) |
| X(i+1)={B(i+1),F(B(i+1))<F(X(i+1))X(i+1),F(B(i+1))⩾F(X(i+1)) | (31) |
其中,
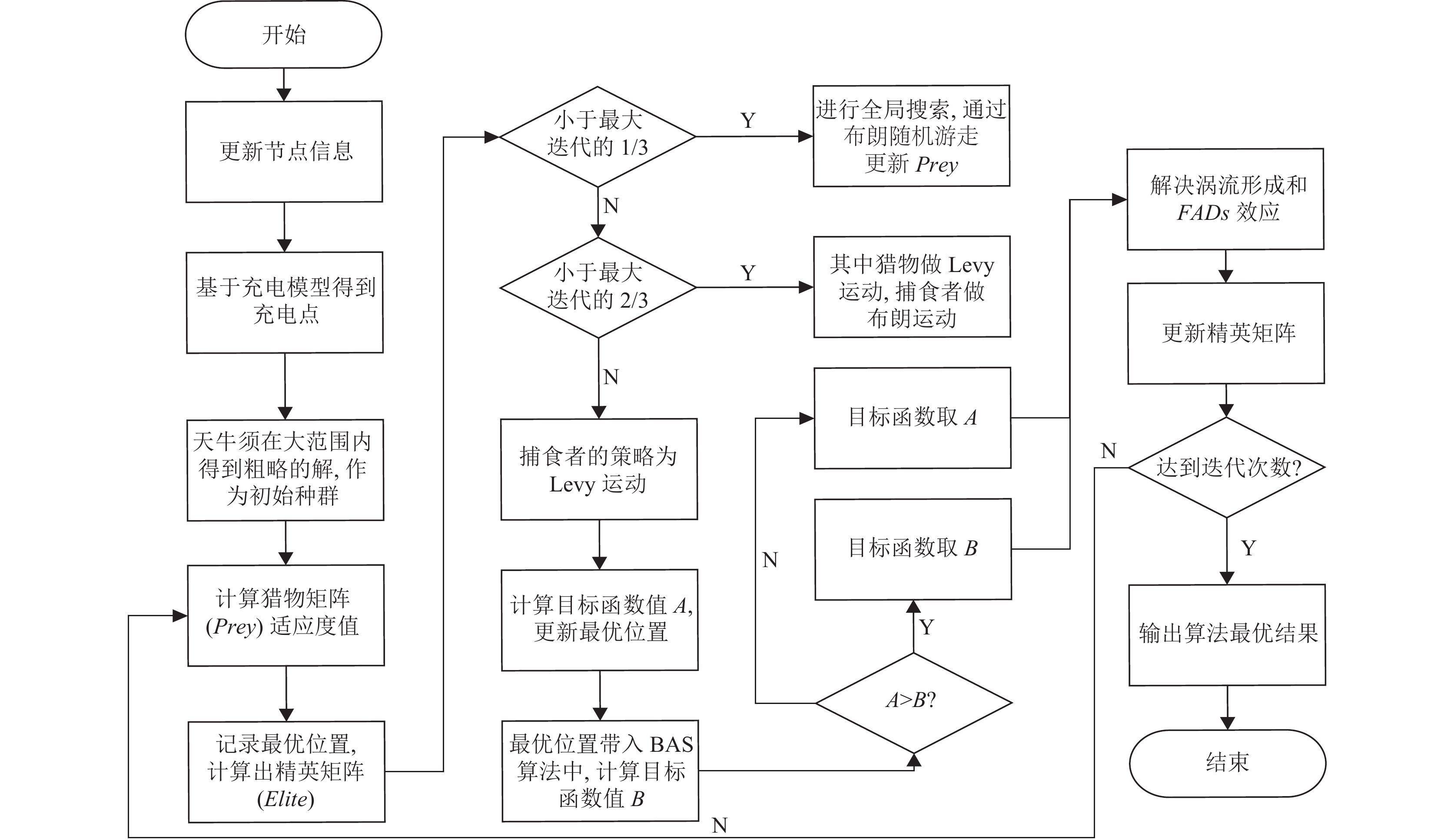
该混合算法既有海洋捕食者算法全局寻优的特性, 又具备天牛须搜索算法的前期收敛快的特性, 算法流程图如图4所示.
|
图 4 BMPA算法流程图 |
算法具体步骤如下.
Step 1. 输入传感器节点的集合, 结合充电模型得到待充节点的位置.
Step 2. 种群初始化, 根据搜索空间每一维的上界和下界, 用天牛须搜索算法搜索一组粗略解当作初始化猎物矩阵, 对每一个猎物个体计算其目标函数值, 然后使用最优个体复制成同规模同纬度的精英矩阵.
Step 3. 在迭代次数范围内, 经过3个阶段更新得到的精英个体, 代入BAS算法继续搜索寻优, 最后与其对比, 最优个体替代原来精英矩阵中相应的个体(一个精英个体即为问题的一个解).
Step 4. 最后, 鱼类聚集装置(FADs)是会改变海洋捕食者觅食行为, 这一策略使在寻优过程中克服早熟收敛问题, 逃离局部极值. 然后计算适应度值, 更新最优位置.
Step 5. 判断是否满足停止条件, 如果不满足则重复Step 3–5, 否则输出算法最优结果.
2.3 BMPA运用到WRSN的充电路径规划上研究多辆无人机的充电方案的问题, 就是要寻找到充电成本最小的无人机路线, 因此, 本文将对4个目标
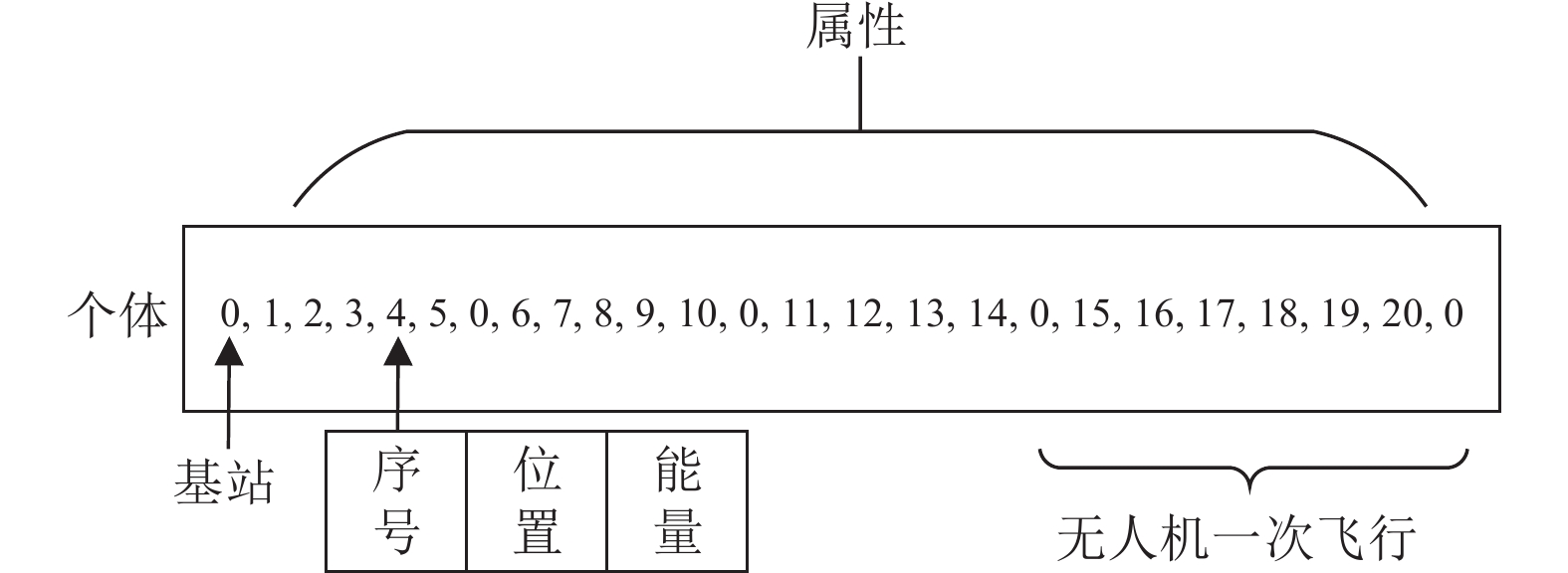
对于无人机充电的路径规划问题, 本文采用整数编码的方式, 有
|
图 5 编码示意图 |
3 仿真和性能分析
本文使用的是Matlab R2022a软件, 根据参考文献[9]给定参数如表1, 搭建实验仿真场景, 将本文改进算法(BMPA)和MPA算法, BAS算法和PreWBAS算法[22]分别在同一场景下进行比较.
假设40个节点分布在100×100平方米的监控区域内, 如图6所示, “○”是待充节点, “×”是基站.
| 表 1 仿真实验参数 |

|
图 6 节点分布图 |
使用本文算法得到的多个无人机的充电轨迹图为图7、图8所示, 图7是原始充电轨迹图, 图8是加入充电模型之后的轨迹图, 可以看出不用去遍历每个节点, 只需要飞行到这些节点所在充电半径内的正六边形正中心的位置即可, 明显飞行停靠次数减少. 表2列出了使用本文算法在有无充电模型下的总飞行路径距离的3次实验数据结果, 可以看出在加入充电模型后总飞行路径是减少了.
3.1 收敛性性能比较为了验证BMPA的收敛性能, 将其在成本目标函数F上进行收敛性能实验, 如图9所示, 本文改进后的算法BMPA对比其他算法, 其收敛速度是最快的, 也获得了最优的解. 4种算法在独立运行10次获得的平均运行时间如图10所示, BAS耗时最低, 随后是MPA (10.18 s)、BMPA (10.89 s)和PreWBAS (11.16 s), 本文算法BMPA运行时间不是最低的原因是, 本文提出的改进策略是替代策略加混合策略, 会有额外的计算. 表3列出了基于4种不同算法下的目标函数和路线, 并且对无人机分配情况做出了说明, 可以看出B型无人机次数比A型多, 说明考虑时间的优先级要高于无人机的本身的成本, 并且本文算法BMPA的充电成本是最低的, 比BAS、MPA和PreWBAS算法的目标函数分别减少了50.90%、4.85%和14.38%.

|
图 7 原始充电轨迹图 |
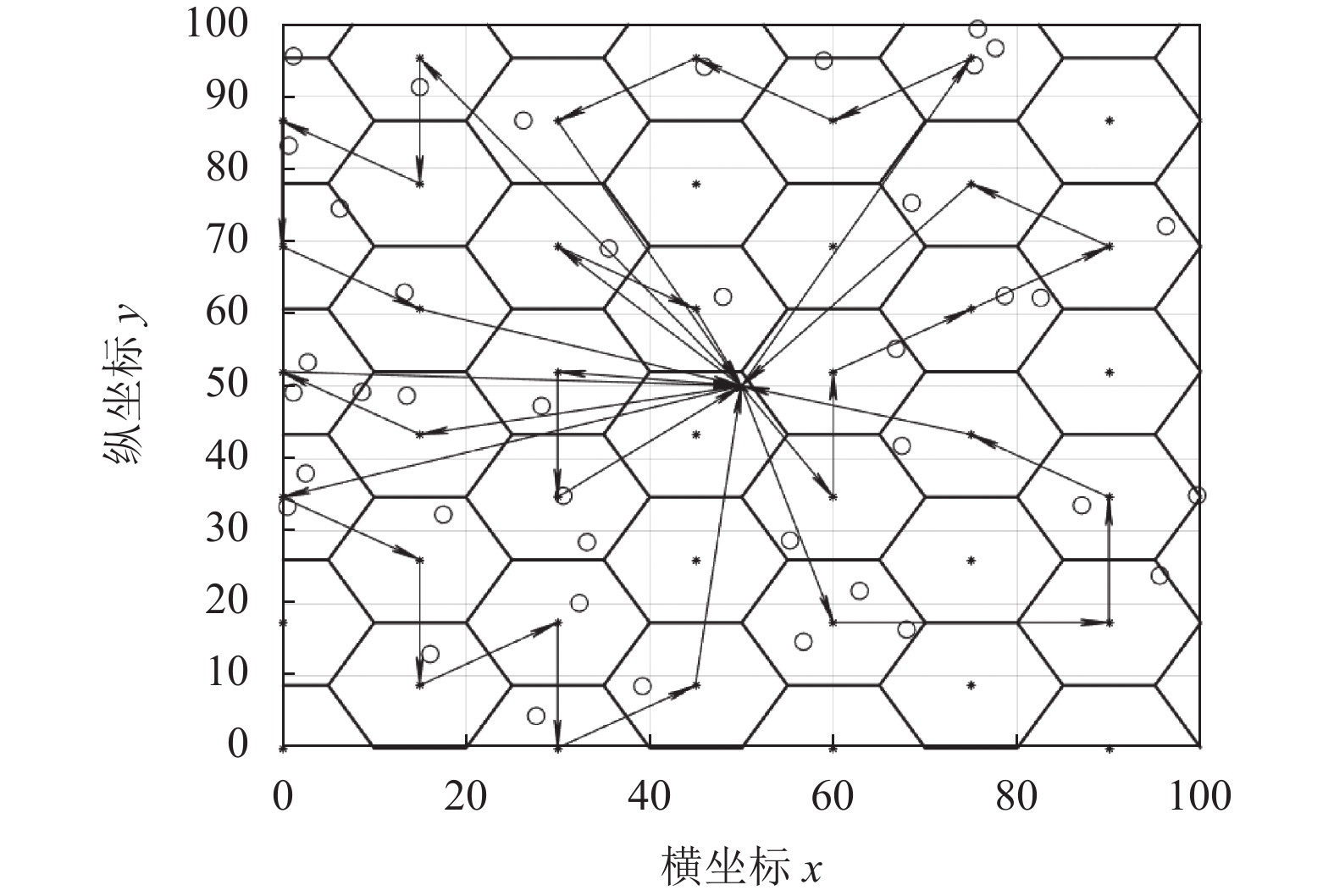
|
图 8 加入充电模型的充电轨迹图 |
| 表 2 本文算法有无充电模型的总路径距离 (m) |
3.2 无人机路径能量消耗分析
在相同的参数设置下进行多次仿真实验, 分析无人机在不同节点数目下飞行消耗, 进一步验证本算法的性能的优越性.
从图11可以看出, 在节点数为40的时候, 本文算法飞行消耗能量比BAS、MPA和PreWBAS算法少36.12%、5.25%和8.03%, 随着节点数增多, 无人机的路径消耗也在增加, 本文提出的算法路径消耗相较于其他对比算法也是最低的.
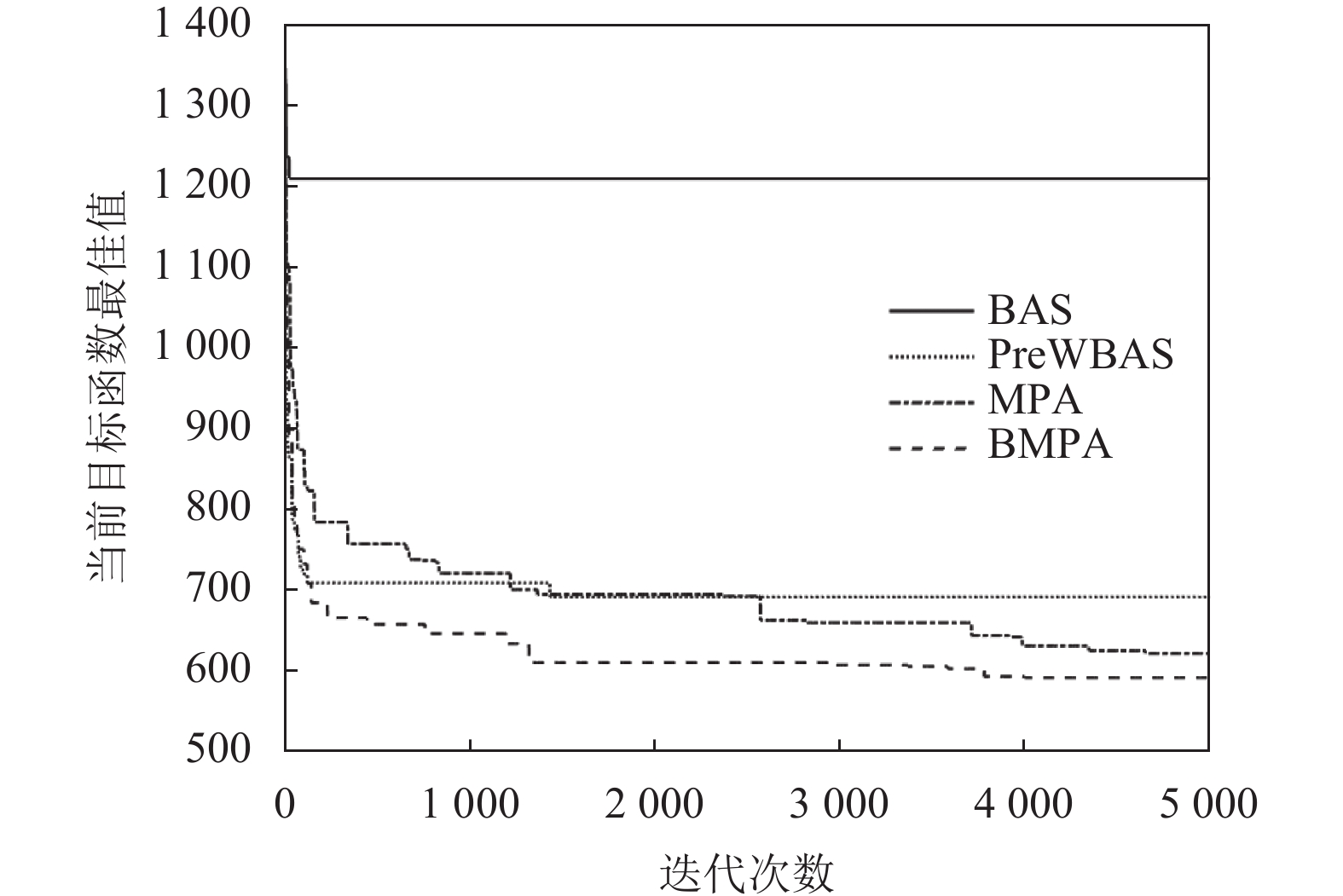
|
图 9 测试问题收敛曲线 |
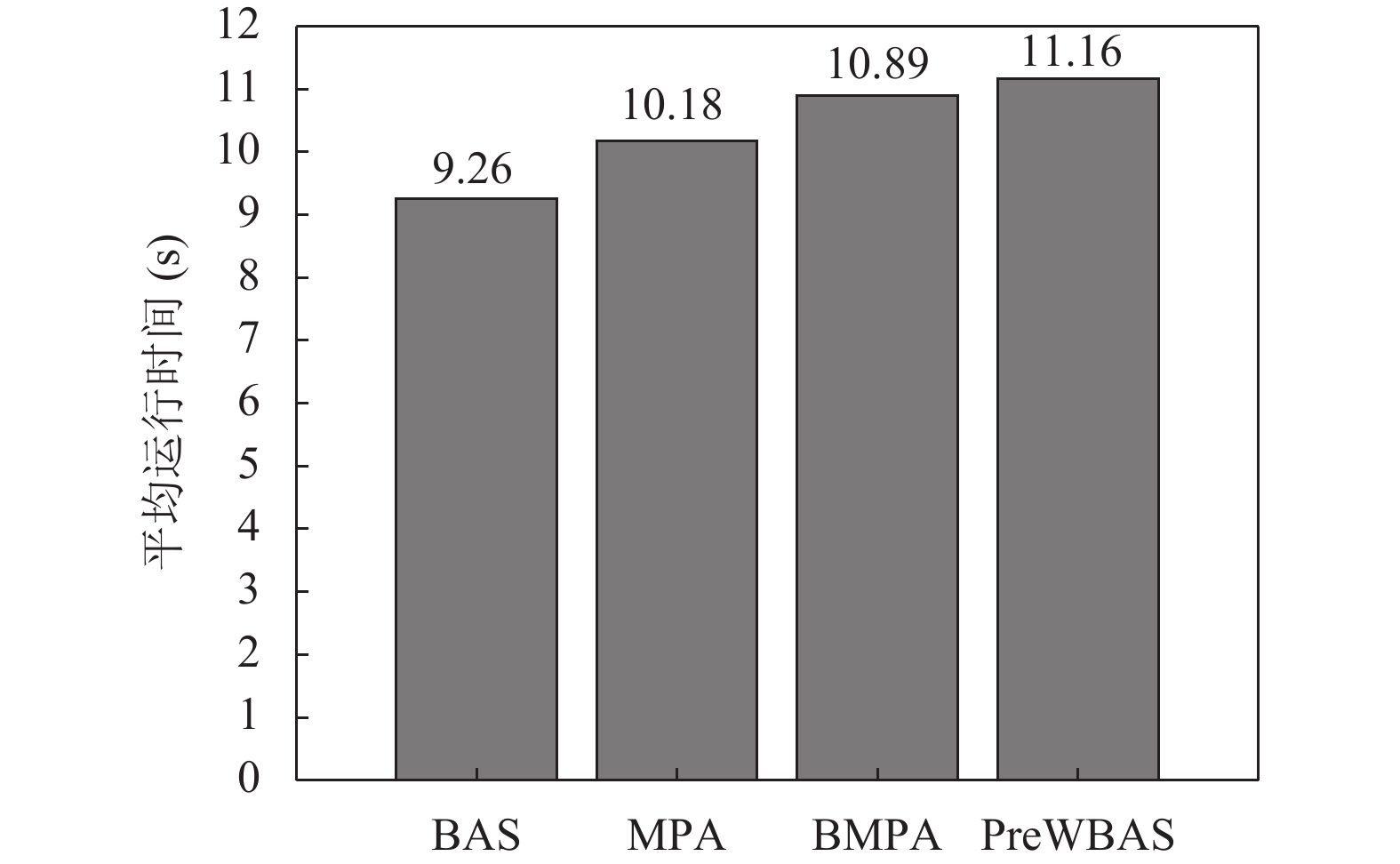
|
图 10 4种算法平均时间对比 |

|
图 11 不同数目节点的无人机路径消耗 |
4 结语
本文通过对无人机充电路径进行分析, 以路径、能耗、时间成本和无人机搭配成本为最小为优化目标, 提出改进的海洋捕食者算法和天牛须搜索算法结合的新算法. 对比传统的海洋捕食者算法和天牛须算法, 提出的算法能有效地降低成本.
在未来的工作里, 将在三维空间内对无人机的部署问题进行研究, 使其更加符合部署实际.
| 表 3 充电成本和路线 |
| [1] |
Kurs A, Karalis A, Moffatt R, et al. Wireless power transfer via strongly coupled magnetic resonances. Science, 2007, 317(5834): 83-86. DOI:10.1126/science.1143254 |
| [2] |
Han GJ, Yang X, Liu L, et al. A joint energy replenishment and data collection algorithm in wireless rechargeable sensor networks. IEEE Internet of Things Journal, 2018, 5(4): 2596-2604. DOI:10.1109/JIOT.2017.2784478 |
| [3] |
Wang HY, Wang JY, Huang M. Building a smart home system with WSN and service robot. Proceedings of the 5th International Conference on Measuring Technology and Mechatronics Automation. Hong Kong: IEEE, 2013. 353–356.
|
| [4] |
Wan LT, Han GJ, Shu L, et al. Distributed parameter estimation for mobile wireless sensor network based on cloud computing in battlefield surveillance system. IEEE Access, 2015, 3: 1729-1739. DOI:10.1109/ACCESS.2015.2482981 |
| [5] |
Khan RA, Shah SA, Aleem M A, et al. Wireless sensor networks: A solution for smart transportation. Journal of Emerging Trends in Computing and Information Sciences, 2012, 3(4): 567-571. |
| [6] |
Wang QH, Kong FZ, Wang M, et al. Optimized charging scheduling with single mobile charger for wireless rechargeable sensor networks. Symmetry, 2017, 9(11): 285. DOI:10.3390/sym9110285 |
| [7] |
吴蕾, 赵英亮, 王黎明, 等. 无线传感器网络节点基于遗传算法的充电路径规划. 单片机与嵌入式系统应用, 2022, 22(3): 61-65. DOI:10.11822/j.issn.1009-623X.2022.3.dpjyqrsxtyy202203016 |
| [8] |
雷蕾, 陈宏滨. 基于萤火虫算法的无线可充电传感器网络的充电策略. 桂林电子科技大学学报, 2021, 41(6): 477-483. DOI:10.16725/j.cnki.cn45-1351/tn.2021.06.012 |
| [9] |
王茜, 崔志华, 王丽芳. 无线可充电传感器网络中的充电路径优化. 小型微型计算机系统, 2021, 42(10): 2167-2172. DOI:10.3969/j.issn.1000-1220.2021.10.025 |
| [10] |
Hong Y, Luo CW, Li DY, et al. Energy efficiency optimization for multiple chargers in wireless rechargeable sensor networks. Theoretical Computer Science, 2022, 922: 193-205. DOI:10.1016/j.tcs.2022.04.024 |
| [11] |
Mukase S, Xia KW. Multi-objective optimization with mayfly algorithm for periodic charging in wireless rechargeable sensor networks. World Electric Vehicle Journal, 2022, 13(7): 120. DOI:10.3390/wevj13070120 |
| [12] |
Jia RH, Wu JH, Lu JF, et al. Energy saving in heterogeneous wireless rechargeable sensor networks. Proceedings of the 2022 IEEE Conference on Computer Communications. London: IEEE, 2022. 1838–1847.
|
| [13] |
Zhao CX, Yao YC, Zhang N, et al. Hybrid scheduling strategy of multiple mobile charging vehicles in wireless rechargeable sensor networks. Peer-to-peer Networking and Applications, 2023, 16(2): 980-996. DOI:10.1007/s12083-022-01428-y |
| [14] |
Faramarzi A, Heidarinejad M, Mirjalili S, et al. Marine predators algorithm: A nature-inspired metaheuristic. Expert Systems with Applications, 2020, 152: 113377. DOI:10.1016/j.eswa.2020.113377 |
| [15] |
Wang JY, Chen HX. BSAS: Beetle swarm antennae search algorithm for optimization problems. arXiv:1807.10470, 2018.
|
| [16] |
Hou YT, Shi Y, Sherali HD. Rate allocation and network lifetime problems for wireless sensor networks. IEEE/ACM Transactions on Networking, 2008, 16(2): 321-334. DOI:10.1109/TNET.2007.900407 |
| [17] |
Houssein EH, Hassaballah M, Ibrahim IE, et al. An automatic arrhythmia classification model based on improved marine predators algorithm and convolutions neural networks. Expert Systems with Applications, 2022, 187: 115936. DOI:10.1016/j.eswa.2021.115936 |
| [18] |
Abdel-Basset M, Mohamed R, Elhoseny M, et al. A hybrid COVID-19 detection model using an improved marine predators algorithm and a ranking-based diversity reduction strategy. IEEE Access, 2020, 8: 79521-79540. DOI:10.1109/ACCESS.2020.2990893 |
| [19] |
Abdel-Basset M, Mohamed R, Elhoseny M, et al. Energy-aware marine predators algorithm for task scheduling in IoT-based fog computing applications. IEEE Transactions on Industrial Informatics, 2021, 17(7): 5068-5076. DOI:10.1109/TII.2020.3001067 |
| [20] |
张潇. 海洋捕食者算法的改进及应用[硕士学位论文]. 成都: 四川师范大学, 2022.
|
| [21] |
陈龙, 金可仲, 蔡雪冰, 等. 基于改进MPA的分层无线传感器网络优化部署. 传感技术学报, 2021, 34(1): 109-117. DOI:10.3969/j.issn.1004-1699.2021.01.017 |
| [22] |
方泗喃, 高萍萍, 肜郝捷, 等. 基于改进天牛须搜索算法的路径规划方法. 信息技术与信息化, 2021(11): 23-28. DOI:10.3969/j.issn.1672-9528.2021.11.006 |
 2023, Vol. 32
2023, Vol. 32



