2. 武汉大学 土木建筑工程学院, 武汉430079;
3. 深圳市腾讯计算机系统有限公司, 深圳 510310
2. School of Civil Engineering, Wuhan University, Wuhan 430079, China;
3. Shenzhen Tencent Computer System Co. Ltd., Shenzhen 510310, China
物体的颜色属性, 是人眼感知世界中重要的组成部分. 物体的颜色在不同光源下会发生改变, 但是人眼能够在不同光源条件下保持对物体颜色感知恒定, 此特性被称作人眼的颜色恒常性. 与人眼不同, 在成像设备采集的数字图像中, 光源会导致图像中的物体颜色发生变化, 这些颜色变化会影响图像下游任务如图像理解[1]、图像分割[2]等算法[3]的性能. 在实际应用中, 拍摄的图像往往会受到多种条件如环境、灯光、天气的影响, 图像的成像质量也因此降低, 需要采用图像处理算法尽可能消除数字图像中场景光源的影响, 将图像中物体的颜色还原到标准光源下, 这类还原图像物体颜色的方法统称为颜色恒常性算法.
颜色恒常性算法可以显著提高计算机对图像场景的理解[4]和对象的识别. 为了去除图像中光源带来的色偏影响, 颜色恒常性算法的步骤多为: 首先估计光照颜色, 然后利用von Kries[5]提出的对角模型对图像进行颜色矫正, 因此光照颜色的估计值准确与否, 是图像最终矫正效果的关键.
颜色恒常性算法通常分为两类, 一类是静态算法, 一类是基于学习的算法. 静态算法具有无监督的特性, 通过分析图像中的颜色统计规律, 寻找图像中的灰色像素, 进行光源估计, 无需对数据进行标注. 例如基于Retinex理论[6]的White Patch[7]、Max RGB[8, 9]和Grey world[10]算法. van de Weijer等人[11]提出Grey Edge算法框架, 通过设定相应的参数就可以实现White Patch, Max RGB和Grey world等算法. 这些算法易于理解计算且相对简单, 但是对图像场景条件有较高的要求, 当图像不满足这些算法的场景要求, 算法的准确率会大幅度降低.
基于学习的算法分为基于传统学习的颜色恒常性算法和基于深度学习的颜色恒常性算法. 基于传统学习的颜色恒常性算法包括相关颜色法[12]、色域映射法[13, 14]和贝叶斯颜色恒常性[15]算法. 这类算法对于数据集同样有着较高的要求, 如果数据集中没有囊括大多数的空间和纹理信息, 将产生不准确的光源估计, 最终影响算法的效果.
基于深度学习的算法在近年来逐渐涌现. 卷积神经网络作为深度学习的经典框架, 通过使用大量数据集进行训练, 能够从多维度提取图像的特征, 得到图像的估计光照值[16-19]. CNN在颜色恒常性算法取得了相对静态算法和传统学习算法更高的效率和更好的效果. 最早是由Bianco等人[20]使用AlexNet和SVR和基于CNN的模型计算光照估计值. Domislović等人[21]使用具有5个卷积层和大小为1×1的卷积核的模型, Hu等人[22]提出的全卷积神经网络Fc4, 通过对图像分块, 对不同图像块赋予不同置信度估计光源, 实现了更高的效率和准确性. 另外还有使用生成对抗式网络算法, 如pix2pix[23]、starGan[24]等, 能够将非标准光源下的图像直接转换称标准光源下的图像, 实现图像颜色恒常性, 也取得了优秀的结果.
本文提出了一种基于深度学习的方法, 采用SqueezeNet全卷积神经网络, 引入了注意力机制和残差模块进行学习训练. 网络使用完整图像作为输入, 通过卷积神经网络, 计算图像不同区域的局部光照颜色, 然后通过设计不同池化汇聚得到图像的全局光照, 最后使用对角模型将图像矫正到标准光源下.
1 光照颜色估计网络SqueezeNet是Iandola等人[25]提出的CNN模型, 是一种轻量级的模型, 能够在保证模型精度的基础上, 提高模型的处理速度. SqueezeNet的核心模块为Fire Module, 其结构如图1所示. 输入的特征图先经过卷积核大小为1×1的卷积层(Squeeze层), 将特征图压缩, 再经过卷积核大小为1×1和3×3的混合卷积层(Expand层), 最后将输出进行拼接(concate), 得到下一模块的输入. 使用1×1的卷积核替换大部分3×3的卷积核, 可以有效减少网络模型参数的数量, 同时达到延迟下采样的效果, 最终产生较大的特征图, 提升网络性能.

|
图 1 Fire Module结构 |
本文基于SqueezeNet的构造的颜色恒常网络模型结构图如图2所示. 色偏图像输入到网络模型中, 经过3×3卷积, 再经过7个Fire Module, 然后连接一个最大池化层、一个6×6卷积层和一个1×1卷积层, 得到不同区域的光照估计值, 最后连接池化层, 通过设计不同的方式汇聚光照估计, 计算得到最终的全局估计光源. 在图2中, 每个Fire Module下方有4个参数. 第1个参数是指Fire Module的输入通道数, 第2个参数意为Fire Module中Squeeze层1×1卷积数量, 第3和第4个参数意为Fire Module中Expand层的1×1卷积数量和3×3卷积数量. Expand层中两种卷积数量的和为Fire Module的输出通道数.
1.1 基于残差连接的Fire Module为了提高模型的光源估计准确性, 降低模型复杂度, 减少过拟合, 根据ResNet[26]的原理, 对模型进行改进. 具体改进如图3所示: 将图1中输出通道数相同的Fire Module添加旁路连接, 也就是对SqueezeNet网络中的Fire3、Fire5、Fire7模块添加残差连接, 将输入的张量和经过Fire Module输出的张量加和后将作为下一个模块的输入. 修改后的Fire Module命名为residual fire module (RFM).

|
图 2 颜色恒常模型结构图 |

|
图 3 RFM的结构示意图 |
通过引入残差连接, 将经过Fire Module的输入特征图和输出特征图相加, 可以实现信息的多层跨越, 解决梯度消失和梯度爆炸的问题; 通过多个层的堆叠, 可以提升神经网络的非线性拟合能力, 提升网络的训练速度和准确度.
1.2 基于注意力机制的残差模块注意力机制是一种资源分配方式, 算法从关注整体到关注重点, 将计算资源分配给更重要的任务. 本文模型基于通道注意力机制, 受SeNet[27]启发, 在RFM网络的基础上, 设计一个Residual Fire Module based SeNet (RFMS), 如图4所示.
如图4所示, 输入的张量除了经过RFM模块以外, 还需要通过平均池化后再经过两个全连接层(FC层), 经过Sigmoid函数对不同特征图通道输出0–1之间权重(ω), 再与原输入张量相乘保持维度一致, 最后与RFM模块输出的张量加和, 以得到下一个模块的输入.

|
图 4 通道注意力机制结构图 |
基于Fire Module添加的全连接层、Sigmoid函数以及张量加和等操作, 就是添加的注意力通道. 由于图像的光照信息常常隐藏在图像的灰色像素中, 使用通道注意力机制, 神经网络可以将算力偏重于对图像的通道信息处理上, 捕捉输入数据中三通道数据相近的像素信息, 更好的理解图像, 提升模型的准确性.
1.3 池化层图像输入到网络模型后, 经过卷积模块和最大池化层(Max Pool)提取特征, 得到局部光照颜色, 最终需要池化层对局部光照颜色整合输出, 得到最终的图像全局光照颜色. 为了评估得到效果最好的池化层, 本文模型测试了3种池化方式.
(1) 加和平均池化(mean pooling): 对模型输出的局部光照颜色值求和, 然后归一化得到全局光照:
| $ L = normali{\textit{z}}e\left(\sum\limits_{i = 1}^n {{L_i}} \right) $ | (1) |
(2) 中值池化(median pooling): 计算局部光照颜色的三通道中值, 然后进行归一化, 得到全局光照:
| $ L = normali{\textit{z}}e(median([{L_1}, {L_2}, \cdots, {L_n}])) $ | (2) |
(3) 置信度加和池化(confidence pooling): 将图3中Conv10的输出通道改为4, 前三维输出图像某区域的光照估计值, 第四维输出该区域的置信度C (confidence), 得到全局光照颜色估计值:
| $ L = normali{\textit{z}}e\left(\sum\limits_{i = 1}^n {{L_i} \cdot {C_i}} \right) $ | (3) |
在颜色恒常性算法中, 为了直观地表示光源的颜色, 我们直接使用光照的色度值表示光源. 在进行光照误差度量时, 光照的亮度可以轻易通过光照向量的模值进行调整, 因此只需要比较估计光照与真实光照之间的向量方向差异, 忽视光照向量模值差异. 光照的色度由红绿蓝三通道组成, 估计光照与真实光照在三维空间的夹角被称为角度误差, 本文模型选取角度误差作为损失函数的修正模型参数. 公式如下:
| $ L = \arccos \left(\frac{{{L_{{\rm{est}}}} \cdot {L_{{\rm{gt}}}}}}{{\left\| {{L_{{\rm{est}}}}} \right\| \times \left\| {{L_{{\rm{gt}}}}} \right\|}}\right) \times \frac{{180^\circ }}{{\text{π}} } $ | (4) |
其中,
为了测试模型效果, 实验选用Color Checker数据集和NUS-8 camera数据集作为原始数据集.
Color Checker数据集由Canon 1D相机拍摄的86张图片和Canon 5D相机拍摄的468张照片组成. 作者在拍摄时在场景中放置了24色卡, 数据集中记录了色卡的坐标, 方便实验人员对色卡进行遮盖, 防止色卡的存在影响模型算法的稳健性. NUS-8 camera数据集与Color Checker数据集类似, 同样有色卡和色卡坐标, 用于计算场景中的光源颜色. 不同的是, NUS-8 camera数据集规模更大, 由8个相机拍摄的1736张图像组成.
原始数据集规模较小, 为了防止模型过拟合, 提升模型最终的效果, 对数据集通过旋转、缩放进行扩充.
图像旋转: 首先设置一个0.1–1的裁剪系数, 对数据集图像进行裁剪, 然后将图像围绕中心随机旋转–30°~30°, 并将裁剪后的图像调整至512×512.
图像缩放: 将旋转后的数据集每张图像的光照颜色值和真实光源值按照0.6–1.4内的随机比例进行缩放, 然后使用Gamma矫正对图像的动态范围进行调整, 对像素值进行归一化.
将扩充后的数据集随机分为3份, 其中任意2份用于训练, 还有1份用于测试, 分别训练出3个模型. 然后使用三折交叉验证, 对不同数据集计算得到的角度误差做几何平均.
2.2 实验设备及训练SqueezeNet是一款轻量级网络, 对于服务器硬件要求不高. 实验设备使用Linux的Ubuntu 16.04版本系统, GPU为GeForce GTX 1080Ti, CPU为i7-4790k, 使用PyTorch框架, Python版本为Python 3.6. 使用在ImageNet上训练好的SqueezeNet参数作为本文模型骨干网络的参数, Adam参数优化器对整个网络权重迭代更新. 所有训练过程中, epoch为2000, batch size为16, 优化器基础学习率为0.0001. 此外, 为防止过拟合, 将模型中的drop out设置为0.5, 网络每一层的weight decay设置为5×10−5.
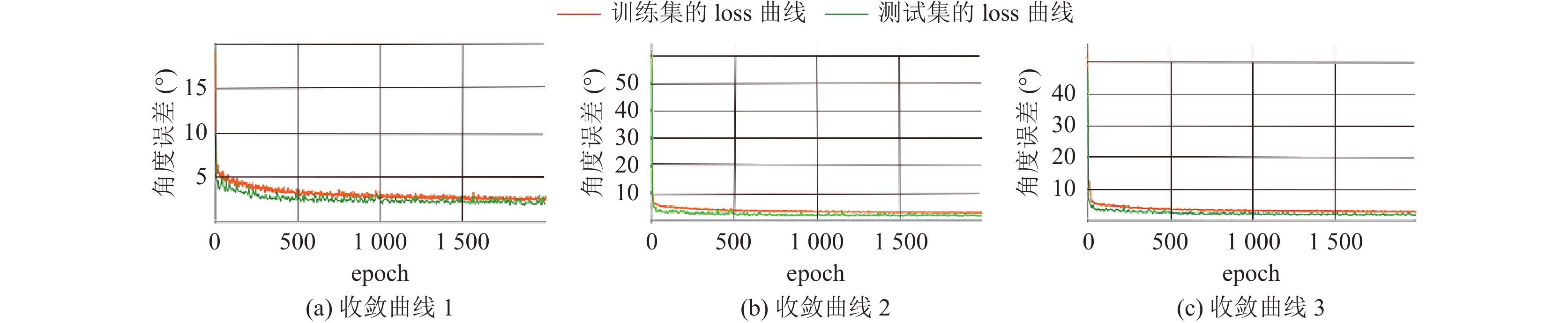
为了提升每个数据集的使用效率, 将数据集平均分为3份, 使用其中的两份作为训练集, 剩下一份作为测试集, 依次训练出3个模型, 然后再将结果做几何平均, 作为最终的算法输出结果. 图5是本文算法的损失函数收敛曲线, 横轴代表训练的迭代次数, 纵轴是角度误差. 从图像中可以看出, 基本上可以在200轮左右趋于平稳, 最终角度误差收敛到1.5左右.
2.3 算法评价指标由于色偏图像是基于网络对图像计算得到的全局估计光源值进行矫正的, 因此图像的估计光源值准确与否是衡量算法可行性的关键. 角度误差作为评价图像估计光源与真实光源偏差的指标, 能够最大程度地反映图像矫正结果, 因此角度误差除了作为损失函数以外, 还是作为评价颜色恒常性算法效果的重要指标. 模型训练完成后, 使用模型对每张测试图像得到的估计光源进行处理, 计算与场景真实光源的角度误差, 统计角度误差的平均值(mean)、中值(median)、三重均值(tri-mean)、最优的25%均值(best 25%)和最差的25%均值(worst 25%), 并将最终得到的结果与其他模型对比, 评价模型的效果.
|
图 5 损失函数收敛曲线 |
3 结果与讨论
RFM模块和RFMS模块的实验结果如表1所示.
| 表 1 实验数据集上的实验结果 |
由表1中结果可以看出, RFM和RFMS模块在角度误差的各项数据上面都有所提升, 说明模块总体上会对于本文模型的效果产生积极的影响. 尤其是RFMS模块, 其在角度误差均值上对模型有0.08的提升, 在三重均值有0.1的提升, 证明了基于注意力机制的残差连接能够帮助模型更有效地获取图像底层信息, 计算图像的估计光源.
针对第1.3节提出的几种池化方式做测试对比, 3种池化方式都基于RFMS模块设计, 实验结果如表2所示.
| 表 2 不同池化方式对聚合全局光照估计的影响 |
实验结果表明, 置信度池化对于模型聚合全局光照的效果最好. 这是因为图像各个部分的光照具有差异性, 简单地对网络输出的图像块的局部光照信息进行加和得到的实验结果不够符合自然规律, 不一定能够得到效果最好的光照估计值; 而置信度池化能够针对各个图像块的光源估计输出一个置信度分数, 使得模型更高效地应用神经网络输出的信息, 提高网络计算估计光源的效率, 因此表现出了更好的性能.
图6显示了静态算法与本文算法颜色恒常处理效果. 从图像的处理结果可以看出: 静态算法对于场景的适应性不足, 在不同光照条件或者不同环境下效果非常不稳定, 最终呈现出不同程度的偏色, 总体在光照弱的环境下偏蓝或偏黄, 在光照强的地方效果较好, 在室外环境下算法效果相对较好, 但在室内环境下算法效果相对较差.
表3是本文算法与常用的静态算法、基于学习的算法的角度误差指标对比.
结果表明, 本文模型的效果与传统静态方法和传统基于学习的方法相比, 在所有指标均有很大程度的提高, 说明基于卷积神经网络的算法模型能够更好地提取图像特征, 理解图像局部之间的关系, 输出更准确的图像光照信息, 且具有很高的稳定性, 适用范围更加广泛, 在不同的光源场景下都有着不错的实验效果, 基于深度学习的算法在和深度学习的方法相比, 在大多数指标下仍然有更好的表现, 体现了本文算法的有效性.
4 结论本研究提出了一种基于全卷积神经网络的颜色恒常性算法. 本文模型以SqueezeNet作为骨干网络, 保证了模型的训练速度, 设计了RFM模块和RFMS模块, 替代SqueezeNet中的Fire Module, 并设计了不同的池化方式汇聚图像块光源信息计算估计光源. 实验结果表明, 基于注意力的残差连接模块能够更好地帮助模型获取图像特征, 理解图像底层信息, 输出图像的局部光源, 使用置信度池化方式估计光源, 能够更高效地汇聚图像光源信息, 矫正色偏图像. 通过在Color Checker数据集和NUS-8 camera数据集上进行训练和测试, 获得了相比于静态方法、传统学习算法和一些深度学习方法更好的效果, 验证了本文算法的有效性.

|
图 6 不同颜色恒常算法效果比较 |
| 表 3 本文算法在实验数据集上与现有算法的比较 |
下一步研究选取更大的数据集进行训练, 提升网络在不同场景下的适应范围; 另外探索基于Transformer等新型的网络框架进行改进; 并将处理好的图像提供给目标检测、语义分割等图像算法, 探究颜色恒常性处理效果对于图像下游任务的影响.
| [1] |
Chen YH, Chao TH, Bai SY, et al. Filter-invariant image classification on social media photos. Proceedings of the 23rd ACM International Conference on Multimedia. Brisbane: ACM, 2015. 855–858.
|
| [2] |
Afifi M, Brown MS. What else can fool deep learning? Addressing color constancy errors on deep neural network performance. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 243–252.
|
| [3] |
Diamond S, Sitzmann V, Julca-Aguilar F, et al. Dirty pixels: Towards end-to-end image processing and perception. ACM Transactions on Graphics, 2021, 40(3): 23. |
| [4] |
Sidorov O. Artificial color constancy via GoogleNet with angular loss function. Applied Artificial Intelligence, 2020, 34(9): 643-655. DOI:10.1080/08839514.2020.1730630 |
| [5] |
Worthey JA, Brill MH. Heuristic analysis of von Kries color constancy. Journal of the Optical Society of America A, 1986, 3(10): 1708-1712. DOI:10.1364/JOSAA.3.001708 |
| [6] |
Land EH, McCann JJ. Lightness and retinex theory. Journal of the Optical Society of America, 1971, 61(1): 1-11. DOI:10.1364/JOSA.61.000001 |
| [7] |
Land EH. The retinex theory of color vision. Scientific American, 1977, 237(6): 108-128. DOI:10.1038/scientificamerican1277-108 |
| [8] |
Funt B, Shi LL. The effect of exposure on MaxRGB color constancy. Proceedings of the 2010 SPIE 7527, Human Vision and Electronic Imaging XV. San Jose: SPIE, 2010. 282–288.
|
| [9] |
Funt BV, Shi LL. The rehabilitation of MaxRGB. Proceedings of the 18th Color and Imaging Conference. San Antonio, 2010. 256–259.
|
| [10] |
Buchsbaum G. A spatial processor model for object colour perception. Journal of the Franklin Institute, 1980, 310(1): 1-26. DOI:10.1016/0016-0032(80)90058-7 |
| [11] |
van de Weijer J, Gevers T, Gijsenij A. Edge-based color constancy. IEEE Transactions on Image Processing, 2007, 16(9): 2207-2214. DOI:10.1109/TIP.2007.901808 |
| [12] |
Finlayson GD, Hordley SD, Hubel PM. Color by correlation: A simple, unifying framework for color constancy. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1209-1221. DOI:10.1109/34.969113 |
| [13] |
Gijsenij A, Gevers T, van de Weijer J. Generalized gamut mapping using image derivative structures for color constancy. International Journal of Computer Vision, 2010, 86(2): 127-139. |
| [14] |
Barnard K. Improvements to gamut mapping colour constancy algorithms. Proceedings of the 6th European Conference on Computer Vision. Dublin: Springer, 2000. 390–403.
|
| [15] |
Brainard DH, Freeman WT. Bayesian color constancy. Journal of the Optical Society of America A, 1997, 14(7): 1393-1411. DOI:10.1364/JOSAA.14.001393 |
| [16] |
Espejo-Garcia B, Mylonas N, Athanasakos L, et al. Towards weeds identification assistance through transfer learning. Computers and Electronics in Agriculture, 2020, 171: 105306. DOI:10.1016/j.compag.2020.105306 |
| [17] |
Gao SB, Zhang M, Li YJ. Improving color constancy by selecting suitable set of training images. Optics Express, 2019, 27(18): 25611-25633. DOI:10.1364/OE.27.025611 |
| [18] |
Hussain MA, Akbari AS. Color constancy adjustment using sub-blocks of the image. IEEE Access, 2018, 6: 46617-46629. DOI:10.1109/ACCESS.2018.2866792 |
| [19] |
Xue SY, Gao SB, Tan MJ, et al. How does color constancy affect target recognition and instance segmentation? Proceedings of the 29th ACM International Conference on Multimedia. ACM, 2021. 5537–5545.
|
| [20] |
Bianco S, Cusano C, Schettini R. Color constancy using CNNs. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Boston: IEEE, 2015. 81–89.
|
| [21] |
Domislović I, Vršnak D, Subašić M, et al. One-net: Convolutional color constancy simplified. Pattern Recognition Letters, 2022, 159: 31-37. DOI:10.1016/j.patrec.2022.04.035 |
| [22] |
Hu YM, Wang BY, Lin S. FC4: Fully convolutional color constancy with confidence-weighted pooling. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu: IEEE, 2017. 330–339.
|
| [23] |
Isola P, Zhu JY, Zhou TH, et al. Image-to-image translation with conditional adversarial networks. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 5967–5976.
|
| [24] |
Choi Y, Choi M, Kim M, et al. StarGAN: Unified generative adversarial networks for multi-domain image-to-image translation. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8789–8797.
|
| [25] |
Iandola FN, Han S, Moskewicz MW, et al. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and < 0.5 MB model size. Proceedings of the 2017 ICLR. 2017.
|
| [26] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [27] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 7132–7141.
|
| [28] |
Finlayson GD, Trezzi E. Shades of gray and colour constancy. Proceedings of the 12th Color Imaging Conference: Color Science and Engineering Systems, Technologies, and Applications. Scottsdale: 2004. 37–41.
|
| [29] |
Shi W, Loy CC, Tang XO. Deep specialized network for illuminant estimation. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer International Publishing, 2016. 371–387.
|
 2023, Vol. 32
2023, Vol. 32


