当今世界新军事变革日新月异, 智能化成为未来军队建设发展的主题. 以智能化、体系化、分布式、自组织为特征的智能化战争以高度分散、灵活机动、动态组合、自主协同的作战体系为依托高效运行, 智能的对抗和决策的对抗最终都体现为作战体系的对抗. 提高对作战体系运行规律的认识、准确描述和评价体系能力是获取体系对抗优势的关键, 也是当前作战规划和评估领域的重点研究方向.

作战体系节点重要度评估作为作战体系建模和应用研究的重要内容, 在现代战争的作战筹划、指挥决策、作战评估等全流程具有重要价值. 当前作战体系模型构建、效能评估方面的研究大多以复杂网络理论和现代作战循环理论为基础开展. 20世纪70年代, 文献[1–3]研究了OODA (observation, orientation, decision and action)环在作战仿真评估和情报分析等领域中的应用. 2002年, Dekker^[4]提出了FINC (force, intelligence, networking and C2)模型对作战体系进行描述, 并使用社会网络分析方法评估作战体系效能. 根据作战循环理论, Cares^{[5, 6]}首次将复杂网络理论与作战体系建模结合在一起, 提出了信息时代交战模型(information age combat model, IACM), 将作战节点分为传感器节点、决策节点、影响节点和敌方目标4种类型, 并提出作战环理念, 将作战体系分解为控制环、催化控制环、催化竞争环和交战环4类元模型, 然后采用IACM模型邻接矩阵的Perron-Frobenius特征值对体系效能进行评估. 借鉴IACM模型思路, 国内学者也开始对作战环模型开展研究. 谭跃进等^[7]将作战环应用于武器装备体系建模中, 并描述了网络拓扑结构对体系整体测度指标的影响. 张春华等^[8]将作战环应用于作战体系效能评估中, 提出了以作战环数量为基础的作战体系网络效能指标和作战装备体系能力评估模型. 文献[9, 10]使用作战环对作战网络进行建模, 并采用作战环数量对体系效能进行评估. 文献[11-13]结合作战环数量和作战环中边的能力对体系效能进行了评估.

结合对相关文献的调研分析可以发现, 文献[4]提出的FINC模型指标体系比较简单, 无法综合考虑作战节点的各方面属性参数, 对后续的体系效能评估精确性影响较大; 文献[5, 6]没有验证基于IACM模型的效能评估方法的有效性; 文献[7-10]仅简单地根据作战体系内的作战环数量对作战体系效能进行评估, 没有考虑作战节点本身的属性参数和作战能力; 文献[11, 12]没有给出边能力的计算方法; 文献[13]针对某个特定敌方目标只考虑了所有作战环效能的最大值作为作战体系对该目标的效能, 而没有考虑体系内各作战环的能力聚合.

1 基于时序功能作战模型的异质作战体系建模

作战体系网络中包含多种类型的节点, 如侦查类的无人侦察机、决策类的指挥控制中心、火力打击类的各类型战机、通信类的中继卫星、保障类的加油机等, 各种类型节点具有不同的属性, 不同类型的节点之间具有不同类型的信息流和关联关系, 如目标信息流、指控命令流、支援保障关系、火力打击关系等, 是一个典型的异质信息网(heterogeneous information network, HIN), 结合超网络模型和异质信息网络模型, 本文建立了基于时序功能作战模型的异质作战体系模型. 将各作战装备抽象为网络中的异质节点, 将装备之间的信息流、物质流、能量流抽象为网络中的异质边, 从作战体系、子网络、武器装备、装备功能、属性参数等不同视角、不同粒度对作战体系进行描述, 其层次模型如图1所示.

为尽量精细地对作战体系进行网络化建模, 同时保留作战体系的复杂网络特性, 本文以功能节点层为对象对作战体系网络进行建模和分析, 建立时序功能作战模型.

本文对作战体系在功能粒度上进行建模, 将每个装备节点分解为一个或多个具有单一功能、执行某一基本作战任务(侦查、指控、火力、通信、保障)的子系统, 并建模为异质信息网络的节点, 即元功能节点; 将连接各元功能节点的物质、信息、能量交互建模为异质信息网中的边.

结合复合网络模型和时序网络模型, 作战体系的时序功能作战模型可定义为:

$ G = ({G_{{\rm{red}}}}, {G_{{\rm{blue}}}}, {E_{{V_{{\rm{red}}}} \times {V_{{\rm{blue}}}}}}, T) $

(1)

该模型定义的作战体系包含红、蓝双方作战体系两个网络, 其中 ${G_{{\rm{red}}}} = ({V_{{\rm{red}}}}, {E_{{\rm{red}}}})$ 代表红方元功能节点网络, ${G_{{\rm{blue}}}} = ({V_{{\rm{blue}}}}, {E_{{\rm{blue}}}})$ 代表蓝方元功能节点网络, ${E_{{V_{{\rm{red}}}} \times {V_{{\rm{blue}}}}}}$ 为红蓝双方元功能节点之间的交互关系集合, T为作战体系处于该状态下的时间戳, ${V_{{\rm{red}}}}$ 和 ${V_{{\rm{blue}}}}$ 分别表示红蓝双方的元功能节点集合, ${E_{{\rm{red}}}}$ 和 ${E_{{\rm{blue}}}}$ 分别表示红蓝双方元功能节点网络内部的交互关系集合. 作战体系的时序功能作战模型如图2所示.

1.1 元功能节点建模

借鉴FINC模型和作战环模型, 本文建立了IDFCS模型. 将作战体系中的元功能节点分为5类, 分别是情报侦查节点(intelligence,I)、指挥决策节点(decision,D)、火力打击节点(fire, F)、通信中继节点(communication, C)和支援保障节点(support, S). 元功能节点其属性向量可表示为:

$ \begin{gathered} v = {\langle} {\begin{gathered} EquipmentID, Identity, NodeType, Level, \\ Capability, {\textit{SupplyDemand}}, {\textit{Defence}}, \\ {\textit{Timestamp}}, Geographic, extend \\ \end{gathered}}{\rangle} \end{gathered} $

(2)

其中, EquipmentID为该元功能节点所属的装备唯一标识ID, Identity为节点身份标识: $ Identity:: = R\left| B \right. $ , R为红方, B为蓝方; NodeType为节点类型: $ NodeType:: = I\left| D \right.\left| F \right.\left| C \right.\left| S \right. $ ; Level为根据节点在其所述类别中的重要程度划分的节点层级: Level={0, 1, 2, 3}, Level=0代表最不重要, Level=1代表一般重要, Level=2代表重要, Level=3代表非常重要, 不同的节点级别影响节点的属性参数取值范围和与其他类型节点发生连接的概率; Capacity为节点能力向量, 表示节点的各能力参数. 不同类型的节点能力向量各不相同, 各类型节点的能力向量内容在后文进行详述; SupplyDemand为节点供应需求; Defence为节点防护能力向量; Timestamp为作战体系当前状态的时间戳; Geographic为节点地理空间信息向量, 包含节点的经度、维度、海拔高度信息; extend为扩展属性向量.

(1)节点能力向量

元侦查功能节点的能力向量为:

$ Capability\_i = \left\langle \begin{gathered} Radius, Accuracy, DetectRate, \\ HavestRate, {\textit{Efficiency}}, extern \\ \end{gathered} \right\rangle $

(3)

其中, Radius表示最大侦查半径, Accuracy表示目标识别精度, DetectRate表示有效探测率, HavestRate表示重要情报获取率, Efficiency表示信息传输效率, extern为能力扩展项.

元决策功能节点的能力向量为:

$ \begin{gathered} Capability\_d = \left\langle \begin{gathered} CoverRate, {\textit{Efficiency}}, ComDis, \\ Delay, Community, extern \\ \end{gathered} \right\rangle \\ \end{gathered} $

(4)

其中, CoverRate表示有效覆盖率, Efficiency表示信息处理效率, ComDis表示通信距离, Delay表示指挥控制延迟, Community表示信息传输效率, extern为能力扩展项.

元火力功能节点的能力向量为:

$ \begin{gathered} Capability\_f = \left\langle \begin{gathered} CombatRadius, KillRadius, Accuracy, \\ RPG, Mobility, {\textit{Efficiency}}, extern \\ \end{gathered} \right\rangle \\ \end{gathered} $

(5)

其中, CombatRadius表示最大作战半径, KillRadius表示毁伤半径, Accuracy表示打击精度, RPG表示弹药剩余数量, Mobility表示机动速度, Efficiency表示信息传输效率, extern为能力扩展项.

元通信功能节点只包含专用的通信中继设备如中继卫星、无人机、飞艇等, 而其他类型元功能节点若包含通信功能, 则将其通信功能归为其能力向量的能力参数, 不再单独分解出一个元通信功能节点. 元通信功能节点的能力向量为:

$ \begin{gathered} Capability\_c = \left\langle \begin{gathered} Radius, {\textit{Efficiency}}, Capacity, \\ Quality, Delay, extern \\ \end{gathered} \right\rangle \\ \end{gathered} $

(6)

其中, Radius表示通信距离, Efficiency表示传输速率, Capacity表示通信容量, Quality表示通信质量, Delay表示通信时延, extern为能力扩展项.

元保障功能节点的能力向量为:

$\begin{split} & Capability\_s = \\ & {\langle}{{\begin{array}{c} {\textit{SupportType}}, Radius, Capacity, \\ {\textit{SupplyEfficiency}}, {\textit{RestoreEfficiency}}, \\ Mobility, {\textit{Efficiency}} , extern \end{array}}}{\rangle} \end{split} $

(7)

其中, SupportType表示保障节点类型: SupportType={0, 1, 2}, SupportType=0为油料补给装备, SupportType=1为弹药补给装备, SupportType=2为火力节点载具(如航母至于战斗机), Radius表示保障距离, Capacity表示供应能力, SupplyEfficiency表示供应速率, RestoreEfficiency表示恢复速率, Mobility表示机动速度, Efficiency表示信息传输效率, extern为能力扩展项.

(2)节点供应需求

节点供应需求表示如式(8):

$ \begin{gathered} {\textit{SupplyDemand}} = \left\langle \begin{gathered} {\textit{AmmoCapacity}}, {\textit{AConsumptionSpeed}}, \\ {\textit{TankCapacity}}, {\textit{FConsumptionSpeed}} \\ \end{gathered} \right\rangle \\ \end{gathered} $

(8)

其中, AmmoCapacity为弹药容量, AConsumptionSpeed弹药消耗速度, TankCapacity为油箱容量, FConsumptionSpeed为燃料消耗速度. 除火力节点外, 其他类型节点无AmmoCapacity和AConsumptionSpeed两个参数.

(3)节点防护能力向量

节点防护能力向量表示如式(9):

$ \begin{gathered} {\textit{Defence}} = \left\langle {Invisibility, Disturb, {\textit{Fencing}}, {\textit{SecFencing}}} \right\rangle \\ \end{gathered} $

(9)

其中, Invisibility为伪装隐身能力, Disturb为干扰拦截能力, Fencing为防护能力, SecFencing为二次防护能力.

(4)节点地理空间信息向量

节点地理空间信息向量表示如式(10):

$ Geographic = \left\langle {Longitude, Latitude, Height} \right\rangle $

(10)

1.2 元功能边建模

由于本文以红方作战体系对蓝方作战体系的作战效能评估为研究内容, 因此评估过程中不需要考虑蓝方节点对红方节点的情报侦查和火力打击活动, 定义蓝方所有节点为红方的目标节点(Target,T), 则时序功能作战模型中共有16种类型的元功能边, 分别是情报侦察: $ {E_{T \to I}} $ , 情报共享 $ {E_{I \to I}} $ , 情报上传 $ {E_{I \to D}} $ , 指挥协同: $ {E_{D \to D}} $ , 指挥控制: $ {E_{D \to I}} $ 、 $ {E_{D \to F}} $ 、 ${E_{D \to {{S}}}}$ , 通信中继: ${E_{D \to {{C}}}}$ 、 ${E_{{{C}} \to {{D}}}}$ 、 ${E_{{{C}} \to {{C}}}}$ , 支援保障: ${E_{{{S}} \to {{I}}}}$ 、 ${E_{{{S}} \to {{D}}}}$ 、 ${E_{{{S}} \to {{F}}}}$ 、 ${E_{{{S}} \to {{C}}}}$ 、 ${E_{{{S}} \to {{S}}}}$ , 火力打击: ${E_{{{F}} \to {{T}}}}$ .

其中友方节点的可达性表如表1所示.

表1中不为×的单元格表示该行类型节点有可能存在指向该列类型节点的连边, 打×的单元格表示该行类型节点不可能存在指向该列类型节点的连边.

红方节点到蓝方节点的可达性表与蓝方节点到红方节点的可达性表各不相同, 如表2、表3所示.

元功能边的属性向量可表示为:

$ e = ({\textit{EdgeType}}, {{Dis}}tan ce) $

(11)

其中, EdgeType为节点类型, Distance为两节点之间的空间距离.

1.3 作战体系网络生成模型

基于时序功能作战模型, 本文设计了IDFCS异质网络生成模型, 其网络生成步骤如下.

Step 1. 给定装备数量与节点数量的比值equip_prob, 元功能节点可能的组合集合combination_set, 网络节点规模network_scope, 节点属性字典node_attribute, 节点存在概率字典node_prob, 边存在概率字典connection_prob.

Step 2. 获取当前系统时间作为各节点Timestamp参数; 获取node_prob中作战体系红蓝双方各类型节点的存在概率、每类节点中不同层级节点的存在概率和红蓝双方各类型保障节点的存在概率, 根据此3个概率循环生成network_scope个节点及其Identity、NodeType、Level的属性值和保障节点SupportType的属性值; 根据equip_prob值为每个节点在[0, equip_prob×network_scope)之间随机生成节点的EquipmentID值, 每生成一个节点的EquipmentID值, 需要将其与其他已生成节点的EquipmentID进行比较, 如果发现相同EquipmentID值, 则判断EquipmentID值相同的元功能节点组合是否属于combination_set, 若属于, 则保留该新节点的EquipmentID值, 并为EquipmentID值相同的节点生成双向边, 若不属于combination_set, 则重新生成随机EquipmentID值并重复上述判断; 然后根据节点的Identity、NodeType、Level属性值和node_attribute中各类节点中各层级节点其他属性值的取值范围随机生成每个节点的剩余属性值; 在生产节点地理空间信息值时, 判断节点的EquipmentID值是否与已生成节点的EquipmentID值存在相等的情况, 若相等, 则将已生成节点的地理空间信息值直接赋给新节点.

Step 3. 根据connection_prob中各类节点中各层级节点之间的有向边存在概率和生成的节点Identity、NodeType、Level属性值, 依次判断每个节点与其他所有剩余节点的连通性, 生成IDFCS网络中的边, 根据节点的地理空间信息属性值计算各连通节点之间的距离作为边的Distance属性值.

Step 4. 以侦查节点的最大侦查半径、决策节点的通信距离、火力节点的最大作战半径、通信节点的通信距离和各边的距离为约束, 判断每条情报侦查边、通信中继边、火力打击边存在的合理性, 若不合理, 则对相关节点的对应约束属性值进行修复使其满足约束.

2 基于作战环和节点能力的异质作战体系效能评估和节点重要度评估

根据文献[7]对作战环的定义, 作战体系中的装备节点可以分为侦查类装备、决策类装备、影响类装备和敌方目标, 作战过程是一个由侦查类装备发现敌方目标, 将目标信息上传至决策类装备, 决策类装备对目标信息进行分析处理后做出相关决策, 并将指挥控制命令下达给影响类装备, 最后由影响类装备对敌方目标实施打击的一个循环过程. 同时包含该4类装备并且以同一个也是唯一一个敌方目标为起始节点和终结节点的闭合回路即为作战环. 包含情报侦察、决策支持、指挥控制和火力打击4种关系的作战环称为标准作战环.

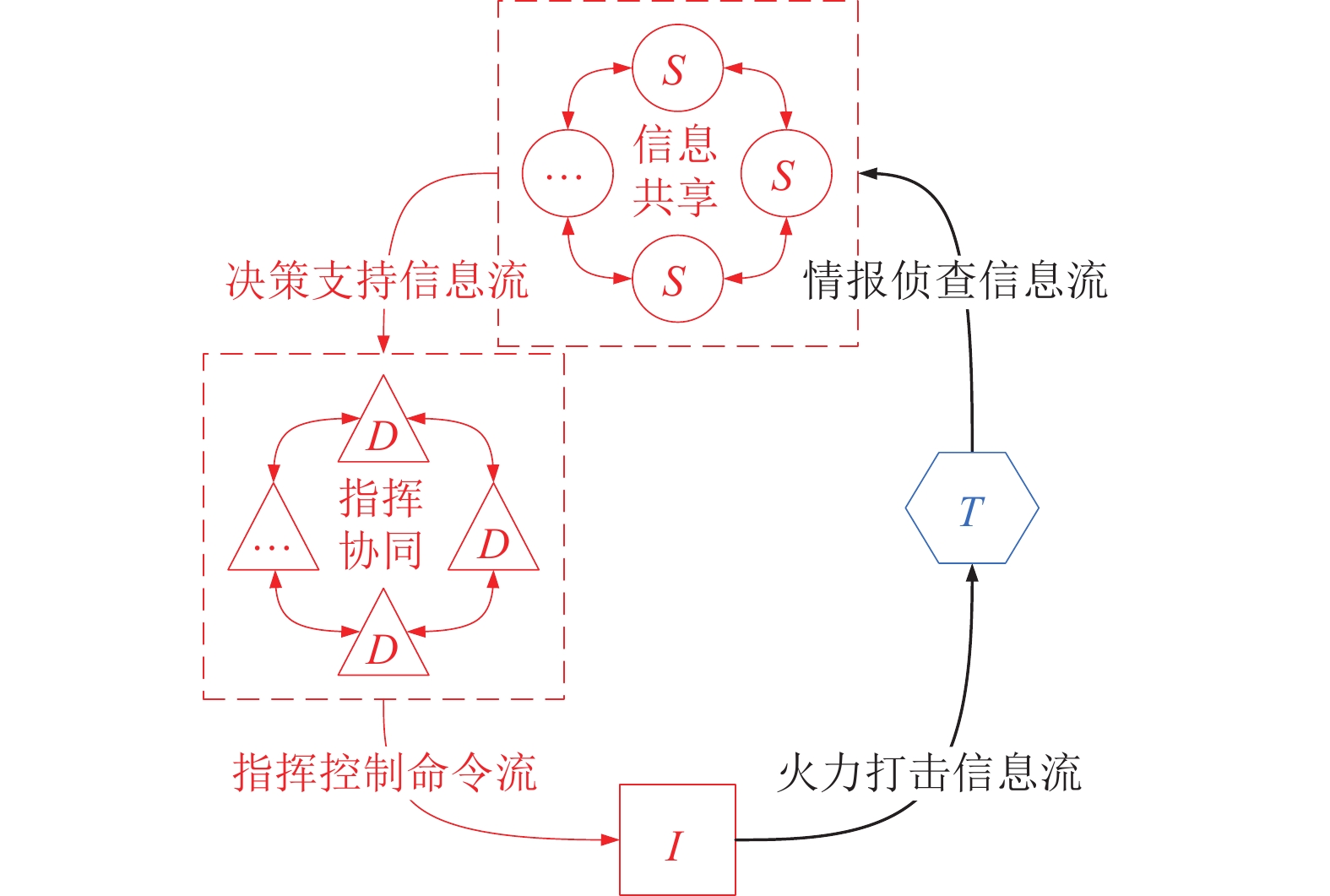
除上述4种交互关系外, 各武器装备之间还可能存在侦查类装备之间的信息共享关系、决策类装备之间的指挥协同关系等, 这种复杂的作战环称为广义作战环, 如图3所示.

一个作战环中, 红方每种类型的装备可能存在多个, 但敌方目标只有一个, 红方各装备通过作战环中的各种交互关系联系在一起, 共同对敌方目标产生作战效能.

在IDFCS模型中, 同一批节点在不同拓扑结构的作战体系下对不同的敌方目标体系将会产生不同的作战效能, 因此对作战体系效能和节点重要度的评估, 应当在对抗环境中开展, 需要同时考虑我方作战体系结构及其与敌方体系的交互关系, 作战环模型能够很好地描述对抗环境下我方作战体系的作战流程和交战体系的交互方式. 基于IDFCS模型的作战环模型如图4所示.

本文基于作战环及和节点能力对作战体系效能进行评估, 并在此基础上对体系内的节点重要度进行评估. 敌我交战体系的作战环数量能够反映我方作战体系对敌方作战体系可选打击方案的多少, 通过对每条作战环上每个节点的能力进行聚合, 即可定量描述我方作战体系对敌方作战体系的作战效能; 完成作战体系效能评估后, 即可采用差值法计算每个元功能节点的体系能力, 进而对装备节点的重要度进行评估. 基于作战环和节点能力的异质作战体系效能评估与节点重要度评估方法如图5所示.

2.1 基于时序功能作战模型的作战环搜索

对作战环的搜索是作战体系效能评估的基础, 当前常用的方法是利用邻接矩阵确定作战环的数量, 但不能求出具体每条作战环包含哪些节点. 本文结合拓扑图环路搜索方法, 设计了基于IDFCS模型的改进深度优先搜索(DFS)算法, 具体流程见算法1.

算法1. 改进深度优先搜索算法

输入: 作战体系网络图G.

输出: 目标节点列表target_nodes, 作战环列表operation_loops.

初始化:

target_loops=set()#用集合对结果进行去重

target_nodes=[]

for each node∈G.node

　if node[‘Identity’]==1

　　target_nodes.append(node)

def dfssearch(G, trace, start)

　bool is_unique=True

　bool has_not_fuel=True

　if start in trace

　　if start in target_nodes

　　　tmp=trace中从start到最后一个元素组成的列表

　　　if len(tmp)>3

　　　　if作战环中包含两个目标节点

　　　　　is_unique=Fales

　　　　if作战环中包含燃油或弹药保障节点

　　　　　has_not_fuel=False

　　　　if is_unique and has_not_fuel

　　　　　target_loops.add(tmp)

　　return

　trace.append(start)

　for each node∈start的一跳下游节点

　　dfs(G, trace, node)

for each node∈target_nodes

　dfs(G, [], node)

该算法能够搜索出节点数大于3且只包括一个蓝方目标节点的作战环, 同时去除了包含燃油和弹药补给节点的环路(因为作战环中的指挥控制命令流在此两类节点处不具备传递性), 这样就能保证搜索到的作战环都包含了基本组成节点(侦查、决策、打击、目标), 并且符合信息流、能量流、物质流的传递逻辑; 在作战环的去重方面, 首先只搜索以蓝方目标节点为起始节点的环路, 其次利用集合类型数据结构对作战环列表的元素进行去重, 能够有效保证作战环的唯一性.

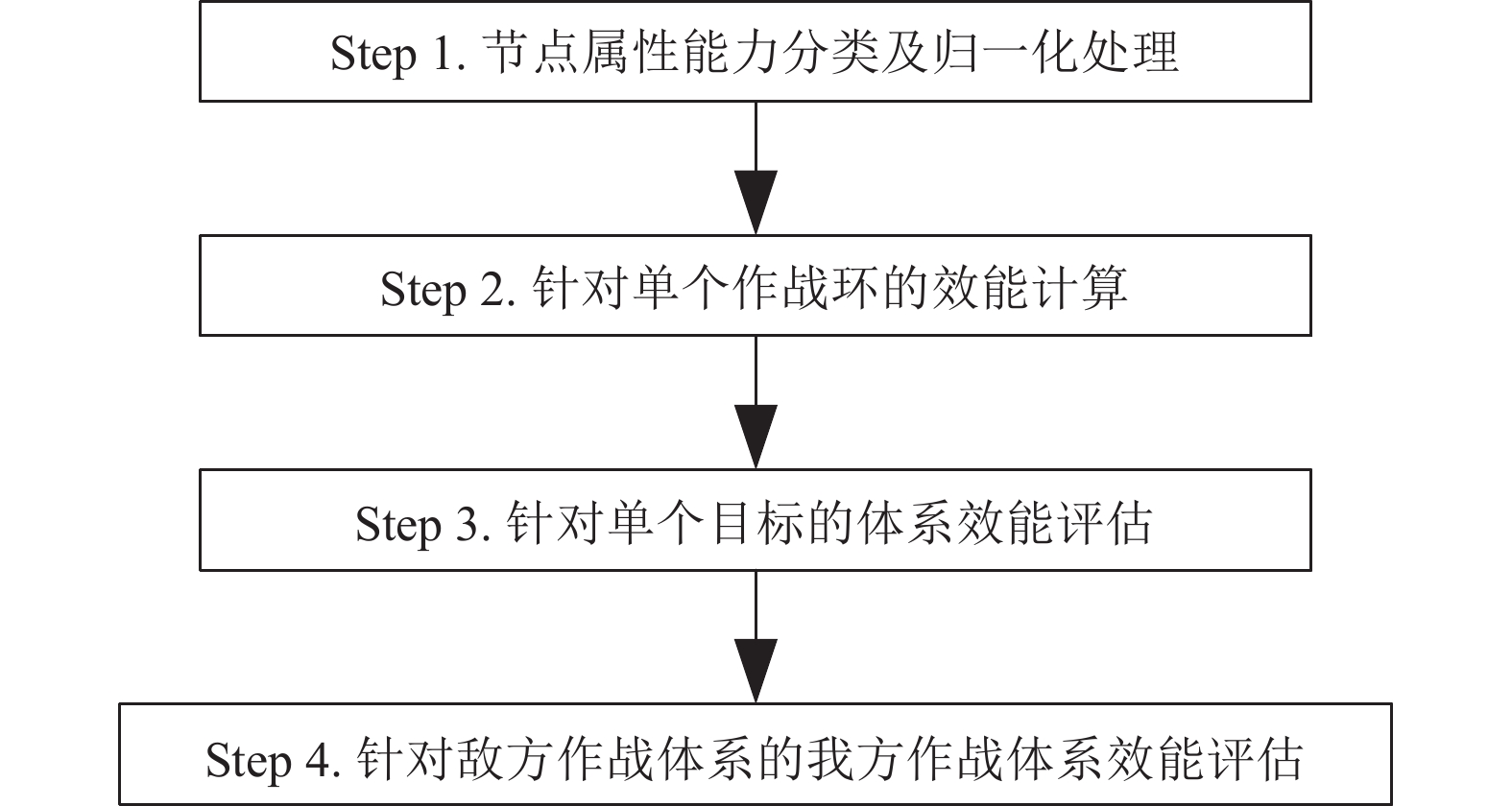
2.2 基于节点能力的体系效能评估

当前基于作战环的体系效能评估方法主要包括两类, 分别是基于作战环数量的体系效能评估方法和基于作战环边能力的效能评估方法, 第1种方法比较简单, 易于理解, 但没有考虑节点和边的属性, 计算结果不够精确; 第2种方法对边能力的计算一般为对节点属性的复杂聚合, 对不同类型的边有不同的聚合方式, 同时对边能力的归一化处理需要借助隶属度函数, 计算方式的设计比较复杂且不够通用. 本文以节点能力作为计算作战环和体系效能的基本要素, 直接对节点属性进行简单的归一化处理和聚合, 从理论上保证了结果的有效性, 同时降低了算法设计的复杂性. 基于节点能力的体系效能评估方法如图6所示.

(1) 节点属性能力分类及归一化处理

本文将节点属性的能力分为两大类: 作战能力和防护能力, 节点作战能力由节点能力向量组成, 并按节点类型进行分类, 由于保障能力在静态作战体系中无法体现, 故将节点作战能力分为侦查、决策、火力、通信4类, 各类型节点的各能力向量分别划分为该4种能力类型; 节点防护能力由节点防护能力向量构成. 节点属性的能力分类如图7所示.

由图7可知, 侦查节点的作战能力属性分为侦查能力属性和通信能力属性, 决策节点的作战能力属性分为决策能力属性, 火力节点的作战能力属性分为火力能力属性和通信能力属性, 通信节点的作战能力属性分为通信能力属性. 对于红方节点, 在进行体系效能评估时仅考虑节点的作战能力, 对于蓝方节点, 在进行体系效能评估时仅考虑节点的防护能力.

在对节点属性进行归一化时, 将属性分为效益型和成本型分别进行处理, 效益型属性指当属性取值越大时, 对体系效能的促进作用越大, 成本型属性指当属性取值越大时, 对体系效能的削弱作用越大. 通过对两种属性的归一化, 将属性值统一到[0, 1]区间内, 消除了量纲不同对计算结果带来的影响. 效益型属性和成本型属性的归一化方法见式(12)、式(13).

$ {\textit{z}} = \left\{ {\begin{array}{*{20}{l}} 0, &{{ I}} \leqslant {{{I}}_{{\text{min}}}} \\ \dfrac{{(I - {I_{\min }})}}{{{I_{\max }} - {I_{\min }}}}, &{{{I}}_{{\text{min}}}} \lt I \lt {I_{\max }} \\ 1, &{\text{ }}I \geqslant {I_{\max }} \end{array}} \right.{\text{ }} $

(12)

$ {\textit{z}} = \left\{ {\begin{array}{*{20}{l}} 1,& {{ I}} \leqslant {{{I}}_{{\text{min}}}} \\ \dfrac{{({I_{\max }} - I)}}{{{I_{\max }} - {I_{\min }}}},& {{{I}}_{{\text{min}}}} \lt I \lt {I_{\max }} \\ 0, &{\text{ }}I \geqslant {I_{\max }} \end{array}} \right.{\text{ }} $

(13)

其中, I为参数的原始值, I_max为该参数取值范围的最大值, I_min为该参数取值范围的最小值.

在各类节点的所有属性中, 除决策节点的指挥控制延迟、通信节点的通信质量(误码率)和通信节点的通信时延3个属性为成本型属性外, 其余属性均为效益型属性.

(2) 针对单个作战环的效能计算

每条作战环包括多个节点, 作战环中的每个节点通过彼此之间的信息、物质、能量交互完成各自能力的聚合, 共同支撑作战环发挥作战效能. 本文对经过归一化处理后的节点属性按照其分类各自进行聚合形成节点的各类能力值, 再对作战环中各个节点的各类能力进行聚合, 形成作战环对某一目标的整体效能. 本文分别采用加权和法和加权积法两种聚合方式对节点各类能力进行聚合并比较其结果. 加权和法和加权积法的计算如式(14)和式(15)所示.

$ {C_i} = \sum\limits_{j = 1}^k {{w_j}{q_{ij}}, \;{w_j} \geqslant 0, \;j = 1, 2, \cdots } , \;k, \sum\limits_{j = 1}^k {{w_j}} = 1 $

(14)

$ {C_i} = \prod\limits_{j = 1}^k {q_{ij}^{{w_j}}} ,\; j = 1, 2, \cdots , k,\; \sum\limits_{j = 1}^k {{w_j} = 1} $

(15)

其中, C_i表示该节点的第i类属性的聚合能力值, q_ij表示节点属于第i类能力的第j个属性, w_j为该属性的权重, k为节点属性中属于第i类能力的属性个数. 由此即可获得某个节点的各类能力聚合值.

对包含某敌方目标的作战环的效能计算, 则需对该作战环中每个节点的各项能力进行聚合. 其聚合方式如式(16)所示.

$ {{\text{C}}_{ol}} = \frac{{\prod {{C_i}} \prod {{C_d}} \prod {{C_f}} \prod {{C_c}} }}{{{C_t}}} $

(16)

其中, C_ol表示作战环ol的作战效能, C_i表示作战环内各我方节点的侦查能力, C_d表示作战环内各我方节点的决策能力, C_f表示作战环内各我方节点的火力能力, C_c表示作战环内各我方节点的通信能力, C_t表示作战环内敌方节点的防护能力.

(3) 针对单个目标的体系效能评估

在敌我交战体系中, 针对某个敌方目标通常存在多个作战环, 则对于敌方某特定目标v^T的我方作战体系效能可由包含该目标的所有作战环效能聚合而成. 如式(17)所示:

$ E{f_{{v^T}}} = \sum\limits_k {{C_{ol_k^{{v^T}}}}} $

(17)

其中, $ {C_{ol_k^{{v^T}}}} $ 为包含目标v^T的第k条作战环.

(4)针对敌方作战体系的我方作战体系效能评估

我方作战体系的效能H可表示为我方体系对敌方体系中每个节点的作战效能的加权和, 其中权重为敌方各节点的重要程度. 具体计算方法如式(18)所示:

$ H = \sum\limits_{{v^{\text{T}}}} {({w_{{v^T}}} \cdot E{f_{{v^T}}})} $

(18)

2.3 作战体系节点重要度评估

(1) 元功能节点重要度评估

本文依据体系贡献度方法对作战体系中的元功能节点进行重要度评估, 某节点的体系贡献度为原体系效能与移除该节点的剩余体系效能之差与原体系效能的比值. 首先采用差值法对每个元功能节点的体系能力进行计算, 然后根据节点能力值计算节点的体系贡献度以对节点体系能力进行归一化. 通过依次计算每个节点的体系贡献度并对节点按其贡献度进行排序, 即可获得元功能节点的体系重要度. 元功能节点体系贡献度计算如式(19)所示:

$ co{n_v} = \frac{{{H_{sys}} - {H_{sys|v}}}}{{{H_{sys}}}} $

(19)

其中, con_v为节点v的体系贡献度, H_sys为原始作战体系的效能, H_sys|v表示将节点v从原作战体系网络中移除后, 剩余网络的体系效能.

(2) 装备节点重要度评估

由于本文的作战体系模型为功能作战模型, 而装备节点为一个或多个元功能节点的组合, 若要对装备节点的重要度进行评估, 需要确定每个装备的元功能节点组合, 并对每个元功能节点组合进行重要度评估. 元功能节点组合的体系贡献度计算如式(20)所示:

$ co{n_{{e}}} = \frac{{{H_{sys}} - {H_{sys|\{ v \in e\} }}}}{{{H_{sys}}}} $

(20)

其中, con_e为装备节点e的体系贡献度, H_sys|{v∈e}表示将原作战体系网络模型中属于装备节点e的元功能节点移除后, 剩余网络的体系效能. 按式(20)依次计算每个装备的体系贡献度后再按其贡献度大小对装备节点进行排序即可获得装备节点的体系重要度.

2.4 算法复杂度分析

在整个作战周期内, 不同的作战阶段对作战效能评估和节点重要度评估的实时性要求各不相同, 因此在选择体系效能评估和节点重要度评估方法时, 需要考虑方法的计算成本和时间消耗. 本节对本文提出的作战体系效能评估方法和节点重要度评估方法的复杂度进行分析, 为算法的选择和优化改进提供依据.

(1) 网络生成算法复杂度分析

网络生成是后续各算法研究、验证的基础, 如何快速生成大量可供实验的、不同规模、准确有效的随机样本, 是网络生成算法研究的目标. 假设网络节点规模为n, 边规模为e, 根据本文提出的网络生成算法, 首先需依次生成n个节点及其属性, 同时在生产每个节点时, 需判断其EquipmentID与已生成节点是否相同, 若相同, 需遍历combination_set判断新旧节点组合是否为集合中的元素以进行节点合并; 然后遍历每个节点, 判断其与其他剩余所有节点的边存在性生成边. 最后遍历每条边对网络进行修复, 则网络生成算法的时间复杂度为:

$ \begin{gathered} {\text{ }}1 + \left| {combination\_set} \right|\frac{{n(n - 1)}}{2} + n(n - 1) + {{e}} = {\rm{O}}({n^2} + e) \\ \end{gathered} $

(21)

(2) 作战环搜索算法复杂度分析

本文提出的作战环搜索算法以深度优先搜索(DFS)算法为基础进行改进, 输入图数据采用树状结构邻接表存储, 目标节点为全部节点的一部分, 数量级与n相同, 在最坏的情况下, 每个节点的后继节点为剩余所有节点, 搜索的最大深度为节点个数n; 每搜索到一个节点需要遍历目标节点列表判断该节点是否为目标节点, 每搜索到一个作战环需要遍历环中的每个节点判断环中是否存在两个以上的目标节点; 同时, 为保证结果的完备性, 需以目标节点集合中的每一个节点为起点进行一次改进DFS搜索. 因此作战环搜索算法的时间复杂度为:

$ \begin{split} & {{ n}}(n + 1)[(n - 1) + {(n - 1)^2} + \cdots+ {(n - 1)^n}] \\ & = n(n + 1)\frac{{{{(n - 1)}^{n + 1}} - n + 1}}{{n - 2}} \\ & = {\rm{O}}({n^{n + 2}}) \end{split} $

(22)

作战环搜索算法只需要在存储搜索过的节点及每个节点的后继节点, 因此其空间复杂度为O(n(n–1))=O(n²).

(3) 作战体系效能评估算法复杂度分析

假设网络中共有k个作战环, 最坏的情况下, 每个作战环包含的节点数为n; 在计算针对单个目标的体系作战效能时, 需要对每个目标计算其所属作战环的聚合值; 在计算我方体系对敌方体系的作战效能时, 需要对针对每个目标的体系作战效能进行聚合, 故作战体系效能评估算法的时间复杂度为:

$ {\rm{O}}(kn) + {\rm{O}}(n) + 1 = {\rm{O}}(kn) $

(23)

(4) 装备节点重要度评估算法复杂度分析

对装备节点的重要度进行评估时, 需要依次移除体系中的我方元功能节点组合并评估剩余网络的体系效能, 每次迭代时分为两步: 1) 对剩余网络进行作战环搜索; 2) 对剩余网络进行体系效能评估. 假设每个装备节点都是由单一的元功能节点构成, 则装备节点重要度评估算法的时间复杂度为:

$ \begin{split} & {\text{ }}{\rm{O}}({k_1}n) + {\rm{O}}({n^{n + 2}}) + {\rm{O}}({k_2}n) + {\rm{O}}({n^{n + 2}}) + \cdots \\ &\qquad\qquad + {\rm{O}}({k_n}n) + {\rm{O}}({n^{n + 2}}) \\ &\qquad\quad = {\rm{O}}({n^{n + 3}}) + {\rm{O}}({k_{\max }}{n^2}) = {\rm{O}}({n^{n + 3}}) \end{split} $

(24)

其中, k₁, k₂,…, k_n为每次移除节点后剩余网络的作战环个数.

可以看出, 本文提出的作战体系效能评估和节点重要度评估方法的时间复杂度随问题规模的扩大呈指数级增长, 是一个典型的NP-hard问题.

3 仿真实验及结果分析

为验证评估方法的有效性, 采用本文提出的IDFCS网络生成模型生成模拟时序功能作战网络对算法进行验证, 并对结果进行了分析.

3.1 实验环境

本文使用华为MateBook X Pro笔记本电脑和阿里云服务器进行使用, 具体配置如表4所示.

3.2 网络生成实验

首先采用不同的初始化参数对本文提出的网络生成模型进行了测试, 生成了不同规模的仿真网络, 并对结果进行了可视化. 节点各属性取值和各类边存在概率采用给定均值和方差通过正态分布随机生成, 部分输入参数设置如表5所示. 对每个规模的网络分别生成3次并对其网络指标值取平均形成统计值.

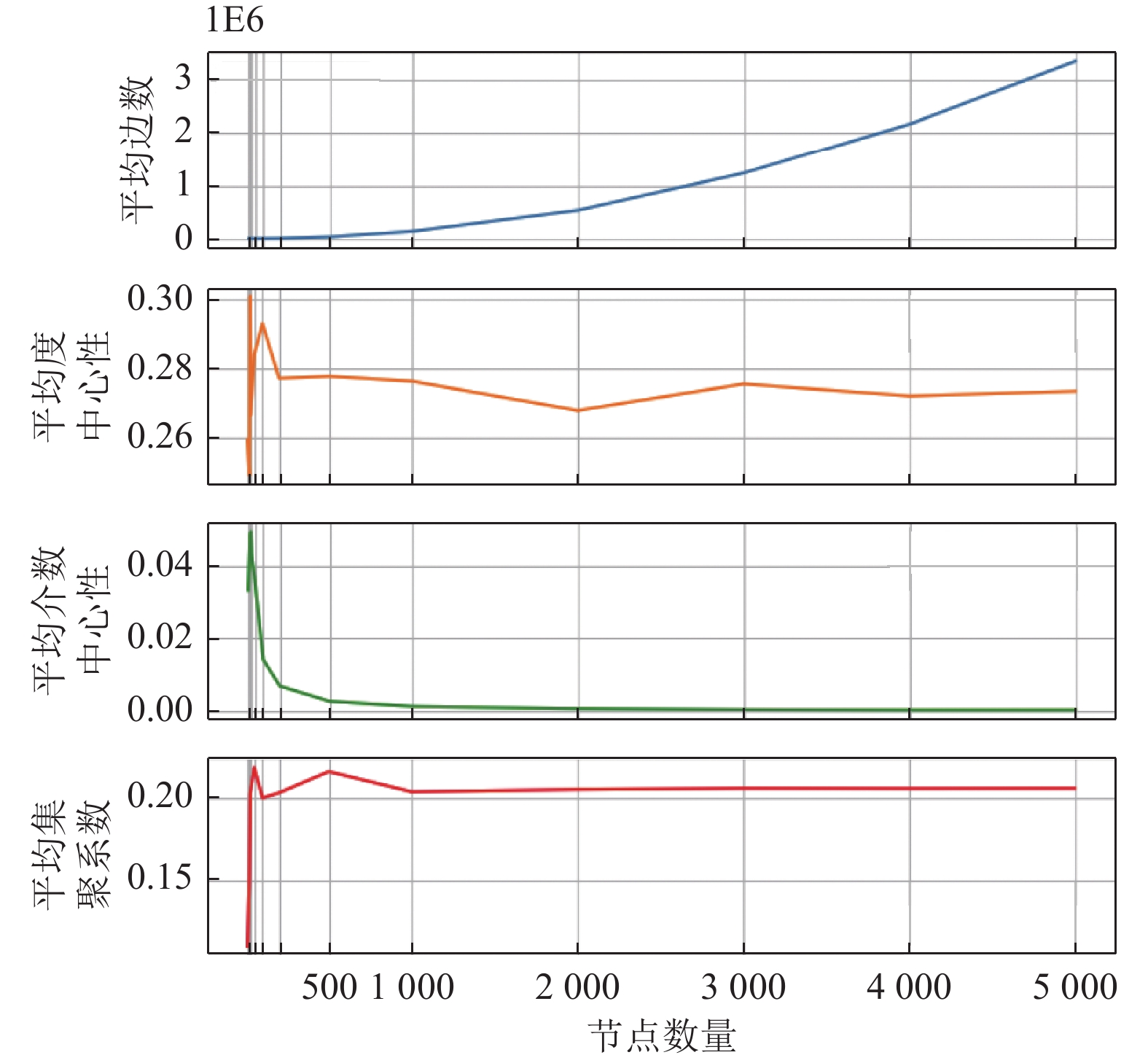
对各规模网络主要统计指标如平均边数、平均度中心性、平均介数中心性和平均集聚系数进行可视化, 结果如图8所示.

可以看出随着网络规模的扩大, 网络平均边数的增长与节点数的增长呈幂函数关系, 表示该网络生成模型的边生成机制较为稳定; 平均度中心性、平均介数中心性和平均集聚系数等网络关键指标值在网络规模较大时趋于平稳, 表示该网络生成模型生成的网络具有独立于网络规模的相同模式, 其生成的网络样本能够很好地应用于机器学习领域.

此外, 本文对生成网络进行了可视化, 以100个节点规模网络为例, 其可视化网络图如图9所示, 图9(a)不同颜色代表红蓝双方, 节点标签代表节点类型; 图9(b)不同颜色和标签代表节点类型.

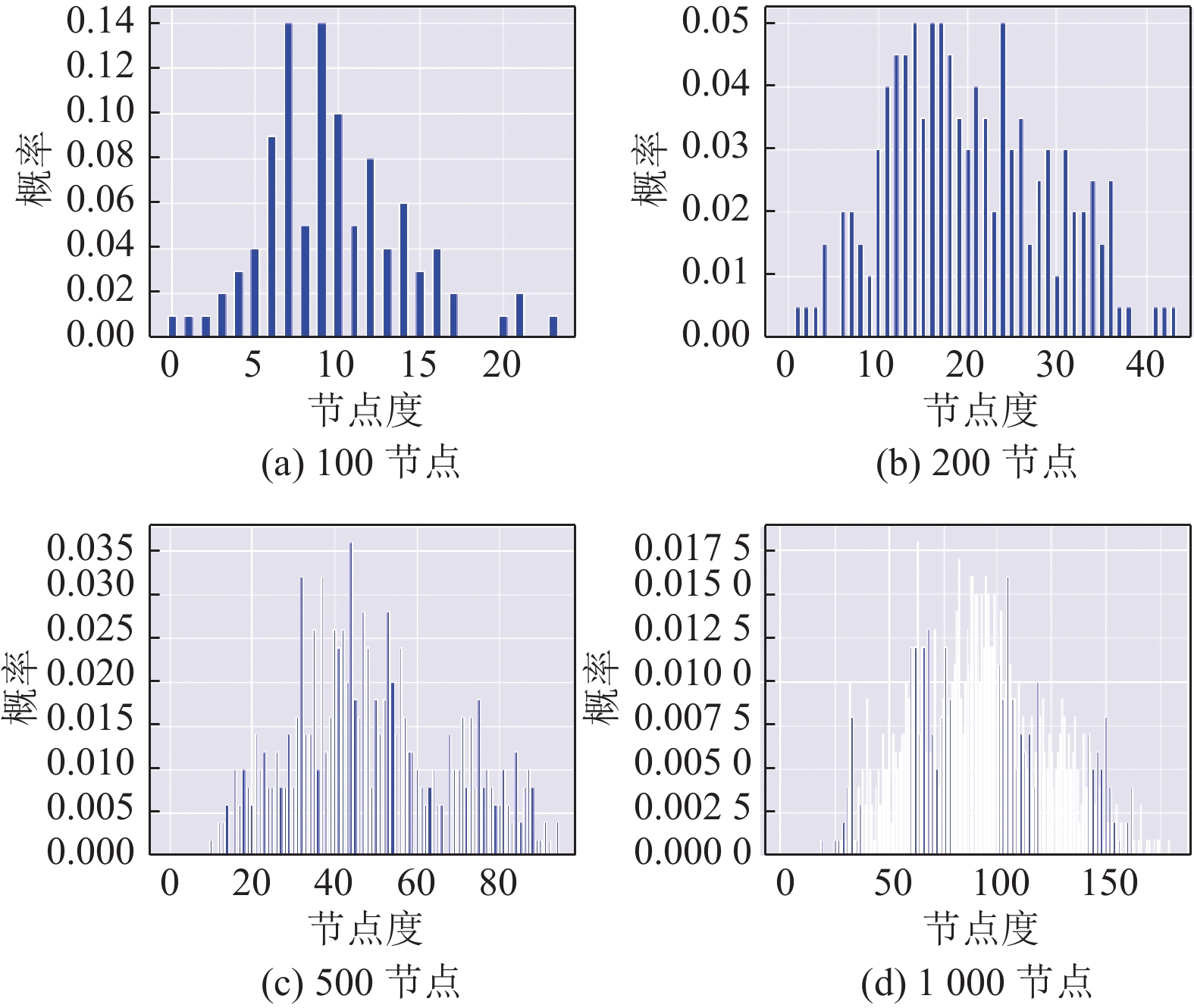
不同规模网络度分布可视化结果如图10所示.

根据不同规模生成网络的可视化结果, 该生成模型生成的样本网络度分布为主峰偏左的偏态分布, 由于作战体系与常规的无标度网络性质并不完全相同, 为保证各作战节点都能在体系中发挥作战效能, 其网络度分布比较均匀, 不会存在大量小度或无度节点, 同时也有一定的无标度性(主峰偏左, 尾部略长).

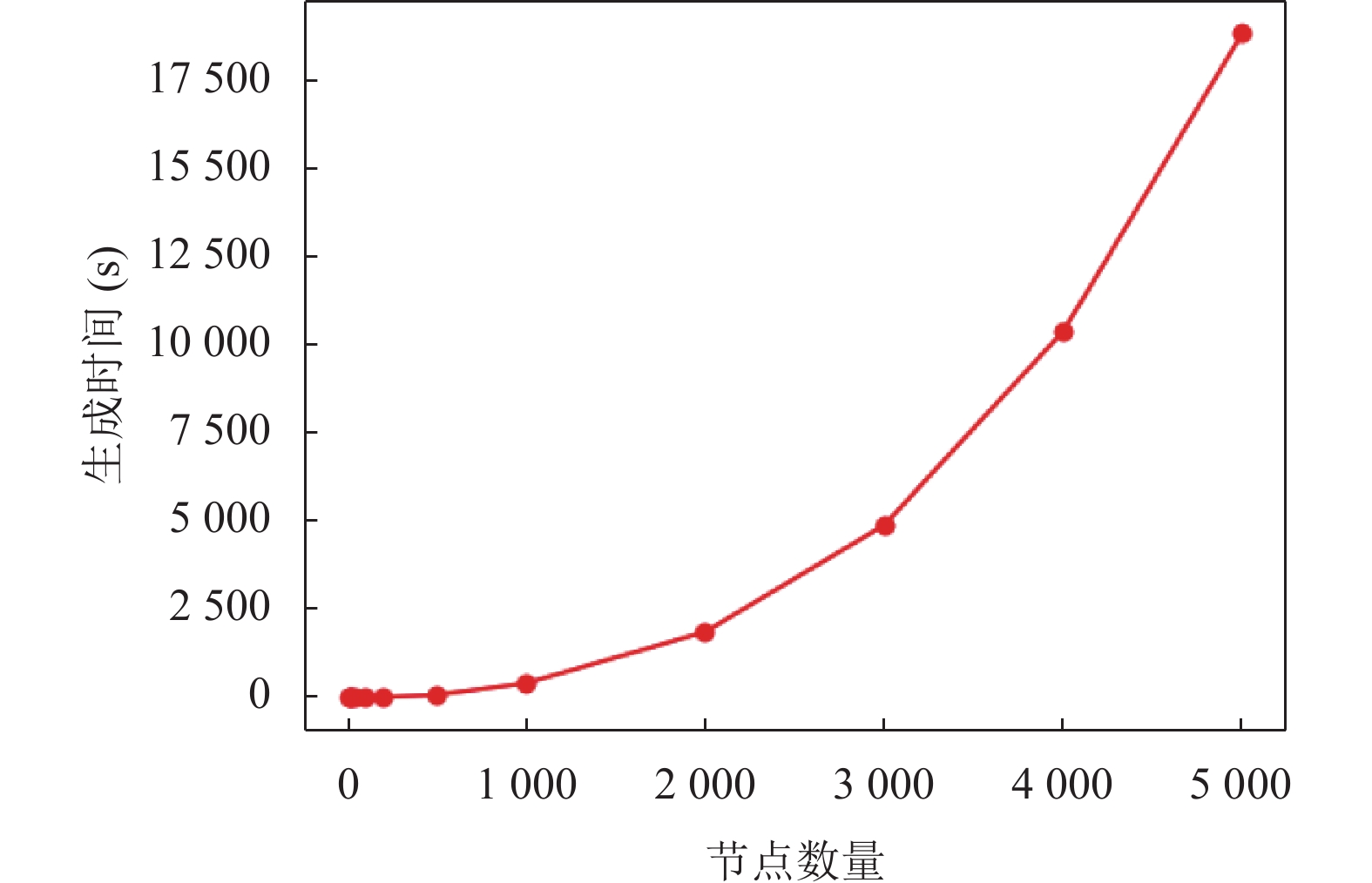
为验证第2.4节网络生成算法复杂度分析的准确性, 本文对不同规模网络的生成时间进行了可视化, 如图11所示.

由图11可知, 网络生成时间与网络规模成幂函数关系, 与第2.4节的分析结果吻合.

3.3 体系效能和节点重要度评估实验

本节采用第2.2节、第2.3节所述方法对第3.2节生成的不同规模网络进行了体系效能和节点重要度评估. 由于实验所用服务器容器资源限制, 部分CPU并行化计算方法无法获得足够的CPU资源, 故只采用串行方法对50节点以下规模的网络进行了评估.

不同规模的算法运行复杂度如表6所示. 对算法在不同规模的网络上的运行时间和节点搜索数量分别按两种方式进行可视化: 1) 对20节点、25节点、30节点规模的抽样网络样本进行可视化; 2) 对全部规模的抽样样本进行可视化. 如表6所示. 可以看出, 该算法的运行复杂度与网络规模成指数关系.

本文对20节点、25节点、30节点、50节点(10节点网络由于规模太小, 无法产生作战环) 4种规模的网络, 每种规模各3个样本共12个网络样本进行了评估, 对每种规模的网络随机抽取一个样本评估结果, 部分指标结果如表7–表10所示.

网络体系效能和装备节点重要度结果如表7–表10所示. 由表7–表10可知: 1) 随着网络连边的增长, 作战环数量也在增长, 并且在网络节点规模为50时, 网络具备体系效应(作战环数量大于边数量); 2) 采用加权和法与加权积法分别计算体系效能和节点重要度时, 所求得的装备节点重要度排名几乎完全一致(除节点数为50的网络中采用该两种方法进行评估时排名为1、2的装备名次互换外, 其他各样本的装备节点重要度排名完全一致), 且与装备节点的介数中心性(若装备为节点组合构成, 则以节点组合的介数中心性之和代表该装备节点的介数中心性; 其他两个网络指标也照此法处理)排名基本一致, 出现排名不同的节点为名次前后差距不大的节点, 表明本文提出的效能评估和节点重要度评估方法能够很好地发现网络中负荷最大、控制性最强的瓶颈节点; 3) 采用本文提出的方法计算的装备节点重要度排名与节点的集聚系数、度中心性排名几乎完全不同, 表明本文对体系效能和节点重要度的评估受该两个指标影响很小; 4) 本文提出的方法能够有效发现体系中层级较高(Level≥2)的控制中心(D类型节点、ID类型节点、DF类型节点、IDF类型节点)和通信中心(C类型节点), 体现了方法的有效性.

3.4 与已有体系效能评估方法的对比

由于已有的基于能力的效能评估方法大多需要特定于应用场景的领域知识对节点或边的能力进行聚合, 不具备通用性, 故本节通过与基于作战环数量的体系效能评估方法进行对比, 验证本文方法的有效性.

以文献[8]提出的作战体系效能评估方法对表10描述的仿真网络进行装备节点重要性评估, 与本文提出方法的实验结果对比如表11所示.

由表11可知, 采用本文提出的方法进行装备节点重要性评估时, 排名前5的装备节点共包含2个侦查类节点, 4个决策类节点, 2个火力类节点, 1个通信类节点, 节点层级分别为3、3、2、2、2; 排名后5的装备节点共包含1个侦查类节点, 1个火力类节点, 4个通信类节点, 节点层级皆为0; 采用文献[8]提出的方法进行装备节点重要性评估时, 排名前5的装备节点共包含2个侦查类节点, 4个决策类节点, 3个火力类节点, 0个通信类节点, 节点层级分别为1、2、2、3、0; 排名后5的装备节点共包含5个通信类节点, 节点层级分别为1、0、2、0、0; 可见本文提出的方法能够更加有效的发现层级较高的决策或通信类节点, 其计算结果更加符合作战体系的实际情况.

4 结论

本文以实际作战体系为研究对象, 以复杂网络理论和现代作战循环理论为理论基础对作战体系的建模和评估方法进行了研究, 提出了一种基于功能作战模型的IDFCS作战体系建模方法及该模型的生成算法, 该模型可扩展性强, 能够较为精确地描述体系节点的能力属性、作战体系的复杂网络形态和体系运行机制, 为后续各项研究的开展打下了基础. 根据作战环理论提出了基于IDFCS模型的体系效能评估方法和节点重要度评估方法, 该方法充分利用节点各能力属性对作战体系效能进行定量分析, 设计简单合理, 通用性强. 最后利用本文提出的模型生成算法生成了不同规模的作战体系样本网络, 并对其效能进行了评估. 实验结果表明, 本文提出的方法能够较为准确地发现仿真网络的结构瓶颈和体系中的重要类型节点及高层级节点, 但在算法复杂度和运行效率方面有较大的提升空间, 具备进一步深入开展研究的学术价值和实际应用价值.