2. 北京卫星导航中心, 北京 100083;
3. 武警部队政治工作部保卫局, 北京 100081
2. Beijing Satellite Navigation Center, Beijing 100083, China;
3. Security Bureau of Political Work Department of Armed Police Force, Beijing 100081, China
传统电子干扰通常采用密集布阵的方式将干扰能量投送至目标区域, 在战场中形成以目标点为中心的能量扇区[1]. 但是在实际电子作战中, 这种“粗放式”电子干扰极易造成电磁误伤. 原因在于干扰设备与目标区域通常距离较远, 通过方向图匹配方法产生的干扰主瓣将覆盖目标区域附近范围较大的区域, 从而导致友方设备遭受电磁误伤. 即使进一步采用定向天线控制干扰波束方向, 甚至在指定方向上采用空间功率合成技术, 也难以避免对目标区域内附近的电子系统产生影响[2]. 因此, 电子干扰方法亟需从传统的“粗放式”干扰向适应现代战场的精确干扰转型. 为解决以上问题, 美国国防部高级计划研究局 (Defense Advanced Research Projects Agency, DARPA) 于2009年发布了跨机构公告DARPA-BAA 09-65文件, 提出了精确电子战 (precision electronic warfare, PREW) 的概念, 旨在对敌方设备进行精确电子干扰[3]. 作为精确电子战的主要手段, 精确干扰的核心思想是采用超稀疏阵列在指定空域内实现干扰信号的相干合成或相消, 以达到仅对指定目标进行干扰, 而不影响友邻设备正常工作的干扰效果, 其本质是在空域上实现干扰能量的精准控制.
尽管现有干扰波形设计技术能在一定程度上满足干扰需求, 但这些方法在空域上的能量控制上精准性不佳, 无法达到精确干扰目的. 文献[4]根据低截获概率针对多个干扰目标, 进行了干扰波形设计的研究. 文献[5]基于功率最小化准则设计了一种单鲁棒性干扰波形设计方法, 有效降低了干扰机的功率需求. 文献[6]基于生成对抗网络设计了一种与目标信号特征相似的干扰波形, 使得干扰波形能够逼近最佳干扰效果. 文献[7]采用恒虚警概率作为环境交互模型, 通过强化学习自适应地调整间歇采样信号的采样时间与转发时间, 实现了对未知雷达信号的干扰. 文献[8]基于Stackelberg博弈模型提出了二次注水的波形设计方法, 极大提高了干扰效能. 但上述文献通常采用单干扰机或密集布阵的干扰阵元, 且并不关注能量的空域分布性能, 因此无法实现干扰信号在指定区域的相干合成或相消.
自精确干扰概念提出以来, 国内外已有文献主要通过设计发射信号自相关阵和单个快拍发射信号的方法进行研究. 文献[9]提出一种基于精确功率传输技术的精确干扰方法, 这种方法建立了关于发射信号自相关阵的半定规划模型, 并通过CVX或YALMIP工具箱进行求解[10, 11]. 在此基础上, 文献[12]充分利用目标设备与友邻设备的位置信息, 以精确干扰中的最坏情况, 即目标区域内平均能量的最小值与保护区域内平均能量的最大值作为优化准则, 有效提升了精确干扰性能. 文献[13]根据以上求解的发射信号自相关阵, 采用循环算法进行秩一估计, 从而获得了精确干扰的可用波形. 可见, 采用发射信号自相关阵作为信号模型无法直接得到精确干扰的可用波形, 必须在求解发射信号自相关阵的基础上进一步恢复才能得到最终结果. 相比之下, 文献[14]则直接求解单个快拍的恒模发射信号, 通过求解采样信号的相位来达到精确干扰的效果. 基于此, 文献[15]对单个快拍发射信号和干扰平台位置进行联合优化, 有效提升了精确干扰效果. 文献[16]根据这类信号模型, 建立了多目标优化模型, 同时实现了精确干扰和栅瓣抑制. 然而, 采用以上信号模型所得到的结果仅是单个快拍发射信号, 在实际干扰时仅有极短时间的干扰效果, 无法对敌目标进行有效干扰.
针对以上问题, 本文旨在设计一种能够直接得到精确干扰波形的快速算法. 首先根据精确干扰空间模型建立关于恒模波形的优化问题; 然后根据Majorization-Minimization (MM) 框架对优化问题中的目标函数进行放缩, 得到了具有闭式解的子问题, 并通过迭代得到可用波形. 最后, 通过仿真实验对比了本文算法与现有算法的精确干扰指标, 并验证了本文在计算复杂度与算法运行时间的优势.
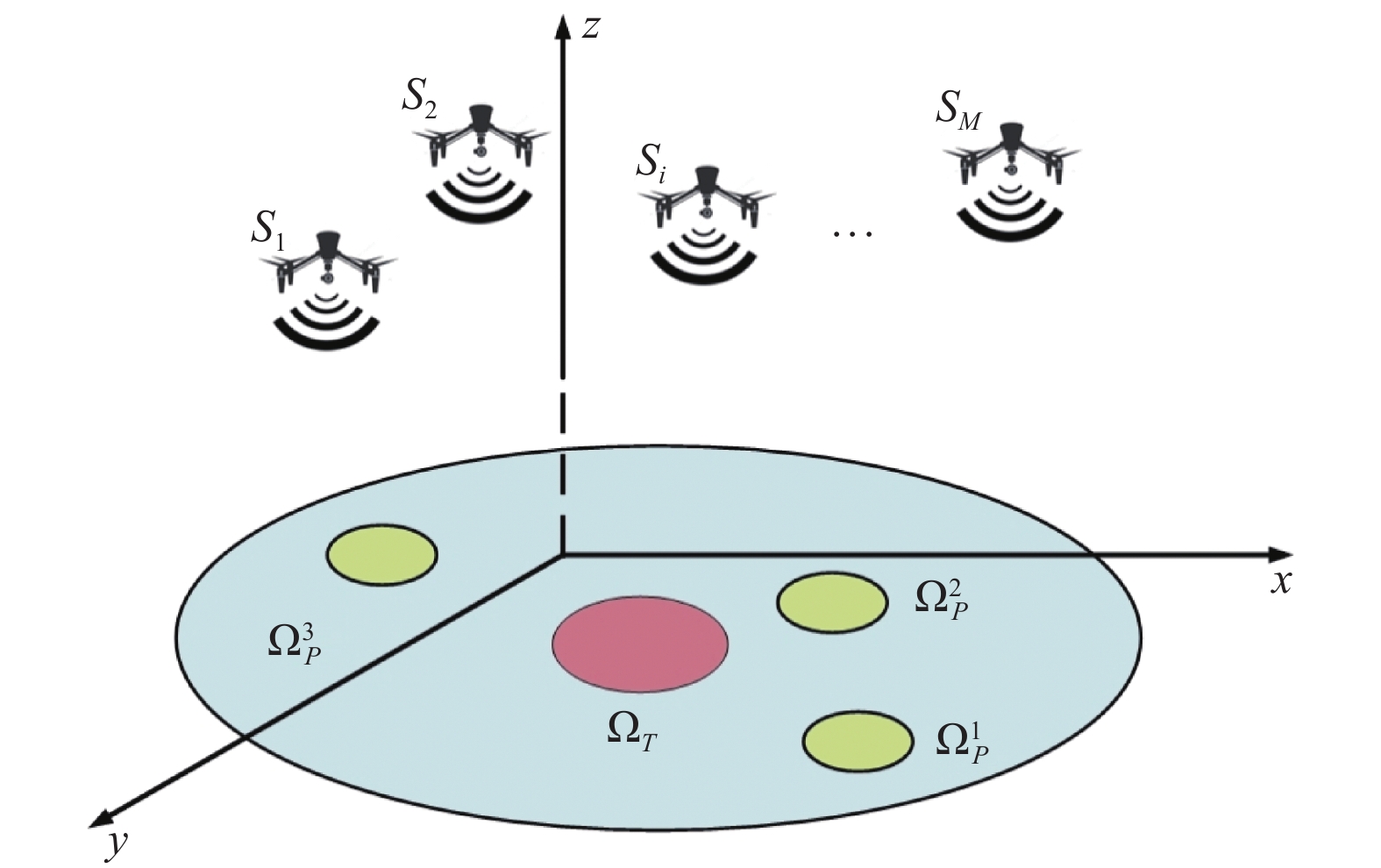
1 数学模型图1所示为精确电子战空间模型, 目标设备
若波形长度为N, 则干扰阵元发射的波形可用如下矩阵形式表示:
| X=[x11x12⋯x1Nx21x22⋯x2N⋮⋮⋱⋮xM1xM2⋯xMN] | (1) |
其中,
由于在分布式阵列和精确干扰的研究中, 信号传播模型通常不考虑多径衰落及阴影衰落的影响[18, 19], 因此各阵元发射信号至xOy平面内任意一点
| a(σ)=[ei2πfτ1‖r1−σ‖2,ei2πfτ2‖r2−σ‖2,⋯,ei2πfτM‖rM−σ‖2]T | (2) |
其中,
| S(σ)=a(σ)HX | (3) |
其中,
| E(σ)=|S(σ)|2=a(σ)HXXHa(σ) | (4) |
|
图 1 精确电子战空间模型 |
对某一区域
| EΩ=∫ΩE(σ)⋅dσ | (5) |
为获得式(5)的解析形式, 将区域
| EΩ=L∑l=1a(σl)HXXHa(σl)ΔS | (6) |
将矩阵
| EΩ=L∑l=1xHA(σl)A(σl)HxΔS=xHQΩx | (7) |
其中,
| {ET=xHQTx=xH(T∑t=1A(σt)A(σt)HΔS)xEP=xHQPx=xH(P∑p=1A(σp)A(σp)HΔS)x | (8) |
其中, T和P分别表示目标区域和所有保护区域内离散网格的数量.
2 快速算法设计精确干扰的目标是在空域上实现能量控制, 其中一种干扰效果评价准则为目标区域合成总能量与保护区域合成总能量之间的差值. 在工程具体设计时, 通常发射恒模波形, 以减轻功率放大器和数模转化器等硬件的负担. 因此, 精确干扰的优化问题写为如下形式:
| {max | (9) |
通过式(8)可知,
| \left\{\begin{gathered} \min {\text{ }}{x^{\text{H}}}Qx \\ {\text{s}}{\text{.t}}{\text{. }}\left| {{x_{mn}}} \right| = 1, {\text{ }}m = 1, 2, \cdots , M, {\text{ }}n = 1, 2, \cdots , N \\ \end{gathered} \right. | (10) |
由于恒模约束的非凸性, 常用的凸优化方法难以求解问题(10). 为此, 本文引入MM框架, 将原问题中的目标函数转化为一系列易于求解的上界函数, 通过迭代不断更新子问题最终得到原问题的近似解[20]. 由于该算法能够有效求解非凸问题, 并具有较低的计算复杂度, 在雷达发射方向图匹配和探测波形设计领域中广为应用[21-24]. 为有效求解问题(10)并取得较好的精确干扰效果, 将MM框架用于精确干扰的波形设计以求解问题(10). 由于问题(10)的目标是最小化
引理1: 设
| \begin{gathered} {x^{\text{H}}}Qx \leqslant {x^{\text{H}}}Lx + 2{Re} \left\{ {{x^{\text{H}}}\left( {Q - L} \right){x_k}} \right\} + x_k^{\text{H}}\left( {L - Q} \right){x_k} \end{gathered} | (11) |
其中,
| \begin{split} Q & = {Q_{{P}}} - {Q_{{T}}} \\ & = \left( {\sum\limits_{p = 1}^P {A({\sigma _p})A{{({\sigma _p})}^{\text{H}}}} - \sum\limits_{t = 1}^T {A({\sigma _t})A{{({\sigma _t})}^{\text{H}}}} } \right)\Delta S \\ & = \left( {\sum\limits_{p = 1}^P {{I_N} \otimes a({\sigma _p})a{{({\sigma _p})}^{\text{H}}}} - \sum\limits_{t = 1}^T {{I_N} \otimes a({\sigma _t})a{{({\sigma _t})}^{\text{H}}}} } \right)\Delta S \\ & = {I_N} \otimes \left( {\sum\limits_{p = 1}^P {a({\sigma _p})a{{({\sigma _p})}^{\text{H}}}} - \sum\limits_{t = 1}^T {a({\sigma _t})a{{({\sigma _t})}^{\text{H}}}} } \right)\Delta S \\ & = {I_N} \otimes Q' \end{split} | (12) |
其中,
根据MM框架和引理1可知, 在第k次迭代时, 问题(10)的上界函数为:
| {\lambda _{\max }}(Q'){x^{\text{H}}}x + 2{Re} \left\{ {{x^{\text{H}}}\left( {Q - L} \right){x_k}} \right\} + x_k^{\text{H}}\left( {L - Q} \right){x_k} | (13) |
由
| \left\{ \begin{gathered} \min {\text{ }}{Re} \left\{ {{x^{\text{H}}}\left( {Q - L} \right){x_k}} \right\} \\ {\text{s}}{\text{.t}}{\text{. }}\left| {{x_{mn}}} \right| = 1, {\text{ }}m = 1, 2, \cdots , M, {\text{ }}n = 1, 2, \cdots , N \\ \end{gathered} \right. | (14) |
由向量空间关系, 可以得到问题(14)的闭式解为:
| {\left( {{x_{k + 1}}} \right)_i} = {{\text{e}}^{{{i}}\phi {{\left( {{{\bar x}_k}} \right)}_i}}}, {\text{ }}i = 1, 2, \cdots , MN | (15) |
其中,
算法1. 基于MM框架的快速波形设计算法
1) 输入:
2) 初始化k = 0;
3) 计算矩阵
4) 计算
5) 循环:
6) k++;
7) 计算
8) 计算
9) 循环结束: 满足迭代停止条件.
3 仿真实验为说明本文算法有效性, 本节基于如下情景进行仿真实验: 目标区域为半径为5 m的圆形区域, 圆心为(0 m, 0 m, 0 m): 保护区域I、II和III分别是以(−20 m, 10 m, 0 m), (10 m , −20 m, 0 m), (20 m, 25 m, 0 m)为圆心, 半径为2 m的圆形区域; xOy平面内区域为[−50 m, 50 m]×[−50 m, 50 m], 离散化网格的尺寸为0.25 m × 0.25 m; 发射信号载频为f = 1 GHz; 本文算法的迭代停止条件设为
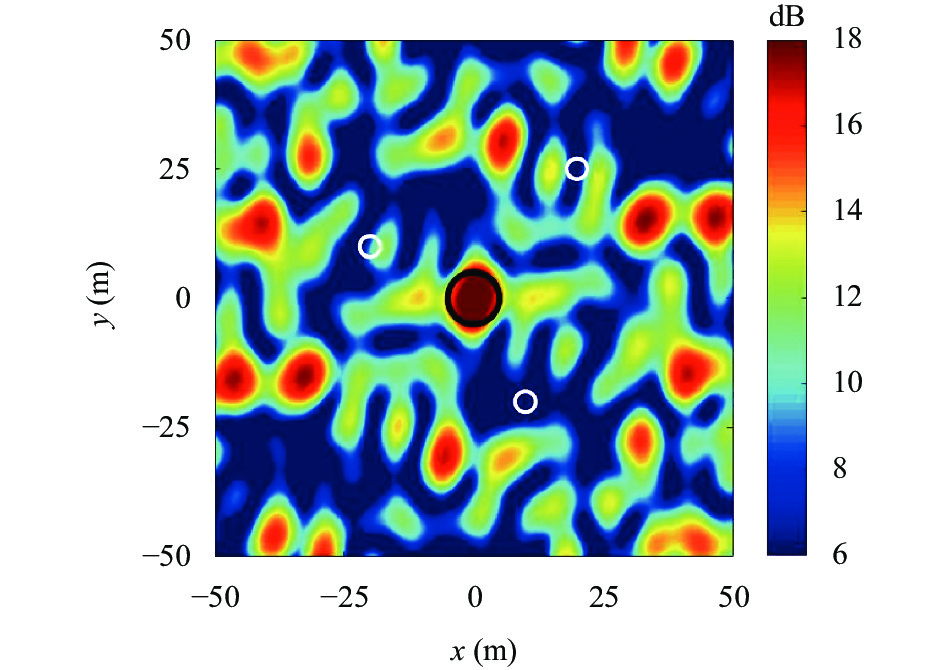
为说明算法产生的精确干扰性能, 本节将本文算法与FEDUS-CA算法进行对比. 干扰平台由M = 10个阵元组成, 并随机分布于高度d = 1000 m的同一平面内, 波形长度为N = 128. 根据式(4), 计算出关注区域内每个离散网格的能量, 除以
图2和图3所示分别为本文算法和FEDUS-CA算法所产生的空域平均能量分布图. 目标区域由黑色圆线标出, 各保护区域分别由白色圆线标出. 红色区域部分表示该处能量较高, 蓝色区域部分表示该处能量较低. 通过对比可以发现, 本文算法比FEDUS-CA算法的目标区域能量更高, 保护区域II和III内能量更低. 通过图2和图3的对比, 可以说明本文算法在空域上具有较好的能量控制性能.
图4进一步对比了两种算法在目标区域和各保护区域随不同采样时刻的能量变化. 需要注意的是, 为突出各算法在不同采样时刻的变化细节, 图4中的能量值没有进行
|
图 2 本文算法产生的空域平均能量分布图 |

|
图 3 FEDUS-CA算法产生的空域平均能量分布图 |

|
图 4 目标区域和保护区域内能量随采样时刻变化 |
3.2 性能分析
为进一步说明本文算法在空域能量控制上的优势, 本节给出了各算法在精确干扰上的具体指标, 并在第4.1节设置的仿真场景中运行50次, 对算法的平均性能进行分析.
表1列出了两个算法的5类性能指标: 分别为优化问题(9)中的目标值AED, 经归一化处理和dB表示的目标区域平均能量AET和保护区域平均能量AEP, 以及有效干扰率
| 表 1 精确干扰指标对比 |
| \left\{ \begin{gathered} {w_{{T}}} = \frac{{\displaystyle\sum\limits_{t = 1}^T {{{I}}\left( {a{{({\sigma _t})}^{\text{H}}}X{X^{\text{H}}}a({\sigma _t}) - {c_{{T}}}} \right)} }}{T} \\ {w_{{P}}} = \frac{{\displaystyle\sum\limits_{p = 1}^P {{{I}}\left( {a{{({\sigma _p})}^{\text{H}}}X{X^{\text{H}}}a({\sigma _p}) - {c_{{P}}}} \right)} }}{P} \\ \end{gathered} \right. | (16) |
其中,
从表1对比结果可见, 本文算法的目标值相对更低, 说明目标区域和保护区域之间的平均能量差值更大, 其目标区域平均能量能达到17.803 dB, 保护区域平均能量低至5.317 dB. 尽管FEDUS-CA算法的目标区域平均能量为17.016 dB, 但其保护区域平均能量达到了6.539 dB, 比本文算法在保护区域内的平均能量高出了1.222 dB. 此外, 本文算法的有效干扰率达到了71.76%, 而FEDUS-CA算法的有效干扰率仅为51.19%, 在干扰成功率的指标上表现较弱, 其误干扰率为38.01%, 也显著高于本文算法的误干扰率22.12%. 经表1中蒙特卡洛实验的验证, 说明本文算法在多项精确干扰指标上优于FEDUS-CA算法.
3.3 复杂度分析为突出本文算法的高效性, 表2给出了本文算法与FEDUS-CA算法的复杂度对比. 从表中对比可见, FEDUS-CA算法比本文算法高出了M3的计算复杂度, 该项是采用内点法解算波形自相关阵所产生. 这说明当干扰平台数量M较多时, FEDUS-CA算法将产生较大的计算负担, 难以应用于干扰平台数量较多的大规模计算. 而本文算法的计算复杂度仅有MN, 仅为问题规模的一次项, 远低于FEDUS-CA算法.
| 表 2 计算复杂度对比 |
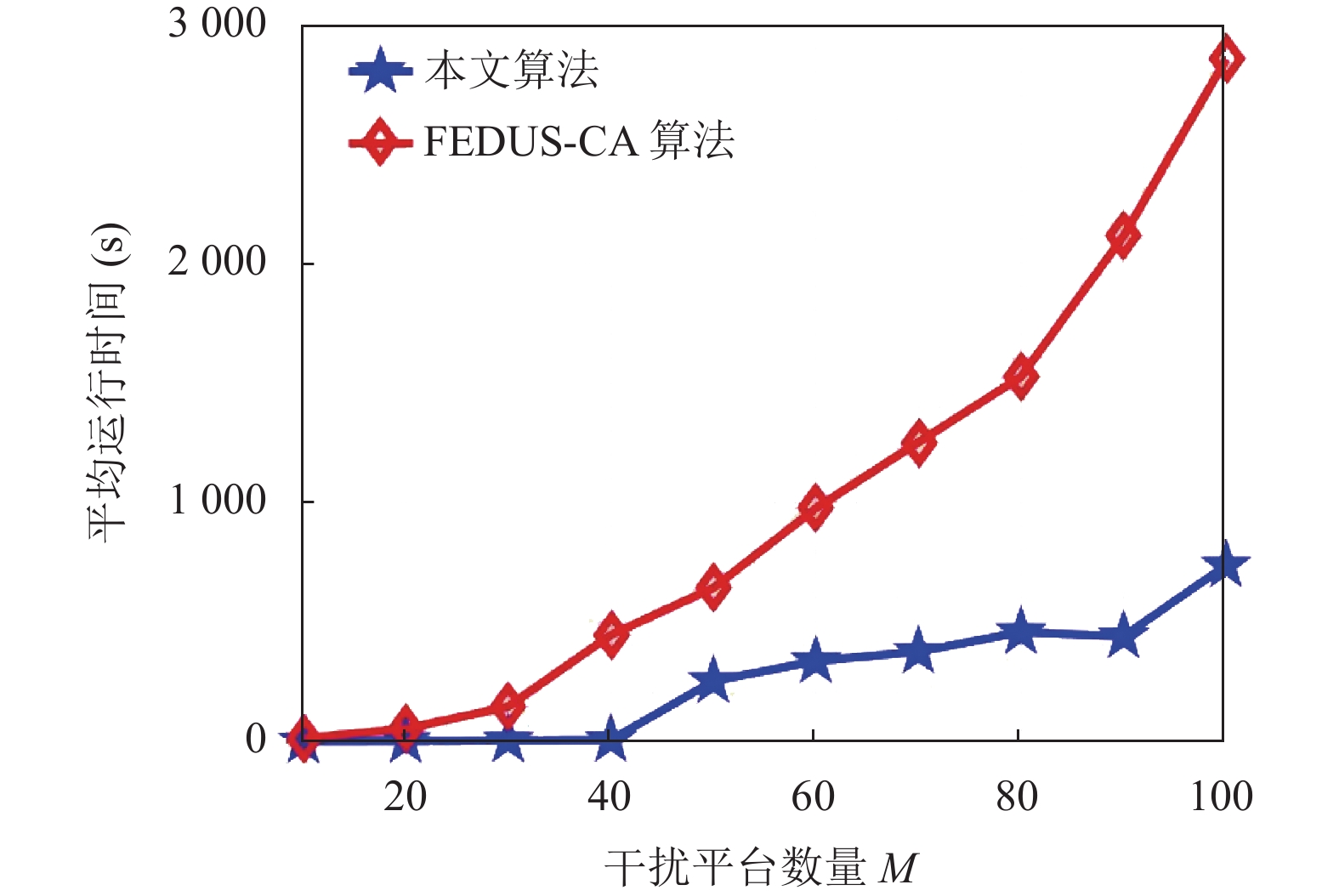
为进一步说明各算法随问题规模的变化, 图5和图6分别给出了各算法平均运行时间随平台数量M和波形长度N的变化曲线. 两种算法在各问题规模下均运行50次并取平均值. 图5在各平台数量下均设置波形长度为N=128, 通过对比可以发现, 本文算法在平台数量在小于等于40时具有远低于FEDUS-CA算法的平均运行时间, 且在平台数量大于40时增长速度更慢. 而FEDUS-CA算法在各干扰平台数量下的平均运行时间均远大于本文算法, 且增长速度较快, 原因在于其计算复杂度中存在M3的高次项.
|
图 5 各算法平均运行时间随干扰平台数量的变化曲线 |
|
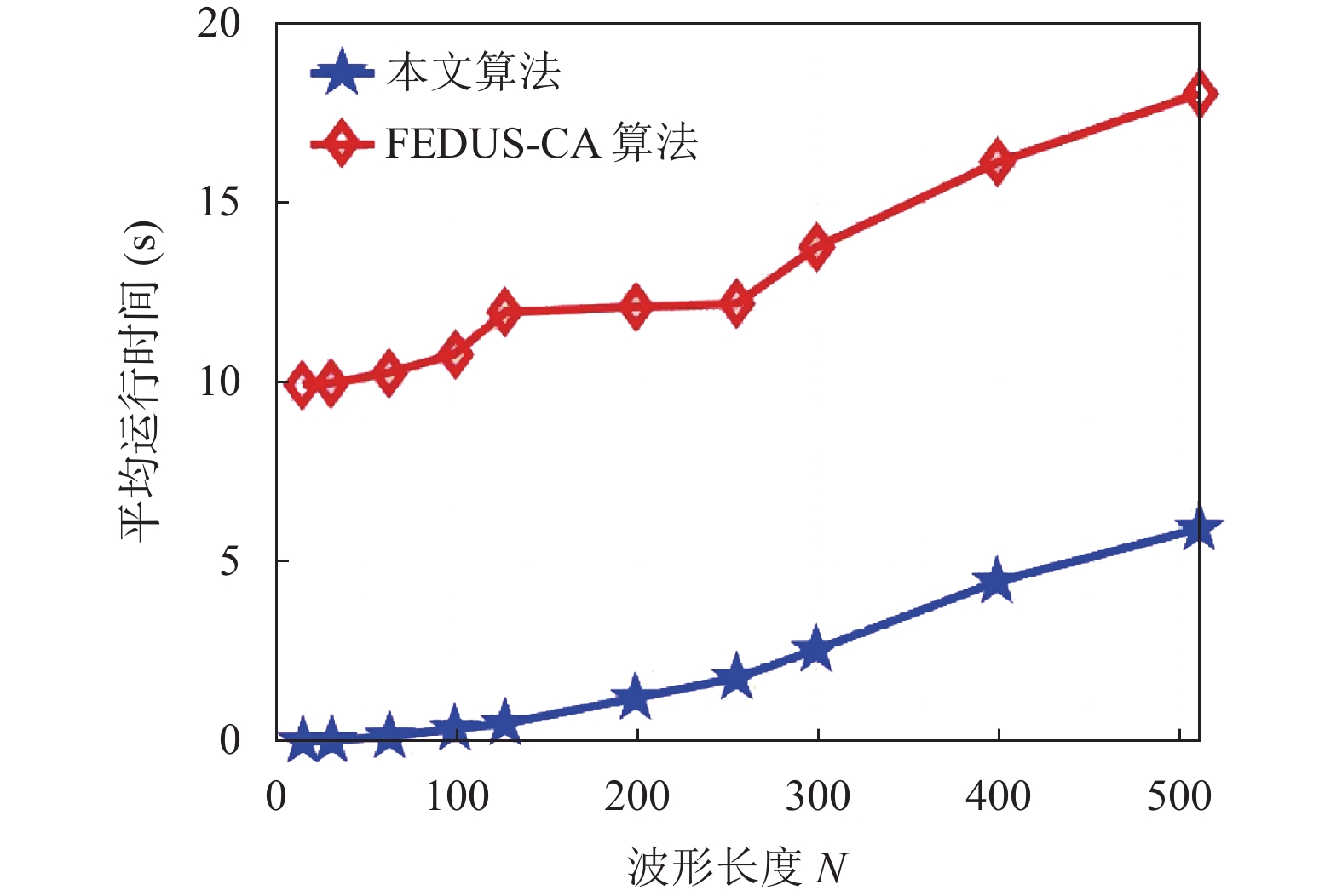
图 6 各算法平均运行时间随波形长度的变化曲线 |
图6设置干扰平台数量为M=10, 在各波形长度下对两种算法均运行了50次, 并对比了其平均运行时间. 通过对比可以发现, 尽管在各波形长度下FEDUS-CA算法的平均运行时间仍高于本文算法, 但两种算法运行时间的增长速度基本相似, 原因在于计算复杂度中关于N的量级相同. 这也进一步说明了在平台数量较多的场景下更适合采用本文算法来设计精确干扰波形.
通过图5和图6对比可见, 本文算法较FEDUS-CA算法在运行时间上更具优势, 解算速度更快, 说明本文算法在对具有移动性的作战目标实施干扰时能够实现快速响应.
4 结论针对现有算法无法快速且有效产生精确干扰波形的问题, 本文提出了一种基于MM框架的快速恒模波形设计算法. 首先根据精确干扰空间模型和信号模型建立了恒模波形的优化问题; 然后根据问题的非凸性, 采用MM框架将二次型目标函数转化为一系列可获得闭式解的子问题, 通过迭代来近似求解原问题的解, 从而获得精确干扰的可用波形; 最后通过仿真实验表明, 本文算法在精确干扰的能量控制性能和计算效率上均优于现有算法.
| [1] |
刘玲. 未来电子战展望. 电子信息对抗技术, 2021, 36(6): 30-33, 99. DOI:10.3969/j.issn.1674-2230.2021.06.007 |
| [2] |
蒋盘林. 精准电子战技术发展初探. 通信对抗, 2010(4): 3-6, 10. |
| [3] |
Strategic Technology Office of the US Defense Advanced Research Projects Agency. Precision electronic warfare (PREW). https://californiastatehospital.com/d/otherfiles/PREW_BAA_24_Aug_09.pdf. (2009-08-09)[2022-08-01].
|
| [4] |
Shi CG, Wang F, Salous S, et al. Adaptive jamming waveform design for distributed multiple-radar architectures based on low probability of intercept. Radio Science, 2019, 54(1): 72-90. DOI:10.1029/2018RS006668 |
| [5] |
Gao J, Wu RH, Zhang JD. An adaptive multi-target jamming waveform design based on power minimization. Entropy, 2020, 22(5): 508. DOI:10.3390/e22050508 |
| [6] |
赵凡, 金虎. 基于GAN的通信干扰波形生成技术. 系统工程与电子技术, 2021, 43(4): 1080-1088. DOI:10.12305/j.issn.1001-506X.2021.04.26 |
| [7] |
陈涛, 张颖, 黄湘松. 基于强化学习的自适应干扰波形设计. 空天防御, 2021, 4(2): 59-66. DOI:10.3969/j.issn.2096-4641.2021.02.010 |
| [8] |
王泓霖, 李伟, 郑家毅, 等. 基于Stackelberg模型的弹载雷达和干扰波形设计. 信号处理, 2020, 36(1): 42-49. |
| [9] |
宋聃, 王伟, 熊子源, 等. 超稀疏阵列下基于波形分集的区域能量聚焦技术研究. 电子与信息学报, 2014, 36(5): 1082-1087. |
| [10] |
Grant M, Boyd S. CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx. (2020-01-01)[2022-08-01].
|
| [11] |
Löfberg J. YALMIP: A toolbox for modeling and optimization in Matlab. Proceedings of the 2004 IEEE International Conference on Robotics and Automation. Taipei: IEEE, 2004. 284–289.
|
| [12] |
Song D, Wang W, Xu ZH, et al. Focused energy delivery with protection for precision electronic warfare. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(6): 3053-3064. DOI:10.1109/TAES.2016.150713 |
| [13] |
Zhang KD, Wang J, Zhou QS, et al. A fast jamming waveform design method for deployment in precision electronic warfare scenario. Proceedings of the 3rd International Academic Exchange Conference on Science and Technology Innovation. Guangzhou: IEEE, 2021. 402–406.
|
| [14] |
Chen SW, Xu CC, Zhang JY. Efficient focused energy delivery with grating lobe mitigation for precision electronic warfare. Signal Processing, 2020, 169: 107409. DOI:10.1016/j.sigpro.2019.107409 |
| [15] |
Yang ZP, Yang SN, Zhou QS, et al. A joint optimization algorithm for focused energy delivery in precision electronic warfare. Defence Technology, 2022, 18(4): 709-721. DOI:10.1016/j.dt.2021.03.001 |
| [16] |
Yang ZP, Zhou QS, Li ZH, et al. Grating lobe suppression in focussed energy delivery for precision electronic warfare. IET Radar, Sonar & Navigation, 2021, 15(11): 1420-1432. |
| [17] |
Li J, Stoica P. MIMO Radar Signal Processing. Hoboken: John Wiley & Sons, 2009. 41–47.
|
| [18] |
Jayaprakasam S, Rahim SKA, Leow CY. Distributed and collaborative beamforming in wireless sensor networks: Classifications, trends, and research directions. IEEE Communications Surveys & Tutorials, 2017, 19(4): 2092-2116. |
| [19] |
Mudumbai R, Hespanha J, Madhow U, et al. Distributed transmit beamforming using feedback control. IEEE Transactions on Information Theory, 2010, 56(1): 411-426. DOI:10.1109/TIT.2009.2034786 |
| [20] |
Sun Y, Babu P, Palomar DP. Majorization-minimization algorithms in signal processing, communications, and machine learning. IEEE Transactions on Signal Processing, 2017, 65(3): 794-816. DOI:10.1109/TSP.2016.2601299 |
| [21] |
Tang B, Liu J, Wang H, et al. Constrained radar waveform design for range profiling. IEEE Transactions on Signal Processing, 2021, 69: 1924-1937. DOI:10.1109/TSP.2021.3065830 |
| [22] |
Chen NK, Wei P, Gao L, et al. Beampattern synthesis and spectral compatibility based MIMO radar waveform design. Digital Signal Processing, 2021, 118: 103211. DOI:10.1016/j.dsp.2021.103211 |
| [23] |
Ma YZ, Wei P, Zhang HG, et al. Closed-form waveform design for MIMO radar transmit beampattern synthesis via integral equality. IEEE Access, 2020, 8: 96837-96844. DOI:10.1109/ACCESS.2020.2996676 |
| [24] |
Liu R, Li M, Liu Q, et al. Joint waveform and filter designs for STAP-SLP-based MIMO-DFRC systems. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1918-1931. DOI:10.1109/JSAC.2022.3155501 |
 2023, Vol. 32
2023, Vol. 32



