计算机视觉技术在目标检测和目标位姿解算方面具有强大的优势. 基于视觉的位姿测量是一种新兴的测量技术, 它从相机采集的图像中提取特征信息来解算目标的相对位置和姿态信息, 这类测量系统具有非接触以及精度高等特点^[1-3]. 视觉测量有多种不同的分类方法, 如根据系统所用摄像机的个数可以分为单目、双目和多目视觉等, 根据获取的图像信息不同, 可以分为二维视觉测量和三维视觉测量. 其中单目视觉测量系统虽不具备深度信息, 但因为其测量结构较为简单, 计算量较小, 对相机的标定和校正过程也较为简单, 在一些相对简单的视觉测量场景中得到了广泛应用^[4,5].

关于位姿测量的研究中, 合作目标是在目标本体上建立的主观标记, 基于合作目标的位姿测量较为成熟, 但是实际工程应用中还有很多问题. 而关于非合作目标位姿解算的工程应用案例较少, 目前仍以科研为主. 赵玉华等^[6]在飞行器表面设置4个激光器组成的合作目标, 建立姿态测量数学模型求解飞行器的姿态. 张勇等^[7]设计了红外合作目标, 提取合作目标中的线特征, 采用灭影线的原理得到无人机的位姿参数. Guo等^[8]将4个非共面的发光二极管作为特征点, 采用Posit算法解算单相机采集图像中目标的相对位置姿态.

在基于合作目标的相机相对位姿解算过程中, 待测图像中的特征点坐标提取以及位姿估计算法是位姿测量系统的两个关键部分^{[9, 10]}. 本文通过图像间的匹配点对从待测图像中提取特征点坐标, 结合合作目标的尺寸信息以及相机标定参数, 解算相机坐标系和目标坐标系间的相对位置和姿态关系. 特征点坐标提取的效率和精度对位姿解算的效率以及解算精度有很大影响, 在实际情况下, 检测精度与效率很难同时保证, 因此需使用合适的匹配算法, 使坐标提取的精度与效率均满足实际应用需求.

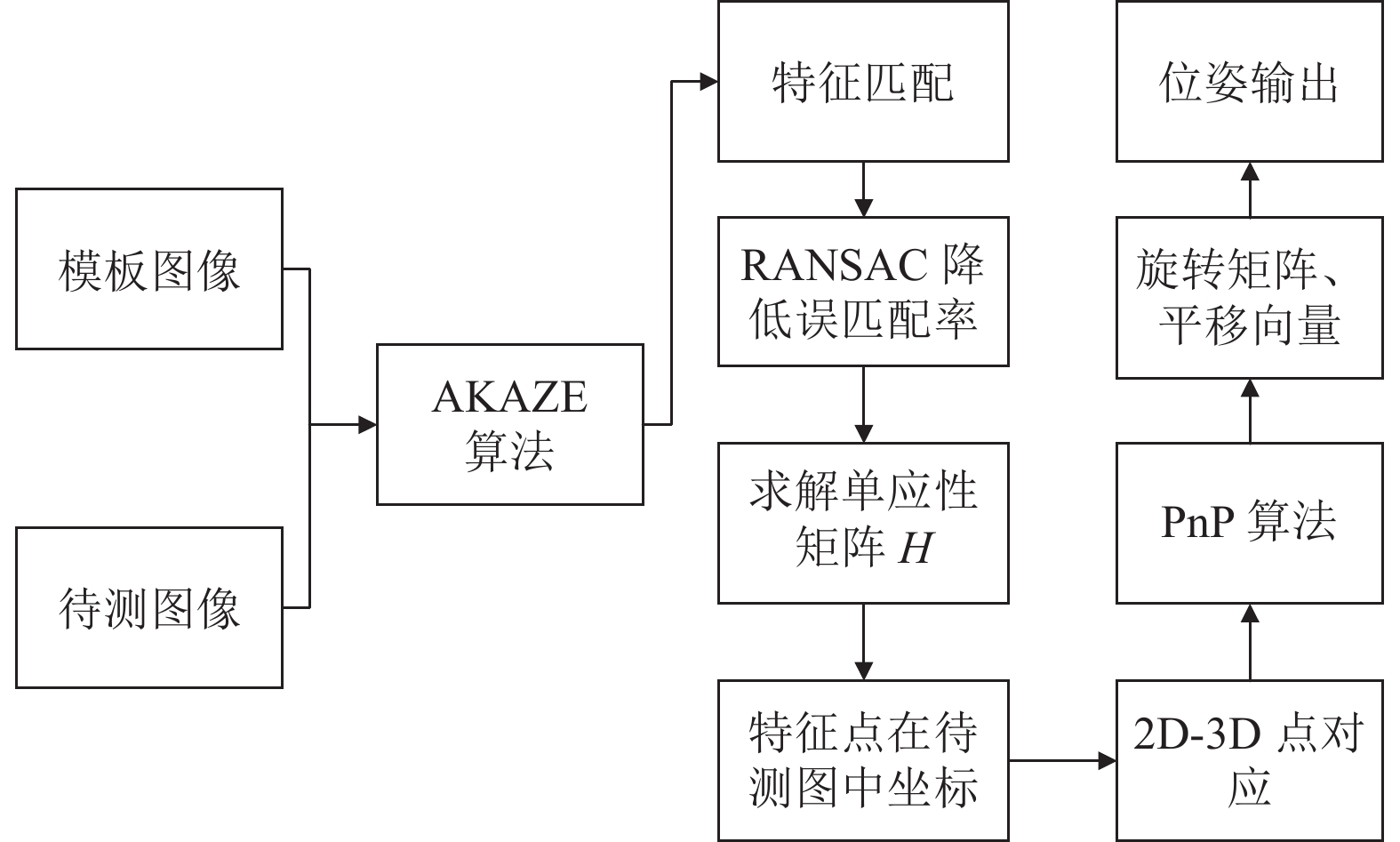
1 方法概述

获取物体和相机的相对位姿的关键在于相机外部参数矩阵的求解. 文中采用的基于AKAZE特征检测算法和4个共面特征点的相机姿态解算方法, 首先需要设计合作目标并采集合作目标的模板图像, 利用数字图像处理技术提取附加到合作目标中的4个特征点的像素坐标, 通过AKAZE特征检测算法分别提取模板图像以及待测图像的关键点, 对关键点描述并进行筛选匹配, 之后计算单应矩阵H, 得到4个特征点在待测图像中的像素坐标. 结合已知的合作目标的尺寸信息, 对2D点和3D点进行一一对应, 之后求解PnP问题解算相机和目标之间的相对位姿. 主要流程如图1所示.

2 基于合作目标的相机位姿解算 2.1 相机标定

视觉测量中为能得到准确的测量数据, 需对相机内参数进行标定. 本文利用6×9大小的棋盘格, 每个棋盘格大小为25 mm×25 mm, 在不同角度拍摄多幅棋盘图像, 利用OpenCV相机标定函数求解内参矩阵和畸变参数, 结果如表1所示.

2.2 合作目标设计

为便于匹配识别待测图像中的合作目标以及输出可靠的位姿信息, 需要合理地设计合作目标. 合作目标的设计图案中应包含足够多的纹理特征, 同时应包含点特征、直线特征、圆特征等易于提取的特征^{[11, 12]}. 文中设计的合作目标为长90 mm, 宽60 mm的矩形, 设计的合作目标如图2(a)所示.

选取的4个特征点为矩形合作目标的4个角点 $ {Q}_{0} $ 、 $ {Q}_{1} $ 、 $ {Q}_{2} $ 、 $ {Q}_{3} $ , 其在图像上的投影点分别为 $ {q}_{0} $ 、 $ {q}_{1} $ 、 $ {q}_{2} $ 、 $ {q}_{3} $ . 首先采集合作目标的模板图像, 对图像进行预处理, 之后通过图像分割、边缘提取等图像处理技术从合作目标的模板图像中提取 $ {q}_{0} $ 、 $ {q}_{1} $ 、 $ {q}_{2} $ 、 $ {q}_{3} $ 的像素坐标( $ {x}_{i} $ , $ {y}_{i} $ ), 提取结果如图2(b)所示.

2.3 AKAZE特征匹配

传统SIFT特征检测存在特征提取和描述子匹配计算量大、计算效率不高的问题, 并且高斯模糊在图像去噪的同时还会将部分边缘纹理信息过滤, 使得边界产生模糊以及丢失图像细节. AKAZE检测算法是采用非线性扩散滤波来构建非线性尺度空间, 能够保留更多的图像边缘特征^[13].

由于特征匹配算法仍具有局限性, 因此文中通过RANSAC (随机抽样一致)算法进一步降低误匹配率, 得到筛选后的匹配点对, 由匹配点对求出两幅图像之间的单应矩阵H, 之后提取 $ {q}_{0} $ 、 $ {q}_{1} $ 、 $ {q}_{2} $ 、 $ {q}_{3} $ 在待测图像中的像素坐标( ${x}'_{i}$ , ${y}'_{i}$ ), 其坐标满足如式(1)的变换关系:

$ \left[ {\begin{array}{*{20}{l}} {x'} \\ {y'} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}&{{h_{13}}} \\ {{h_{21}}}&{{h_{22}}}&{{h_{23}}} \\ {{h_{{\text{3}}1}}}&{{h_{{\text{32}}}}}&{\text{1}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{l}} x \\ y \\ 1 \end{array}} \right] = H\left[ {\begin{array}{*{20}{l}} x \\ y \\ 1 \end{array}} \right] $

(1)

其中, $ (x, y) $ 和 $(x', y')$ 为正确匹配点对分别在模板图像和待测图像中对应的像素坐标, H矩阵为3×3大小的矩阵.

2.3.1 构造非线性尺度空间

非线性扩散滤波将图像的亮度变化描述为通过提升尺度参数控制扩散的过程, 可以通过式(2)所示的非线性扩散滤波方程表示:

$ \frac{{\partial L}}{{\partial t}} = div(c(x, y, t) \cdot \nabla L) $

(2)

其中, $ L $ 代表图像亮度信息, $ div $ 为散度信息, $ \nabla L $ 代表图像梯度, 为传导函数, 能够使扩散自适应于图像的局部特性结构. $ t $ 为尺度参数, $ t $ 的值越大, 图像的表示形式也越简单.

AKAZE算法通过快速显示扩散(FED)方法进行若干次循环完成非线性扩散滤波方程的计算来构造非线性尺度空间. 将式(2)中方程离散化可得式(3):

$ {L^{i + 1}} = \left( {I + \tau A\left( {{L^i}} \right)} \right){L^i}, \quad (i = 0, 1, \cdots , n - 1) $

(3)

其中, $ I $ 为单位矩阵, $ \tau $ 表示时间步长, $ A\left({L}^{i}\right) $ 是图像 $ {L}^{i} $ 的传导矩阵, 用变化步长 $ {\tau }_{j} $ 代替恒定步长 $ \tau $ , FED算法周期如式(4) :

$ {L^{i + 1, j + 1}} = \left[ {I + {\tau _j}A\left( {{L^i}} \right)} \right]{L^{i + 1, j}}, \quad (j = 0, \cdots , n - 1) $

(4)

与传统的SIFT、SURF算法不同, AKAZE构建的尺度空间中, 每层图像的大小都与输入图像保持一致, 共有 $ O $ 组, 每组 $ S $ 层, 每层参数计算如式(5):

$\left\{ { \begin{array}{*{20}{l}} {\sigma _i}(o, s) = {\sigma _0}{2^{o + s/S}} \\ o \in [0, 1, \cdots , O - 1] \\ {s \in [0, 1, \cdots , S - 1], \; i \in [0, 1, \cdots , M]} \end{array}} \right. $

(5)

其中, $ {\sigma }_{i} $ 代表尺度参数, $ M=O\times S $ 是全部尺度空间包含的图像总数. 以时间单位 $ {t}_{i} $ 替代尺度参数 $ {\sigma }_{i} $ 可得式(6):

$ {t_i} = \frac{1}{2}\sigma _i^2, \; i \in [0, \cdots , N] $

(6)

2.3.2 特征点提取与描述

AKAZE算法通过从尺度空间中寻找不同尺度下的黑塞矩阵局部极大值点来检测特征点. 黑塞矩阵的计算公式如式(7) :

$ {L_{{\rm{Hessian}}}} = {\sigma ^2}\left( {{L_{xx}}{L_{yy}} - L_{xy}^2} \right) $

(7)

AKAZE提出了改进局部差分二值描述符(M-LDB描述符)来生成描述子, M-LDB描述符从划分好的网格中进行尺度为 $ \sigma $ 的采样, 使用采样点的梯度值和灰度值等信息完成二值描述符的建立^[14]. AKAZE特征算法得到的描述子具有旋转不变性、尺度不变性、光照不变性等特性.

2.4 PnP算法

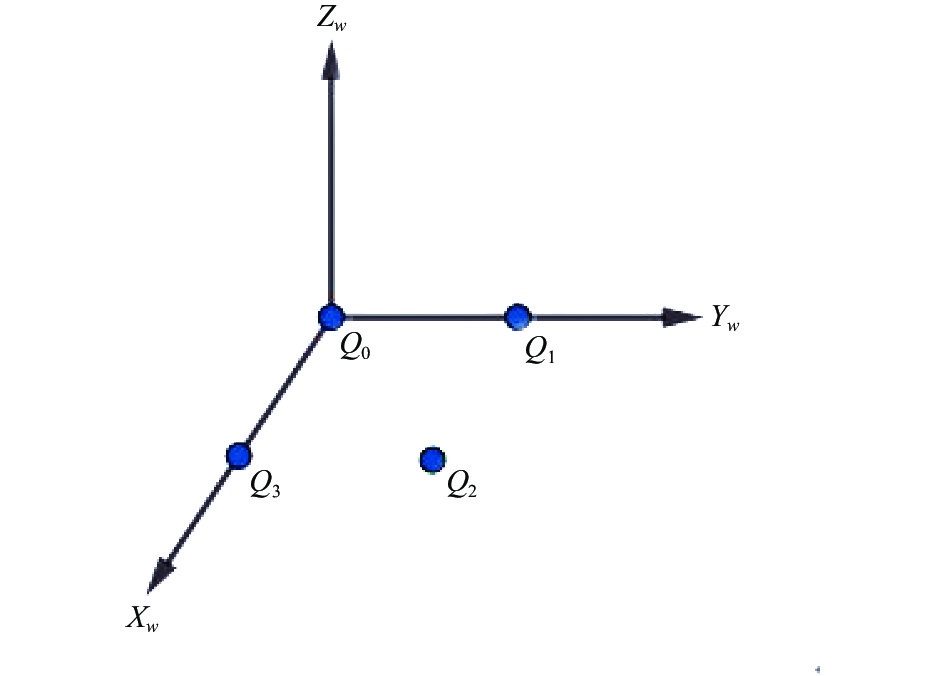
PnP (perspective-n-point)问题又称为给定控制点的位姿测量问题, 在已知N个三维空间点的坐标以及空间点在图像上的投影, 计算相机和目标的相对位姿^[15]. 文中以 $ {Q}_{0} $ 为原点, 采用如图3所示的方式定义目标坐标系 $ O{X}_{w}{Y}_{w}{Z}_{w} $ .

随着n取不同的值, 解决PnP问题也有不同的方法. 当n=1, 2时, 约束条件太少, 此时求解PnP问题会得到无数个解; 当n=3时, 约束条件个数等于未知数个数, 至多可有4个解; 当n=4时, 若4个点共面, 可以求得唯一解, 若4个点不共面, 至多有5个解; 当n=5时, 可以将PnP问题转化为几个P3P问题或P4P问题; 当n>6时, PnP问题可通过线性求解方法求得唯一解.

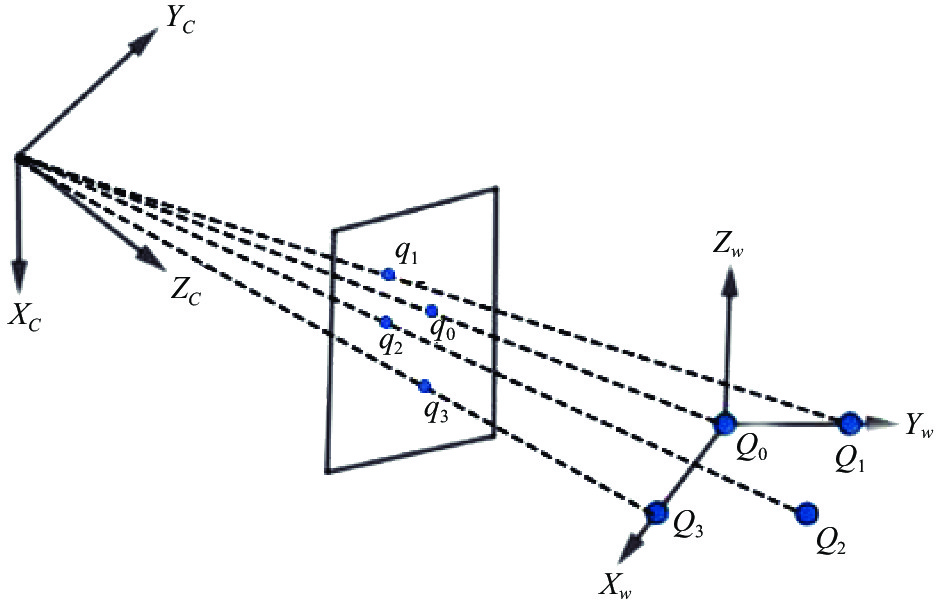
综上所述, 设计了具有4个共面特征点的合作目标, 以此来确定相机坐标系和目标坐标系之间唯一的位姿关系. PnP位姿解算示意图如图4所示.

利用PnP算法对相机和目标的相对位姿进行解算, 实现流程如下.

(1)输入相机内参矩阵和畸变系数.

(2)输入4对2D-3D点对.

(3)调用solvePnP函数求解旋转向量和平移向量.

(4)将旋转向量转换为旋转矩阵, 解算相对位姿.

设解算得到的旋转变换矩阵为 $ R $ , 平移向量为 $ T $ , 目标坐标系下某点 $ {(X}_{w} $ , $ {Y}_{w} $ , $ {Z}_{w}) $ 到相机坐标系下所对应点(X_C, Y_C, Z_C)的转换关系如下:

$ \left[ {\begin{array}{*{20}{l}} {{X_C}} \\ {{Y_C}} \\ {{Z_C}} \end{array}} \right] = R\left[ {\begin{array}{*{20}{l}} {{X_w}} \\ {{Y_w}} \\ {{Z_w}} \end{array}} \right] + T $

(8)

3 实验分析

以Visual Studio 2017为实验平台, 结合了OpenCV计算机视觉开源库、Eigen计算库, 利用实验对所提方法进行了验证.

3.1 匹配实验

对几种经典提取算子的优缺点进行了比较, 如表2.

从表2可以看出, Harris适应环境能力不足, ORB和HOG特征未能解决尺度不变性的问题, SIFT和SURF算法具有较好的旋转不变性和尺度不变性等特性, 故对同一幅待匹配图像, 利用SIFT、SURF、AKAZE这3种不同的算法进行了关键点提取和匹配, 效果如图5(a)–图5(c). 为了提升目标检测及位姿估计的实时性, 实验中对相机采集的图像进行了压缩, 从而减少图像的处理量.

对不同算法提取的关键点数量和检测用时进行比较, 结果如表3所示.

利用AKAZE算法对不同角度、不同距离、不同光照以及部分目标遮挡等条件下采集的90幅图像进行目标检测, 其中正确匹配图像数量为82, 检测准确率为91.1%, 平均检测耗时0.263 s. 实验表明, 当尺度变化、旋转变化过大或者待测目标被严重遮挡时容易造成检测失败.

3.2 位姿解算实验

预先标定相机相对于合作目标的位置和旋转参数, 分别进行平移和旋转测试实验, 与标定参数进行对比, 以验证算法的有效性.

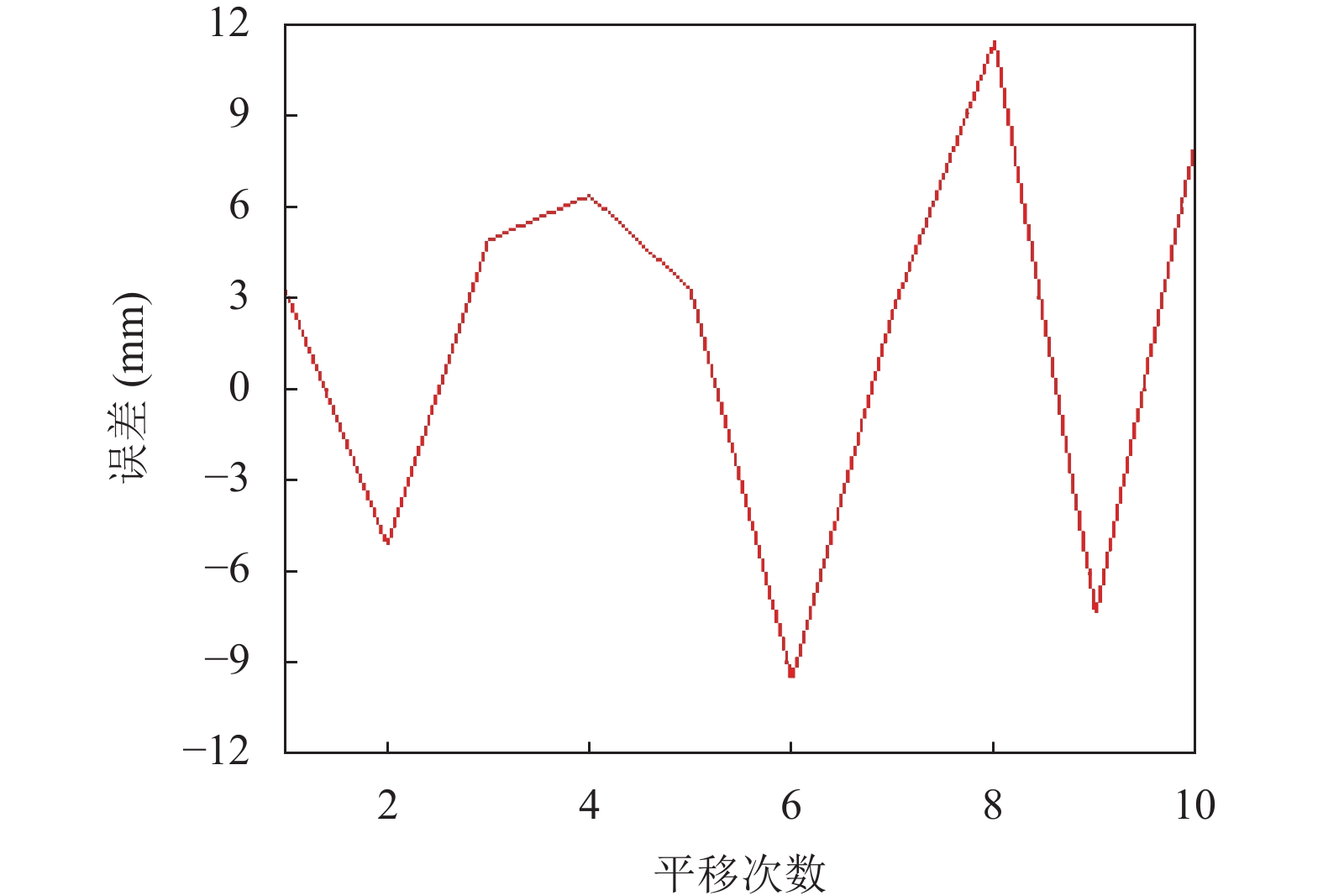
3.2.1 平移测试实验

将相机分别沿 $ {X}_{w} $ , $ {Y}_{w} $ , $ {Z}_{w} $ 轴进行平移, 每次平移25 mm, 每次平移后, 采集当前图像进行解算, 并对位置参数测量误差进行计算. 初始位置时, 相机在目标坐标系中的坐标为(40.83, 20.14, 650.64). 以沿 $ {Y}_{w} $ 正方向平移为例, 测量结果如表4所示, 图6为 $ {Y}_{w} $ 方向平移误差曲线.

由图6可以看出, 沿着 $ {Y}_{w} $ 正方向平移, 平移参数测量的绝对误差在12 mm内. 同理, 将相机分别沿 $ {X}_{w} $ 、 $ {Z}_{w} $ 轴方向平移, 测量结果与沿 $ {Y}_{w} $ 方向类似, 考虑到相机安装与移动过程中造成的影响, 误差在允许范围内.

3.2.2 旋转测试实验

采用如图7(a)所示的旋转平台. 相机位置固定不动, 将合作目标固定在旋转工作台上, 目标坐标系坐标轴应与转台坐标系坐标轴平行, 合作目标平面的初始位置大致与相机光轴垂直. 图7(b)为转台与合作目标.

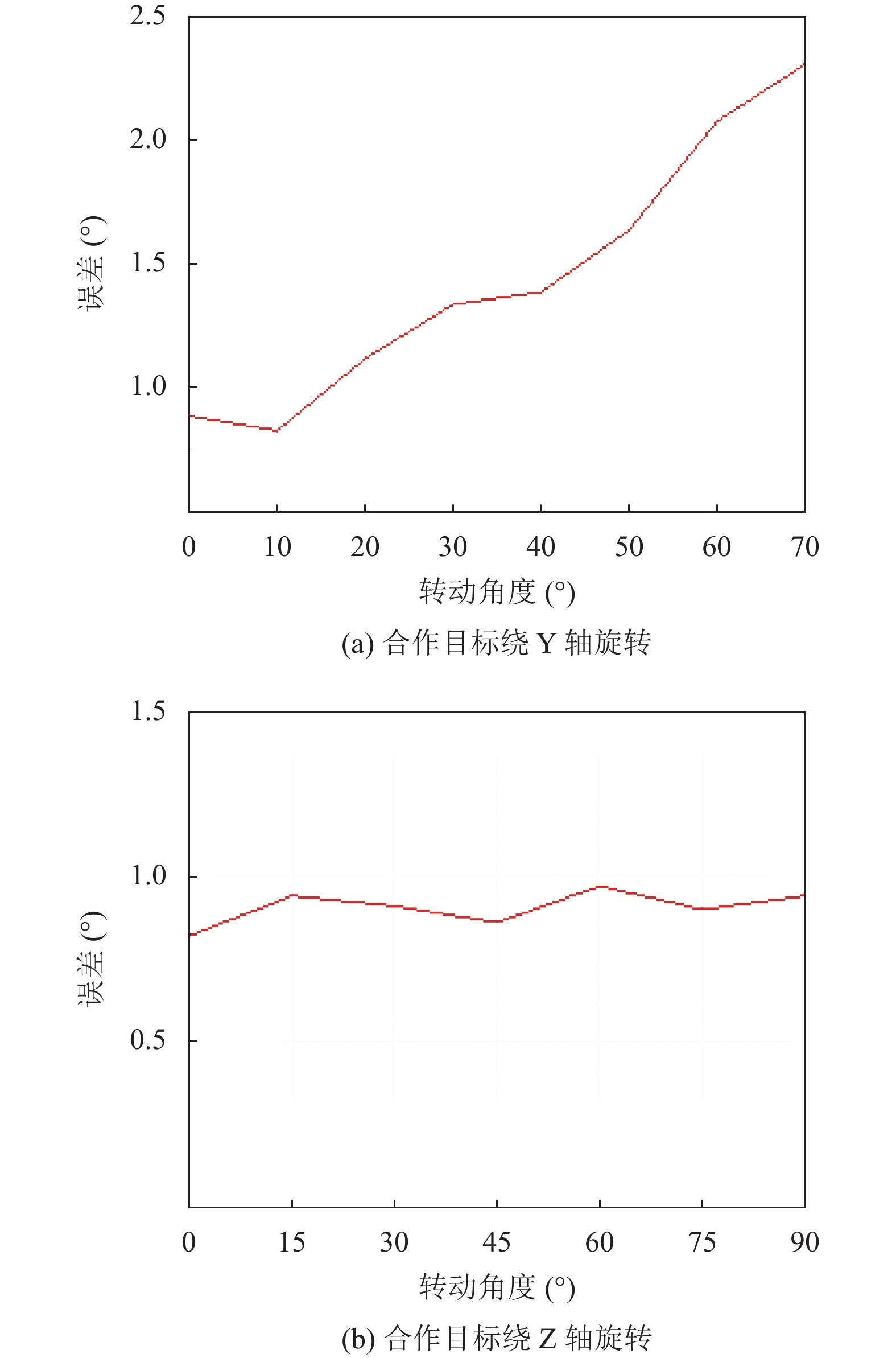
将合作目标分别绕Z轴以及Y轴进行旋转, 每转动一次, 采集图像获取相机对应单幅图像的位姿参数, 计算旋转参数的测量误差, 测量结果如图8(a)、图8(b)所示.

由图8(a)可知, 当合作目标绕Y轴旋转时, 随着旋转角度的增大, 测量误差也会随之增大, 且角度越大测量误差越大, 误差不超过2.5°, 这是由于相机与合作目标平面夹角增大时, 采集的图像也会产生一定的几何畸变, 测量误差也会增大. 由图8(b)可知, 合作目标绕Z轴旋转, 角度的变化不会对测量精度造成太大影响.

4 结论

本文采用了一种基于AKAZE特征检测算法和PnP算法的单目相机位姿估计方法, 对目标检测以及位姿解算分别进行了实验验证. 结果表明, 该方法得到的相机与目标间的相对位姿与真实结果接近, 验证了本文方法的有效性.