2. 深圳大学 电子与信息工程学院, 深圳 518060
2. College of Electronics and Information Engineering, Shenzhen University, Shenzhen 518060, China
能源分配问题是地区发展需要面临的一个难题, 对于未来一段时间内地区的能源分配数值进行预测, 使得能源被充分利用, 既能保证该地区的发展, 还能减少对环境造成的污染, 所以对于所需能源的具体值进行预测是一项非常有必要的工作[1-3]. 而能源分配往往需要考虑到该地区的气候环境因素, 同时还要将以往能源分配的数值作为参考值, 这是典型的时序预测问题.
对于传统的时序预测, 有包括卡尔曼滤波预测[4]、时间序列预测[5]和差分整合滑动平均自回归模型预测[6]等方法, 而此类传统方法预测精度低[7]且预测耗时很长. 利用神经网络预测能更快更好的解决上述问题, 循环神经网络(recurrent neural network, RNN)作为最早使用的算法结构容易出现梯度爆炸的问题, 而且其预测的结果基本仅取决于过去超短时期的数据. 后续为了改进RNN遗忘性大这一问题, 引入了传统的长短期记忆网络(long short-term memory, LSTM)这一种时间循环神经网络, LSTM的记忆门与遗忘门可以处理传入的短期数据, 在预测问题上可以减缓梯度爆炸或者梯度消失的问题; 虽然传统的LSTM模型在相比RNN时有了很大的进步, 但仍然存在3个问题: (1)预测多元问题效果差. LSTM模型在面对多元预测问题上, 往往都是将原始数据直接传入网络中生成对应的预测结果; (2)统计窗口小. LSTM模型进行大量的数据预测时, 很难将过去较长一段时期的数据纳入计算范围, 模型投入过多的数据不但浪费算力甚至会影响结果的准确性; (3)时间复杂度高. LSTM模型预测所花费的时间随所需预测的数量的增加而变长. 另一方面, Informer模型[8]常被用于预测能源分配问题, 该模型预测速度快且在中长距离预测和多元预测问题上都有较好的表现, 但在此任务上该模型效果不好.
本文针对上述问题, 提出了Conv1d-LSTM模型, 引入计算机视觉中的卷积核[9, 10]作为统计窗口, 提取出结合了多元的环境因素与能源分配的数值的特征; 设置较大的计算窗口可以让网络接收到更久远的信息; 采用并联多个LSTM组件的方法可进行快速地长序列预测. Conv1d-LSTM模型面对多元数据集时, 相较于其他经典算法有着更高的精度. 本文将采用平均绝对误差MAE (mean absolute error)、均方根误差RMSE(root mean square error)、平均绝对百分比误差MAPE (mean absolute percentage error)和运行时长作为评价指标. 通过实验发现, Conv1d-LSTM模型较其他模型具有更低的MAE和RMSE, 在短距离预测MAPE仅为4.4%, 同时在运行速度上也有着一定优势.
1 算法结构 1.1 输入与输出 1.1.1 输入原始数据
输出是未来P个连续时间预测的能源分配数值及环境因素数值, 可以表示为
相较于传统的LSTM模型, Conv1d-LSTM模型继承了LSTM内部的结构, 仍然保留了遗忘门、输入门、输出门等结构, 但输入序列不再从原始数据中直接获得, 而是将多组能源分配的数值以及该区域的环境因素数值传入卷积神经网络中.
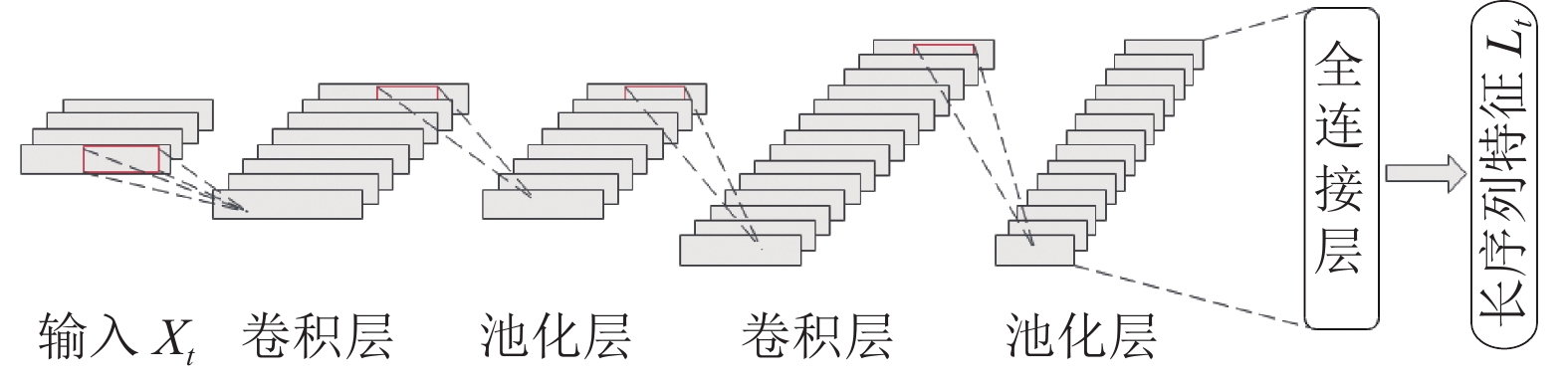
如图1所示, 输入序列Xt通过多个卷积层和池化层, 最后经过全连接层提取出特征向量Lt , 将生成的特征向量传入LSTM的相关组件中.
|
图 1 卷积神经网络(CNN)提取数据特征 Fig. 1 data features extracted by convolution neural network |
卷积层Conv1d中输入为Xin (k, Lin), 输出为Xout (n, Lout), 其计算公式如下:
| Xout=WD⋅D0+WD⋅D1+⋯+WD⋅Dk−1+bn | (1) |
| Lout=Lin+2∗p−(ks−1)s+1 | (2) |
其中, WD为卷积核的权值; D0–Dk–1为k个原始数据; b为偏置量; Lin为输入的矩阵的第二维度; n为卷积核数量, p为填充数量; ks为卷积核的尺度; s为卷积核每次移动的步长.Xout为输出数值, Lout为维度值.
卷积层计算方式如图2, 假设输入为Xin (3,

|
图 2 卷积层结构 Fig. 2 convolutional layer structure |
平均池化层和激活函数ReLU维度计算公式与卷积层同理, 数值计算公式如下:
| Pout=P′in+Pin+P″in3 | (3) |
| Rout=max | (4) |
其中,
将输入Xt传入通过多层卷积池化以及全连接层的卷积神经网络后获得长序列特征向量Lt , 记为:
| {L_t} = Conv1d\left( {{X_t}} \right) | (5) |
其中, 计算结果Lt为t时刻前k次能量分配的原始数据通过卷积神经网络(convolutional neural networks, CNN)提取出的特征参数, k为超参数, 用于设定每个特征包含多少组的数据.
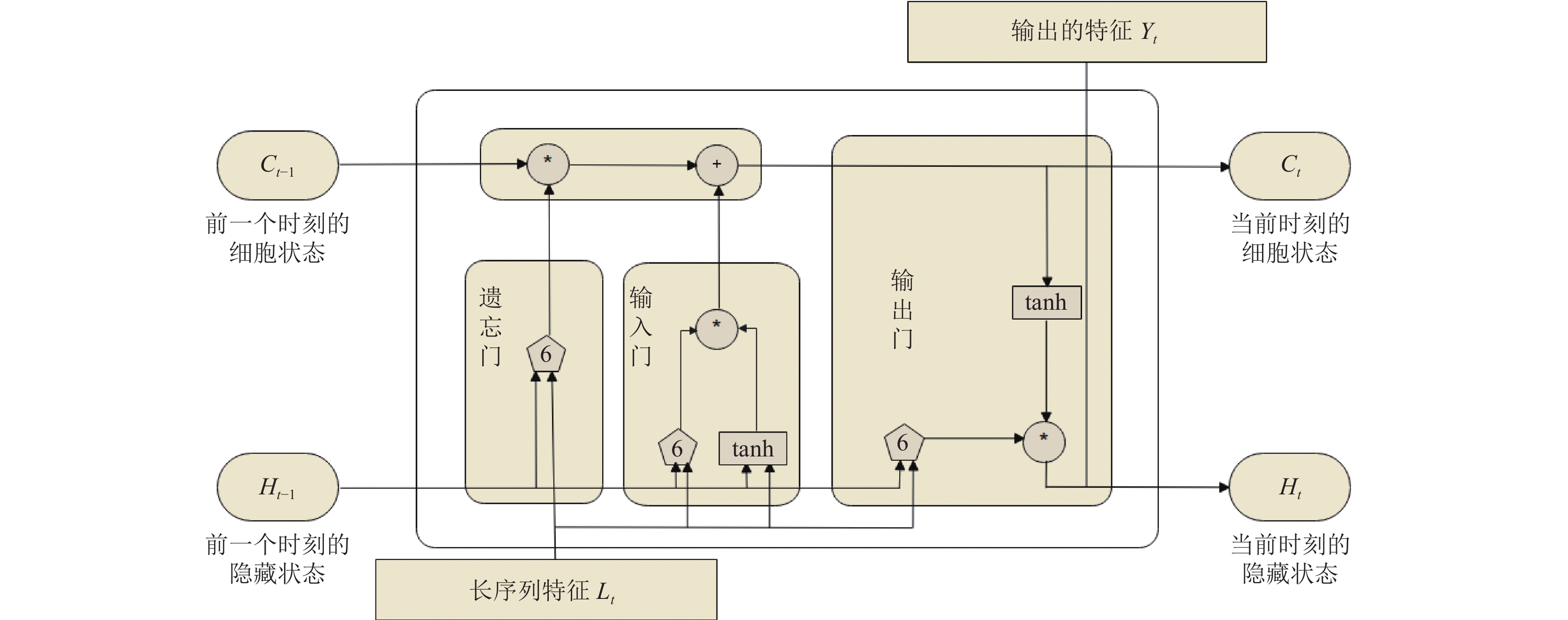
LSTM模型如图3, 将每个时刻通过卷积神经网络生成的长序列特征Lt传入模型计算如下, 激活函数:
| \sigma \left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} | (6) |
| \tanh \left( x \right) = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} | (7) |
遗忘门ft , 输入参数为前一时刻的隐藏状态Ht–1及特征向量Lt:
| {f_t} = \sigma \left( {{W_f} \cdot \left[ {{H_{t - 1}}, {L_t}} \right] + {b_f}} \right) | (8) |
输入门it , 输入参数与遗忘门一样:
| {i_t} = \sigma \left( {{W_i} \cdot \left[ {{H_{t - 1}}, {L_t}} \right] + {b_i}} \right) | (9) |
当前细胞状态Ct , 输入参数由遗忘门的输出ft 、输入门的输出it 、上一时刻细胞状态值Ct–1及特征向量Lt组成:
| {C_t} = {f_t} \cdot {C_{t - 1}} + {i_t} \cdot \tanh \left( {{W_C} \cdot \left[ {{H_{t - 1}}, {L_t}} \right] + {b_C}} \right) | (10) |
输出门ot , 输入参数为前一时刻隐藏状态Ht–1、当前细胞状态值Ct及特征向量Lt :
| {o_t} = \sigma \left( {{W_o} \cdot \left[ {{H_{t - 1}}, {L_t}} \right] + {b_o}} \right) | (11) |
更新后的当前隐藏状态Ht :
| {H_t} = {o_t} \cdot \tanh \left( {{C_t}} \right) | (12) |
输出预测出的长序列值Yt :
| {Y_t} = {o_t} \cdot \tanh \left( {{C_t}} \right) | (13) |
|
图 3 LSTM模型 Fig. 3 LSTM model |
2 计算方法 2.1 单步计算 2.1.1 单步训练
模型单步训练流程如图4, 假设输入Xt0由10个原始数据Dt0–Dt9组成, 即
| {\textit{MSELoss}}\left( {p, t} \right) = {\left( {p - t} \right)^2} | (14) |

|
图 4 Conv1d-LSTM单步训练 Fig. 4 single-step training of Conv1d-LSTM |
预测值Yt0与真实值Dt10通过
模型单步预测流程如图5, 假设预测第1个未知值Dt10, 则将Dt0–Dt9组成1个输入Xt0传入模型, 即可获得预测值Yt0. 若预测后续值如Dt11, 则将Dt1–Dt9和预测值Yt0组成1个输入Xt1传入模型, 获得预测值Yt1. 按照此方法反复计算直到获得所有预测值

|
图 5 Conv1d-LSTM单步预测 Fig. 5 single-step prediction of Conv1d-LSTM |
2.2 多步计算 2.2.1 多步训练
由于单步训练的时间复杂度与LSTM一样, 长距离预测时会导致模型性能下降严重, 故设计出一组并联的Conv1d-LSTM结构来提升模型性能. 模型多步训练流程如图6, 假设一次性输入Xt0和Xt1, 分别由3个原始数据Dt0–Dt2和Dt1–Dt3组成, 即
模型多步预测流程如图7, 假设预测两个未知值Dt4、Dt5, 则将输入

|
图 6 Conv1d-LSTM多步训练 Fig. 6 multistep training of Conv1d-LSTM |

|
图 7 Conv1d- LSTM多步预测 Fig. 7 multistep prediction of Conv1d-LSTM |
3 实验分析 3.1 实验数据集
为了评估Conv1d-LSTM模型的性能, 本文使用了从公开数据集(rp5.ru)下载的由比利时切维斯机场气象站收集的当地相关数据. 该数据共29列, 其中1列时间、1列能源分配数值和27列环境因素, 环境因素包括1列光照度、24列从当地采集到的西北角至东南角的气压和湿度数值以及2列匿名环境因素. 其采样时间间隔为10分钟, 共19736行原始数据.
3.2 实验配置实验服务器配置CPU: Intel Xeon E5-2620 v4, GPU: GTX1080Ti×4 (显存11 GB), 操作系统: CentOS Linux release 7.6.1810 (Core), 训练和测试均在单块显卡上进行, 软件使用Python 3.8、PyTorch 1.7.0、cuda 10.1. 见表1.
| 表 1 服务器配置和环境 Table 1 server configuration and environment |
3.3 参数选择 3.3.1 普通参数
各个模型内部权值矩阵W, 其内部数值分布是以均值为0, 标准差为1的正态分布; 损失值Loss, 由于L2损失较L1损失对异常值更为敏感且惩罚更重, 故本实验使用MSELoss为损失函数.
3.3.2 超参数统计窗口train_window, 默认值为92; LSTM组件内部隐藏层大小hidden_size, 默认值为100; 优化器选择Adam[11], 学习率learning_rate, 初始值为0.001; 每批次数据量batch, 默认值为32; 迭代次数epoch, 默认值为100.
3.4 实验过程训练模型时, 全部使用超参数的默认值, 一批次输入124个原始数据, 即统计窗口92, 可截出32个连续的原始数据片段, 使得传入CNN的batch数量为32, 并获得相应的长序列特征. 将获得的长序列特征传入LSTM结构中, 同时传出对应的预测值
测试模型时, 以平均绝对误差MAE (mean absolute error), 均方根误差RMSE (root mean square error)和平均绝对百分比误差MAPE (mean absolute percentage error), 其具体表达式为:
| MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} | (15) |
| {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } | (16) |
| {\textit{MAPE}} = \frac{{100{\text{%}} }}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_i} - {{\hat y}_i}}}{{{{\hat y}_i}}}} \right|} | (17) |
其中, n为测试的样本数目; yi和
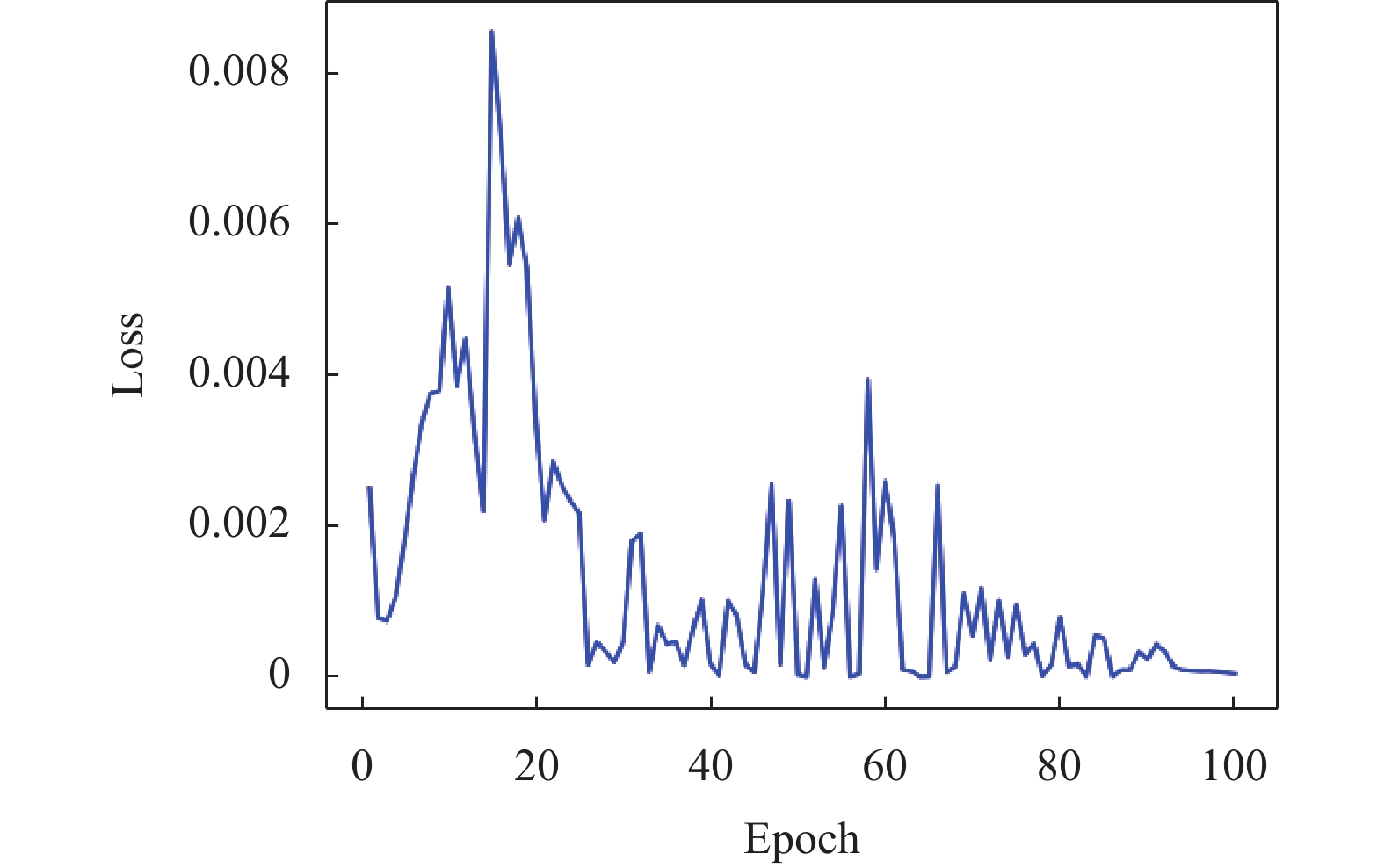
|
图 8 损失值Loss变化 Fig. 8 the change of Loss |
3.5 实验结果
实验选择传统LSTM模型, Informer模型与Conv1d-LSTM模型接收上述数据进行学习并预测后续能源分配的具体数值, 分别预测未来间隔为24次 (4 h)、96次 (16 h)、192次 (32 h)以及216次 (36 h)的能源分配数值, 比较其MAE、MSE、MAPE以及运行时长, 见表2.
| 表 2 不同模型的实验结果 Table 2 experimental results of different models |
如表2所示, 使用Conv1d-LSTM模型时, 间隔24次时的超短预测间隔平均绝对误差(MAE)仅为0.0338, 其预测效果远好于Informer模型, 较传统LSTM模型的效果也有小幅提升; 同样, Conv1d-LSTM在中长预测间隔中, 如间隔96次、间隔192次、间隔216次时的MAE、RMSE均远低于Informer和LSTM模型, MAPE也在始终保持在100%以下.
运行时长用于记录训练好的模型从加载到最后预测出结果的耗时. 传统的LSTM模型面对越来越长的预测任务时, 运行时长也会随之变久, 而Conv1d-LSTM模型随着任务间隔变长所消耗的时间增多不明显, 相较于传统的LSTM模型有着速度上的绝对优势.
3.6 预测波形为了直观体现Conv1d-LSTM模型在预测问题上的优势, 本文采用Python 3.8中的第三方库matplotlib绘制预测折线图, 数据由模型预测后直接导入该第三方库. 图9、图10展示了预测未来24次间隔的能量分配值, 图展示了未来192次间隔的能量分配值, 横坐标为间隔次数, 纵坐标为能源分配数值, 能源分配数值为原始数据放缩在(−1, 1)区间内归一化后的数值.

|
图 9 各模型24次间隔预测图 Fig. 9 the 24-time interval prediction graph of each model |

|
图 10 各模型96次间隔预测图 Fig. 10 the 96-time interval prediction graph of each model |
如图9、图10可知, Informer模型在预测此类能源分配任务时几乎没有波动, 从实验结果的MAPE远高于100%和展示的波形可以看出, Informer模型不具备对该任务预测能力; LSTM模型在24次间隔即短间隔时预测能力较好, 但在96次中长预测间隔中性能严重下滑, 折线图中LSTM的波形只会在(−1.0, −0.7)之间徘徊, 故在更长间隔的任务中LSTM模型也将不具备预测能力; 本文提出的Conv1d-LSTM模型, 在24次短间隔的预测结果与真实值接近, 且中长距离的预测结果波形与真实数据波形走势接近, 仍然具有很好的预测能力.
4 总结与展望 4.1 当前存在的问题(1) Conv1d-LSTM模型中运用了神经网络来进行计算, 属于黑箱模型, 无法从原理上找到问题的突破口, 目前阶段主要是以计算出结果来对比真实值, 再利用对比结果进行反推从而达到调优模型性能的目的.
(2) Conv1d-LSTM的模型在该能源分配任务上效果显著, 但其泛化能力还有待验证.
(3)目前关于能源分配的问题还未有成熟的计算体系, 难以从理论上构建更加有效的预测模型, 现阶段仍需要组合搭建不同的网络来尝试解决此类问题.
4.2 发展动向(1)随着“双碳”政策的提出, 越来越多的人重视能源的相关问题, 也有更多的科研工作者投身该方向的研究. 文中使用的Informer模型虽不适合本文的任务, 但该模型也是我国科研工作者提出的有关能源分配预测的新算法模型.
(2)未来的能源分配任务将会根据能源分配预测的特点, 从数学角度出发, 寻找对能源分配具有高影响力的环境因素, 通过对不同地方采集到的数据进行先筛选归类, 再从算法的角度组合可用的模块或搭建合适的模型.
4.3 总结能源分配的具体数值具有一定的规律性, 非常适合用深度学习的方法来挖掘其内部各个数据间的关系, 故我们需要搜集大量的当地环境因素数据如温度、湿度及PM2.5等. 本文提出的Conv1d-LSTM用于进行能源分配数值的预测, 拥有传统LSTM短距离的高精确度, 同时还能通过扩大感受野来预测长期数值, 预测的速度也不会因任务的长短不同而发生较大变化. 测试结果也表明, 通过当地的环境因素数值及能源分配数值来训练Conv1d-LSTM模型, 能够准确地预测该地一段时间内能源所需分配的具体数值, 能够达到节能或是充分利用能源的目的.
| [1] |
施冬梅, 肖锋. 基于改进长短时记忆网络的驾驶行为检测方法研究. 汽车工程, 2021, 43(8): 1203-1209, 1262. DOI:10.19562/j.chinasae.qcgc.2021.08.011 |
| [2] |
张亚伟, 陈瑞凤, 徐春婕, 等. 基于LSTM-LightGBM模型的车站环境温度预测. 计算机测量与控制, 2022, 30(1): 20-25. DOI:10.16526/j.cnki.11-4762/tp.2022.01.004 |
| [3] |
黄冬梅, 王唱, 胡安铎, 等. 基于CNN-BiLSTM的潮汐电站潮位预测. 水力发电, 2021, 47(10): 80-84. DOI:10.3969/j.issn.0559-9342.2021.10.016 |
| [4] |
陈军, 陶巍, 吕英飞, 等. 基于卡尔曼滤波的短期负荷预测. 电气开关, 2014, 52(2): 43-45. DOI:10.3969/j.issn.1004-289X.2014.02.013 |
| [5] |
李东东, 覃子珊, 林顺富, 等. 基于混沌时间序列法的微网短期负荷预测. 电力系统及其自动化学报, 2015, 27(5): 14-18. DOI:10.3969/j.issn.1003-8930.2015.05.03 |
| [6] |
李晨熙. 基于ARIMA模型的短期电力负荷预测. 吉林电力, 2015, 43(6): 22-24. DOI:10.3969/j.issn.1009-5306.2015.06.007 |
| [7] |
马得银, 孙波, 刘澈. 基于天气信息的短期冷热电负荷联合预测方法. 电网技术, 2021, 45(3): 1015-1022. DOI:10.13335/j.1000-3673.pst.2020.0794 |
| [8] |
Zhou HY, Zhang SH, Peng JQ, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proceedings of the 35th AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2021. 11106–11115.
|
| [9] |
甘昕艳, 唐晓年. 基于CNN的时序数据关联规则挖掘模型. 计算机仿真, 2021, 38(3): 282-285, 326. DOI:10.3969/j.issn.1006-9348.2021.03.058 |
| [10] |
陈海鹏, 周越豪, 王趁录, 等. 基于改进的CNN-LSTM短期风功率预测的系统旋转备用经济性分析. 高电压技术, 2022, 48(2): 439-446. DOI:10.13336/j.1003-6520.hve.20201850 |
| [11] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv:1412.6980, 2014.
|
| [12] |
Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature, 1986, 323(6088): 533-536. DOI:10.1038/323533a0 |
 2023, Vol. 32
2023, Vol. 32



