洪水是世界上最具破坏性的自然水文气象灾害之一^[1], 其危害有引起城市内涝、河流洪水、山洪滑坡等, 历史见证了由暴雨洪水所造成的重大人员伤亡和财产损失. 然而, 目前世界各地仍然处于暴雨洪水灾害的威胁下, 例如2021年河南郑州“7·20”特大暴雨灾害事件, 引发了舆论的高度关注^[2]. 而发展可靠和有效的洪水预报模型将有助于对暴雨洪水事件进行预判, 将为相关部门提供及时的预警提醒, 从而提前制定灾害应对措施, 洪水预报已经成为一项重要的非工程性防洪减灾举措^[3]. 因此, 发展洪水预报模型是暴雨洪涝灾害预警的关键研究内容, 为保障城市远离洪涝灾害提供重要支撑.

国内外学者针对洪水预报模型的研究已取得了大量研究成果, 目前主流的洪水预报模型大致可分为两种类型, 即基于物理原理的模型和基于数据驱动的模型^{[4, 5]}. 一方面, 传统物理模型从水文原理出发, 存在着诸如原理复杂, 水文参数定标难, 合理的模型开发周期长等问题. 另一方面, 随着数字水利工作的全面部署完成以及计算机领域中数据挖掘算法的快速发展, 水利与计算机学科的交叉融合逐渐成为科研进步的强大动力. 其中, 基于数据驱动的洪水预报模型是目前水文预报领域的研究热点^[6]. 丰富的机器学习理论逐渐被应用于洪水预报模型的扩展和提升中. 时间序列预测模型是机器学习领域一类重要的任务, 该模型常常应用于股票证券、能源电力、交通流量等预测. 单一水文要素规律的模拟与预测也属于时序预测任务, 而相关水文要素的预测问题尚待大量的研究. 传统的时间序列预测模型常常采用移动平均法、指数平均法、AR、MA及ARMA等方法. 如果数据的平稳性满足一定的要求, 水文要素的时序预测问题也能得到解决, 例如文献[7]将ARMA和ARIMA模型应用于Dez大坝水库月流量的预测问题中. 而深度学习作为机器学习的重要分支, 复杂的网络模型结构使其具备高效的特征表达能力, 这为解决传统时序预测模型的局限性提供了新思路. 常见的深度学习网络包括循环神经网络(RNN)、长短时记忆网络(long short-term memory networks, LSTM)模型、门控单元神经网络(GRU)、卷积神经网络(CNN)、注意力机制、变分自编码器等. 其中RNN、LSTM及GRU模型是处理时间序列问题的最优选择. 最新的研究^[8-11]表明, LSTM模型被广泛地应用于水文要素的时序预测任务中.文献[8]研究LSTM模型在洪水预警领域的可行性, 并指出LSTM模型克服了物理模型参数多, 定标复杂的问题. 文献[9]将LSTM模型应用于合流制管网溢流(combined sewer overflow, CSO)问题, 这有助于理解CSO的结构行为, 提升城市水资源的利用效率.文献[10]利用LSTM模型提升韩国汉江大桥站水位预测的准确度, 有效地解决了汉江大桥站季节性变化很大, 水位改变非常迅速的问题. 文献[11]将LSTM模型应用于我国沂沭泗流域中的石梁河水库水位, 并取得相对较为满意的预测效果. 大量的成功应用表明LSTM模型在水文要素预测问题的可行性. 基于LSTM模型的组合方法^[12-14]在最近的研究中呈现出热门的趋势, 例如文献[12]为降低降雨-径流预测的时间成本, 将KNN方法与LSTM进行了组合, 其中KNN方法成为更新因子, 有助于提升LSTM方法在实时洪水预报系统中的可行性;文献[13]将attention机制内嵌在 LSTM 中, 并用贝叶斯优化来加速超参数的调整, 从而实现了水库日流量的准确预报; 文献[14]尝试将Seq2Seq模型与LSTM模型进行了组合, 从而实现对烟台市门楼水库水质的准确预测. 由此可见, 这些组合模型的提出源于实际应用所存在的局限性.不同组合模型各有所长, 要根据具体问题视情况而定. 本文关注到这类问题——实际模型的输入即水文要素的测量值会受到水利现场设施环境、人类活动等因素的影响, 导致水文要素的测量值是一个非平稳的时间序列, 而且水文要素关系复杂导致的有效特征提取困难, 水位预测精度低等问题不利于准确的模型训练和预测, 因而准确的洪水预报模型除了需要选择合适的时间序列模型还需要考虑采集数据的预处理, 以便得到平稳时间序列的准确预测模型^[15]. 奇异谱分析(SSA)是一种先进的时频分析方法^[16], 可以从数据中提取趋势项、波动项和噪声成分, 已被广泛用于水文数据的预处理^[17,18]. 文献[17]针对水文时间序列月径流多尺度非平稳性等特点, 提出基于奇异谱分析的月径流组合预测模型并应用于月径流预报, 提高了云南省水文站月径流预报的准确度. 文献[18]将奇异谱分析应用于数据预处理阶段, 对径流数据进行去噪来提高径流序列的平稳性和可预测性, 提出的奇异谱分析—灰狼优化—支持向量回归(SSA-GWO-SVR)模型提高了黑河正义峡的月径流预测精度, 并且能很好地预测径流峰值. 由此可见, 将奇异谱分析方法应用于数据预处理阶段可以提高时序数据的平稳性和可预测性, 而LSTM神经网络具有记忆的特点, 可以处理时间序列中的长期依赖性^[19]. 基于此, 本文提出一种基于奇异谱分析分解与长短期记忆神经网络(SSA-LSTM)的组合模型的短期水位时间序列预测方法. SSA-LSTM模型的主要工作原理是, SSA方法将观测到的时间序列分解为周期、趋势和噪声分量, 接着利用LSTM方法对去噪后的序列进行预测, 得到最终的预测值^[20]. 为了验证SSA-LSTM模型的有效性, 本文利用涡河流域的涡阳闸监测点近50年的水位数据对模型进行了训练和验证, 并将实验结果与LSTM模型进行了对比, 验证了所提出方法的高可靠和低误差特性, 更适用于水位预测的应用.

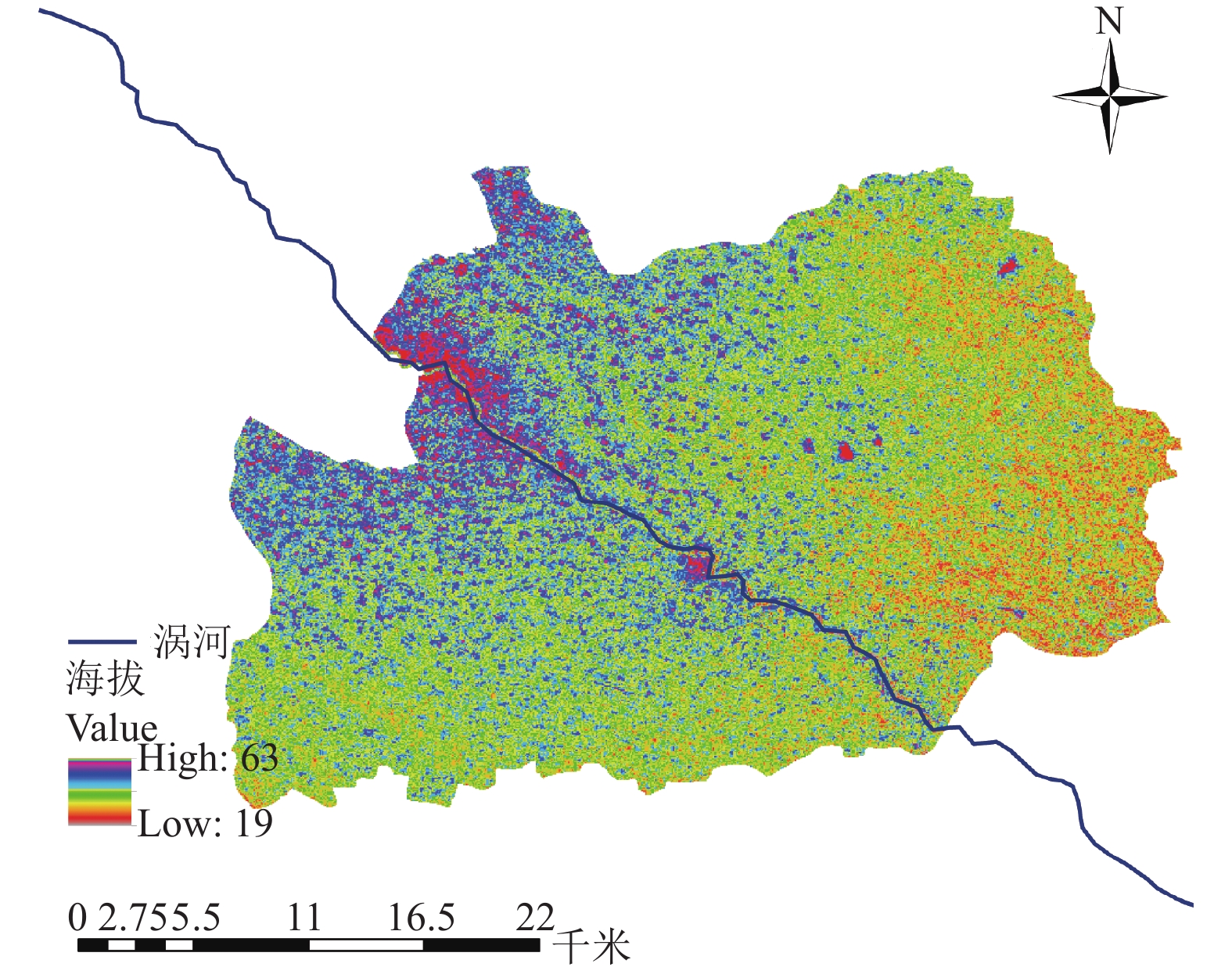
为了验证SSA-LSTM模型在日水位预测应用的有效性, 本研究利用涡河流域涡阳闸的历史数据开展, 涡阳流域位于安徽省亳州市涡阳县, 属暖温带半湿润季风气候, 降雨季节性变化明显, 多集中于夏季(6–8月). 涡阳县的地理位置如图1所示, 涡阳县地势平缓, 平均海拔不超过35 m, 境内涡河横跨东西, 将涡阳分为涡南涡北两个地区. 涡河是涡阳流域第一大河, 淮河的第二大支流, 位于淮河北岸, 于安徽省怀远县城附近流入淮河. 涡阳闸位于涡阳县城东涡河干流上, 始建于1958年, 1963年9月完工, 工程历时5年.

图 1

Fig. 1

图 1 涡阳县地理位置信息图

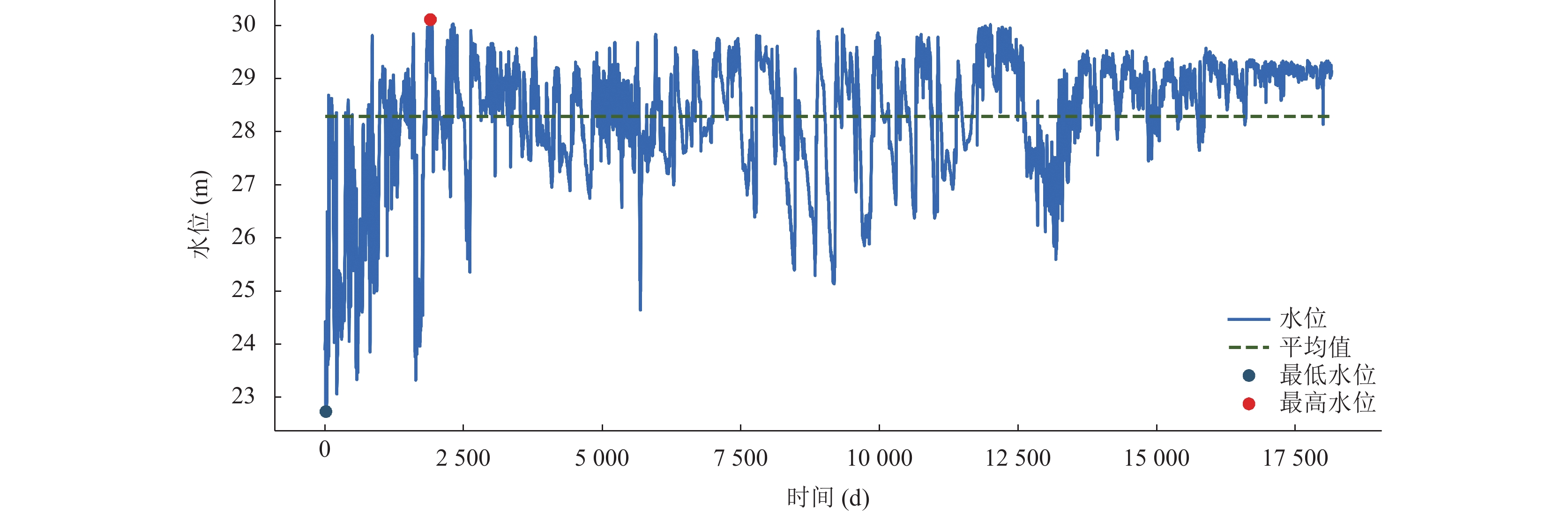
本研究取1971年5月至2020年12月涡阳闸的闸上水位为数据研究对象, 数据随时间的变化如图2所示, 该历史数据采样周期为1天, 其中最高水位为1976年的30.15 m, 最低水位为1971年的22.73 m. 为了将径流数据的时间序列重构为一个标准的机器学习数据集, 通常采用滑动窗口法对数据进行预处理, 窗口的大小是一个可变参数, 通常被称为时间步长^[21]. 因此, 本文采取滑动窗口法对原始数据进行加工, 得到了时间步长为7、14、21、28、35天的机器学习数据集, 并且取前40年水位数据作为训练集用于调整所建立模型的权重和偏差, 后10年水位数据作为测试集验证模型的性能.

图 2

Fig. 2

图 2 涡阳闸1971-05-01至2020-12-31闸上游日水位时序图

为了从复杂水文要素关系中提取有效特征, 并提高水位预测精度, 本文在考虑水文采集数据预处理问题同时选择合适的时间序列预测模型从而得到准确的洪水预报模型. 接下来将对SSA数据预处理方法和LSTM时间序列预测方法, 以及SSA-LSTM组合模型进行分别介绍.

为了避免水文数据采集中伴随的噪声对模型预测的干扰, 需要借助非线性时间序列数据处理方法对水文序列进行处理, 目前常见的非线性时间序列处理方法包括小波分解(wavelet decomposition)、经验模态分解(empirical mode decomposition, EMD)、奇异谱分析(singular spectrum analysis, SSA)等, 本文选择奇异谱分析处理涡阳闸水位时序数据. 奇异谱分析是一种处理非线性、非平稳时间序列数据的方法, 基于由时间序列构造的轨迹矩阵的奇异值分解(SVD), 通过分解和重构轨迹矩阵, 提取出趋势、信号、谐波成分和噪声^[20]. SSA的主要步骤包括嵌入、奇异值分解(SVD)、分组、对角线平均.

嵌入操作通过滑动窗口的方式将原始的一维时间序列 $ {X^*} = ({x_1}, {x_2}, {x_3}, \cdots , {x_N}) $ 映射成一个列向量序列, 称为轨迹矩阵 $X$ . 窗口大小决定 $X$ 的形状, 长度为 $M$ 的窗口映射成的轨迹矩阵如下所示:

其中, $K = N + 1 - M$ . $M$ 的大小取决于具体问题, 一般小于 $N/3$ ^[16].

奇异值分解(singular value decomposition, SVD)是一种对矩阵进行特征分解的方法, 与实对称矩阵对角化不同的是, 奇异值分解并不要求矩阵是方阵^[15]. SVD通常用于分解原始序列, 提取包含独立信息的奇异值和奇异向量, 其在降维、数据压缩、推荐系统等领域有广泛的应用^[22].

具体来说, 设 $U$ 和 $V$ 为矩阵 $X$ 的左奇异向量和右奇异向量, $ \Sigma $ 为矩阵 $X$ 的奇异值, 轨迹矩阵 $X$ 被表示如下:

其中, $U$ 、 $V$ 为正交矩阵, ${V^{\rm{T}}}$ 为矩阵 $V$ 的转置, $\Sigma $ 为对角矩阵.

方阵 $Y = {X^{\rm{T}}}X(K \times K)$ 由式(3)得到:

其中, ${X^{\rm{T}}}$ 为轨迹矩阵 $X$ 的转置, $ {\sqrt {{\sigma _1}} ^2}, {\sqrt {{\sigma _2}} ^2}, \cdots , {\sqrt {{\sigma _L}} ^2} (L \leqslant K) $ 为矩阵 $Y$ 的特征值. 由式(3)得 $ \Sigma = diag (\sqrt {{\sigma _1}} , \sqrt {{\sigma _2}} , \cdots , \sqrt {{\sigma _L}} )({\sigma _1} \geqslant {\sigma _2} \geqslant \cdots \geqslant {\sigma _L} > 0) $ .

所以, 轨迹矩阵 $X$ 可以被表示成:

最终, 轨迹矩阵 $X$ 可以被表示成若干正交矩阵的和:

其中, ${X_i} = \sqrt {{\sigma _i}} {U_i}V_i^{\rm{T}}$ .

分组操作将第2.1.2节中SVD分解出的矩阵( ${X_1}, {X_2}, \cdots , {X_L}$ )进行重新组合. 首先, 下标集合 $\{ 1, 2, \cdots , L\} $ 被分成 $p$ 个不相交的子集 ${I_1}, {I_2}, \cdots , {I_p}$ . 令 $I = \{ {i_1}, {i_2}, \cdots , {i_n}\} $ , 则第 $I$ 组矩阵构成的复合矩阵被表示为:

分组后, 轨迹矩阵 $X$ 的表达式如式(7)所示:

在这一步中, 对角线平均法将式(7)中的每个矩阵 ${X_{{I_i}}}$ 重构成一个长度为 $N$ 的新序列 $R{C_t} = {y_1}, {y_2}, \cdots , {y_N}$ , 即SSA分解后的序列. 假设 ${X_{{I_i}}}$ 为 $M \times K$ 维矩阵, ${y_k}$ 的计算公式如式(8)所示:

其中, ${M^*} = \min \{ M, K\} $ , ${K^*} = \max \{ M, K\} $ , $N = K + M - 1$ , $M < K$ 时, $y_{ij}^* = {y_{ij}}$ , 否则 $y_{ij}^* = {y_{ji}}$ .

一个单独的分量 $R{C_t}$ 可以由式(8)得到, 每个分量的奇异值占总奇异值的百分比 $ \sqrt {({\sigma _t})} /\displaystyle\sum _{i = 1}^p\sqrt {({\sigma _i})} (t = 1, 2, \cdots , p) $ 就是该分量的贡献. 选取 $d$ 个贡献最大的分量, 原始时间序列可以近似地由 $d$ 个分量的和表示 ${X^*} \approx R{C_1} + R{C_2} + \cdots + R{C_d}$ , 剩下的分量 ${R_{d + 1}}, {R_{d + 2}}, \cdots , {R_p}$ 被视作噪声.

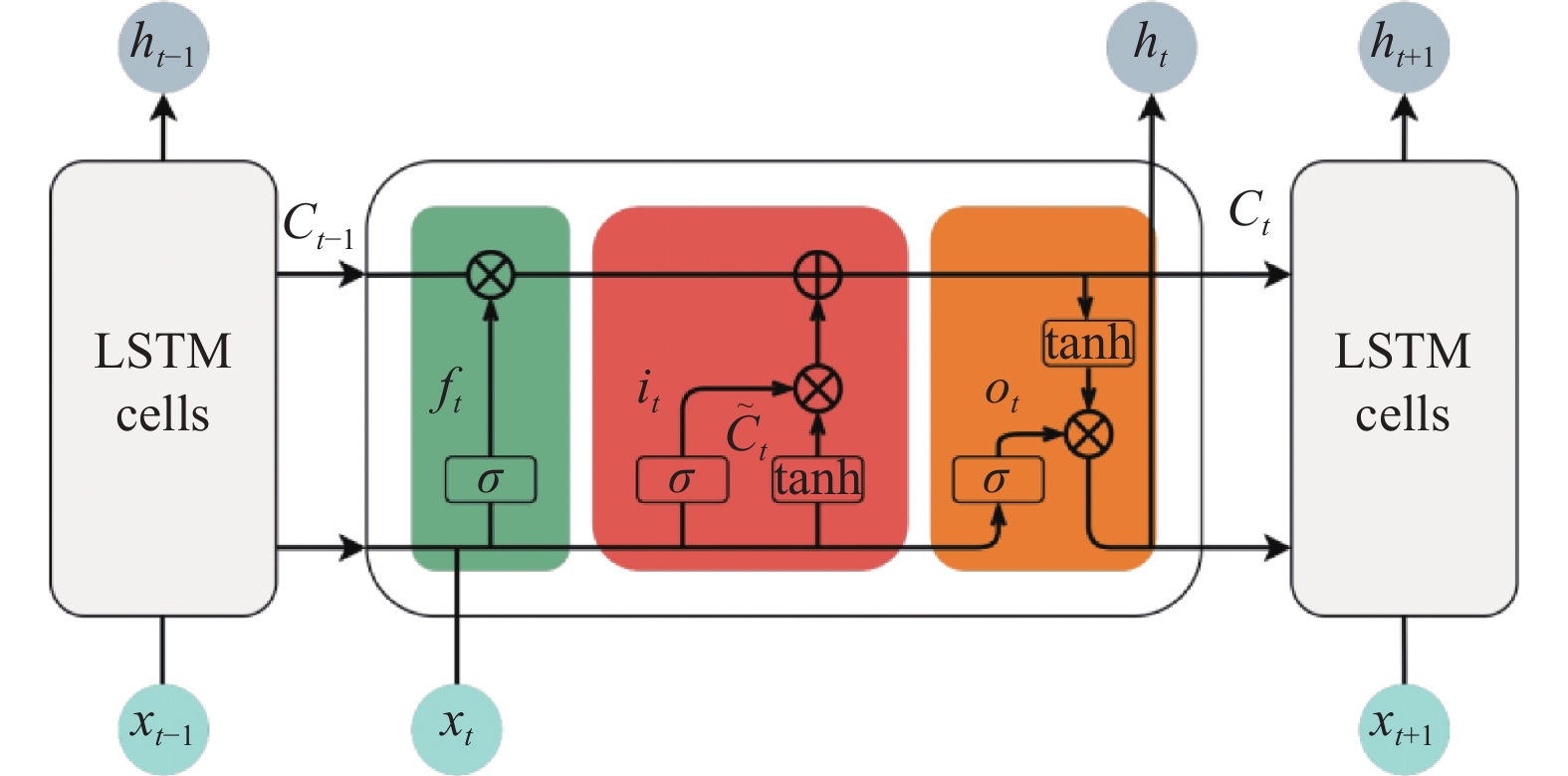
本文所研究的水位数据是一种典型的时间序列数据. 目前深度学习RNN模型被广泛用于处理时间序列数据, 然而, 由于多次反向传播导致的梯度消失或梯度爆炸, RNN在学习长期依赖性方面有局限性^[23]. LSTM是一种特殊的循环神经网络^[19], 解决了RNN在长序列数据训练过程中的梯度消失和梯度爆炸问题^[23]. 如图3所示, LSTM使用一个称为细胞状态的特定单元来存储短期和长期信息, 其余结构包括遗忘门、更新门、输出门. 遗忘门决定哪些信息被保留下来, 更新门决定哪些值被用来更新信息, 而输出门根据遗忘门和更新门的过滤结果, 决定最终的输出值. LSTM的公式如下:

图 3

Fig. 3

图 3 LSTM结构图

其中, ${x_t}$ 为输入向量, ${h_t}$ 为隐藏状态向量. ${f_t}$ 、 ${i_t}$ 、 ${o_t}$ 和 ${C_t}$ 分别为遗忘门、更新门、输出门和细胞状态; ${W_f}$ 、 ${W_i}$ 、 ${W_o}$ 和 ${W_C}$ 为权重矩阵; ${b_f}$ 、 ${b_i}$ 、 ${b_o}$ 、 ${b_C}$ 为偏置向量. $\sigma $ 和 $\tanh $ 为激活函数.

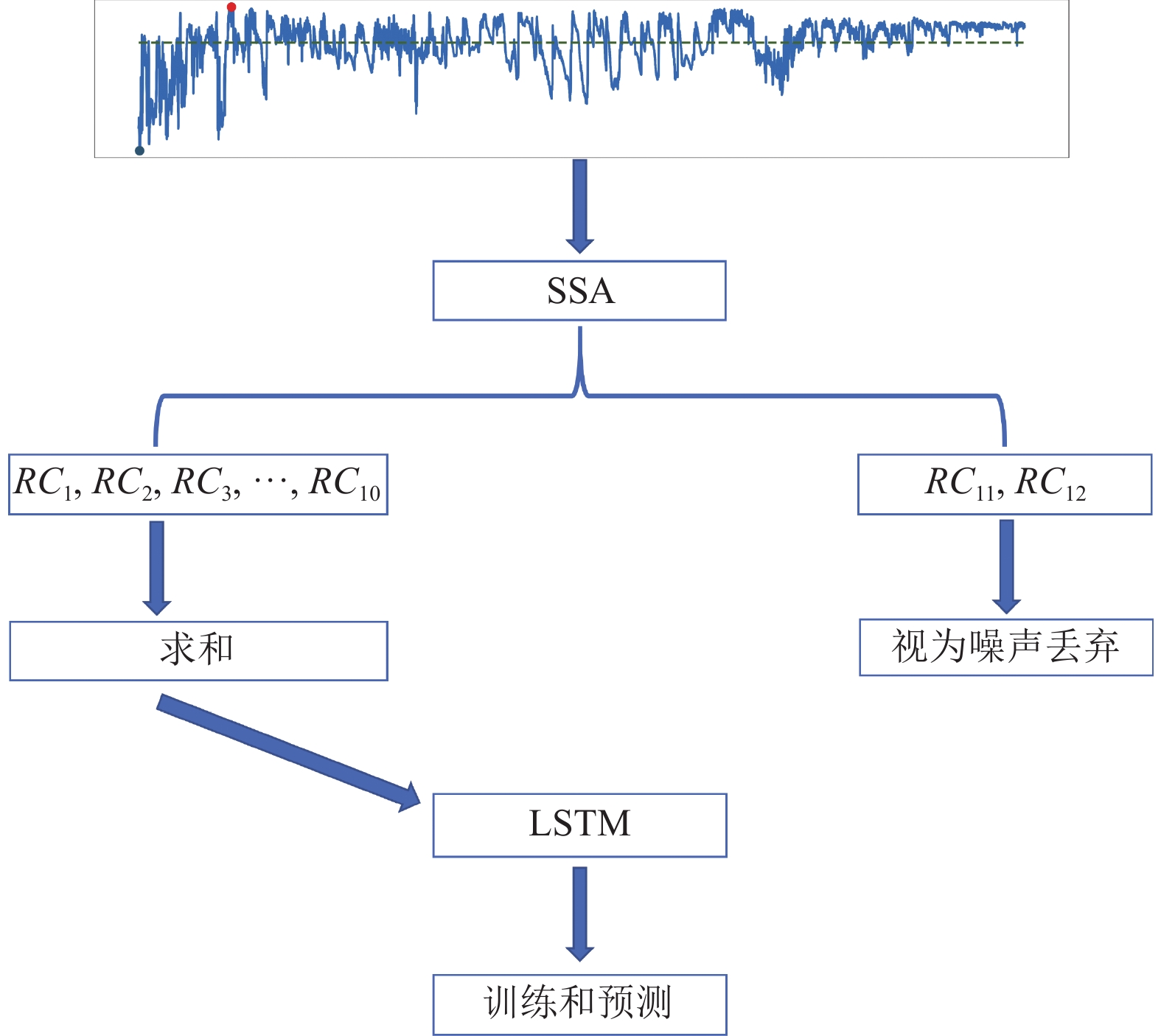
本文提出一种改进的水位预测模型SSA-LSTM, 该模型首先利用奇异谱分析将原始时间序列分解为趋势项和噪音项, 然后将去除噪音后的序列用于LSTM模型的训练和验证, 模型流程如图4所示, 其基本实现方式如下.

图 4

Fig. 4

图 4 模型开发流程图

(1) 首先, 对涡阳闸水位时序数据 $S$ 应用SSA奇异谱分析, 通过设置嵌入窗口长度为12, 得到包含趋势项和噪声项的12个分量 $R{C_1}, R{C_2}, \cdots , R{C_{12}}$ . 由第2.1.2节中的式(3)计算得到每个分量对应的奇异值 $ \sqrt {{\sigma _t}} $ , 每个分量的奇异值占总奇异值的百分比 $\sqrt {{\sigma _t}} /\displaystyle\sum\nolimits_{i = 1}^{12} \sqrt {{\sigma _i}} \;(t = 1, 2, \cdots , 12)$ 为该分量对原始序列的贡献, 按照贡献大小对分量进行排序 $(R{C_1} > R{C_2} > \cdots > R{C_{12}})$ .

(2) 为了突出原始序列的趋势特征, 以及最大程度地保留序列信息, 贡献较小的分量 $R{C_{11}}, \; R{C_{12}}$ 被当作噪声去除. 为了避免累积误差, 不对每个分量进行单独预测, 剩余分量 $R{C_1}, \; R{C_2}, \cdots , \;R{C_{10}}$ 的和重构成一个新的时间序列 $S' = R{C_1} + R{C_2} + \cdots + R{C_{10}}$ 用于替代原始水位时序数据^[15].

(3) 最后, LSTM模型对去噪和重构后的序列进行拟合.

(4) 在实验部分, 首先验证了SSA-LSTM模型的有效性, 然后探索其在不同时间步长下的表现.

为了量化评估SSA-LSTM模型的性能, 本研究选取3种常见的统计评价指标, 即决定系数 ${R^2}$ 、均方根误差RMSE、平均绝对误差百分比MAPE.

决定系数 ${R^2}$ , 又称拟合优度, 可定义为模型中预测值与观测值的离散程度之比, 取值范围为 $[ - \infty , 1]$ . ${R^2}$ 的大小反应模型拟合程度的高低, 越接近于1, 模型拟合程度越好; 接近0, 表示模拟结果接近观测值的平均值水平, 即总体结果可信, 但过程模拟误差大; 远远小于0, 模型拟合程度差, 结果不可信. ${R^2}$ 的公式如式(10)所示:

RMSE、MAPE用于计算模型预测值与观测值的误差水平, 公式如式(11)和式(12)所示:

其中, $N$ 表示样本总数; ${{{P}}_i}$ 、 ${O_i}$ 分别表示第i个样本的预测值和观测值; $\bar O$ 表示观测值的平均值. R²最大, RMSE、MAPE最小的模型被认为是性能最好的模型.

为了验证SSA-LSTM模型的有效性, 本文利用涡河流域的涡阳闸监测点近50年的水位数据对模型进行了训练和验证, 其中前80% (40年)为训练集, 用于调整所建立模型的权重和偏差; 后20% (10年)为测试集, 并将实验结果与LSTM模型进行了对比. 第3.1节展示了通过SSA方法对水位序列进行分解和重构的结果. 第3.2节展示了不同时间步长(time step)下LSTM和SSA-LSTM模型性能, 并根据不同评估指标分析了SSA-LSTM模型的性能.

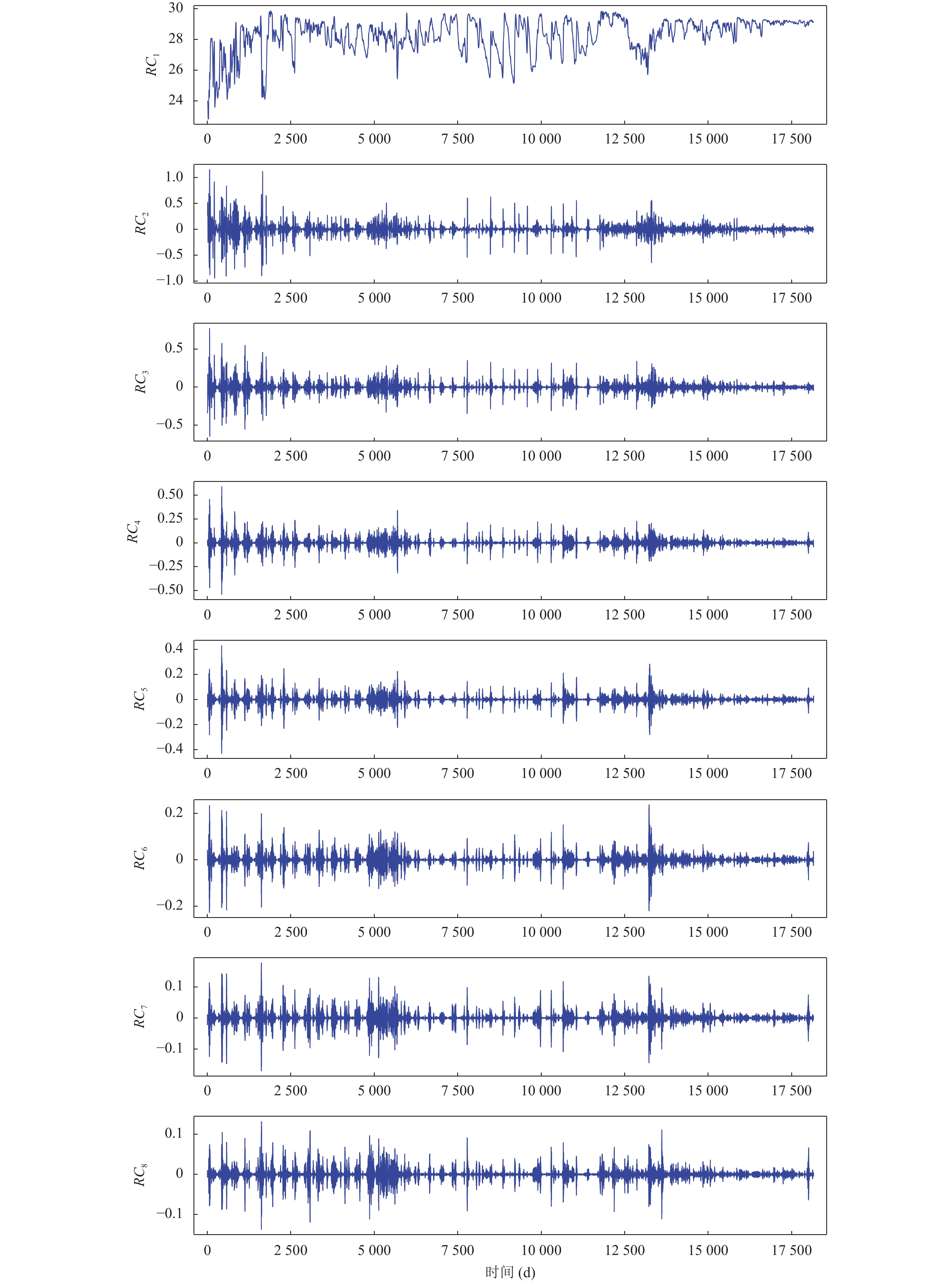
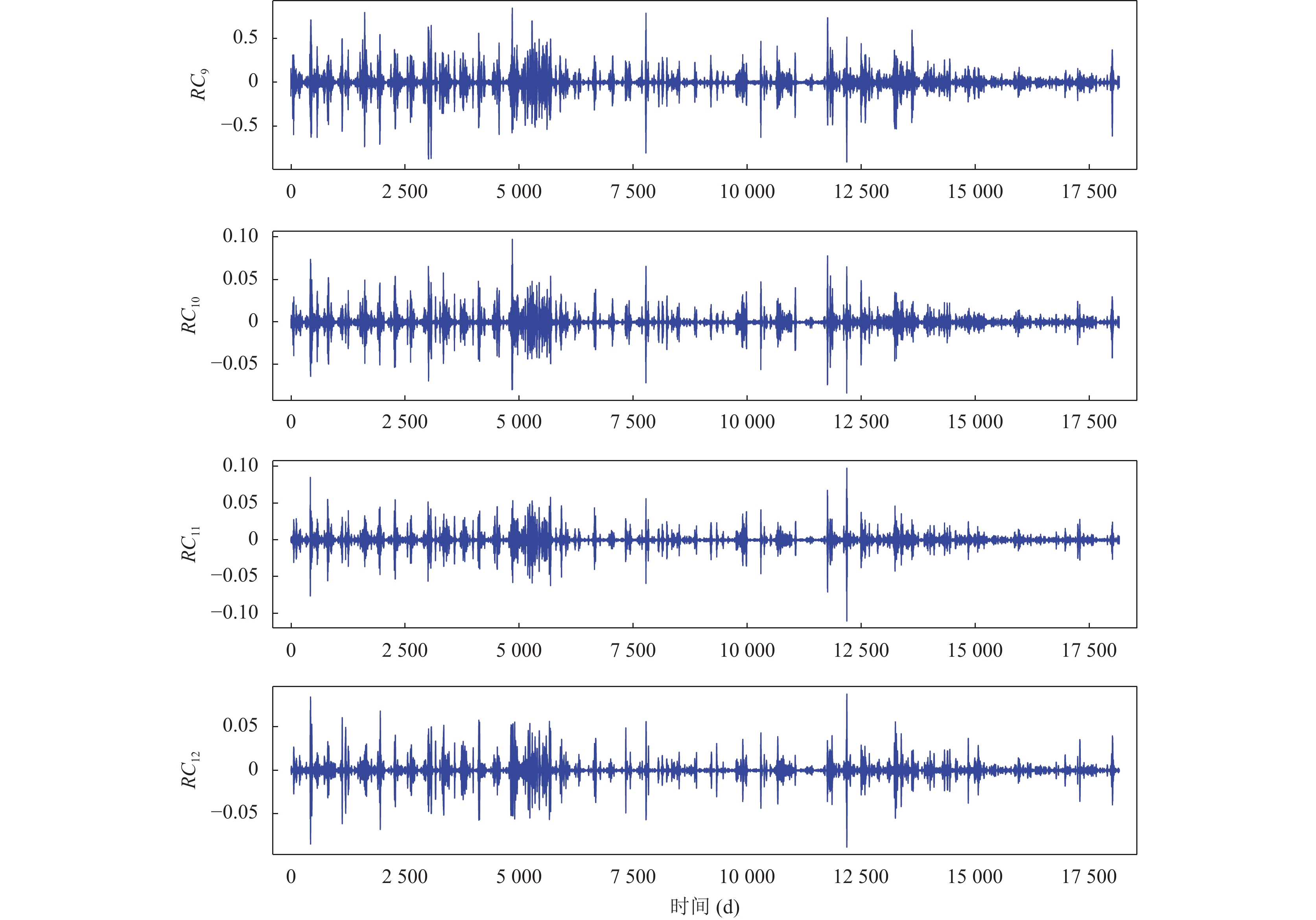
本研究使用SSA分解技术提高模型的预测能力. 图5展示了用SSA方法对涡阳闸闸上水位数据进行奇异值分解的结果. 通过设置嵌入窗口长度为12, 水位数据被分解成12个分量, 根据每个分量对原始序列的贡献, 即所占百分比, 对分量排序, 得到 $R{C_1}, \; R{C_2}, \cdots , R{C_{12}} \; (R{C_1} > R{C_2} > \cdots > R{C_{12}})$ . 由图5可以看出, $R{C_1}$ 分量体现了数据的主要趋势, 包含水位时间序列的绝大部分信息. 随着分量贡献的减少, 分量的幅度逐渐变小, 噪声值逐渐增加, $R{C_{11}}, \; R{C_{12}}$ 几乎不含任何信息, 对原始序列没有明显影响, 在后续操作中, 将其视为噪声去除^[24]. $R{C_1}, \; R{C_2}, \cdots , \;R{C_{10}}$ 重构后的水位序列如图6所示, 去除噪声后的序列几乎保留了原始序列的所有主要趋势分量和波动分量, 而不包含序列特征信息的噪声被去除, 说明SSA可以在保留水位序列主要特征的同时极大程度地减少数据中的无用信息, 从而避免模型被噪声干扰.

图 5-1

Fig. 5-1

图 5

Fig. 5

图 5 水位序列经过SSA分解得到的12个分量

图 6

Fig. 6

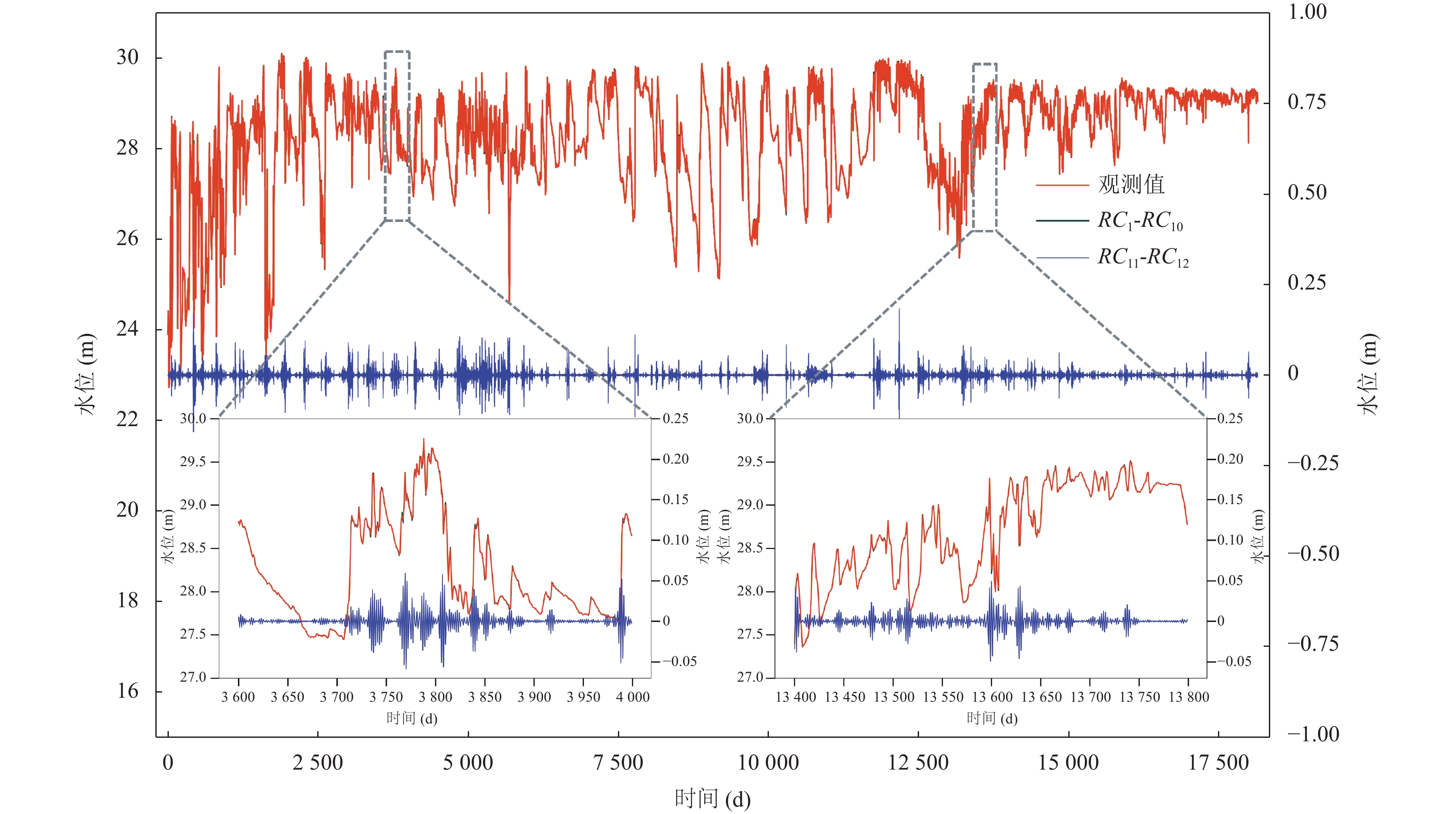
图 6 SSA分解重组后的水位序列

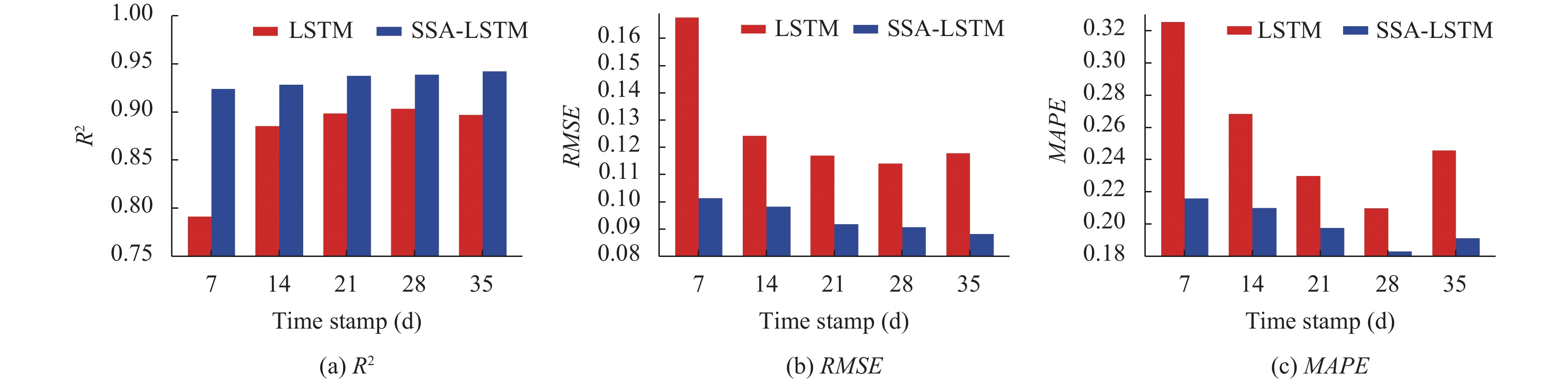
本节评估了LSTM、SSA-LSTM模型在不同时间步长(7、14、21、28、35)下的单步预测性能, 通过 ${R^2}$ 、RMSE、MAPE这3种统计评价指标探究两种模型在不同时间步长下的表现, 模型表现如表1所示. 考虑LSTM模型参数和超参数不同可能影响模型的训练过程和性能, 对LSTM、SSA-LSTM两种模型中的LSTM结构设置相同的参数, 参数的选择如表2所示. 如图7(a)所示, SSA-LSTM的 ${R^2}$ 系数明显优于LSTM模型, 说明SSA-LSTM模型在水位序列预测中具有更好的性能, 这可能是因为SSA过滤了水位时间序列中的一部分不含任何信息的噪声分量, 而保留了趋势和周期分量, 从而使得模型在避免噪声干扰的同时获得了更多的特征. 当时间步长为28天时的时候, LSTM模型表现出了最差的性能, ${R^2}$ 系数为0.791. 随着时间步长的增加, LSTM模型的 ${R^2}$ 系数首先增加, 然后下降. 这可能是因为LSTM具有提取时间序列长期特征的能力, 但随着时间步长的增加, 模型获得了冗余信息. 同时表明LSTM提取长期特征的能力并不能抵消冗余信息造成的影响. SSA-LSTM模型在时间步长为7天时, ${R^2}$ 系数为0.923, 随着时间步长的增加, SSA-LSTM模型的 ${R^2}$ 系数逐步增加, 当时间步长为35天时, SSA-LSTM模型的 ${R^2}$ 系数达到最高, 为0.942, 该时间步长下两种模型在测试集上的预测曲线如图7所示. 这可以解释为SSA-LSTM模型通过将原始序列分解成噪声、趋势和波动分量, 可以较好地过滤长序列中的冗余信息, 并提取出水位序列中更多的特征. 图8(b)和图8(c)展示了LSTM、SSA-LSTM模型的RMSE值和MAPE值在不同时间步长下的变化趋势, 与 ${R^2}$ 系数基本一致. 值得一提的是, SSA-LSTM模型在时间步长为21天和28天时的RMSE、MAPE出现了相反的结果, 即RMSE减小, MAPE增加, 这可能是因为受到了异常值的影响. 基于以上分析, LSTM模型在较小时间步长时可以提取长序列中的额外信息, 从而提升模型的表现, 但过长的时间步长会产生冗余信息, LSTM提取长期特征的能力并不能抵消冗余信息造成的影响. 相反, SSA-LSTM模型的表现随着时间步长的增加而提升, 这说明SSA-LSTM模型可以过滤掉长序列中的无用信息, 如噪声等, 同时可以提取出额外的特征信息, 如周期信息、趋势信息等. SSA-LSTM模型在各个时间步长上的性能均优于LSTM模型.

表 1(Table 1)

表 1 LSTM、SSA-LSTM模型在不同时间步长下的 ${R^2}$ 、RMSE、MAPE对比 评价指标 模型 时间步长 7 14 21 28 35 ${R^2}$ LSTM 0.791 0.885 0.898 0.903 0.896 SSA-LSTM 0.923 0.928 0.937 0.938 0.942 RMSE LSTM 0.167 0.124 0.116 0.114 0.117 SSA-LSTM 0.101 0.098 0.091 0.090 0.088 MAPE (%) LSTM 0.325 0.268 0.230 0.209 0.245 SSA-LSTM 0.216 0.207 0.197 0.183 0.191

表 1 LSTM、SSA-LSTM模型在不同时间步长下的 ${R^2}$ 、RMSE、MAPE对比

表 2(Table 2)

表 2 LSTM结构及参数选择 参数 值 参数 值 Optimizer Adam Hidden layers 16 Learning rate 0.001 Activation function ReLU Loss function MSE Epochs 700

表 2 LSTM结构及参数选择

本文提出一种基于奇异谱分析分解—长短期记忆神经网络的组合模型(SSA-LSTM)的短期水位时间序列预测方法, SSA方法(奇异谱分析)将观测到的时间序列分解为周期、趋势和噪声分量, 接着利用LSTM(长短期记忆)方法对去噪后的序列进行预测, 得到最终的预测值. 这种组合模型具有以下优点: 1)有效解决水文要素测量值被水利现场设施环境、人类活动等因素影响所导致的非平稳性; 2)有效解决水文要素关系复杂导致的有效特征提取困难, 水位预测精度低等问题. 为了验证SSA-LSTM模型的性能, 将该模型应用于涡阳闸闸上水位的预测任务, 并与LSTM模型进行了比较. 实验结果证明, SSA-LSTM模型可以提取出序列中的周期、趋势、噪声分量, 具有良好的非线性序列预测能力, 克服了LSTM模型容易受到长序列中冗余信息影响的缺点. 随着时间步长的增加, SSA-LSTM模型具有更好的预测性能. 在各个时间步长下, SSA-LSTM模型的可靠性和预测准确度均明显优于LSTM模型. SSA-LSTM模型的高可靠和低误差特点可以为城市防洪、灌溉、供水等水利措施的合理调度提供决策依据.

图 7

Fig. 7

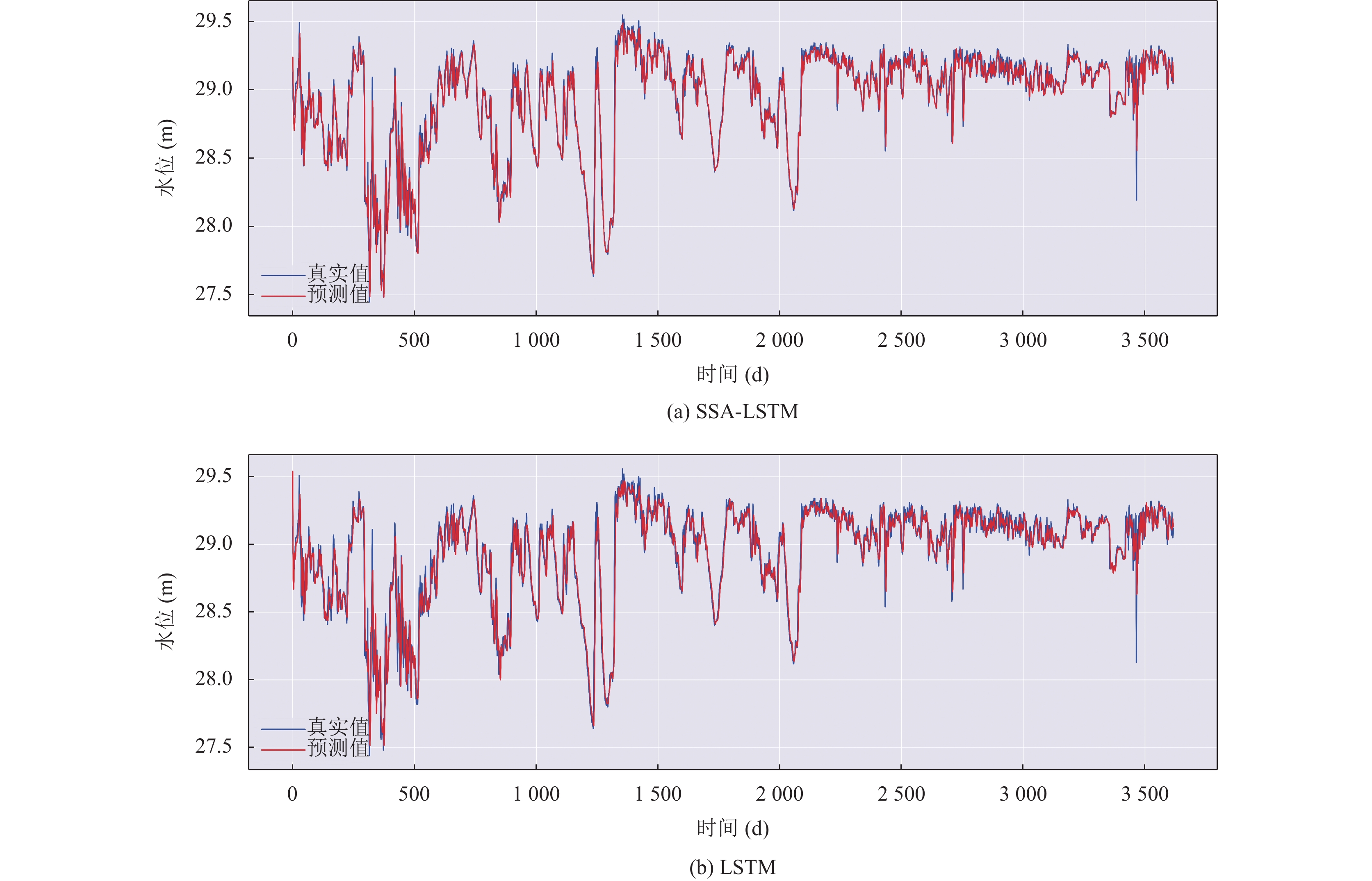
图 7 时间步长为35的条件下, SSA-LSTM与LSTM模型在测试集上的预测曲线

图 8

Fig. 8

图 8 LSTM、SSA-LSTM在不同时间步长下的指标对比