作为比特币^[1]的核心技术, 区块链是一种去信任化的分布式新型计算范式^[2], 巧妙地融合了P2P网络、哈希运算、非对称加密等多种相关技术. 其核心优势是去中心化, 能够摆脱对单一可信第三方的依赖, 在无需相互信任的分布式网络中实现去中心化信用交易与协作^[3]. 区块链技术凭借其去中心化、可追溯、防篡改等特性, 在数字支付、金融服务、风险管理、物联网等领域拥有广阔的应用前景^[4]. 但区块链账本固有的单链式结构也带来了可扩展性差、吞吐量低、高延迟、高能耗等缺陷^[5], 与主流支付工具存在巨大的性能差异^[6].

为了解决区块链的性能瓶颈问题, 基于有效无环图(directed acyclic graph, DAG)的分布式账本技术被提出, 这种技术将区块链固有的单链式结构转变为有向无环图的形态, 使账本具有高并发的特性^[7]. 近年来诞生了许多代表性的DAG区块链系统^[8], 如文献[9]介绍了Byteball共识算法的原理, 在Byteball中, 引入12个见证人, 见证人用来记录存储单元. 当用户发起交易时, 由一个顶端单元开始通过选择算法选择一个最优父单元, 直到构成一条到达创世单元的最佳路径称为主链. DAG的每个顶端单元直接或者间接到达主链, 把主链编号为MCI, 创世单元的MCI设置为0, 向后逐渐加1, 主链上最先直接或者间接单元的MCI是不在主链上的单元的MCI. 在发生双重支付时, MCI小的存储单元被认为是有效的. 但是当存储单元数量比较少时, 可能会发生双花问题, 因为存储单元太少, 使一些交易长期得不到确认, 此时攻击者可以发起交易, 制造另一条链, 并且让其成为主链; 而且交易确认的时间也是不确定的, 导致实时性不行. 文献[10]提出IOTA共识机制, 是针对物联网场景的应用, 物联网中的设备可以作为区块链的参与节点. 在IOTA中, 一个区块存放一个交易, 每个新加入的交易将会被放在后面指向之前的两个交易. 相较于链式区块链, IOTA结构具有较好的可扩展性, 同时能够处理大量的交易信息, 减少了共识的时间. 但是由于IOTA的交易验证是通过计算累积权重的方式, 在交易量比较少时, 容易出现交易长时间得不到确认, 导致交易时延太长. 在文献[11]提出的Conflux系统是对比特币系统的扩展, 通过使用DAG提升比特币系统的扩展性. Conflux采用主链共识机制, 主链共识算法采用GHOST协议, 通过挑选出子树最多的交易来延长主链, 也是主链延迟选择策略, 由于依然使用工作量证明机制算法(proof of work, PoW), Conflux的劣势是耗时耗资源, 并且主链延迟选择会导致主链不一致. 文献[12]提出了哈希图(hashgraph)共识算法. 哈希图主要通过八卦协议和虚拟投票来达成分布式节点的共识. 八卦协议让分布式节点每过一个时间间隔进行点对点的区块信息交换, 目的是让每一个节点知道每一个区块. 区块的共识通过虚拟投票来实现, 也就是节点基于本地账本来执行一种基于图论连通性的算法, 达成特定连通性条件的区块即达成共识. 哈希图的不足之处在于其容易受到女巫攻击的影响, 攻击者可以以极低的成本创建大量区块来使非法交易达成共识并且交易时延太长. Nano (原名Raiblocks)^[13]也是一种典型的DAG区块链系统, Nano系统采用了一个账户一条链的平行链结构, 每个用户只需要记录自己的交易, 从而实现交易的并行执行和秒级确认速度. DAG区块链结构最大的弊端来自于异步通信造成的全局无序状态^[14]. 因此对于DAG式区块链中共识算法的研究尤为重要, 目前Nano区块链采用的是一种被称为开放代表投票(ORV)的共识机制, 这实际上是基于委托权益证明(DPOS)的一种变体.

DPOS共识机制^[15]通过全网节点进行投票产生代理节点, 由代理节点代表普通节点进行验证和维护账本, 从而降低交易时延及网络能耗. 但DPOS在实际应用过程中还存在权益分配不合理等问题, 因此相关研究人员对基于传统区块链的DPOS共识机制做了很多改进^[16-18]. DAG式区块链作为一种新型区块链结构, 在共识机制的设定方面与传统区块链有许多不同, 但关于此方面的研究还很不成熟. Nano系统^[13]采用的ORV共识机制便存在资源和节点权益分配不合理的问题. 本文针对上述问题提出了一种基于DPOS改进的DAG式区块链共识算法, 称为OERV (open election representative voting). 基于Nano区块链的平行DAG链式结构, 建立了一种新的代表选举模型, 并对共识流程进行优化设计, 旨在优化节点资源和权益的分配, 提高系统稳定性和安全性.

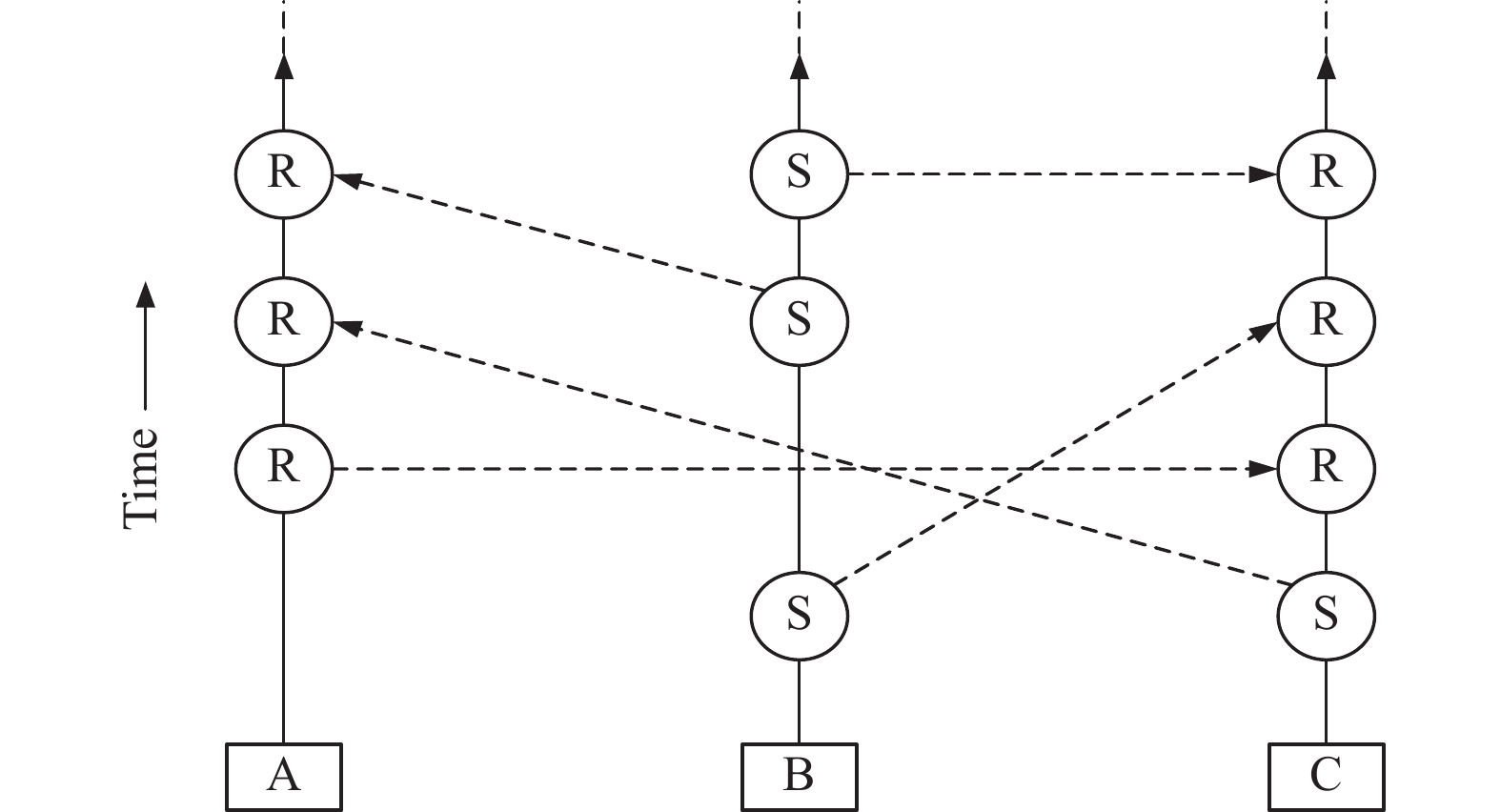
1 Nano设计概述 1.1 Block-lattice区块点阵结构

Nano使用了一种基于有向无环图(DAG)的并行区块链结构, 称为区块点阵(block-lattice), 如图1所示, S代表发送交易, R代表接收交易. 在block-lattice中, 每个节点(账户)都有自己的链, 节点自行决定是否将有效交易添加到其本地分类账中, 每个节点都持有所有链的副本.

点阵结构是指每个账户都有自己的一条独立区块链, 每个区块就一笔交易, 点指的是每个区块, 区块可以是发送交易或者接收交易. 所以每次转账都会生成两个新的区块, 在交易时, 在发送方账户与接受方账户的链结构中均通过PoW的方式各生成一个新区块. Block-lattice结构允许异步传输操作, 因为单个交易不必与其他账户交易一起包含在块中. Block-lattice将共享的全局账本(如比特币)转换为一组非共享的异步账本, 从而加快交易时间. 在Nano中有4种不同类型的块, send用于发送交易, receive用于接收交易, change为改变账户的代表, open (receive)用于创建账户, 新账户的第一个块必须是open (receive)块.

在block-lattice中, 需要两个交易来完成价值转移, 而不是通过单个交易来转移价值. 如图1所示, 发送者生成发送交易将从发送账户的余额中扣除资金, 而接收者也需要生成匹配的接收交易将资金添加到接收账户的余额中. 为了完成交易, 节点会计算一个区块并将其发送给一组对等点, 这些对等点又会将其发送给其他对等点. 当区块通过网络传播时, 代表们将对其进行投票. 一旦达到了一定的投票门槛, 交易就被认为是确定的.

图2所示, 账户A拥有第一个接收区块, 然后发送交易给账户C, 账户C接收交易, 将信息保存在本地自己区块链并且对账户A回复验证, 账户A也会将交易过程保存在本地区块链, 账户B对账户A和账户C交易过程进行备份存储.

当一个发送块被网络验证后, 交易被挂起为未结算状态并且不可逆转, 即交易一旦发起便不可撤销, 私钥一旦丢失就无法对账户进行任何操作. 接收者可以随时将资金加入自己的账户, 只需要生成相应的接收块并通过网络进行验证, 验证通过后交易被标记为结算状态.

1.2 ORV公开代表投票共识机制

Nano使用公开代表投票(ORV)作为其共识机制, 这实际上是一种委托权益证明(DPoS)机制的变体. 在ORV中, 运行全节点的任何人都可以成为一个代表, 并从其他用户那里获得投票权重. 任何账户在任何交易中都可以随时自由选择(包括它自己)或更改代表, 该代表将代表它进行交易投票.

这些代表账户配置在保持在线的节点上, 并对他们在网络上看到的交易的有效性进行投票, 他们的投票权重是委托给他们的账户余额的总和. 如果代表账户下线, 其投票权重将不用于帮助保护网络, 直至他们上线.

ORV中有两种代表: 主要代表(principal representative, PR)和非主要代表. 要成为主要代表(PR), 该代表账户必须至少有0.1%的在线投票权重委托给它. 但两种代表类型之间唯一的区别是只有PR发出的投票会被其他节点转播, 以减少网络的带宽消耗, 帮助网络更快地达成共识.

这些投票在节点之间共享和转播, 它们会被统计并与可用的在线投票权重进行比较. 每个节点(无论是否是代表)在看到足够多的代表投票超过其本地投票权重阈值后(默认情况下大于在线投票权重的50%), 认为该交易已被确认, 然后独立地将该笔交易巩固为不可逆转. 当网络上的交易之间发生冲突时, 代表们会将他们的投票集中到该冲突交易上, 从而快速解决分叉问题.

由于网络上没有交易费用, ORV还使用了工作证明机制来防止垃圾邮件攻击. 所有4种交易类型都有一个必须正确计算的PoW工作字段, 大约需要5 s来完成, 1 μs来验证. 这使正常进行交易的用户只需要少量的计算能力, 但恶意行为者需要投入大量计算能力才能进行攻击.

1.3 ORV存在的问题

虽然ORV机制对DAG结构区块链的共识算法效率有很大的改善, 但还是存在节点资源和权益分配不均衡等问题. 首先ORV机制中对主要代表节点的选举方式过于单一, 即每个投票人将自己的一票投给最满意的候选者, 得票多者取胜. 这种方法不易充分表达民意, 如果一个节点获取或控制了绝大多数节点的投票, 则可能选出超级节点, 没有考虑到全体选民的选举意愿. 其次ORV机制中主要代表拥有决定性投票资格且无法进行监督, 对区块链的去中心化性质造成了很大的威胁. 最后ORV机制是一种异步的最终一致性共识算法, 为了让投票尽快在网络上进行传播, 采用了gossip流言传播方式, 对所有不确定性投票进行无差别转播, 由于网络带宽等影响会导致每个节点收到的信息差异过大, 网络很难保持正确同步, 造成大量通信开销的同时带来了共识安全隐患.

2 OERV公开选举代表投票共识机制

针对上述ORV共识存在的问题, 本文设计了一种代表选举模型对ORV共识机制加以改进, 提出了OERV公开选举代表投票共识机制. OERV主要改进的地方有:

1) 优化代表选举规则, 建立了一种新的代表选举模型. 使用borda计数法选举主要节点, borda计数法是一种排序投票法. 每个选民在选票上对所有候选人进行排序, 每个候选人按照不同的排序名次获得相应的波达数或积分, 积分最高的候选人赢得选举. 同简单多数规则相比, borda计数法较不容易选出有争议的人士, 但投票结果较容易受策略选举的影响, 有利于充分表达民意.

2) 制定新的共识规则, 降低主要代表节点的影响力, 以二次投票的方式保证了普通代表节点对最终投票结果的参与度, 大大增加了网络的去中心化程度.

重新设计共识流程, 普通节点不需要广播任何不确定性投票, 减少不必要的资源消耗, 增强网络账本一致性.

2.1 代表选举模型

(1) 节点类型

本文代表选举模型涉及3类节点角色: 普通节点、全节点、代表节点、主要代表节点.

普通节点是系统中占比最大的节点类型, 不需要维护其他节点账本, 不参与代表选举, 可以在任意交易中随时自由选择或更改代表来代替他们投票, 可以对代表节点进行偏好投票以此选举主要代表节点. 全节点是维护系统正常运行的重要角色, 需要维护所有节点账本, 及时接收代表投票并更新账本, 委托投票权重达到法定代表权重的全节点可以申请成为代表节点. 代表节点包括普通代表节点和主要代表节点, 普通代表节点除了维护全局账本外, 还需要对节点生成的交易块进行有效性验证并投票. 主要代表节点通过加权borda计数法进行排序选举, 其与普通代表节点的区别在于, 共识算法的第一阶段投票只有主要代表节点进行投票.

(2) 代表选举模型

本文设计的代表选举模型分为两个阶段: 代表选举阶段和主要代表选举阶段. 由于代表选举需要消耗一定通信资源, 如果频繁更新代表列表会造成很多不必要的资源浪费, 且少数投票权重委托并不会对选举结果造成影响. 所以本模型规定代表选举阶段间隔周期较长, 但同一代表选举阶段周期中将进行多轮主要代表选举. 可以在减少资源浪费的同时, 保证代表节点间的轮换, 及时降低出错率高的代表节点的影响力, 维护网络的正常运行. 本文设计的代表选举模型结构如图3所示.

1) 代表选举阶段

节点在发起交易时, 需要在区块中指定全节点以委托其代表自己投票, 节点可以在任何交易中随时自由选择或更改代表. 当某一全节点的委托投票权重达到法定代表权重时, 全节点可以申请成为普通代表节点, 参与交易区块的有效性投票, 并以此获得竞选主要代表节点的资格.

2) 主要代表选举阶段

本文将代表节点的投票行为和全体节点的选择意愿纳入主要代表选举机制中, 主要分为3个部分: borda得分计算、borda加权系数计算、有效得分排序.

首先普通节点对所有的代表节点进行偏好投票. 设全网普通节点数共有N个, 全节点均不参与偏好投票. 为了防范所有的主要代表节点都是恶意节点的极端情况, 代表节点数RN需大于等于主要节点数PN的两倍. 本文暂定RN=2PN, 则设2PN个代表节点为 $ {x}_{1}, {x}_{2}, \cdots, {x}_{2PN} $ , 如果一个普通节点的偏好次序为:

$ {x_1} \gt {x_2} \gt \cdots \gt {x_{2PN}} $

(1)

则代表节点 $ {x}_{1}, {x}_{2}, \cdots, {x}_{2PN} $ 的得分依次为:

$ 2PN, 2PN - 1, \cdots, 1 $

(2)

对第 $ k $ 个普通节点的偏好, 可以记为:

$ {p}_{ij}^{k}=\left\{ {\begin{array}{c}1, 第k个普通节点的偏好为{x}_{i}\gt {x}_{j}\\ 0\text{, }第k个普通节点的偏好为{x}_{j}\gt {x}_{i}\end{array} } \right.$

(3)

若 $ i = j $ , 则取 $ p_{ij}^k = 1 $ , 创建第 $ k $ 个普通节点的偏好矩阵, 如式(4)所示:

$ {r}_{k}=\left[\begin{array}{cccc}{p}_{11}^{k}& {p}_{12}^{k}& \cdots & {p}_{1n}^{k}\\ {p}_{21}^{k}& {p}_{22}^{k}& \cdots & {p}_{2n}^{k}\\ \vdots & \vdots & \ddots & \vdots \\ {p}_{n1}^{k}& {p}_{n2}^{k}& \cdots & {p}_{nn}^{k}\end{array}\right],\; n=2PN $

(4)

则第 $ k $ 个普通节点给第 $ i $ 个代表节点的borda评分为: $ {p}_{i}^{k}={\displaystyle \sum _{j=1}^{n}{p}_{ij}^{k}}, n=2PN $ , 由此构造所有普通节点对所有代表节点的评分矩阵, 如式(5)所示:

$ B=\left[\begin{array}{cccc}{p}_{1}^{1}& {p}_{1}^{2}& \cdots & {p}_{1}^{N}\\ {p}_{2}^{1}& {p}_{2}^{2}& \cdots & {p}_{2}^{N}\\ \vdots & \vdots & \ddots & \vdots \\ {p}_{n}^{1}& {p}_{n}^{2}& \cdots & {p}_{n}^{N}\end{array}\right],\; n=2PN $

(5)

则所有普通节点对第 $ i $ 个代表节点的累计borda评分为式(6):

$ {p}_{i}={\displaystyle \sum _{k=1}^{n}{p}_{i}^{k}},\; n=N $

(6)

然后根据代表节点的投票行为计算borda加权系数, 目的在于提高频繁出现错误投票行为的代表节点成为主要代表节点的难度. 如果代表节点因为某种原因导致投错票/没有投票时, 计数器将会将该行为对应的失误次数(m)加一, 用以计算该节点的borda加权系数, 如果失误次数(m)超过网络允许的最大失误次数(M)将停止计数, 该代表节点会在下一轮被淘汰. 具体计算如式(7):

$ \begin{array}{l}{\rho }_{i}=1-{\displaystyle \sum _{e=1}^{E}\left(\frac{{m}_{ie}}{{M}_{e}} \times{\theta }_{e}\right)}, \\ ({m}_{ie}\leqslant {M}_{e}, 1\leqslant i\leqslant 2PN, 1\leqslant e\leqslant E\text{, }0\leqslant {\theta }_{e}\leqslant 1)\end{array} $

(7)

其中, 变量含义如表1所示.

由式(7)可知, 代表节点i的错误投票行为次数m越多, 其borda加权系数越小, 反之其borda加权系数越趋近于100%.

本阶段最后将通过式(8)计算每个代表节点的最终有效得分, 根据有效得分对代表节点进行排序并确定主要代表节点:

$ {V}_{i}={\rho }_{i}{p}_{i}={\rho }_{i}{\displaystyle \sum _{k=1}^{n}{p}_{i}^{k}},\; (n=N,\; 0\leqslant {\rho }_{i}\leqslant 1) $

(8)

其中, $\; {\rho _i} $ 为节点i的borda加权系数, $ {p_i} $ 为所有普通节点对第 $ i $ 个代表节点的累计borda评分. 由式(8)可知, 节点出现错误投票行为次数越多, $ \;{\rho _i} $ 越小, borda评分的有效占比就越小; 反之最终有效得分越趋近实际borda评分.

3) 代表选举流程

本文定义一个普通代表选举周期为RT, 一个主要代表选取周期为PT. 一个主要代表的选取会经历4个环节: 委托投票权重计算、borda得分计算、borda加权系数计算、有效得分排序. 委托投票权重是代表选取模型最基础的部分, 全节点需得到一定规格的委托投票权重才能申请成为代表节点; 然后所有节点对代表节点进行偏好投票, 以支持这些代表节点竞选主要代表节点, 偏好投票数据将通过borda计数法进行处理并计算得分; borda加权系数计算可以制约代表节点的错误/怠惰投票行为, 提高出错率高的代表节点成为主要代表节点的难度: 本模型最后会根据代表节点的borda得分和borda加权系数计算其有效得分并排序, 排序靠前的代表节点将成为主要代表节点.

具体选举过程算法描述如算法1所示.

算法1. selectRepresentative()
Input: N (number of ordinary nodes), RN (number of representative nodes), PN (number of principal representatives nodes), S (set of ordinary nodes)
Output: S1 (set of representative nodes), S2 (set of principal representatives nodes)
1) selectS1(S, r)
2)　pvSetr ← proxyVoting(S, r) //统计第r轮委托投票权重 3)　For pvSetr i: 4)　　pvNi = addpv(pvSetr) //计算节点i在第r轮的委托投票权重 5)　　If pvNi ≥ Legalpv //判断节点i是否满足代表节点条件
6)　　　　 S1 ← i
7)　End For
8) selectS2(S, S1, r)
9)　For x
10)　　bordaVoteSetr.x ← bordaVote(S, S1, r.x) //开始第r–x轮borda投票 11)　　For bordaVoteSetr.x j: 12)　　　bvSjr = bordacount(bordaVoteScorer.x)//borda计数法计算节点j的borda得分 13)　　End For 14)　　ErrorNj ← ErrorNje ← Errorcounting(e, j) //统计节点j的错误投票行为 15)　　For ErrorNj j 16)　　　　 $\rho _j^{{{r.x}}}$ ← ErrorNj //计算节点j在第r–x轮的borda加权系数 17)　　End For 18)　　For Validbordar.x(bvSj, $ \rho _j^{{{r.x}}} $ ) j 19)　　　vScorejr.x ← Validbordar.x(bvSj, $ {\rho _j} $ ) //计算节点j在第r–x轮的有效borda得分 20)　　　vScoreSetr.x(vScorejr.x) 21)　　End For 22)　　vsSortr.x(vScoreSetr.x, S1) //根据有效得分对代表节点(S1)进行排序
23)　　 S2 ← vsSortr.x //根据有效得分排名选取第r–x轮的主要代表节点
24)　　End For

2.2 OERV共识过程

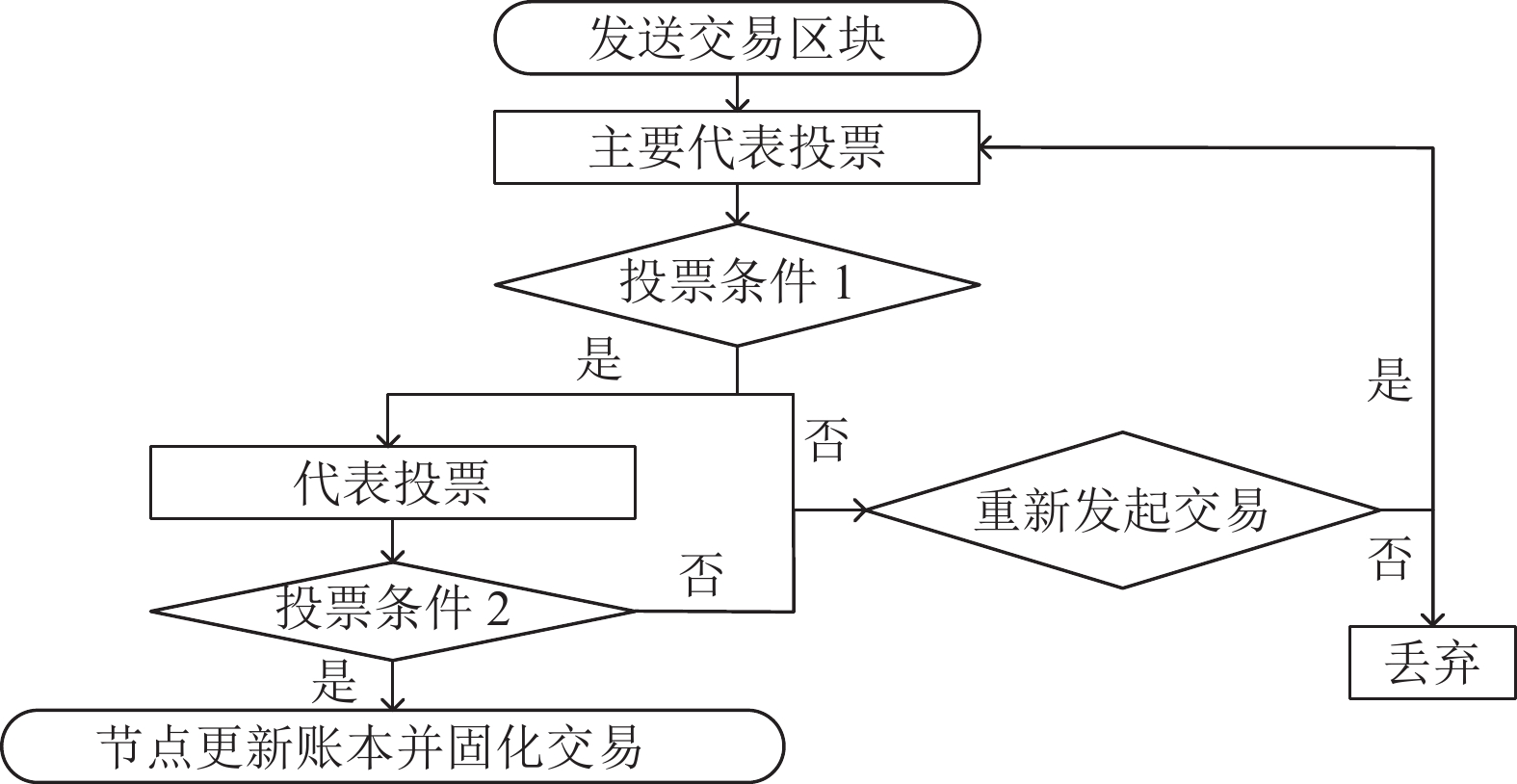
OERV算法的共识过程如图4. 首先根据代表选举模型对节点进行分级, 一个普通代表选举周期为CT (cycle time), 一个主要代表选取周期为PT (principal time). 为了进行交易, 节点需要向所有主要代表发布一个块, 然后主要代表对他们在网络上看到的交易的有效性进行投票, 即投票条件1是主要代表对交易的有效性投票, 并广播给其他所有代表节点(判断为无效的交易会直接丢弃或者重新发起交易区块, 主要代表投票重新投票确认交易区块有效性. 否则所以所有的投票都应该是“确认有效”). 而投票条件2为代表节点(包括主要代表和普通代表)对交易确认上链进行投票, 当委托投票权重超过在线权重阈值(默认情况下大于在线投票权重50%)且达到法定人数(默认情况下大于70%主要代表节点)后, 确定自己的投票并广播给全节点和发起交易的节点. 当全节点和发起交易的节点收到达到法定人数(默认情况下大于50%代表节点)的在线投票数(包括主要代表和普通代表)后, 更新本地账本, 并固化该交易为不可逆转.

OERV共识机制优化了投票和节点传播协议, 在主要代表进行一次投票后, 所有的代表节点需进行第2次投票. 由于代表节点数量很少, 主要代表节点更少, 所以这个过程耗费的资源也很少, 达成投票共识的速率不会低于原ORV共识机制. 此外普通节点不应该转播任何不确定的投票, 会造成不必要的资源浪费, 也会放大交易异步性带来的账本同步问题. 在OERV共识机制中, 投票还未进行初步确认时, 只在代表节点中进行传播, 普通节点只需对代表节点的投票结果进行再次确认, 在减少资源浪费的同时可以提高共识效率和账本一致性.

3 模型分析及实验

由于OERV共识机制采用的是Nano网络的底层DAG数据结构: block-lattice. 每个账户只需记录和维护自己的交易账本, 因此所有的交易都可以并行执行. 代表选举的第1阶段数据来源于节点的日常交易块, 不需要额外投票并采集, 第2阶段除了普通节点的投票, 还参考了代表节点的验证投票行为, 增强了普通节点出现怠惰投票时系统对代表节点的监督和制约. 共识流程的两次投票验证过程只在代表节点之间进行, 普通节点只需对已经进行初步确认的二次投票结果进行验证, 在减少通信开销的同时提高系统效率. OERV共识算法对资源和节点权益进行了合理划分, 交易数据验证简单, 带宽消耗低, 可以达到秒级确认速度. 本次仿真实验采用golang语言编写, 使用go-libp2p库实现了一个小型仿真网络, 并将其部署到阿里云ECS服务器上(10个服务器, 每个服务器分别部署2, 4, 6,…, 20个节点).

3.1 吞吐量测试

区块链技术的最终目标之一是替换传统的基础应用模式, 为了证明其可行性, 吞吐量是衡量区块链并发能力的硬性指标之一. 吞吐量(transactions per second, TPS)代表了区块链每秒能处理的交易数量, 可以很好地评估区块链网络的性能.

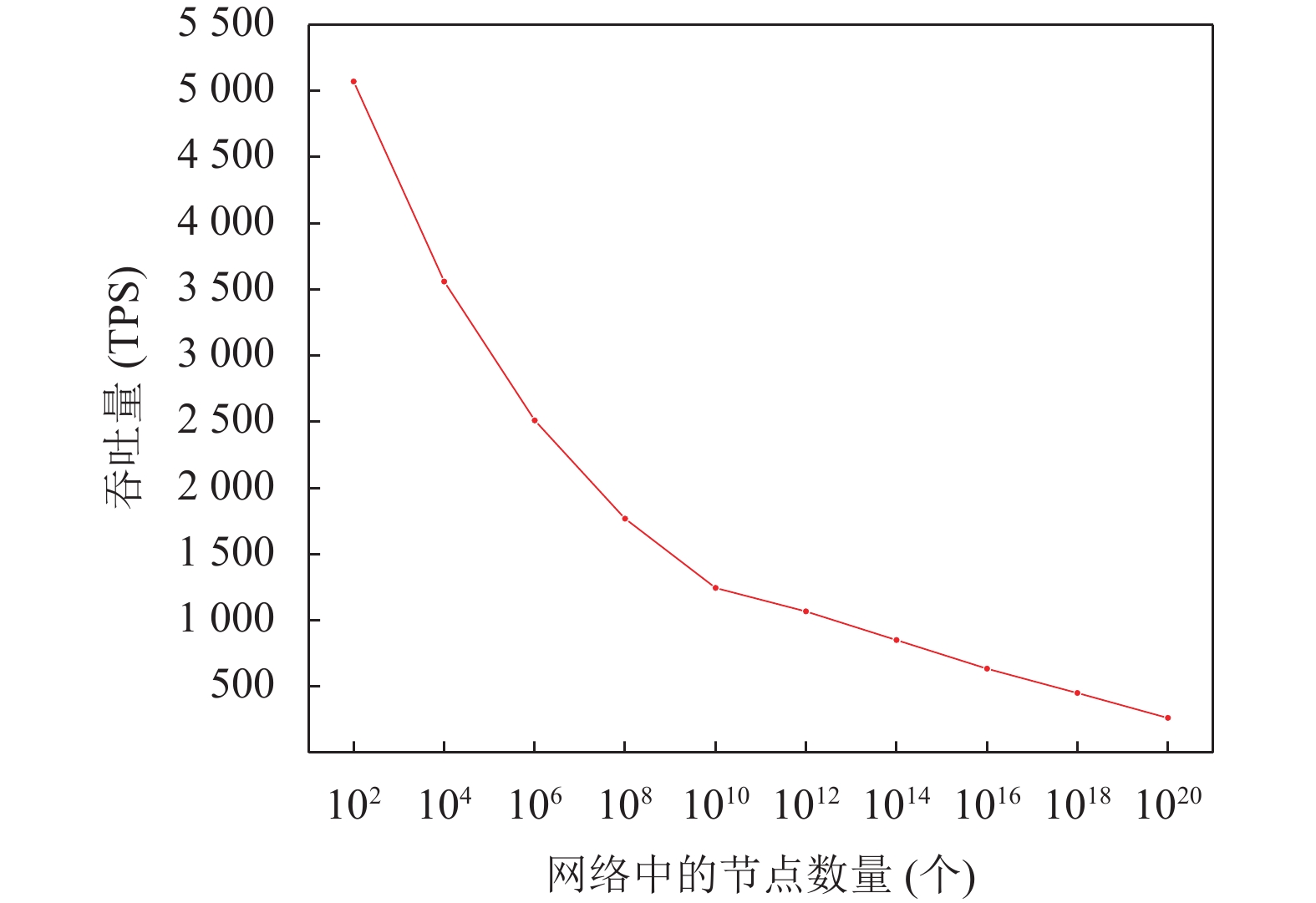
从图5可以看出, 随着每个ECS服务器上部署的节点数的增加, 吞吐量会由于硬件限制而下降, 但每个账户的交易块发送都是异步的, 不需要像传统区块链一样等待矿工打包. 由于block-lattice结构中每个交易块都非常小, 验证和确认时间非常短, 当每个ECS服务器上部署节点数少于4个时, 其吞吐量接近3 000 TPS. 但是在实际环境中每台计算机应该只部署一个节点, 所以吞吐量会更高(Nano网络声称其TPS理论上可以达到7 000 TPS).

3.2 时延测试

区块链中的时延指的是从创建交易到网络首次确认该交易被接收所花费的时间. 由于在OERV中交易时延是瞬时的, 所以本节只考虑一致性时延即共识时延. 本文中的共识时延指的是区块从被主要代表接收后到普通节点对该交易进行固化的时间间隔. 共识时延越低, 区块就能更快被固化为不可更改的状态, 便能减少出现网络拥堵和账本双花的可能性.

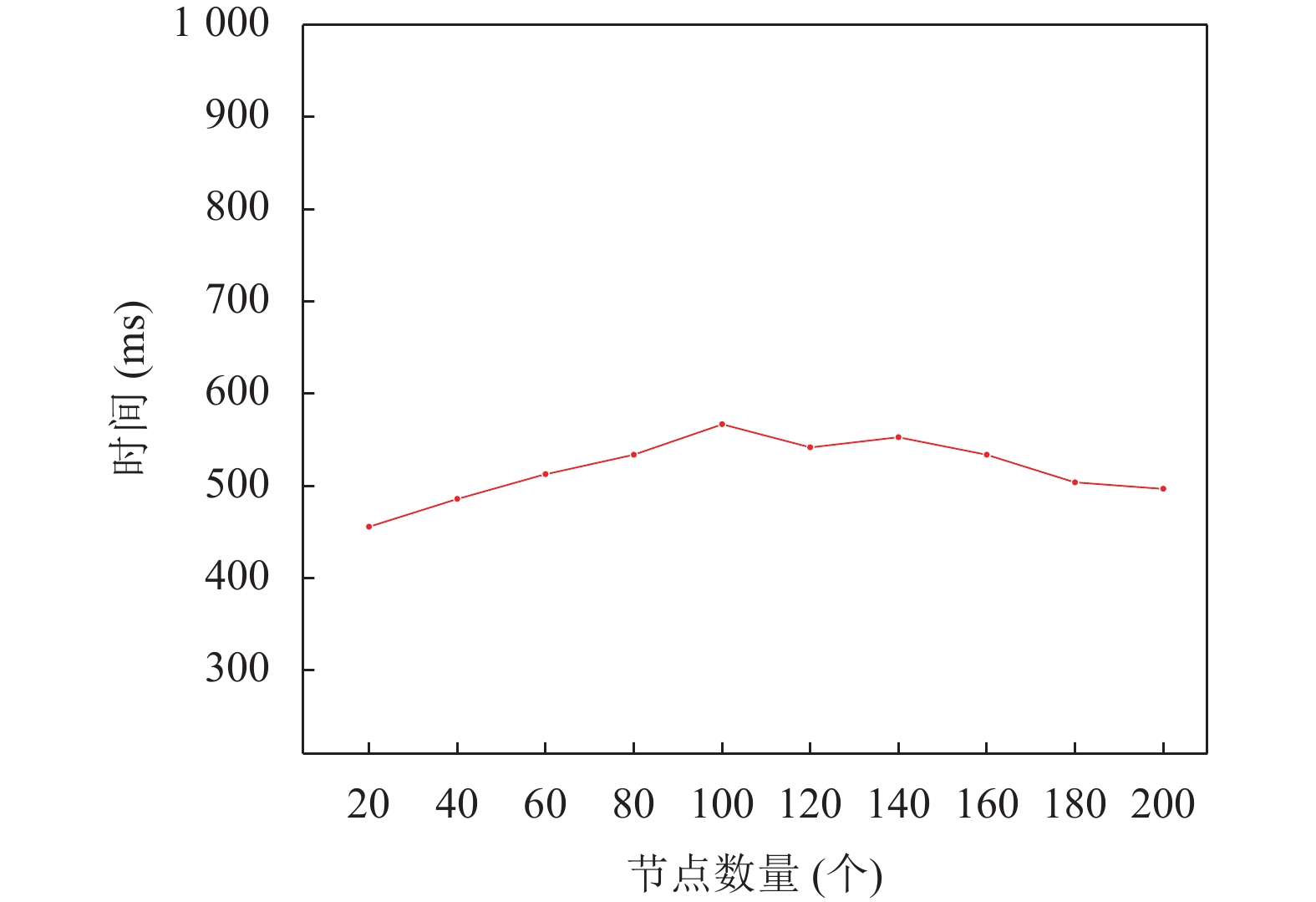
从图6可以看出, 随着节点的数量从20增加到200, 一致性时延持续增加, 但总体能控制在400–600 ms之间. 交易区块能够在秒级时间间隔内被固化.

4 结论与展望

区块链在许多行业中具有广泛的应用前景. 但传统的单链式结构区块链存在吞吐量瓶颈问题. 为解决其性能瓶颈, 一种基于有向无环图结构的新型账本技术被提出, 但目前基于DAG型区块链系统的共识机制并不成熟. 本文针对典型DAG型区块链系统Nano网络的OERV共识机制存在的安全性问题进行改进, 提出了一种基于代表选举模型的公开选举代表投票共识机制, 即OERV. 本模型将主要代表节点的权益进行合理分配, 提高了网络安全性. 实验结果表明, OERV算法性能优于传统链式区块链, 能够在不牺牲系统效率的同时增强系统的稳定性和安全性, 对于推动DAG型区块链共识机制的研究有着重要的现实意义.