随着多媒体技术的发展和移动互联网技术的普及, 作为重要的数字化信息载体, 数字图像被广泛地应用于各个领域中. 然而, 在当前开放的网络环境中, 数字图像所面临潜在的诸如监听、篡改、盗用及伪造等安全风险也不容小觑. 为有效保护敏感图像数据的安全, 数字图像加密技术孕育而生, 并已然成为信息安全领域的研究重点之一.

混沌信号所具有的长期不可预测性和其对初始状态的极度敏感性使得混沌系统在安全通信领域得到迅速的发展^[1]. 迄今为止, 通过将混沌理论与神经网络^[2]、量子计算^[3]、压缩感知^{[4, 5]}和元胞自动机^[6]等技术相结合, 提出了许多高安全性且视觉上无语义特征的图像加密算法. 此外, 随着研究的深入, 一些科研人员有针对性地对遥感、光学以及医学领域中数字图像的特征进行分析, 进而提出相应的隐私数据保密技术^[7-9]. 例如在文献[9]中, Jeevitha等结合二维多层离散小波分解和边缘图设计出适用于MRI (magnetic resonance imaging)图像的加密算法. 然而, 前面所提及到的数据加密方案均存在一个共同的缺陷, 即最终生成的密文图像具有统计类噪声特性. 特别是近年来随着深度学习技术的不断创新和突破, 基于数据驱动的深度人工神经网络模型可以智能化地对公用信道中传输的无视觉意义的密文数据进行解密分析、恶意攻击以及非法拦截等.

为了对密文图像的外观进行保护, Bao等在文献[10]中介绍了一种先加密后嵌入的算法框架. 在该方案中, 首先通过现有的加密技术手段完成对明文图像的内容保护. 其次, 再通过提升离散小波变换嵌入方法将具有统计伪随机特性的秘密图像嵌入到可公开获取的载体图像中. 随后, Wang等^[11]和Chai等^[12]分别将并行压缩感知模型和二维压缩感知模型引入到Bao的加密框架中, 以降低不必要的存储资源和传输花销. 然而, 正如在文献[13]中所指出的, 压缩感知模型的本质是线性投影(或线性测量), 因此其不能有效地抵御一系列基于明文分析的安全攻击模型. 不过通过采用明文数据的特征值、哈希值^[14]或者分块计数器模式^[15]来更新测量矩阵的策略恰好可以弥补这一点缺陷. 其他方面, 对于现有的基于变换域嵌入的视觉安全加密算法, 如多分辨率奇异值分解嵌入^[16]、舒尔分解嵌入^[17]和斜变换嵌入^[18], 由于在嵌入阶段中存在截断误差和误差扩散效应, 因此很难得到较好的视觉安全性和重建质量.

针对上述问题, 本文首先提出一新颖的分段混沌映射, 并对其混沌性能进行分析和对比. 其次, 将该分段混沌映射与P张量积压缩感知模型、数字隐写编码方法相结合, 设计出一种新颖的具有视觉安全性的图像加密算法. 该加密算法主要由压缩加密和随机嵌入这两个阶段组成. 首先在第1阶段中, 通过Arnold置乱策略、线性测量和双向扩散对明文图像进行压缩加密, 获得无语义特征的中间秘密图像. 在第2阶段中, 在不扩大载体图像分辨率的情况下, 利用隐写编码嵌入生成最终视觉安全的密文图像.

1 相关知识 1.1 超混沌Qi系统

考虑到Qi等^[19]所提出的四维超混沌系统具有复杂的非线性动力学行为, 且在相空间中, 其运动轨迹的遍历范围广, 因此适用于图像加密领域. 该四维超混沌系统的数学定义如式(1)所示:

$ \left\{ {\begin{array}{*{20}{l}} {\dot x = a(y - x) + y{\textit{z}}{\text{ }}} \\ {\dot y = b(x + y) - x{\textit{z}}{\text{ }}} \\ {\dot {\textit{z}} = - c{\textit{z}} - ew + xy{\text{ }}} \\ {\dot w = - dw + f{\textit{z}} + xy} \end{array}} \right. $

(1)

其中, 符号a, b, c, d, e和f为可调的系统控制参数, 而 $ \left[ {x, {\text{ }}y, {\text{ }}{\textit{z}}, {\text{ }}w} \right] $ 则为该混沌系统的4个输出状态变量, $ \dot{{x}} $ 表示对 $ x $ 执行微分运算. 当 $ a = 50, {\text{ }}b = 24, {\text{ }}c = 13, {\text{ }}d = 8, $ $ e = 33, {\text{ }}f = 30 $ 时, 式(1)中存在两个大于0的李雅普诺夫指数, 表明该非线性动力系统进入超混沌状态. 再将该系统的初始参数分别设为5, 7, 9 和11, 步长设为0.000 1, 则通过四五阶龙格库塔法所得到的混沌吸引子如图1所示.

1.2 P 张量积压缩感知模型

相比于传统的一维压缩感知模型, P张量积压缩感知模型可以在测量矩阵与像素值矩阵的维度不匹配的情况下完成对明文数据的线性压缩^[20]. 将明文图像和正交小波包稀疏基分别记为 $ X \in {\mathbb{R}^{q \times q}} $ 和 $ \Psi \in {\mathbb{R}^{q \times q}} $ , 其中上标 $ q \times q $ 为矩阵维度. 则明文图像的稀疏分解过程可表示为:

$ X = \Psi \times S $

(2)

其中, 矩阵 $ S \in {\mathbb{R}^{q \times q}} $ 表示为明文图像在 $ \Psi $ 域中的稀疏系数矩阵. 则在PTP-CS模型中, 对明文图像X进行压缩的过程可表示为:

$ \begin{split} \\ Y = \Phi _ \triangleright ^P \times X = \left( {\Phi \otimes P} \right) \times X = \left( {\Phi \otimes P} \right) \times \Psi \times S \end{split} $

(3)

其中, 符号 $ _ \triangleright ^P $ 和 $ \otimes $ 分别表示为P张量积和克罗内克积. 假设, $ \Phi \in {\mathbb{R}^{m \times n}} $ , $ P \in {\mathbb{R}^{t \times t}} $ , $ m < n $ , $ t = \left\lfloor {q \times {n^{ - 1}}} \right\rfloor $ , 并将测量矩阵 $ \Phi $ 重写为向量的形式, 即为 $ \Phi = \left[ {{\varphi _1}, {\varphi _2}, \cdots, {\varphi _n}} \right] $ , 则矩阵的P张量积可以写为:

$ \Phi \otimes P = \left( {{\varphi _1}P, \cdots, {\varphi _n}P} \right) = \left( {\begin{array}{*{20}{c}} {{\varphi _{11}}P}& \cdots &{{\varphi _{1n}}P} \\ \vdots & \ddots & \vdots \\ {{\varphi _{m1}}P}& \cdots &{{\varphi _{mn}}P} \end{array}} \right) $

(4)

于是有 $ \Phi \otimes P \in {\mathbb{R}^{(m \times t) \times (n \times t)}} $ , 且 $ Y \in {\mathbb{R}^{\left( {mq \times {n^{ - 1}}} \right) \times q}} $ . 其中, 系数 $ m{n^{ - 1}} $ 和 $ q{n^{ - 1}} $ 分别叫做矩阵的压缩率和放大系数. 在本文所提算法中, 矩阵P设置成维度为2的单位阵, 而矩阵 $ \Phi $ 则由所提出的一维分段混沌映射所构建.

2 所提出的分段混沌映射 2.1 分段混沌映射的定义

本文所提出的具有分式结构的一维分段混沌映射的数学迭代式如式(5)所示. 其中, 符号 $\; \beta \in \left[ { - 0.25, {\text{ 0}}.25} \right] $ 和x分别为该映射的可调参数和输出变量.

$ {x_{i + 1}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{2\cos \left( {\beta {\text{π}} {x_i}} \right)}}{{2x_i^4 + 1}} - {x_i}, {\text{ }}0 \leqslant {x_i} \leqslant 2{\text{ }}} \\ { - \dfrac{{2\cos \left( {\beta {\text{π}} {x_i}} \right)}}{{2x_i^4 + 1}} - {x_i}, {\text{ }} - {\text{2}} \leqslant {x_i} < 0} \end{array}} \right. $

(5)

其中, 分式结构 $\pm {{2\cos (\beta {\text{π}} {x_i})} \mathord{\left/ {\vphantom {{2\cos (\beta \pi {x_i})} {(2x_i^4 + 1)}}} \right. } {(2x_i^4 + 1)}}$ 用于分离相空间中相邻演化轨道的两个点, 且常数“1”用于防止分式无意义. 另外, 相减部分则是将该非线性映射的输出范围限制在区间[−2, 2]内.

2.2 性能分析与对比

分岔图反映非线性动力系统在确定的初始条件下所产生的时间序列的长期演化状态, 其中包括稳定状态、非稳定状态、周期状态和混沌状态^[21]. 接着, 将所提出的分段混沌映射的初始状态 $ {x_0} $ 随机设置成1.2, 绘制出该一维混沌映射的分岔图, 如图2所示. 可以看出, 与经典一维Logistic混沌映射不同, 即其所生成的时间序列经历稳定态→非稳定态→周期态→混沌态等4个不同演化阶段, 本文所设计的非线性映射始终处于混沌状态, 且具有更宽的遍历范围.

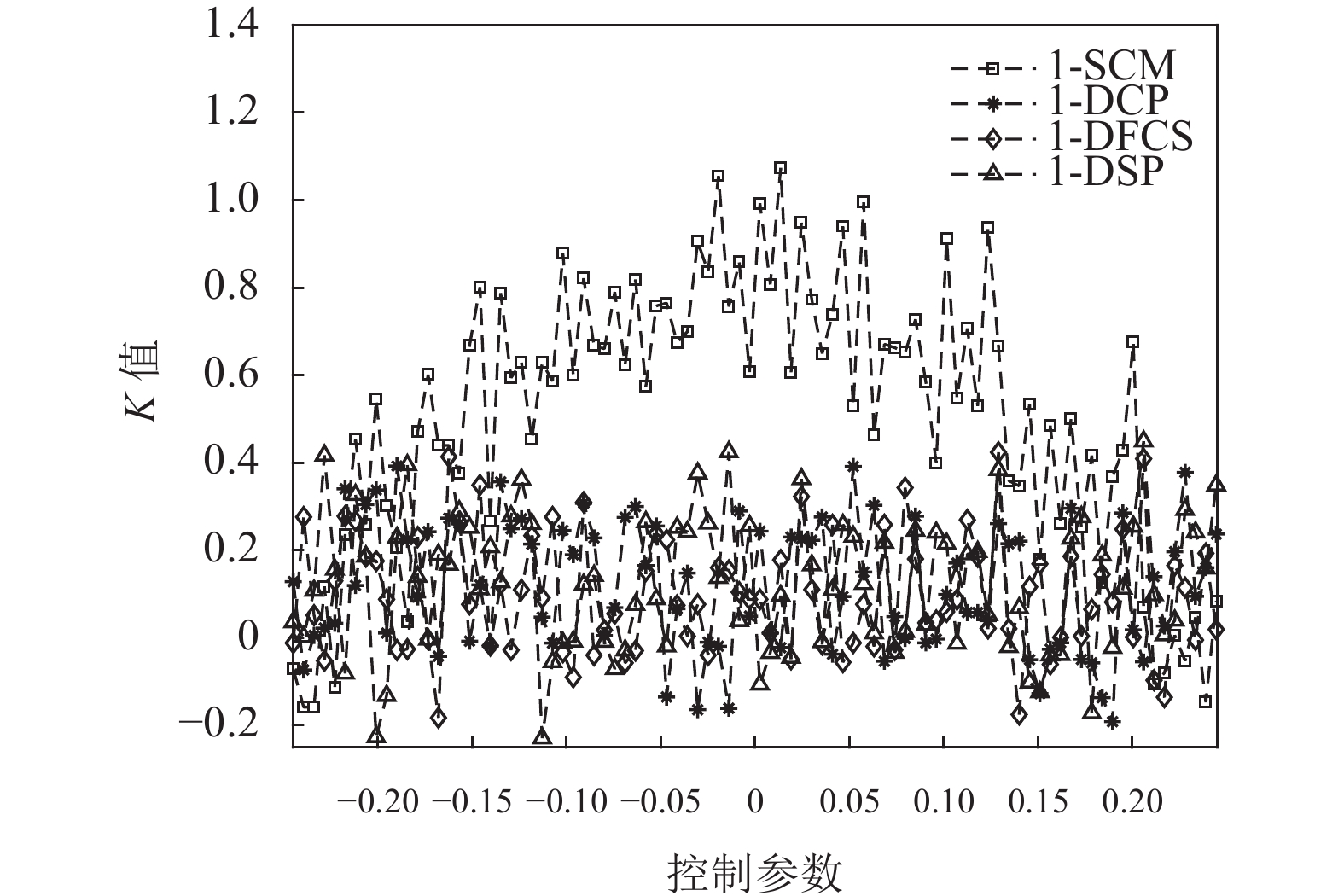
0-1测试是一种用于衡量非线性系统是否存在混沌现象的测试方法^[22]. 与其他评估方法相比, 此方法最大的优点是在测试过程中不需要对时间序列进行相空间重构. 对于混沌序列Q而言, 其0-1测试的数值结果可由式(6)计算得到:

$ \left\{ {\begin{array}{*{20}{l}} K = \mathop {\lim }\limits_{n \to \infty } \ln \left( {\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^n {\left( {{{\left[ {p\left( {i + n} \right) - p\left( i \right)} \right]}^2} + {{\left[ {s\left( {i + n} \right) - s\left( i \right)} \right]}^2}} \right)} } \right) \\ \qquad \times \ln {{\left( n \right)}^{ - 1}} \\ {p\left( n \right) = \displaystyle\sum\limits_{i = 1}^n {Q\left( i \right)\cos \left( {ir} \right){\text{ }}} } \\ {s\left( n \right) = \displaystyle\sum\limits_{i = 1}^n {Q\left( i \right)\sin \left( {ir} \right){\text{ }}} } \end{array}} \right. $

(6)

其中, 变量r和N分别被设置为 $ \left[ {0.25{\text{π}}, 0.8{\text{π}}} \right] $ 和1 000. 接下来, 图3给出了若干个一维混沌映射在控制参数不同取值下所产生的混沌序列的0-1测试结果. 可以清楚地看出, 与文献[23-25]中所介绍的一维非线性映射相比, 本文所提出的映射的K值更大且更宽, 说明所设计的分式结构映射具有良好的混沌性能.

3 视觉安全图像加解密算法

本文所提出的视觉安全图像加密算法主要由基于PTP-CS模型的压缩加密阶段和基于矩阵编码的信息嵌入阶段两部分组成, 其加密流程如图4的上半部分所示. 从图中可以看出, 在密码流的控制下, 明文图像首先经过稀疏化分解、Arnold置乱、压缩和双向异或扩散以生成没有视觉语义特征的秘密图像. 其次, 再在空域­中通过矩阵编码嵌入将秘密图像随机地隐藏到载体图像中, 得到具有视觉安全性的密文图像. 所提加密算法的技术细节如下.

3.1 压缩加密阶段

步骤1. 首先, 对明文图像 $ {P_1} \in {\mathbb{N}^{N \times N}} $ 执行二维离散小波包变换以得到明文稀疏系数矩阵 $ {P_2} \in {\mathbb{R}^{N \times N}} $ , 其次, 为了进一步提升矩阵 $ {P_2} $ 的稀疏度和重建图像的视觉质量, 对其进行阈值处理和二维Arnold置乱操作, 并将该过程所生成的系数矩阵记作 $ {P_3} \in {\mathbb{R}^{N \times N}} $ . 另外, Arnold置乱可以通过式(7)表示, 其中, 坐标 $ \left[ {{i_{n - 1}}, {\text{ }}{j_{n - 1}}} \right] $ 和 $ \left[ {{i_n}, {\text{ }}{j_n}} \right] $ 分别为置乱前后系数矩阵中元素的位置, 序列 $ {X_a} $ 和 $ {X_b} $ 是在密钥的控制下由超混沌Qi系统所产生的伪随机序列, 而符号mod则表示取模操作.

$ \left[ {\begin{array}{*{20}{c}} {{i_n}} \\ {{j_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{X_a}} \\ {{X_b}}&{{X_a} \cdot {X_b} + 1} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{i_{n - 1}}} \\ {{j_{n - 1}}} \end{array}} \right]{\text{ }}\bmod {\text{ }}\left[ {\begin{array}{*{20}{c}} N \\ N \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right] $

(7)

步骤2. 通过加模操作对给定的初始状态和明文图像的平均像素值进行处理. 在运算得到的新初始状态下, 迭代新分段混沌映射若干次以获得混沌序列 $ {X_c} $ . 然后, 再根据式(8)对该序列进行进一步处理. 其中, 常量d为抽样距离.

$ W(i) = 1 - 2{X_c}(di), {\text{ }}i = 1, {\text{ }}2, {\text{ }}3, {\text{ }}\cdots $

(8)

接着对混沌抽样序列W以按列的方式重塑为二维矩阵并执行归一化处理, 得到测量矩阵 $ \Phi $ , 如式(9)所示:

$ \Phi = \sqrt {\frac{4}{N}} \left[ {\begin{array}{*{20}{c}} {{W_1}}&{{W_{{N \mathord{\left/ {\vphantom {N 8}} \right. } 8} + 1}}}& \cdots &{{W_{{{N(N - 2)} \mathord{\left/ {\vphantom {{N(N - 2)} {16 + 1}}} \right. } {16 + 1}}}}} \\ {{W_2}}&{{W_{{N \mathord{\left/ {\vphantom {N 8}} \right. } 8} + 2}}}& \cdots &{{W_{{{N(N - 2)} \mathord{\left/ {\vphantom {{N(N - 2)} {16 + 2}}} \right. } {16 + 2}}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{W_{{N \mathord{\left/ {\vphantom {N 8}} \right. } 8}}}}&{{W_{{N \mathord{\left/ {\vphantom {N 4}} \right. } 4}}}}& \cdots &{{W_{{{{N^2}} \mathord{\left/ {\vphantom {{{N^2}} {16}}} \right. } {16}}}}} \end{array}} \right] $

(9)

将矩阵P设置为 $ \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] $ , 并对矩阵 $ {P_3} $ 执行如式(10)和式(11)所示的操作, 即可得到压缩图像 $ {P_5} $ . 其中, 变量 $ {P_{\max }} $ 和 $ {P_{\min }} $ 分别记为矩阵 $ {P_4} $ 中的极值.

$ {P_4} = \Phi _ \triangleright ^P \times {P_3} = \left( {\Phi \otimes P} \right) \times {P_3} $

(10)

$ {P_5} = \left\lfloor {\left( {{2^8} - 1} \right) \times \left( {{P_4} - {P_{\min }}} \right) \times {{\left( {{P_{\max }} - {P_{\min }}} \right)}^{ - 1}}} \right\rfloor $

(11)

步骤3. 由于文献[13]中指出压缩感知模型的本质是线性映射, 因此不能有效抵抗选择明文攻击, 有必要对压缩图像执行扩散操作以使得明文图像发生细微的差别都将产出存在具有巨大差异且无语义的秘密图像. 首先, 在给定初始状态的情况下, 量化超混沌Qi系统迭代若干次生成的两条混沌序列, 获得整数序列 $ {X_d} $ 和 $ {X_e} $ . 然后通过模拟退火算法对这两条序列进行优化^[26], 具体步骤如下.

(1) 对两条整数序列做差( $ X_{d}-X_{e} $ )以得到目标序列L.

(2) 如果 $ {L_i} \geqslant 0 $ , 则最优解为 $ {D_i} = {L_i} $ . 否则, 计算出阈值 $ {P_c} = \exp \left( { - \left| L \right| \cdot {i^{ - 1}}} \right) $ 和概率 $ {P_t} = \exp \left( { - {i^{ - 1}}} \right) $ .

(3) 如果 $ {P_c} \geqslant {P_t} $ , 则最优解为 $ {D_i} = {L_i} $ . 否则, 最优解为 $ {D_i} = {X_d} \oplus {X_e}{\text{ }}\bmod {\text{ }}256 + 1 $ .

接下来对压缩图像执行双向异或扩散操作, 如式(12)所示. 其中, 变量 $ {m_0} \in \left[ {0, 255} \right] $ 和 $ {m_1} \in \left[ {0, 255} \right] $ 为外部密钥, $ D^{(1)} $ 表示序列 $ D $ 中的第1个元素值.

$ \left\{ {\begin{array}{*{20}{l}} {P_6^{(1)} = {m_0} \oplus P_5^{(1)} \oplus {D^{(1)}}{\text{ }}} \\ {P_6^{(n)} = P_6^{(n - 1)} \oplus P_5^{(n)} \oplus {D^{(n)}}{\text{ }}} \\ {P_7^{({\rm{end}})} = {m_1} \oplus P_6^{({\rm{end}})} \oplus {D^{({\text{end}})}}{\text{ }}} \\ {P_7^{({\rm{end}} - i)} = P_7^{({\rm{end}} - i + 1)} \oplus P_6^{({\rm{end}} - i)} \oplus {D^{({\text{end}} - i)}}} \end{array}} \right. $

(12)

3.2 嵌入阶段

就现有的图像加密算法而言, 其所产生的密文图像具有明显的伪随机特性. 因该类密文图像在公用网络中传输时, 极易遭到人工神经网络模型的拦截、窃听、伪造以及恶意攻击等. 基于此, 本文将采用基于矩阵编码的嵌入方法为加密数据提供视觉上的保护.

步骤1. 在初始状态情况下, 对迭代超混沌Qi系统若干次生成的序列 $ {X_f} $ 进行排序, 并用得到的索引值序列对加密图像 $ {P_7} $ 执行索引置乱, 得到矩阵 $ {P_8} $ .

步骤2. 在算法1的控制下, 在空域中将加密数据通过隐写编码的方式嵌入到非涉密传输介质-载体图像中. 至此, 加密过程完成.

算法1. 基于隐写编码的空域嵌入算法
输入: 秘密图像 $\scriptstyle {P_8} $ , 载体图像 $\scriptstyle H \in {\mathbb{N}^{N \times N}} $
输出: 具有视觉安全性的密文图像 $\scriptstyle V \in {\mathbb{N}^{N \times N}} $
(1) [m, n] = size( $\scriptstyle {{\mathit{P}}_8}$ )(2) for i = 1:mn end (3) 　　 T1 = bitand( $\scriptstyle {P_8} $ (i), 192, “int16”); (4) 　　 T2 = bitand( $\scriptstyle {P_8} $ (i), 48, “int16”); (5) 　　 T3 = bitand( $\scriptstyle {P_8} $ (i), 12, “int16”); (6) 　　 T4 = bitand( $\scriptstyle {P_8} $ (i), 3, “int16”); (7) 　　 Z(1) = bitshift(T1, –6); Z(2) = bitshift(T2, –4); (8) 　　 Z(3) = bitshift(T3, –2); Z(4) = T4; (9) 　　 for j = 1:4 do (10) 　　 a = bitget(H(i), 1); (11) 　　 b = bitget(H(i), 2); (12) 　　 c = bitget(H(i), 3); (13) 　　 $\scriptstyle su = {\text{ }}c \times 1 \oplus b \times 2 \oplus a \times 3 $
(14) 　　 if su != Z(i) do
(15) 　　　 $\scriptstyle s = {\text{ }}su \oplus Z(i) $
(16)　　　 if bitget(H(i), 4–s) == 0 do
(17) 　　　　 v = 1;
(18) 　　　 else
(19)　　　　 v = 0;
(20) 　　　 end do
(21) 　　　 I(i) = bitset(H(i), 4–s, v)
(22) 　　 end do
(23) 　 end do
(24) 　 V(4i–3) =I(1); V(4i–2) =I(2);
(25) 　 V(4i–1) =I(3); V(4i) =I(4);
(26) end do

3.3 解密过程

本文提出的加密算法所对应的解密流程如图4下半部分所示. 当解密方通过安全通道获得解密密钥以后, 可以对视觉有意义的密文图像进行以下操作来恢复出其所携带的明文敏感数据.

步骤1. 首先, 利用接收到的解密密钥迭代超混沌Qi系统和新提出的分段混沌映射以生成若干条混沌序列, 进而构建出解密过程中所需的密码流.

步骤2. 通过矩阵解码算法和索引逆置乱操作从隐写的密文图像中提取出加密图像 $ {P_7} $ .

步骤3. 在密码流的控制下, 对加密图像执行双向的逆异或扩散, 并再利用量化参数 $ {P_{\max }} $ 和 $ {P_{\min }} $ 进行逆量化操作, 得到压缩后的明文稀疏系数矩阵.

步骤4. 根据优化算法, 使用矩阵 $ \Phi $ 和 $ P $ 从 $ P_{4} $ 中恢复出明文系数矩阵 $ {P_3} $ .

步骤5. 再通过对系数矩阵 $ {P_3} $ 执行二维Arnold置乱和逆离散小波包变换, 得到最终的解密图像.

4 实验结果与分析 4.1 仿真实验结果

实验平台为搭载在I7-8550U CPU和16 GB内存笔记本电脑上的Matlab 2020B. 仿真实验中, 新分段混沌映射的初始状态和控制参数分别设为0.678和0.2, 而超混沌Qi系统的3个初始状态分别为0.238, 0.471, −1.2和0.39. 另外, 参数 $ d{\text{ = 15}} $ , $ {m_0} = {m_1} = 127 $ , 压缩率为0.25, 稀疏基选为多贝西小波.

随机选择分辨率为 $ 512 \times 512 $ 的两幅明文图像和两幅可公开获取的载体图像进行仿真实验, 且所得到的实验结果如图5所示. 可以看出, 明文图像被有效地压缩并加密成类噪声的中间秘密图像, 实现了对明文图像数据的内容保护. 除此之外, 生成的密文图像具有视觉上的语义, 与相应的载体图像高度相似. 其他方面, 从密文图像中恢复出的解密图像与对应的明文图像在视觉上并无差别.

接下来, 采用定量的评估方法, 即峰值信噪比(peak signal-to-noise ratio, PSNR)和平均结构相似度(mean structural similarity, MSSIM)^[18], 来对所提加密方案的重构效果和视觉安全性进行评价. 测得两组实验中明文图像与解密图像, 载体图像与密文图像之间平均PSNR和MSSIM值分别为36.680 4 dB, 0.947 7和43.949 0 dB, 0.995 0. 从得到的实验数值结果可以看出, 在不受到噪声等因素的干扰情况下, 所提出的算法具有不错的视觉安全性和解密质量.

4.2 安全性分析 4.2.1 穷举攻击分析

密钥空间和密钥敏感性是抵御穷举攻击的两个重要评估指标. 在本文所提出的视觉安全加密算法中, 混沌系统被应用于加密过程的各个阶段, 包括并行压缩、双向扩散加密以及随机嵌入. 由于混沌序列对初始状态极度敏感, 因此所提加密算法具有相当高的密钥敏感性. 其他方面, 将所采用的两个混沌系统的初始状态作为外部密钥, 则在双精度数据类型的条件下, 本算法总的密钥空间约为 $ {10^{120}} $ , 远远大于标准理论值^[1], 即 $ {2^{100}} $ . 值得一提的是, 其他的一些参数, 如 $ {m_0}, {\text{ }}{m_1}, {\text{ }}d $ 以及量化参数 $ {P_{\max }} $ 和 $ {P_{\min }} $ , 均可以作为密钥以提升算法在抵抗穷举攻击方面的能力.

4.2.2 统计攻击分析

直方图反映在自然图像中像素值的分布比例. 接下来, 将分辨率均为 $ 512 \times 512 $ 的两张明文图像(Lena和Peppers)和两张载体图像(Baboon和Sailboat)分别单独地传入所提加密算法进行统计分析实验, 其实验结果绘制在图6中. 首先, 从图中可以看出, 生成的中间秘密图像的像素值分布近似均匀, 表明明文图像的统计特征信息得到有效的隐藏, 同时也防止在加密的第2阶段中嵌入信息不对称的漏洞. 其次, 明文图像的直方图与对应的载体图像的直方图极为相似, 同时在第4.1节中也给出了这两者之间的定量数值结果, 即43.949 0 dB和0.995 0. 另外, 相比于现有的非视觉安全的图像加密而言, 本文所提加密算法从两个方面来抵抗统计分析攻击. 其一是通过压缩加密和双向扩散操作来消除明文特有的统计信息, 其次是采用隐写编码方法来隐藏加密的统计信息. 通过上述分析可知, 所本文介绍的图像加密算法具有不错的抗统计分析的性能.

4.2.3 差分攻击分析

差分分析是一种常用且可行的攻击方法. 密码分析者首先构造出多个特殊的明文图像并单独地对它们进行加密, 然后通过分析多个明文-密文对之间的关系, 以推导出加密方案所采用的密码流. 接下来, 采用像素变化率(number of pixels change rate, NPCR)和归一化平均变化强度(unified average changing intensity, UACI)^[27]等评估指标来定量衡量本文提出的加密算法在抵抗差分攻击方面的能力. 本实验的数值结果如表1所示. 值得一提的是, 由于本算法所产生的密文图像具有视觉安全性. 因此, 在实验前须将嵌入阶段移除. 从实验结果数据来看, NPCR和UACI值接近文献[15]给出的理论值, 即99.59%和33.55%, 且相比于文献[1, 11]具有更大的指标值, 表明本文介绍的加密算法具有不错的抵御差分攻击的能力.

4.3 健壮性分析

视觉安全的密文图像在传输信道中传输时, 不可避免地会遭到噪声的污染或数据丢包. 接下来, 为模拟出这两种攻击的效果, 人为地在密文图像中分别单独地添加 $ 30 \times 30 $ 的掩模块, 不同强度的盐椒噪声和斑点噪声. 实验结果如图7所示. 可以清楚地看到, 在不同强度的噪声和剪切攻击干扰下, 解密图像在视觉上仍具有一定的语义和可读性, 并且所提算法在抗椒盐噪声攻击方面具有很好的抵御能力. 此外, 由于本文介绍的加密算法具有强大的雪崩效应, 即当密文图像中的某一像素值发生细微变化时, 所产生的误差会逐步扩散到整个解密图像中, 这可以看作是对追求极高安全性的一种让步.

4.4 时间复杂度分析

加密算法的时间复杂度在很大程度上决定了其本身的执行效率^[27]. 针对分辨率均为 $ N \times N $ 的明文图像和载体图像. 首先, 在密码流的构造阶段, 利用 $ \Theta \left( {\left( {d \cdot {C_R} + 1} \right){N^2}} \right) $ 的时间复杂度来对新设计的分段混沌映射和四维超混沌Qi系统进行迭代, 生成混沌序列(符号C_R为预设的压缩率). 在PTP-CS阶段, 二维Arnold置乱操作所消耗的时间复杂度为 $ \Theta \left( {{N^2}} \right) $ . 其次, 在加密阶段中, 压缩图像进行双向的扩散操作共占用时间复杂度 $ \Theta \left( {2{N^2}} \right) $ . 最后, 将秘密图像随机地嵌入非涉密传输介质中, 而这部分操作所占用的时间复杂度为 $ \Theta \left( {4{C_R} \cdot {N^2}} \right) $ . 因此, 本文所提加密算法总的时间复杂度为 $\Theta ( ( ( d + 4 ) \cdot {C_R} + 4 ){N^2} )$ .

就分辨率为 $ 512 \times 512 $ 的明文图像“Lena”而言, 其加密过程中, 各个部分所消耗的时间占总加密时间的百分比如图8所示. 可以看出, 密码流生成阶段与嵌入阶段占据约90%的总时间. 因此, 本文建议以分块的形式对明文图像进行加密处理以提高运行速度. 首先, 分块操作可以大大减少混沌映射的迭代次数, 便于在加密过程中同步处理图像的各个子块. 其次, 这种处理手段有助于提高凸优化重建算法的收敛速度.

4.5 算法对比

为了突出本文所介绍的隐私图像加密算法的优越性, 本小节将从视觉安全性、重建质量等两个方面把本文所提算法与其他先进的加密算法进行对比实验, 所得到的数值结果如表2和表3所示.

对于视觉安全的加密算法而言, 载体图像与密文图像之间的PSNR和MSSIM值越大, 表明其视觉安全性越好. 表2列出了几种视觉有意义图像加密算法的视觉安全性对比实验的数值结果. 从得到的数据来看, 本文提出的加密算法所生成的密文图像具有最好的视觉质量. 相比文献[11]中所介绍的加密算法, 视觉安全性提高近8.5 dB. 同时, 也说明基于矩阵编码的信息嵌入技术对载体图像原始特征信息的损害较小.

在本文所提出的方案中, 将从以下两个方面来提高解密图像的重构质量. 首先, 在PTP-CS模型中, 通过对明文系数矩阵进行阿诺德置乱, 可以有效缓解测量矩阵的有限等距性质的限制, 从而提高重构图像的质量^[13]. 其次, 采用完全可逆的编码嵌入方法来消除截断损失. 在不同解密算法中, 从密文图像中恢复出的解密图像的重构质量如表3所示. 可以看出, 与其他压缩加密算法相比, 本文提出的算法具有更好的压缩性能.

5 结论与展望

针对公用信道中的敏感明文数据, 本文基于张量积压缩感知模型、混沌理论和数字隐写编码嵌入提出了一种具有视觉安全性的加密算法以实现对明文图像的同步加密和隐写. 在本项工作中, 在新提出的分段混沌映射和超混沌Qi系统的共同控制下, PTP-CS模型和二维阿诺德置乱策略可以有效地提升所提算法的压缩性能. 同时, 所采用的编码嵌入方法保证了类噪声秘密数据的高度不可感知性. 最后, 仿真实验的数值结果和综合分析表明所提出的加密算法具有足够的安全性以够抵御常见的多种攻击. 下一步工作, 将对循环生成对抗网络模型(cycle generative adversarial network model, cycle GAN)进行研究并将其引入到图像加密领域.