为深入推进“碳达峰”“碳中和”工作, 我国开展了一系列工作推进新能源相关产业的发展. 其中, 电动汽车(electric vehicle, EV)作为低碳环保的新能源汽车近年来销量骤增. 2021年新能源汽车销量333.41万辆, 新能源汽车在中国乘用车市场的渗透率从2017年的2.4%快速增长至2021年的16.0%, EV已成为中国最受欢迎的新能源汽车类型^[1]. 随着EV的快速发展, 其相关配套设施也面临巨大挑战^[2], 充电设施配置落后及EV就近充电导致区域内充电资源配置不均衡等问题, 使得充电站容易产生排队过长的现象, 同时也会对电网稳定运行产生冲击. 在目前EV配套设施发展还未跟上EV发展脚步的环境下, 通过智能信息化的方法引导用户的充电行为, 合理地最大化利用区域内充电资源是目前亟需解决的问题. 我国目前针对电动汽车充电策略已开展了许多研究. 文献[3]提出一种考虑实时交通的充电调度方法, 该方法通过历史数据对路况进行模拟, 考虑充电站中充电选项的排队情况, 对EV进行统一调度, 提高了充电站的利用率. 该方法仅以减少充电时间为目的, 并未考虑EV出行成本, 存在一定的局限性.

文献[4]提出了一种快充站配置优化的方法, 考虑站内分布式电源和储能, 基于遗传算法求解充电站最小运行成本. 文献[5]考虑了库存电池问题对充电站运行的影响, 将充电站模型与电池约束的调度模型结合, 同时考虑分时电价以最大化利用充电资源. 文献[6]聚焦于减少EV充电对电网的影响, 提出一种价格与激励联合需求相应的调度方法, 减少了负荷波动和EV调度成本. 上述文献主要针对充电站运行成本和调度成本进行研究, 在EV出行和充电效率上的研究相对较少.

综上所述, 目前已有研究主要着眼于价格激励方面, 没有综合考虑EV出行和充电成本以及充电站实际容量. 本文提出一种电动汽车优化调度模型, 该模型可以找出最优充电价格, 并且不会显著增加总行驶时间. 其中, 总行驶时间包括抵达充电站所需的时间、排队等待时间、充电时间以及到达目的地所需的时间. 本文对充电网络进行建模并计算总行程时间, 同时考虑了每个充电选项的排队率和充电成本.

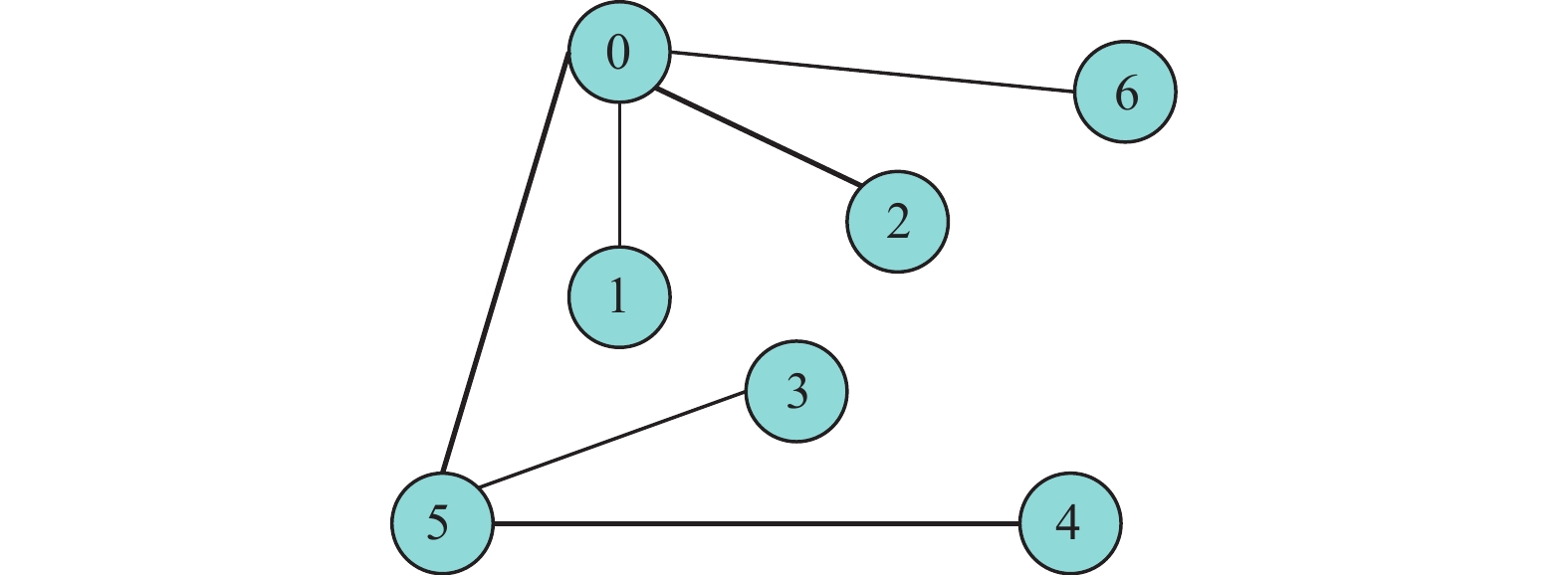
1 网络模型

根据图理论将EV充电网络简化为拓扑结构 $G = (N, R)$ , 其中, $ N $ 代表充电站的集合, j = $\text{1}\text{, }\text{2}\text{, }\cdots, {N}$ , R代表如图1所示的节点之间的道路路段集合, 不同节点间的道路等级不同. 考虑每个充电站提供直流快充和交流慢充两种充电选项, 每种充电方式都会产生一个队列, 每个队列都有特定的服务费率、等待时间和价格. 队列长度受EV充电率和充电时间等因素的影响. 队列长度决定了EV进行充电前所需的等待时间. 同时, EV充电率也会一定程度上受到价格的影响. 在本文所提出的模型中, 第i( ${i}\in \text{1, 2, }\cdots,{I}$ )个EV在时刻t的充电行为会受到当前荷电状态 ${\textit{SoC}}_{{t}}$ (state of charge, SoC)、当前位置 ${{L}}_{{i}}$ 和预期目的地 $ {D}_{i} $ 的影响. 为了保证EV与充电站信息的实时性, 所有充电站和EV信息都通过车联网互联并进行实时信息交换. 如果一辆EV计划从起点行驶至一个目的地节点, 而它当前的SoC表明它的剩余电量不足以支撑其行驶至终点, 那么它就不得不寻找充电站充电. 另一方面, EV车主也可能更倾向于在快速充电站以更快的速率充电, 而不是在其附近的充电站使用慢速充电设施进行充电.

2 考虑多目标优化的数学模型 2.1 出行时间模型与排队模型

EV的总出行时间包括从当前地点行驶至充电站的时间、充电站充电时间和从充电站行驶至终点的行驶时间, 具体计算公式如下:

$ {t_{L, D}} = {t_{L, j}} + t_j^n + {t_{j, D}} $

(1)

其中, $ {t_{L, j}} $ 和 $ {t_{j, D}} $ 分别为充电前路径行驶时间和充电后路径行驶时间. $ t_j^n $ 为在充电站j使用充电选项n所花费的时间, 包括等待时间和充电时间.

为了确保EV有足够电量支撑其行驶至充电站, 式(1)中的 ${\textit{S}_{L, j}}$ 必须小于 ${{\textit S}_{m} }$ , ${{\textit{S}}_{m} }$ 为EV基于其当前SoC下可以行驶的最大距离. EV基于当前时刻t的SoC可行驶的最大距离计算公式如下:

$ {{\textit{S}}_m} = \frac{{({\textit SoC}_t - {\textit SoC}_0){B_C}}}{{\Delta E}} $

(2)

其中, $ {B_C} $ 为EV电池容量, ${\textit SoC}_0$ 为EV的SoC最小值, ${\textit{SoC}}_{{t}}$ 为当前荷电状态, $ \Delta E $ 为EV单位里程能耗, 其计算公式如下^[7]:

$ \left\{ {\begin{array}{*{20}{l}} {\Delta {E_f} = - 0.004v + 0.247 + 1.520/v} \\ {\Delta {E_m} = 0.004v + 0.179 + 5.492/v} \\ {\Delta {E_s} = - 0.001v + 0.210 + 1.531/v} \\ {\Delta {E_b} = - 0.002v + 0.208 + 1.553/v} \end{array}} \right. $

(3)

其中, $ \Delta {E_f} $ 、 $ \Delta {E_m} $ 、 $ \Delta {E_s} $ 和 $ \Delta {E_b} $ 分别代表了EV在快速路、主干路、次干路和支路4个等级的单位里程能量消耗.

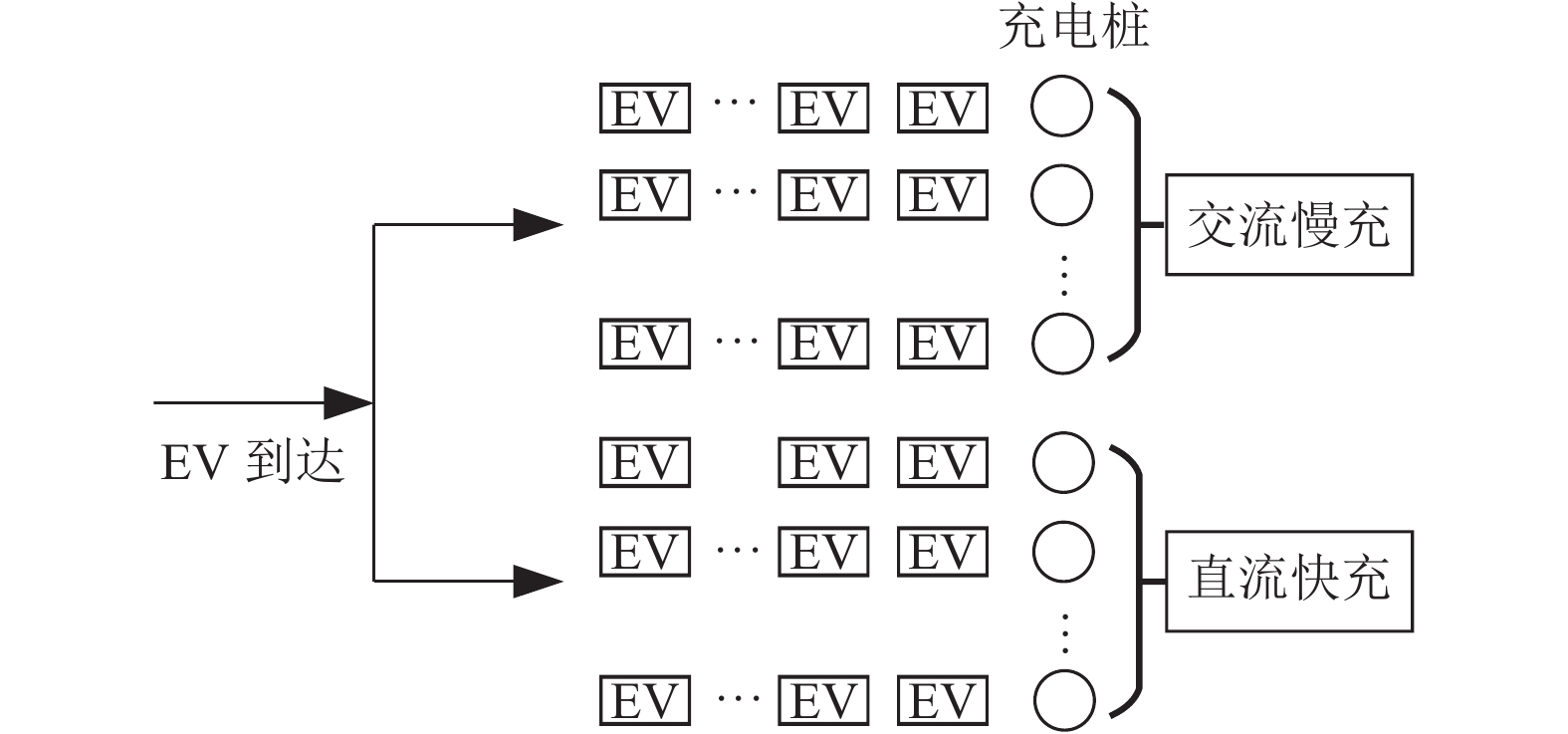
在充电高峰时段, 由于充电需求增加, EV在到达充电站时会需要排队等候. 图2为具有多种充电选项的充电站排队系统. 为了预估车站每个充电选项的等待时间, 本文使用M/M/s/K模型^[8], 其中, 第1个M代表马尔科夫链的EV到达时间分布; 第2个M代表马尔科夫链的计费时间分布; s代表服务器数量; K代表系统容量, 即充电站可停放的电动汽车数量.

在排队模型中, 如果充电站有空闲的充电位置, 每个到达充电站的EV都可以立即充电; 如果所有的充电桩都在使用中, EV则需要在队列中等待, 直到一个充电桩进入空闲状态. 每个充电站有3个队列, 每个充电选项一个都会有一个队列, 每个队列中的EV由s个服务器提供服务. $ \gamma _j^n $ 表示充电站j的充电选项 ${n}\text{=}\text{1, 2}$ 的服务时间, 每个服务器都以指数服务速率运行. $ {\lambda _j} $ 为第j个充电站的EV平均排队率, EV到达充电站的过程遵循 $ {\lambda }_{j} $ 的泊松分布. 充电设施和EV排队率可影响充电站的服务率, 而一天中不同时间的EV平均排队率可以从历史数据中得出. 基于马尔可夫链原理^[9], 推导出 M/M/s/K 排队过程的状态转移图如图3所示, 其中链的每个状态对应于队列中EV的数量. 当新的EV到达或充电完成离开充电站时, 排队过程将进入不同的状态. 这种状态转换本质上是一个随机过程, 其中, $ {X}_{r} $ 为代表链在步骤r处的值的随机变量. 这个具有状态空间 $\mathbb{R},\; \mathbb{R} ={\rm{\{ 1,2,3,}}\cdots\}$ 的随机过程由于具有式(4)的属性而表现出马尔可夫链的性质.

$ \begin{split} P({X_{r + 1}} &= j\left| {{X_r} = i, } \right.{X_{r - 1}} = {x_{r - 1}}, \cdot \cdot \cdot , {X_0} = {X_0}) \\ & =P({X_{r + 1}} = j\left| {{X_r} = i)} \right. \\ \end{split} $

(4)

上述随机过程的状态转移概率矩阵 $ P $ 可用式(5)表示^[10]:

$ P = \left[ {\begin{array}{*{20}{c}} { - \lambda }&\lambda &0&{ \cdot \cdot \cdot }&0&0 \\ \gamma &{ - (\lambda + \gamma )}&\lambda & \cdots &0&{} \\ 0&{2\gamma }&{ - (\lambda + 2\gamma )}& \cdots &0&{\vdots} \\ \vdots &{\vdots}&{\vdots}&{\ddots}& \vdots & \\ 0&0& \cdots &{}&\lambda &0 \\ 0&0& \cdots &{}&{ - (\lambda + k\gamma )}&\lambda \end{array}} \right] $

(5)

其中, k为充电站的容量, $ \lambda $ 为排队率, $ \gamma $ 为服务时间.

在概率矩阵 $ P $ 中, ${P^{\rm{T}}}{\pi ^{\rm{T}}} = {0^{\rm{T}}}$ , $ \pi $ 为包含平稳分布的行向量, 假设占用率为 $ \varepsilon = \dfrac{\lambda }{{k\gamma }} $ , 得到第 $ r $ 个平稳分布:

$ {\pi _r} = {\pi _0}\frac{{{\lambda ^r}}}{{n!{\gamma ^r}}} = \frac{{{{(k\varepsilon )}^r}}}{{r!}}{\pi _0} $

(6)

当r=0, 1, 2, ···, k+r=K时:

$ {\pi _{c + r}} = {\pi _0}{\varepsilon ^r}\frac{{{{(k\varepsilon )}^k}}}{{k!}} $

(7)

$ {\frac{1}{\pi_0}} = \sum\limits_i^k {\left( {\frac{1}{{i!}}{{\left( {\frac{\lambda }{\gamma }} \right)}^i} + \sum\limits_{j = k + 1}^R {\frac{1}{{{K^{j - k}}}}} } \right)\left( {\frac{1}{{k!}}} \right)} \left( {\frac{\lambda }{\gamma }} \right) $

(8)

队列长度为:

$ q = {\pi _0}\frac{{\varepsilon {{\left( {k\varepsilon } \right)}^k}}}{{k!{{\left( {1 - \varepsilon } \right)}^2}}}\left[ {1 - {\varepsilon ^{R - k}} - \left( {R - k} \right){\varepsilon ^{R - k}}\left( {1 - \varepsilon } \right)} \right] $

(9)

每个充电站内都包含直流快充与交流慢充两个充电选项n=1, 2, 每个充电站考虑排队论中的律特法则^[11], 每次充电所花费的时间为:

$ t_j^n = \frac{{q_j^n}}{{{\lambda _j}(\gamma _j^n - {\lambda _j})\left( {1 - \pi _j^R} \right)}} + \frac{{(90{\text{%}} - {{\textit{SoC}}_t}){B_C}}}{{\varphi {P^n}}} $

(10)

其中, $ \pi _j^R $ 为第j个充电站在第R个状态下的概率转移矩阵. $ \varphi $ 为充电效率, $ {P^n} $ 为充电选项n的充电机功率.

2.2 动态定价模型与充电成本

每个EV的充电成本取决于充电站与站内充电桩当前排队率来决定. 同时, 大量的电动汽车接入会对电网造成冲击, 电网企业通过对电价分时调整来应对EV的高峰充电^{[12, 13]}, 根据文献[12]中的分时定价标准, 充电电价如表1所示.

为了缓解高峰期充电站的充电压力, 本文提出一种动态定价模型, 该模型考虑了充电站内的排队率来实时改变充电费率:

$ {p_E} = \lambda s_j^n + {p_s} $

(11)

其中, $ {p_s} $ 为当前时段的电价, $ s_j^n $ 为充电 $ j $ 内充电选项n的充电服务费.

在充电站j中使用充电选项n的EV充电成本计算公式如下:

$ c_j^n = (90{\text{%}} - {\textit{SoC}}_t){B_C}{p_E} $

(12)

2.3 优化调度模型

本文提出一种优化的调度模型, 综合考虑以包括充电成本和时间成本的总成本最小为目标. 根据式(1)和式(13), 调度模型的目标函数可建模为如下所示:

$ \min\; {F = a{t_{L, D}} + } c_j^n $

(13)

其中, $ a $ 是关于时间的耗费系数.

约束条件如下:

$ {{\textit S}_{L, j}} \leqslant \frac{{{B_C}{\textit SoC}_t^{}}}{{\Delta E}} $

(14)

$ t_j^n < \eta t_{L, D}^{n, M} $

(15)

$ P_j^{{\rm{load}}, \max } \leqslant P_{{\rm{grid}}}^{{\rm{load}}, \max } $

(16)

其中, $ \eta $ 为时间约束系数, $ t_{L, D}^{n, M} $ 为起点至充电站和充电站至终点距离最短并使用第n个充电选项的等待时间. ${P^{{\rm{load}}}}$ 、 $P_j^{{\rm{load}}, \max }$ 和 $P_{{\rm{grid}}}^{{\rm{load}}, \max }$ 分别为EV负载、第j个充电站所能容纳的最大负载和电网所能容纳的最大负载.

3 基于DEB-ABC算法的EV优化调度模型 3.1 DE-BABC算法

人工蜂群(artificial bee colony, ABC)算法是一种受蜜蜂启发的流行算法, 由Karaboga^[14]提出, 其灵感来自蜂群中蜜蜂的觅食行为. ABC对于多变量函数优化问题具有较好的全局搜索能力, 其在诸如旅行商问题之类的路径搜索问题中表现出明显优势^{[15, 16]}. 但是传统的ABC算法在大规模计算时接近全局最优解时容易陷入局部最优, 后期搜索速度减慢等缺点, 本文提出一种引进差分进化算法(differential evolution, DE)的DEB-ABC算法, 同时引入全局最优位置来提高ABC算法的局部搜索能力. DE算法的个体学习方式使得其具有收敛速度快的优点, 所以改进的算法弥补了ABC算法易局部最优和收敛速度慢的缺陷.

在ABC算法中, 蜜源代表搜索空间中优化问题的可能解决方案, 蜜源的花蜜量代表该解决方案的适合度. ABC算法定义了3种类型的蜜蜂: 雇佣蜂、跟随蜂和侦察蜂. 算法的机制如下: 雇佣蜂首先在其记忆中的食物源附近执行邻域搜索, 然后他们回到蜂房表演舞蹈, 舞蹈通知跟随蜂每个解决方案的适应度. 每个跟随蜂观察并选择食物源, 采用轮盘赌法基于与食物源适应度成比例的概率执行另一个邻域搜索. 跟随蜂倾向于从雇佣蜂发现的食物中选择好的食物来源. 雇佣蜂和跟随蜂通过执行邻域搜索来与现有的解进行比较从而产生新的解, 应用贪婪方法来决定是否接受新的扰动解. 如果一个解决方案在预先设定的试验次数后无法改进, 那么它将被放弃. 与非改进解决方案, 即局部最优相关联的雇佣蜂被放弃, 然后它将变成侦察蜂. 侦察蜂以大步长随机探索搜索空间, 寻找新的解决方案.

DEB-ABC算法中, 首先初始化TN个蜜蜂个体, 雇佣蜂与跟随蜂数量相同, 对于 ${f}\in\text{1, 2, 3, }\cdots,{TN}$ , ${l}\in \text{1, 2, 3, }\cdots,{D}$ , D为目标函数的变量数, 每个随机产生的可行解 $ {x_f} $ 的种群初始化方程为:

$ {x_f} = {L_l} + \theta ({T_l} - {L_l}) $

(17)

其中, $ {T_l} $ 和 $ {L_l} $ 为第 $ l $ 维解的上下界, ${\theta}$ 为[0, 1]上的随机数.

对于传统ABC算法来说, 雇佣蜂只沿着当前食物源的邻域的一个方向搜索并与原食物源位置比较, 然后选择更优位置. 在改进的ABC算法中, 引入DE算法的搜索方程, 将搜索方向增至3个邻居, 从而增加收敛速度. 式(18)为位置更新方程:

$ {v_{fl}} = {x_{g1, l}} + \tau \left( {{x_{g2, l}} - {x_{g3, l}}} \right) $

(18)

其中, ${g1}$ , ${g2}$ , ${g3}$ 为种群中随机的3个不同个体. 为扩大搜索范围, $ \tau $ 服从高斯分布, 平均值为0.5, 方差为0.1.

每个观察蜂根据轮盘赌方法选择一个食物源, 其概率公式如下:

$ p(f) = \frac{{fit(f)}}{{\displaystyle\sum\limits_{f = 1}^{TN} {fit(f)} }} $

(19)

其中, $ fit(f) $ 为可行解 $ {x_f} $ 的适应度值. 计算公式如下:

$ fit(f) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{1 + {F_f}}}, \begin{array}{*{20}{c}} {}&{{F_f} \geqslant 0} \end{array}} \\ {1 + \left| {{F_f}} \right|, \begin{array}{*{20}{c}} {}&{{F_f} < 0} \end{array}} \end{array}} \right. $

(20)

其中, $ {F_f} $ 为目标函数值.

为提高算法的局部搜索能力, 将全局最优位置^[17]引入观察蜂搜索方程, 改进后的搜索方程为:

$ {v_{fl}} = {x_{{\rm{gbest}}, l}} + \sigma \left( {{x_{g1, l}} - {x_{g2, l}}} \right) $

(21)

其中, ${g1}$ , ${g2}$ 为种群中随机两个邻居, ${x_{{\rm{gbest}}, l}}$ 为第 $ l $ 维空间的最优解. $\sigma$ 服从高斯分布, 平均值为0, 方差为0.3, 从而将搜索范围限制在 ${x_{{\rm{gbest}}, l}}$ 周围.

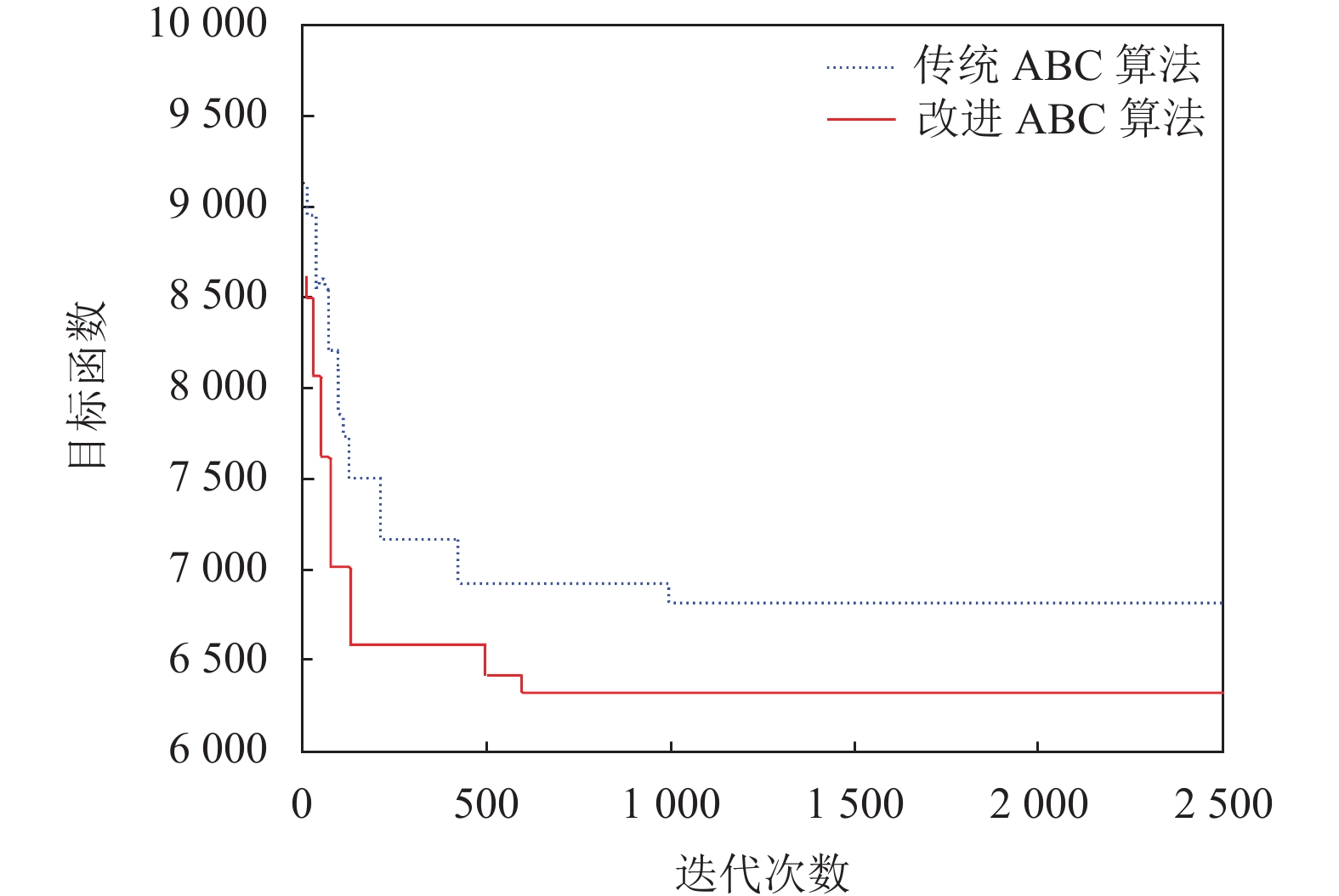
为验证所提改进算法的优越性, 本文在经典组合优化问题TSP问题^[18]上分别对标准ABC算法和改进的ABC算法进行实验验证, 如图4所示, 结果表明, 本文所提出的算法拥有更快收敛速度与更好的优化效果.

3.2 DEB-ABC算法求解优化模型

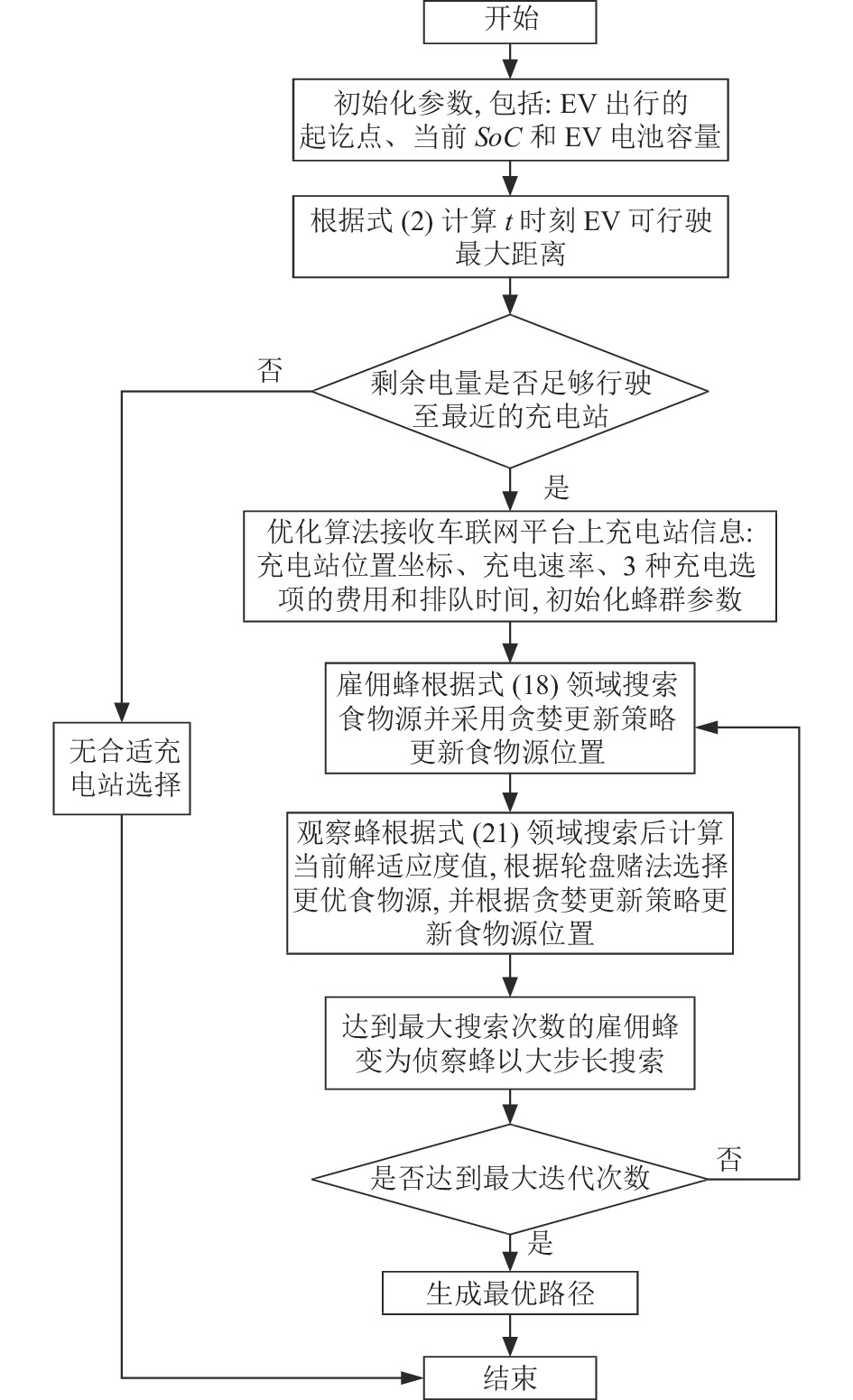
在所提出的模型中, 当车联网平台和EV驱动程序之间共享信息时, 使用优化算法在每次迭代中收集可能的解决方案, 计算每个解的适应度值, 优化算法计算模型后输出最优路径进而为EV车主提供最新的路线选择. 优化算法的输入包括: 充电站位置图、充电站规格、EV当前SoC、EV的最大能耗、始发地和目的地. 优化算法求解EV优化调度模型流程图如图5所示.

4 算例分析 4.1 实验参数

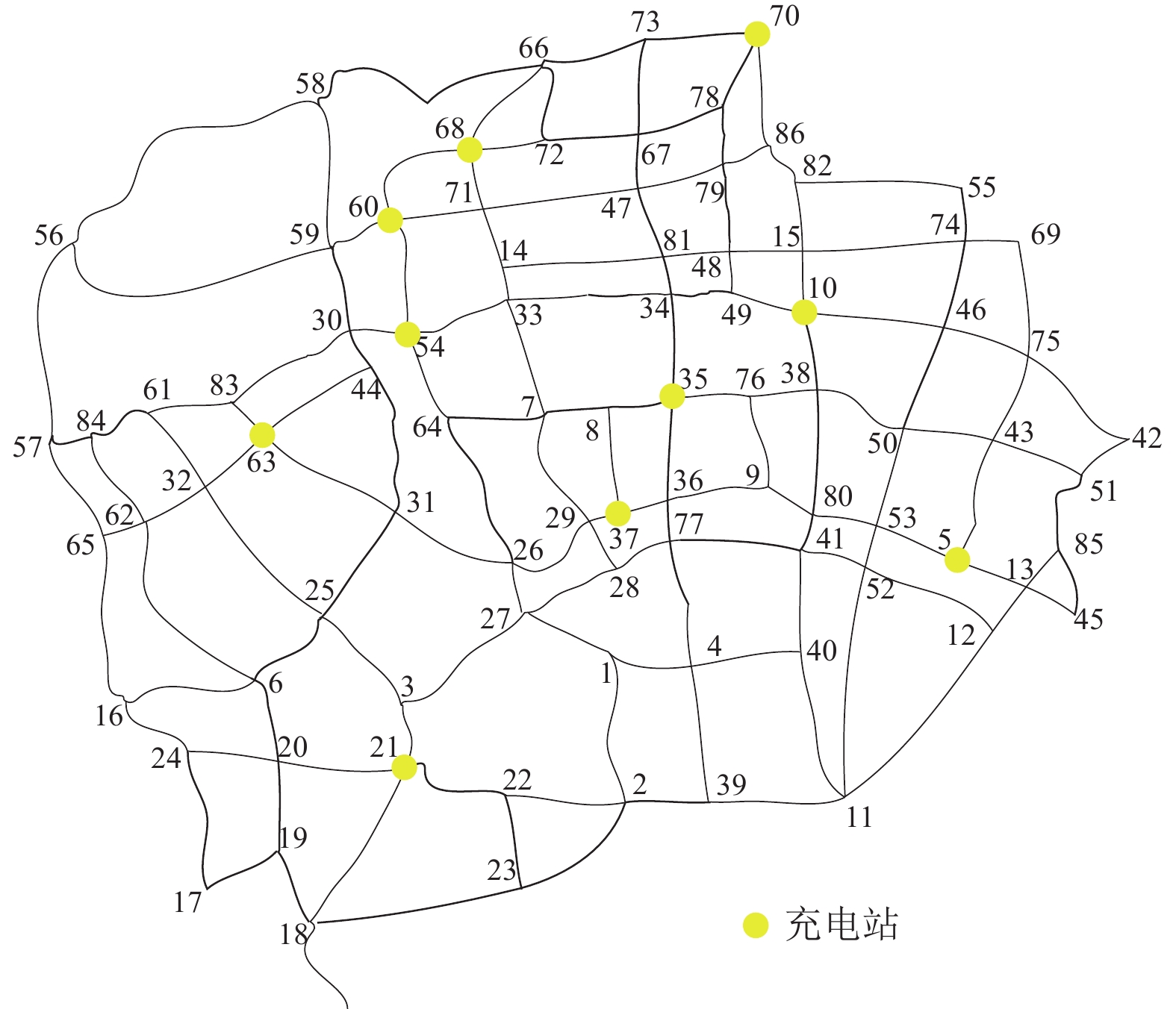
为了验证所提优化模型的有效性, 本文以南京市某典型区域为基础, 在Matlab上对充电网络进行仿真验证, 如图6所示, 网络包含86个交通节点和10个充电站. 具体实验参数如下: 每个充电站都包含直流快充和交流慢充两个充电选项, 站内的充电桩数目在10–20的范围内均匀分布, 充电机功率及充电效率参数如表2所示. 选择BYD E6、特斯拉Model Y和宝马530le三种车型共计1 500辆车为仿真车辆, 所有车辆初始状态时的SoC为高斯分布 ${{N}}_{\textit{SoC}}\text{(0.8, }{\text{0.1}}^{\text{2}}\text{)}$ ^[19], 3种车型参数如表3所示, EV到达每个充电站的概率建模为泊松分布. 每个充电站内的充电选项的插座数量均匀分布在110的范围内. 假设EV以60 km/h的速度行驶^[20], 设置每千米能耗为0.13 kWh, 时间约束系数为1.5, 时间耗费系数为45 元/h^[12].

4.2 仿真结果分析

本文研究了平均等待时间、出行时间、动态定价的充电成本和充电站EV排队率. 等待时间包括排队时间和充电时间, 行程时间包括行驶时间和等待时间. 队列占用参数表示当前占用的队列长度, 表示为充电站最大队列长度的一部分.

通过将本文中的调度模型(模型1)与文献[21]中的充电调度模型(模型2)和文献[22] (模型3)进行对比, 模型2考虑了等待时间实行就近充电策略, 但没有将EV行驶路径和充电成本考虑在内就近充电, 模型3为考虑了充电运营成本与电池损耗的充电策略. 结果验证本文中提出的优化调度模型具备有效性,

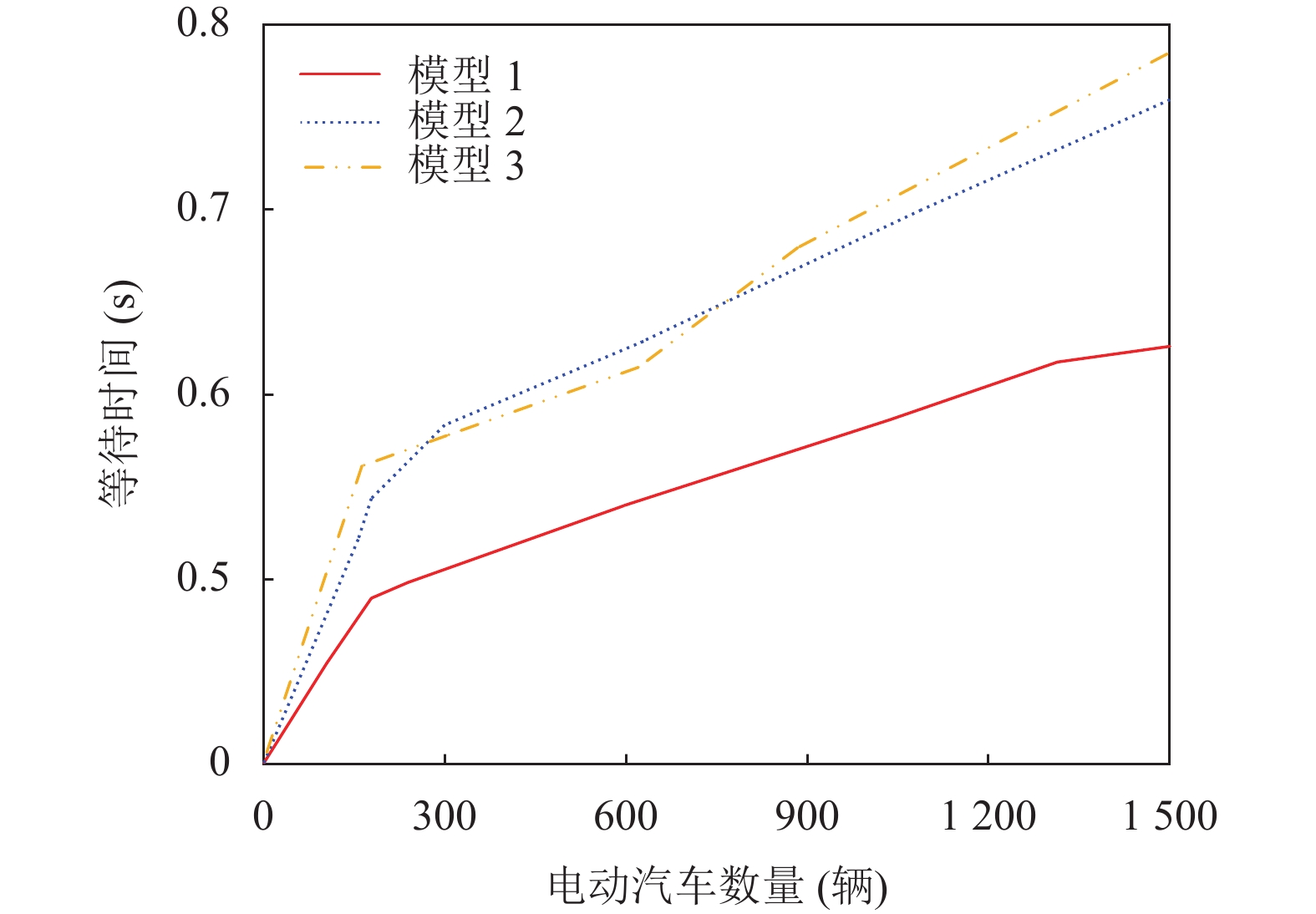
将平均等待时间进行归一化处理, 得到充电站EV的归一化平均等待时间如图7所示. 图中, 由于充电桩的数量是有限的, 当EV数量增多时充电需求同时增加, 平均等待时间随之上升. 结果表明, 与模型2和模型3相比, 本文所提出的充电方案考虑了两种充电选项, 缩短了等待时间. 调度模型同时考虑了每个充电选项的排队延迟, 并通过车联网平台获得每个充电站中排队等待相关信息, 从而减少每个充电站的排队时间.

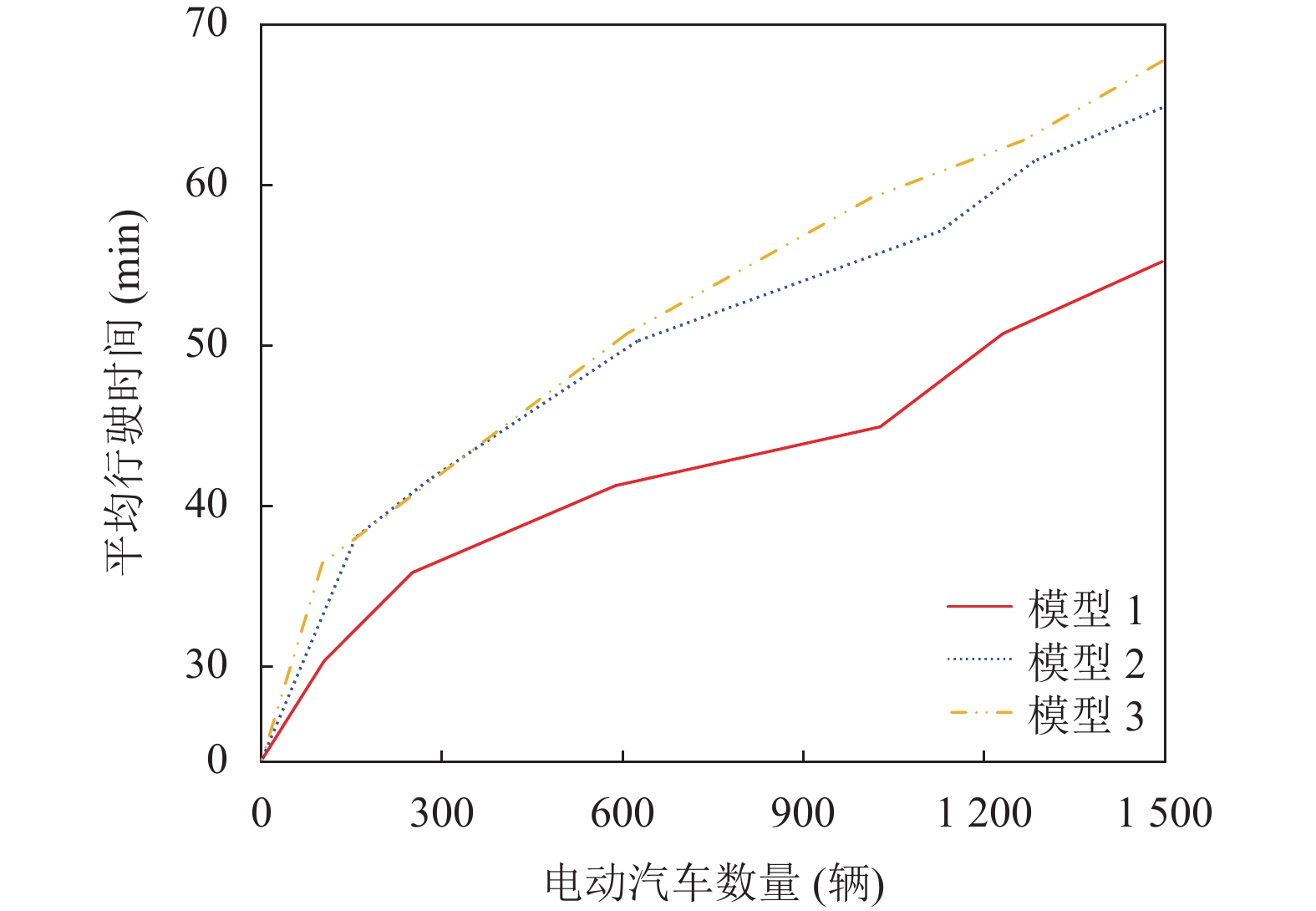
图8为模型1、模型2和模型3中平均行程时间的比较. 模型2采取的就近充电策略会使EV拥挤在少数几个充电站内, 模型3也并未考虑充电站内的排队情况, 造成充电队列长度过长, EV需要等待更长的时间. 与模型2和模型3相比, 本文提出的调度模型根据排队模型计算充电站每个充电选项对应的等待时间, 通过减少充电时排队等待时间进而减少总行驶时间.

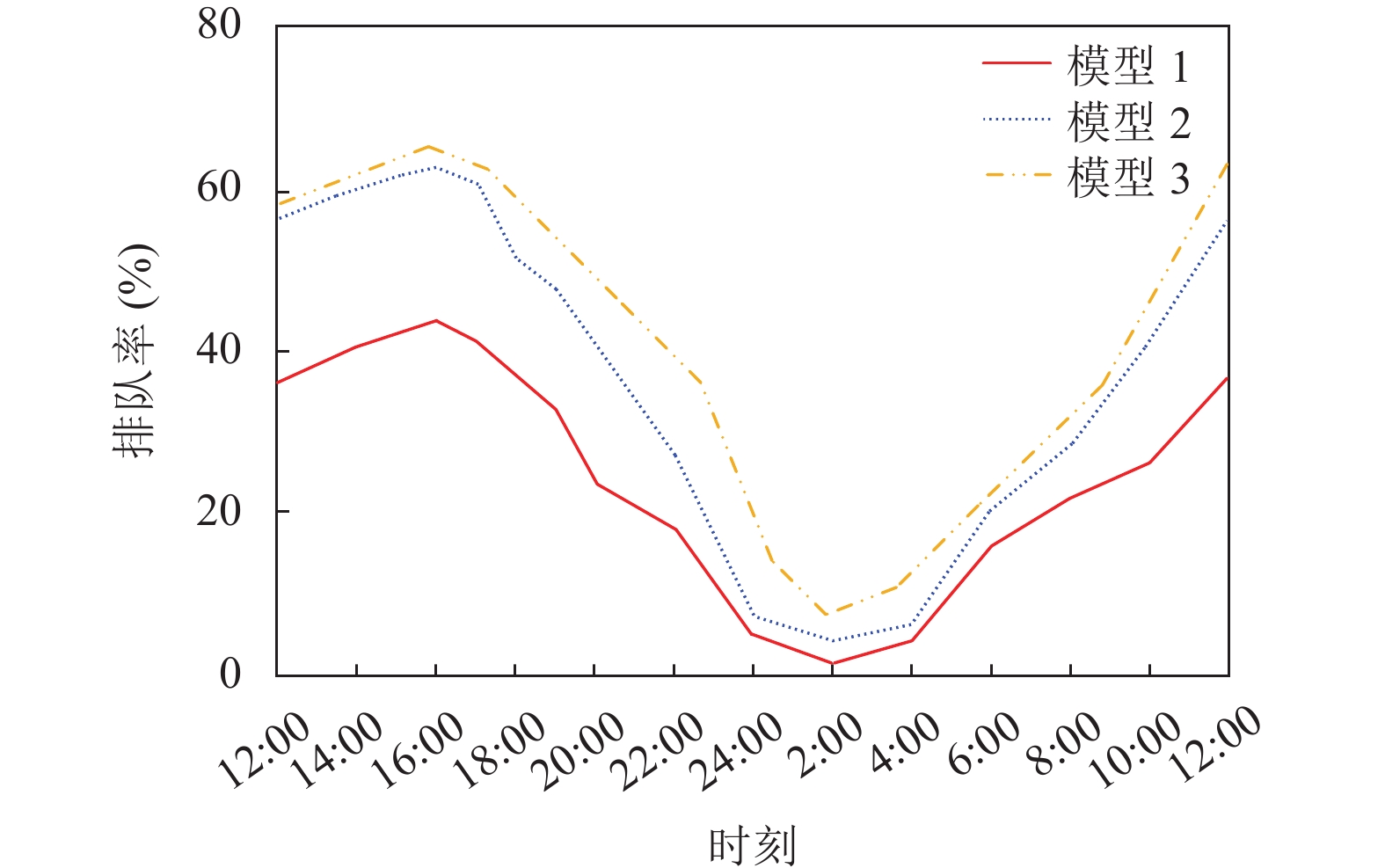
图9给出了3个模型在繁忙区域的充电站平均排队率的比较. 由图9可得, 由于就近充电策略没有综合考虑充电站的队列信息, 所以模型2的平均队列排队率较高, 而只考虑运营成本的模型3拥有更高的排队率. 模型1中的EV在可用的充电站之间分布地更加均匀, 从而减轻热点地区充电站的压力, 提高区域内充电站的利用率.

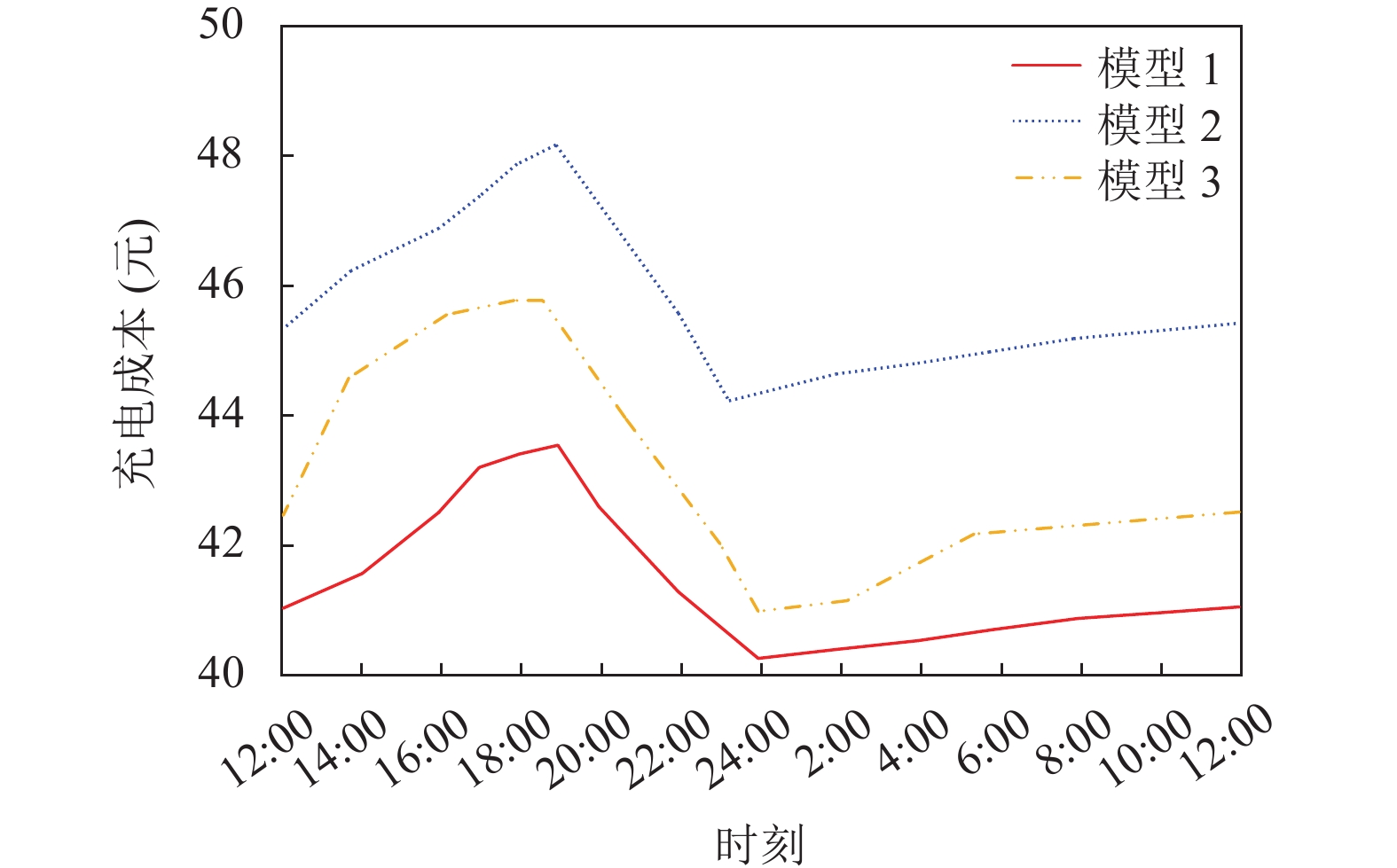
由于每个充电选项的价格会受到不同充电站和时间段的影响, 因此在本文提出的模型1中考虑了不同充电站的每个充电选项的实时价格. 图10显示了一天中不同时段的平均充电成本, 模型1产生了较低的平均充电成本. 模型3考虑了充电时间和行驶成本, 相较于模型1并未考虑动态的价格因素, 所以充电成本略高于模型1. 而模型2在计算路线时没有考虑价格信息, 所以其平均充电成本明显高于本文提出的模型1和模型3.

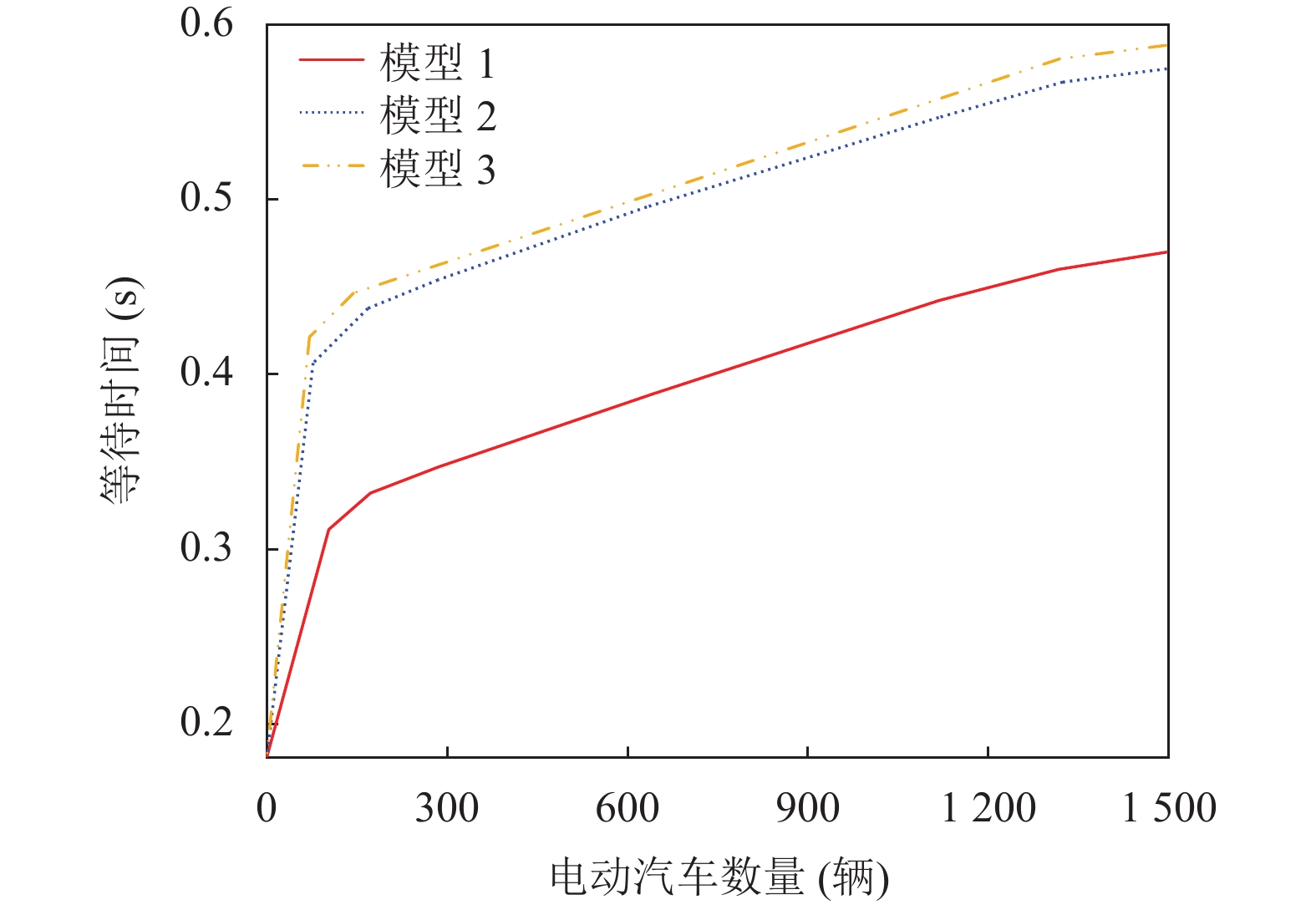
图11为在EV负载高峰期间采取动态定价策略的平均等待时间. 如图11所示, 较高的价格促使许多EV车主选择部分充电或避免在高峰期充电, 从而缩短平均等待时间. 为了减少大量EV接入电网对电能质量造成的影响,

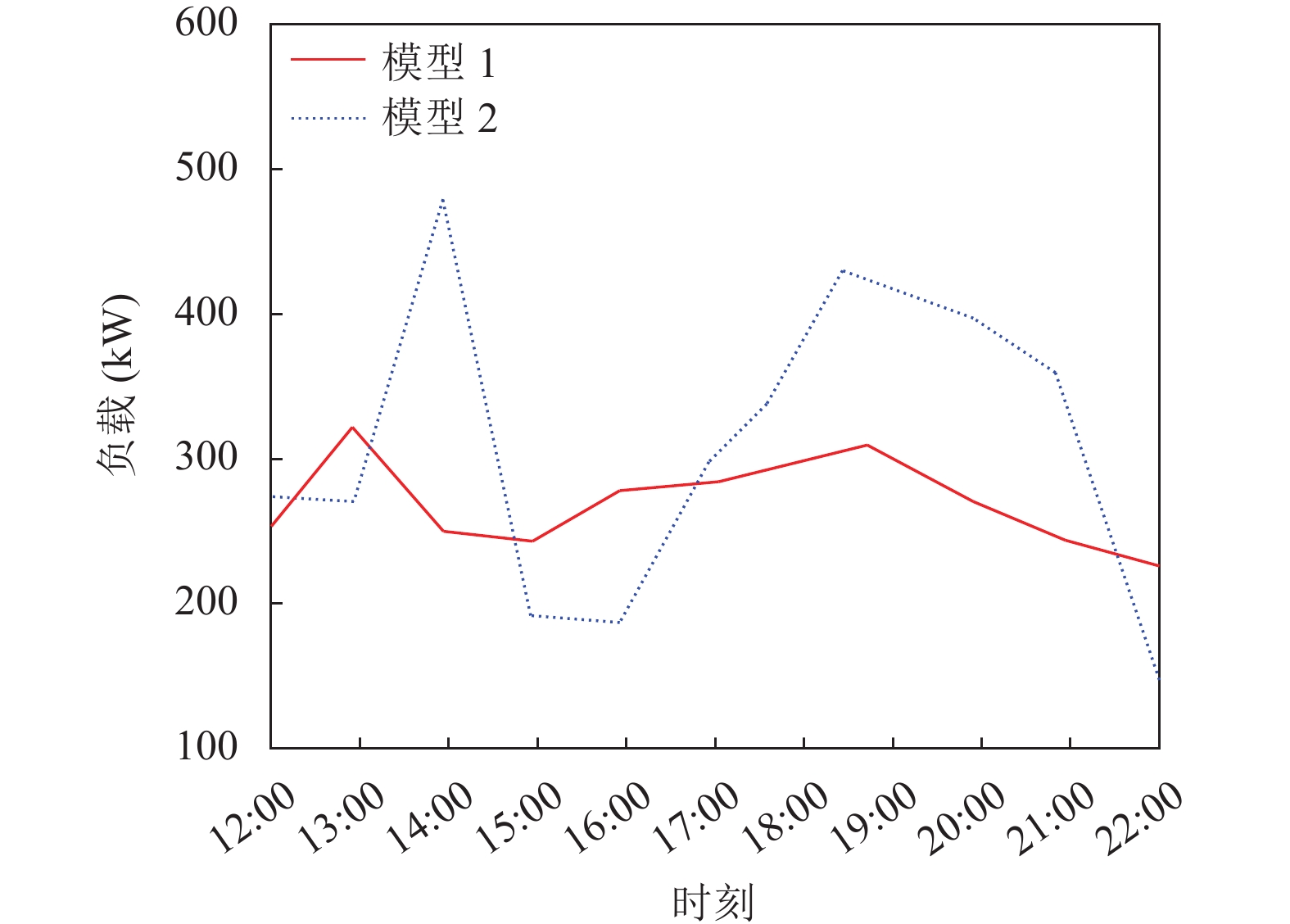
通过模型1中增加充电站内的服务费用以及电网在不同时段执行不同的电价动态定价模型来影响充电价格, 可以减少EV负载和居民用电高峰期之间的重叠. 图12显示了两种模型对于充电网络EV充电负载的影响. 模型1与模型2相比, 模型1通过向EV车主提供与首选充电选项的队列长度和充电价格相关的信息, 有效地提高了充电站内充电设施的使用率, 使得不同时段内负载更加均衡, 从而降低了负载高峰期对于电网的影响程度.

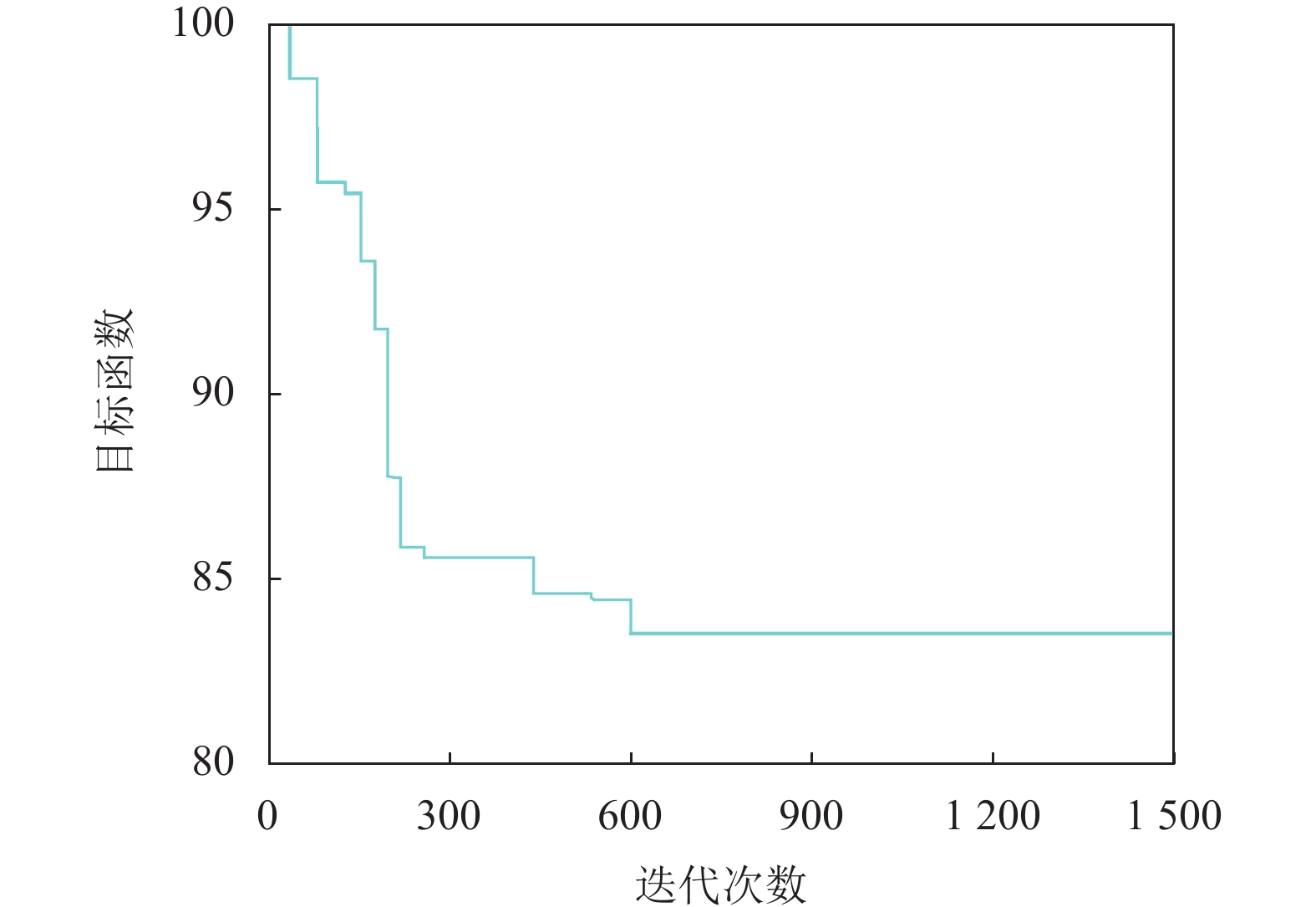
图13显示了所提出的改进的ABC算法在优化模型上的收敛性测试结果. 如图13所示, 本文提出的基于改进ABC算法的优化模型在经过596次迭代后收敛到最优解.

表4为1 500辆EV的情况下模型1、模型2和模型3优化后的数据. 可见本文提出的模型1相较于模型2和模型3所需要的包括平均等待时间、充电成本以及平均行驶时间的总成本都有所减少.

5 结论

本文提出一种优化调度模型, 该模型综合考虑了EV总行驶时间、充电站排队率和充电成本, 并基于改进的人工蜂群算法进行求解. 对于每个充电站内同时考虑了直流快充和交流慢充两个充电选项, 并根据队列长度和时间段分别设置不同的充电费率. 算例结果表明, 本文提出的优化模型可有效减少EV排队时间、充电成本和总行驶时间, 均衡地分配了充电资源, 提高了区域内充电资源的利用率, 减少了电网侧的负荷波动.