2. 长安大学 信息工程学院, 西安 710064
2. School of Information Engineering, Chang’an University, Xi’an 710064, China
信息科学技术的快速发展使得多媒体信息如图像、视频、语音等被广泛地应用在互联网平台上, 在开放共享的平台上能够便捷地实现信息交换的同时, 也存在信息泄露的隐患, 因此, 对信息进行加密的技术应运而生. 由于图像能够非常直观地传达出所需要的表达的信息, 而且对图像的加密方案可以很容易地移植到对其他多媒体信息的加密, 因此, 图像加密被广大学者所研究.
现如今, 多种技术在图像加密领域得到了应用, 其中, 基于混沌系统的图像加密方案由于其计算效率高的特点而吸引了学者们的广泛关注. 随着混沌理论的不断发展, 其特性逐渐被挖掘出来[1]. 同时将混沌理论与压缩感知[2, 3]、细胞自动机[4]、DNA (deoxyribo nucleic acid)编码[5]、S盒技术[6]等相结合提出了许多图像加密算法. 这些方案的主要思想就是将明文图像转换成类噪声图像, 使得黑客无法从中获取有用的信息, 这在一定程度上保护了数字图像信息的内容, 但是在传输的过程中极易引起黑客的注意, 受到恶意的攻击造成信息的泄露和丢失. 考虑到这种视觉无意义图像加密算法的缺陷, 结合密码技术和隐藏技术的可视化图像加密[7, 8]应运而生.
Bao等人[9]提出了具有VMIE算法, 首先利用现有的图像加密算法把一幅明文图像加密成类噪声图像, 然后将密文数据拆分并通过整数小波变换(integer wavelet transform, IWT)嵌入到另一幅具有视觉意义的载体图像中. 值得注意的是, 通过本方案选取的载体图像是明文图像的4倍, 这无疑增大了存储空间和传输带宽负担. 但幸运的是, 压缩感知技术的引入使得这一问题得到了解决. Chai等人[10]将压缩感知技术引入到可视化图像加密中, 在该方案中, 首先对明文图像的稀疏系数进行置乱, 然后利用压缩感知技术进行压缩加密, 最后在小波域中将压缩后的密文矩阵与明文图像分辨率相等的载体图像的系数矩阵进行融合得到视觉有意义的密文图像. 由于该嵌入操作过程存在截断误差, 所以解密方不可能在没有任何数据损失的情况下提取出原始秘密图像, 进而不可避免地会降低解密图像的质量. 为此, Wang等人[11]将最低有效位(least significant bit, LSB)嵌入算法和IWT结合提出了一种新的无损嵌入的方法. 首先, 利用IWT对载体图像进行分解, 得到LL, LH, HL, HH相等的4部分, 然后将秘密图像转换为二进制格式, 通过LSB嵌入算法把秘密二进制位分离并分别嵌入到载体图像的3个高频里, 利用三维猫映射来打乱嵌入信息的顺序. 考虑加密算法的鲁棒性, Zhu等人[12]基于块压缩感知和奇异值分解嵌入提出了一鲁棒的VMIE算法, 采用分块的形式将通过增益系数调节密文图像中像素点后的幅值嵌入到对宿主图像进行奇异值分解得到的对角矩阵中, 实现了调中大型规模的图像的并行处理. 现有可视化加密方案由于变换域嵌入受误差扩散效应的影响, 或是所采用的无损嵌入方式存在量化误差或舍入误差所造成的数据丢失等, 其视觉安全性和解密质量还存在可优化的空间.
为解决上述问题, 本文首先基于余弦函数提出了一个新余弦混沌映射, 并将其应用于可视化图像加密领域. 一维混沌映射相较于高维混沌映射具有简单易实现的优势, 但是其密钥空间小. 在此基础上所设计的新余弦混沌映射在保留一维混沌系统优势的情况下改善了其密钥空间小的缺陷. 经过实验分析, 与其他现有的一维混沌映射相比, 所提出的新余弦混沌映射具有更好的混沌性能. 其次通过二维Arnold置乱算法、线性测量以及双向加模扩散操作对明文图像的小波包系数矩阵进行压缩加密. 最后, 为了保证嵌入数据位置的随机性, 将载体图像进行细胞自动机混合置乱后通过LSB嵌入算法无损地隐藏在秘密图像中以得到具有视觉意义的密文图像.
1 相关知识 1.1 二维超混沌系统考虑到二维超混沌系统[13]具有多个系统参数和状态变量, 不易破解, 将其用于图像加密可以提高算法中密码流的不可预测性和其敏感性. 该二维超混沌系统的数学定义如式(1)所示:
| {xn+1=ayn+by2nyn+1=cxn+1+dyn | (1) |
其中, a, b, c, d为系统的控制参数, 而xn和yn则为该混沌系统的两个输出状态变量. 当控制参数a = 1.68, c = −1.1时, 其相应的混沌吸引子如 图1所示.
1.2 贝叶斯压缩感知压缩感知理论[14]可以用矩阵的形式被表述为:
| y=Φx=Φφs | (2) |
其中,
|
图 1 二维超混沌系统的吸引子图 Fig. 1 Attractor graph of 2D hyperchaotic system. |
2 所提出的分段混沌映射 2.1 新余弦混沌映射的数学定义
在本节, 基于余弦函数提出了一个新的一维混沌映射. 所提混沌映射的数学表达式如下:
| xn=cos((μxn−1(1−xn−1)3)−1) | (3) |
其中, μ > 0是实际控制参数, x为该映射的迭代输出变量.
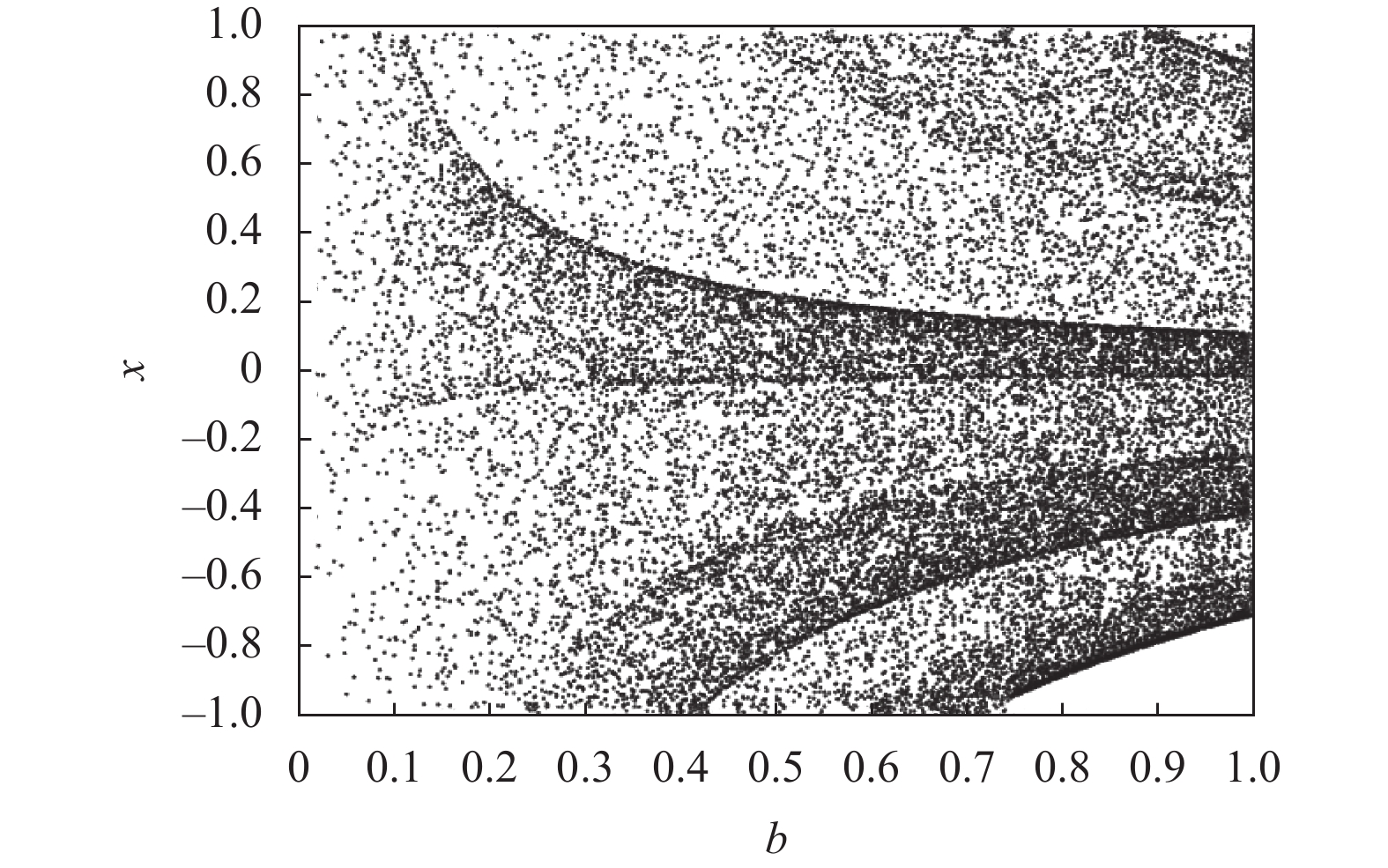
2.2 改进型混沌系统的性能分析给定系统的控制参数和初始值会生成一组时间序列. 通过观察系统的分岔图, 可以确定系统的长期状态[16]. 为了更直观地分析所提出的混沌映射的性能, 在初始状态x0随机设置为0.72的情况下, 将新设计的一维混沌系统的分岔图绘制于图2. 可以看出, 本文所提出的混沌映射在参数u的整个区间范围内一直处于混沌状态.
0-1测试是一个能够衡量时间序列是否有混沌的一种测试算法[17], 通过输出结果是否接近于1来判别混沌现象的产生. 对于一个常数c ∈ (0, π), 序列T(j) (j = 1, 2, …, N)可以通过式(4)计算:
| Kc=lim | (4) |
| M_{c}(n)=\frac{1}{N} \sum_{j-1}^{n}\left(\left[p_{c}(j+n)-p_{c}(j)\right]^{2}+\left[q_{c}(j+n)-q_{c}(j)\right]^{2}\right) | (5) |
| p_{c}(n)=\sum_{j=1}^{m} T(j) \cos (j c) | (6) |
| q_{c}(n)=\sum_{j=1}^{n} T(j) \sin (j c) | (7) |
图3绘制了不同一维混沌映射的0-1测试结果, 可以看出相较于其他映射, 本文所提出的混沌映射的K值接近1, 这表明在整个控制参数范围内系统的混沌性是可以被保证的.

|
图 2 CCM的分岔图 Fig. 2 Bifurcation diagram of CCM |

|
图 3 若干个混沌映射的0-1测试图 Fig. 3 0-1 test graphs of several chaotic maps |
3 视觉安全加密算法设计
本节是对加密算法的详细描述, 主要包括两个阶段, 其加密流程图如图4所示. 第1阶段是预加密阶段, 在此阶段, 通过Arnold置乱以及受控的混沌测量矩阵对经过小波包分解后的明文图像进行压缩和加密. 此外再通过双向加模扩散消除图像的统计特性, 得到类噪声图像. 第2阶段是嵌入阶段, 为了增强嵌入数据的随机性, 将载体图像先进行生命游戏置乱, 并借助LSB算法将类噪声图像信息嵌入到载体图像中, 将携带秘密信息的载体图像进行GOL反置乱, 获得具有视觉意义的密文图像. 值得一提的是无损嵌入方式保证了选择任意载体图像都不会导致秘密图像信息的丢失. 这里假设选取大小均为

|
图 4 所提图像加密算法的流程图 Fig. 4 Flow chart of the proposed image encryption algorithm. |
3.1 预加密阶段
步骤1. 首先用小波包变换对明文图像进行分解, 得到小波包系数矩阵P1.
步骤2. 为了使稀疏效果更好, 设置阈值TS, 将小波包系数矩阵的绝对值小于等于TS的元素全部置为0, 从而提高重建图像的质量, 阈值处理后的矩阵记为P2.
| {P_1}(abs({P_1}) \leqslant TS) = 0 | (8) |
步骤3. 将内部密钥U1: [x0, y0]作为混沌系统的初始值迭代超混沌系统500+2MN次, 舍弃前500次以移除混沌系统的瞬时效应, 生成两条混沌序列, 选取其中的一条混沌序列S1用作后续的置乱操作.
步骤4. 对混沌序列进行升序排列得到相应的索引序列
| \begin{split} \left[\begin{array}{l}{x}_{n}\\ {y}_{n}\end{array}\right]=&\left[\begin{array}{cc}1& Sa(i, j)\\ Sb(i, j)& Sa(i, j)\times Sb(i, j)+1\end{array}\right]\\ &\cdot \left[\begin{array}{l}{x}_{n-1}\\ {y}_{n-1}\end{array}\right]\mathrm{mod}\left[\begin{array}{l}M\\ N\end{array}\right]+\left[\begin{array}{l}1\\ 1\end{array}\right] \end{split} | (9) |
其中, (xn–1, yn–1)和(xn, yn)分别表示置乱前后的坐标, i和j代表索引序列的坐标.
步骤5. 将内部密钥U2: [a, v0]作为系统的初始值和抽样间距d迭代新一维混沌系统生成伪随机数vn, 然后根据式(10)对vn进行等距抽样. 其中, j是为了消除混沌系统的暂态效应而设置的某一固定正整数.
| {S_i} = 1 - 2 \times {v_{j + id}}{\text{, }}i = 0, {\text{ }}1, {\text{ }}2, {\text{ }}3, \cdots | (10) |
步骤6. 通过式(10)对抽样得到的混沌序列Sn进行归一化处理得到大小为W×N测量矩阵
| \varPhi = \sqrt {\frac{2}{W}} \left[ {\begin{array}{*{20}{c}} {{S_1}}&{{S_{W + 1}}}& \cdots &{{S_{W(N - 1){\text{ + }}1}}} \\ {{S_2}}&{{S_{W + 2}}}& \cdots &{{S_{W(N - 1) + 2}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{S_W}}&{{S_{2W}}}& \cdots &{{S_{WN}}} \end{array}} \right] | (11) |
步骤 7. 用
| {P_4} = \varPhi \times {P_3} | (12) |
步骤8. 量化过程. 为了将经过压缩感知测量后的输出矩阵的值限制在[0, 255]范围内, 在扩散过程之前进行量化. 如式(13)所示. 其中, pmin和pmax表示矩阵P4中所有元素的最小值和最大值, 它们也需要当作密钥由发送方通过秘密信道传送给接收方, 量化后的秘密矩阵记为P5.
| {P_5} = \left\lfloor {\frac{{255 \times ({P_4} - pmin)}}{{pmax - pmin}}} \right\rfloor | (13) |
步骤9. 使用内部密钥U3: [a, v1]作为改进混沌系统的初始值, 迭代混沌系统m+2W×N次, 丢弃前m次, 得到混沌序列S2, 然后使用混沌序列S2构造用于扩散的密码流O, 构造公式如式(14)所示:
| O={\rm mod}({floor}({S}_{2}\times {10}^{10}){, } \; 256) | (14) |
步骤10. 对矩阵P5进行双向加模扩散处理从而得到加密的图像P7, 式(15)和式(16)分别为前向扩散和后向扩散, 其中n = 1, 2, …, W×N, P6是前向扩散的结果, A0, A1是明文像素值.
| \left\{ \begin{gathered} P_6^{(1)} = {A_0} + P_5^{(1)} + {O^{(1)}}\bmod {\text{ }}256 \\ P_6^{(n)} = P_6^{(n - 1)} + P_5^{(n)} + {O^{(n)}}\bmod {\text{ }}256 \\ \end{gathered} \right. | (15) |
| \left\{ \begin{gathered} P_7^{(end)} = {A_1} + P_6^{(end)} + {O^{(end)}}\bmod {\text{ }}256 \\ P_7^{(end - n)} = P_7^{(end - n + 1)} + P_6^{(end - n)} + {O^{(end - n)}}\bmod {\text{ }}256 \\ \end{gathered} \right. | (16) |
步骤1. 将内部密钥U2: [x0, y0]作为混沌系统的初始值迭代超混沌系统m+M×N次, 舍弃前m次, 生成两条混沌序列Q1和Q2.
步骤2. 通过式(17)比较序列Q1和Q2中每个元素的大小, 得到大小为1×MN的一个新序列Q. 当Q (j)=1, 它是一个活细胞, 当Q (j) = 0, 它是一个死细胞, j = 1, 2, …, M×N. 接着, 将序列Q调整为一个大小为M×N的矩阵, 将其作为初始单位进行生命游戏置乱, 得到置乱矩阵T.
| Q(j) = \left\{ \begin{gathered} 1, {\text{ }}{Q_1}(i, j) \geqslant {Q_2}(i, j) \\ 0, {\text{ }}{Q_1}(i, j) < {Q_2}(i, j) \\ \end{gathered} \right. | (17) |
步骤3. 通过对置乱矩阵T进行排序得到索引序列T1, 然后利用索引排序置乱将载体图像中C的每个元素置乱, 得到置乱后的矩阵C1.
步骤4. 将矩阵C1的像素值矩阵进行四等分分割以获得矩阵大小均为0.5N×0.5N的矩阵Wn (n = 1, 2, 3, 4).
步骤5. 接下来通过LSB算法将P7嵌入到矩阵Wn中. 算法描述如式(18)所示. 其中, 符号
| \left\{ \begin{gathered} W_1^n(1, 2) = P_7^n(1, 2), {\text{ }}W_2^n(3, 4) = P_7^n(3, 4) \\ W_3^n(5, 6) = P_7^n(5, 6), {\text{ }}W_4^n(7, 8) = P_7^n(7, 8) \\ \end{gathered} \right. | (18) |
步骤6. 最后, 对组合后的矩阵W进行反GOL置乱生成具有视觉意义的密文图像H.
4 解密算法解密算法与加密算法是互逆的. 解密方可以由密钥生成的密码流和受控的混沌测量矩阵对密文图像H进行一系列逆操作, 包括提取、解密及重建等, 进而成功得到解密图像. 具体解密过程如下.
步骤1. 首先将接收到的密钥迭代新混沌系统构造解密过程中的密码流和受控的混沌测量矩阵φ.
步骤2. 将GOL置乱后得到的密文图像记为H1, 通过LSB提取算法从矩阵H1中提取出加密矩阵P7.
步骤3. 根据式(19)和式(20)进行双向的逆加模扩散操作, 将置乱后的矩阵P5从加密矩阵中求解出来.
| \left\{ \begin{gathered} P_6^{(end)} = P_7^{(end)} - {A_1} - {O^{(end)}}\bmod {\text{ }}256 \\ P_6^{(end - n)} = P_7^{(end - n)} - P_7^{(end - n + 1)} - {O^{(end - n)}}\bmod {\text{ }}256 \\ \end{gathered} \right. | (19) |
| \left\{ \begin{gathered} P_5^{(1)} = P_6^{(1)} - {A_0} - {O^{(1)}}\bmod {\text{ }}256 \\ P_5^{(n)} = P_6^{(n)} - P_6^{(n - 1)} - {O^{(n)}}\bmod {\text{ }}256 \\ \end{gathered} \right. | (20) |
步骤4. 对逆扩散得到的矩阵P5进行逆量化操作, 如式(21)所示:
| {P_4} = \frac{{{P_5} \times (pmax - pmin)}}{{255}} + pmin | (21) |
步骤5. 根据贝叶斯重构算法从压缩加密矩阵P4中恢复出稀疏矩阵P3.
步骤6. 对矩阵P3进行逆Arnold置乱和逆二维小波包变换得到最终的解密图像, 解密过程完成.
5 实验结果 5.1 仿真环境设置实验在Matlab R2020a仿真平台和一台2.90 GHz CPU、8 GB内存, 操作系统为微软Windows 10的台式机上进行. 加密过程中所设置的内部密钥[x0, y0, a, v0, v1] =[−0.1, 0.2, 4, 0.678, 0.789], 其余的加密参数设置为压缩比CR = 0.25, d = 25, TS = 25.
5.2 加解密结果随机选取两组大小均为512×512的明文图像和载体图像进行仿真实验, 实验结果如图5所示.

|
图 5 视觉安全图像加密算法的加解密结果 Fig. 5 Encryption and decryption results of visual security image encryption algorithm. |
直观来看, 图5(a)和图5(e)是明文图像及其相应的解密图像, 可以看出本文所提出的方案在解密过程中能够高度还原出明文图像; 图5(c)是经过压缩加密后的秘密图像, 其大小是明文图像的1/4, 证明所提出方案具有很好的压缩性能; 图5(b)和图5(d)是载体图像和密文图像, 可以看出该方案最终的加密结果产生了一幅几乎和载体图像无差别的图像, 在一定程度上保证了明文图像内容和视觉上的安全性.
另外, 分别计算两组实验中明文图像和解密图像以及载体图像和密文图像的峰值信噪比(peak signal- to-noise ratio, PSNR)[18]和平均结构相似度(mean structural similarity, MSSIM)[19]两个指标来定量分析解密图像的质量和密文图像的不可感知性. 前者的平均值为37.3499 dB, 0.9400, 后者的平均值为47.1338 dB, 0.9973. 经过定量分析可知本算法具有良好的视觉安全性和解密质量.
5.3 性能分析 5.3.1 密钥分析密钥空间的大小决定VMIE算法抵抗暴力攻击的能力. 理论上, 如果加密系统的密钥空间大于2100, 则认为在当前计算速度下, 加密系统可以有效抵抗穷举攻击. 在我们所提出的方案中, 将二维超混沌系统以及新一维混沌映射的初始值作为加解密过程中的密钥, 即x0, y0, a, v0, v1. 如果计算机的精度为10–14, 密钥空间就能达到(1014)5 = 1070, 远远大于2100. 除此之外, 一些参数也可以作为辅助密钥, 如CR, d, TS, pmax, pmin 来提高算法的安全性, 因此我们所提出的方案有足大的密钥空间以抵抗暴力攻击.
5.3.2 直方图分析直方图直观地反映了图像中各个灰度值的分布情况. 由于本文所提出的方案最终生成的是具有视觉意义的图像, 可以通过分析载体图像和密文图像的相似程度来衡量抵抗直方图分析攻击的能力. 本文引入直方图相交距离(数学表达式见式(22))来评估载体图像和密文图像之间的相似程度.
| H(C, E) = \sum\limits_{k = 1}^L { \min ({C_k}, {E_k})} \cdot {\left( {\sum\limits_{k = 1}^L {{E_k}} } \right)^{ - 1}} | (22) |
其中, C和E分别是载体图像和密文图像的直方图, 每个包含L个单元. H(C, E)的值越接近1, 表示两个直方图之间的相似程度越高. 实验结果如表1所示. 从表中可以看出, 距离非常接近1, 表明所提出的方案具有非常好的视觉安全性.
| 表 1 直方图分析的实验结果 Table 1 Experimental results of histogram analysis. |
5.3.3 相关性分析
相关系数通常用来评估图像中相邻像素之间的相关关系. 对于有意义的图像来说, 相邻像素之间的相关系数应该接近1, 有效的密码系统可以显著减小图像的相关性. 为了评估相邻像素之间的相关性, 选取大小为512×512的明文图像Lena和与其大小相等的载体图像Baboon进行实验, 得到秘密图像和隐写图像. 在测试中, 从明文图像、秘密图像、载体图像、隐写图像中随机选择10000对相邻像素, 然后相关系数在水平、垂直、对角线方向通过式(23)计算:
| {r_{xy}} = \frac{{E(x - E(x))E(y - E(y))}}{{\sqrt {D(x)} \sqrt {D(y)} }} | (23) |
其中, 符号x和y记作是相邻的像素,
常用像素变化率(number of pixels change rate, NPCR)和归一化平均变化强度(unified average chang-ing intensity, UACI)[20]来衡量明文图像的敏感性, 上述两个指标通常用于对处理后的图像进行定量和定性分析, 以确定图像是否能抵抗差分攻击. 将原始明文图像和修改像素值后的明文图像分别加密, 比较明文图像的微小变化对秘密图像产生的, 这里不考虑其嵌入过程, 实验结果如表3所示. 从表中数值可以看出, 在原始明文图像和修改后的明文图像总的像素值保持不变的情况下, 通过所提出方案产生的秘密图像的NPCR和UACI的值均接近于理论值, 这表明本文提出的VMIE算法具有一定的抗差分攻击的能力.
5.3.5 视觉安全性分析对于VMIE算法来说, 其视觉安全性是通过载体图像和密文图像的相似程度来衡量的. 定量的来看, 分别计算本文载体图像与密文图像的峰值信噪比和平均结构相似性并将其结果记录于表4中, 进而与现有加密方案进行对比分析. 从表4中可以看出在本文所提出方案中, 载体图像和密文图像之间的PSNR平均达到47.7354 dB, 平均结构相似性平均达到0.9978, 远远优于其他方案, 保证了加密方案具备非常不错的视觉安全性.
5.3.6 解密质量分析由于本文所提出的加密方案采用了无损嵌入的过程, 理论上来说嵌入和提取操作是完全可逆的, 这也意味着载体图像的选取不会影响解密质量. 但本方案在加密过程中存在量化过程和取整操作, 会在一定程度上影响解密图像的质量. 因此, 对于本方案的解密质量进行测试和评估是有必要的. 选取与对比文献相同的图像进行实验, 仿真实验得到的数据列于表5中. 从表中可以看出, 不管选择哪幅载体图像都没有对本算法的解密质量产生影响, 明文图像和解密图像的PSNR和MSSIM都达到了理想值, 明显优于其他方案. 经分析可知所提VMIE算法具有良好的解密质量.

|
图 6 像素相关性分析 Fig. 6 Pixels correlation analysis: (a)−(c) are correlation plots of plain image “Couple” in horizontal, vertical and diagonal direc- tions; (d)−(f) are correlation plots of secret image in horizontal, vertical and diagonal directions; (g)−(i) are correlation plots of carrier image “Airplane” in horizontal, vertical and diagonal di- rections; (j)−(l) are correlation plots of cipher image in horizon- tal, vertical and diagonal directions, respectively. |
| 表 2 各图像的相关系数 Table 2 Correlation coefficients of plain image, secret image, carrier image and cipher image. |
| 表 3 抗差分攻击分析的实验结果 (%) Table 3 Experimental results of differential attack analysis. |
5.3.7 鲁棒性分析
考虑到隐写图像在信道传输过程中可能会遭受不同类型噪声的攻击和裁剪攻击, 这在一定程度上为重建图像增加了难度, 因此一个好的加密方案需要具备能够抵抗噪声攻击和裁剪攻击的能力. 通过在密文图像上加入不同强度的椒盐噪声、乘性噪声、高斯噪声以及 30×30裁剪块来测试我们的方案抵抗噪声攻击和裁剪攻击的能力. 实验结果如图7所示. 可以看出, 即使在不同强度的噪声攻击及裁剪攻击的干扰下, 解密图像中仍然能清晰地呈现出人物的轮廓信息. 由此来看, 本算法具有一定的抗噪抗裁剪能力.
5.4 时间复杂度分析一个好的加密算法不但要保证其安全性, 还应考虑其时间复杂度. 本节从以下4个阶段分析本文所提出的视觉意义图像加密算法的时间开销. 第1阶段为密钥流生成阶段, 迭代二维超混沌系统和新余弦混沌映射生成混沌序列需要
| 表 4 视觉安全性分析的实验结果 Table 4 Experimental results of visual safety analysis |
| 表 5 解密质量分析的实验结果 Table 5 Experimental results of decryption quality analysis |

|
图 7 鲁棒性分析的实验结果 Fig. 7 Experimental results of robustness analysis. |
选取图像尺寸为512×512的明文图像进行加密, 将4个阶段所占用的加密时间以百分比的形式呈现在图8中, 可以看出嵌入阶段约占整个加密时间的3/5. 因此, 当对大规模图像进行加密时建议采取分块处理的方式处理各个子图像块, 以实现并行操作, 提高加密算法的运行效率.

|
图 8 每个阶段所消耗的时间占总加密时间的百分比 Fig. 8 The percentage of time consumed by each part to the total encryption time. |
6 结论
本文基于新余弦混沌映射和BCS模型提出了一种VMIE算法, 实现了对明文信息视觉和内容的双重保护. 在密钥流生成阶段, 新余弦混沌映射和二维超混沌系统共同控制以生成该加密算法所需的密钥流, 提高加密系统的安全性. 在加密阶段, 借助BCS模型, 经过二维Arnold置乱、线性测量以及双向加模扩散生成视觉无意义的秘密图像, 保证了图像的内容安全. 在嵌入阶段, 将秘密图像通过LSB嵌入算法无损地隐藏在经过处理的载体图像中, 以完成对秘密图像的视觉加密. 最后, 仿真实验和性能分析表明所提出方案满足各项安全评估指标, 且能够抵抗常见的各种攻击, 适合于图像安全通信. 在未来, 进一步探究在保证算法安全高效实现的前提下提高明文图像的稀疏率以达到更高的压缩率是有意义的.
| [1] |
Özkaynak F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dynamics, 2018, 92(2): 305-313. DOI:10.1007/s11071-018-4056-x |
| [2] |
蒋东华, 刘立东, 王兴元, 等. 基于细胞神经网络和并行压缩感知的图像加密算法. 图学学报, 2021, 42(6): 891-898. |
| [3] |
朱礼亚, 张曦, 张亮. 基于并行压缩感知与混沌映射的图像加密方案设计. 微电子学与计算机, 2019, 36(10): 96-102. DOI:10.19304/j.cnki.issn1000-7180.2019.10.019 |
| [4] |
Yang YG, Tian J, Lei H, et al. Novel quantum image encryption using one-dimensional quantum cellular automata. Information Sciences, 2016, 345: 257-270. DOI:10.1016/j.ins.2016.01.078 |
| [5] |
黄林荃, 刘会, 王志颖, 等. 结合混沌映射与DNA计算的自适应图像加密算法. 小型微型计算机系统, 2020, 41(9): 1959-1965. DOI:10.3969/j.issn.1000-1220.2020.09.027 |
| [6] |
吕群, 薛伟. 结合混沌系统和动态S-盒的图像加密算法. 小型微型计算机系统, 2018, 39(3): 607-613. DOI:10.3969/j.issn.1000-1220.2018.03.038 |
| [7] |
Wang XY, Liu C, Jiang DH. A novel triple-image encryption and hiding algorithm based on chaos, compressive sensing and 3D DCT. Information Sciences, 2021, 574: 505-527. DOI:10.1016/j.ins.2021.06.032 |
| [8] |
蒋东华, 刘立东, 陈颖频, 等. 基于分数阶Chen超混沌系统和压缩感知的可视化图像加密算法. 小型微型计算机系统, 2022, 43(11): 2387–2393.
|
| [9] |
Bao L, Zhou YC. Image encryption: Generating visually meaningful encrypted images. Information Sciences, 2015, 324: 197-207. DOI:10.1016/j.ins.2015.06.049 |
| [10] |
Chai XL, Gan ZH, Chen YR, et al. A visually secure image encryption scheme based on compressive sensing. Signal Processing, 2017, 134: 35-51. DOI:10.1016/j.sigpro.2016.11.016 |
| [11] |
Wang H, Xiao D, Li M, et al. A visually secure image encryption scheme based on parallel compressive sensing. Signal Processing, 2019, 155: 218-232. DOI:10.1016/j.sigpro.2018.10.001 |
| [12] |
Zhu LY, Song HS, Zhang X, et al. A robust meaningful image encryption scheme based on block compressive sensing and SVD embedding. Signal Processing, 2020, 175: 107629. DOI:10.1016/j.sigpro.2020.107629 |
| [13] |
张修引, 曾齐红, 邵燕林, 等. 二维超混沌系统的研究及在图像加密中的应用. 计算机技术与发展, 2020, 30(5): 103-108. DOI:10.3969/j.issn.1673-629X.2020.05.020 |
| [14] |
Donoho DL. Compressed sensing. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [15] |
Ji SH, Xue Y, Carin L. Bayesian compressive sensing. IEEE Transactions on Signal Processing, 2008, 56(6): 2346-2356. DOI:10.1109/TSP.2007.914345 |
| [16] |
Hua ZY, Zhou YC, Huang HJ. Cosine-transform-based chaotic system for image encryption. Information Sciences, 2019, 480: 403-419. DOI:10.1016/j.ins.2018.12.048 |
| [17] |
Mansouri A, Wang XY. A novel one-dimensional chaotic map generator and its application in a new index representation-based image encryption scheme. Information Sciences, 2021, 563: 91-110. DOI:10.1016/j.ins.2021.02.022 |
| [18] |
Parah SA, Sheikh JA, Loan NA, et al. Utilizing neighborhood coefficient correlation: A new image watermarking technique robust to singular and hybrid attacks. Multidimensional Systems and Signal Processing, 2018, 29(3): 1095-1117. DOI:10.1007/s11045-017-0490-z |
| [19] |
Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [20] |
Wu Y, Noonan JP, Agaian S. NPCR and UACI randomness tests for image encryption. Cyber Journals: Multidisciplinary Journals in Science and Technology, Journal of Selected Areas in Telecommunications, 2011, 1(2): 31. |
 2023, Vol. 32
2023, Vol. 32



