基于混合策略的改进哈里斯鹰优化算法

引用本文

张海林, 陈泯融. 基于混合策略的改进哈里斯鹰优化算法. 计算机系统应用, 2023, 32(1): 166-178.http://www.c-s-a.org.cn/1003-3254/8911.html

Zhang HL, Chen MR. Improved Harris Hawks Optimization Algorithm Based on Hybrid Strategy. Computer Systems and Applications, 2023, 32(1): 166-178(in Chinese).http://www.c-s-a.org.cn/1003-3254/8911.html

基于混合策略的改进哈里斯鹰优化算法

张海林, 陈泯融

华南师范大学计算机学院, 广州 510631

收稿日期：2022-06-11; 修改日期：2022-07-06; 采用时间：2022-07-20; csa 在线出版时间：2022-09-08

基金项目：国家自然科学基金(61872153, 61972288)

通讯作者：陈泯融, E-mail: chenminrong@scnu.edu.cn.

摘要：针对原始哈里斯鹰优化算法(HHO)存在的收敛精度低、收敛速度慢、易陷入局部最优等不足, 提出了一种基于混合策略的改进哈里斯鹰优化算法(HSHHO). 首先, 在种群初始化阶段引入Sobol序列, 生成均匀分布的种群, 提高种群的多样性, 有利于提高算法的收敛速度; 其次, 引入limit阈值, 令算法在一定迭代次数没有获得更优值后执行全局探索操作, 提高算法跳出局部最优解的能力, 改善HHO在迭代后期只执行开发阶段而易陷入局部最优的缺陷; 最后, 提出一种动态的反向学习机制, 提高算法的收敛精度以及跳出局部最优的能力. 在9个基准函数和6个CEC2017函数上进行测试, 与其他多种优化算法、HHO变体作对比, 验证所提出策略的有效性, 并进行Wilcoxon符号秩检验、Friedman检验和Quade检验等非参数检验. 实验结果表明, HSHHO在收敛速度、寻优精度和统计测试方面具有较为优秀的性能. 最后, 还应用到焊接梁设计优化问题, 结果表明改进的算法对于带约束的实际工程优化问题也具有更好的效果.

关键词: 函数优化哈里斯鹰优化算法 Sobol序列 limit阈值动态反向学习

Improved Harris Hawks Optimization Algorithm Based on Hybrid Strategy

ZHANG Hai-Lin, CHEN Min-Rong

School of Computer Science, South China Normal University, Guangzhou 510631, China

Abstract: Original Harris hawks optimization (HHO) has low convergence accuracy and slow convergence speed and is easy to fall into local optimum. In view of these problems, an improved HHO based on a hybrid strategy (HSHHO) is proposed. Firstly, the Sobol sequence is introduced in the population initialization stage to generate a uniformly distributed population, which enriches the diversity of the population and helps to improve the convergence speed of the algorithm. Secondly, the limit threshold is introduced to make the algorithm perform global exploration when it does not obtain a better value within a certain number of iterations. This can improve the ability of the algorithm to jump out of a locally optimal solution and solve the problem that HHO is prone to fall into a locally optimal solution in late iterations because it only executes the development phase. Finally, a dynamic backward learning mechanism is proposed to improve the algorithm’s convergence accuracy and ability to jump out of the local optimum. The proposed algorithm is tested by nine benchmark functions and six CEC2017 functions and compared with various optimization algorithms and HHO variants. As a result, this study verifies the effectiveness of the proposed strategies and performs Wilcoxon signed rank test, Friedman test, and Quade test. The experimental results show that HSHHO has great performance in terms of convergence speed, optimization accuracy, and statistical tests. Furthermore, the proposed algorithm is applied to the design optimization of welded beams. The results show that HSHHO also has a positive effect on practical engineering optimization problems with constraints.

Key words: function optimization Harris hawks optimization (HHO) Sobol sequence limit threshold dynamic opposition-based learning

优化问题是指寻求问题的最佳解决方案, 即求目标函数的最大值或者最小值. 优化问题广泛存在于工程设计、医学、科学研究、经济管理等领域^[1], 有效地处理优化问题对于各领域都存在重大的帮助. 然而, 一些传统的数学优化方法例如拟牛顿法、共轭梯度法和顺序二次规划比较复杂, 受限性高, 对于各种复杂的、不可微的优化问题无法高效求解^[2]. 元启发式算法因其不受限于具体问题、不需要梯度等信息、思想简单等备受人们关注, 广泛用于优化求解问题^[3]. 在元启发式算法中有一类是基于群体智能的方法, 该类方法是模拟自然界中群体的行为, 通过群体的智慧寻求最优解, 如粒子群算法(particle swarm optimization, PSO)^[4]、蝙蝠算法(bat algorithm, BA)^[5]、灰狼优化算法(grey wolf optimizer, GWO)^[6]、鲸鱼优化算法(whale optimization algorithm, WOA)^[7]、樽海鞘算法(salp swarm algorithm, SSA)^[8]、蝴蝶优化算法(butterfly optimization algorithm, BOA)^[9], 飞蛾扑火算法(Moth-flame optimization algorithm, MFO)^[10]等. 群智能优化算法是近年来倍受关注的研究领域之一, 基于群体智能的方法不受具体问题的各种约束限制、通用性强、容易实现、优化效率高, 已经应用于许多实际问题, 展现了良好的应用前景.

哈里斯鹰优化算法(HHO)是Heidari等人^[11]在2019年提出的一种基于群体智能的元启发算法, 模拟了哈里斯鹰合作觅食以及多种策略包围猎物的行为. 哈里斯鹰算法包含了探索和开发两个阶段, 通过猎物逃逸能量在两个阶段之间切换. 哈里斯鹰对比其他的群体智能优化算法有较强的竞争力^[12], 已经应用在各种优化问题上. Hussain等人^[13]将HHO用于特征选择; Rodriguez-Esparza等人^[14]将HHO应用到图像分割领域; 刘小宁等人^[15]将HHO用于求解作业车间调度问题. Gharehchopogh等人^[16]将HHO用于求解旅行商问题. 但是, 根据无免费午餐(NFL)定理^[17], 没有算法能在所有优化问题上取得优异效果. HHO也存在收敛精度低、收敛速度慢、探索与开发阶段不平衡等问题. 针对哈里斯鹰优化算法展开研究, 对它的一些不足进行改进, 完善哈里斯鹰优化算法, 提高算法的性能和效率, 并应用于函数优化问题以及一些实际的问题, 有效地提高解决实际优化问题的效率, 具有非常重要的理论和现实意义. 近年来, 有很多研究针对哈里斯鹰算法的改进, 如Chen等人^[18]将混沌策略、多种群策略和差分进化策略引入HHO中; Kamboj等人^[19]将正余弦算法结合到HHO中, 增强了HHO的性能. Al-Betar等人^[20]在探索阶段对于随机个体采用了3种选择策略, 并引入了3个新的选择策略版本, 探讨3个版本对于算法性能的影响. Hussien等人^[21]提出了一种改进的基于对抗学习、混沌局部搜索和自适应技术相结合的哈里斯鹰优化算法.

上述文献在一定程度上提升了HHO的性能, 但是HHO在收敛速度、收敛精度、跳出局部最优等方面仍有较大的提升空间. 本文提出了一种基于混合策略的改进哈里斯鹰优化算法(HSHHO). 利用Sobol序列生成更为均匀分布的初始种群, 使得种群在初始阶段便能尽可能地均匀分布在搜索空间, 提高了种群的多样性, 更好地进行全局搜索, 提高了算法的收敛速度. 设定limit阈值, 在一定迭代次数后种群仍无法获得更好的解时, 执行全局搜索阶段, 弥补HHO在迭代后期只执行局部开发而导致容易陷入局部最优的不足. 提出一种动态的反向学习机制, 提高算法的收敛精度以及跳出局部最优的可能性. 通过多个单模态、多模态的基准函数和CEC2017函数测试, 验证了所提出算法的有效性, 并应用到焊接梁设计优化这种实际工程设计优化问题上.

1 哈里斯鹰优化算法(HHO)

HHO是一种新型的群体智能优化算法. 该算法模拟了哈里斯鹰的捕食特点, 分为探索和开发两个阶段, 并通过猎物逃逸能量进行这两个阶段的切换. 哈里斯鹰最大的特点便是合作觅食, 并能根据环境的变化和猎物的逃逸模式表现出多种攻击模式. 在HHO中, 哈里斯鹰个体组成候选解, 每一次迭代中适应度最高的个体视为猎物.

1.1 探索阶段

在这一阶段, 哈里斯鹰通过两种策略更新自己的位置, 一是基于随机选择的一个个体信息和自身信息进行探索, 二是基于目前的最优个体以及所有个体的平均信息进行探索, 两种策略的执行机会相等, 由参数q决定, 数学模型如下:

$ \begin{split} &{X_i}(t + 1) = \\ &\left\{ {\begin{array}{*{20}{l}} {{X_{{\rm{rand}}}}(t) - {r_1}\left| {{X_{{\rm{rand}}}}(t) - 2{r_2}{X_i}(t)} \right|},&{q \geqslant 0.5} \\ {({X_{{\rm{prey}}}}(t) - {X_m}(t)) - {r_3}(LB + {r_4}(UB - LB))},&{q < 0.5} \end{array}} \right. \end{split} $

(1)

其中, X_i(t+1)和X_i( t)分别代表了第i个个体在第t+1次迭代和第t次迭代时的位置, q, r₁, r₂, r₃, r₄是0–1之间的随机数, UB和 LB代表搜索空间的上下界, X_rand(t)指t时刻在种群中随机选择的一个个体, X_prey(t)指t时刻时种群中适应度最高的个体, X_m(t)是t时刻种群所有个体的平均位置, 其定义如下:

$ {X_m}(t) = \frac{1}{N}\sum\limits_{i = 1}^N {{X_i}(t)} $

(2)

其中, N代表种群中的个体数目.

1.2 探索阶段转向开发阶段

在HHO算法中, 定义了猎物逃逸能量E, 模拟猎物在逃跑过程中的体力消耗. 当|E|≥1时, 算法执行探索阶段, 模拟哈里斯鹰寻找猎物的过程, 当|E|<1时, 哈里斯鹰追捕猎物, 进入开发阶段. 猎物逃逸能量E的变化公式如下:

$ {E_1} = 2 \times \left(1 - \frac{t}{T}\right) $

(3)

$ E = {E_2} \times {E_1} $

(4)

其中, E₂代表能量的初始值, 范围在−1到1之间, 在每次迭代时随机产生, T代表最大迭代次数.

1.3 开发阶段

为了较为真实地模仿哈里斯鹰实际的围攻行为, HHO引入了4种策略. 定义参数r表示猎物在哈里斯鹰突袭前能成功逃脱(r<0.5)或不能成功逃脱(r≥0.5)的机会. 根据参数r和猎物逃逸能量E共同决定采用哪种策略.

1.3.1 软围攻

当|E|≥0.5且r≥0.5时, 猎物体力充沛, 通过一些随机的跳跃行为来试图逃脱包围圈. 在这个过程中, 哈里斯鹰对猎物进行高空软包围操作, 不断消耗猎物的能量, 待猎物精疲力竭后, 进行猛扑捕获猎物. 采用数学模型描述如下:

$ {X_i}(t + 1) = \Delta X(t) - E\left| {J{X_{{\rm{prey}}}}(t) - {X_i}(t)} \right| $

(5)

$ \Delta X(t) = {X_{{\rm{prey}}}}(t) - {X_i}(t) $

(6)

其中, ΔX(t)指t时刻最优个体与个体i的位置差值, J是指猎物在逃跑过程时的跳跃行为, 值为2(1–r₅), r₅是0–1之间的一个随机数.

1.3.2 硬围攻

当|E|<0.5且r≥0.5时, 猎物精疲力竭, 没有足够的能量和机会进行逃跑. 哈里斯鹰这时采取硬围攻的方式, 对猎物进行猛扑.

$ {X_i}(t + 1) = {X_{{\rm{prey}}}}(t) - E\left| {\Delta X(t)} \right| $

(7)

1.3.3 渐进式快速俯冲的软围攻

当|E|≥0.5且r <0.5时, 猎物有足够的能量成功逃跑. 这时, 哈里斯鹰会采取更加智能的软包围策略, 进行多次俯冲行为, 逐渐调整自己的方向和位置. 这个策略下, 哈里斯鹰采取两个步骤. 第1个步骤的规则如下:

$ Y = {X_{{\rm{prey}}}}(t) - E\left| {J{X_{{\rm{prey}}}}(t) - {X_i}(t)} \right| $

(8)

然后, 判断这次俯冲有没有取得更好的效果, 如果没有取得更优值, 哈里斯鹰在接近猎物时会突然做出不规则的快速俯冲:

$ Z = Y + S \times LF(D) $

(9)

其中, D是指优化问题的维度, S是一个1×D维的随机向量, LF是莱维飞行^[22] . LF的表达式如下:

$ LF(x) = 0.01 \times \dfrac{{u \times \sigma }}{{{{\left| v \right|}^{\frac{1}{\beta }}}}}, \sigma = {\left( {\dfrac{{\tau (1 + \beta ) \times \sin\left(\dfrac{{\pi \beta }}{2}\right)}}{{\tau \left(\dfrac{{1 + \beta }}{2}\right) \times \beta \times {2^{\left( {\frac{{\beta - 1}}{2}} \right)}}}}} \right)^{\frac{1}{\beta }}} $

(10)

其中, u, v是(0, 1)之间的随机数, $\;\beta $ 是常量1.5. 因此, HHO在渐进式快速俯冲的软围攻策略的更新公式为:

$ {X_i}(t + 1) = \left\{ {\begin{array}{*{20}{c}} {Y, }&{F(Y) < F({X_i}(t))} \\ {Z, }&{F(Z) < F({X_i}(t))} \end{array}} \right. $

(11)

1.3.4 渐进式快速俯冲的硬围攻

当|E | <0.5且 r <0.5时, 猎物有机会逃跑, 但是体力不足. 哈里斯鹰形成一个硬包围圈, 缩小它们群体和猎物之间的平均距离, 然后采取俯冲捕获猎物. 数学模型如下:

$ \dot Y = {X_{{\rm{prey}}}}(t) - E\left| {J{X_{{\rm{prey}}}}(t) - {X_m}(t)} \right| $

(12)

$ \dot Z = \dot Y + S \times LF(D) $

(13)

$ {X_i}(t + 1) = \left\{ {\begin{array}{*{20}{c}} {\dot Y, }&{F(\dot Y) < F({X_i}(t))} \\ {\dot Z, }&{F(\dot Z) < F({X_i}(t))} \end{array}} \right. $

(14)

1.3.5 基本HHO算法步骤

步骤1. 设置种群大小N和最大迭代次数T.

步骤2. 随机初始化种群, 计算个体适应度, 得出目前最优个体.

步骤3. 对于每个个体, 更新初始能量E₂, 猎物逃逸能量E, 跳跃强度J.

步骤4. 若|E|≥1, 执行探索策略, 使用式(1)更新位置, 若|E|＜1, 执行开发策略, 根据E和随机参数r分别使用式(5), 式(7), 式(11), 式(14)更新位置.

步骤5. 计算更新个体位置, 更新目前最优个体.

步骤6. 判断是否到达算法停止条件, 若是, 算法结束, 否则, 返回步骤3.

1.3.6 基本HHO缺陷

原始的哈里斯鹰优化算法采取随机初始化种群的方式产生初始种群, 这使得种群在初始阶段不能够均匀地分布在搜索空间中, 难以全面地搜索空间, 使得种群多样性不足. 在算法的后期, HHO只执行局部搜索行为, 使得算法易陷入局部最优解. 另外, 虽然HHO相比其他一些群体优化算法具有较好的性能, 但其搜索精度仍有提高的空间.

2 混合策略改进的哈里斯鹰优化算法

针对第1.3.6节中描述的哈里斯鹰优化算法缺陷, 提出了3种改进策略. 针对原始的哈里斯鹰优化算法采取随机初始化种群的方式产生初始种群而使得种群多样性不足的问题, 利用Sobol序列产生均匀分布序列, 提高种群的多样性, 有利于提高算法的收敛速度. 引入limit阈值策略, 在一定阈值的迭代次数后若算法仍未获得更优解, 则对个体执行全局搜索策略帮助算法跳出局部最优, 改善算法在迭代后期只执行局部搜索而容易陷入局部最优的不足. 提出一种动态的反向学习策略, 提高算法的收敛精度, 也有助于帮助算法跳出局部最优.

2.1 Sobol序列初始化种群

种群初始状态的分布极大地影响着算法的收敛速度和收敛精度^[3] . 在原始的HHO算法中, 种群采用随机化的方式产生. 然而, 这种伪随机方式产生的种群个体分不均匀, 使得算法难以对整个搜索空间进行搜索, 影响了算法的收敛速度和精度. 相比之下, Sobol序列^[23]是一种用确定性拟随机数产生的低差异化序列, 它能尽可能地将点均匀分布在搜索空间中. 用Sobol序列生成种群的表达式如下:

$ {X_i} = LB + {S_n} \times (UB - LB) $

(15)

其中, LB和UB为搜索空间的下界和上界, S_n∈[0, 1]是Sobol序列所产生的随机数.

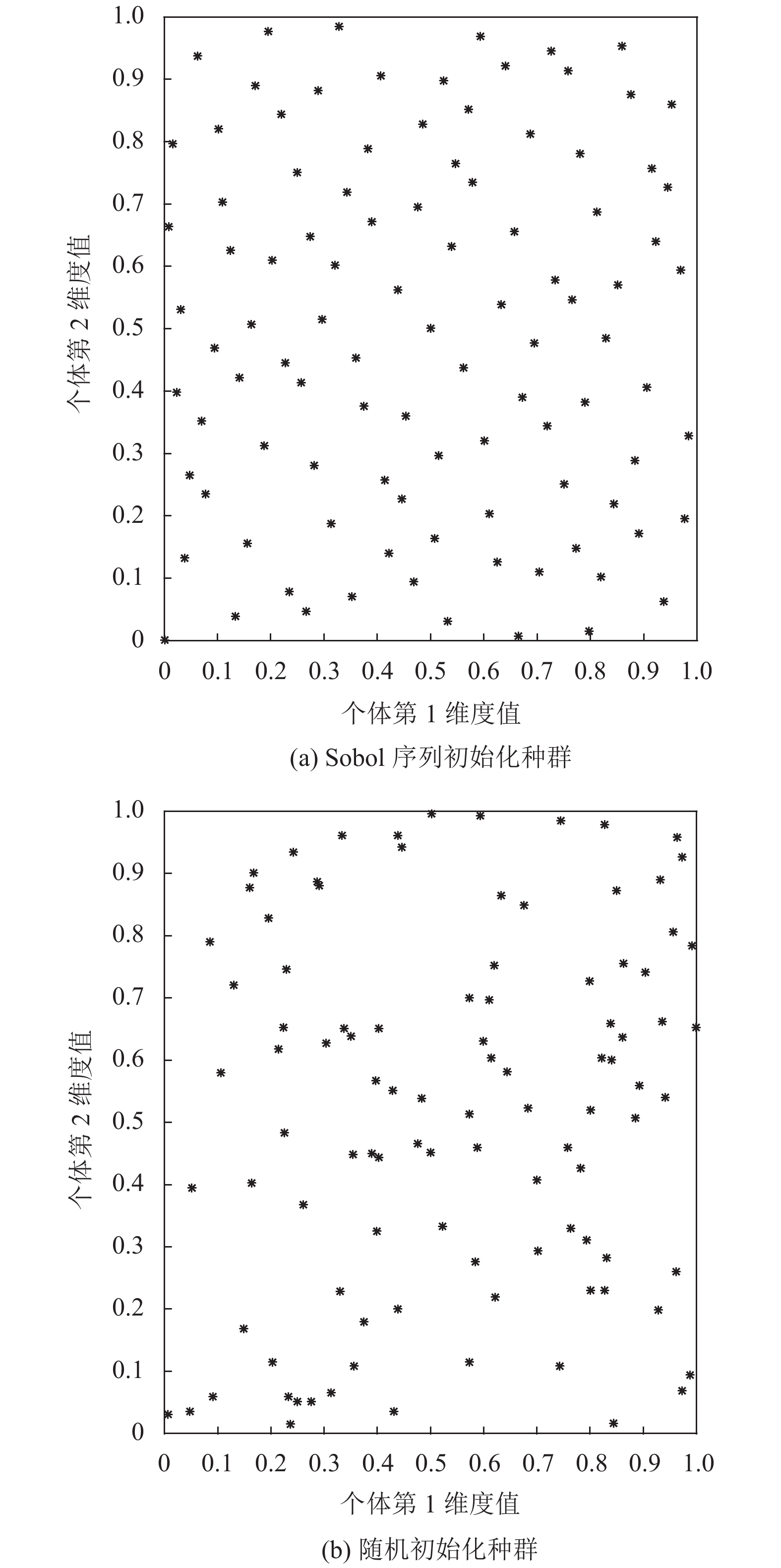
假设搜索空间为2维空间, 下界和上界分别为0和1. 采用随机化初始种群和采用Sobol序列初始化种群的种群个体分布如图1所示.

图 1 Sobol序列生成种群和随机生成种群对比

由图1可得, 采用Sobol序列初始化的种群比随机初始化的种群分布更加地均匀, 这使得算法能够更好地在搜索空间进行全局搜索, 增加了种群的多样性, 提高了算法的收敛速度. 因此, 本文采用Sobol序列初始化种群.

2.2 limit阈值执行全局搜索阶段

在HHO算法中, 当猎物逃逸能量|E|≥1时算法执行全局探索, |E|<1时算法执行局部开发. 根据式(3)和式(4), 可得E随迭代次数变化而变化的图2.

图 2 猎物逃逸能量E变化图

由图2可得, 在迭代次数超过总迭代次数的一半时, |E|一直小于1. 这说明在迭代的后期, 算法只执行局部开发阶段, 这容易导致算法陷入局部最优.

受人工蜂群算法(artificial bee colony algorithm, ABC)^[24]中引入limit阈值观察解的停滞次数而舍弃食物源的启示, 将limit阈值机制引入HHO算法中. limit阈值机制是指预先设定好一个限制次数(limit), 观察在这个限制次数内最优解是否停滞, 如果算法在limit阈值的迭代次数内没有获得更好的最优解, 则进行一定操作. 通过分析, HHO算法在迭代的后期只执行局部开发阶段, 不执行全局搜索阶段而容易陷入局部最优. 因此加入limit阈值机制, 在一定迭代次数后, 算法仍无法获得更好的解, 则使用式(1)对个体执行全局搜索操作生成新个体, 如果新个体的适应度比原个体好, 就用新个体取代原个体, 帮助算法跳出局部最优. 本文的limit取值为5.

2.3 动态反向学习

反向学习是Tizhoosh^[25]于2005年提出的, 其基本思想是为当前解产生一个基于反向学习的解, 同时考虑当前解以及其反向解, 扩大搜索范围.在该解的位置上和其相反位置上同时进行搜索, 能提高获得更优解的可能性. 假设搜索空间为D维, 那么个体X_i在第j维的反向解定义为:

$ {\tilde X_{ij}} = L{B_j} + {\textit{UB}}_j - {X_{ij}} $

(16)

其中, X_ij∈(LB_j, UB_j), j∈1, 2, …, D, UB_j和LB_j是第j维的上下限. 反向学习能够利用自身位置信息生成反向解, 在当前解的反方向上进行探索, 使候选解更有可能获得高质量的解.

但是, 基础的反向学习也有一定局限性. 考虑到在迭代前期自身位置信息的不可靠, 参考价值不大, 因此利用自身位置信息生成的反向解质量也不高. 随着迭代次数的增加, 自身位置信息越来越好, 那么生成的反向解也越来越能够达到真正的反向效果.

因此, 本文提出一种动态的反向学习机制, 给自身位置信息加入动态因子以更好地引导反向解的产生, 表达式如下:

$ {\tilde X_{ij}} = L{B_j} + {\textit{UB}}_j - r \times {X_{ij}} $

(17)

$ r = \sin \left(\frac{t}{T}\right) $

(18)

随着迭代次数t的增加, 动态系数r的值也非线性地越来越大, 代表着个体自身位置随着迭代次数的增加越来越有参考价值. 相比原始的反向学习, 本文所提出的动态反向学习能够生成更好的反向解.

对所有个体进行动态反向学习操作, 并将新产生的反向解群体与原群体混合作适应度的排序, 选择适应度最高的N个个体作为新种群.

2.4 改进算法HSHHO流程图及描述

HSHHO的流程如图3所示. HSHHO的执行步骤如下.

图 3 HSHHO流程图

步骤1. 设置种群大小N和最大迭代次数T.

步骤2. Sobol序列初始化种群, 计算个体适应度, 得出目前最优个体.

步骤3. 对于每个个体, 更新初始能量E₂, 猎物逃逸能量E, 跳跃强度J.

步骤4. 若|E|≥1, 执行探索策略, 使用式(1)更新位置, 若|E|＜1, 执行开发策略, 根据E和随机参数r分别使用式(5), 式(7), 式(11), 式(14)更新位置.

步骤5. 判断在设置的limit阈值内, 种群能否获得更优值, 如果不能则执行探索策略尝试跳出局部最优, 使用式(1)更新位置, 若更新后的位置优于原位置则用更新后的位置取代原位置.

步骤6. 对所有个体使用式(17)进行动态反向学习操作, 将得到的新种群与原种群混合, 贪婪选择前N个最好的个体作为新种群的个体.

步骤7. 计算更新后的个体位置, 更新目前最优个体.

步骤8. 判断是否到达算法停止条件, 若是, 算法结束, 否则, 返回步骤3.

2.5 时间复杂度分析

假设种群中个体数目为N, 问题维度为D, 迭代次数为T. 在原始的HHO算法中, 时间复杂度主要有3部分构成: 初始化、适应度评价、个体位置更新. HHO的时间复杂度为O(N)+O(T×N)+O(T×N×D).

在提出的HSHHO中, 引入Sobol序列初始化种群不会增加额外的时间复杂度. limt阈值进行全局搜索的时间复杂度为O(T×N×D)+O(T×N), 其中O(T×N×D)为执行全局搜索过程产生新个体的时间, O(T×N)为适应度评价时间. 动态反向学习的复杂度为O(T×N×D)+O(T×2N), 其中O(T×N×D)为对个体产生动态反向学习解的时间, O(T×2N)为适应度评价时间.

综上, HSHHO的时间复杂度为O(N)+ O(4×T×N)+O(3×T×N×D), 与原始HHO算法复杂度在数量级上是相同的, 因此并没有增加太多复杂度.

3 仿真实验与结果分析 3.1 实验设置

为了验证提出的HSHHO算法在解决数值优化问题上的性能, 实验选取了9个经典的标准测试函数和6个CEC2017复杂函数中进行评估. 算法在函数上运行得到的结果越小, 代表搜索精度越高. 在9个经典的标准测试函数中, F₁–F₄为单模态函数, 用于检验算法的开发性能, F₅–F₇为多模态函数, 用于检验算法的探索性能和跳出局部最优解的能力, F₈–F₉为固定低维度的多模态函数, 用于检验算法的稳定性. 9个经典的标准测试函数的细节见表1. 在6个CEC2017测试函数f₁–f₆中, 存在单模态、多模态、复合函数等情况, 比较复杂, 用于检验算法在解决复杂的数值优化问题的能力. CEC2017测试函数的细节见表2.

表 1 基准测试函数

函数	维度	范围	最优值	特征
${F_1}(x) = \displaystyle\sum\limits_{i = 1}^n {x_i^2} $	30	[−100, 100]	0	单峰
${F_2}(x) = \displaystyle\sum\limits_{i = 1}^n {\left\| {{x_i}} \right\|} + \prod\limits_{i = 1}^n {\left\| {{x_i}} \right\|} $	30	[−10, 10]	0	单峰
${F_3}(x) = \displaystyle\sum\limits_{i = 1}^{n - 1} {\left[ {100{{({x_{i + 1}} - x_i^2)}^2} + {{({x_i} - 1)}^2}} \right]} $	30	[−30, 30]	0	单峰
${F_4}(x) = \displaystyle\sum\limits_{i = 1}^n {i{x^4} + random[0, 1]} $	30	[−1.28, 1.28]	0	单峰
${F_5}(x) = - 20{\rm{exp} }\left( - 0.2\sqrt {\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} } \right) - {\rm{exp} }(\dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\cos (2\pi {x_i})} ) + 20 + {\rm{e} }$	30	[−32, 32]	0	多峰
${F_6}(x) = \dfrac{\pi }{n}\left\{ {10\sin (\pi {y_1}) + \displaystyle\sum\limits_{i = 1}^{n - 1} {({y_i} - 1} {)^2}\left[ {1 + 10{{\sin }^2}(\pi {y_{i + 1}})} \right] + {{\left( {{y_n} - 1} \right)}^2}} \right\}$ $ + \displaystyle\sum\limits_{i = 1}^n {u({x_i}, 10, 100, 4)} $ ${y_i} = 1 + \dfrac{{{x_i} + 1}}{4}u({x_i}, a, k, m) = \left\{ {\begin{array}{*{20}{l}} {k{{({x_i} - a)}^m}},&{{x_i} > a} \\ 0,&{ - a < {x_i} < a} \\ {k{{( - {x_i} - a)}^m}},&{{x_i} < - a} \end{array}} \right.$	30	[−50, 50]	0	多峰
${F_7}(x) = 0.1\left\{ { { {\sin }^2}(3\pi {x_1}) + \displaystyle\sum\limits_{i = 1}^n { { {({x_i} - 1)}^2}[1 + \sin^2(3\pi {x_i} + 1)]} + { {({x_n} - 1)}^2}[1 + \sin^2(2\pi {x_n})]} \right\} +$ $\displaystyle\sum\limits_{i = 1}^n {u({x_i}, 5, 100, 4)} $	30	[−50, 50]	0	多峰
${F_8}(x) = \displaystyle\sum\limits_{i = 1}^{11} { { {\left[{a_i} - \dfrac{ { {x_1}(b_i^2 + {b_i}{x_2})} }{ {b_i^2 + {b_i}{x_3} + {x_4} } }\right]}^2} }$	4	[−5, 5]	0.00030	多峰
${F_9}(x) = - \displaystyle\sum\limits_{i = 1}^4 { {c_i}\exp \left( - \displaystyle\sum\limits_{j = 1}^6 { {a_{ij} }{ {({x_j} - {p_{ij} })}^2} } \right)}$	6	[0, 1]	−3.322	多峰

表 1 基准测试函数

表 2 CEC2017测试函数

算法的参数设置见表3. 所有实验都在64位Windows 7 操作系统上进行, CPU为 i5-3320M, 主频为2.60 GHz.

表 3 参数设置

3.2 与其他智能优化算法的对比

在本节实验中, 将提出的HSHHO算法与近些年提出的一些新型智能优化算法在9个经典的标准测试函数中作比较. 比较的算法有原始的哈里斯鹰优化算法HHO、鲸鱼优化算法WOA^[7]、樽海鞘算法SSA^[8]、灰狼优化算法GWO^[6]、蝴蝶优化BOA^[9]、飞蛾扑火优化算法MFO^[10]. 每个算法的个体数量设置为30, 运行30次, 每次的迭代次数为500代. 结果如表4所示. 从平均值的角度看, HSHHO在9个基准测试函数上都优于其他对比的算法或者基本相当. 在函数F₁和F₂上, HSHHO能稳定寻得函数最优值0, 其他算法无法寻得最优值. 对于函数F₃, 只有HSHHO能找到函数的最优值. 在函数F₄以及F₆–F₈上, HSHHO在最优值、平均值、最差值以及标准差上均优于其他算法. 在函数F₅上, HSHHO与HHO的性能相当, 优于其他算法. 综上所述, HSHHO算法的性能较为优异.

表 4 与其他智能优化算法的对比

函数名称	函数最优值	算法	最优值	平均值	最差值	标准差
F₁	0	HSHHO	0	0	0	0
		HHO	1.3807E–113	3.2883E–94	9.524E–93	1.7375E–93
		WOA	4.1547E–87	3.1799E–74	5.9442E–73	1.1539E–73
		SSA	3.8758E–08	1.2992E–07	6.5591E–07	8.442E–08
		GWO	2.9928E–29	7.1766E–28	6.7464E–27	1.3178E–27
		BOA	1.1045E–11	1.2793E–11	1.4112E–11	7.505E–13
		MFO	0.31305	3005.769	20001.3664	5348.395
F₂	0	HSHHO	0	0	0	0
		HHO	5.5027E–62	3.3844E–50	1.0025E–48	1.8295E–49
		WOA	5.1941E–58	1.6473E–47	4.9395E–46	9.0181E–47
		SSA	0.31304	2.3002	6.673	1.5948
		GWO	1.1168E–17	1.1966E–16	3.9049E–16	8.8778E–17
		BOA	1.4425E–09	4.0689E–09	5.7363E–09	1.4955E–09
		MFO	0.14525	35.618	80.0211	19.6937
F₃	0	HSHHO	0	2.4213E–06	7.17E–05	1.3086E–05
		HHO	6.991E–05	0.019353	0.15148	0.03021
		WOA	27.1882	28.0909	28.7735	0.47633
		SSA	25.2621	96.364	1561.0287	110.763
		GWO	25.4961	26.6839	27.9564	0.63448
		BOA	28.878	28.9391	28.9846	0.026588
		MFO	260.2402	2672814.0339	79942991.6776	14594024.3112
F₄	0	HSHHO	2.0666E–07	8.2863E–05	0.00032113	8.2162E–05
		HHO	4.0259E–06	0.00015572	0.0012088	0.00022079
		WOA	4.2163E–05	0.0024214	0.01296	0.0028111
		SSA	0.051068	0.17139	0.35208	0.074745
		GWO	0.00050151	0.0019334	0.0037542	0.00096206
		BOA	0.00043866	0.001401	0.0024265	0.00056823
		MFO	0.090447	4.795	35.0181	7.9582
F₅	0	HSHHO	8.8818E–16	8.8818E–16	8.8818E–16	0
		HHO	8.8818E–16	8.8818E–16	8.8818E–16	0
		WOA	8.8818E–16	3.7303E–15	7.9936E–15	2.3603E–15
		SSA	1.3404	2.4724	4.9895	0.56719
		GWO	6.839E–14	9.468E–14	1.1102E–13	1.3636E–14
		BOA	4.2639E–09	6.0963E–09	7.2641E–09	5.9714E–10
		MFO	1.1035	14.4128	19.9641	7.4618
F₆	0	HSHHO	1.5705E–32	1.8778E–07	2.0043E–06	3.9041E–07
		HHO	4.5249E–09	5.139E–06	2.5202E–05	6.1599E–06
		WOA	0.0039956	0.037074	0.29058	0.053503
		SSA	1.9035	7.1311	18.8941	2.7254
		GWO	0.0065551	0.033561	0.071201	0.015182
		BOA	0.38915	0.63306	1.0414	0.17009
		MFO	3.0402	208.6657	5842.8266	1064.2755
F₇	0	HSHHO	1.3498E–32	3.0545E–06	4.5569E–05	9.1472E–06
		HHO	1.3431E–06	0.00011693	0.00074199	0.00016114
		WOA	0.10553	0.62506	1.5405	0.30762
		SSA	0.01646	20.4511	54.0221	15.4907
		GWO	0.21316	0.59833	1.1092	0.23258
		BOA	2.5491	2.9139	2.9999	0.13588
		MFO	2.1435	6478.8439	193519.5135	35326.354
F₈	0.00030	HSHHO	0.00030773	0.0003337	0.00043424	2.8012E–05
		HHO	0.0003083	0.0003439	0.00048665	3.6928E–05
		WOA	0.00030786	0.00067821	0.0022519	0.00048581
		SSA	0.00030751	0.002154	54.0221	0.0049558
		GWO	0.00030769	0.0058614	0.020367	0.0089002
		BOA	0.00030941	0.00037616	0.00049217	5.4588E–05
		MFO	0.0004934	0.00091382	0.0016554	0.00033782
F₉	−3.322	HSHHO	−3.3211	−3.3013	−3.2765	0.010533
		HHO	−3.2907	−3.1006	−2.7214	0.12886
		WOA	−3.3217	−3.266	−3.058	0.080149
		SSA	−3.322	−3.2242	−3.1719	0.055428
		GWO	−3.322	−3.2692	−3.0867	0.074232
		BOA	−3.1138	−2.866	−2.2105	0.2296
		MFO	−3.322	−3.2342	−3.1376	0.060702

表 4 与其他智能优化算法的对比

3.2.1 Wilcoxon符号秩检验结果

为了进一步说明HSHHO与其他算法效果的差异性, 还进行了Wilcoxon符号秩检验^[26] . 当检验结果p的值小于0.05时, 可认为HSHHO与该对比的算法在某函数上具有明显的差异, NaN表示两种算法基本没有差异. 从表5中可以看出, HSHHO与对比的几种算法在绝大部分函数上都有明显的效果差异. 符号 $ + / \approx / - $ 表示HSHHO与其他算法在平均值上对函数结果的优劣统计. 对比HHO算法, HSHHO在7个函数上有明显优异的结果, 另外2个函数上没有明显差异, 但是HSHHO平均值仍然要比HHO好. 与其他算法相比, 除在F₉与WOA算法效果基本相当, HSHHO在所有函数上对比其他算法都有明显的效果.

表 5 Wilcoxon符号秩检验结果

3.2.2 函数收敛性分析

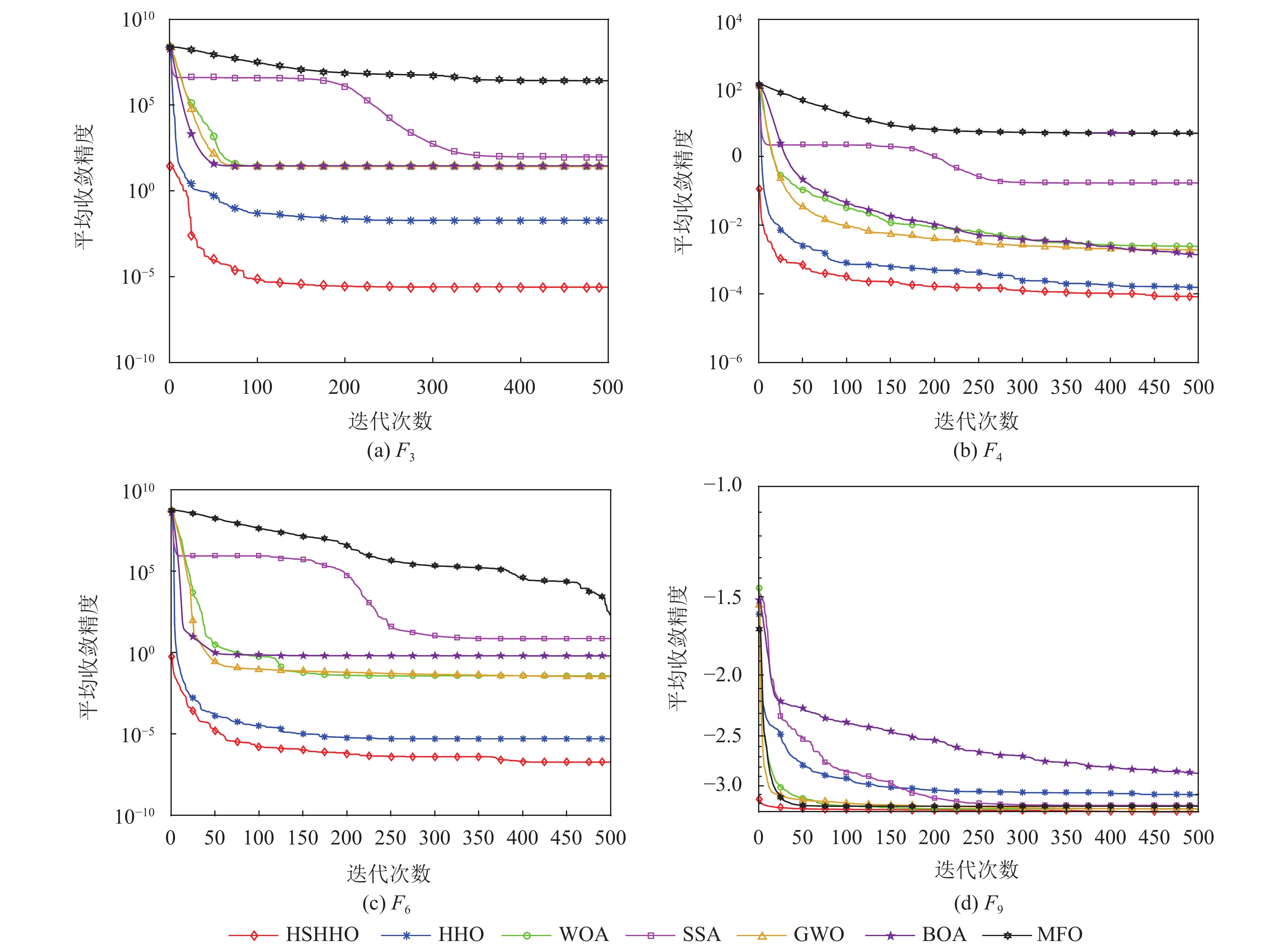
图4展示了部分函数的收敛图. 从图中可以看出, 在所有函数上, 相比于其他算法, HSHHO的收敛速度较快, 收敛精度较高. 由于使用了Sobol序列进行种群初始化, 增加了种群的多样性, HSHHO在迭代开始就能取得较好的结果, 在迭代中期和后期, 有limit策略使用全局搜索阶段和动态反向学习策略, HSHHO能够稳定且快速收敛, 波动性较小.

图 4 部分函数收敛图

3.3 与其他HHO变体的对比

本节实验将HSHHO算法与一些具有较好性能的HHO改良版本进行对比, 包括: HHO-SCA^[19]、QR-HHO^[27]、THHO^[20] . 表6展示了在9个经典的标准测试函数的效果对比. 可以看出, HSHHO在大部分函数上的平均值都是最好或者相当. 与HHO-SCA相比, HSHHO在所有函数上均优于它或者效果基本相当. 与QRHHO相比, HSHHO仅在F₄和 F₈上的平均值略低于它. HSHHO在所有函数上均比THHO的效果要好. 在函数F₅上, 几种算法的效果基本相当. HSHHO的标准差相较于其他算法也较小, 说明所提出的算法稳定性较好. 对结果执行Friedman检验^[28]和Quade检验^[29], 结果如表7所示, HSHHO的排名均是最高, 表明所提出的算法对比其他算法拥有更好的性能.

表 6 与其他HHO变体的对比

函数	指标	HSHHO	HHO-SCA	QRHHO	THHO
F₁	平均值	0	1.86E–91	0	3.11E–102
F₁	标准差	0	9.49E–91	0	1.57E–101
F₂	平均值	0	2.46E–51	3.55E–268	2.27E–51
F₂	标准差	0	1.11E–50	0	9.67E–51
F₃	平均值	2.4213E–06	1.43E–02	1.16E–01	6.80E–03
F₃	标准差	1.3086E–05	2.01E–02	1.06E–01	9.17E–03
F₄	平均值	8.2863E–05	1.22E–04	8.04E–05	2.02E–04
F₄	标准差	8.2162E–05	1.10E–04	5.36E–05	2.23E–04
F₅	平均值	8.8818E–16	8.88E–16	8.88E–16	8.88E–16
F₅	标准差	0	0	0	0
F₆	平均值	1.8778E–07	1.13E–05	9.37E–05	8.15E–06
F₆	标准差	3.9041E–07	1.5E–05	4.81E–05	1.37E–05
F₇	平均值	3.0545E-06	0.000113	1.42E–03	9.24E–05
F₇	标准差	9.1472E–06	0.000166	5.11E–04	1.47E–04
F₈	平均值	0.0003337	3.45E–04	3.12E–04	3.64E–04
F₈	标准差	2.8012E–05	4.03E–05	4.79E–06	3.99E–05
F₉	平均值	−3.3013	−3.09	−3.27	−3.16
F₉	标准差	0.011	1.09E–01	7.71E–02	1.18E–01

表 6 与其他HHO变体的对比

表 7 Friedman和Quade检验结果

3.4 算法改进策略的有效性分析

本部分实验探讨所提出的HSHHO的各种所添加策略的有效性. 用HHO-S1代表仅加入Sobol序列进行种群初始化策略, HHO-S2代表仅加入limit阈值执行全局搜索策略, HHO-S3代表仅加入动态反向学习策略. 如表8所示, 加入的3种策略分别在所有9个函数上对于平均值效果都有一定程度的提升, 也减小了标准差, 说明了所提出策略的有效性. HSHHO综合了这3种策略, 取得的效果是最好的.

表 8 不同的改进策略对基准测试函数影响的对比

函数名称	指标	HHO	HHO-S1	HHO-S2	HHO-S3	HSHHO
F₁	平均值	3.2883E–94	0	9.0903E–144	0	0
F₁	标准差	1.7375E–93	0	4.7253E–143	0	0
F₂	平均值	3.3844E–50	0	2.8719E–85	0	0
F₂	标准差	1.8295E–49	0	9.9755E–85	0	0
F₃	平均值	0.019353	0.0089207	0.0032989	5.189E–06	2.4213E–06
F₃	标准差	0.03021	0.012052	0.0070753	2.8421E–05	1.3086E–05
F₄	平均值	0.00015572	0.00018112	0.00011726	0.0001069	8.2863E–05
F₄	标准差	0.00022079	0.00017185	0.00019234	8.4685E–05	8.2162E–05
F₅	平均值	8.8818E–16	8.8818E–16	8.8818E–16	8.8818E–16	8.8818E–16
F₅	标准差	0	0	0	0	0
F₆	平均值	5.139E–06	7.4502E–06	1.7013E–06	3.1892E–07	1.8778E–07
F₆	标准差	6.1599E–06	1.1414E–05	2.6264E–06	7.9073E–07	3.9041E–07
F₇	平均值	0.00011693	4.5443E–05	2.138E–05	9.24E–05	3.0545E–06
F₇	标准差	0.00016114	5.4336E–05	3.7823E–05	1.7431E–05	9.1472E–06
F₈	平均值	0.0003439	0.00036826	0.00040329	0.0003725	0.0003337
F₈	标准差	3.6928E–05	0.00017428	0.00022602	8.9816E–05	2.8012E–05
F₉	平均值	−3.1006	−3.289	−3.1587	−3.2096	−3.3013
F₉	标准差	0.12886	0.013469	0.085015	0.095855	0.010533

表 8 不同的改进策略对基准测试函数影响的对比

3.5 在CEC2017函数上的对比

将HSHHO用于更复杂的部分CEC2017函数优化, 以测试HSHHO在复杂函数优化上的性能. 将结果与正余弦优化算法SCA^[30]、HHO进行对比, 如表9所示. 表9中的平均值是实际运行所得结果与该函数理论最优值之间的差值. HSHHO在6个函数上的平均值效果相比HHO均有提高, 说明HSHHO在复杂的函数优化上也具有较好的性能. HHO在6个函数上的平均值均比SCA算法要好.

表 9 在CEC2017函数上的对比

3.6 焊接梁设计问题

焊接梁设计问题^[31]是一个经典的工程设计优化问题, 目的是为了在约束条件下寻找最优的焊缝厚度(h)、长度(l)、高度(t)和钢筋厚度(b)这4个变量从而使得焊接梁的制造成本最小. 焊接梁设计问题的数学模型如下:

$ \left\{ {\begin{array}{l} X = [{x_1}, {x_2}, {x_3}, {x_4}] = [h, l, t, b] \\ \min f(X) = 1.10471x_1^2{x_2} + 0.04811{x_3}{x_4}(14.0 + {x_2}) \\ {\rm{s.t.}} \\ {g_1}(X) = \tau (X) - {\tau _{\max }} \leqslant 0 \\ {g_2}(X) = \sigma (X) - {\sigma _{\max }} \leqslant 0 \\ {g_3}(X) = \delta (X) - {\delta _{\max }} \leqslant 0 \\ {g_4}(X) = {x_1} - {x_4} \leqslant 0 \\ {g_5}(X) = P - {P_c}(X) \leqslant 0 \\ {g_6}(X) = 0.125 - {x_1} \leqslant 0 \\ {g_7}(X) = 1.10471x_1^2 + 0.04811{x_3}{x_4}(14.0 + {x_2}) - 5.0 \leqslant 0 \\ {\rm{Range}}:\;0.05 \leqslant {x_1} \leqslant 2.00, 0.25 \leqslant {x_2} \leqslant 1.30, \\ 2.00 \leqslant {x_3} \leqslant 15.00 0.05 \leqslant {x_4} \leqslant 2.00 \end{array} } \right.$

(19)

其中,

$\left\{ { \begin{gathered} \tau (X) = \sqrt {{\tau {'2}} + 2{\tau {'}}{\tau {''}}\frac{{{x_2}}}{{2R}} + {\tau {''2}}} , \;{\tau {'}} = \frac{P}{{\sqrt 2 {x_1}{x_2}}} \\ {\tau {''}} = \frac{{MR}}{J},\; M = P(L + \frac{{{x_2}}}{2}) \\ R = \sqrt {\frac{{x_2^2}}{4} + {{\left(\frac{{{x_1} + {x_3}}}{2}\right)}^2}} ,\; J = 2\left\{ {\sqrt 2 {x_1}{x_2}\left[ {\frac{{x_2^2}}{{12}} + {{\left(\frac{{{x_1} + {x_3}}}{2}\right)}^2}} \right]} \right\} \\ \sigma (X) = \frac{{6PL}}{{{x_3}x_4^2}} \\ \delta (X) = \frac{{4P{L^3}}}{{E{x_3}x_4^2}},\; {P_c}(X) = \frac{{4.013E\sqrt {x_3^2x_4^6} }}{{{L^2}}}\left(1 - \frac{{{x_3}}}{{2L}}\sqrt {\frac{E}{{4G}}} \right) \\ P = 60000lb, L = 14in, E = 30 \times {10^6}psi, G = 12 \times {10^6}psi \\ {\tau _{\max }} = 13600psi, {\sigma _{\max }} = 30000psi, {\delta _{\max }} = 0.25in \\ \end{gathered} } \right.$

(20)

将HSHHO在焊接梁设计问题上的结果与HHO、RANDOM^[32]、GA^[33]、ESs^[34]算法作对比, 如表10所示. 每个算法执行的次数为30次.

表 10 求解焊接梁设计问题的最优解对比

表10展示了几种算法在焊接梁设计问题上寻求到的最优的对于焊缝厚度(x₁)、长度(x₂)、高度(x₃)和钢筋厚度(x₄)这4个变量的取值及对应的成本(最优值). 从表10中可得, HSHHO在对比的几种算法中得到的最优值是最好的, 能够进一步表明HSHHO在解决焊接梁设计问题这种带约束条件的实际工程实际问题也有良好效果, 能够减少焊接梁设计的制造成本.

4 结束语

为了改善哈里斯鹰优化算法收敛精度低、收敛速度慢、易陷入局部最优等缺陷, 本文提出了一种基于混合策略的改进哈里斯鹰优化算法(HSHHO). 利用Sobol序列的均匀性生成尽可能均匀分布搜索空间的种群, 提高种群的多样性, 提高算法的收敛速度; 针对HHO在后期只执行开发阶段而导致容易陷入局部最优的问题, 引入limit机制, 在一定迭代次数后若算法仍不能取得更好的值, 则执行全局搜索阶段帮助跳出局部最优; 提出一种动态反向学习机制以更好地生成反向解, 提高算法的收敛精度和跳出局部最优的能力. 在多个标准基准测试函数以及复杂的CEC2017函数上对提出的算法(HSHHO)进行测试, 实验结果表明, HSHHO算法拥有良好的性能, 有效改进了HHO的缺陷. 将改进的算法进一步应用到焊接梁设计问题这种带约束条件的实际工程实际问题上, 同样也取得了较好的效果. 未来的工作是将改进的算法进一步应用于更多的实际问题.

参考文献

[1]	Jiang QP, Shao F, Lin WS, et al. Optimizing multistage discriminative dictionaries for blind image quality assessment. IEEE Transactions on Multimedia, 2018, 20(8): 2035-2048. DOI:10.1109/TMM.2017.2763321
[2]	Krishna AB, Saxena S, Kamboj VK. A novel statistical approach to numerical and multidisciplinary design optimization problems using pattern search inspired Harris hawks optimizer. Neural Computing and Applications, 2021, 33(12): 7031-7072. DOI:10.1007/s00521-020-05475-5
[3]	Dokeroglu T, Sevinc E, Kucukyilmaz T, et al. A survey on new generation metaheuristic algorithms. Computers & Industrial Engineering, 2019, 137: 106040.
[4]	周蓉, 李俊, 王浩. 基于灰狼优化的反向学习粒子群算法. 计算机工程与应用, 2020, 56(7): 48-56. DOI:10.3778/j.issn.1002-8331.1904-0203
[5]	Chen MR, Huang YY, Zeng GQ, et al. An improved bat algorithm hybridized with extremal optimization and Boltzmann selection. Expert Systems with Applications, 2021, 175: 114812. DOI:10.1016/j.eswa.2021.114812
[6]	Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007
[7]	龙文, 蔡绍洪, 焦建军, 等. 求解大规模优化问题的改进鲸鱼优化算法. 系统工程理论与实践, 2017, 37(11): 2983-2994. DOI:10.12011/1000-6788(2017)11-2983-12
[8]	Mirjalili S, Gandomi AH, Mirjalili SZ, et al. Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 2017, 114: 163-191. DOI:10.1016/j.advengsoft.2017.07.002
[9]	Arora S, Singh S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Computing, 2019, 23(3): 715-734. DOI:10.1007/s00500-018-3102-4
[10]	Mirjalili S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-based Systems, 2015, 89: 228-249. DOI:10.1016/j.knosys.2015.07.006
[11]	Heidari AA, Mirjalili S, Faris H, et al. Harris hawks optimization: Algorithm and applications. Future Generation Computer Systems, 2019, 97: 849-872. DOI:10.1016/j.future.2019.02.028
[12]	Li CY, Li J, Chen HL, et al. Enhanced Harris hawks optimization with multi-strategy for global optimization tasks. Expert Systems with Applications, 2021, 185: 115499. DOI:10.1016/j.eswa.2021.115499
[13]	Hussain K, Neggaz N, Zhu W, et al. An efficient hybrid sine-cosine Harris hawks optimization for low and high-dimensional feature selection. Expert Systems with Applications, 2021, 176: 114778. DOI:10.1016/j.eswa.2021.114778
[14]	Rodríguez-Esparza E, Zanella-Calzada LA, Oliva D, et al. An efficient Harris hawks-inspired image segmentation method. Expert Systems with Applications, 2020, 155: 113428. DOI:10.1016/j.eswa.2020.113428
[15]	刘小宁, 魏霞, 谢丽蓉. 混合哈里斯鹰算法求解作业车间调度问题. 计算机应用研究, 2022, 39(6): 1673-1677. DOI:10.19734/j.issn.1001-3695.2021.11.0640
[16]	Gharehchopogh FS, Abdollahzadeh B. An efficient Harris hawk optimization algorithm for solving the travelling salesman problem. Cluster Computing, 2022, 25(3): 1981-2005. DOI:10.1007/s10586-021-03304-5
[17]	Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. DOI:10.1109/4235.585893
[18]	Chen H, Heidari AA, Chen HL, et al. Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Future Generation Computer Systems, 2020, 111: 175-198. DOI:10.1016/j.future.2020.04.008
[19]	Kamboj VK, Nandi A, Bhadoria A, et al. An intensify Harris hawks optimizer for numerical and engineering optimization problems. Applied Soft Computing, 2020, 89: 106018. DOI:10.1016/j.asoc.2019.106018
[20]	Al-Betar MA, Awadallah MA, Heidari AA, et al. Survival exploration strategies for Harris hawks optimizer. Expert Systems with Applications, 2021, 168: 114243. DOI:10.1016/j.eswa.2020.114243
[21]	Hussien AG, Amin M. A self-adaptive Harris hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection. International Journal of Machine Learning and Cybernetics, 2022, 13(2): 309-336. DOI:10.1007/s13042-021-01326-4
[22]	Yang XS. Firefly algorithm, lévy flights and global optimization. In: Bramer M, Ellis R, Petridis M, eds. Research and Development in Intelligent Systems XXVI. London: Springer, 2010. 209–218.
[23]	Joe S, Kuo FY. Remark on algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Transactions on Mathematical Software, 2003, 29(1): 49-57. DOI:10.1145/641876.641879
[24]	Chen MR, Chen JH, Zeng GQ, et al. An improved artificial bee colony algorithm combined with extremal optimization and Boltzmann selection probability. Swarm and Evolutionary Computation, 2019, 49: 158-177. DOI:10.1016/j.swevo.2019.06.005
[25]	Tizhoosh HR. Opposition-based learning: A new scheme for machine intelligence. Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Vienna: IEEE, 2006. 695–701.
[26]	Demšar J. Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research, 2006, 7: 1-30.
[27]	Fan Q, Chen ZJ, Xia ZH. A novel quasi-reflected Harris hawks optimization algorithm for global optimization problems. Soft Computing, 2020, 24(19): 14825-14843. DOI:10.1007/s00500-020-04834-7
[28]	García S, Fernández A, Luengo J, et al. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Information Sciences, 2010, 180(10): 2044-2064. DOI:10.1016/j.ins.2009.12.010
[29]	Derrac J, García S, Molina D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. DOI:10.1016/j.swevo.2011.02.002
[30]	郎春博, 贾鹤鸣, 邢致恺, 等. 基于改进正余弦优化算法的多阈值图像分割. 计算机应用研究, 2020, 37(4): 1215-1220. DOI:10.19734/j.issn.1001-3695.2018.10.0779
[31]	Sadollah A, Bahreininejad A, Eskandar H, et al. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Applied Soft Computing, 2013, 13(5): 2592-2612. DOI:10.1016/j.asoc.2012.11.026
[32]	Ragsdell KM, Phillips DT. Optimal design of a class of welded structures using geometric programming. Journal of Manufacturing Science and Engineering, 1976, 98(3): 1021-1025.
[33]	Deb K. Optimal design of a welded beam via genetic algorithms. AIAA Journal, 1991, 29(11): 2013-2015. DOI:10.2514/3.10834
[34]	Mezura-Montes E, Coello CAC. A simple multimembered evolution strategy to solve constrained optimization problems. IEEE Transactions on Evolutionary Computation, 2005, 9(1): 1-17. DOI:10.1109/TEVC.2004.836819