1 引言

随着大数据和信息技术的迅速发展, 企业越来越依赖信息管理系统进行组织实施和管理业务. 现代信息系统支持企业内部不同业务流程的执行, 可以从信息系统中提取出描述业务流程执行的事件数据. 过程挖掘^{[1, 2]}是一门较新的研究学科, 它介于数据挖掘和过程建模和分析之间. 它可以通过从当前信息系统的事件日志中提取信息来发现、监控和改进实际的流程. 过程挖掘由3组不同的函数组成, 包括挖掘(discovery)、一致性检查和优化(enhancement).

在业务流程管理系统应用中, 业务过程的实际运行受资源分配、组织协调、过程瓶颈等各个方面的影响, 可能导致业务实际执行不满足预期的模型描述^[3]. 一致性检查^[4]是用以检查业务过程运行事件数据与其行为定义模型之间符合情况的方法. 早期的一致性检查方法主要基于令牌重放(token-based replaying)^[5], 但是当偏差过多时, 这种方法会导致不明确结果^[4]. 为了以一种明确的方式解释和量化偏差, Adriansyah^[6]提出了对齐的方法, 通过将观察到的行为序列映射到流程模型所描述的可执行序列中, 再根据对齐结果可以查看是否存在缺失行为或不当行为.

目前, 对齐已成为一种主流的一致性检查方法. 最优对齐的查找是一个NP-hard问题, 复杂度较高, 为了提高对齐的效率, 部分研究者提出了基于分解技术的一致性检查方法, Polyvyanyy等^[7]提出了简化的RPST(refined process structure tree)结构对业务流程进行分解. Schuster等^[8]利用过程树的层次结构进行一致性检查, 并采用分而治之的思想计算近似的对齐结果. 除分解方法外, 还可以通过降低搜索空间的方法降低算法的复杂度. Song等^[9]利用全局日志的统计信息, 采用启发式规则和迹重放等方法降低搜索空间. 田银花等^[10]提出了新的快速对齐方法(rapid align), 以代价函数为约束条件, 使得搜索空间无冗余结点. 韩咚等^[11]通过计算事件日志的花型模型, 减少计算乘积模型与可达图的次数, 进而提高对齐的效率.

然而, 这些方法都属于离线一致性检查方法, 需要全局的日志信息作为输入, 且日志中的每一条迹都必须是完整的^[12]. 并且只能在流程全部执行完后进行偏差分析, 并不能在流程运行的过程中发现偏差并及时调整. 因此运行时一致性检查成为当前一致性检查研究的新问题^[6,13,14]. 运行时一致性检查是指将业务流程运行时所产生的数据流作为输入, 判断是否与参考模型中的行为一致^[14]. 其难点在于, 针对每个新产生的事件, 如何有效缓解因计算最优对齐结果所带来的高复杂性.

Burattin^[13]提出了一种动态量化偏差行为的方法, 通过构造支持过程重放的一致性迁移系统, 可以实现在线分析事件流. 但是这种方法无法定位出偏差发生的位置. Burattin等^[14]还提出了根据流程活动的所有行为模式来计算运行时一致性的方法, 可以实现从中间阶段进行监控(热启动). 但这两种方法为了性能的提升都降低了结果的准确率, 只能得到对齐的近似解.

目前主流的运行时一致性检查方法是一种计算事件流和过程模型之间最优前缀对齐的方法^[6]. 部分研究在该方法的基础上提出了一定的改进, Zelst等^[15]提出一种增量计算前缀对齐的算法, 通过复用先前计算的前缀对齐提高了求解性能. Schuster等^[16]在Zelst等^[15]的基础上通过增量扩展搜索空间和重用先前计算的中间结果简化A*算法^[6]. 这些方法都可以得到前缀对齐的最优解, 虽然保证了结果的最优性, 但是会导致过高的时间复杂度和巨大的内存消耗.

针对基于A*算法的前缀对齐方法^[6,15,16]并没有考虑到过程模型的结构性信息, 具有一定的局限性, 同时计算最优前缀对齐的复杂度过高. 为了解决这些问题, 本文提出了一种基于RPST的一致性监控树模型, 利用过程模型的结构信息进行偏差的快速定位, 同时, 一致性监控树可以动态保存运行时的状态, 采用动态规划的思想, 在计算前缀对齐时, 复用结构化片段的最优前缀对齐, 并采用重置机制保证结果的最优性, 在减少内存资源消耗的同时保证了对齐的最优解. 将本文的方法与已有方法^[15,16]进行比较说明, 验证了本文的算法在保证最优前缀对齐结果有效的基础上, 提高了运行效率并节省了内存空间.

本文的其余部分结构如下: 第2节介绍基本概念, 第3节介绍一致性监控树的概念. 第4节介绍具体的算法实现. 第5节对提出的算法进行实验评估, 并给出实验结果. 第6节提出总结与展望.

2 基本概念

下面给出一个现实世界的订单处理流程图, 如图1所示: 活动A代表收到订单并检查, 活动C表示处理订单, 在活动C之前任意次更改订单, 即活动B. 之后, 产品发货(D), 同时, 将发送发票(E), 随后, 向客户发送邮件或者寄信通知. 完成前面的所有活动之后, 将订单存档(H), 至此, 订单处理流程结束.

以该订单处理流程为动机例子, 本节主要介绍迹, 事件日志, 事件流, 过程模型, 对齐, 前缀对齐, RPST的相关概念.

定义1 (迹, 事件日志)^[6]. 设A是一个所有活动集合. 若活动序列 $\sigma \in A^*$ , 则称 $\sigma $ 是一条迹. 若 $\exists L \in \beta (A^*)$ 是迹的一个有限非空多重集, 则称L为一个事件日志.

定义2 (事件流)^[15]. 设C是作为时刻序号的非负整数集合, A是所有可能的活动的集合. 事件流S是这两个集合组成的二维序列 $C \times A$ 上的无界序列, 表示为 $S \in (C \times A)^*$ .

定义3 (过程模型)^[17]. 基于BPMN^[18]的过程模型为 $PM = (T, G, F)$ , 其中: T表示任务集合. G表示网关, 包括XOR网关、OR网关和AND网关. F表示控制流关系. 主要连接两个元素对象, 并显示元素对象的执行顺序, 对象可以是T或G.

定义4 (常规对齐)^[6]. 设A是活动的集合, $\sigma \in A^*$ 是一个活动序列, $PM = (T, G, F)$ 是一个过程模型, 且 $\gt \gt \notin A \cup T$ , $\sigma $ 和N的对齐 $\gamma \in ({A^{ \gt \gt }} \times {T^{ \gt \gt }})$ 是满足如下条件的一个序列:

1) $ \gamma $ 的第1行元素(排除 $ \gt \gt $ )为活动序列, 该序列等于迹 $\sigma $ ;

2) $ \gamma $ 的第2行元素(排除 $ \gt \gt $ )为模型中的移动序列, 可以使模型从开始任务到达结束任务.

我们将对齐记为 ${\gamma _M}(\sigma )$ , 并将合法移动 $(a, t) \in {\gamma _M}$ 进行分类:

$(a, \gt \gt )$ 称为日志移动, 其中 $a \in A$ ;

$( \gt \gt , t)$ 称为模型移动, 其中 $t \in T$ ;

$(a, t)$ 称为同步移动, 其中 $a \in A$ , $t \in T$ .

其中, 偏差由日志移动和模型移动表示: 日志移动表示的是在迹中所观察到的事件是模型不允许发生的, 模型移动表示的是根据模型本应该发生的事件在迹中并没有被观察到. 通常情况下, 一条迹会对应多个对齐结果, 成本函数为每个可能的移动分配一个成本, 具有最低成本的对齐即为最优对齐. 标准成本函数为每个日志移动和模型移动分配的成本为1, 为每个同步移动分配成本为0.

例如, 以图1的过程模型为例, 对迹 ${\sigma _1} = \lt A, D, F, G, H \gt $ 的最优对齐结果为 $ \lambda ({\sigma }_{1}) $ , 如图2所示, 其中 $( \gt \gt , C)$ 、 $( \gt \gt , E)$ 是模型移动, 成本为2, $(G, \gt \gt )$ 是日志移动, 成本为1, 其他均为同步移动, 成本为0, 所以该对齐结果的总成本为3.

前缀对齐是在常规对齐上的改进, 以实现运行时一致性检查的对齐结果, 不需要显示从开始到结束所有事件的对齐结果, 只需要显示当前发生事件的对齐结果, 每当新的事件发生时, 对齐结果都有可能改变.

定义5 (前缀对齐)^[6]. 设A是活动的集合, $\sigma \in A^*$ 是一个活动序列, $PM = (T, G, F)$ 是一个过程模型, 且 $\gt \gt \notin A \cup T$ , $\sigma $ 和 $PM$ 的前缀对齐 ${\gamma ^{{\rm{pre}}}} \in {({A^{ \gt \gt }} \times {T^{ \gt \gt }})^*}$ 是一个满足如下条件的一个序列:

1) $ \gamma $ 的第1行元素(排除 $ \gt \gt $ )为活动序列, 该序列就是迹 $\sigma $ ;

2) $ \gamma $ 的第2行元素(排除 $ \gt \gt $ )为模型中的移动序列 ${\sigma _M}$ , 该序列由PM中的任务T组成. 且存在一个移动序列 ${\sigma {'}}$ , 使得 ${\sigma _M} \cdot {\sigma {'}}$ 的发生, 可以使模型从初始任务到达结束任务.

例如, 迹 $\sigma_{2}=\lt A, D, F\gt$ 与图1的过程模型的前缀对齐的结果为 $( > > , C)$ , 如图3所示, 该对齐结果的第一行的最后一个活动不需要是模型的最后一个活动H. 其中 $( > > , C)$ 和 $( > > , E)$ 是模型移动, 成本为2, 没有日志移动, 其他均为同步移动, 所以总成本为2.

过程结构树RPST是将流程模型的图结构划分成一系列单入口单出口的模块(SESE)^[7], 图4将图1的过程模型分解为SESE片段, 并按照嵌套关系组织成层次结构, 这个层次结构表示为一棵树, 即RPST, 如图5所示.

定义6 (RPST)^[7]. $RPST = (RN, r, child)$ , 其中: RN为树的结点集合; r为树的根结点; child表示结点之间的父子关系.

给定PM为BPMN的流程图, PM的RPST是所有规范SESE^[7]片段的集合. 规范片段可以分为4种类型. 这4种类型分别为多边片段(polygon fragment)、键片段(bond fragment)、平凡片段(trivial fragment)、刚性片段(rigid fragment)^[7], 在图4中, 用P表示多边片段, B表示键片段, 普通叶子结点为平凡片段.

3 基于RPST的一致性监控树

本文提出了一种基于一致性监控树的前缀对齐算法, 利用RPST的结构化特点, 保存运行时的状态信息, 提高算法的性能. 首先介绍基于RPST的一致性监控树的概念.

因为原始的RPST片段中的子结点是呈无序状态的, 无法显示流程活动的执行依赖关系, 所以本文使用的是改进后的有序的过程结构树RPST来构造一致性监控树, 这个监控树可以体现流程模型中任务结点的执行顺序.

如图6所示, 基于RPST的一致性监控树不仅可以表示事件之间的依赖关系, 还存储了计算前缀对齐所需的相关信息.

一致性监控树具有以下几个特点:

(1) 叶子结点是任务结点.

(2) 非叶子结点是非任务结点, 并有以下4种类型: XOR、AND、LOOP、Polygon. 这4种类型分别对应过程模型中的选择结构、并行结构、循环结构、顺序结构. 其中XOR、AND的子结点是无序的, LOOP、Polygon的子结点是有序的.

定义7 (一致性监控树结点). $ CMN = (RN, type, pre, post, shortest, acts) $ , 其中:

RN表示该CMN结点关联的RPST结点;

type表示结点类型, 结点分为任务结点和非任务结点, 非任务结点又分为Polygon (多边结点), XOR (选择结点)、AND (并发结点)和LOOP (循环结点), 其中, XOR、AND、LOOP都属于RPST中的键片段;

pre表示当前结点的前置结点, 即发生在该结点之前, 会影响该结点发生的前一个结点;

post表示当前结点的后置结点, 即发生在该结点之后, 受该结点影响的后一个结点;

shortest表示该结点的最短路径, 即该结点完成所需的最少的任务结点数;

acts表示与该结点相关的活动, 即该结点片段所包含的任务结点的集合.

图6中显示了一致性监控树结点的所有信息, 其中, 前置结点和后置结点的判定方法是由当前结点的父结点类型决定的. 结合图1中的过程模型可知, 前置结点和后置结点表示的是事件之间的依赖关系. 如事件D (产品出货)依赖于事件C (处理订单), 所以D的前置结点为C, C的后置结点为D, 只有在订单处理完成以后, 产品才能出货.

本文提出的前缀对齐算法需要根据成本来计算最优前缀对齐, 对于任务结点, 如果在事件流中缺失, 成本为1, 对于非任务结点, 如表1所示, 不同类型的结点成本的计算并不相同, shortest记录了每个结点的初始成本, 即最短路径.

一致性监控树结点CMT根据与其相关联的RPST结点RN进行转化, 接下来给出结点的转化算法, 如算法1.

算法1. 结点转化算法(rn_to_cmn)

输入: RPST tree, 及结点 RN: rn

输出: CMT的结点CMN: cmn

1 type $\scriptstyle \leftarrow $ tree.get_type(rn)

2 pre $\scriptstyle \leftarrow $ pre_node(rn)

3 post $\scriptstyle \leftarrow $ post_node(rn)

4 acts $\scriptstyle \leftarrow $ get_acts(rn)

5 if type is trivial then

6　 if rn is task node then

7　　 cmn $\scriptstyle \leftarrow $ (rn, task, pre, post, acts)

8 else if type is bond then

9　 if rn is AND node then

10　　 cmn $\scriptstyle \leftarrow $ (rn, AND, pre, post, acts)

11　 else if rn is XOR node then

12　　 cmn $ \scriptstyle \leftarrow $ (rn, XOR, pre, post, acts)

13　 else if rn is LOOP node then

14　　 cmn $\scriptstyle \leftarrow $ (rn, LOOP, pre, post, acts)

15　 end if

16 else if type is Polygon then

17　 cmn $ \scriptstyle \leftarrow $ (rn, Polygon, pre, post, acts)

18 end if

结点转化算法根据结点类型的不同将RPST中的结点转化为CMT中的结点. 在转化的过程中根据RPST的结构特点获取每个CMT结点的相关属性信息. 首先输入RPST的结点, 获取该结点的前置结点, 后置结点以及相关活动, 接下来判断该结点的类型, 如果是平凡片段, 则转化为CMT的任务结点(代码第5–7行), 如果是键片段, 则继续判断其是否为循环结点、选择结点或并行结点(代码第8–14行). 如果是多边片段, 则转化为相应的多边结点(代码第16–17行).

一致性监控树CMT是由一致性监控树结点CMN组成的, 下面介绍一致性监控树的定义.

定义8 (一致性监控树). ${\rm{CMT}} = (CMN, r, rt, ms)$ , 其中:

CMN表示树中一致性监控树结点CMN集合;

$r \in CMN$ 表示一致性监控树的根结点;

rt表示一致性监控树关联的RPST树;

ms: $CMN \to MS$ 为结点集合到监控状态集合的映射, 给定结点 $n \in CMN$ , $ms(n) \in MS$ 为结点n的当前监控状态; 监控状态 $ms(n) = (status, las, cost, seq, unt)$ , 其中:

status表示结点的匹配状态;

las表示结点的最新对齐步;

cost表示结点的成本, 记录从开始结点到当前结点的总成本;

seq表示结点的对齐步序列, 这个对齐步序列就是最优前缀对齐;

unt表示缺失的任务结点, 对应于传统对齐中的模型移动.

在一致性监控过程中, 为了表示出结点的匹配状态, 需要知道每个结点的决定性结点, 因此还为每一个非任务结点定义了决定性任务结点, 非任务结点的完成状态由其孩子结点的完成状态决定, 如表2所示.

同时, 本文的方案还考虑了事件之间的冲突关系, 例如, 在XOR结点的孩子结点之间就是冲突的, 如果XOR结点之下的孩子结点完成了不止一个, 则只能选择其中一个孩子结点中的事件进行对齐, 并且要在结果中表明冲突关系.

4 基于一致性监控树的前缀对齐算法

本文使用一致性监控树的结构, 采用动态规划算法求事件流和过程模型的最优前缀对齐. 当事件流中有新的事件发生时, 首先计算出事件流和模型的因果对齐, 再利用结点状态动态的记录结点的对齐步、成本及当前的最优前缀对齐, 并随着事件流的更新不断更新最优前缀对齐, 并将结果记录在CMT的根结点中.

4.1 因果对齐

在一致性监控过程中, 每到一个事件, 都要与一致性监控树中的对应任务结点进行匹配, 并更新其他相关结点的匹配状态. 为了表示事件与结点的匹配情况, 定义了以下4种匹配状态, 如表3所示.

当没有事件发生时, 结点的初始匹配状态为未触发(inactivated), 只有该结点的acts中的活动有发生, 该结点状态才会变为触发(activated). 只有任务结点存在匹配(matched)和不匹配状态(unmatched), 当该任务结点的前置结点pre为触发状态时, 该结点状态为匹配, 否则为不匹配.

因果对齐将匹配状态存储在对齐步中, 以便显示与当前事件有依赖关系的事件是否完成.

定义9(对齐步(aligned step)). 设A是活动的集合, T是事件的集合. 对齐步为 $als = (ord, a, t, status)$ , 其中:

ord为该对齐步的标识, 表示事件发生的次序;

$a \in A$ 表示迹中的活动, 即当前对齐步的活动;

$t \in T$ 表示与a对应的模型中的事件;

status为该对齐步的匹配状态.

每到一个新的事件, 都将其与一致性监控树对应的任务结点进行对齐, 根据树中结点的状态得到对应的对齐步, 并更新树中该结点与其祖先结点的匹配状态.

为了在因果对齐中表示事件的依赖关系, 还需要用输入流将对齐步连接起来, 如果得到的对齐步的状态是匹配的, 那么直接在前置结点的最近对齐步和当前对齐步中建立因果流, 如果不匹配, 则需要通过一致性监控树查找未对齐片段. 并根据通过未对齐片段在当前对齐步和最近对齐步之间建立因果流.

定义10 (未对齐片段(unaligned fragment)). $uaf = (src, tar, shortest)$ , 其中:

src表示源结点, 即最近处于触发状态的前置结点.

tar表示目标结点, 即当前对齐步对应任务结点.

shortest表示从源结点到目标结点的最短路径, 即最小成本.

未对齐片段的搜索算法如算法2.

算法2. 未对齐片段搜索算法(find_uaf)

输入: 当前CMN结点t, 一致性监控树CMT

输出: 未对齐片段uaf

1 currnode $\scriptstyle \leftarrow $ t

2 uaf.shortest $\scriptstyle \leftarrow $ 0

3 while true do

4　 prenode $\scriptstyle \leftarrow $ pre_node(currnode)

5　 unalignedtask.add(prenode.acts)

6　 uaf.tar $\scriptstyle \leftarrow $ t

7　 if prenode is activated or start node then

8　　 uaf.src $\scriptstyle \leftarrow $ prenode

9　　 end while

10　 end if

11　 uaf.shortest $\scriptstyle \leftarrow $ uaf.shortest+

　　prenode.shortest

12　 currnode $\scriptstyle \leftarrow $ prenode

13 return uaf

算法2可以根据给定的CMN结点t, 在CMT中搜索到未对齐片段uaf, 目标结点tar为当前结点t(代码第6行), 通过不断搜索前置结点的状态来确定源结点src(代码第4行和第12行), 源结点为最近的处于触发状态的前置结点(代码7–9行), 并在搜索的过程中统计未对齐片段的最小成本shortest(代码第11行). 设算法中CMT的结点数为n, 那么该算法的时间复杂度为 ${\rm{O}}(n)$ .

最近对齐步为源结点中的最近对齐步, 通过搜索未对齐片段uaf, 可以找到当前对齐步与监控树中最近对齐步之间所有未触发的前置结点, 构建前置链条. 并计算出缺失的最少活动数, 从而可以计算成本. 同时, 在当前的对齐步与最近的对齐步之间建立因果流, 因果流记录了事件发生的顺序关系, 在后续计算最优前缀对齐的过程中, 可以通过这个关系查找到最优对齐序列.

例如, 对迹 ${\sigma _1} = \lt A, D, F, G, H \gt $ 和图1的过程模型, 根据一致性监控树计算出对应的因果对齐结果, 如图7所示.

由图7可知, 对齐步2、3、4的状态为未匹配(unmatched), 存在未对齐片段. 事件F和G为冲突事件. 以对齐步2为例, 此时迹中的活动为D, 在监控树中对应任务结点D, 该结点的前置结点为C, C的状态为未触发, 则继续寻找前置结点, C的前置结点为A, A的状态为匹配, 已触发, 则A为源结点. A的最近对齐步为1, 从A到D的前置链条为A→C→D, 根据每个结点的shortest可得到uaf的最短路径为1. 在对齐步1和2之间建立因果流, 并显示未对齐片段.

4.2 基于CMT的最优前缀对齐算法

基于CMT的最优前缀对齐算法是通过动态规划的思想, 利用结点状态记录成本和匹配序列的信息, 每到一个新的事件, 计算对齐步和对应结点的成本元组, 并更新对应结点以及所有相关结点的成本元组, 通过结点的监控状态的比较和因果流计算出最优的前缀对齐序列, 并将其存储在根结点中. 算法如算法3所示.

算法3. 基于CMT的最优前缀对齐算法

输入: 事件流 $\scriptstyle S \in (C \times A)^*$ , 一致性监控树CMT

输出: 最优前缀对齐 $\scriptstyle \gamma $

1 i $\scriptstyle \leftarrow $ 1

2 while truedo

3　 e $\scriptstyle \leftarrow $ S(i)

4　 t $\scriptstyle \leftarrow $ CMT.domatch(e) //t为CMN结点

5　 als $\scriptstyle \leftarrow $ (i, e, t, null)

6　 p $\scriptstyle \leftarrow $ pre_node(t)

7　 if p.status is finished then

8　　 als $\scriptstyle \leftarrow $ (i,e,t,matched)

9　　 CMT.ms(t) $\scriptstyle \leftarrow $ (matched, als,

　　　CMT.ms(p).cost, als,null)

10　 else

11　　 als $ \scriptstyle \leftarrow $ (i, e, t, unmatched)

　　//查找未对齐片段

12　　 uaf $\scriptstyle \leftarrow $ find_uaf(t)

13　　 CMT.ms(t) $\scriptstyle \leftarrow $ (unmatched, als,

　　　CMT.ms(uaf.src).cost+uaf.shortest,

　　　als, CMT.ms(uaf.src).unt+uaf.unt)

14　 end if

15　 update_note_state(t, CMT.ms(t))

16　 $\gamma $ $ \leftarrow $ CMT.ms(r).seq

17　 return $\gamma $

18　 i $ \leftarrow $ i+1

19 end while

算法3是基于CMT的前缀对齐算法, 事件流S和CMT作为算法输入, 根据事件流中的事件变化更新CMT的监控状态ms, 每接收一个新的事件e, 就在CMT中找到对应的CMN结点t(代码3–4行), 根据前置结点的状态判断对齐步是否匹配, 如果前置结点已完成, 则状态为matched, 并更新当前结点的监控状态(代码7–10行). 如果前置结点未完成, 则状态为unmatched, 并寻找未对齐片段(代码12–13行), 并根据未对齐片段的源结点的状态信息更新当前结点的监控状态(代码第15行).

计算完对齐步和当前结点的监控状态之后, 还需要利用动态规划的方法更新与当前结点相关的所有结点的监控状态(代码第16行), 只有当新的监控状态比原来的的监控状态更优的情况下, 才需要更新结点状态. 更新算法如算法4所示.

算法4. 结点状态更新算法(update_note_state)

输入: 当前CMN结点t, t的监控状态CMT.ms(t)

输出: 一致性监控树CMT

1 preseq=null

2 f=father(t)

3 currstep=t.als

4 if CMT.ms(t).seq>CMT.ms(f).seqor

(CMT.ms(f).seq=CMT.ms(t).seq and

CMT.ms(f).cost<CMT.ms(t).cost) then

5 　CMT.ms(f)=CMT.ms(t)

6 end if

7 if f is Polygon then

8　 preseq.add(currstep)

9　 while CMT.ms(f).las!=start.las do

10　　 prestep=get_before_als(currstep)

11　　 preseq.add(prestep)

12　　 currstep=prestep

13　 end while

14　 CMT.ms(f).seq=preseq

15 end if

16 update_node_state(f, CMT.ms(f))

17 reset_node(t, CMT)

18 return CMT

在更新算法中, 只有当父结点类型为Polygon时, 才需要计算当前对齐步的前缀对齐序列(代码7–15行), 父结点的对齐序列为所有孩子结点的对齐序列, 通过该算法, 最终才能将最优的对齐序列存放在根结点当中.

在更新结点的过程中, 除更新当前结点以外, 还需要遍历该结点的所有后置结点, 需要判断更新结点的后置结点需不需要重置(代码第17行), 通过比较当前结点的成本与当前结点到后置结点(已激活)的最短路径之和是否小于后置结点原来的成本, 如果成本更小, 则将后置结点中触发的结点重置为未触发, 具体实现如算法5所示.

算法5. 重置算法(reset_node_state)

输入: 当前CMN结点t, 一致性监控树CMT

输出: 一致性监控树CMT

1 cost=CMT.ms(t).cost

2 while true do

3　 postnode=post_node(t)

4　 if postnode is inactived then

5　　 cost=cost+postnode.shortest

6　 else if postnode is actived then

7　　 if postnode.cost>cost then

8　　　 CMT.ms(postnode)=(inactived, 0, null, null, null)

9　　 end if

10　 end if

11 end while

12 return CMT

通过重置算法, 可以更新后置结点的状态信息, 使得在新的事件到来时, 可以根据新的状态计算最优的前缀对齐结果, 保证结果的最优性.

根据算法1–5, 以图1的模型为例, 当迹为 ${\sigma _1} = \lt A, D, F, G, H \gt $ 时, 最优前缀对齐的结果为序列 $ \lt A, D, F, H \gt $ , 成本为2, 缺失任务为C和E. 本文的对齐结果为最长的匹配序列, 成本为缺失的任务数. 同时, 每个结点的匹配状态显示了与该结点有依赖关系的活动是否完成, 即该结点的前置结点的完成情况. 这在传统的前缀对齐算法中是无法体现的.

5 实验评估

本节使用不同的数据集评估基于CMT的最优前缀对齐算法的性能. 将本文的算法与文献[16]中涉及的算法(如表4)进行比较, 这些算法在PM4Py开源库^[19]中均有实现, 主要对比算法的执行时间和内存消耗. 本文的算法实现可在线访问: https://gitee.com/workingspace/conformance-monitoring-all.

本文采用3组真实的数据集, 如表5所示.

本文所有实验基于如下环境: Intel(R) Core(TM) i7-10710U CPU@1.10 GHz 1.61 GHz, 16 GB内存, Windows 10 64位操作系统, Python 3.7, JDK 11.

5.1 实验步骤

首先, 为了得到算法输入所需的过程模型, 需要通过Inductive Miner^[23]的过程挖掘算法从数据集中挖掘出合适的过程模型, 该过程模型用Petri网表示. 基于A*算法的在线一致性检查算法直接将过程模型和事件流作为输入, 得到最优前缀对齐结果. 本文算法的过程模型基于BPMN, 所以需要将Petri网转化为对应的BPMN, 作为算法的模型输入. 再结合事件流的输入得到对应的最优前缀对齐. 统计这几组算法的执行时间和内存消耗, 并显示对比结果.

5.2 准确性评估

使用来自CCC 19的数据集验证本文算法结果的准确性, 利用服从度^[4]量化一致性检查的结果. 因为OCC的前缀对齐结果是最优解^[16], 所以实验只需验证CMT算法与OCC算法得到的结果服从度是否相同, 如果相同, 则证明CMT算法得到的前缀对齐是最优解. 服从度为对齐中同步移动占总移动长度的比例^[12]. 在OCC算法的对齐结果 $\lambda $ 中, 记同步移动数为 $syn(\lambda )$ , 成本移动数为 $dev(\lambda )$ , 成本移动包括模型移动和日志移动, 服从度的公式记为:

$ C = \frac{{syn(\lambda )}}{{syn(\lambda ) + dev(\lambda )}} $

其中, 总移动长度为同步移动数和成本移动数的总和. 在本文的最优对齐结果 ${\lambda ^{{\rm{CMT}}}}$ 中, 最长匹配序列对应 $\lambda $ 中的同步移动, 迹中的序列的长度对应 $\lambda $ 中的同步移动和日志移动. 成本对应模型移动. 记 $cost({\lambda ^{{\rm{CMT}}}})$ 为运用CMT算法得到的成本(最小代价). n为最长匹配序列的长度, m为迹的长度. 则本文算法的服从度公式记为:

$ {C_{{\rm{CMT}}}}({\sigma _L}) = \frac{n}{{m + cost({\lambda ^{{\rm{CMT}}}})}} $

因为n与 $syn(\lambda )$ 均表示迹与模型相符合的事件序列, $syn(\lambda ) + dev(\lambda )$ 和 $m + cost({\lambda ^{{\rm{CMT}}}})$ 均表示迹的长度和模型移动个数的总和, 所以 ${C_{{\rm{CMT}}}}$ 和 $C$ 所表示的内涵是相同的.

根据两种算法分别计算CCC 19中20个迹的服从度, 结果如图8所示.

通过对比可知, 这20个迹(事件序列)的结果中, CMT算法有14个迹的服从度与OCC完全相同. 分析数据集可知, 造成另外6个迹的服从度不同的原因是迹中的事件发生了循环. 在发生循环事件时, 本文的算法只考虑一次循环中的事件, 所以服从度较OCC会有所降低. 实验结果证明了在不考虑循环事件的前提下, 可以计算出前缀对齐的最优解.

5.3 效率评估

针对3组数据集, 计算平均每个迹所需的时间, 得到如图9所示的结果.

图9的结果显示, 本文算法在时间性能上有明显的提升, 这3组数据集中每个迹的执行时间都有明显的减少.

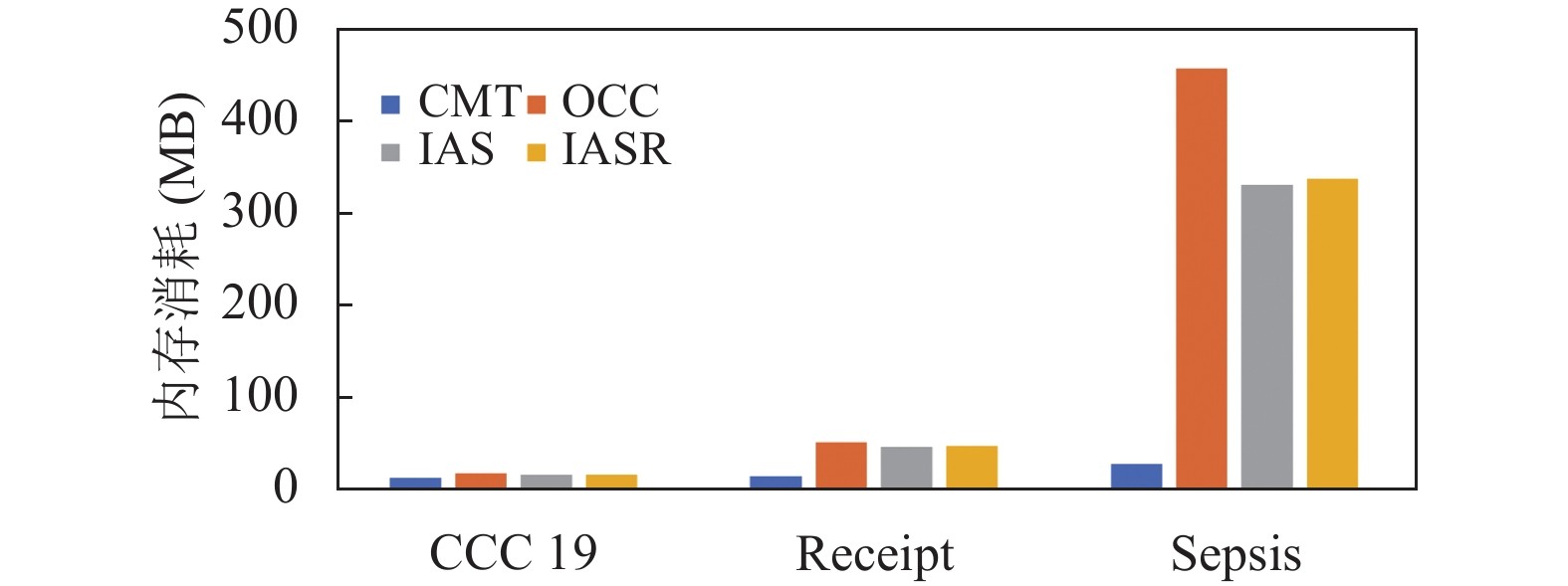
同时利用这3组数据集对比这4种算法的内存消耗, 如图10所示.

对于数据集CCC 19, 4种算法的内存消耗差别不大, 但是基于CMT的算法的内存消耗还是比基于A*的算法少. 而对比另外两组数据集, 基于A*的算法的内存均远远大于基于CMT的算法. 尤其是数据集Sepsis, 这组的内存消耗差距是最明显的. 从图10可以看出, 数据量越大, 内存消耗越大, 但是基于CMT的算法的内存消耗增长较为平缓. 相较于基于A*的算法在减少内存消耗上更有优势.

综上表明, 基于CMT的前缀对齐算法具有较高的性能优势. 因为运行时一致性检查无法获得完整的迹, 每到一个新事件, 最优前缀对齐的结果都有可能发生改变, 传统的基于A*的算法的方法是使用线性规划重新计算最优前缀对齐, 这种方法会导致过高的时空复杂度. 而本文的算法利用重置机制保证结果的最优性, 如果最优前缀对齐发生改变, 只需要将一致性监控树中当前对齐步所在结点之后的所有结点状态重置为初始状态, 就可以保证之后计算的对齐结果也是最优的.

6 总结与展望

针对业务过程运行时一致性检查的复杂度过高的问题, 本文基于RPST提出了一致性监控树CMT, 利用过程模型的结构性信息进行偏差的快速定位, 并利用基于CMT的动态规划算法求解事件流与过程模型的最优一致性检查结果. 最后, 将本文方法与其它在线一致性检查方法进行性能比较分析, 比较了它们的准确率和效率. 结果表明, 本文提出的方法在保证了有效性的同时提升了性能. 但是, 如果过程模型中存在循环结构, 本文的方法只考虑一次成本最小的局部对齐, 因此, 在未来的工作中, 将考虑当过程模型中存在循环结构时, 计算出循环多次执行时的最优前缀对齐结果.