交叉验证(cross validation)作为一种评价算法性能的方法在实际中得到广泛的应用. 在统计机器学习中, 无论是进行模型选择, 还是算法性能对比交叉验证都体现特有的价值. 当前交叉验证有多种形式, 文献[1]的综述中提到的标准 $k$ 折交叉验证, Monte-Carlo交叉验证, repeated learning-testing交叉验证, 文献[2]正则化交叉验证, 文献[3] 5×2交叉验证等. 文献[4]组块3×2交叉验证估计分析每组训练集和验证集数据重叠个数, 能够得到相对稳定的泛化误差估计.

结合几个学习器的结果产生一个聚合结果的集成学习算法, 不仅可以减少分类器的方差也能够提高模型的分类准确性和鲁棒性. 目前有很多成功的集成学习方法能够提高模型的泛化能, 如linear ensemble^[5], weighted average ensemble learning^[6], collaborativefiltering ensemble^[7], multi-label ensemble learning^[8], neural network ensemble^[9]等, 这些方法从不同的角度构建多个基学习器来提高系统的泛化能力, 这些集成学习有些涉及交叉验证的方法, linear ensemble^[5]中数据集被分成3个子集, 测试集由每个用户的最后6个评级组成, 验证集由每个用户的测试集之前的4个评级组成, 训练集由剩下的每个用户的评级组成. Multi-label ensemble learning^[8]在使用RBF (径向基函数神经网络)模型时, 在两个原型向量之间选择交叉点进行交叉操作. Neural network ensemble^[9]研究将模糊性和交叉验证相结合能够得到可靠的集成泛化误差估计, 以及这种类型的集成交叉验证有时可以改进模型的性能.

虽然目前关于集成学习的泛化性能的研究取得了很大成功, 但是关于集成学习的多样性理解, 关于集成学习方法的损失函数以及误差分析还需要进一步研究, 而交叉验证作为一种评价算法性能的优良方法如果能够被充分应用到集成学习中, 可以得到更好的集成学习方法. 考虑组块3×2交叉验证^[4]和正则化交叉验证^[2]具有稳定的泛化性能, $k$ 折交叉验证^[10]是一种常用的交叉验证方法, 并且当前很多集成学习感兴趣于结合来自不同模型的预测产生更高的预测, 本文应用组块3×2交叉验证和 $k$ 折交叉验证得到的数据集的切分建立模型并对预测进行集成产生新的预测, 并对集成学习的预测进行误差分析.

1 集成学习

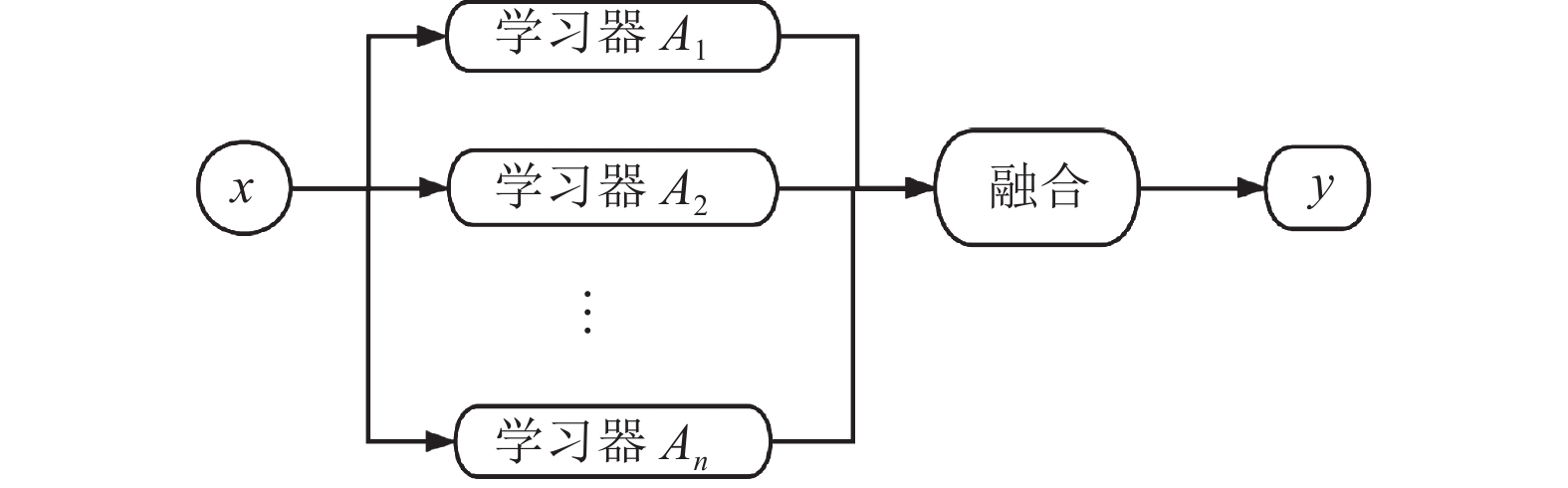
集成学习的基本思想是通过一个回归器(分类器)来融合多个回归(分类)模型. 在分类问题中, 采用对不同模型输出值进行投票选择分类结果. 在回归问题中, 可以对输出的结果进行加权平均得到最后输出值. 一般集成学习具有比个体学习器更好的泛化性能. 文献[11]提出一组分类器经过集成可以得到比其中性能最优的个体学习器更加准确的预测. 文献[12]理论证明弱学习器可以提升为强学习器, 该理论为通过集成学习得到强学习器指明前进的方向. 图1给出一个常用的集成学习框架. 集成学习代表性的算法有bagging^[13], boosting^[14]和ECOC (error-correcting output codes)^[15].

集成学习算法^[16]一般可以分两个阶段进行: (1)生成或者训练一组学习器; (2)对分类(回归)结果进行合并. 在训练一组学习器时, 要构建具有充分多样性的学习器达到较好的聚合效果有很多方法, 一种常见的方法是对训练样例进行随机子抽样进行训练, 另外采用交叉验证方法, 将一部分数据作为训练集, 一部分作为验证集也是一种有效方法. 当前好用的交叉验证方法有很多, 本文考虑应用 $k$ 折交叉验证^[10]和组块3×2交叉验证^[4]进行集成学习.

2 基于交叉验证的集成学习

基于组块3×2交叉验证和 $k$ 折交叉验证的集成学习方法思路如下:

(1)应用组块3×2交叉验证和 $k$ 折交叉验证得到切分的数据集在单个学习器中进行训练, 得到单个学习器在每个样本点的预测值和单个学习器预测的平均绝对误差.

(2)在保证误差越大权重越小的前提下, 分析预测误差得到不同的权重.

(3)用计算得到的权重分别去乘对应学习器的预测值, 也就是得到经过集成学习的新的预测.

(4)计算集成学习的新预测的误差、偏差平方和以及方差.

2.1 $k$ 折交叉验证在每个样本点的预测

设容量为 $n$ 的样本集 ${D_n} = \left\{ {{\nu _1}, {\nu _2}, \cdots , {\nu _j}, \cdots , {\nu _n}} \right\}$ , 其中 ${\nu _j} = ({x_j}, {y_j})$ , ${x_j}$ 是输入向量, ${y_j}$ 是相应的输出, 用 ${f}_{i}= {A}_{i}({D}_{n}), \; i=1, 2, \cdots , M$ 表示应用算法 ${A_i}$ 在数据集 ${D_n}$ 上进行训练得到的预测函数, ${\hat y_i} = {f_i}(x)$ 表示输入 $x$ 在学习器 ${A_i}$ 中的预测值.

$k$ 折交叉验证^[10]它是把样本量大小为 $n$ 数据集切分成大小几乎相等且互不相交的 $k$ 折. 如将数据集 ${D_n}$ 划分为不相交的 $k$ 份, 分别为 ${F_1}, {F_2}, \cdots , {F_k}$ , 用 $\left| {{D_n}} \right| = n$ 和 $\left| {{F_t}} \right| = m$ 分别表示数据集 ${D_n}$ 和第 $t$ 份 ${F_t}$ 包含的样本个数, 则 $n = km$ , 依次用切分的 $k$ 折中的每一折作为验证集, 其余 $k - 1$ 折作为训练集训练模型.

$k$ 折交叉验证一般将随机切分重复 $t$ 次, 通常情况下 $t = 5$ , 或者 $t = 10$ , 则样本集中第 $j$ 个样本点的预测为:

${\hat y_{ij}} = \frac{1}{t}\sum\limits_{v = 1}^t {pred_v^{(i)}({x_j})} , \; v = 1, 2, \cdots , t$

(1)

其中, $pred_v^{(i)}({x_j})$ 表示第 $j$ 个样本点在学习器 ${A_i}$ 中第 $v$ 次重复时的预测值, ${\hat y_{ij}}$ 表示通过学习器 ${A_i}$ 得到的第 $j$ 个样本点的平均预测值.

2.2 组块3×2交叉验证在每个样本点的预测

组块3×2交叉验证^[4]将数据集均衡地分成四份, 每一份所包含的样本数大致相同, 并且每一类别在每份数据集中的个数也基本相同, 然后将4份中的任意两份两两结合, 将互为补集的两个组合看为对数据集中的一次切分, 得到3组切分数据集, 每两组训练集重叠的样本个数和测试集重叠的样本个数相同, 具体是把数据集 ${D_n}$ 分成互不相交且元素个数几乎相等的4个子集, 记为 ${S_i}, \; i = 1, 2, 3, 4$ , 然后两两结合, 有6种组合分成 $\left\{ {\left( {{S_1}, {S_2}} \right), \left( {{S_3}, {S_4}} \right)} \right\}, \left\{ {\left( {{S_1}, {S_3}} \right), \left( {{S_2}, {S_4}} \right)} \right\}, \left\{ {\left( {{S_1}, {S_4}} \right), \left( {{S_2}, {S_3}} \right)} \right\}$ 这样得到3组数据集的切分, 用在每一组数据集的切分上做一次标准的2折交叉验证. 再把3组2折交叉验证的结果进行平均得到每个样本点的平均预测结果.

${\hat y_{ij}} = \frac{1}{3}\sum\limits_{q = 1}^3 {pred_q^{(i)}({x_j})} , q = 1, 2, 3$

(2)

其中, $pred_q^{(i)}({x_j})$ 表示对组块3×2交叉验证的第 $q \; (q = 1, 2, 3)$ 组切分的数据在学习器 ${A_i}$ 中训练得到的第 $j$ 个样本点的预测值, ${\hat y_{ij}}$ 表示通过学习器 ${A_i}$ 得到的第 $j$ 个样本点的平均预测值.

2.3 权重分析

在回归任务中, 损失函数 $L({f_i}(x), y)$ 表示预测和观测值之间的差异. 则在容量为 $n$ 的数据集上不同模型的平均绝对值损失函数 ${\overline L_i}, \; i = 1, 2, \cdots , M$ 可以定义为:

${\overline L_i} = \frac{1}{n}\sum\limits_{j = 1}^n {L({f_i}({x_j}), {y_j})} = \frac{1}{n}\sum\limits_{j = 1}^n {\left| {{f_i}({x_j}) - {y_j}} \right|}$

(3)

在应用交叉验证训练单个学习器后, 对单个学习器预测的处理分析是集成学习算法重要部分. 用 ${\overline L_i}, \; i = 1, 2, \cdots , M$ 分别表示不同模型对应的平均绝对值损失. 下面用平均绝对值损失来计算不同模型在集成学习中的权重, 考虑到绝对值损失越大, 权重越小, 这里应用式(4)的方法来取权重.

式(4)中 ${L_Z}$ 表示不同模型平均绝对损失的总和, $N{L_i}, \; i = 1, 2, \cdots , M$ 表示不同模型对应的新的损失, ${w_i}, \; i = 1, 2, \cdots , M$ 表示不同模型对应的权重.

$\left\{ { \begin{split} &{L}_{{{Z}}}={\displaystyle \sum _{i=1}^{M}{\overline{L}}_{i}=\frac{1}{n}}{\displaystyle \sum _{i=1}^{M}{\displaystyle \sum _{j=1}^{n}\left|{f}_{i}({x}_{j})-{y}_{j}\right|}}, \; i=1, 2, \cdots , M\\ &N{L}_{i}=\frac{{L}_{Z}}{{\overline{L}}_{i}}, \; i=1, 2, \cdots , M\\ &{w}_{i}=\frac{N{L}_{i}}{{\displaystyle \sum _{i=1}^{M}N{L}_{i}}}\text{, }i=1, 2, \cdots , M\end{split} } \right.$

(4)

2.4 集成学习的预测值

集成学习之后每个样本点的新的预测为每个样本点的预测结果与相应的权重的乘积之和, 集成学习的每个样本点的预测可以表示为:

$e{\hat y_j} = \sum\limits_{i = 1}^M {{{\hat y}_{ij}}} {w_i}, \; i = 1, 2, \cdots , M$

(5)

集成学习的平均绝对值损失为:

${L_e} = \frac{1}{n}\sum\limits_{j = 1}^n {\left| {e{{\hat y}_j} - {y_j}} \right|}$

(6)

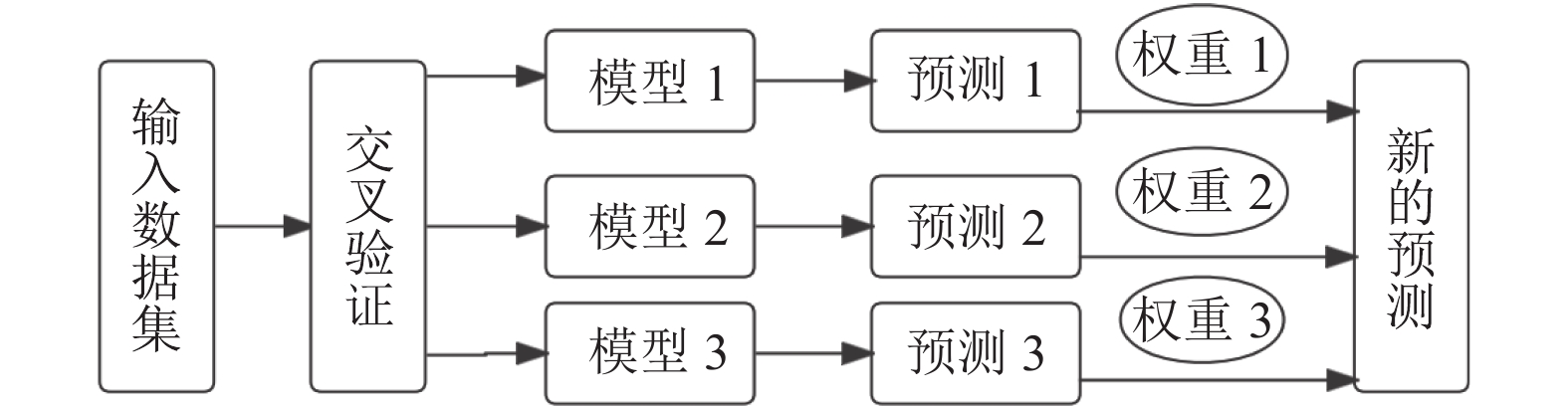
假设有3个基学习器, 图2给出具体的集成学习算法分析图.

3 集成学习的误差分解

集成学习有两种经典的误差分解方法, 一种是误差-分歧分解^[9], 另一种是偏差-方差分解^[17], 一般把每个学习器的泛化误差分解成噪声、偏差和方差的和. 考虑到固有噪声是模型在当前任务上产生的较难估计的一项, 文献[17]泛化误差被分解为偏差项(表示学习器误差期望)和方差项(反映模型对训练数据变化的稳定性).

用 $f$ 表示目标函数, $A$ 表示单个学习器. 以回归任务为例, 使用相同的样本去训练不同的模型产生的平方误差可以分解为:

$\begin{split} err(A) &= { E}[{(A - f)^2}] \\ & = { E}[{(A - E[A] + E[A] - f)^2}] \\ & = {(E[A] - f)^2} + { E}[{(A - E[A])^2}] \\ & = bias(A{{\text{)}}^2} + {var} (A) \end{split}$

(7)

在包含 $M$ 个学习器 ${A_1}, {A_2}, \cdots , {A_M}$ 的集成问题中, 可以与文献[11]中偏差-方差-协方差分解类似将式(7)中的分解进行拓展. 文献[12]在假设单个学习器的权重相同的情形下, 集成学习的平均方差, 平均偏差, 和平均协方差定义为:

$\left\{ { \begin{split} &\overline {{{bias}}} (A) = \frac{1}{M}\sum\limits_{i = 1}^M {(E[{A_i}] - f)} \\ &\overline {{{var}}} (A) = \frac{1}{M}\sum\limits_{i = 1}^M {E({A_i} - E[{A_i}} ]{)^2}\\ &\overline{ { covariance }}(A)=\\ &\dfrac{1}{M(M-1)} \displaystyle\sum_{i=1}^{M} \displaystyle\sum_{\substack{j=1 \\ j \neq i}}^{M} E\left(A_{i}-E\left[A_{i}\right]\right) E\left(A_{j}-E\left[A_{j}\right]\right) \end{split} } \right.$

(8)

集成以后的平方误差 $err(A)$ 可以分解成:

$\begin{split} err(A) =& \overline {bias} {(A)^2} + \frac{1}{M}\overline {{var} } (A) \\ & + \left(1 - \frac{1}{M}\right)\overline {{{covariance}}} (A) \end{split}$

(9)

集成学习的平方误差和协方差项有很大关系, 协方差越小, 说明集成学习效果越好. 但是考虑不同的学习器在相同数据集上得到的误差不同, 也就是不同学习器的性能不同, 因此结合不同学习器的预测误差对不同的学习器赋予不同的权重也是一种集成学习的方法. 用 ${w_1}, {w_2}, \cdots , {w_M}$ 表示不同学习器的权重, 用权重去乘以每个学习器的平均预测值 $E({A_i})$ 再求和得到 $\displaystyle\sum\limits_{i = 1}^M {{w_i}} E({A_i})$ , 那么集成学习的偏差、方差可以定义为:

$bias(A) = \left(\sum\limits_{i = 1}^M {{w_i}E[{A_i}]} \right) - f$

(10)

${var} (A) = E{\left(\sum\limits_{i = 1}^M {{w_i}} {A_i} - E\left[\sum\limits_{i = 1}^M {{w_i}} {A_i}\right]\right)^2}$

(11)

基于交叉验证的集成学习的平方误差 $err(A)$ 可以分解成式(12):

$\begin{split} err(A) =& { E}\left[{\left(\sum\limits_{i = 1}^M {{w_i}{A_i}} - f\right)^2}\right] \\ = &{ E}\left[{\left(\sum\limits_{i = 1}^M {{w_i}{A_i}} - E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right] + E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right] - f\right)^2}\right] \\ = &{\left(E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right] - f\right)^2} + { E}\left[{\left(\sum\limits_{i = 1}^M {{w_i}{A_i}} - E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right]\right)^2}\right] \\ & + E\left[2\left(E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right] - f\right)\left(\sum\limits_{i = 1}^M {{w_i}{A_i}} - E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right]\right)\right] \\ = &{\left(E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right] - f\right)^2} + { E}\left[{\left(\sum\limits_{i = 1}^M {{w_i}{A_i}} - E\left[\sum\limits_{i = 1}^M {{w_i}{A_i}} \right]\right)^2}\right] \\ = & bias(A{{\text{)}}^2} + {var} (A) \end{split}$

(12)

4 实验分析

考虑到基于交叉验证的集成学习的预测误差在一般情况下会比单个学习器的预测要小. 为了更进一步分析基于交叉验证的集成学习的误差, 下面先在模拟数据集上进行模拟实验进行验证, 再在真实数据集wine quality-white上进行验证.

4.1 模拟数据的实验

本文针对回归问题进行分析, $X = ({x_1}, {x_2}, \cdots , {x_p})$ 表示 $p$ 维输入向量, 取 $p = 6$ , $X$ 由基于MASS包的 $mvrnorm()$ 函数的多元高斯正态分布的随机数产生, $Y = rnorm(n)$ 表示服从标准正态分布的 $n$ 个随机数. 实验分析在样本量 $n$ 发生变化时, 基于 $k$ 折交叉验证和组块3×2交叉验证集成学习的预测误差和单个学习器的预测误差的变化. 在这里考虑3个回归模型, 具体如下.

(1)广义线性回归模型

广义线性回归是一种经典的线性模型, 在给定输入的情形下, 它可以学得一个模型预测输出, 使得预测准确率尽可能高, 误差尽可能小. 在本文的模拟实验中, 指数分布族取的是高斯分布 $(family = gaussian())$ .

(2)支持向量机回归

假设输出模型 $f(x)$ 与真实输出 $y$ 之间的偏差最多为 $\varepsilon$ 才可接受, 也就是说 $\left| {f(x) - y} \right| \gt \varepsilon$ 时需要计算损失, 相当于以 $f(x)$ 为中心, 构建一个宽度为 $2\varepsilon$ 的间隔带^[18], 在训练样本属于间隔带的情况下, 认为预测是正确的.

(3)随机森林回归

随机森林一般采用bootstrap sampling方法进行抽样, 对抽取的每个样本子集建树, 随后输出每棵树的预测结果. 对于回归问题, 一般通过简单平均法对每棵树的结果求均值作为最终的预测结果, 本文实验中随机森林参数设置 $ntree = 100, \; mtry = 6$ .

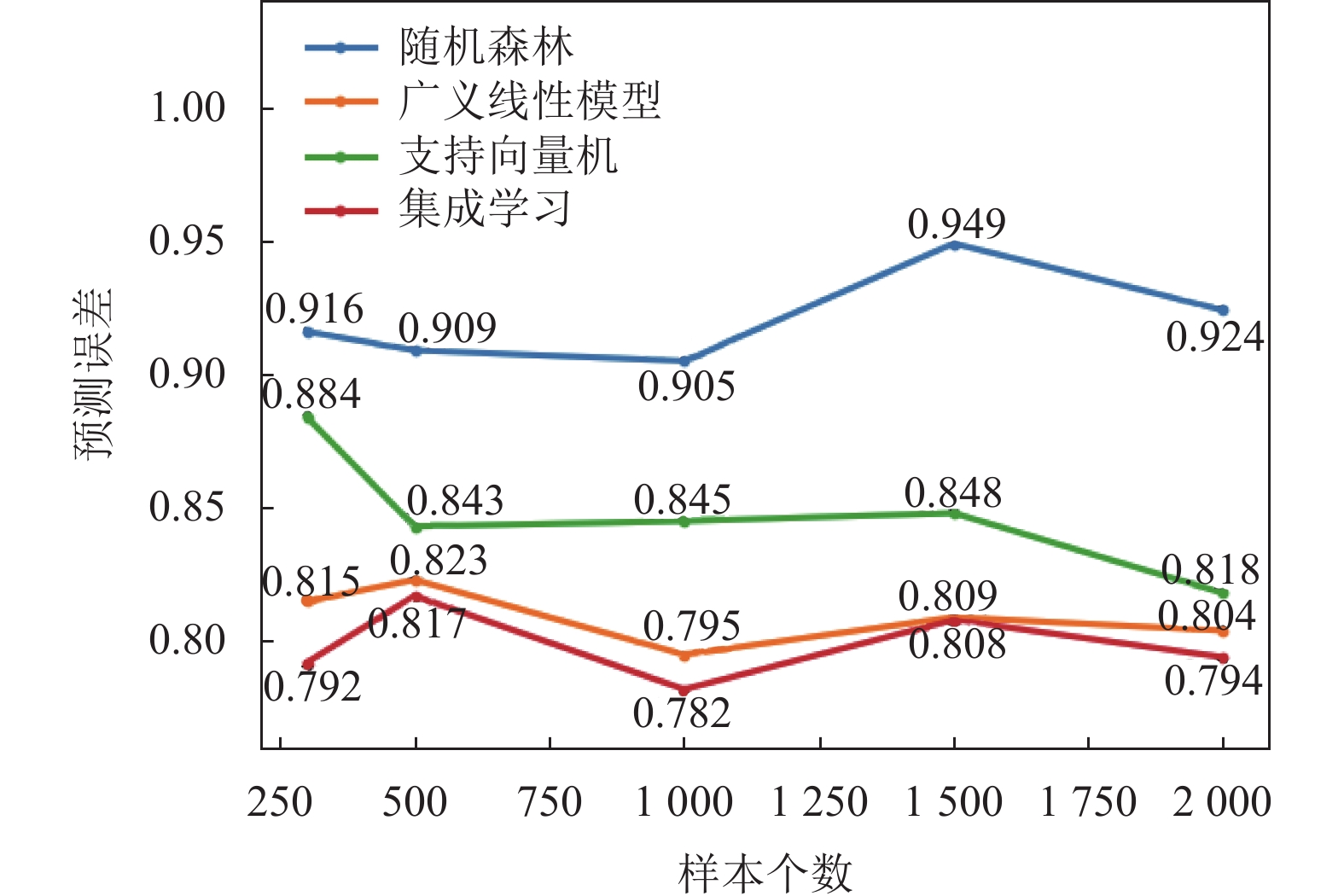
由图3可以看到在组块3×2交叉验证的情形下, 随着样本个数的变化, 随机森林, 广义线性模型, 支持向量机3个模型与集成学习相比, 集成学习的预测误差的均值比其他3个模型的均值都小. 由图4可以看到基于 $k$ 折交叉验证的集成学习得到的预测误差比随机森林和支持向量机得到的预测误差小, 但是比广义线性模型的预测误差大.

表1是具体的不同学习器的预测误差的数值, 具体可以看到随着样本个数的变化在应用组块3×2交叉验证和 $k$ 折交叉验证进行集成学习的误差均小于单个学习器的预测误差均值, 而且在广义线性模型和支持向量机模型中随着样本个数的增加, 误差均值有逐渐减少的趋势, 并且在大部分情形下组块3×2交叉验证比 $k$ 折交叉验证进行集成学习的误差相对更小.

表2和表3为不同模型的偏差平方 $(bias{(A)^2})$ 和方差, 从中可见组块3×2交叉验证的集成学习偏差的平方和方差比基于 $k$ 折交叉验证的集成学习小.

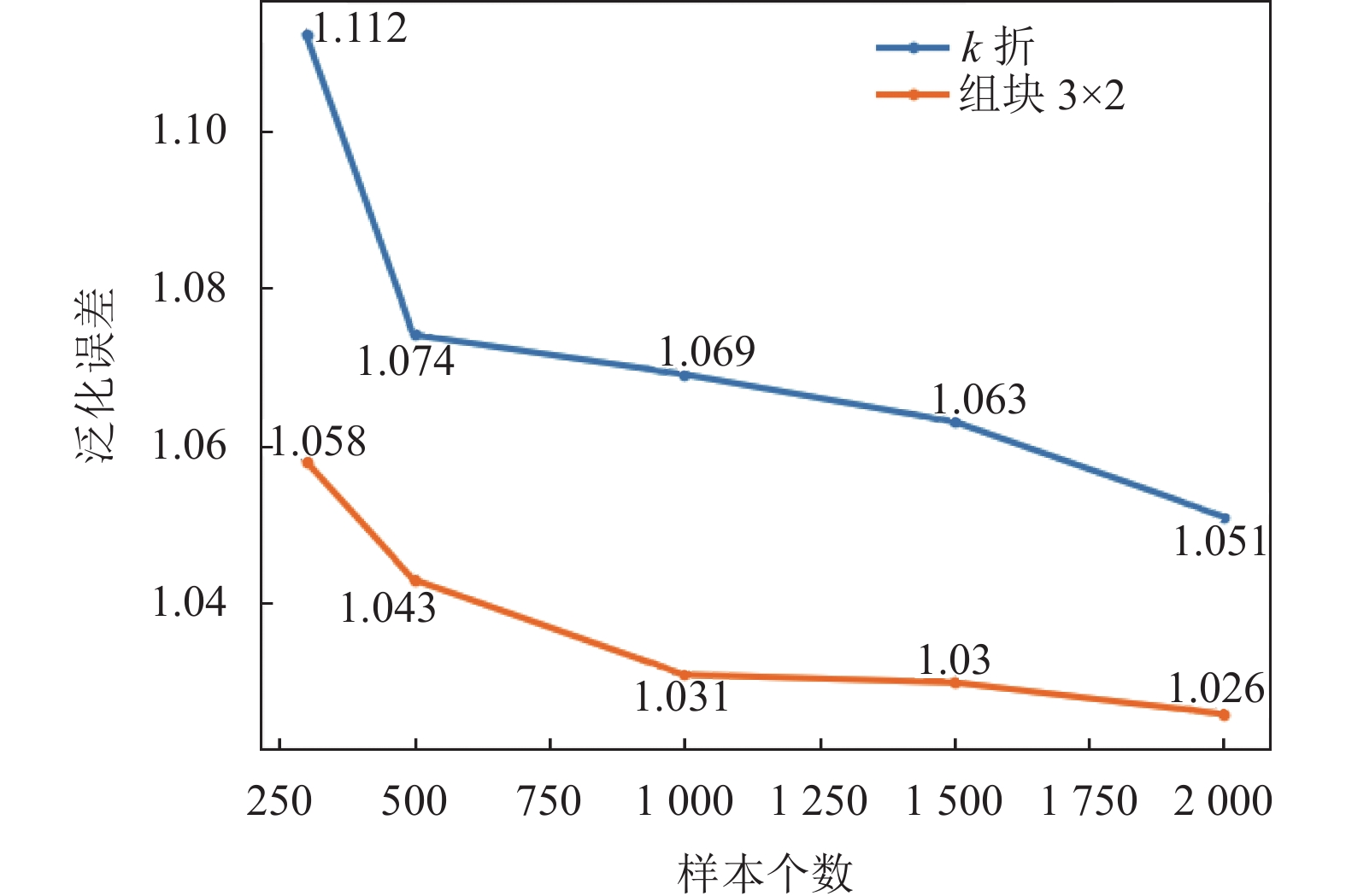
图5可以发现集成学习的泛化误差随着样本量的增大在逐渐减少, 并且基于组块3×2交叉验证的集成学习的泛化误差比基于 $k$ 折交叉验证的集成学习的泛化误差小.

4.2 真实数据的实验

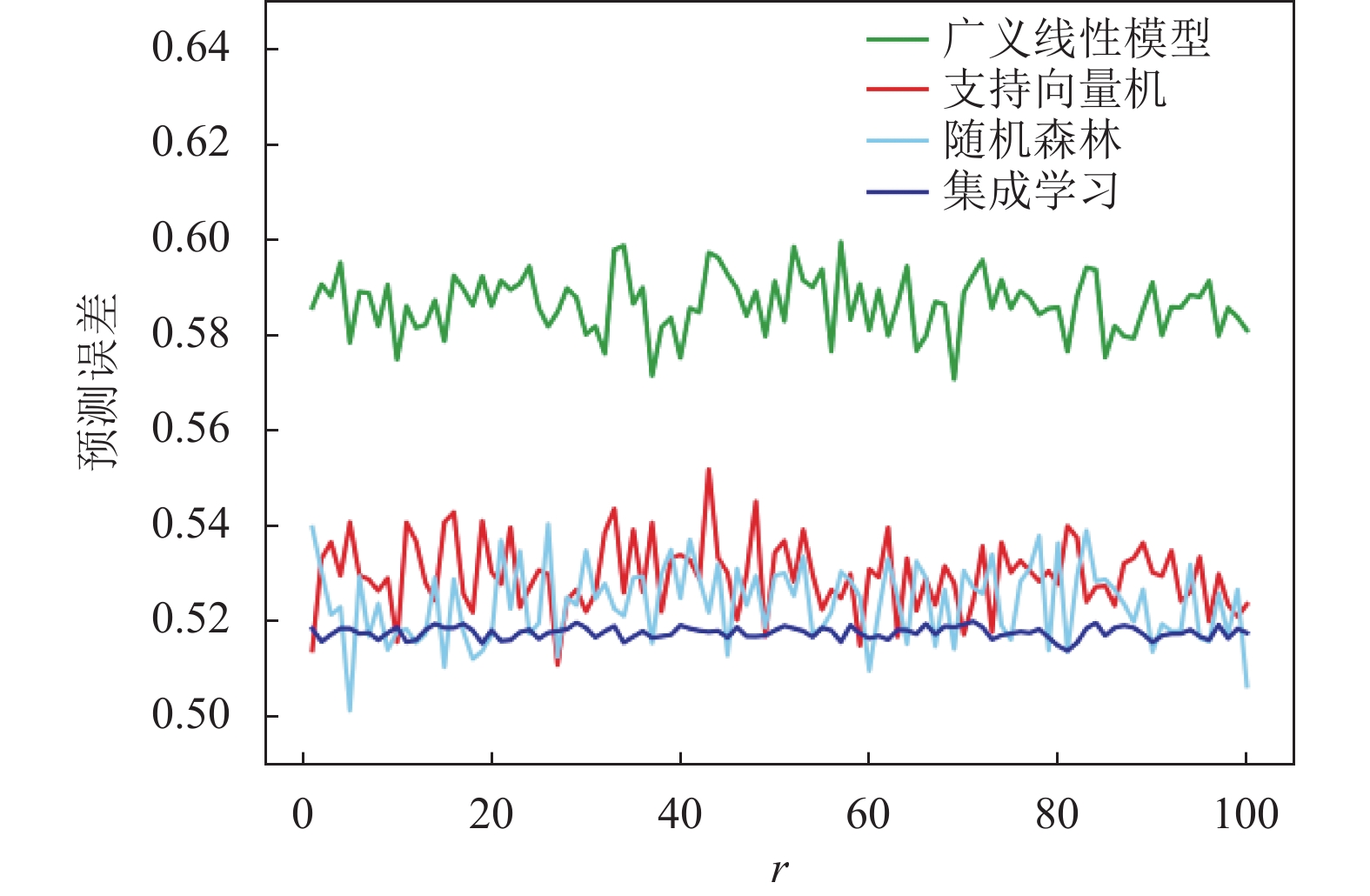
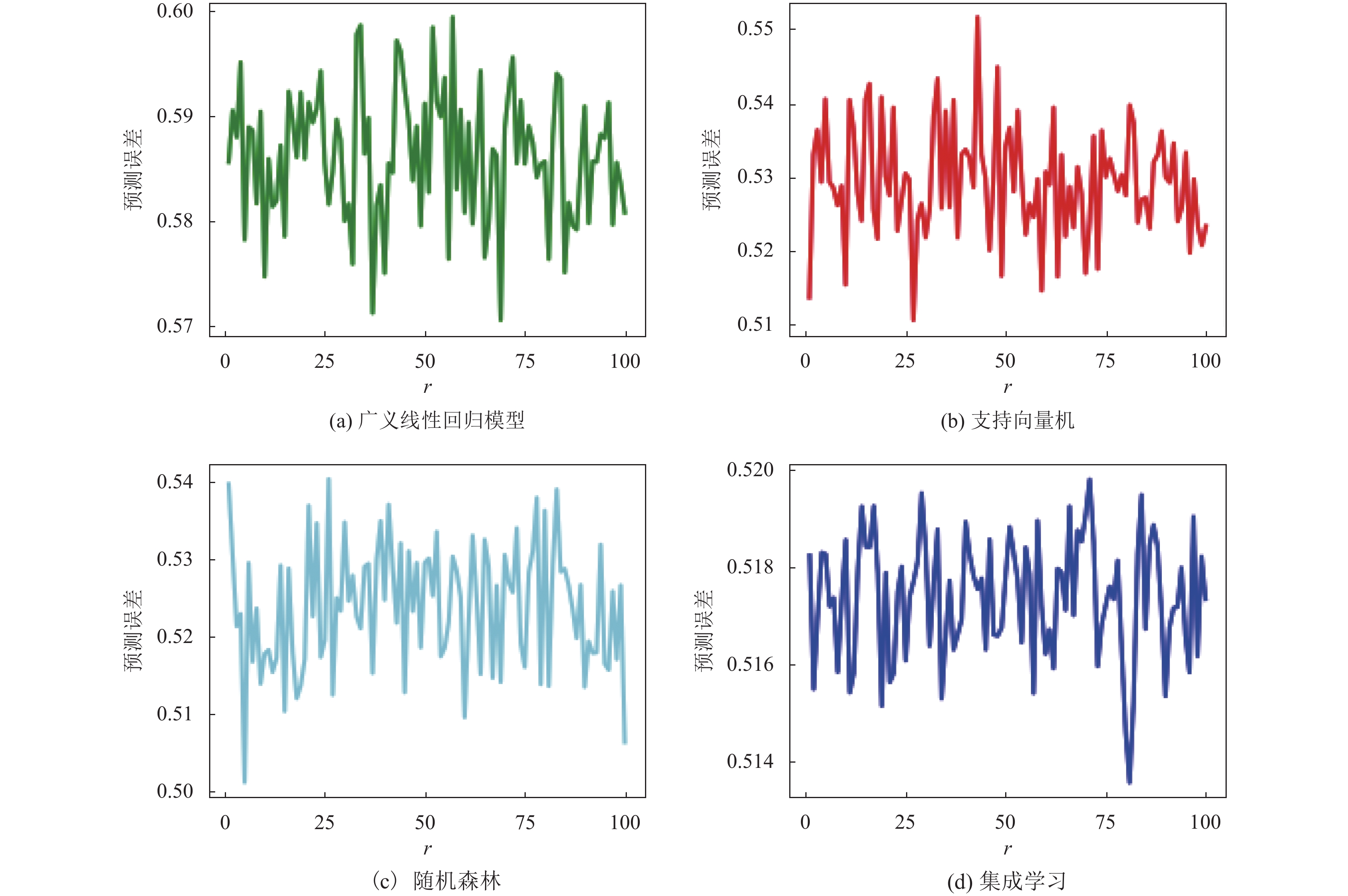
在真实数据集wine quality-white上基于组块3×2交叉验证进行实验, 在相同情形下重复实验r次, r=1, 2, …,100, 图6和图7表示不同模型下的预测误差图, 从图7可以看到广义线性回归模型的大部分数据的预测误差处于0.57到0.60之间, 支持向量机回归的大部分数据的预测误差处于0.51到0.55之间, 随机森林做回归任务的大部分数据的预测误差处于0.50到0.54之间, 而集成学习的大部分数据的预测误差处于0.516到0.519之间. 因此随机森林, 广义线性模型, 支持向量机3个模型与集成学习相比, 从图6可以明显看出基于组块 $3 \times 2$ 交叉验证集成学习的预测误差的均值比其他3个模型小.

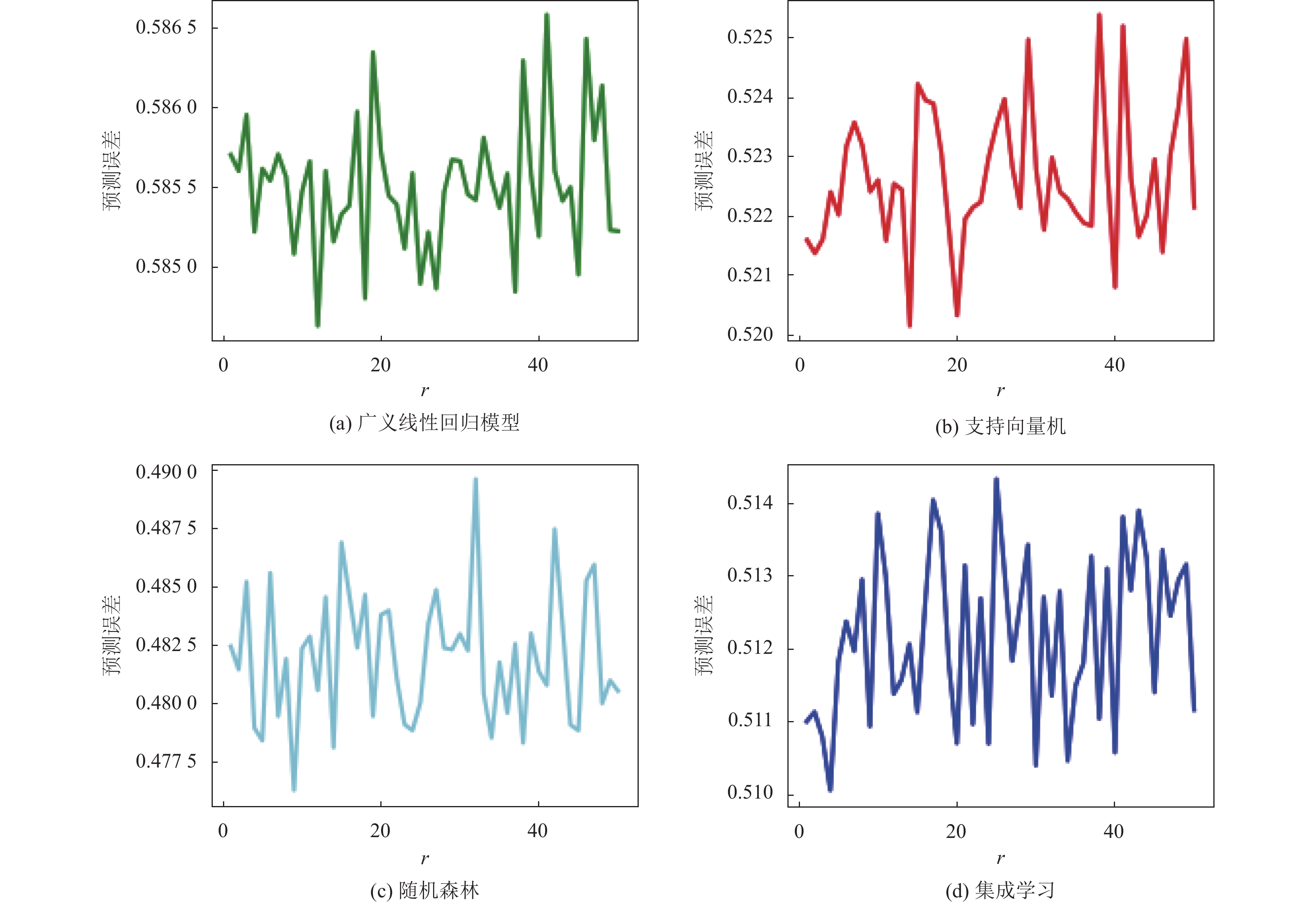
在真实数据集wine quality-white上基于 $k$ 折交叉验证进行实验, 图8表示不同模型下的预测误差图, 从图8可以看到广义线性回归模型的大部分数据的预测误差处于0.585到0.5865之间, 支持向量机回归的大部分数据的预测误差处于0.520到0.525之间, 随机森林做回归任务的大部分数据的预测误差处于0.4775到0.4900之间, 而集成学习的大部分数据的预测误差处于0.510到0.514之间. 基于 $k$ 折交叉验证的集成学习的预测误差小于广义线性模型和支持向量机的误差, 但是比随机森林的预测误差大. 因此基于组块3×2交叉验证集成学习的预测误差比基于 $k$ 折交叉验证的集成学习在wine数据集上集成效果更好.

5 结论

本文分析基于交叉验证的集成学习方法, 重点分析基于组块3×2交叉验证和基于 $k$ 折交叉验证的集成学习, 与其他单个学习器相比, 集成学习误差更小, 方差更加稳定. 并且通过模拟实验验证基于组块3×2交叉验证的集成学习比基于 $k$ 折交叉验证的集成学习的预测误差更小, 模型更加稳定.