情绪是人类对外界环境或人际事件的刺激所产生的一组情感状态, 积极的情绪对于人的社会活动至关重要, 正确地识别人类情绪也是社会稳定发展的前提. 情绪识别与人机交互密切相关, 情绪识别技术的发展有助于提升人机交流质量和计算机的智能性, 此外, 情绪识别技术也广泛应用于心理学、医疗等领域. 当识别情绪状态时, 语言和动作等非生理信号可以被刻意伪装, 而EEG信号记录了情绪状态与大脑活动的关系[1], 可以真实的反映情绪的动态变化, 并且基于脑电信号的情绪识别技术的实现对于一些特殊疾病患者也易于实现. 近些年来, 很多研究学者将脑电情绪识别作为研究的重点, 结合机器学习和深度学习实现了较高的准确率, 相比于机器学习, 深度学习可以深层次提取特征. 特征提取是情绪识别中非常重要的一环, 选择合适的脑电信号成分可以提升情绪识别准确率. Liu等人[2]对数据进行经验模态分解和微分熵特征提取, 设计了电极最佳放置位置, 最后将处理后的数据输入二维卷积神经网络进行情绪识别实验. Chen等人[3]对预处理后的数据进行模式分解后提取平均近似熵特征, 接着将特征输入到LIBSVM分类器中, 最终在唤醒度和效价上的分类准确率为74.88%和82.63%. 刘鹏等人[4]利用AR模型功率谱估计方法及小波包分解算法对脑电特征进行组合, 采用栈式自编码神经网络对其进行识别, 平均识别率为81.5%和80.3%. 很多研究者将特征提取方法与深度学习相结合, 相较于传统的机器学习算法分类效果有所提升. Alhagry等人[5]将长短时记忆网络(LSTM)和循环神经网络(RNN)结合起来进行特征学习, 在DEAP数据集上的唤醒和效价的分类准确率分别为85.65%和85.45%. Yang等人[6]保留了通道间的空间信息, 对于单个频段及其组合频段的数据进行分类, 结果显示多频段组合的分类效果更好, 在DEAP数据集上唤醒度和效价分类准确率为90.24%和89.45%. Yin等人[7]对脑电信号进行标定和分段, 将提取微分熵特征后的数据作为融合图卷积神经网络和长短时记忆神经网络的深度学习模型的输入, 最终在唤醒度和效价上的平均分类准确率为: 90.45%和90.60%.
同一实验中不同个体EEG反应模式存在显著性差异, 很多文献并未考虑个体差异及环境因素对识别准确度的影响. 本文进行了去基线信号干扰研究和脑电通道筛选优化, 结合连续卷积神经网络提出一种情绪识别方法. 实验中对于DEAP数据集中受试者的基线信号和实验脑电信号数据分别进行微分熵特征提取, 将结果的差值根据电极分布映射为二维矩阵, 将得到的4个不同频带的二维矩阵在频率维度进行堆叠, 最终将多通道数据输入连续卷积神经网络进行分类. 去基线干扰方法可以减少情绪诱发前状态对于实验的干扰影响进而提高识别准确率, 对于脑电通道进行筛选可以减少实验训练时间, 将数据处理后组合为多通道的输入形式可以从不同频带提取特征的同时保留其空间特征, 该方法在公开数据集DEAP上进行了验证.
1 方法 1.1 频率模式分解EEG信号可以根据带内相关性和行为状态等划分为表1所示的5种不同的频率模式[8]. 情绪识别实验中一般使用滤波的方式对原始信号进行分解, 文献[6]将脑电信号分解到各个频带探索单频带和组合频带的分类效果, 其结果证明全频带组合的方式提取特征进行分类效果最好, 本文依据此结论将使用滤波器将原始脑电信号分为θ、α、β、γ四个频段, 将4个频段组成为多通道形式并在此基础上进行实验.
| 表 1 脑电信号模式 |
1.2 脑电信号特征提取 1.2.1 微分熵
微分熵具有分辨脑电模式低频带和高频带的平衡能力, 可以准确反映刺激的反应程度变化. 因此本实验采用微分熵算法来表示一段固定长度脑电信号的复杂程度. 微分熵是香农信息熵在连续变量上的推广形式[9], 设Xi为脑电信号, 其原始表达式为:
| D(x)=−∫E(x)log[E(x)]dx | (1) |
其中, E(x)指的是连续的脑电信号的概率密度函数. Shi等人[10]证明, 对于近似服从高斯分布N(μ, σ2)的一段随机变量的微分熵等于其在特定频段上能量谱的对数, 其具体表达式为:
| D(x)=−∫+∞−∞1√2πσ2e−(x−μ)22σ2log[1√2πσ2e−(x−μ)22σ2]dx=12log2πeσ2 | (2) |
原始脑电信号比较复杂, 不服从正态分布, 但是一段脑电信号经过2–44 Hz的带通滤波后近似服从高斯分布. 表达式中的π与e为常数, 只要获得了
| final_vnm=trial_vnm−base_vnk | (3) |
其中,
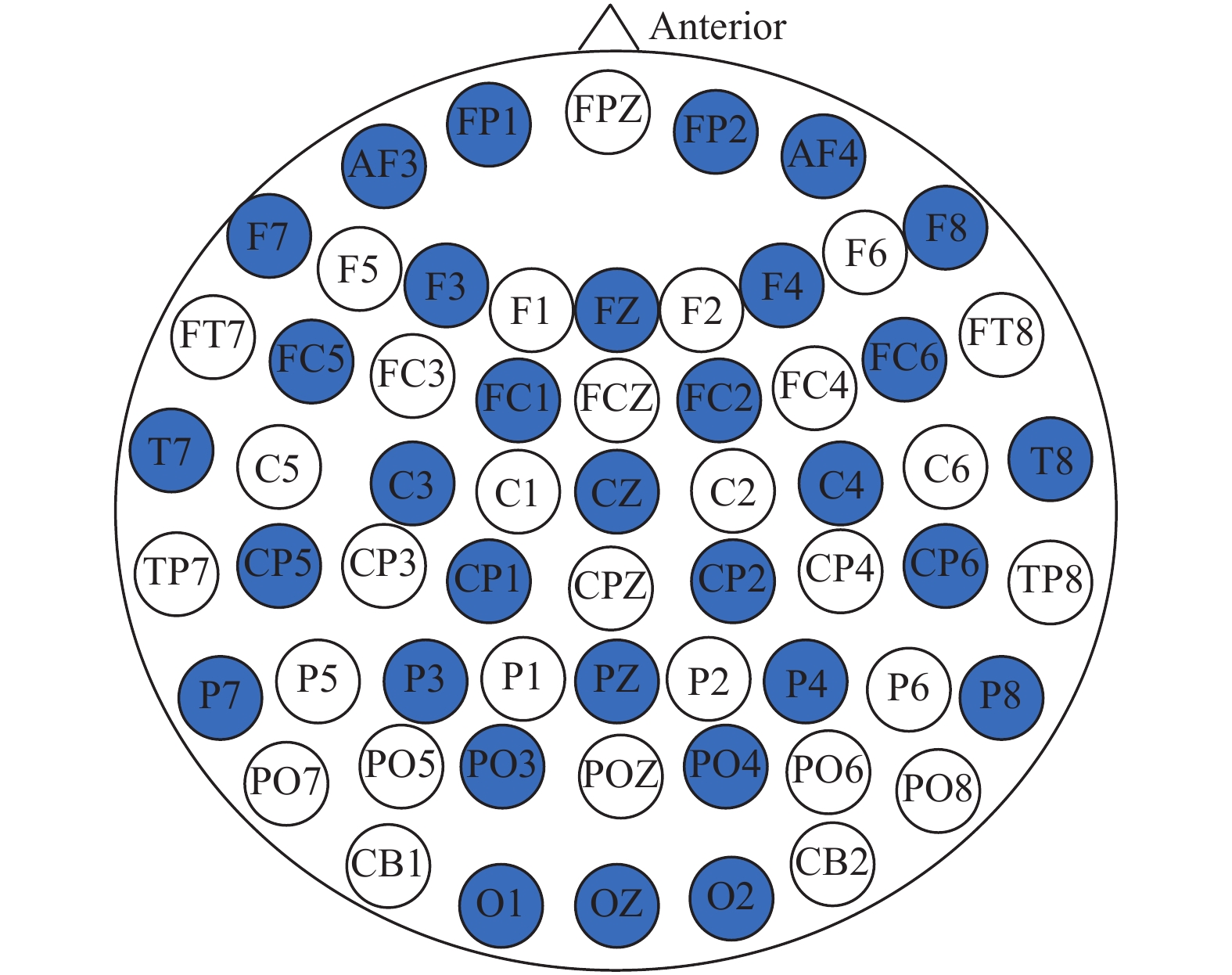
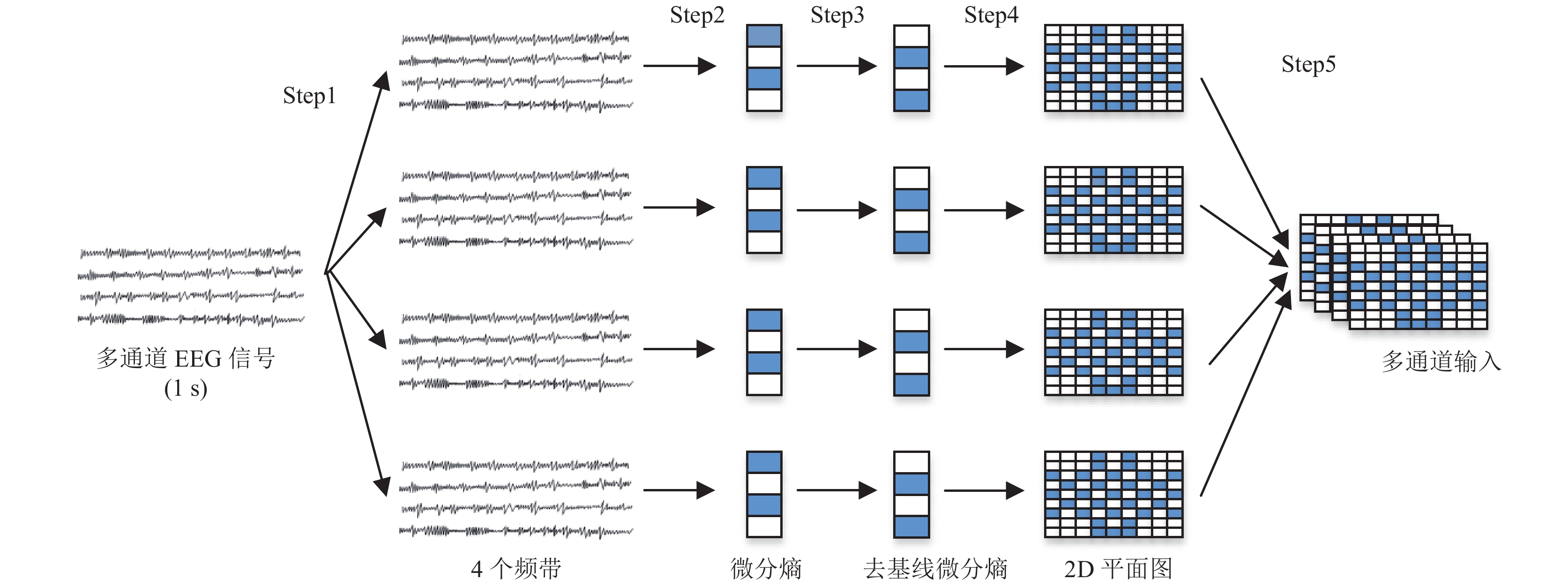
不同个体之间生理信号差异很大, 同一个体在不同的时刻和环境也会有很大的差异[11]. 对于受试者来说, 每个音乐视频播放之前会产生一段静息态信号, 这段静息态信号对后面刺激情况下的实验脑电信号有一定的影响, 所以本实验用的方法是用情绪诱发状态下的脑电信号微分熵减去平静状态下的脑电信号(即基线信号)微分熵, 将结果按照图1的国际10–20系统电极[12]放置位置构造出一个9×9的二维矩阵, 剩余位置使用零填充. 本文实验按照图2的方法将得到θ、α、β、γ四个频带的二维矩阵, 为了进行充分的特征提取, 将4个二维矩阵在频率维度进行堆叠得到多通道形式的输入, 将4通道数据作为连续卷积神经网络的输入进行特征提取与分类. 具体的特征提取与转化过程如图2所示.
|
图 1 国际10–20系统平面图 |
|
图 2 特征提取与转化流程图 |
1.3 连续卷积神经网络
卷积神经网络中的运算量主要集中在卷积层, 使用较小的卷积核和较少的卷积层数可以提升模型运行速度[13]. 经典卷积神经网络中卷积层后面是池化层, 作用是筛选前一层的特征的同时减少下一层计算量, 但是在情绪识别领域卷积操作提取的特征有限, 使用池化层容易丢失有效的特征信息并且池化层会增加模型深度进而导致过拟合[14]. 池化层并不是必须条件, He等人[15]在图像处理实验中减少了池化层的个数, 但是结果却并没有影响. 因此在本文设计的卷积神经网络模型中弃用池化层, 使用连续卷积的形式减少模型深度, 降低过拟合的风险.
连续卷积神经网络最终构建的模型如图3所示. 模型包含7层, 第1层为输入层, 将处理后的数据输入卷积模型; 第2层至第5层为卷积层, 多次卷积是为了提取更深层次的数据特征; 第6层为具有1024个神经元的全连接层, 最后一层为输出层, 使用Softmax分类器进行分类.

|
图 3 连续卷积神经网络 |
因为脑电数据样本集数量有限, 卷积操作容易使原始数据特征丢失, 为了保证输入输出的尺寸一致, 采用same模式进行填充, 卷积核大小一般设置为奇数可以保证对称填充. 经过多次实验, 最终确定第2层至第4层卷积层采用大小为3的卷积核, 步长设置为1, 卷积核个数由64逐层加倍. 在输入全连接层之前进行特征降维, 因此设计第5层卷积核大小为1, 卷积核个数为64个. 连续卷积神经网络模型使用的激活函数为SELU函数, batch size大小设置为128, 学习率为10–6, 采用交叉熵损失函数加L2正则化避免过拟合, Adam算法对目标函数进行优化, L2正则化权重系数设置为0.5, dropout设置为0.5.
2 数据集和数据预处理 2.1 DEAP数据集情绪识别实验中通常会采用离散模型和维度模型来构建情绪空间. 其中, 维度模型认为情绪空间可以由二维的效价-唤醒度(arousal-valence, VA)坐标体系表示[16]. Koelstra等人[17]利用情绪维度模型建立了DEAP数据集, 被各种基于EEG的情绪识别研究所广泛使用. 相对于电影来说, 音乐视频能够使人更快地进入状态, 诱发情绪速度较快, 所以本文使用DEAP数据集来验证情绪识别方法. 在DEAP数据集中, 受试者共32名(16名男性, 16名女性), 平均年龄为26.9岁. 实验中要求每位受试者观看40段1 min长的音乐视频, 同时记录其观看视频过程中的生理信号, 每观看结束一段视频, 受试者按照自己的真实感受进行自我评估, 采样流程如图4所示.
在信号采集阶段, 采样率为512 Hz, 采样通道为40通道, 包括32通道脑电信号, 8通道的眼电信号、肌电信号等. DEAP数据集提供了预处理版本, 在预处理版本中EEG信号被下采样到128 Hz, 保留了32个通道的数据, 脑电信号数据频率范围在4–45 Hz. 受试者每个音乐视频保留63 s的脑电信号数据, 其中前3 s为观影前受试者在平静状态下的基线信号, 随后60 s是在情绪诱发状态下的实验脑电信号. 实验采用唤醒度(arousal)与效价(valence)两项进行情绪分类评估, 分别表示的是受试者在观看音乐视频的兴奋状态和愉悦度, 分值为1–9, 以5为阈值将其分为积极和消极.

|
图 4 实验流程图 |
2.2 数据预处理
本文实验中为了增大数据样本量, 首先将实验脑电信号以1 s为单位进行分割, 每位受试者观看一个音乐视频可以得到60段实验脑电样本数据, 处理后的实验脑电数据集大小为40 (通道数)×128 (分段长度)×60 (片段数). 本文讨论的是基于脑电信号的情绪识别, 所以选取DEAP数据集中的前32通道脑电信号数据. 使用巴特沃斯滤波器将脑电信号分解到θ、α、β、γ四个频带上, 选用微分熵算法对于每个频带的脑电信号进行特征提取. 后续实验将讨论基线信号的影响, 因此受试者的基线信号也按照该步骤进行处理分为3 s的基线信号片段、3个1 s的基线信号片段.
3 脑电情绪识别实验 3.1 去基线干扰实验为了研究基线信号对于脑电情绪识别的影响, 本文针对基线信号微分熵的选取进行了实验, 分别将受试者一段基线信号的微分熵、每秒基线信号微分熵均值、最后一秒基线信号(即有刺激的实验脑电前一秒)微分熵作为该名受试者的基线信号微分熵特征. 一般情绪识别实验不使用基线信号, 因此为了体现本文方法的优越性设置了对比实验. 采用经典的脑电情绪识别方法提取60 s脑电信号微分熵特征输入到卷积神经网络中, 对比实验没有考虑平静状态对于情绪诱发时的影响, 网络结构与图3相对应. 采用十折交叉验证方法对连续卷积神经网络模型进行测试, 首先将处理后的样本数据随机打乱, 进行归一化处理后按照9:1的形式分为训练集和测试集. 将每位受试者进行十折交叉验证后的平均准确率作为该受试者的准确率.
实验结果如表2所示, 未结合基线信号的情况下在唤醒度和效价上的分类准确率为69.69%与67.85%. 将所有基线信号DE特征与实验脑电信号DE的偏差作为连续卷积神经网络的输入, 在唤醒度和效价上的分类准确率为89.80%和88.68%, 结合基线信号DE均值进行情绪识别在唤醒度和效价上的分类准确率为89.66%和88.74%, 结合最后一秒基线信号的DE特征进行实验在唤醒度和效价上的分类准确率为95.95%和95.54%. 图5显示的是32名受试者在唤醒度和效价上的分类准确率. 可以明显地看到结合基线信号的3种实验结果远高于不使用基线信号的结果. 其中, 结合所有基线信号DE及基线信号DE均值进行分类实验得到的结果相差不大, 使用最后一秒基线信号DE得到的结果相比其他两种情况提升了6个百分点, 并且几乎所有受试者的分类准确率都高于90%. 相对来说, 未使用基线信号的情绪识别率较低. 由此分析可知, 结合基线信号采用去基线干扰方法能够提升情绪识别准确率, 证明了该方法的有效性.
| 表 2 分类准确率对比 (%) |
3.2 通道选择
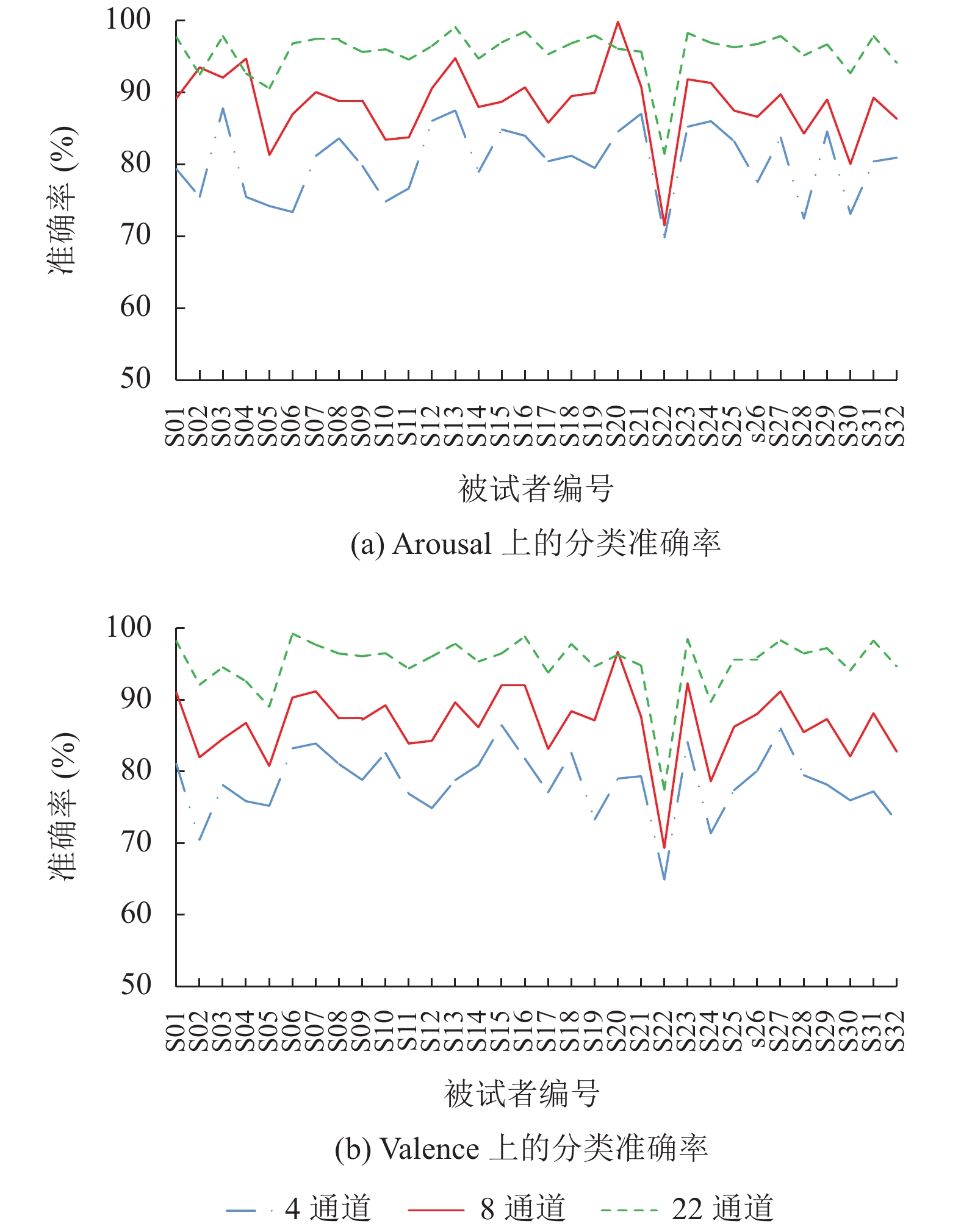
在脑电情绪识别的实验中, 选择合适的脑电通道个数可以降低计算复杂度. 本文实验使用预处理后的DEAP数据集来探索电极通道个数对于识别准确率的影响, 进而选择出最佳的脑电通道个数. 脑区的前额、前半脑区和颞叶这3部分区域控制着人类的情绪波动[18], 因此根据该结论, 选择了3种不同的电极分布, 在10–20国际系统中对应为: 1) 4通道(FP1、FP2、T7、T8); 2) 8通道(FP1、FP2、T7、T8、CP5、CP6、P7、P8); 3) 22通道(FP1、FP2、AF3、AF4、F7、F3、FZ、F4、F8、FC5、FC1、FC2、FC6、T7、C3、CZ、C4、T8、CP5、CP6、P7、P8). 图6显示了32名受试者在3种不同通道上的分类准确率, 4通道数据在唤醒度和效价上的分类准确率为80.40%和78.41%, 选用8通道数据的分类结果为87.78%和86.31%, 22通道数据在唤醒度和效价上的平均准确率为95.63%和95.13%. 由结果可知, 22通道的平均分类准确率高于4通道与8通道的平均分类准确率, 且22通道的平均分类准确率接近32通道的平均分类准确率, 由此可以推断DEAP数据中的FP1、FP2、AF3、AF4、F7、F3、FZ、F4、F8、FC5、FC1、FC2、FC6、T7、C3、CZ、C4、T8、CP5、CP6、P7、P8电极通道包含了大部分我们所需要的情感识别信息.

|
图 5 32名受试者的分类准确率 |
|
图 6 不同通道数据的分类准确率 |
3.3 同类研究结果对比
为了体现本文情绪识别方法的科学性, 将与同样采用DEAP数据集的情绪分类实验结果进行对比. 文献[3]首先计算脑电信号的LZ (Lempel-Ziv)复杂度和小波细节系数, 将计算平均近似熵后的数据输入到LIBSVM分类器中进行分类实验. 文献[5]结合LSTM和RNN模型直接从原始的数据中学习特征, 在唤醒度和效价上的平均准确率为85.65%和85.45%. 文献[6]对于单个频段及其组合频段的数据使用三维卷积神经网络进行分类. 文献[7]将脑电数据进行分段, 分别提取微分熵特征后构成特征立方体作为融合图卷积神经网络和长短时记忆神经网络的深度学习模型的输入, 最终平均分类准确率为90.45%和90.60%. 由表3可知, 本文所提出的识别方法在唤醒度和效价上的平均准确率均高于其他4种方法, 说明本文方法在DEAP数据集上进行情绪识别的效果更好, 具有一定的研究价值.
4 结论与展望本文对DEAP情绪数据集脑电数据进行特征提取和分类, 通过去基线干扰及通道选择的研究, 最终采用DEAP数据集中32名受试者每段音乐视频数据中的最后一秒基线信号和60 s实验脑电数据在22通道的情况下进行情绪识别实验, 在唤醒度和效价上的平均分类准确率为95.63%和95.13%. 实验结果证实了结合基线信号能够有效地提升分类准确率, 采用连续卷积模型也可以将特征中的有效信息进一步的提取出来, 同时选择对情绪识别影响较大的部分通道代替全通道能够使数据量大大减少, 降低计算复杂度.
| 表 3 同类研究结果对比 (%) |
在本文的实验研究中, 采用的是提取微分熵特征, 提取的特征类型较为单一, 在接下来的工作中, 考虑对脑电信号不同的特征提取方式进行组合, 提取到更深层次的特征, 同时, 本文采用DEAP数据集中的32通道脑电信号, 并未使用剩余的8通道生理信号, 在后续的实验中希望将眼电信号等生理信号与脑电信号结合起来, 研究出更好的特征提取和分类的方式进行情绪识别.
| [1] |
Hämäläinen M, Hari R, Ilmoniemi RJ, et al. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics, 1993, 65(2): 413. DOI:10.1103/RevModPhys.65.413 |
| [2] |
Liu SQ, Wang X, Zhao L, et al. Subject-independent emotion recognition of EEG signals based on dynamic empirical convolutional neural network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2021, 18(5): 1710-1721. DOI:10.1109/TCBB.2020.3018137 |
| [3] |
Chen T, Ju SH, Ren FJ, et al. EEG emotion recognition model based on the LIBSVM classifier. Measurement, 2020, 164: 108047. DOI:10.1016/j.measurement.2020.108047 |
| [4] |
刘鹏, 乔晓艳. 基于栈式自编码神经网络的脑电信号情绪识别. 测试技术学报, 2021, 35(2): 145-151. DOI:10.3969/j.issn.1671-7449.2021.02.009 |
| [5] |
Alhagry S, Fahmy AA, El-Khoribi RA. Emotion recognition based on EEG using LSTM recurrent neural network. International Journal of Advanced Computer Science and Applications, 2017, 8(10): 355-358. |
| [6] |
Yang YL, Wu QF, Fu YZ, et al. Continuous convolutional neural network with 3D input for EEG-based emotion recognition. Proceedings of the 25th International Conference on Neural Information Processing. Berlin, Siem Reap: Springer, 2018. 433–443.
|
| [7] |
Yin YQ, Zheng XW, Hu B, et al. EEG emotion recognition using fusion model of graph convolutional neural networks and LSTM. Applied Soft Computing, 2021, 100: 106954. DOI:10.1016/j.asoc.2020.106954 |
| [8] |
Zhang X, Yao LN, Kanhere SS, et al. MindID: Person identification from brain waves through attention-based recurrent neural network. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 2018, 2(3): 149. |
| [9] |
Zheng WL, Lu BL. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. DOI:10.1109/TAMD.2015.2431497 |
| [10] |
Shi LC, Jiao YY, Lu BL. Differential entropy feature for EEG-based vigilance estimation. Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Osaka: IEEE, 2013. 6627–6630.
|
| [11] |
Jirayucharoensak S, Pan-Ngum S, Israsena P. EEG-based emotion recognition using deep learning network with principal component based covariate shift adaptation. The Scientific World Journal, 2014, 2014: 627892. |
| [12] |
Acharya JN, Hani AJ, Cheek J, et al. American clinical neurophysiology society guideline 2: Guidelines for standard electrode position nomenclature. The Neurodiagnostic Journal, 2016, 56(4): 245-252. DOI:10.1080/21646821.2016.1245558 |
| [13] |
程越, 刘志刚. 基于轻量型卷积神经网络的交通标志识别方法. 计算机系统应用, 2020, 29(2): 198-204. DOI:10.15888/j.cnki.csa.007264 |
| [14] |
涂文博, 袁贞明, 俞凯. 无池化层卷积神经网络的中文分词方法. 计算机工程与应用, 2020, 56(2): 120-126. DOI:10.3778/j.issn.1002-8331.1809-0177 |
| [15] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [16] |
Mehrabian A. Pleasure-arousal-dominance: A general framework for describing and measuring individual differences in temperament. Current Psychology, 1996, 14(4): 261-292. DOI:10.1007/BF02686918 |
| [17] |
Koelstra S, Muhl C, Soleymani M, et al. DEAP: A database for emotion analysis using physiological signals. IEEE Transactions on Affective Computing, 2012, 3(1): 18-31. DOI:10.1109/T-AFFC.2011.15 |
| [18] |
Zheng WL, Guo HT, Lu BL. Revealing critical channels and frequency bands for emotion recognition from EEG with deep belief network. Proceedings of the 7th International IEEE/EMBS Conference on Neural Engineering. Montpellier: IEEE, 2015. 154–157.
|
 2023, Vol. 32
2023, Vol. 32



