实时异构系统的应用非常广泛, 例如无人驾驶系统, 无人机系统, 工业控制系统等. 一个异构系统通常由一组处理器组成, 处理器之间通过总线相连, 能够进行数据通信. 随着处理器的增多, 当今的应用程序并行程度也变得越来越高, 并且这些应用中的任务拥有明显的数据依赖^[1-3]. 比较典型的应用有快速傅里叶变换^[4]和高斯消元^[5]. 异构系统中的处理器拥有不同的计算性能和能量消耗, 在执行并行应用时相较于同构系统拥有明显的优势^{[6, 7]}.

但由于严峻的运行环境, 处理器在运行过程中偶尔也会发生错误. 错误一般分为两种, 暂时性错误和永久性错误. 暂时性错误会造成任务执行结果的错误, 进而造成整个应用执行出错, 通常因为辐射、高温和电磁干扰等环境因素导致. 永久性错误产生的原因是处理器设计方面的缺陷, 一旦发生永久性错误, 除非更换处理器, 否则该处理器不能继续执行任务^[8]. 两种错误都会导致系统可靠性的下降. 可靠性指的是一个调度成功执行的概率, 现在已经逐渐成为评判一个系统性能好坏的标准之一, 并且已在一些相关标准中定义, 例如IEC 61508和ISO 9000^[9]. 复制技术是一个有效的提升系统可靠性的解决方案. 在使用了复制技术的系统中, 只要任务的任意一个副本执行成功, 那么该任务被认为执行成功^[3]. 复制技术会通过增加任务的执行次数来提升任务的执行成功率, 进而提升系统的可靠性. 然而, 系统中需要执行的任务增加了, 应用的执行时间会变长, 系统的实时性会下降.

为了解决实时异构系统中的并行应用调度问题, 最早Wang等人采用了遗传算法^[9]. 但是遗传算法的时间复杂度较高, 不适用于大规模的任务调度. HEFT算法是一个经典的启发式算法^[6], 它的调度策略是, 先为任务分配优先级, 构造任务优先队列, 然后不断出队, 为出队的任务选择完成时间最早的处理器, 最终可以得到一个较短的应用执行时间. 此外, 还有基于复制的调度算法. 该类算法的核心在于减少任务之间数据传递产生的时间成本, 从而达到减小整个应用执行时间的目的^[10]. 上述的3种算法都没有考虑到处理器中可能出现错误导致最终应用执行结果出错.

为了提升系统的可靠性, 前人提出了很多容错调度算法. 容错调度算法大多使用了复制技术来提升系统的可靠性. 复制技术分为两种, 一种为积极复制, 另一种为被动复制. 积极复制技术是在任务调度前, 就对任务进行复制. 而被动复制需要系统额外配备一个错误检测器, 每当一个任务执行完成后, 错误检测器都会对任务的结果进行检测, 假如任务结果错误, 再对执行失败的任务进行复制^[11]. 被动复制技术大多被用于节能调度算法, 其在任务执行出错后才会复制任务, 并且重新执行任务^{[12, 13]}. 使用被动复制技术可以有效地减少系统执行任务的数量, 从而达到节能的效果. 两种复制技术都对应用的执行时间有不同程度的增加, 但相比于被动复制, 积极复制对于硬件的要求不高, 对实时性的影响较小, 因此很多同时考虑可靠性和实时性的容错调度算法都采用了积极复制技术进行容错, 例如FTSA算法^[14]、DB-FTSA算法^[15]、DBSA算法^[16]. 其中FTSA算法同时考虑系统中出现的暂时性错误和永久性错误, DB-FTSA只考虑暂时性错误, DBSA只永久性错误. 这3个算法都面向实时异构系统, 在提升系统可靠性的同时, 兼顾了系统的实时性. 其中考虑了永久性错误的容错调度算法, 一定要将同一任务的两个副本任务分配至不同的处理器, 这样才能保证其中一个处理器出现永久性错误后, 任务在另一个处理器上依然能执行成功. 而HRRM^[8]面向异构云计算系统, 不考虑实时性的约束, 更加侧重于节省系统的算力资源, 在保证系统可靠性的同时, 尽量减少系统中的任务冗余. 这些采用了积极复制技术的容错调度算法的执行过程包含为两个部分, 调度策略和复制策略. 调度策略是指为每个任务分配执行优先级, 然后调度至合适的处理器. 复制策略指的是为每个任务制定合理的复制次数.

本研究提出了一个面向实时异构系统的, 基于积极复制技术的容错调度算法 (fault-tolerant scheduling algorithm with replication strategy of minimum impact on real-time performance, FTSA-RSMI). 由于处理器执行任务时, 出现的错误大多为暂时性错误^{[7, 8]}, 因此该算法针对实时异构系统中出现的暂时性错误, 在满足实时性约束的条件下, 最大化系统的可靠性. 本研究和上述研究的不同点及主要贡献如下.

(1)本文提出了一个全新的复制策略, 该复制策略会优先复制任务集中对实时性影响最小的任务. 基于这个复制策略, 本文提出了一个全新的基于积极复制技术的面向实时异构系统的容错调度算法FTSA-RSMI.

(2)实验证明FTSA-RSMI能够在截止期限的约束下高效地提升系统的可靠性, 例如, 在调度随机生成DAG应用时, FTSA-RSMI能够得到90.68%的系统可靠性, 而DB-FTSA只能得到40.17%的系统可靠性. 在调度真实应用分子动力学代码时, FTSA-RSMI得到的系统可靠性比DB-FTSA高15%.

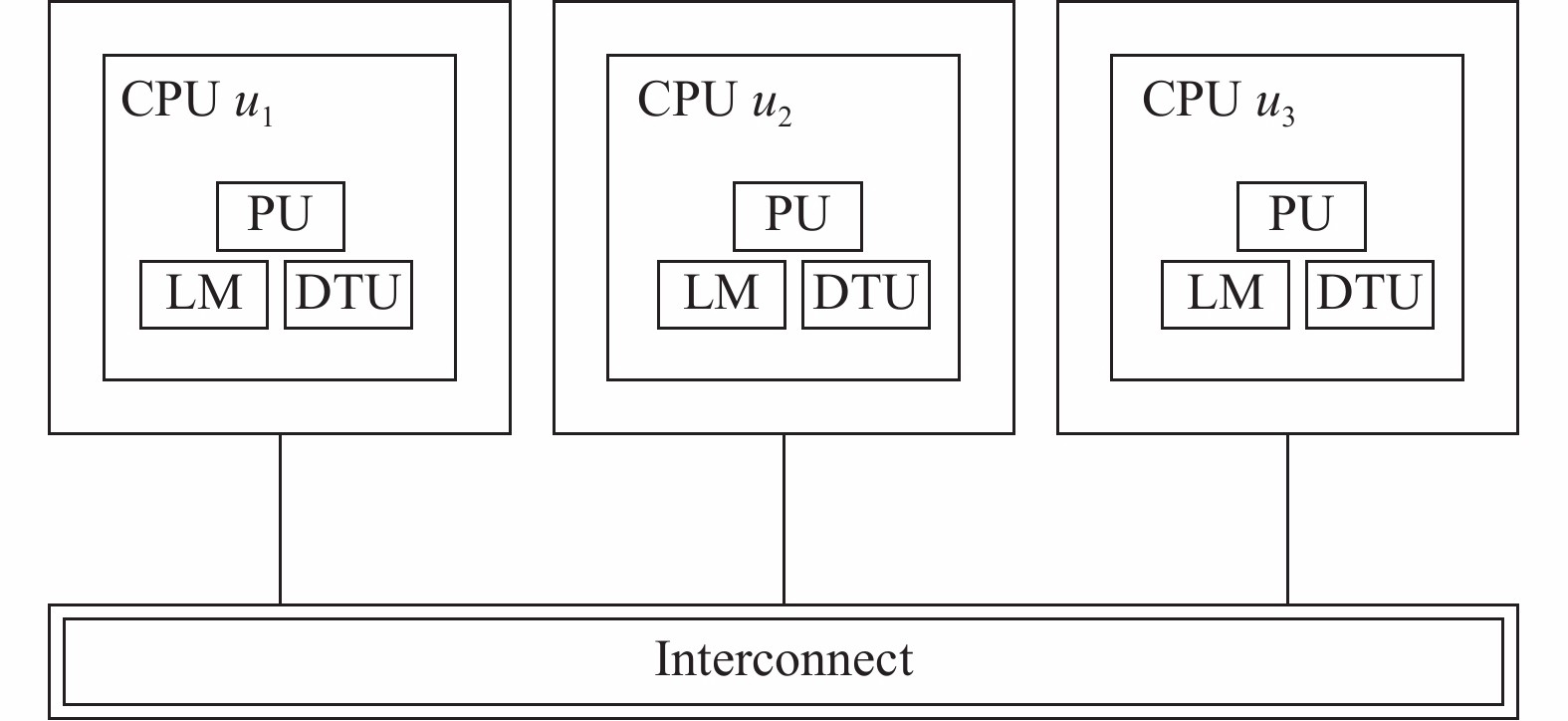
1 模型及问题阐述 1.1 系统模型

定义一个由m个全连通的处理器组成的异构多处理器系统, 使用U={u₁, u₂, u₃, …, u_m}来表示这个处理器集, 其中不同的处理器拥有不同的运行速度. 图1给出了一个由3个处理器u₁, u₂, u₃组成的系统架构模型.

每个处理器模块分别由3个模块组成, 处理器单元(processing unit, PU)、本地内存(local memory, LM)以及数据传输单元(data transfer unit, DTU). PU负责一系列的计算操作. LM是一个小型的低延时的存储并且负责在PU的执行过程中供PU访问. DTU负责实现处理器和存储之间的数据传输操作. 处理器之间的信息交流通过互连进行, 例如总线. 假设所有处理器间通信都在没有争用的情况下进行.

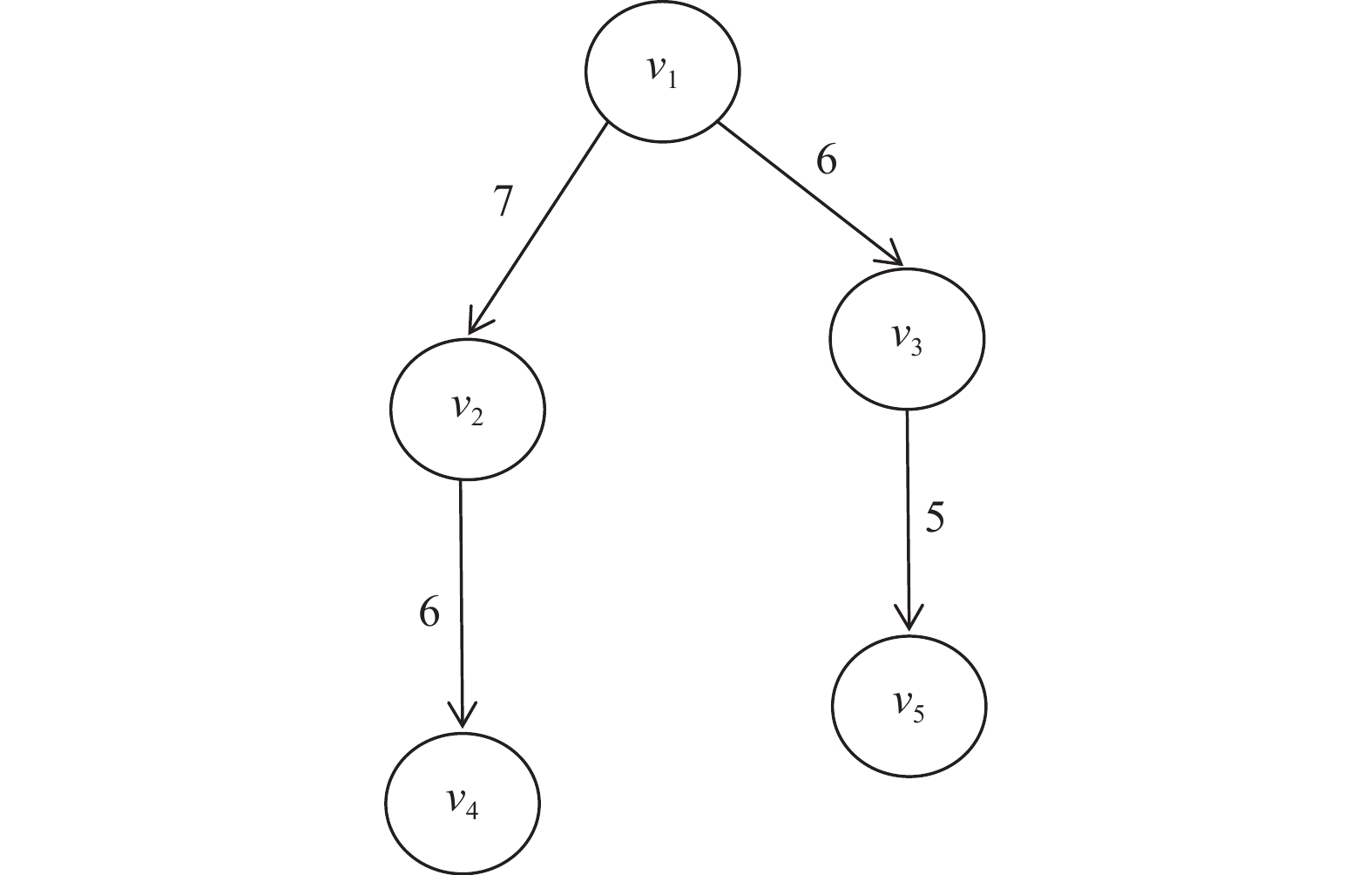
1.2 应用模型

一个并行应用通常使用一个有向无环图(DAG)来表示, 其中的节点表示任务, 边表示任务间的数据依赖^[17-19]. 使用一个四元组来表示一个DAG应用G=(V, E, C, W). V={v₁, v₂, v₃, …, v_n}用来表示DAG中的节点任务集, 其中n表示任务节点的数量. E用来表示任务之间的交流边集, e_ij表示DAG中的边, 表示任务v_i和任务v_j之间存在数据依赖. C表示的是数据传递消耗的时间集, c_ij表示任务v_i和任务v_j在分配至不同处理器时数据传递消耗的时间. W是一个m×n的矩阵, 其中m表示处理器数量, n表示应用中的任务数量, w_ik表示任务v_i在处理器u_k上的执行时间. 定义pre(v_i)表示任务v_i的前驱任务集合, suc(v_i)表示任务v_i的后继任务集合. 一个没有前驱任务的任务被称为入口任务, 被定义为v_entry, 一个没有后继任务的任务被称为出口任务, 被定义为v_exit. 如果一个DAG拥有多个出口任务或者多个入口任务, 那么一个零权值依赖的虚拟出口任务或入口任务将会生成并被添加至图中. 图2展示了一个包含5个任务的并行应用.

图2中的应用将会被执行在图1中的系统中. 表1展示了一个3×5的表格, 表示的是图2中的所有任务在3个不同处理器上的执行时间. 例如, 任务v₁在处理器u₂上的执行时间为8个单位时间, 用公式表示为w₁₂=8.

1.3 错误模型

假定处理器的故障率是恒定的, 处理器在连续执行一段时间时, 出现暂时性错误的概率服从泊松分布^{[1,2,8,14,20,21]}. 那么任务v_i在被分配至处理器u_k上执行一次的成功率计算方式如式(1)^{[1, 2,8, 22]}:

$ R({v_i}, {u_k}) = {{\rm{e}}^{ - {\lambda _k}{w_{ik}}}} $

(1)

其中, λ表示处理器的故障率. 在使用了复制技术的系统中, 只要该任务的其中一个副本(包括原始任务)执行成功, 该任务被认为执行成功, 那么当系统中执行了p个任务v_i的副本时, 任务v_i的执行成功率的计算方式如式(2):

$ R({v_i}) = 1 - \mathop \prod \limits_{\beta = 1}^p (1 - R({v_i}^{b\beta }, pro({v_i}^{b\beta })) $

(2)

其中, v_i^bβ表示任务v_i的副本, pro(v_i^bβ)表示执行任务v_i^bβ的处理器. 整个应用的可靠性等于应用中所有任务执行成功率的乘积, 计算方式如式(3):

$ R(G) = \mathop \prod \limits_{i = 1}^n R({v_i}) $

(3)

1.4 问题阐述

FTSA-RSMI用来解决实时异构系统中出现的暂时性错误导致的可靠性下降的问题, 问题的描述如下: 输入一个包含n个任务节点的DAG应用G=(V, E, C, W), 一个由m个处理器U={u₁, u₂, u₃, …, u_m}组成的实时异构系统, 以及应用的截止期限D, 目标是设计一个高效的容错调度算法, 在截止期限的约束下, 使用复制技术复制任务, 然后将所有任务调度至处理器执行, 并且最大化系统的可靠性. 可以表示为: 在满足式(4)的条件下, 最小化式(5).

$ makespan \Leftarrow D $

(4)

$ R(G) = \mathop \prod \limits_{i = 1}^n R({v_i}) $

(5)

2 容错调度算法(FTSA-RSMI)

一个使用了积极复制技术的容错调度算法包含两个部分, 调度策略和复制策略. 调度策略决定了任务的执行次序和处理器选择规则. 复制策略决定了任务集中的所有任务的复制次数. FTSA-RSMI会动态的根据截止期限来调整任务复制的数量, 在截止期限的约束下, 最大化系统的可靠性. 下文将首先给出调度策略, 然后给出复制策略, 之后会详细地描述FTSA-RSMI的执行过程, 最后会给出一个例子用来比较DB-FTSA和FTSA-RSMI的区别.

2.1 调度策略

FTSA-RSMI使用经典的向上等级法(upward rank)来确定任务的执行优先级. 定义rank_u(v_i)作为任务v_i的优先级, 计算方式如式(6):

$ ran{k_u}({v_i}) = \overline {{w_i}} + \mathop {\max }\limits_{{v_j} \in suc({v_i})} (\overline {{c_{ij}}} + ran{k_u}({v_j})) $

(6)

其中, 出口任务v_exit的优先级为 $\overline {{w_{{\rm{exit}}}}} $ , $\overline {{w_i}} $ 表示任务v_i在所有处理器上的平均执行时间, $\overline {{c_{ij}}} $ 表示任务v_i和任务v_j的平均交流时间. 任务的rank_u越高, 任务的执行次序就越前. 表2展示了图2中所有的任务优先级计算结果和执行次序.

FTSA-RSMI在为任务选择处理器时, 都会遍历所有处理器, 并且选择其中完成时间最早的处理器. 定义est(v_i, u_k)为任务v_j在处理器u_k上的开始时间, f(v_i)为任务的v_i的完成时间, 那么处理器选择策略可以表示为:

$ f({v_i}) = \mathop {\min }\limits_{{u_k} \in U} \{ {\textit{est}}({v_i}, {u_k}) + {w_{ik}}\} $

(7)

任务v_i在处理器u_k上开始执行前, 处理器必须要是空闲的, 并且任务v_i需要的输入数据都已经被传递至处理器u_k. 所以est(v_i, u_k)的计算方式如下:

$ est({v_i}, {u_k}) = \max \{ \mathop {\max }\limits_{{v_p} \in pre({v_i})} \{ f({v_p}) + {c_{pi}}\} , idle({u_k})\} $

(8)

任务v_p是任务v_i的前驱集合中的任意一个任务, 需要注意的是, 假如任务v_p和任务v_i被分配至同一个处理器执行, 那么两个任务之间的依赖数据不需要在处理器之间进行传递, c_pi=0. idle(u_k)表示处理器的空闲时刻, 即当前处理器上当前正在执行的最后一个任务的结束时刻. 当所有的任务都被分配至处理器之后, 整个应用的执行时间通过式(9)计算出来:

$ makespan(G) = \mathop {\max }\limits_{{v_i} \in V} \{ f({v_i})\} $

(9)

其中, makespan即为整个应用的执行时间, 在本文中也称之为调度长度.

调度策略的算法如算法1.

算法1. 调度策略算法

1) 遍历任务集, 使用式(6)计算任务优先级.

2) 按照任务的优先级与任务之间的依赖关系构造任务执行队列.

3) while 队列不为空 do

4) 出队一个任务, 遍历处理器集, 依照式(7)选择任务完成时间最早的处理器.

5) 依照式(1)和式(2)可以计算出任务的执行成功率.

6) end while

7) 依照式(7)计算整个应用的执行时间makespan.

2.2 复制策略

对于一个任务集S而言, 定义S_com表示任务集中那些复制次数达到α次的任务子集, 定义S_inc表示任务集中那些复制次数未达到α次的任务子集. 将任务集S_inc中的任务v_i复制1次后, 新的任务集S_i将会生成, 用公式表示为 ${S_i} - S = \{ {v_i}^x\} $ , 其中的v_i^x为任务v_i的新副本. 使用上文给出的调度策略, 调度任务集S_i, 就能够得到新的应用执行时间makespan(S_i). 这样一来, 复制任务v_i对系统当前的实时性造成的影响IMP(v_i)可以通过式(10)计算:

$ IMP({v_i}) = makespan({S_i}) - makespan(S) $

(10)

为了尽可能地减小任务复制对系统实时性造成的影响, FTSA-RSMI优先复制当前任务集S中对系统实时性影响最小的任务v_rep(S), v_rep(S)的查找方式如式(11):

$ IMP({v_{rep(s)}}) = \mathop {\min }\limits_{{v_i} \in {S_{{\rm{inc}}}}} \{ IMP({v_i})\} $

(11)

在实际的实验过程中, 每增加一个任务的复制次数, 调度长度都会增加. 当任务的复制次数大于2次后, 系统的可靠性增长速度变得缓慢. 为了避免超过截止期限, 任务的最大复制次数被设置为2次. 表3展示了查找任务集S={v₁, v₂, v₃, v₄, v₅}中对实时性影响最小的任务的过程.

表3中的第1行表示所有的任务复制次数为0, 任务集S={v₁, v₂, v₃, v₄, v₅}, 应用的执行时间makespan=23. 第2行表示将任务v_i复制一次后, 新的任务集S₁={v₁, v₁^b0, v₂, v₃, v₄, v₅}生成, 使用上文的调度策略调度这个任务集, 可以得到应用的执行时间makespan=27, 那么复制任务v₁对于系统实时性的影响IMP(v₁)=4. 根据式(9)可知, 对于任务集S={v₁, v₂, v₃, v₄, v₅}, 应该被复制的任务为v₄, 该任务对当前系统实时性的影响最小, IMP(v₄)=1.

2.3 FTSA-RSMI执行过程

FTSA-RSMI的执行过程分为以下4步. 第1步, 将任务的最大复制次数α设置为0, 构造原始任务集; 第2步, 使用复制策略复制任务后调度任务集, 记录调度结果; 第3步, 重复执行第1步和第2步, 直至所有任务的复制次数都达到α次, 然后将任务的最大复制次数α设置为2, 重新执行第1步和第2步; 第4步, 一旦调度结果中的应用执行时间大于截止期限, 那么算法停止, 从记录中选择出, 应用执行时间小于截止期限的, 可靠性最大的调度结果.

FTSA-RSMI的算法如算法2.

算法2. FTSA-RSMI

输入: DAG应用G={V, E, C, W}, 截止期限D, 处理器集U={u₁, u₂, u₃, …, u_m}

输出: 一个实现了容错的调度结果, 应用执行时间makespan, 系统可靠性R(G)

1) for α = 0; α<=2;α++ do

2) while makespan<=D 且任务集中仍有部分任务的复制次数小于α do

3) 使用复制策略复制任务集中的任务.

4) 使用调度策略调度任务集, 并得到makespan, R(G).

5) end while

6) end for

7) 从记录中选择出makespan<=D且R(G)最大的调度结果.

FTSA-RSMI的时间复杂度的计算步骤如下.

第1步. 计算调度策略的时间复杂度. FTSA-RSMI会遍历整个任务集并计算任务的优先级, 这一步操作的时间复杂度为O(n). 在计算完任务优先级后, FTSA-RSMI会不断地从任务集中取出优先级最高的任务, 遍历处理器集, 为该任务选择处理器, 这一步的时间复杂度为O(m×n).

第2步. 计算复制策略的时间复杂度. FTSA-RSMI会遍历整个任务集, 不断地增加任务的复制次数, 然后调度整个任务集, 遍历完成后, 选择出对实时性影响最小的任务. 这一步的时间复杂度为O(m×n×n).

第3步. 计算整个算法的时间复杂度. FTSA-RSMI会不断地复制任务, 在最坏的情况下, 每个任务均被复制两次. 这一步的时间复杂度即为O(m×n×n×n). 因此整个算法的时间复杂度为O(m×n+m×n³).

2.4 实例分析

图3给出了在截止期限为32时, 分别使用DB-FTSA和FTSA-RSMI调度图2中的DAG应用的结果. 其中处理器u₁, u₂, u₃的故障率分别为0.008, 0.006, 0.007, 任务在不同处理器上的执行时间在表1中给出, 任务之间的交流时间在图2中给出. 图中的矩形表示任务的副本集, 由白色填充的圆角矩形表示原始任务, 由灰色填充的圆角矩形表示复制任务, 任务v₁^b0即是任务v₁的复制任务. 图3(a)表示使用DB-FTSA调度图2中的应用至图1中的系统, 最终得到的调度结果. 表4中给出了每个任务的开始时刻和结束时刻, 以及每个原始任务的执行成功率.

DB-FTSA的复制策略是按照任务执行优先级的顺序依次复制任务, 但是当它将任务v₂的复制次数增加一次后重新调度任务集, 得到的应用执行时间超过了截止期限, 因此DB-FTSA最终只复制了任务v₁. 最终系统可靠性计算过程为99.81%×95.31%×95.89%×95.31%×95.89%=83.37%.

FTSA-RSMI的复制策略是优先复制任务集中对实时性影响最小的任务. 按照这个复制策略, 任务v₂, v₄, v₅被依次复制. 最终系统可靠性的计算过程为96.56%×99.71%×95.89%×99.89%×99.84%=92.07%.

3 实验结果和讨论

在本节中, FTSA-RSMI将会和DB-FTSA比较从而评估其性能. DB-FTSA解决的问题和FTSA-RSMI相同, 同样只考虑实时异构系统中出现的暂时性错误, 采用了积极复制技术提高系统的可靠性, 但是两个算法的调度策略的实现不同, 复制策略也完全不同. 为了测试算法性能, 实验进行了两组仿真测试. 很多研究都采用了TGFF来随机生成DAG应用^{[1,2,6,8,15,16]}, 因此实验数据第一组为使用TGFF随机生成的DAG应用, 另一组为真实世界的应用. 仿真平台是一个配备了2.8 GHz Intel CPU和8 GB内存的电脑, 应用模型和处理器的模型通过Java语言模拟.

3.1 实验参数和指标

随机生成的应用是通过TGFF生成的, 使用这个软件需要输入以下的参数: (1) n, 任务的数量; (2) CCR, 任务之间信息传递的平均时间与平均执行时间的比值, 将会从{0.1, 0.5, 1, 5}中选取; (3)任务的入度, 即任务的前驱数量; (4)任务的出度, 即任务的后继数量; (5) $\overline w $ , 任务的平均执行时间. 在实验中, 任务的数量会从10到100之间选取. 为了避免其他因素对实验结果造成影响, 所有随机生成的应用的最大入度和最大出度都设置为4.

系统设置为由4个全连通的处理器组成的异构系统. 为了模拟处理器的故障, 处理器的故障率将会随机地从区间[6×10⁻⁴, 14×10⁻⁴]中选取. 实验将会保证单个任务在不同处理器上的执行时间不同, 以保证处理器的异构性.

实验使用了两个评估指标如下: (1)系统可靠性, 一个调度成功执行的概率; (2) PSS, 应用中的所有任务在截止期限前完成的概率, 可以通过计算调度成功的次数和总调度次数的比值得到. 在本文中, 只要应用调度后执行时间小于截止期限, 那么认为该次调度成功. 总调度次数在实验中被设置为11, PSS值越大, 证明算法越能保证系统的实时性.

3.2 随机生成应用

本节将会展示4组实验结果. 因为DB-FTSA和FTSA-RSMI都能够针对截止期限不断地调整任务复制数量来保证实时性, 所以截止期限的选取非常重要. 为了确保实验的合理性, 在使用两个算法调度前, 我们都会先使用HEFT算法调度一次. HEFT算法已经被证明在异构系统中的实时性任务调度问题中表现优秀, 而且经常用来作为实时性调度算法的对比算法, 但是HEFT算法不具有容错能力, 因此在设置实验中的截止期限 $D$ 时, 我们将会先用HEFT将所有任务调度一次, 得到应用的执行时间makespan, 最后通过 $D = makespan \times 1.5$ 计算得到.

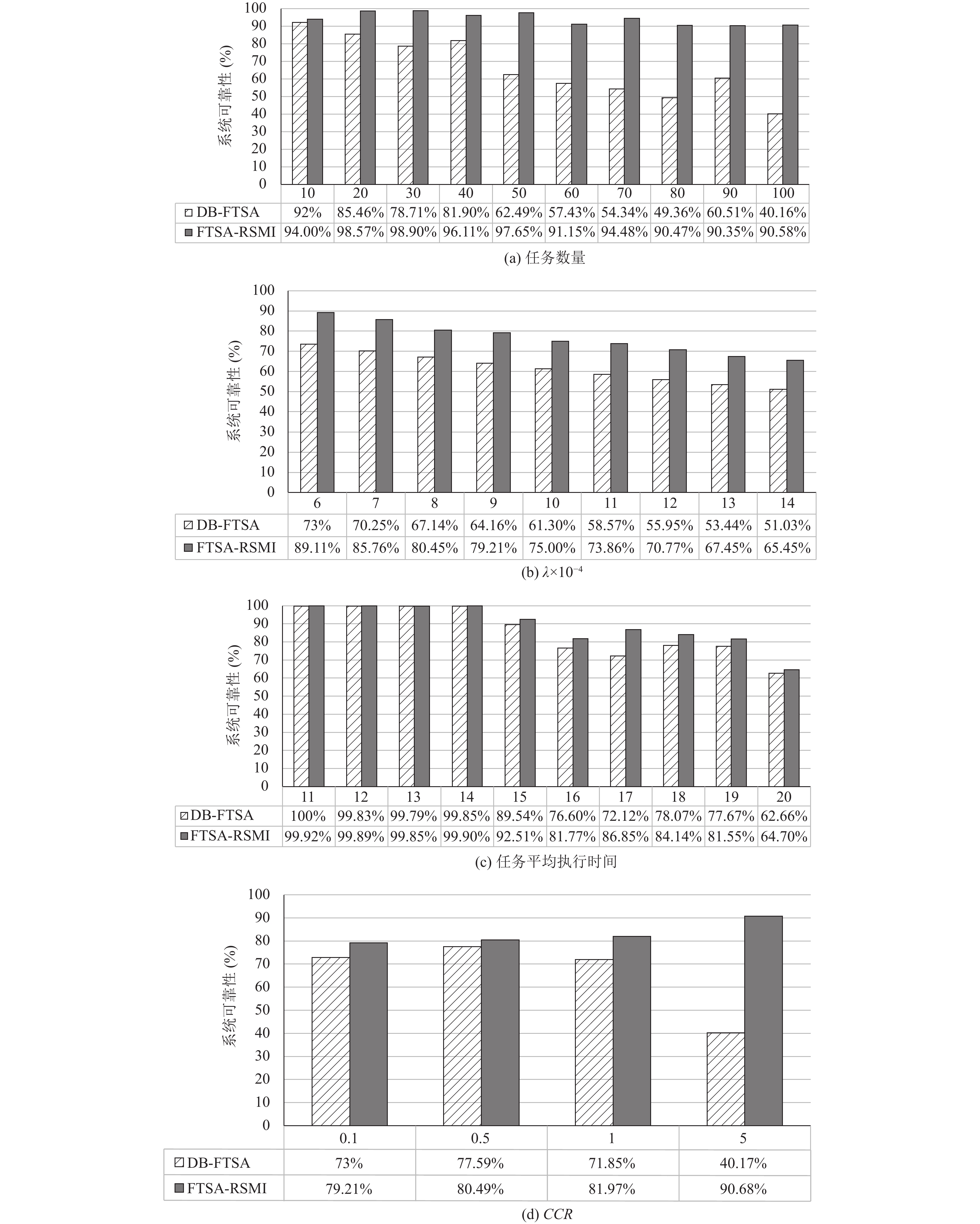
图4(a)展示了在CCR=5, 任务平均执行时间 $\overline w = 15$ 以及任务数量从10增加到100的条件下, 分别使用DB-FTSA和FTSA-RSMI调度应用后得到的系统可靠性结果. 可以明显地看到无论任务数量如何变化, FTSA-RSMI的系统可靠性都是大于DB-FTSA的. 当任务数量等于100时, FTSA-RSMI的可靠性优于DB-FTSA 50%.

图4(b)展示了在CCR=1, 任务数量n为50的情况下, 不断增加处理器的故障率, 分别使用DB-FTSA和FTSA-RSMI调度应用后得到的系统可靠性结果. 随着故障率的变化, 两个算法得到的系统可靠性都下降了, 但是FTSA-RSMI始终高于DB-FTSA.

图4(c)展示了在截止期限 $D = 300$ , 任务数量等于50, 以及任务平均执行时间不断增加的条件下, 分别使用DB-FTSA和FTSA-RSMI调度应用后得到的系统可靠性结果. 随着任务平均执行时间不断增加, 系统的实时性约束不断严格, 两个算法得到的系统可靠性总体上都呈下降的趋势.

图4(d)展示了在任务数量等于50, 任务平均执行时间等于15, CCR从0.1增加到5的条件下, 分别使用DB-FTSA和FTSA-RSMI调度应用得到的系统可靠性. 当CCR等于5时, 两个算法的系统可靠性差距达到最大为50%.

3.3 真实应用

在这个实验中, 我们将会用3个真实世界的应用来测试算法的性能, 分别是高斯消元(Gaussian elimination)、快速傅里叶变换(fast Fourier transform) 和分子动力学代码(molecular dynamics code). 这些应用的结构都是已知的, 所以我们只需要设置CCR和任务的平均执行时间 $\overline w $ .

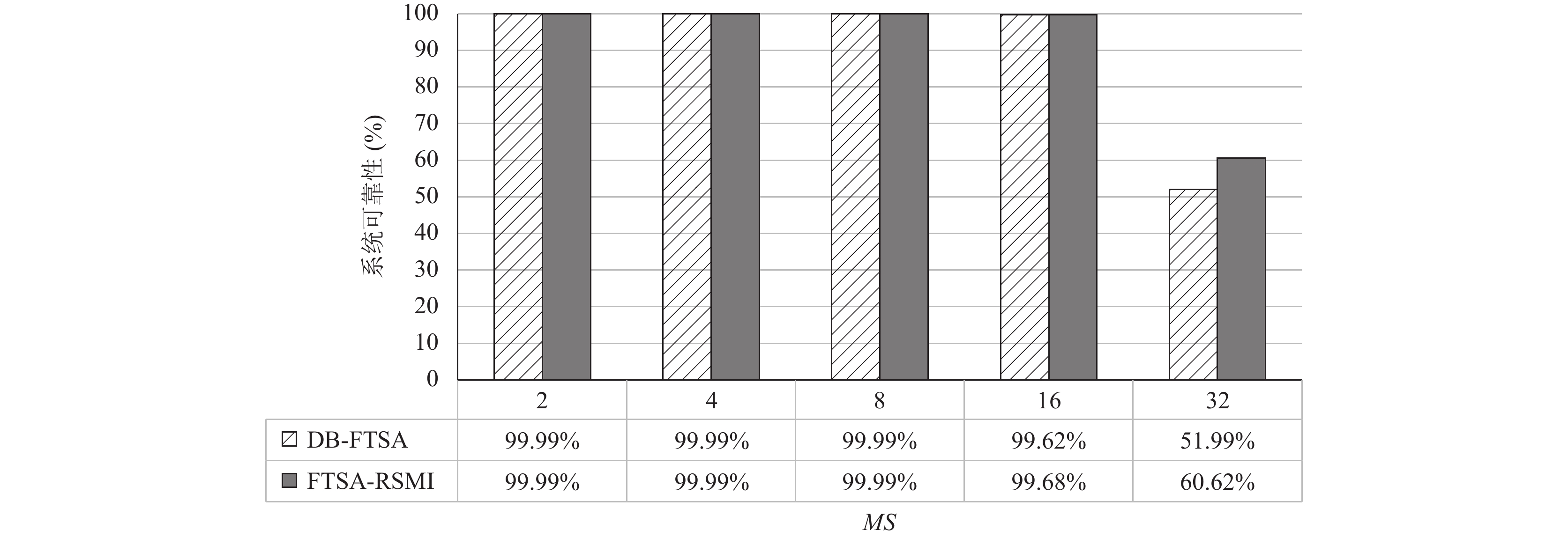
在高斯消元中, MS用来定义高斯消元问题中的系数矩阵的大小, 同时也被用于计算高斯消元应用中的任务数量, 用公式表示为式(12):

$ n = \frac{{M{S^2} + MS - 2}}{2} $

(12)

在调度成功率方面, DB-FTSA和FTSA-RSMI调度应用得到的调度成功率PSS均为1. 图5展示了在任务平均执行时间 $\overline w = 15$ , CCR=1, 以及截止期限 $D = MS \times (\overline w + \overline w \times CCR)$ 的情况下, 不断增加系数矩阵大小, 分别使用DB-FTSA和FTSA-RSMI调度高斯消元应用得到的可靠性结果. 从图中可以看出, 随着系数矩阵MS不断增加, FTSA-RSMI的可靠性依然是高于DB-FTSA的.

在快速傅里叶变换实验中, 我们使用VS来表示快速傅里叶变换应用需要输入的参数. 应用的截止期限计算方式如式(13):

$ D = (2 \times {\log _2}VS + 1) \times (\overline w + \overline w \times CCR) $

(13)

实验结果表明3种算法的调度成功率PSS均为1. 图6展示了在任务平均执行时间 $\overline w $ =15, CCR=1的情况下, 不断增加VS, 分别使用DB-FTSA和FTSA-RSMI调度快速傅里叶变换应用得到的可靠性对比. 从图6中可以看到当VS大于32时, 所有算法得到的可靠性都下降了. 但是当VS等于32时, FTSA-RSMI得到的可靠性依然是最高的.

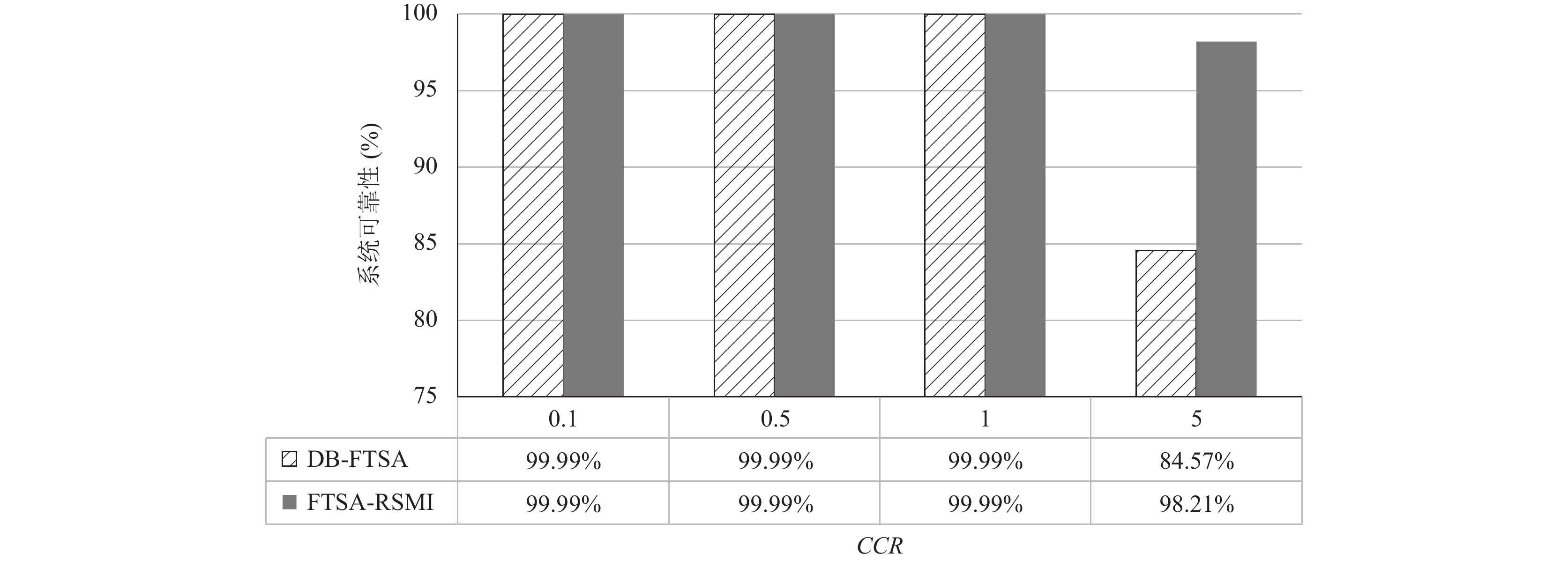
分子动力学代码拥有一个不规则的任务结构, 需要考虑两个参数CCR和任务平均执行时间 $\overline w $ .

两种算法在这个实验中得到的PSS都是1. 图7展示了分别使用DB-FTSA和FTSA-RSMI在任务平均执行时间 $\overline w = 15$ , 任务数量n=40, 截止期限D=500的情况下, CCR从0.1到5, 调度分子动力学代码的系统可靠性结果. 当CCR=5时, DB-FTSA得到的可靠性为84.57%, 但是FTSA-RSMI得到的可靠性依然能够达到98.21%.

对于调度3个真实世界的应用而言, DB-FTSA和FTSA-RSMI都能有效的提升系统的可靠性, 但是当截止期限约束较为严格时, FTSA-RSMI有明显的优势.

4 结论与展望

在本文中, 一个新的基于复制策略的容错调度算法FTSA-RSMI被提出. FTSA-RSMI针对异构实时系统中的出现的暂时性错误, 确保实时并行应用能在截止期限前完成并且得到一个较高的系统可靠性. FTSA-RSMI不断地增加对系统实时性影响最小的任务的复制次数, 从而提高系统的可靠性. 实验结果证明FTSA-RSMI在严格的截止期限的约束下依然能够保证比DB-FTSA更高的系统可靠性. 在未来研究实时性调度问题时, 我们会尽量减少系统中的任务冗余, 并且将系统的节能也纳入研究范畴.