异构无线传感器网络(heterogeneous wireless sensor network, HWSN)是由不同性能的节点被随机安置到监测区域组成的, 能够准确地采集数据, 可以适应各种复杂、恶劣的环境, 不仅广泛应用于互联网, 更适用于军事、医疗、工业等领域, 但是因为无线传感器网络的电源能量有限, 维护成本高, 所以如何有效利用传感器节点能量, 保证网络稳定性及通信能力的条件下延长网络生存周期成为目前研究的重要问题.

目前, 可以通过优化各种网络特性参数和寿命最大化技术来提高WSNs性能^[1], 其中, 分簇路由协议因其简单高效而成为研究重点^[2]. 其中低功耗自适应集簇分层协议LEACH (low energy adaptive clustering hierarchy)^[3]是WSNs最早的分簇路由协议, 算法复杂度较低, 但是按轮随机选取簇头, 忽略了簇头节点剩余能量, 数据使用单跳传输等问题导致了负载分布不均衡, 最终出现耗能快、生存周期短等情况^[4]. 于是研究者们提出了很多改进的LEACH算法来提高性能. 为了避免簇头不合理选择造成的能耗不均衡, Ngangbam等人^[5]提出的LEACH-C算法通过主次簇头协作并兼顾两者的剩余能量和相对距离等因素, 均匀分布簇头和网络能耗. Verma等人^[6]提出了FLEC利用高能量节点作为簇头改进LEACH. 并结合他们簇头的数据, 传输到基站, 为了支持LEACH算法, 减少簇头损坏时选择新簇头所消耗的时间和精力, 引入了新机制为每个簇分配副簇头. Dutt等人^[7]提出的CREEP算法通过修改双层异构网络中的簇首选择阈值, 来克服原算法在计算和簇首选举过程复杂性较高的缺点.

上述针对LEACH算法的改进虽然在不同程度上降低了网络能耗, 但是LEACH-C和FLEC算法在同构网络环境中运行, 面对各节点性能、参数不等的异构网络环境, 仍存在簇头选举精度不高等缺点; 而CREEP算法在簇头选举中在多跳路径的选择中, 并未设置合理的参数来限制下一跳的选择, 会出现路径不合理的现象, 造成数据传输过程额外耗能. 这些缺点使得WSN无法有效延长网络寿命.

因此本文在异构网络环境下, 引入多目标优化方法^[8]考虑能量、覆盖范围等因素来提高簇头选举精度; 使用模拟退火(simulated annealing, SA)算法^[9]增强哈里斯鹰(Harris hawks optimization, HHO)算法^[10]的局部搜索能力; 最后使用改进哈里斯鹰算法选出最佳数据传输路径.

1 系统模型 1.1 网络模型

为了研究改进的路由算法对网络的影响, 对网络模型进行假设.

(1)传感器节点被随机不均匀分布在大小为A×A的二维正方形区域内.

(2)传感器中存在高级节点和普通节点. 高级节点的能量高于普通节点, 两者的数据存储、传输、处理能力相同. 且所有节点都具有唯一的身份标识号ID.

(3)传感器节点随机被分散布置后将国定或轻微移动, 网络部署后不再进行人为干涉.

(4)任意两个节点之间的最大距离不超过其最大通信半径, 可以计算任意节点到BS的距离.

(5)无线发射功率可以自我调控, 可自主选择发射功率. 节点之间的传输链路可以在任意(双向)方向上传输数据.

(6)传感器节点可以知悉自身剩余能量并可以对冗余数据进行融合.

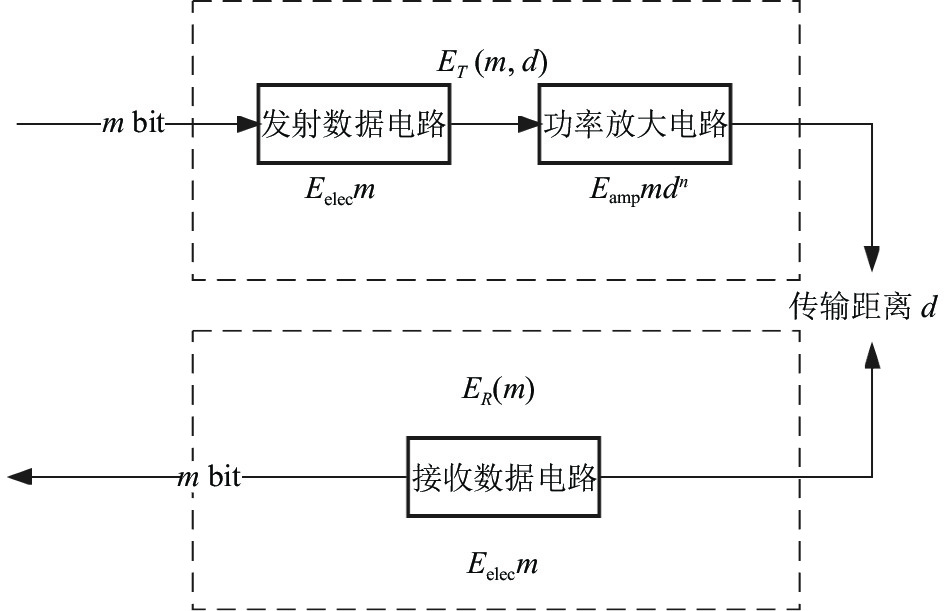
1.2 能耗模型

考虑到传感器节点电量有限, 能耗更是WSNs路由协议设计过程中的重要考虑因素, 所以对于无线信道能耗模型的研究将有助于路由算法的设计^[11,12], 本文将采用图1所示的无线通信能耗模型.

该模型的实行与距离阈值 $ {d_0} $ 有关, 发送 $ m $ bit数据的能耗公式如式(1):

$ {E_T}(m, d) = \left\{ {\begin{array}{*{20}{l}} {m{E_{{\rm{elec}}}} + m{\varepsilon _{fs}}{d^2}, \; d \lt {d_0}} \\ {m{E_{{\rm{elec}}}} + m{\varepsilon _{mp}}{d^4}, \; d \geqslant {d_0}} \end{array}} \right. $

(1)

接收 $ m $ bit数据的能耗公式如式(2):

$ {E_R}(m) = m{E_{{\rm{elec}}}} $

(2)

数据融合的能耗公式如式(3):

$ {E_m} = (N + 1)m{E_{{\rm{DA}}}} $

(3)

$ {d_0} = \sqrt {\frac{{{\varepsilon _{fs}}}}{{{\varepsilon _{mp}}}}} $

(4)

其中, $ {\varepsilon _{fs}} $ 是自由空间模型下发送电路的损耗系数, 当 $ d \geqslant {d_0} $ 时使用该模型; $ {\varepsilon _{mp}} $ 是多路衰减模型下发送电路的损耗系数, 当 $ d \lt {d_0} $ 时使用该模型; ${E_{{\rm{elec}}}}$ 是发射电路的能量; ${E_{{\rm{DA}}}}$ 是单位数据融合能耗; $ N $ 是簇内节点数.

2 LEACH-MHO算法

大多数分簇路由算法在簇头选择时基于概率纯随机选择, 未考虑节点覆盖范围、通信成本等因素, 导致整个网络能量负载不均衡, 降低了网络生存时间. LEACH-MHO算法由LEACH改进而来, 选择异构网络使得其实用性得到提升. 同构网络与异构网络主要区别于两个方面: 参数不同, 可以随环境而改变; 协议不同, 可以融合在一起, 共同作用.

LEACH-MHO算法的主要目的是提高簇头选举的精度, 寻找最佳数据传输路径, 降低数据传输过程中的能耗, 使数据传输更加稳定高效.

2.1 簇的建立阶段 2.1.1 适应度函数

适应度函数(fitness function)的设计直接影响到改进算法的收敛速度和能否找到最优解. 在簇头选举过程中, 相比较LEACH-C算法, 本文算法还考虑了覆盖范围、接近度和通信成本3个因素来选择簇内最佳节点作为簇头, 确保选举合理性和簇首节点的均匀分布. 为了优化网络中簇的结构, 均衡各个簇之间的能量消耗, 适应值函数的设计主要考虑以下4个因素.

1)覆盖范围. 根据覆盖半径得到最优覆盖范围, 由式(5)表示:

$ {N_{{\rm{Cov}}}} = r({N_i}) $

(5)

在网络中, 该节点所覆盖的半径被描述为 $ r({N_i}) $ . 因此第1个目标等式如式(6):

$ Maximi{\textit{z}}e \_ {F_1} = \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{N_{{\rm{Cov}}}}({N_i})} $

(6)

2)节点剩余能量. 由于簇首节点需要更多的剩余能量来接收簇内成员节点的数据并进行数据融合, 因此, 选择簇内剩余能量最高的节点作为簇首更能有效地实现数据的传输.

$ {E_{{\rm{Res}}}} = {E_T} - ({E_{{\rm{Coll}}}} + {E_{{\rm{Tran}}}} + {E_{{\rm{Rec}}}} + {E_{{\rm{Agg}}}}) $

(7)

一个SN的总能量称作 $ {E_T} $ , 数据收集期间使用的能量称作 ${E_{{\rm{Coll}}}}$ , 用于传输数据的能量称作 ${E_{{\rm{Tran}}}}$ , 用于接收数据的能量称作 ${E_{{\rm{Rec}}}}$ , 用于聚合数据的能量称作 ${E_{{\rm{Agg}}}}$ . 因此, 第2个目标等式如式(8):

$ {{{{Maximi{\textit{z}}e}}}} \_ {F_2} = \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{E_{{\rm{Res}}}}({N_i})} $

(8)

3)接近度. 该协议根据相邻两个节点的距离来查找相邻节点的接近度, 由式(9)表示:

$ {N_{{\rm{Prox}}}} = \frac{1}{{{N_T}}}\sum\limits_{i = 1}^{{N_T}} {d(n, i)} $

(9)

一个网络中的SNs总数是 $ {N_T} $ , 相邻节点之间的距离是 $ d(n, i) $ . 因此, 第3个目标等式如式(10):

$ {{Minimi{\textit{z}}e}} \_ {F_3} = \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{N_{{\rm{Prox}}}}({N_i})} $

(10)

4)通信成本. 相邻节点通信所需的成本计算如式(11):

$ {C_{{\rm{Com}}}} = \frac{{d_{{\rm{Avg}}}^2}}{{d_0^2}} $

(11)

相邻两个节点之间的平均距离描述为 $d_{{\rm{Avg}}}^2$ , $ d_0^2 $ 表示簇半径. 因此, 第4个目标等式如式(12):

$ {{{Minimi{\textit{z}}e}}} \_ {F_4} = \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{C_{{\rm{Com}}}}({N_i})} $

(12)

适应度功能的发展是以一种可以在规定的矛盾目标范围内建立权衡的方式. 本文多目标适应度函数在每个目标上, 权值 $ {W_i} $ 乘以这个目标值. 最后, 通过将多个值相加使得不同的目标转换为一个单标量目标函数. 本节设计的适应值函数^[13]为:

$ \begin{split} Fitness =& {W_1} \times {F_1} + {W_2} \times {F_2} + {W_3} \times {F_3} + {W_4} \times {F_4} \\ =& {W_1} \times \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{E_{{\rm{Cov}}}}({N_i})} + {W_2} \times \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{E_{{\rm{Res}}}}({N_i})} \\ & + {W_3} \times \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{N_{{\rm{Prox}}}}({N_i})} + {W_4} \times \frac{1}{{{N_T}}}\sum\limits_{i = 1}^N {{C_{{\rm{Com}}}}({N_i})} \end{split} $

(13)

其中, 权值 $ {W_i} $ 的和为1, 每个 $ {W_i} $ 介于0到1, $ 1 \leqslant i \leqslant 4 $ . 这里的主要目标是最大化适应度的值, 满足所有目标的节点将被选择为一个CH. 在每个簇中所选择的CH负责直接或通过其他跳数将数据包转发给BS.

2.1.2 簇的形成过程

最初, 为了形成簇, 传感器节点需要识别相邻的中继节点. 这些消息中列出了属性激活标志、图层ID、节点的位置、簇ID和节点ID. 对于CH输出停止/激活传感器节点和中继节点或簇头, 相应需要激活标志和节点的位置. 此处使用Haversine距离公式^[14]是为了识别距离, 由式(14)表示:

$ {\textit{Diff}}{_{{\rm{Nodes}}}} = Lo{c_{Ni}} - Lo{c_{Nj}} $

(14)

$ Lo{c_{Ni}} $ 和 $ Lo{c_{Nj}} $ 表示两个节点的位置. 节点与基站之间的距离由式(15)给出:

$ {\textit{Diff}}{_{{\rm{toBS}}}} = Lo{c_{Ni}} - Lo{c_{{\rm{BS}}}} $

(15)

$Lo{c_{{\rm{BS}}}}$ 表示基站的位置. 邻近节点通过距离公式找到, 可由式(16)给出:

$ \begin{split} Dis =& \sin {\left(\frac{{{{\textit{Diff}}_{{\rm{Nodes}}}}}}{2}\right)^2} + \cos (Lo{c_{Ni}}) \\ & \times \cos (Lo{c_{Nj}}) \times {\left(\sin \left(\frac{{{{\textit{Diff}}_{{\rm{toBS}}}}}}{2}\right)\right)^2} \end{split} $

(16)

如果出现任何节点不可用或已死亡, 那么簇的形成过程将重新开始.

2.2 稳定传输阶段

经过筛选的簇头将从簇内成员收集来的信息进行处理, 找出网络传输的最佳路径, 将数据转发到基站.

2.2.1 基于模拟退火的HHO算法(SHHO)

HHO算法原理简单、控制参数少、全局搜索能力出色, 逐渐被应用于物联网领域. 该算法受到哈里斯鹰捕猎的启发, 结合Levy飞行实现对复杂多维问题的求解. HHO算法通过模仿哈里斯鹰群体捕猎、突袭式围捕策略实现算法的全局寻优^[15]. 该算法用数学公式来模拟现实中哈里斯鹰在不同机制下捕捉猎物的策略, 可应用于分簇路由协议的数据传输阶段的优化问题中. 该算法主要由3个部分组成: 全局搜索阶段、搜索与开发转换阶段、局部开发阶段.

但是HHO算法容易陷入局部最优. 因此当每次迭代结束之后, 将SA嵌入到HHO算法中^[16], 以提高其局部搜索性. 并且这种嵌入方法将提高算法的开发能力, 利用SA改进当前的最佳解.

改进后的算法步骤如下.

Step 1. 种群初始化. 根据搜索空间每一维的上界和下界, 初始化每个个体.

Step 2. 计算初始适应度. 将适应度最优的个体位置设为当前猎物位置.

Step 3. 位置更新. 先通过更新猎物逃逸能量, 然后根据逃逸能量和生成的随机数执行搜索或开发行为中对应的位置更新策略.

Step 4. 计算适应度. 计算位置更新后的个体适应度, 并与猎物适应度值进行比较, 若位置更新后的个体适应度值优于猎物, 则以适应度值更优的个体位置作为新的猎物位置.

Step 5. 引入模拟退火(SA).

重复Step 3–5, 当算法迭代次数达到最大迭代次数时. 输出当前猎物位置作为目标的估计位置.

上述流程可以看出SHHO算法复杂度取决于种群的初始化、适应度评估和位置更新过程. 首先, 考虑到所有可能的解, 初始化过程的复杂度是 $ {\rm{O}}(N) $ ; 其次, 更新过程中的复杂度是 $ {\rm{O}}(T \times N) + {\rm{O}}(T \times N \times Dim) $ , 其中包含更新搜索代理位置和寻找最佳解, $ T $ 表示最大迭代次数, $ Dim $ 是搜索空间的维度; 然后, 利用SA可以确定复杂度 $ {\rm{O}}(T \times t \times S) $ , 其中是SA的迭代次数, $ S $ 是SA的搜索策略; 最后得到SHHO算法复杂度为 $ {\rm{O}}(N \times T + N \times T \times Dim + N + T \times t \times S) $ .

2.2.2 基于SHHO的路径寻优

为了找到网络中将在CH上聚合的数据传输给BS的最佳路径, 提出了基于SHHO的路径寻优过程, 分为3个步骤: 初始化、路径选择策略、数据通信和路径变更.

(1) 初始化

SHHO可以根据其位置向量并结合Levy飞行实现对复杂多维问题的求解. 所以, 这里的SHHO需要种群和所有从CH到基站的可用路径. 在二维笛卡尔空间中, 每条路径上的CH都有自己的位置 $C{H_{i, j}} \in R \; (i = 1, 2, 3 , \cdots, n)$ . 路径中每个CH的位置存储在矩阵中, 如式(17):

$ C{H_{{\rm{pos}}}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {C{H_{1, 1}}} \\ {C{H_{2, 1}}} \\ \vdots \\ {C{H_{d, 1}}} \end{array}}&{\begin{array}{*{20}{c}} {C{H_{1, 2}}} \\ {C{H_{2, 2}}} \\ \vdots \\ {C{H_{d, 2}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots \\ \cdots \\ \ddots \\ \cdots \end{array}}&{\begin{array}{*{20}{c}} {C{H_{1, n}}} \\ {C{H_{2, n}}} \\ \vdots \\ {C{H_{d, n}}} \end{array}} \end{array}} \right] $

(17)

其中, CHs的个数描述为n, d表示路径数, 第i个CH的维数表示为 $ C{H_{i, j}} $ . 用拟合的方法计算所有CHs中最适合加入到最佳路径中的CHs的评估值.

$ {{Evaluate \_ value \_ of}} \_ CH = E(CH) $

(18)

主要以吞吐量、节点能量和链路质量3个目标进行评估, 以避免SN故障和交通控制. CHs的吞吐量由式(19)估计:

$ Th = \sum\limits_{i = 1}^n {C{H_i}\left[ {{{D}}{{{S}}_{C{H_i}}}(Lo{c_{C{H_i}}}, Lo{c_{BS}})} \right]} $

(19)

在式(19)中, 从CHs传输到BS的最大数据量(单位: b/s)被描述为 $C{H_i}\left[ {{{D}}{{{S}}_{C{H_i}}}(Lo{c_{C{H_i}}}, Lo{c_{{\rm{BS}}}})} \right]$ . CHs的数据传输速度用 $ DS_{{CH}_i} $ 表示, CHs的位置到BS表示为 $(Lo{c_{C{H_i}}}, Lo{c_{{\rm{BS}}}})$ . 利用式(7)估计了CHs的能量. 估计路径中CHs的能量, 而不是估计节点的能量. 链路质量根据从相邻CH接收的(接收信号强度)^[17]估计. 由式(20)表示:

$ Lin{k_Q} = \left\{ \begin{array}{*{20}{l}} {very {\textit{-}} good, } \\ {good, } \\ {bad, } \\ {very {\textit{-}} bad} \end{array} \right. \begin{array}{*{20}{l}} {{\rm{if}}}\; {RSS \lt - 10 \; {\rm{{{dBm}}}}} \\ {{\rm{if}}}\; {RSS \lt - 20 \; {\rm{dBm}}} \\ {{\rm{if}}}\; {RSS \lt - 30 \; {\rm{dBm}}} \\ {{\rm{if}}}\; {RSS \lt - 40 \; {\rm{dBm}}} \end{array} $

(20)

CHs的评估值由式(21)表示:

$ \begin{split} E(CH) = Ev{a_1} \times Th + Ev{a_2} \times {E_{{\rm{Res}}}} + Ev{a_3} \times Lin{k_Q} \end{split} $

(21)

其中, $ Ev{a_i} $ 表示评估系数, 介于0到1之间. 各路径中CHs的评估值以矩阵形式存储, 如式(22):

$ C{H_{{\rm{Eva}}}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {E(C{H_{1, 1}}} \\ {E(C{H_{2, 1}}} \\ \vdots \\ {E(C{H_{d, 1}}} \end{array}}&{\begin{array}{*{20}{c}} {C{H_{1, 2}}} \\ {C{H_{2, 2}}} \\ \vdots \\ {C{H_{d, 2}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots \\ \cdots \\ \ddots \\ \cdots \end{array}}&{\begin{array}{*{20}{c}} {C{H_{1, n}})} \\ {C{H_{2, n}})} \\ \vdots \\ {C{H_{d, n}})} \end{array}} \end{array}} \right] $

(22)

BS的位置可以由 $ Lo{c_{{\rm{BS}}}} $ 表示, 并在部署的笛卡尔空间中设置为(0, 0)的维数:

$ B{S_{{\rm{pos}}}} = Lo{c_{{\rm{BS}}}} $

(23)

(2) 路径选择策略

路径选择是通过计算最佳邻近CHs (基于评估值)来进行的. 确定的最佳相邻近CHs, $CH_i^{{\rm{Eva}}}$ 将与其他CHs的 $X_{C{H_{{\rm{old}}}}}^i$ 一起更新, 并确定最佳路径由式(24)给出:

$ {P_{{\rm{best}}}} = CH_i^{{\rm{Eva}}} - {\lambda _i} \times \left(r \times \left(\frac{{CH_i^{{\rm{Eva}}} + B{S_{{\rm{pos}}}}}}{2}\right) + X_{C{H_{{\rm{old}}}}}^i\right) $

(24)

在式(24)中新发现的CHs的位置表示为 $CH_i^{{\rm{Eva}}}$ , CHs为最佳, 初始CHs的位置表示为 $ X_{C{H_{{\rm{old}}}}}^i $ , r表示0到1之间的随机数. 第i次迭代的系数被描述为i, 它由式(25)生成:

$ {\lambda _i} = 2 \times r \times PD $

(25)

其中, 路径密度用PD表示. 路径密度是根据当前可用的跳数来定义的. 由式(26)表示:

$ PD = \left(\frac{{{N_{CHs}}}}{{{N_{CHs}} + {N_{{\rm{BS}}}}}}\right) $

(26)

在式(26)中, CHs和BS的数量表示为 $ {N_{CHs}} $ 和 ${N_{{\rm{BS}}}}$ ( ${N_{{\rm{BS}}}} = 1$ , 网络只有一个BS).

(3) 数据传输和路径变更

网络中一旦确定了最佳路径, 将会启动数据传输过程. 在传输过程中, 它利用能量将数据包传输到基站, 会导致CHs的死亡或其能量的减少. 因此, 在每次迭代中, 该算法在启动数据传输之前都会定期监控路径. 如果任何节点的能力不足以传输数据, 将从路径中删除, 并选择备用路径. 路径变更由式(27)表示:

$ {P_{{\rm{alt}}}} = NEW\_{P_{{\rm{best}}}}, \; {\rm{if}} \; {E_{{\rm{Res}}}}(C{H_i}) \lt threshol{d_{{\rm{min}}}} $

(27)

由式(27)可知, 如果任何CH的能量小于最小阈值, 则将从可用路径中识别出新的最佳路径, 并描述为 ${E_{{\rm{Res}}}}(C{H_i})$ 小于最小阈值. 其中, 最小阈值是 $ {E_{i, j}}(C{H_i}, C{H_j}) $ , 即从一个CH向下一个CH传输数据所需的能量. 基于SHHO的路由过程如图2所示.

最后, 该方法基于覆盖范围、节点剩余能量、接近度和通信成本4个目标选择了最优CHs; 通过基于SNs分布密度的不等聚类方法划分网络区域中的节点进行成簇, 降低网络中形成空簇的概率, 相比较CREEP算法, 本文算法路径选择更加合理, 通信成本更低, 同时提升数据转发的准确性.

3 仿真和性能分析

本文在macOS平台下的Matlab R2020a仿真实验环境中, 将本文算法与LEACH (m=0.1, a=2)算法^[3]、LEACH-C算法^[5]和CREEP算法^[7]进行实验对比分析. 实验参数如表1所示.

3.1 100 m×100 m网络部署区域仿真分析

在100 m×100 m的网络区域中, 4种算法死亡节点数量随时间变化曲线对比情况如图3所示, 当节点都死亡约90%时, LEACH算法迭代了约2800次, LEACH-C算法迭代了约3000次, CREEP算法迭代了约5000次, 而效果较好的LEACH-MHO算法迭代了约6300次, 由此可见对比其余3种算法, LEACH-MHO的网络生存周期更长.

图4表示BS收到的数据包数量. 在迭代次数到达2800次之前, CREEP算法的包传递数较低于LEACH-C算法; 超过5500次, 4种算法的包传递数都处于平稳状态, 而本文算法的包传递数比CREEP算法略高出20.5%, 并且本文算法与CREEP算法的包传递数明显高于LEACH算法与LEACH-C算法.

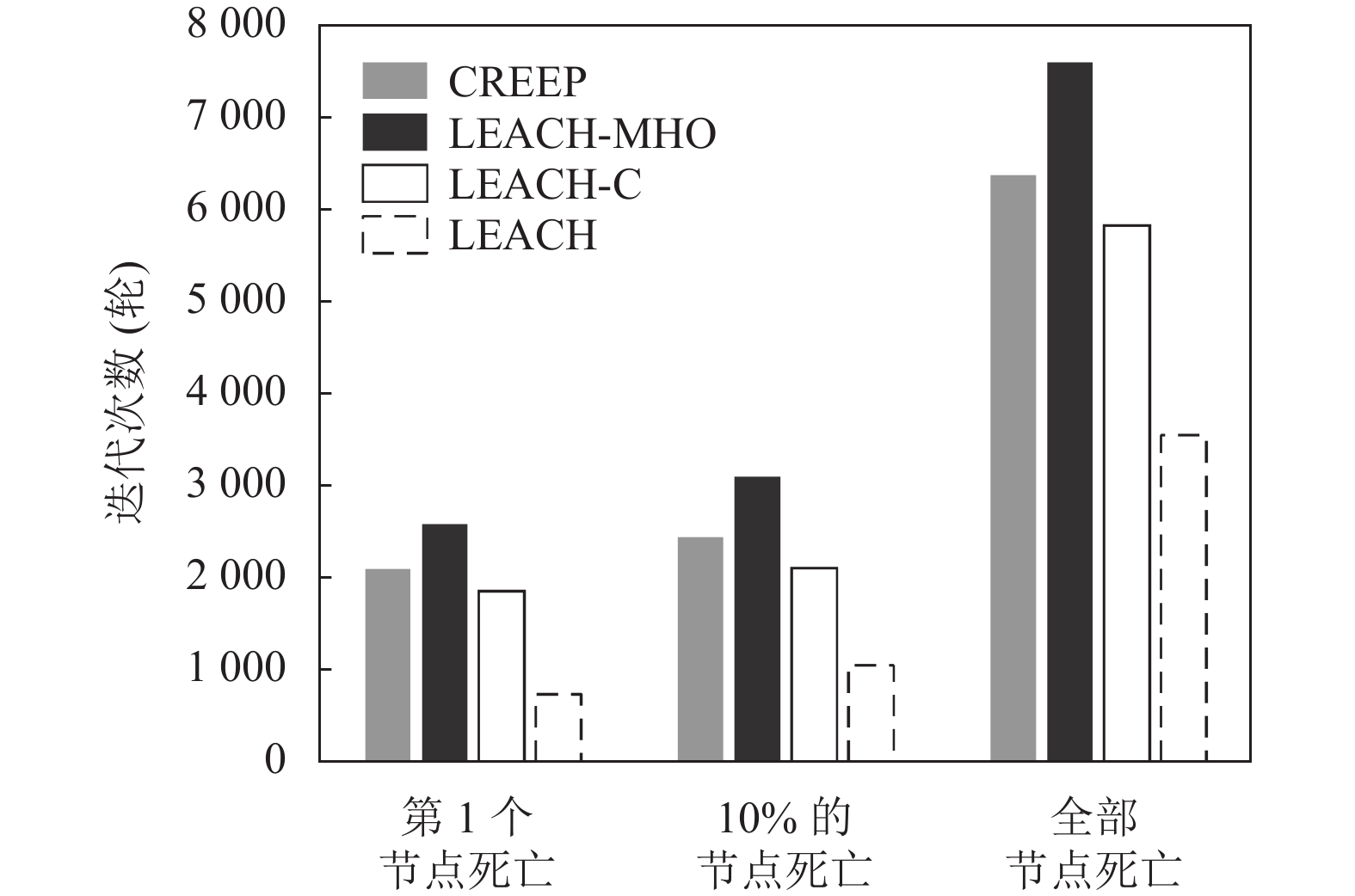
图5是100 m×100 m监测区域中4种算法分别在第1个节点死亡、10%的节点死亡、全部节点死亡出现的迭代次数. 同一阶段下, 迭代次数多高, 说明该网络生存周期越长.

3.2 200 m×200 m网络部署区域仿真分析

在200 m×200 m的网络区域中, 4种算法节点在各阶段死亡的情况变化曲线对比情况如图6–图8所示.

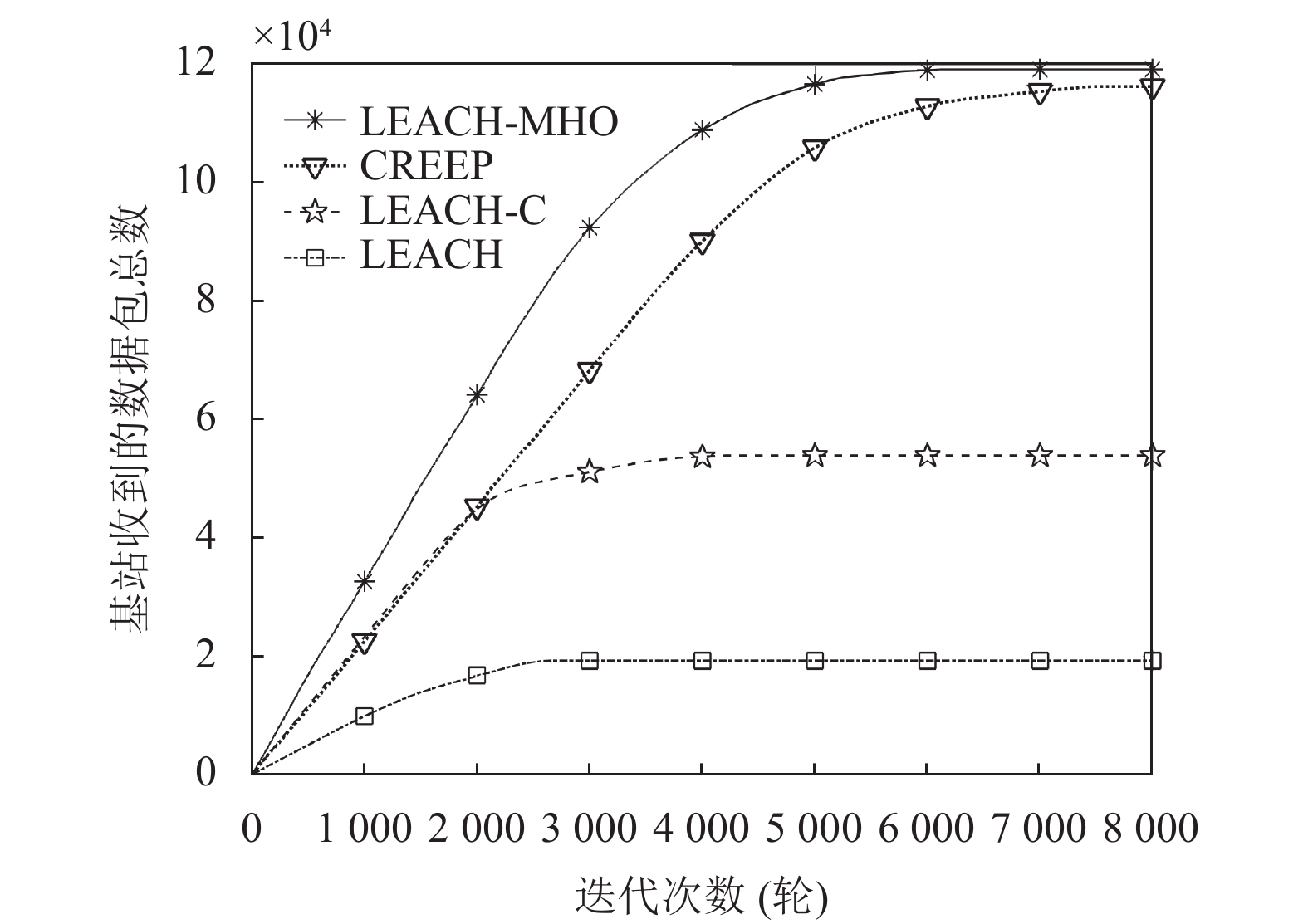
图6与图7体现的效果与上述100 m×100 m网络区域中的效果除了具体数据外, 算法的性能优劣情况大致相同. 图7数据表示, 本文算法的包传递数比CREEP算法略高出2.5%, 比LEACH算法明显高出510.4%.

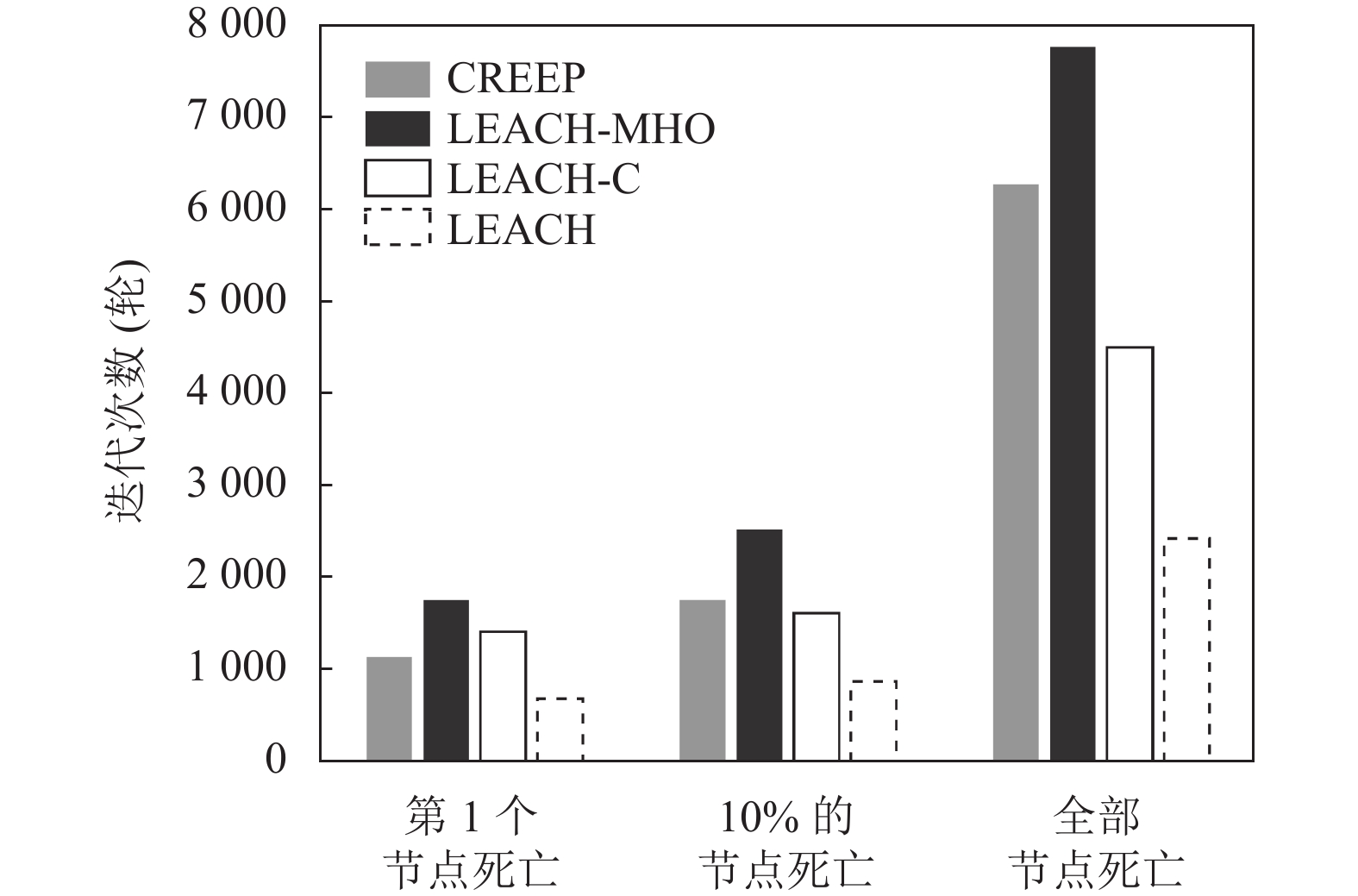
由图8的数据得到, 与对比算法进行比较, 本文算法的寿命比CREEP算法高出22.18%, 比LEACH-C算法高出77.83%, 比LEACH算法高出180.52%. 由此可见, 对比其余3种算法, LEACH-MHO的网络生存周期更长.

4 结论与展望

本文针对LEACH协议存在的簇头选举精度不高、数据传输能耗过大的问题, 考虑接近度、通信成本, 剩余能量和节点覆盖范围因素, 通过多目标优化方法改进簇头选举; 同时考虑到数据传输阶段更加耗能, 提出基于改进HHO算法的路径选择策略, 出现任何能量小于阈值的节点, 都会在网络中识别出新的最佳路径. 仿真结果表明, 提出的LEACH-MHO算法在网络生存周期、能耗方面都优于CREEP、LEACH-C、LEACH算法. 下一步的工作为三维空间中WSNs的寿命最大化进行研究.