1 引言

全景视频拼接技术通过图像配准、图像拼接、畸变校正、图像融合等步骤, 可快速获得宽视角、高精度、小畸变、无重影、实时性好的全景图像, 被广泛应用于智能交通、遥感探测、医学影像、计算机视觉、模式识别等领域.

图像配准作为全景视频拼接的基础, 它将传统摄像头拍摄的两个或多个图像的重合区域进行特征点相似度配准. 经典的匹配算法有SIFT和SURF (speeded-up-robust features), 之后相继出现的ORB、BRISK等加速优化算法以牺牲匹配准确率为代价来满足实时性要求. SURF算法通过盒子滤波器近似SIFT算法中二阶高斯函数的方式对源积分图像进行卷积运算, 极大地提高了算法速度^[1]. 因此, 进一步对SURF算法进行加速优化研究, 使其在保证高精度特征提取的同时达到实时性要求, 对全景视频监控领域具有深远意义和应用前景.

近年来, 随着图像处理器(graphic processing unit, GPU)的发展, 很多学者采用GPU并行架构对算法进行优化加速, 很大程度上提高了全景图像拼接效率. 王艳梅等^[2]基于OpenCL平台, 从数据传输、内存访问、负载均衡等方面优化SURF算法, 具有较好的可移植性. 刘金硕等^[3]利用GPU的内存模型和线程映射实现了SURF算法的统一计算设备架构 (computing unified device architecture, CUDA)加速. 徐晶等^[4]结合SURF算法和SVM算法进行特征提取和分类, 检测速度提升了5–9倍. 郭景等^[5]基于OpenCL平台提出了一种特征点检测的并行实现方法, 对旋转、缩放和模糊等处理都具有较好的自适应性. 卢嘉铭等^[6]基于CUDA平台进行图像拼接和融合, 实现了4K分辨率全景图像显示输出. 周亮君等^[7]基于GPU并行加速使得SURF算法较普通PC架构速度提高了约5倍.

本文基于CUDA架构并行化原理, 对SURF算法中计算Hessian响应值、非极大值抑制、确定特征点主方向、生成特征描述符等步骤进行GPU加速处理, 并基于FLANN和RANSAC算法进行图像配准, 采用双向匹配策略提高图像配准精度.

本文第2节介绍了传统SURF特征检测算法原理; 第3节阐述了基于CUDA的SURF优化算法实现过程和采用双向匹配策略的图像配准步骤; 第4节分析了实验结果; 第5节得出结论并提出展望.

2 SURF特征匹配算法

SURF算法是基于SIFT的加速鲁棒特征检测算法, 其速度比SIFT算法快10倍^[8]. 主要包括特征点的检测和描述两大步骤.

2.1 特征点检测 2.1.1 计算积分图像

定义灰度图像 $ I $ 在任意像素点 $ X\left( {x, y} \right) $ 处的积分图像 $I_{\sum} \left( x \right)$ 为: 输入图像 $ I $ 中原点和 $ X $ 构成的矩形区域内所有像素点的灰度值之和, 如式(1)所示, 则如图1所示, 任意矩形区域ABCD的积分图像为每个顶点区域积分图像的简单求和, 如式(2)^[9]:

$ I_{\sum} \left( X \right) = \sum\nolimits_{i = 0}^x {\sum\nolimits_{j = 0}^y {I\left( {i, j} \right)} } $

(1)

$ I_{\sum}ABCD = I_{\sum} A + I_{\sum} D - I_{\sum} B - I_{\sum} C $

(2)

2.1.2 构建Hessian矩阵

图像 $ I_{\sum} $ 上像素点 $ X\left( {x, y} \right) $ 在尺度 $ \sigma $ 处的Hessian矩阵被定义为:

$ H\left( {x, \sigma } \right) = \left[ {\begin{array}{*{20}{c}} {L_{xx}\left( {X, \sigma } \right)}&{L_{xy}\left( {X, \sigma } \right)} \\ {L_{xy}\left( {X, \sigma } \right)}&{L_{yy}\left( {X, \sigma } \right)} \end{array}} \right] $

(3)

其中, $ L_{xx}\left( {X, \sigma } \right) $ 是图像 $I_{\sum}$ 与高斯二阶偏导数 $ \dfrac{{{\partial ^2}}}{{\partial {x^2}}}g\left( \sigma \right) $ 的卷积, $ L_{xy}\left( {X, \sigma } \right) $ 和 $ L_{yy}\left( {X, \sigma } \right) $ 类似.

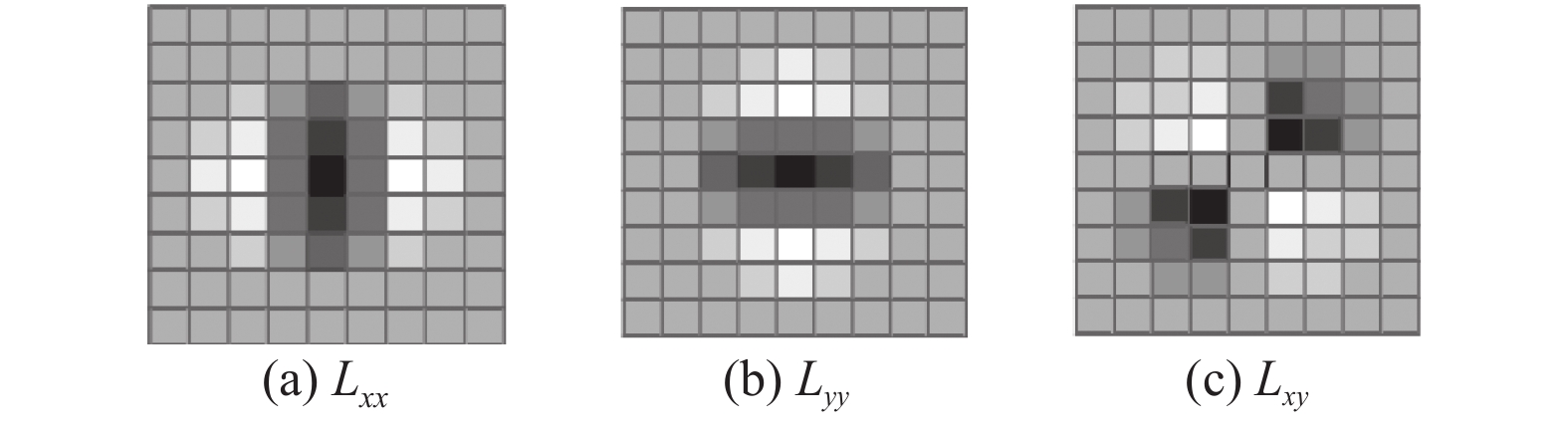
SURF算法利用不同权重大小的盒子滤波器进行二维高斯滤波, 从而近似二阶高斯偏导数(如图2所示), 该过程可利用积分图像降低计算成本^[10].

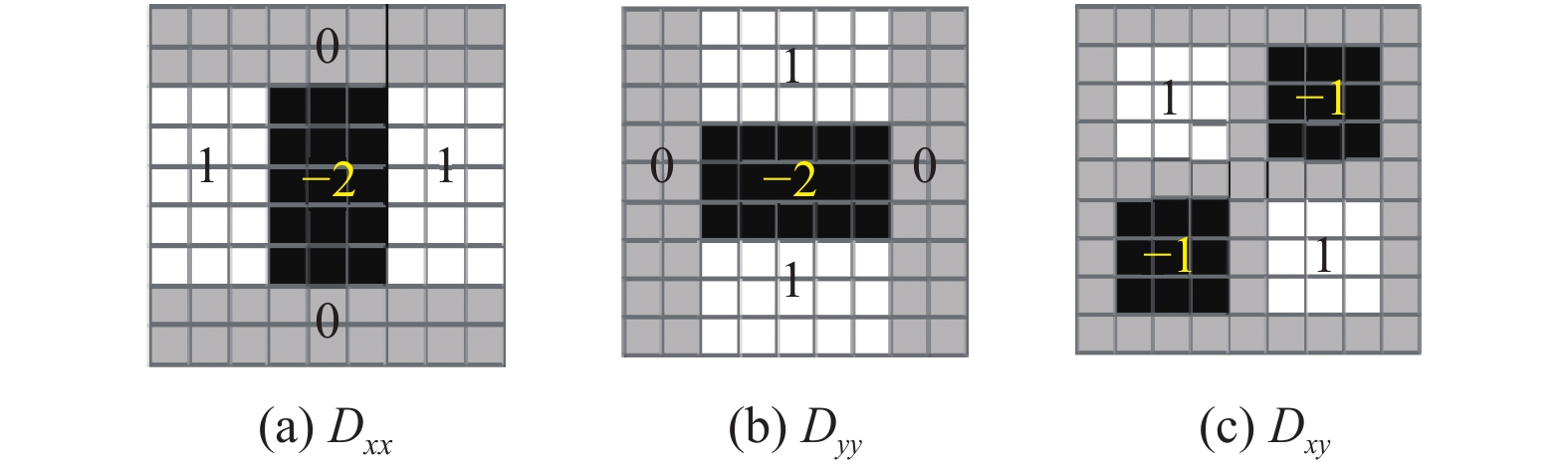
图3中9×9盒子滤波器是尺度 $ \sigma = 1.2 $ 的高斯近似, 代表最高空间分辨率, 分别表示为 $ D_{xx} $ 、 $ D_{yy} $ 、 $ D_{xy} $ , 则Hessian矩阵判别式(DOH值)被定义为:

$ det \left( H \right) = D_{xx}D_{xy} - {\left( {\omega D_{xy}} \right)^2} $

(4)

为提高计算效率引入权重 $ \omega $ , 其值常取0.9.

2.1.3 构建尺度空间

SURF算法通过增加盒子滤波器的大小来构建尺度空间. SURF尺度空间被分为若干层(octave), 图3中9×9盒子滤波器为SURF尺度空间第一层, 用来计算最小尺度( $ {\sigma _0} = 1.2 $ )的Hessian响应值, 每层采样间隔(interval)增加一倍, 相邻层盒子滤波器大小按6个像素步长递增, 由式(5)便可得到如图4所示的SURF尺度空间模板大小^[11].

$ L = 3 \times {2^{octave}} \times interval + 1 $

(5)

不同层对应尺度为:

$ s = {\sigma _0} \times \frac{L}{9} = 1.2 \times \frac{L}{9} $

(6)

2.1.4 特征点检测

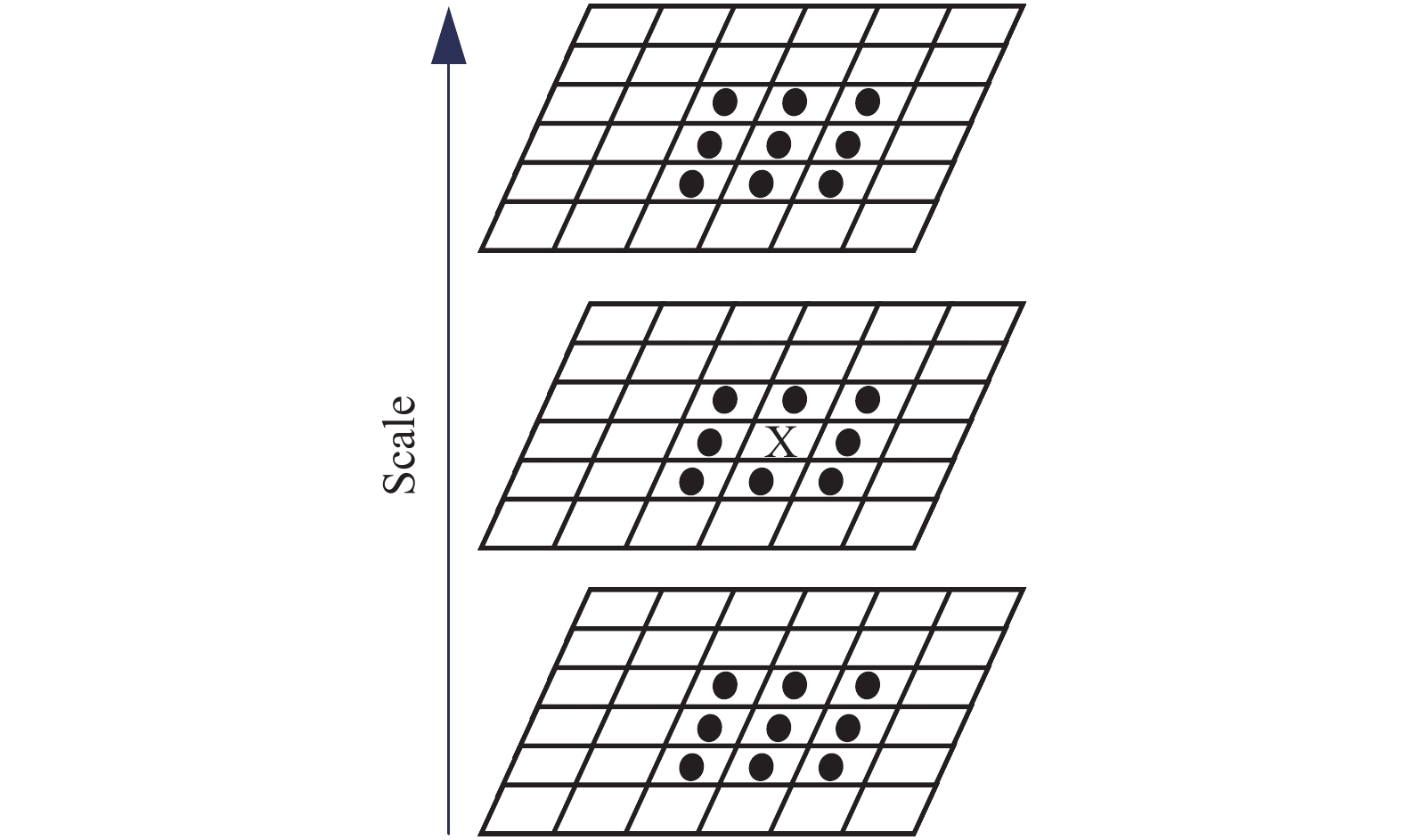
SURF算法采用3×3×3邻域非极大值抑制来检测特征点, 如图5所示, 将由式(4)计算得到的每个像素点DOH值, 与其3×3×3邻域中的26个点进行比较, 若该点的模最大, 则初步定为极值点. 然后去除不稳定和能量较弱的兴趣点, 将det(H)值大于阈值的点精选出来作为最终的特征点^[12].

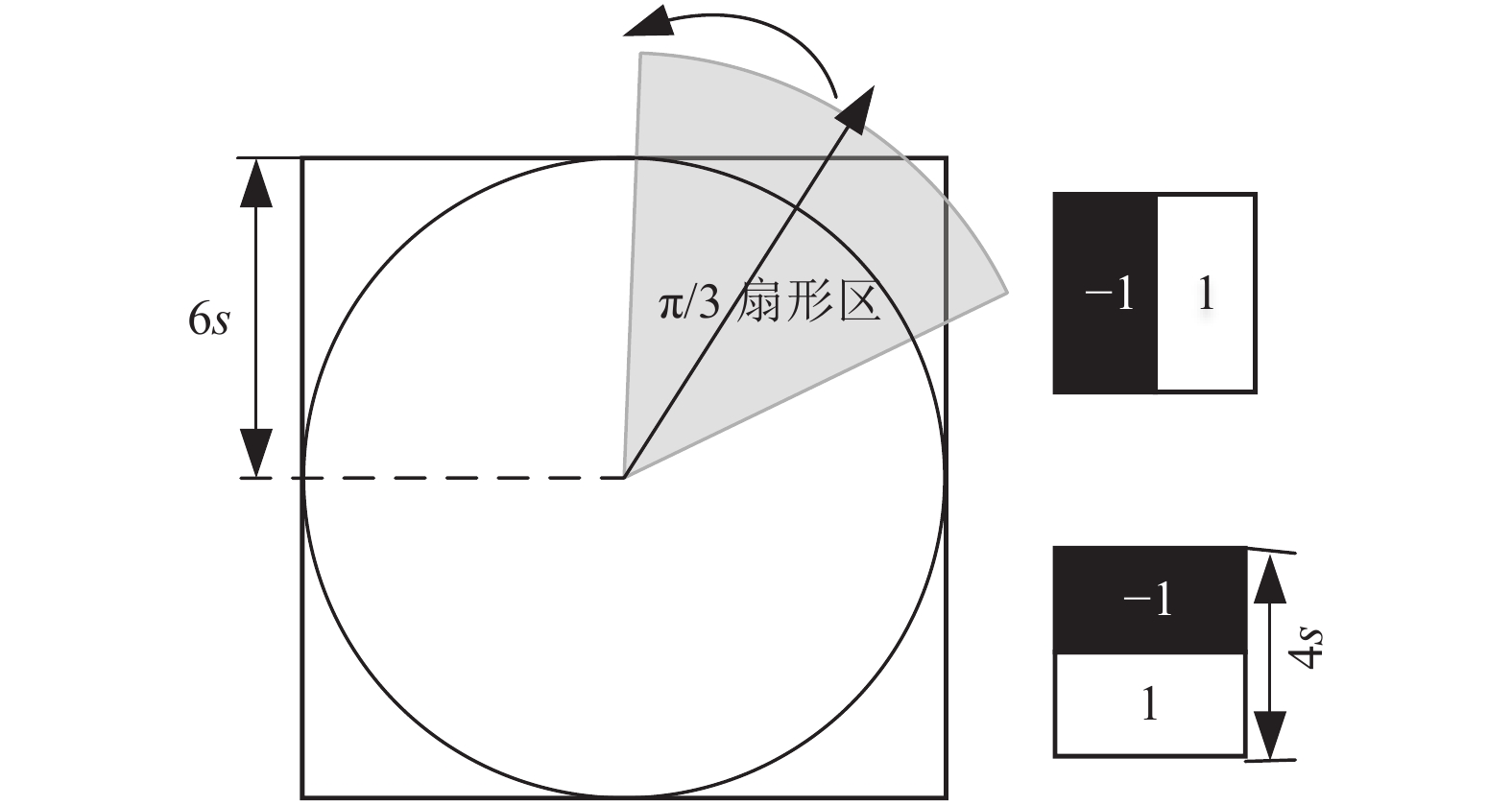
2.2 特征点描述 2.2.1 确定特征点主方向

为保证图像旋转不变性, SURF算法通过计算特征点邻域内Haar小波响应来确定每个特征点的主方向^[13]. 如图6所示, 以特征点为中心, 利用尺寸为4s的Haar小波模板, 计算半径为6s的圆形邻域内 $ x $ 和 $ y $ 方向上的小波响应 $ d_x $ 、 $ d_y $ ; 并统计沿逆时针方向滑动的 $ {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. } 3} $ 扇形滑窗内所有特征点的水平和垂直响应之和, 得到一个局部方向向量 $ \left( {m_\omega , \theta_ \omega } \right) $ . 定义所有窗口中最长的向量为特征点的主方向, 如式(9)所示^[14]:

$ m_\omega = \sum\nolimits_\omega {d_x} + \sum\nolimits_\omega {d_y} $

(7)

$ \theta_ \omega = \arctan \frac{{\displaystyle\sum\nolimits_\omega {d_x} }}{{\displaystyle\sum\nolimits_\omega {d_y} }} $

(8)

$ \theta = \theta _\omega \left| {\max } \right.\left\{ {m_\omega } \right\} $

(9)

2.2.2 生成特征点描述符

如图7所示, 以特征点为中心, 特征点主方向为 $ x $ 轴, 构建一个边长为20s的方形区域, 并将其等分成4×4个边长为5s的正方形子区域, 计算每个子区域中模板尺寸为2s的Haar小波响应, 得到4维特征描述子向量:

$ V = \left( {\sum d_x, \sum d_y, \sum \Big| {d_x} \Big|, \sum \Big| {d_y} \Big|} \right) $

(10)

其中, $ d_x $ 、 $ d_y $ 为 $ x $ 和 $ y $ 方向的Haar小波响应^[12].

如此, 16个子区域可得到该特征点的16×4=64维描述符. 对SIFT算法的128维描述符进行降维, 大大提高了特征检测速度.

3 SURF并行优化

CUDA是NVIDIA公司推出的并行计算平台, 兼容CPU逻辑处理能力和GPU并行计算能力, 可实现CPU+GPU异构并行优化^[15]. GPU通过CUDA流进行异步数据传输, 为不同CUDA流分配不同任务, 可实现数据并行和任务并行, 大大缩短程序执行时间^[16]. CUDA有6种内存模型: 全局内存、本地内存、常量内存、共享内存、纹理内存和寄存器内存, 从左到右内存的读写速度递增^[17].

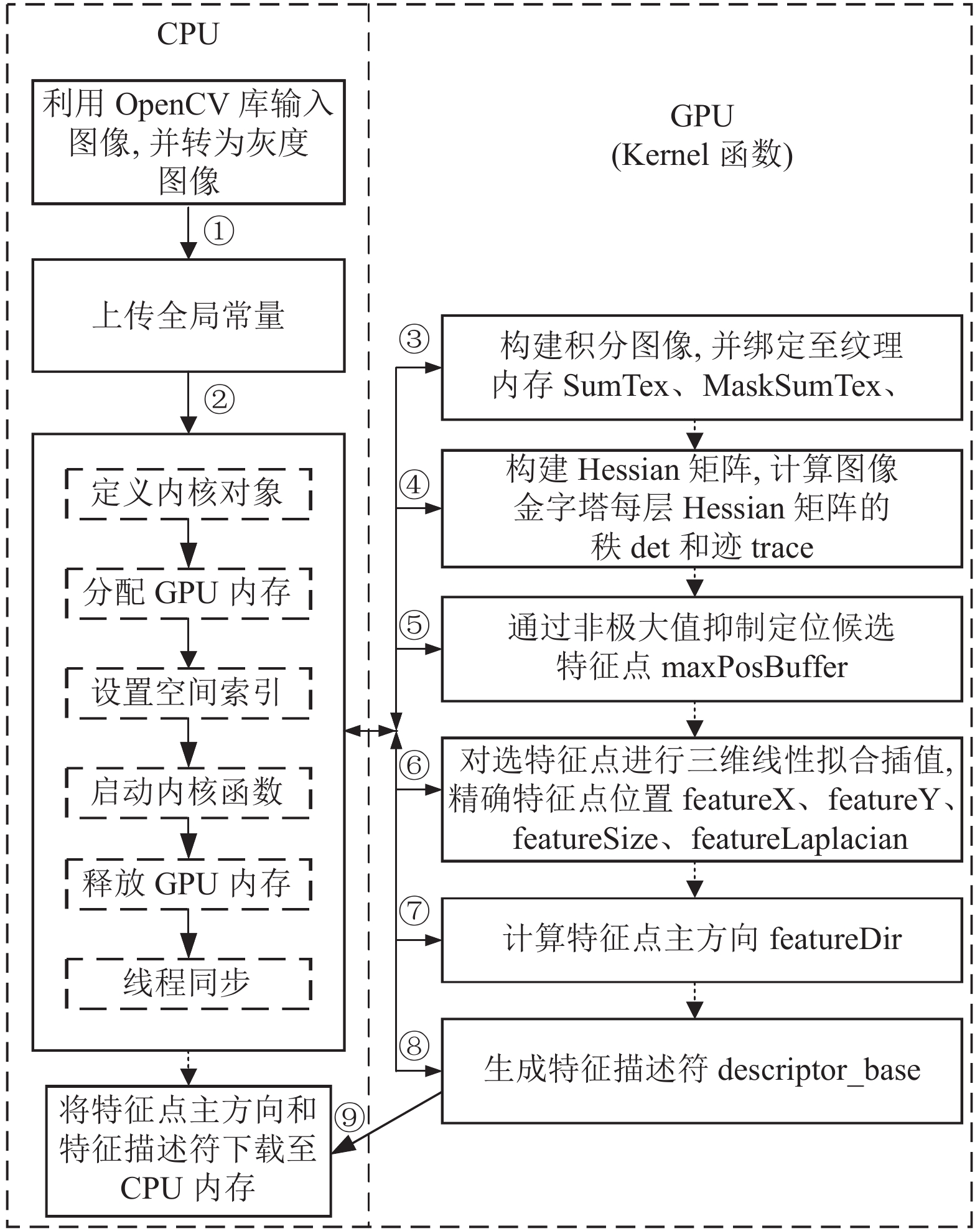
基于上述SURF算法关键技术的研究, 为提高算法速度, 本文基于CUDA并行架构编程模型, 通过将一些固定参数设置为常量内存、将各个步骤间相互传递使用的参数设置为共享内存、将积分图像设置为纹理存储结构, 从而加快参数传输和内存访问; 并创建计算Hessian响应、非极大值抑制、确定特征点主方向、计算特征描述符等Kernel函数, 实现数据和任务并行加速处理, 其并行加速优化流程如图8所示.

3.1 特征点检测 3.1.1 基于前缀加法的积分图像计算

前缀加法即通过分段计算数组元素之和, 应用到图像处理中, 即将图像行和列分成多个段, 构造多层扫描数据, 计算并更新从行或列起始位置到该段末的像素和, 行与行的计算并列, 列与列的计算并列, 从而有效减少计算冗余^[17]. 具体算法流程如算法1.

$ I_{\sum} \left( {x, y} \right) = I_{\sum} \left( {x - 1, y} \right) + i(x, y) $

(11)

$ I'_{\sum} \left( {x, y} \right) = I_{\sum} \left( {x, y - 1} \right) + I_{\sum} \left( {x, y} \right) $

(12)

算法1. 基于前缀加法的积分图像并行计算流程

1) 输入源图像, 将其转化成灰度图像并绑定为纹理内存.

2) 从左向右遍历源图像行像素点, 计算所遍历行像素点灰度和, 则积分图像该位置像素为式(11).

3) 从上向下遍历积分图像列像素点, 计算所遍历列像素点灰度和, 则积分图像当前遍历位置像素为式(12).

4) 将积分图像绑定为纹理内存.

3.1.2 计算Hessian响应值

SURF算法在构建尺度空间、计算Hessian矩阵以及计算特征点描述符等步骤中均可利用积分图像简化算法步骤. 因此, 本文算法将源图和积分图像绑定为纹理内存, 从而通过坐标较快地获取texture存储器的数据, 加快Kernel函数数据传输.

尺度空间金字塔不同层计算相互独立, 可构建不同尺度的Hessian矩阵; 同层不同像素点的Hessian响应值计算也相互独立. 因此, 本文基于图像级和像素级同时并行优化, 设计如下算法流程如算法2.

算法2. 计算Hessian矩阵响应值算法

1) 在CPU端将源图及相关参数上传至GPU全局内存.

2) 创建不同方向具有不同权重大小的盒子滤波器模板, 并将其存储于常量内存.

3) 为Kernel函数分配与图像大小相同的索引指数, 即为每个像素点分配一个内核线程, 用于并行计算不同像素点在 $\scriptstyle x $ 方向、 $\scriptstyle y $ 方向及 $\scriptstyle xy $ 方向的高斯二阶偏导数, 进而确定每个像素的Hessian响应值.

4) 为金字塔每层图像分配内存空间, 进行不同层Hessian响应值的并行计算.

3.1.3 非极大值抑制

特征点检测实质就是进行3×3×3邻域非极大值抑制, 然后通过三维线性插值法确定亚像素级特征点位置^[18]. 该过程是在尺度空间像素级上进行的, 故而同理, 进行像素级和图像级的并行加速优化, 设计如算法3所示流程. 为进一步提高特征点检测效率, 本文算法利用积分图像对边界效应引起的边界空白区域像素进行预处理, 简化特征点检测步骤; 通过原子操作, 确保在多个并行线程间共享内存的读写保护. 特征点检测结果如图9, 图9(a)为文献[9]串行算法检测结果, 图9(b)为本文算法检测结果.

算法3. 非极大值抑制算法流程

1) 创建Haar小波滤波器模板并设置为常量内存.

2) 创建掩码积分图并绑定为纹理内存.

3) 创建Kernel函数, 为每个像素分配索引空间, 遍历中间层图像的所有像素, 设置阈值剔除对照度低的点.

4) 当前点与其周围26个点比较, 进行非极大值抑制.

5) 通过三维二次曲线拟合对候选特征点插值, 并将该候选特征点坐标、Laplace迹以及索引号存入向量组.

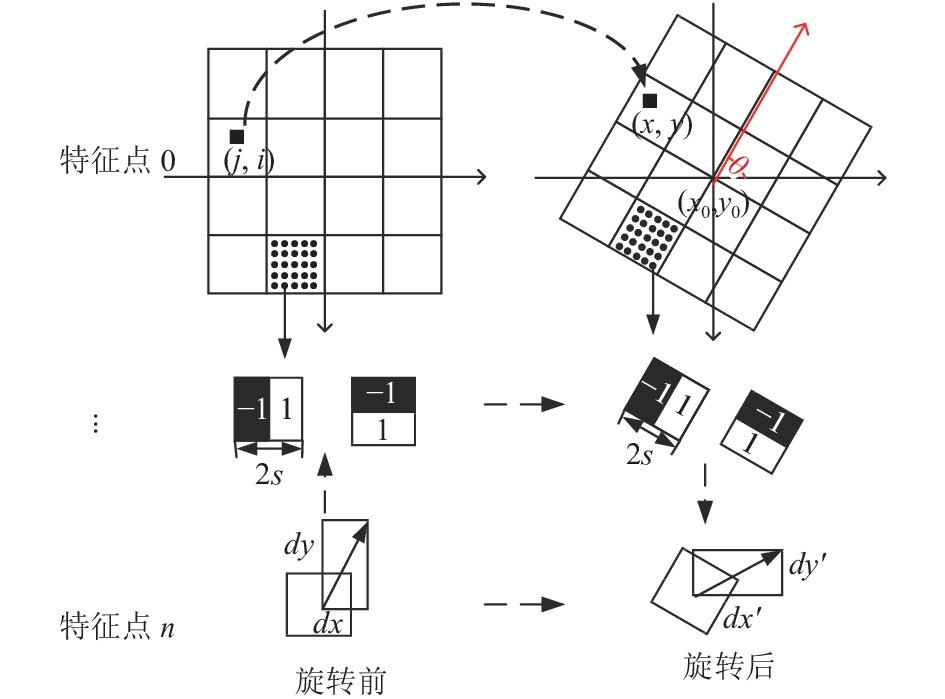
3.2 特征点描述 3.2.1 寻找特征点主方向

寻找特征点主方向时, 各特征点主方向计算相互独立, 计算圆形域内各像素Haar小波响应及扇形域内响应值累加求和同样相互独立. 因此, 并行化处理时, 为每个特征点分配一个线程块, 该特征点每个邻域像素点被分配在线程块的每个线程中, 其算法流程如算法4.

$ angle = \arctan \frac{{d_x}}{{d_y}} $

(13)

算法4. 寻找特征点主方向算法流程

1) 使用大小为4s的小波在半径为6s的圆中对 $\scriptstyle x $ 和 $\scriptstyle y $ 方向梯度进行采样, 利用积分图像计算 $\scriptstyle x $ 、 $\scriptstyle y $ 方向的Haar小波响应值 $\scriptstyle d_x $ 、 $\scriptstyle d_y $ .

2) 使用 $\scriptstyle \sigma = 2s $ 的高斯加权函数对 $\scriptstyle d_x $ 、 $\scriptstyle d_y $ 进行高斯加权, 通过式(13)计算向量的方向角angle, 并将其分别存储在共享内存s_X、s_Y、s_angle中.

3) 用60°的滑动窗口以0.2弧度步长进行旋转, 每个线程并行计算每个窗口内采样点的Haar小波响应值之和sumx, sumy.

4) 通过式(7)和式(8)计算特征向量的长度 $\scriptstyle m_\omega $ 和方向 $\scriptstyle \theta_ \omega $ , 得到方向矢量 $\scriptstyle \left( {m_\omega , \theta_ \omega } \right) $ , 取最长矢量对应方向为主方向.

3.2.2 生成特征点描述符

计算主方向时, 使用 $ 4s \times 4s $ 的正窗计算半径为6s圆域内的Haar响应, 因此可借助积分图像简化运算; 而计算描述符时, 使用 $2s \times 2s$ 的倾斜窗计算边长为21s倾斜方形域内的Haar特征, 如图10所示, 因此不能利用积分图像快速计算. 点 $ \left( {i, j} \right) $ 旋转前对应积分图像的位置 $ \left( {x, y} \right) $ 为式(14)^[19]:

$ \left\{ \begin{gathered} x = x_0 - j \times scale \times \sin \theta + i \times scale \times \cos \theta \\ y = y_0 + j \times scale \times \cos \theta + i \times scale \times \sin \theta \\ \end{gathered} \right. $

(14)

为防止误匹配, 本文引入高斯权重, 并给远离特征点的点赋予较小权值. 生成的描述符如图11所示, 图11(a)为文献[9]串行算法生成描述符结果, 图11(b)为本文算法生成描述符结果. 其算法流程如算法5.

$ \left\{ \begin{gathered} d'_x = \omega \left( { - d_x \times \sin \theta + d_y \times \cos \theta } \right) \\ d'_y = \omega \left( {d_x \times \cos \theta + d_y \times \sin \theta } \right) \\ \end{gathered} \right. $

(15)

算法5. 生成特征点描述符算法流程

1) 定义采样间隔和尺度大小, 通过点旋转公式(式(13))把点旋转到主方向上, 并通过最近邻插值计算“倾斜窗”所有像素.

2) 以特征点为中心, 沿主方向构建 $\scriptstyle 20s \times 20s$ 方形邻域.

3) 在线程块内分配 $\scriptstyle 5 \times 5 $ 的线程子区域, 使用 $\scriptstyle 2s \times 2s$ 的模板计算窗口内 $\scriptstyle x $ 、 $\scriptstyle y $ 方向的Haar小波响应 $\scriptstyle d_x $ 、 $\scriptstyle d_y $ , 并利用式(15)对 $\scriptstyle d_x $ 、 $\scriptstyle d_y $ 进行高斯加权处理.

4) 对4×4个边长为 $\scriptstyle {\text{5}}s $ 的方形区域分别累加求和, 得到每个特征点的4×4×4维描述符, 并对其标准化处理.

3.3 特征点匹配

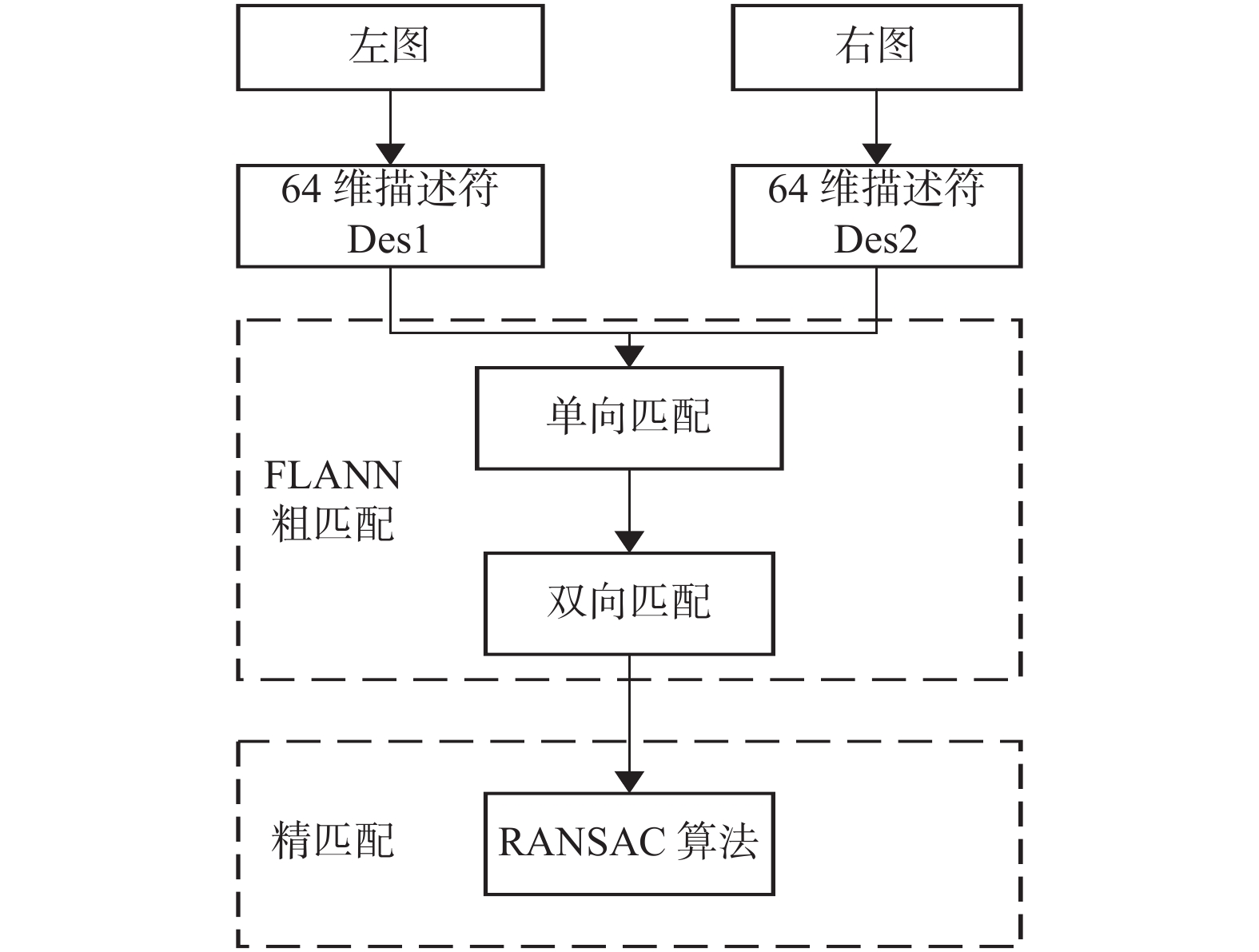
SURF算法用欧氏距离表征描述符的相似程度, 进而完成匹配^[20]. 设特征点p和q的描述符为 $ Des_p $ 和 $ Des_q $ , 则其欧氏距离为式(16), 其中i为描述符的维度. 若某图像特征点最近邻距离 $ d_1 $ 与次近邻距离 $ d_2 $ 的比值小于匹配阈值(式(17)), 则表示此特征点与待匹配图像中欧式距离最近的特征点匹配^[20]. 本文首先通过FLANN算法进行最近邻近似匹配, 提高匹配效率; 然后采用RANSAC算法进行精匹配, 并采用双向匹配策略在传统算法上进一步优化, 提高算法精度, 其流程如图12所示.

$ d = \sqrt {\sum i{{\left( {Des_p\left( i \right) - Des_q\left( i \right)} \right)}^2}} $

(16)

$ \frac{d_1}{d_2}＜r=0.8 $

(17)

FLANN算法即快速最近邻搜索, 其算法复杂度低, 匹配结果如图13所示, 由图13可知FLANN算法存在误匹配对, 需要进一步的筛选^[21]. 本文通过RANSAC(随机采样一致性)算法进行提纯. RANSAC算法, 是用迭代的方法通过重复随机取样来计算两幅图像的最优单应性矩阵H, 利用矩阵变换模型(式(18))剔除误匹配点, 从而完成图像配准^[22]. RANSAC算法具有很好的旋转不变性, 精细化匹配效果如图14所示, 图中很好地剔除了误匹配点.

$ \left( {\begin{array}{*{20}{c}} {x'} \\ {y'} \\ 1 \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {h_{11}}&{h_{12}}&{h_{13}} \\ {h_{21}}&{h_{22}}&{h_{23}} \\ {h_{31}}&{h_{32}}&1 \end{array}} \right]\left( {\begin{array}{*{20}{c}} x \\ y \\ 1 \end{array}} \right) $

(18)

其中, $ h_{11} $ 、 $ h_{12} $ 、 $ h_{21} $ 、 $ h_{22} $ 为缩放及旋转因子, $ h_{13} $ 、 $ h_{23} $ 为平移因子, $ h_{31} $ 、 $ h_{32} $ 为仿射因子, $ x $ 、 $ y $ 分别为当前图像的横纵坐标, $ x' $ 、 $ y' $ 为变换后图像的坐标.

4 实验分析 4.1 实验方案

已有基于GPU的SURF加速算法有基于OpenCL和CUDA架构两个版本, 两者运行效率相当, OpenCL架构可移植性好, 但其内存等需要程序员自己管理, 而CUDA架构由开发环境进行管理, 这无疑降低了编程的难度. 因此, 本文采用更高一级别的CUDA架构实现SURF特征检测算法加速, 利用7张分辨率不同的图像设计两组实验, 从而验证本文算法的实时性和准确性. 结果表明, 本文算法与传统SURF算法具有相同的匹配精度, 而对于特征提取速度有显著提升. 其主要实验环境平台为: 软件集成开发环境: Visual Studio 2015; 开源库: CUDA 9.1, OpenCV 3.4.13; 硬件运行平台: Intel(R) Core(TM) i5-8500 CPU @ 3.00 GHz; 显卡: NVIDIA GeForce GT 730; 操作系统: Windows 10 64位.

4.2 SURF算法优化方案 4.2.1 内存访问优化

CUDA内存模型中全局内存读写速度最慢, 因此, 文献[7]算法中引入共享内存, 将计算Hessian响应、非极大值抑制、三线性插值等过程关联提高算法速度. 本文在此基础上引入常量内存、纹理访问和原子操作进一步优化, 具体方案如下.

(1)使用常量内存替换全局内存, 限制只读访问机制, 减少内存带宽, 提升算法性能.

(2)在访问原图、积分图、掩码积分图等二维数据时, GPU内具有高速处理的纹理缓存, 因此, 本文算法在函数体外声明纹理参照系, 将这些二维数据绑定为纹理内存, 使用纹理操作在Kernel函数中通过坐标较快的获取texture存储器数.

(3)使用原子操作, 确保在多个并行线程间共享内存的读写保护, 从而高效得到正确特征点序列.

4.2.2 程序设计优化

在程序编写中, 对现有GPU加速算法主要采取以下优化方案.

(1)尽可能将多个缓存数据打包合并一次传输, 减少数据传输时的时间开销.

(2)减少函数调用和循环语句, 必要时在循环语句前使用“#pragma unroll”指令控制循环次数, 减少不必要的循环.

4.2.3 匹配精度优化

无论是SURF欧式距离匹配算法还是其他匹配算法均存在一定误匹配, 因此, 本文在传统FLANN和RANSAC匹配算法上进行匹配度优化. 本文将FLANN粗匹配和RANSAC精匹配结合剔除误匹配点, 并引入双向匹配策略进一步提高配准精度, 最后通过计算配准精度验证算法性能.

4.3 实验结果

由算法实现过程知, 特征点检测过程性能与输入图像分辨率及其复杂度有关, 计算特征描述符与特征点数量有关, 因此, 为验证本文算法的准确度, 设计了文献[9]串行算法与本文优化算法对比实验, 如表1和表2所示, 分别记录了7组不同分辨率图像特征点检测和特征点描述过程的运行时间, 其实验结果取10次试验的平均值.

由表1可以看出, 特征检测过程运行时间随着图像分辨率的增大而增大, 其中传统串行算法耗时尤为明显; 本文算法与文献[9]检测特征点数相同, 由式(19)得检测精度可高达99.81%. 对于分辨率为800×600的图像, 其复杂度较低, 检测到的特征点数目较少, 算法运行时间较短, 检测精度可达到100%. 去掉该图, 得到如图15所示特征点检测时间对比图, 可见本文算法在保证检测精度的同时, 大大优化了特征检测速度.

$ 检测精度=\frac{正确特征点数}{正确特征点数+错误特征点数} $

(19)

如表2所示, 记录了6组不同分辨率图像特征描述步骤的运行时间, 从而可得到如图16所示特征描述时间对比. 由此可见, 特征描述过程运行时间随着图像检测特征点数的增大而增大, 其中文献[9]串行算法耗时尤为明显. 根据式(20)计算生成特征描述符精度, 相比于文献[9], 本文算法得到的特征描述符精度高达97.97%, 且图16本文算法大大节省了特征描述用时.

$ 描述精度=\frac{正确特征描述符}{正确特征描述符+错误特征描述符} $

(20)

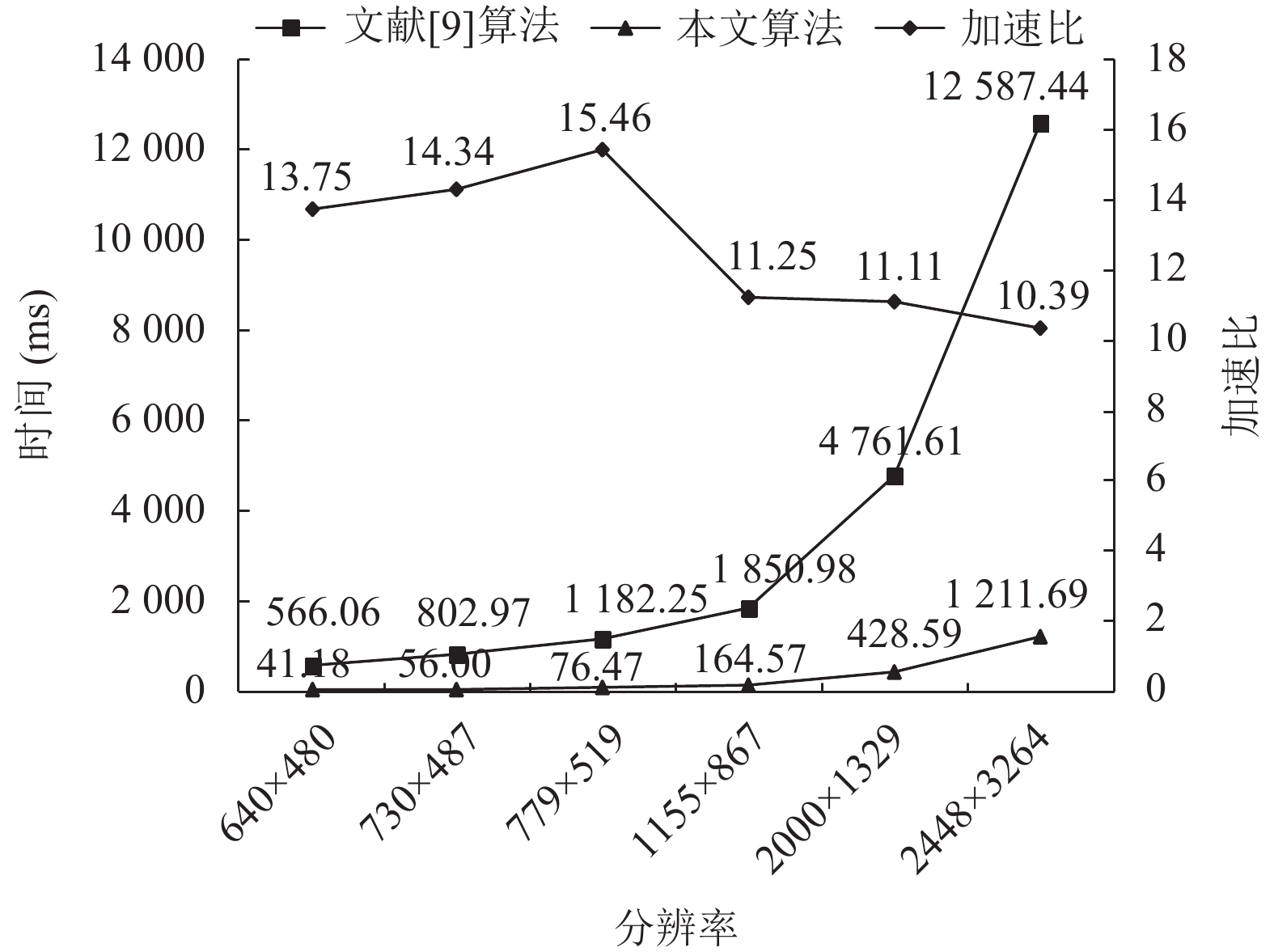
基于上述实验过程, 统计了本文并行算法与文献[9]串行算法的总耗时和加速比(如表3所示), 进而可得到其时间对比折线图(如图17所示). 图17也证实了上述结论, 随着分辨率的增大, 传统串行算法耗时严重, 而本文算法对不同分辨率的图像均可实现平均10倍以上的加速比, 加速效果较好. 然而, 由于随着图像分辨率的增大以及图像复杂度的增加, 检测到的特征点数量增大, 进而算法的并行化程度增大, GPU的并行计算能力也增强; 当分辨率与特征点数增大到一定程度时, GPU内存竞争导致加速比逐渐下降, 故而出现如图17所示下降趋势.

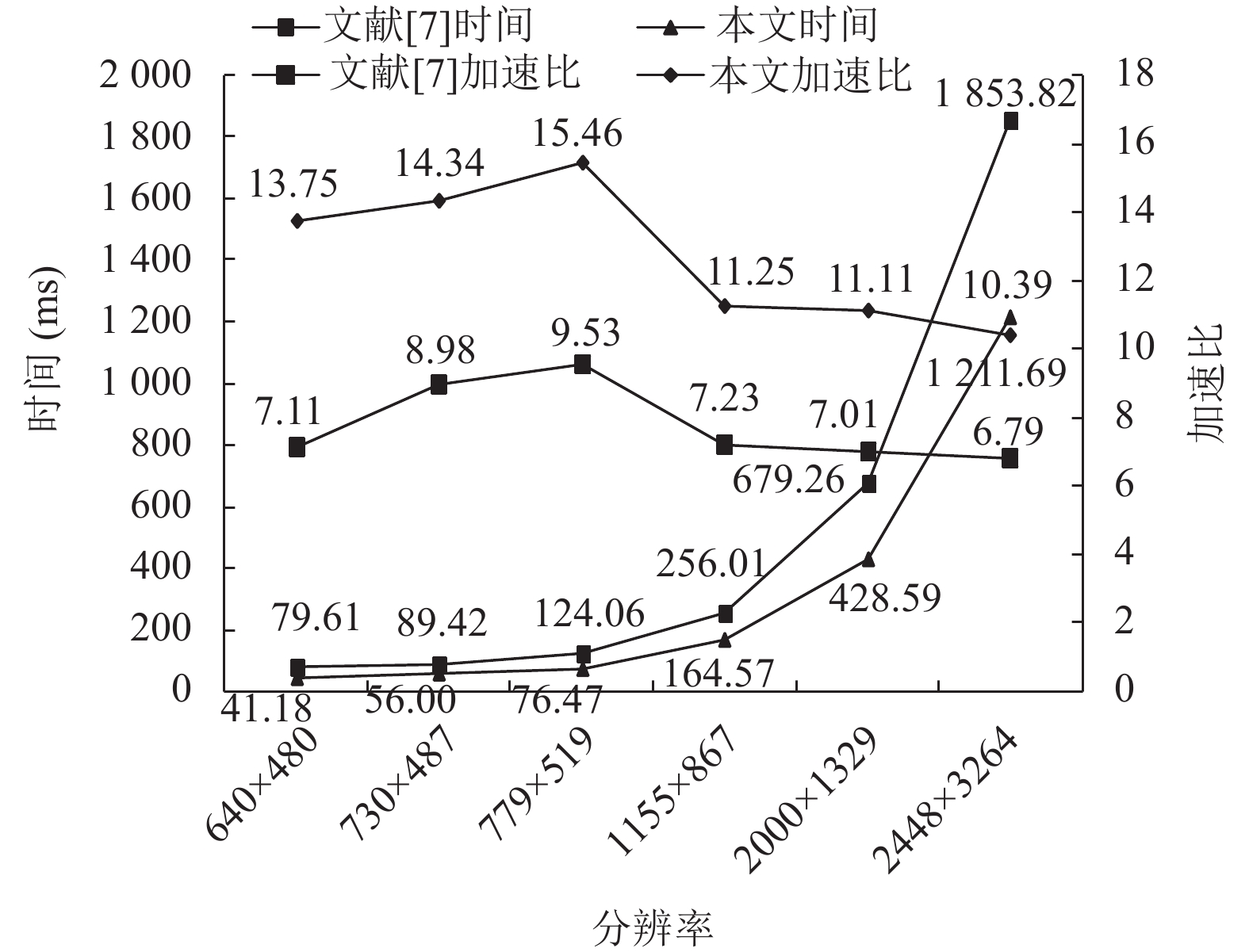
为突出本文算法的先进性, 设计了本文算法与已有CUDA加速算法的对比实验, 如表4所示记录了文献[7]与本文算法的运行时间及加速比, 可以看出, 文献[7]算法检测速度至少提高了6倍, 而本文优化算法对不同分辨率图像均可实现10倍以上的加速比. 从加速比折线图(图18)也可明显看出, 本文算法在提高算法效率方面具有很大优势.

4.4 特征匹配优化实验结果

为验证本文算法的普适性, 本文在传统SURF算法最近邻匹配基础上进行了精细匹配实验, 采用双向匹配策略对传统FLANN和RANSAC算法进行优化, 从而提高匹配精度.

选用4组具有代表性的不同分辨率的图像进行匹配度分析: 从不同仰角拍摄的室内图像office、光线比较暗的图像temple、纹理比较复杂的图像train和水平位置拍摄的不同方位图像intersection, 得到实验效果分别如图19–图22所示, 从图中可以看出, 无论是室内图像还是户外图像, 对于不同纹理、不同光强、不同角度的图像, 本文算法均有较好的配准效果.

为客观评价配准效果, 本文利用式(21)计算匹配精度, 得到如表5所示对比实验结果.

$ 配准精度=\frac{正确匹配数}{正确匹配数+错误匹配数} $

(21)

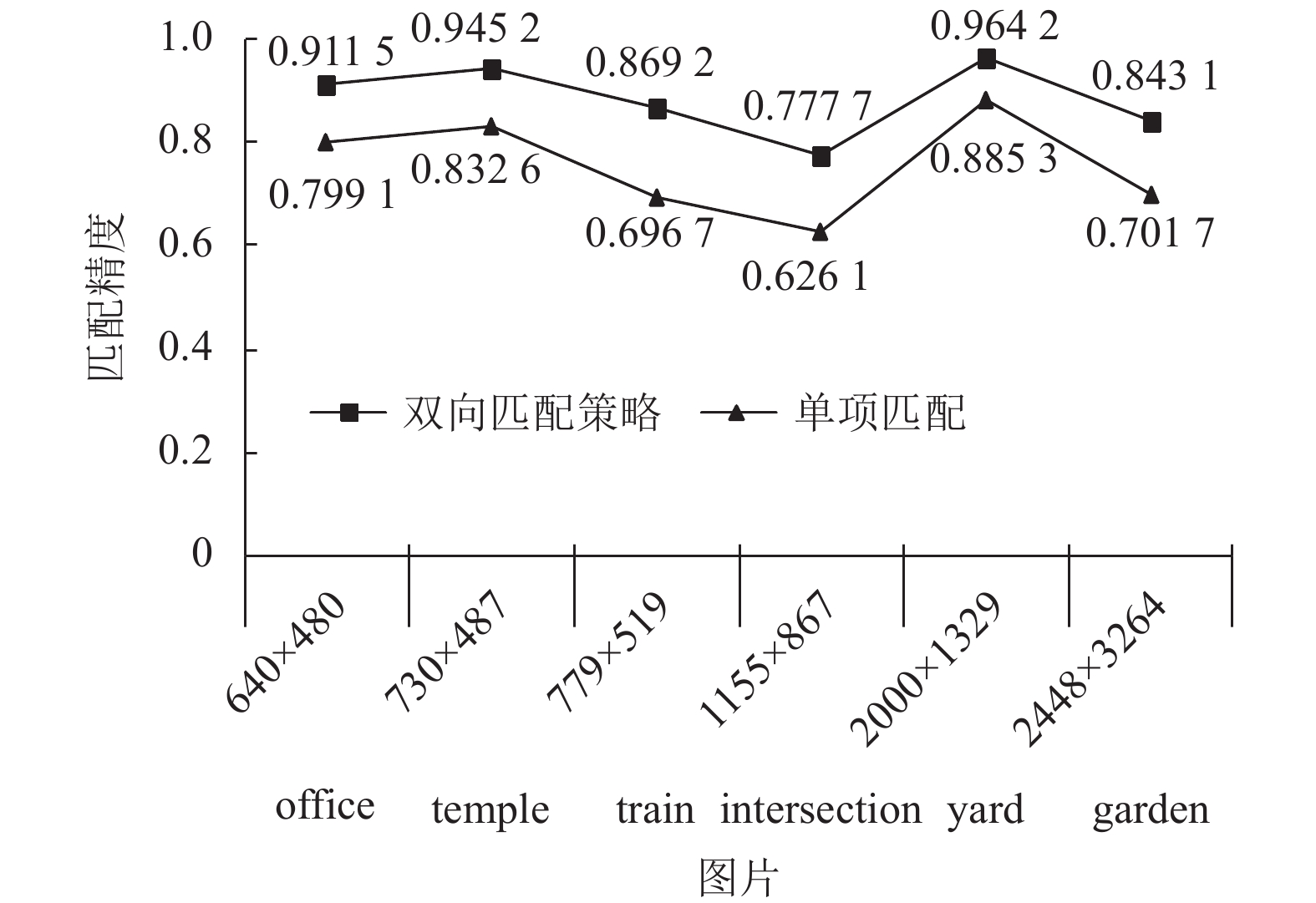
图像的复杂程度、光线强弱、重叠区域大小等都会对配准精度有一定的影响. 为显著比较算法优化前后精度, 得到如图23所示精度对比曲线, 从图中可以看出, 本文优化算法配准精度明显提升, 最高配准精度可达到96%, 进一步说明本文算法具有较好的鲁棒性.

5 结论与展望

本文提出了一种基于CUDA架构的并行SURF算法, 通过对计算Hessian响应、非极大值抑制、计算特征点主方向及生成特征描述符等步骤的并行加速优化, 从而提升算法性能. 本文给出了详细的算法流程, 并以此提出一种基于FLANN和RANSAC算法的双向配准方法. 实验结果表明: 本文算法对不同分辨率图像的特征提取均能实现10倍以上的加速比, 且配准精度最高可达到96%, 具有较好的实时性和鲁棒性, 对获取全景视频图像具有深远意义. 后续工作基于本文CUDA加速的配准算法, 对视频图像序列进行拼接, 并通过融合处理实时生成大尺度无重影的全景图像, 为全景视频监控提供有力的技术支撑.