近年来, 由于云计算的广泛应用, 使其逐渐成为各行各业的研究热点^{[1, 2]}. 云存储作为云计算的重要组成部分, 以其存储成本低、访问方式简单等优势也逐渐受到了人们的青睐. 借助云存储平台, 数据所有者不仅可以通过云服务器存储数据, 还可以通过云服务器与其他用户共享数据^{[3, 4]}.

在云存储环境中, 当数据所有者将其数据上传到云服务器进行存储和共享时, 可能会存在一些安全问题. 首先, 当云服务器或者共享用户接收到数据时, 需要验证数据的正确性. 其次, 数据所有者的数据中可能包含其敏感信息. 当数据所有者通过云服务器共享数据时, 不希望将自己的敏感信息泄露给云或共享用户. 因此, 如何确保云服务器中数据的可认证性和敏感信息隐藏成为亟待解决的关键问题.

数字签名是保证数据的可认证性、完整性和不可否认性的重要技术. 然而, 数据所有者为了在数据共享的过程中不泄露自己的敏感信息, 需要对敏感信息对应的数据进行适当的修改. 为了保证修改后的数据能够通过云服务器或者共享用户的验证, 数据所有者一般选择将数据先进行加密, 再进行签名. 然后将加密后的数据以及相应签名上传到云服务器^[5]. 但是, 如果共享数据是被加密过的, 那么传统的数字签名方案只能保证加密数据的正确性, 而无法保证原始数据的正确性.

为了解决该问题, 2005年, Ateniese等人^[6]首先提出了可净化签名的概念. 可净化签名允许数据所有者在对数据进行签名的同时指定一个净化者, 净化者能够修改数据所有者指定的部分数据. 并且净化者能够在不与数据所有者交互的前提下, 为修改后的数据生成有效签名, 使得修改后的数据也能通过云服务器或者共享用户的验证. 因此, 可净化签名能够被用来解决云存储环境下共享数据的可认证性与敏感信息隐藏. 之后, Miyazaki等人^[7]提出了基于双线性对的可净化签名方案. Agrawal等人^[8]提出了一个标准模型中强透明度的可净化签名方案. 但是上述可净化签名方案效率低下. 考虑到这个问题, 2013年, 文献[9]利用Waters签名技术, 提出了一个标准模型中高效的基于身份可净化签名方案. 2014年, 文献[10]提出了一个基于属性的可净化签名方案. 2016年, 文献[11]提出了一个没有随机谕言机的高效的可净化签名. 然而, 以上可净化签名方案功能单一, 并不适用于实际应用场景. 为了解决该问题, 2017年, 文献[12]提出了一种支持树形访问结构的属性基可净化签名方案. 2019年, 文献[13]提出了一个高效的不可链接的可净化签名. 2020年, 文献[14]提出了一种基于环签名和短签名的可净化签名方案. 文献[15]将可净化签名引入到了智能医疗场景中, 提出了一个基于可净化签名的智能移动医疗场景隐私保护方案. 文献[16]使用Affine消息鉴别码提出了一个基于身份的陷门可净化签名. 此外, 为了保证共享数据的可认证性、完整性以及敏感信息隐藏, 文献[17]和文献[18]分别提出了一种基于可净化签名的云存储数据完整性审计方案.

但是, 现有的大部分可净化签名方案有以下两个问题: 很多方案依赖于传统公钥基础设施或者基于身份密码学, 这使得大多方案存在昂贵的证书管理开销或者复杂的密钥托管缺陷; 此外, 现有方案都没有考虑数据访问控制的问题, 如果数据所有者的数据存储在云服务器后, 能被任何用户访问, 那么可能会造成数据滥用的问题.

针对上述问题, 本文提出了一个云存储中无证书的可净化签名方案. 具体而言, 本文的贡献如下.

(1) 由于无证书密码学^[19]固有的结构优势, 所提方案摆脱了传统公钥基础设施中昂贵的证书管理开销、消除了基于身份密码学中复杂的密钥托管缺陷.

(2) 所提方案实现了云存储环境下数据的可认证性和敏感信息隐藏. 此外, 所提方案加入了访问控制, 使得存储在云服务器中的数据只能被授权用户访问.

(3) 安全分析表明了所提方案的安全性; 性能分析表明, 与其他相关方案相比, 所提方案的计算代价和通信代价是可接受的.

1 背景知识 1.1 双线性映射

设 $q$ 是一个大素数, ${\mathbb{G}_{\text{1}}}$ 是阶数为 $q$ 的加法循环群, ${\mathbb{G}_{\text{2}}}$ 是阶数为 $q$ 的乘法循环群. ${\mathbb{G}_{\text{1}}}$ 到 ${\mathbb{G}_{\text{2}}}$ 的双线性映射 $e:{\mathbb{G}_1} \times {\mathbb{G}_1} \to {\mathbb{G}_2}$ 满足如下性质.

(1) 双线性: 如果对任意的 $X, Y \in {\mathbb{G}_1}$ 和 $a, b \in \mathbb{Z}_q^*$ , 等式 $e(a \cdot X, b \cdot Y) = e{(X, Y)^{a \cdot b}}$ 成立, 那么就称该映射为双线性映射.

(2) 非退化性: 映射不把 ${\mathbb{G}_1} \times {\mathbb{G}_1}$ 中的所有元素映射到 ${\mathbb{G}_2}$ 中的单位元. 即对于元素 $X, Y \in {\mathbb{G}_1}$ , 满足 $e(X, Y) \ne {1_{{\mathbb{G}_2}}}$ .

(3) 可计算性: 对于任意的 $X, Y \in {\mathbb{G}_1}$ , 存在一个有效算法计算 $e(X, Y)$ .

1.2 困难问题和安全假设

(1) 离散对数问题(DL问题): 假设 ${\mathbb{G}_{\text{1}}}$ 是一个加法循环群, $P$ 是 ${\mathbb{G}_{\text{1}}}$ 的生成元. 对于未知的 $x \in \mathbb{Z}_q^*$ , 给定元组 $(P, \; x \cdot P \in {\mathbb{G}_1})$ , DL问题是计算 $x \in \mathbb{Z}_q^*$ .

(2) 离散对数假设(DL假设): 对任意的概率多项式时间敌手 $\mathcal{A}$ , $\mathcal{A}$ 能够解决DL问题的概率是可忽略的.

(3) 计算性Diffie-Hellman问题(CDH问题): 假设 ${\mathbb{G}_{\text{1}}}$ 是一个加法循环群, $P$ 是 ${\mathbb{G}_{\text{1}}}$ 的生成元. 对于未知的 $a, b \in \mathbb{Z}_q^*$ , 给定元组 $(P, \; a \cdot P, \; b \cdot P \in {\mathbb{G}_1})$ , CDH问题是计算 $a \cdot b \cdot P$ .

(4) 计算性Diffie-Hellman假设(CDH假设): 对任意的概率多项式时间敌手 $\mathcal{A}$ , $\mathcal{A}$ 能够解决CDH问题的概率是可忽略的.

1.3 系统模型

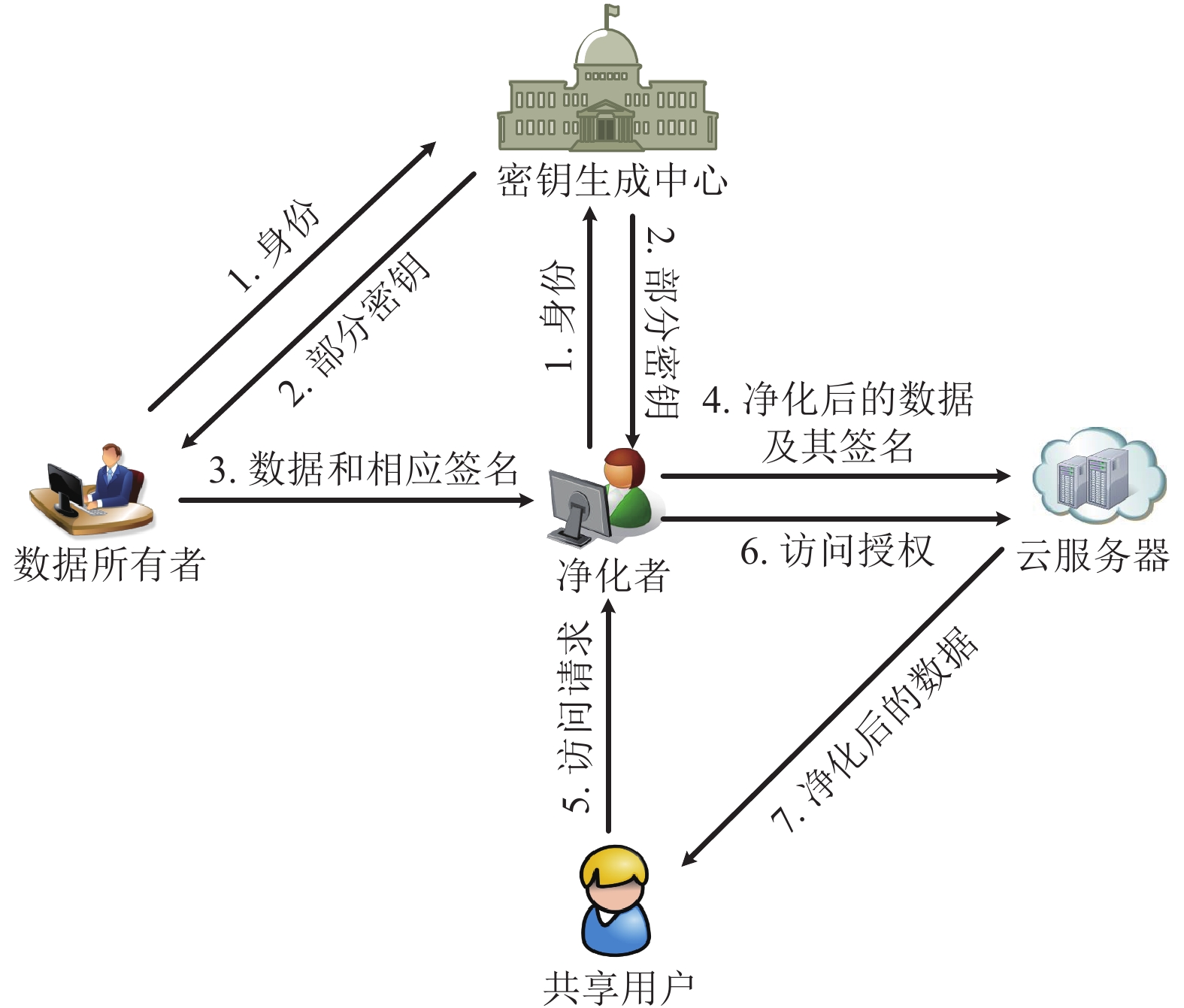
本文的系统模型如图1所示, 其中包括5个实体: 密钥生成中心(KGC)、数据所有者(DO)、净化者(Sanitizer)、云服务器(CS)以及共享用户(User).

(1) 密钥生成中心(KGC): 一个可信实体, 具有强大的计算能力, 负责整个系统的初始化, 为系统生成主密钥和公开参数. 此外, 在接收到DO和Sanitizer的身份后, 为DO和Sanitizer生成相应的部分密钥.

(2) 数据所有者(DO): 一个可信实体, 有大量的数据需要存储在云服务器. 此外, DO会将其数据和相应签名发送给Sanitizer, 并指定数据中需要净化的敏感信息, 让净化者执行净化.

(3) 净化者(Sanitizer): 一个半可信实体, 负责对DO数据中的敏感信息进行净化, 并为净化后的数据生成有效签名. 然后, 将净化后的数据和相应签名发送给CS进行存储和共享.

(4) 云服务器(CS): 一个半可信实体, 具有丰富的存储空间和强大的计算能力, 负责对净化后的数据进行存储和维护. 此外, 在接收到Sanitizer的访问授权时, 验证授权的正确性, 并将净化后的数据发送给User.

(5) 共享用户(User): 它主要是指需要访问数据所有者数据的用户.

在该模型中, DO和Sanitizer首先分别将其身份发送给KGC进行注册, KGC为DO和Sanitizer分发部分密钥. 然后, DO为原始数据生成相应的签名, 并指定原始数据中需要净化的敏感信息数据块. 最后, DO将原始数据、敏感信息对应的数据块索引以及相应签名发送给Sanitizer. Sanitizer接收到数据后, 对敏感信息对应的数据块执行净化, 并将净化后的数据和相应签名发送到CS进行存储和共享. 然后, CS验证数据和签名的正确性. 当User需要使用数据时, 会向发送访问请求. Sanitizer收到请求后为用户生成访问授权, 并将其发送给CS. 访问授权通过CS的验证后, CS会将净化后的数据发送给User.

1.4 安全需求

(1) 正确性: 当接收到Sanitizer发送的数据和相应签名时, CS应确保数据和相应签名的正确性. 此外, 当接收到Sanitizer生成的访问授权时, CS需确保访问授权的正确性.

(2) 指定Sanitizer: 只有被DO指定的Sanitizer才能够执行净化.

(3) 不变性: 除了DO指定的敏感信息数据块外, Sanitizer不能对其他数据生成有效签名.

(4) 隐私性: DO数据中的敏感信息不应暴露给CS和User.

(5) 访问控制: 只有User才能够访问云服务器中的数据.

(6) 消除密钥托管: DO和Sanitizer的私钥不需要由KGC进行托管.

2 本文方案

方案由6个算法组成, 包括系统初始化算法, 密钥生成算法, 签名生成算法, 净化算法, 验证算法和访问算法.

2.1 系统初始化算法

该算法由KGC执行, 输入安全参数 $k$ , KGC执行如下过程生成系统参数 $params$ 和主密钥 ${\textit{msk}}$ .

(1) KGC选择阶数同为 $q$ 的一个加法循环群 ${\mathbb{G}_1}$ 以及一个乘法循环群 ${\mathbb{G}_2}$ , 其中 $q$ 为一个大素数. 令 $P$ 为 ${\mathbb{G}_1}$ 的生成元. 然后选择双线性映射 $e:{\mathbb{G}_1} \times {\mathbb{G}_1} \to {\mathbb{G}_2}$ .

(2) KGC选择 $\lambda \in \mathbb{Z}_q^*$ 作为主密钥, 即 ${\textit{msk}} = \lambda$ . 并计算系统公钥 ${P_{{\rm{pub}}}} = \lambda \cdot P$ .

(3) KGC选择3个安全的哈希函数 ${H_1}:{\{ 0, 1\} ^*} \to \mathbb{Z}_q^*$ 、 ${H_2}:{\{ 0, 1\} ^*} \to \mathbb{Z}_q^*$ 、 ${H_3}:{\{ 0, 1\} ^*} \to {\mathbb{G}_1}$ .

KGC保存主密钥 ${\textit{msk}} = \lambda$ , 公开系统参数 $params = \{ q, {\mathbb{G}_1}, {\mathbb{G}_2}, e, P, {H_1}, {H_2}, {H_3}, {P_{{\rm{pub}}}}\}$ .

2.2 密钥生成算法

该算法由KGC, DO和Sanitizer执行. 输入主密钥 ${\textit{msk}} = \lambda$ , 系统参数 $params$ , KGC、DO和Sanitizer执行如下过程.

(1) 当接收到DO的身份 $I{D_o}$ 后, KGC随机选择 ${y_o} \in \mathbb{Z}_q^*$ , 并计算 ${Y_o} = {y_o} \cdot P$ , ${h_o} = {H_1}(I{D_o}||{Y_o})$ , ${d_o} = {y_o} + {h_o} \cdot \lambda $ . KGC将 $({Y_o}, {d_o})$ 作为DO的部分密钥, 并通过安全信道发送给DO.

(2) 当接收到Sanitizer的身份 $I{D_s}$ 后, KGC随机选择 ${y_s} \in \mathbb{Z}_q^*$ , 并计算 ${Y_s} = {y_s} \cdot P$ , ${h_s} = {H_1}(I{D_s}||{Y_s})$ , ${d_s} = {y_s} + {h_s} \cdot \lambda $ . KGC将 $({Y_s}, {d_s})$ 作为Sanitizer的部分密钥, 并通过安全信道发送给Sanitizer.

(3) DO随机选择 ${x_o} \in \mathbb{Z}_q^*$ 作为自己的秘密值, 并计算 ${X_o} = {x_o} \cdot P$ . 然后DO设置私钥为 $s{k_o} = ({d_o}, {x_o})$ , 相应的公钥为 $p{k_o} = ({Y_o}, {X_o})$ .

(4) Sanitizer随机选择 ${x_s} \in \mathbb{Z}_q^*$ 作为自己的秘密值, 并计算 ${X_s} = {x_s} \cdot P$ . 然后Sanitizer设置私钥为 $s{k_s} = ({d_s}, {x_s})$ , 相应的公钥为 $p{k_s} = ({Y_s}, {X_s})$ .

2.3 签名生成算法

该算法由DO执行, 输入DO的原始数据 $M$ 、私钥 $s{k_o} = ({d_o}, {x_o})$ , DO执行如下过程为原始数据生成相应签名.

(1) DO将原始数据 $M$ 分为 $n$ 个数据块, 即 $M = \{ {m_1}, {m_2}, \cdots, {m_n}\} $ , 其中 ${m_i} \in \mathbb{Z}_q^*$ , $i \in [1, n]$ . 并选择 $name \in \mathbb{Z}_q^*$ 作为 $M$ 的标识符. 假设数据 $M$ 中需要净化的敏感信息数据块的集合为 $K$ , 即 $K \subseteq [1, n]$ .

(2) 对于原始数据 $M$ 中每个数据块 ${m_i} \in \mathbb{Z}_q^* \; (i \in [1, n])$ , DO随机选择 ${r_i} \in \mathbb{Z}_q^*$ , 并计算 ${R_i} = {r_i} \cdot P$ , $\alpha = {H_2}(I{D_o}||{X_o}||{Y_o})$ , ${\nu _i} = {H_3}(name||{R_i})$ .

(3) DO为不需要净化的数据块计算签名 $ {\sigma }_{i}={d}_{o}\cdot {\nu }_{i}+ {x}_{o}\cdot {m}_{i}\cdot \alpha \cdot {R}_{i} \; (i\in [1, n]且i\notin K) $ .

(4) DO为需要净化的敏感信息数据块计算签名 ${\sigma _i} = {d_o} \cdot {\nu _i} + {x_o} \cdot {m_i} \cdot \alpha \cdot {r_i} \cdot {X_s} \; (i \in K)$ , 并计算转换值 $\;{\beta _i} = {x_o} \cdot {R_i} \; (i \in K)$ . 一般而言, 一份数据中敏感信息的数量并不多, 因此, DO只需要为某几个需要净化的数据块单独计算签名即可.

(5) DO将 $(M, K, {\{ {\sigma _i}\} _{i \in [1, n]}}, {\{ {R_i}\} _{i \in [1, n]}}, {\{ {\beta _i}\} _{i \in K}})$ 发送给Sanitizer, 并在本地删除这些信息.

2.4 净化算法

该算法由Sanitizer执行. 当接收到DO发送信息后, Sanitizer执行如下过程对数据 $M$ 中的敏感信息数据块执行净化.

(1) Sanitizer首先对集合 $K$ 中的数据块执行净化, 通常, Sanitizer使用通配符替换敏感信息所对应的数据块, 生成净化后的数据 $M' = \{ {m'_1}, {m'_2}, \cdots, {m'_n}\} $ . 其中当且仅当 $i \in [1, n]$ 且 $i \notin K$ 时 ${m_i} = {m'_i}$ , 否则 ${m_i} \ne {m'_i}$ .

(2) Sanitizer通过如下方式将集合 $K$ 中的数据块所对应的签名转换为经过净化后的数据块的有效签名:

$ \begin{split} {{\sigma '_i }}&=\left\{ {\begin{array}{l}{\sigma }_{i}-{m}_{i}\cdot \alpha \cdot {x}_{s}\cdot {\beta }_{i}+{{m'_i}}\cdot \alpha \cdot {\beta }_{i}, \; i\in K \\ {\sigma }_{i}, \; i\in [1, n]且i\notin K\end{array}} \right.\\ &={d}_{o}\cdot {\nu }_{i}+{x}_{o}\cdot {{m'_i}}\cdot \alpha \cdot {R}_{i}\end{split} $

(1)

(3) Sanitizer将 $(M', {\{ {\sigma '_i}\} _{i \in [1, n]}}, {\{ {R_i}\} _{i \in [1, n]}})$ 发送到CS进行存储和维护, 并在本地删除这些信息.

2.5 验证算法

当接收到Sanitizer发送的数据和相应签名后, CS执行如下过程进行验证.

(1) CS计算 ${h_o} = {H_1}(I{D_o}||{Y_o})$ , $\alpha = {H_2}(I{D_o}||{X_o}||{Y_o})$ , ${\nu _i} = {H_3}(name||{R_i})$ , $\sigma = \displaystyle\sum\limits_{i = 1}^n {{\sigma '_i}}$ , $\mu = \displaystyle\sum\limits_{i = 1}^n {{m'_i} \cdot {R_i}}$ .

(2) CS通过式(2)是否成立来判断接收到的数据和签名是否正确:

$ e(\sigma , P) = e\left(\sum\limits_{i = 1}^n {{\nu _i}} , {Y_o} + {h_o} \cdot {P_{{\rm{pub}}}}\right) \cdot e(\alpha \cdot \mu , {X_o}) $

(2)

如果式(2)成立, CS存储数据和相应签名; 否则, CS拒绝存储数据和相应签名.

2.6 访问算法

该算法由User、Sanitizer和CS执行, 具体过程如下.

(1) User利用其身份 $I{D_u}$ 和DO数据的标识符 $name$ 生成访问请求 $\omega = {H_3}(I{D_u}||name)$ , 并将 $\omega $ 发送给Sanitizer.

(2) Sanitizer接收到访问请求 $\omega $ 后, 计算 ${\delta _\omega } = {d_s} \cdot \omega $ , 为User生成访问授权 $(\omega , {\delta _\omega })$ , 并将 $(\omega , {\delta _\omega })$ 发送给CS.

(3) CS接收到访问授权 $(\omega , {\delta _\omega })$ 后, 计算 ${h_s} = {H_1}(I{D_s}|| {Y_s})$ , 然后CS通过式(3)验证授权的正确性:

$ e({\delta _\omega }, P) = e(\omega , {Y_s} + {h_s} \cdot {P_{{\rm{pub}}}}) $

(3)

如果式(3)成立, CS将净化后的数据 $M'$ 发送给User.

3 安全分析与性能评价 3.1 安全需求分析

本节对第1.4节中的安全需求进行分析.

(1) 正确性: CS根据式(2)是否成立来判断接收到的数据和签名是否正确; 此外, CS根据式(3)是否成立来判断接收到的访问授权是否正确.

式(2)的正确性:

$ \begin{split} e\left(\sigma , P\right) &= e\left(\sum\limits_{i = 1}^n {{{\sigma '}_i}} , P\right) \\ & = e\left(\sum\limits_{i = 1}^n {\left({d_o} \cdot {\nu _i} + {x_o} \cdot {m'_i} \cdot \alpha \cdot {R_i}\right)} , P\right) \\ & = e\left(\sum\limits_{i = 1}^n {{d_o} \cdot {\nu _i}} , P\right) \cdot e\left(\sum\limits_{i = 1}^n {{x_o} \cdot {m'_i} \cdot \alpha \cdot {R_i}} , P\right) \\ & = e\left(\sum\limits_{i = 1}^n {{\nu _i}} , {d_o} \cdot P\right) \cdot e\left(\alpha \cdot \sum\limits_{i = 1}^n {{m'_i} \cdot {R_i}} , {x_o} \cdot P\right) \\ & = e\left(\sum\limits_{i = 1}^n {{\nu _i}} , \left({y_o} + {h_o} \cdot \lambda \right) \cdot P\right) \cdot e\left(\alpha \cdot \mu , {X_o}\right) \\ & = e\left(\sum\limits_{i = 1}^n {{\nu _i}} , {Y_o} + {h_o} \cdot {P_{{\rm{pub}}}}\right) \cdot e\left(\alpha \cdot \mu , {X_o}\right) \\ \end{split} $

式(3)的正确性:

$ \begin{split} e({\delta _\omega }, P) &= e({d_s} \cdot \omega , P) = e(\omega , {d_s} \cdot P) \\ & = e(\omega , ({y_s} + {h_s} \cdot \lambda ) \cdot P) \\ & = e(\omega , {Y_s} + {h_s} \cdot {P_{{\rm{pub}}}}) \end{split} $

(2) 指定Sanitizer: 在本方案中, 需要净化的数据块的签名为 ${\sigma _i} = {d_o} \cdot {\nu _i} + {x_o} \cdot {m_i} \cdot \alpha \cdot {r_i} \cdot {X_s} \; (i \in K)$ , 其中 ${X_s}$ 表示Sanitizer的公钥. 根据Diffie-Hellman协议, 只有使用Sanitizer的私钥 ${x_s}$ 才能执行净化. 因此, 在本方案只有Sanitizer才能执行净化, 其他任何敌手无法执行净化, 本文方案满足指定Sanitizer的安全需求.

(3) 不变性: 在本方案中, 不允许净化的数据块的签名为 $ {\sigma }_{i}={d}_{o}\cdot {\nu }_{i}+{x}_{o}\cdot {m}_{i}\cdot \alpha \cdot {R}_{i} \; (i\in [1, n]且i\notin K) $ . 如果Sanitizer想要净化这一部分数据块, 就需要DO的私钥 ${x_o}$ , 而 ${x_o}$ 存在于 ${X_o} = {x_o} \cdot P$ , 这可以被看作是DL问题. 根据DL问题, Sanitizer无法获得 ${x_o}$ . 因此, Sanitizer无法对这部分数据块执行净化, 本文方案满足不变性.

(4) 隐私性: Sanitizer会使用通配符替换敏感信息对应的数据块, 因此, CS和User不能获得DO的敏感信息, 本文方案满足隐私性.

(5) 访问控制: Sanitizer使用自己的私钥为User生成访问授权, 因此, 只有User才能访问云服务器中的数据.

(6) 消除密钥托管: 由于无证书密码学固有的结构优势. 在本文方案中DO和Sanitizer的私钥不需要由KGC进行托管.

3.2 功能比较

本节将所提方案和文献[17, 18]进行功能对比. 在比较过程中只考虑文献[17, 18]中和可净化签名相关的部分. 功能比较如表1所示, 其中 $ {\text{F1}} $ 表示正确性; $ {\text{F2}} $ 表示指定Sanitizer; $ {\text{F3}} $ 表示不变性; $ {\text{F4}} $ 表示隐私性; $ {\text{F5}} $ 表示访问控制; $ {\text{F6}} $ 表示消除密钥托管. 从表1中可以看出, 文献[17]不满足指定Sanitizer和访问控制, 并且文献[17, 18]都不满足不变性. 此外, 文献[17, 18]是基于身份下的可净化签名, 故都存在密钥托管的缺陷. 因此, 只有本文方案满足第1.4节中的所有安全需求.

3.3 计算代价比较

为了确保公平比较, 应采用相同的80 bit安全性. 由于文献[17, 18]和本文方案都使用了双线性映射, 故选择双线性映射 $e:{\mathbb{G}_1} \times {\mathbb{G}_1} \to {\mathbb{G}_2}$ , 群 ${\mathbb{G}_1}$ 的阶数为 $q$ , $q$ 是512 bit的素数. 基于MIRACL Crypto SDK^[20]得到密码学操作的执行时间并列举在表2中, 其硬件设备为2.90 GHz i5 CPU和16 GB内存的台式电脑, 操作系统是 ${\text{64}}$ 位 ${\text{Windows 10}}$ . 表3给出了文献[17, 18]和所提方案的计算代价比较, 其中 $n$ 代表数据块的数量, $K$ 代表需要净化的数据块的数量.

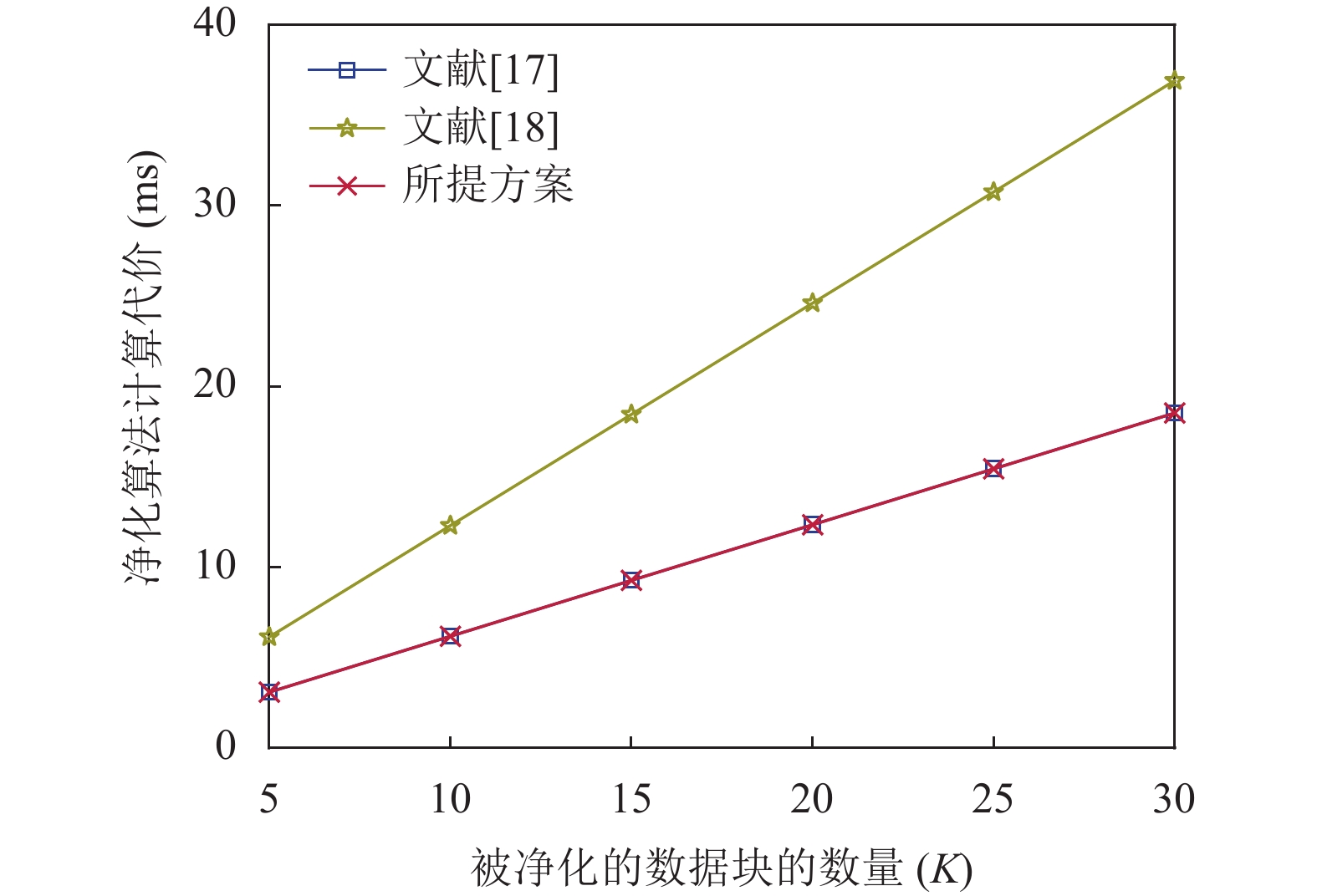
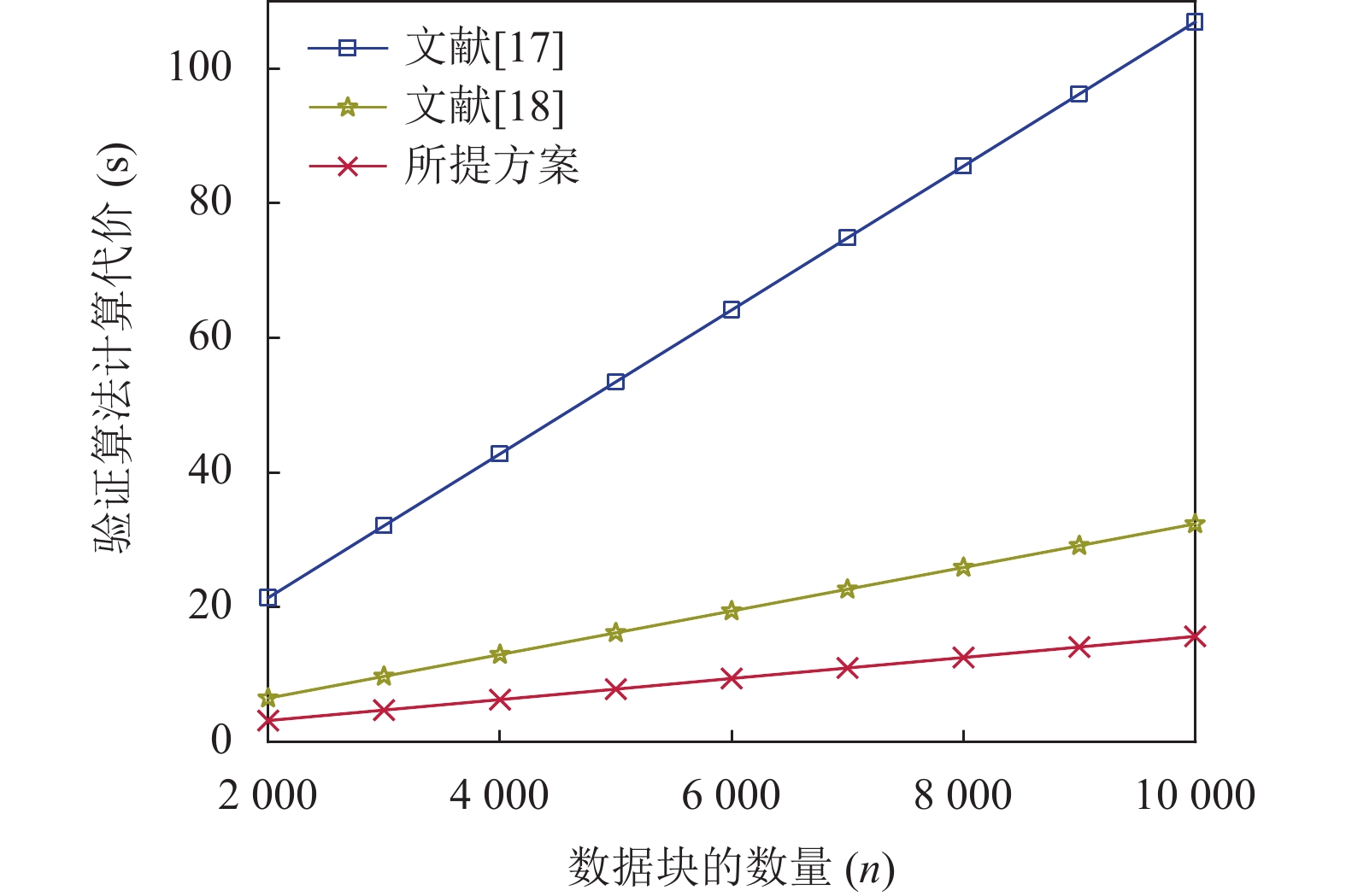
图2–图4分别表示签名生成算法, 净化算法和验证算法的计算代价比较. 由图2和图3可以看出, 所提方案在签名生成算法和净化算法中的计算代价优于文献[18], 而与文献[17]基本相同. 虽然所提方案的计算代价与文献[17]基本相同, 但是文献[17]的功能性较差, 它不满足指定Sanitizer、不变性、访问控制以及消除密钥托管, 而所提方案满足所有的安全需求. 因此, 整体而言, 所提方案优于文献[17]. 由图4可知, 在验证算法中, 随着数据块数量的增加, 所提方案的计算代价明显优于文献[17, 18]. 更进一步, 根据总体的计算代价而言, 所提方案优于文献[17, 18]. 综上所述, 所提方案更加适用于解决云存储环境中共享数据的可认证性与敏感信息隐藏.

3.4 通信代价比较

为了更实际的比较通信代价, 本文设定如下: ${\text{|}}{\mathbb{G}_{\text{1}}}{\text{|}}$ , ${\text{|}}\mathbb{Z}_q^*{\text{|}}$ 分别为512 bit和160 bit. 表4比较了文献[17, 18]与所提方案的通信代价. 在通信代价的比较中, 我们主要对每个方案的主密钥长度, 签名长度, 净化签名长度以及访问授权长度进行比较.

由表4可以看出, 首先所提方案的主密钥长度少于文献[17], 而与文献[18]相同. 其次, 所提方案与文献[17, 18]具有相同的签名长度和净化签名长度. 最后, 文献[18]的访问授权长度少于所提方案. 据此可以看出所提方案的整体通信代价优于文献[17], 但是略高于文献[18]. 由于所提方案在功能和计算代价方面优于文献[18], 故所提方案多出的通信代价是可接受的.

4 结论

为了解决现有可净化签名方案的问题, 本文提出了一个云存储中无证书的可净化签名方案, 能够使得数据所有者在隐藏其敏感信息的情况下, 通过云服务器与其他用户共享数据. 本文方案解决了基于身份可净化签名方案中的密钥托管问题; 并且所提方案加入了访问控制, 使得只有授权用户才能访问云服务器中的数据. 此外, 与现有方案相比, 本文方案能够满足所提的所有安全需求; 并且本文所提方案的计算代价优于现有方案. 因此, 本文所提方案更加适用于解决云存储中共享数据的可认证性与敏感信息隐藏问题.