计算机系统应用  2023, Vol. 32 Issue (1): 214-223   PDF    
引用本文
祝一帆, 安云哲, 夏秀峰. 数据流环境下基于距离的离群点检测算法. 计算机系统应用, 2023, 32(1): 214-223.http://www.c-s-a.org.cn/1003-3254/8879.html   
Zhu YF, An YZ, Xia XF. Distance-based Outlier Detection Algorithm in Data Streams. Computer Systems and Applications, 2023, 32(1): 214-223(in Chinese).http://www.c-s-a.org.cn/1003-3254/8879.html   
数据流环境下基于距离的离群点检测算法
祝一帆, 安云哲, 夏秀峰     
沈阳航空航天大学 计算机学院, 沈阳 110136
收稿日期：2022-04-28; 修改日期：2022-06-01; 采用时间：2022-06-13; csa 在线出版时间：2022-11-18
基金项目：国家自然科学基金(61702344)
通讯作者：祝一帆, E-mail: sorrysorrysjhg@126.com.
摘要：面向滑动窗口的连续离群点检测问题是数据流管理领域中的重要问题. 该问题在信用卡欺诈检测、网络入侵防御, 地质灾害预警等诸多领域发挥着重要作用. 现有算法大多需要利用范围查询判断对象之间的位置关系, 而范围查询的查询代价大, 无法满足实时性要求. 本文提出基于滑动窗口模型下的查询处理框架GBEH (grid-based excepted heap). 首先, 它以网格为基础构建索引GQBI (grid queue based index)管理数据流. 该索引一方面维护数据流之间的位置关系, 另一方面利用队列维护数据流的时序关系. 其次, GBEH提出离群点检测算法PBH (priority based heap). 该算法利用查询范围与网格单元格的相交面积计算该单元格中包含于查询范围对象数目的数学期望, 并以此为基础构建基于小顶堆执行范围查询, 从而有效降低范围查询代价, 实现高效检测. 理论分析和实验验证GBEH的高效性和稳定性.
关键词: 数据流    离群点    基于距离    对象维护    
Distance-based Outlier Detection Algorithm in Data Streams
ZHU Yi-Fan, AN Yun-Zhe, XIA Xiu-Feng     
College of Computer Science, Shenyang Aerospace University, Shenyang 110136, China
Abstract: The detection of continuous outliers for sliding windows is an important problem in data stream management, which plays an important role in many fields such as credit card fraud detection, network intrusion prevention, and early warning for geological hazards. Most of the existing algorithms require the use of the range query to determine the positional relationship between objects, but the cost of the range query is usually high, which cannot meet real-time requirements. Therefore, this study proposes the grid-based excepted heap (GBEH), a query processing framework based on sliding windows. Specifically, GBEH proposes a grid queue based index (GQBI) on the basis of the grid to manage data streams, which maintains the positional relationship between data streams and the temporal relationship of data streams. Furthermore, GBEH proposes an outlier detection algorithm, namely, the priority based heap. This algorithm calculates the mathematical expectation of the number of objects in the cell that is included in the query range by use of the intersection area of the query range and the cell and on this basis, establishes an execution range query based on the min-heap. In this way, it effectively reduces the cost of range queries and achieves efficient detection. Theoretical analysis and experiments verify the efficiency and stability of GBEH.
Key words: data stream     outlier     distance-based     objects maintenance    

基于滑动窗口的离群点检测问题是数据流[1]管理中的一类重要问题, 在欺诈检测、计算机网络安全、股票投资战术规划、医疗和公共卫生异常检测等方面都发挥着重要作用. 例如: 当在股票市场寻求短期投资机会时, 投资者可能会寻找与大多数同类股票行为显著不同的异常股票. 这种不正常的股票通常是市场中的热点或被遗忘的宝藏. 这两者都可能对应潜在的优秀投资机会. 更具体地说, 如图1所示给定两个股票s1和s2, 投资者可以定义一个距离函数来测量它们的差异, 例如:考虑股票价格变化百分比和它们的公司利润变化百分比. 若两只股票具有的相似公司利润表现, 但价格变化百分比差异为200%, 则它们将具有差异分数d(s1, s2) = |(s1.price_gain% – s2.price_gain%) – (s1.profit_gain% – s2.profit_gain%)| = 2. 对于此应用, 如果投资者确信2是一个很好的阈值, 表明两个股票的行为差异足够大. 他可以将邻居搜索的距离阈值R设为2, 从而找到其想要的异常股票. 根据Hawkins[2]的描述, “离群点是一个与其他观察值偏差太大的观察值, 以致引起人们怀疑它是由不同的机制产生的”. 许多学者针对离群点检测问题展开研究, 并提出了多种度量数据是否“离群”的定义. 本文针对基于距离的离群点检测问题展开研究, 它是数据流环境下最常见的一种定义.

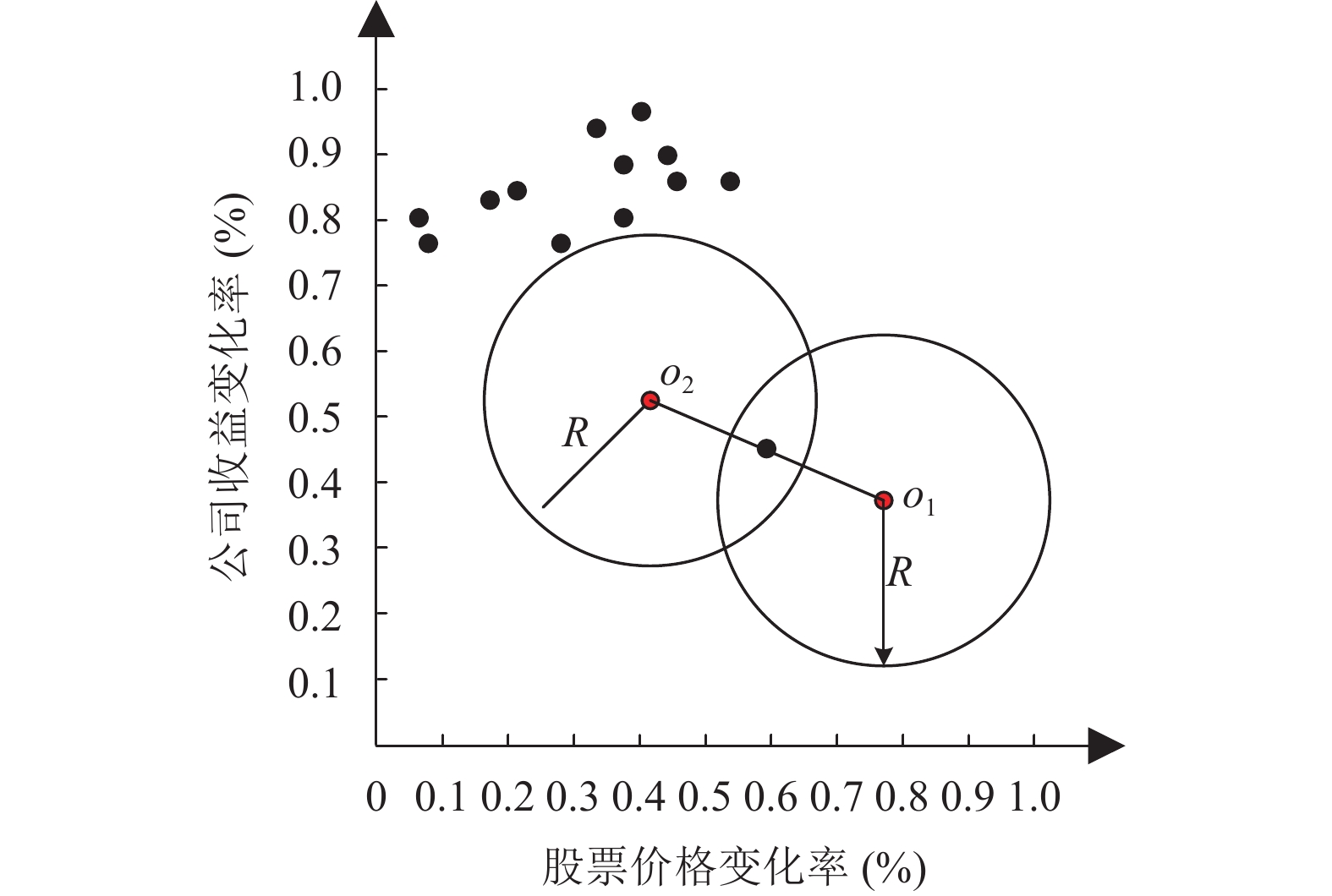
图 1 基于距离的离群点类型

文献[3]首次研究了静态数据集下基于距离阈值的离群点检测问题, 该文献定义如果在给定数据集中, 若与数据对象o间距离不大于R的对象少于k个, 那么对象o就被认定为离群点. 随后, 文献[4-6]提出了几种基于距离离群点的变体定义. 如图1所示, 当k=2时, 基于距离阈值的离群点为o1、o2, 它们在R范围内的邻居个数均为1.

本文研究滑动窗口模型下基于距离阈值的离群点连续检测问题. 滑动窗口模型存在两种定义形式: 基于对象个数的窗口和基于时间的窗口. 为了叙述方便, 本文只考虑前者. 给定窗口W<N, s>,N表示窗口中的对象个数, s表示窗口滑动时流入/流出窗口的对象个数.

目前, 文献[3, 4,7, 8]已经广泛研究了面向静态数据的基于距离的离群点检测问题. 近几年来, 诸多研究[9-18]关注于数据流环境下的离群点检测问题. 文献[13]研究分布式环境下的离群点检测问题. 文献[14]研究高维数据集中的离群点检测. 具体而言, 文献[9]针对基于计数滑动窗口模型的 ${{O}}_{\text{thres}}^{\left({k, R}\right)}$ 检测问题提出了对应的解决方案. 文献[10]则提出了两种解决方案: 第1种对文献[9]所提方案进行了改进, 使其可以支持基于时间滑动窗口模型的基于距离离群点检测. 第2种则提出了全新的微集群思路. 以上3种解决方案都利用了滑动窗口间的对象重叠特性, 从而避免了每个窗口上的重复计算所带来的巨大开销. 第3种解决方案则利用集群的思想进行有效剪枝, 降低每个数据对象邻居搜索时的成对距离计算代价. 文献[11]提出适用于基于距离阈值和其变形的检测框架, 该框架利用数据流间的时间关系, 减少重复查询次数. 文献[16]针对高维密集连续的数据流, 提出可扩展的分布式离群点检测框架. 文献[18]基于对偶性将相似数据点由相似查询以增量方式进行统一处理, 有效应对多重动态性挑战.

然而, 上述解决方案存在以下不足: (1)未将资源集中利用在少数离群点候选者的维护上, 而是将其用于大多数对象的邻居计算和记录方面; (2)未利用数据流点之间的时间关系, 即在未来的窗口中谁能够更长时间地存在. 这导致现有算法时间复杂度高, 无法满足用户实时性的需求.

在现有研究的基础上, 本文提出查询处理框架GBEH (grid-based excepted heap). 它根据查询参数构建网格, 统计各单元格内的对象数目, 利用对象间的时序关系降低候选离群点的维护代价.

本文的主要贡献如下:

(1) 提出索引GQBI (grid queue based index)管理数据流. 它根据查询参数R设置网格的划分粒度. 理论分析可知, 当单元格的长度被设置为2R时, 算法可通过访问2d个单元格确定其是否为离群点. 显然, 当数据维度为常数时, 算法可在较低复杂度下实现离群点检测. 另一方面, GQBI利用网格管理数据流, 实现数据流的高效维护.

(2) 提出基于小顶堆的离群点查询算法. 给定新流入窗口的数据流o, PBH (priority based heap)提交以o为圆心, R为半径的范围查询判断o是否为离群点. 为加快查询处理速度, PBH根据查询范围, 各单元格相交的面积和单元格包含的对象数目设置单元格的优先级, 根据优先级建立小顶堆加快查询处理速度并获取对象可能成为离群点的最晚时间.

(3) 设计了详细的性能评价实验. 基于3个真实数据集的实验结果表明, 本文提出的GBEH查询处理框架可高效处理数据流上基于距离的离群点检测, 且具有较强的稳定性.

本文第1节介绍数据流上基于距离离群点检测的相关定义并回顾相关工作; 第2节详细描述本文检测框架GBEH, 包括GQBI索引、基于索引的离群点检测算法PBH; 第3节给出实验结果和分析.

1 背景知识 1.1 背景知识

根据评价方式不同, 基于距离的离群点可被定义为以下3种形式: ${{O}}_{\text{thres}}^{\left({k, }{r}\right)}$ 离群点, ${{O}}_{{k}\text{max}}^{\left({k, n}\right)}$ 离群点和 ${{O}}_{{k}\text{avg}}^{\left({k, n}\right)}$ 离群点. 它们分别表示基于阈值的离群点, 基于k近邻的离群点和基于k平均距离的离群点. 如文献[19]所述, 基于阈值的离群点计算代价较小, 更适合在流环境下使用. 因此, 本文基于该定义展开研究. 具体地, 给定参数k和r, 若数据集合D中与o距离不小于r的对象个数少于k, 则称o为D中的离群点. 为方便描述, 给定D{o1, o2, …, on}中任意对象oi, 如果Dist(o, oi) ≤ r, 那么oi被称为对象o的邻居. 换句话说, 如果对象o的邻居个数不小于k, 则称o为非离群点. 反之, 则称o为离群点. 接下来, 本节正式介绍问题定义.

问题定义. 数据流环境下基于距离的离群点检测.给定基于距离的离群点检测查询q(W, S, k, R), q监听窗口中的数据, 当窗口滑动时返回W中的离群点.

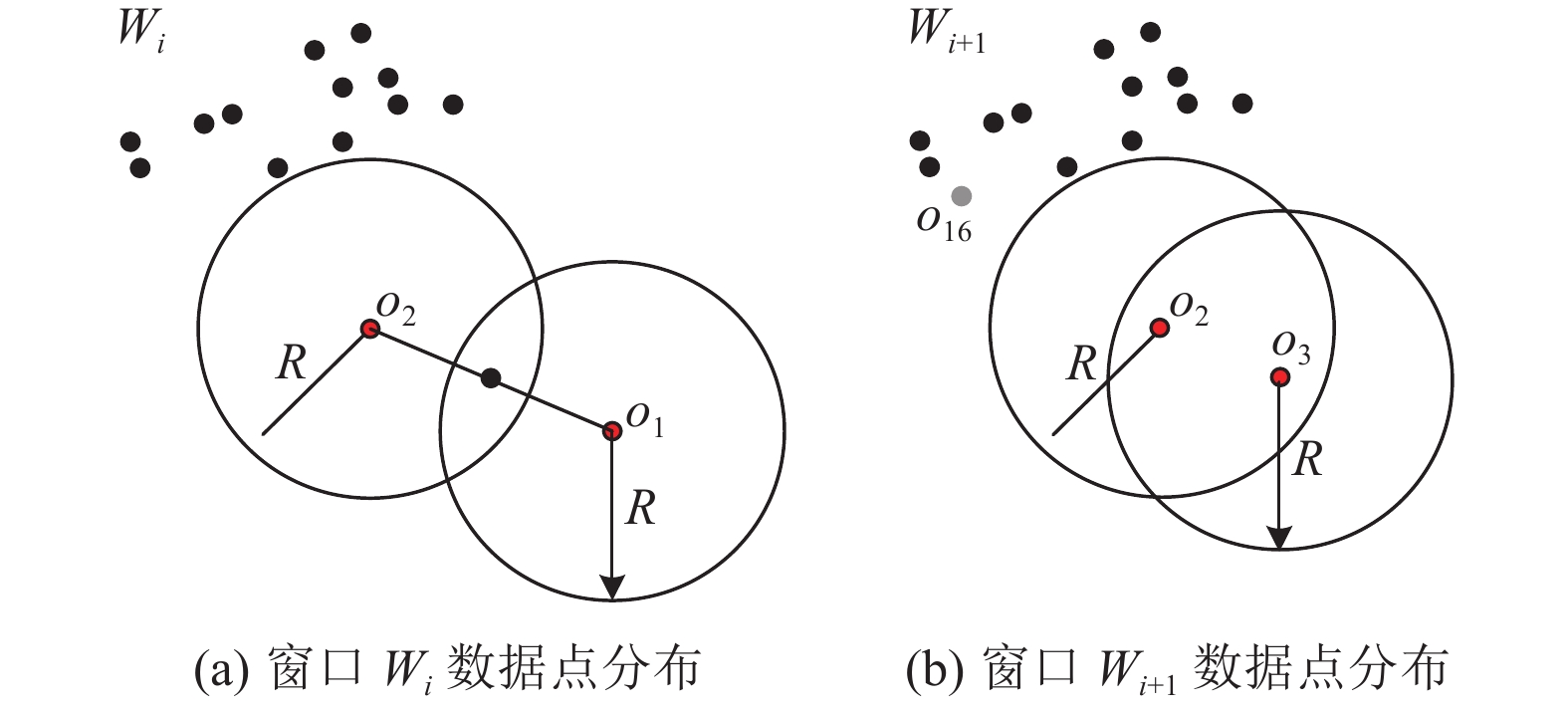
如图2(a)–图2(b)所示, 当k=2, s=1时, 窗口Wi中基于距离的离群点为o1和o2, 它们的邻居个数为1, 小于2. 当窗口从Wi滑动到Wi+1后, 窗口Wi+1中离群点变为o2和o3.

1.2 相关工作及问题

鉴于此类问题的重要性, 许多学者研究了基于滑动窗口的离群点连续检测问题. 现有研究成果的核心思想是利用数据流之间的时序关系和位置关系识别数据流中不能成为离群点的对象、潜在离群点和离群点. 这样一来, 算法只需考虑后两类对象便可支持连续离群点检测. 这些算法通常利用范围查询判断对象之间的位置关系, 而范围查询的代价通常对数据流分布、查询参数和窗口长度较为敏感, 当窗口中对象数目多或数据呈倾斜分布时, 查询代价大, 实时性差.

图 2 基于滑动窗口的 ${{O}}_{\text{thres}}^{\left({k, R}\right)}$ 离群点

在介绍相关算法之前, 本节首先介绍对象前/后邻居的概念. 给定滑动窗口中对象o和它的邻居o', 如果T(o)>T(o'), 则称o'是o的前邻居. 反之, 如果T(o)<T(o') , 则称o'是o的后邻居.显然, 如果o的后邻居个数超过k, 那么o在它流出窗口前不会称为离群点. 在这种情况下, 本文称之为安全对象.

在以往研究中, 代表性算法包括STROM[20]、MCOD[10]以及Thresh_LEAP[11]等. STROM为每个对象o分配最小邻居队列o<p, l>. 其中,o.p是一个列表, 它维护o的k'(k'<k)个前邻居, o.l记录o的后邻居个数. 当有数据oin流入窗口时, exact-Strom查找距离oin小于r的对象. 假设R(oin)为查询结果集. 算法将R(oin)中流入时间最晚的k个对象加入oin.p. 与此同时, 对于R(oin)中的每个对象o, 算法将o.p 增加到o.p+1, 将o.l中最先流入窗口的数据从o.l中移除. 显然, 当o.p增加到k时, o在其生命周期内都不会成为离群点. 然而, 该算法不仅要针对每个对象执行范围查询, 而且要为每个对象消耗O(k)的空间代价维护前邻居列表. 针对此问题, MCOD算法被提出. 它利用微集群的思想, 将窗口中对象尽可能地划分到一组半径为r/2的球{b1, b2, …, bm}内. 这样一来, 对于任意球bi, 由于其内部对象互为邻居, 如果bi内对象个数不少于k, 则bi中对象均为非离群点. 然而, 该算法对数据分布和维度较为敏感. 当维度较高或数据分布呈均匀分布时, 只有少量球中对象多余k. 在这种情况下, 算法仍然需要划分较高的代价维护非安全对象的前邻居信息. 与MCOD 相比, Thresh_LEAP算法利用高速流的特性降低前邻居的维护代价. 但是, 该算法对流速s较为敏感. 当流速较低时, 该算法仍然需要消耗较高的空间代价. Cao等提出了适用于基于距离和KNN离群点检测的LEAP框架[11]. 此框架以候选离群点与其第k个邻居的最小距离为阈值, 以滑片为单位, 按照滑动到达时间逆序搜索对象的临时k近邻. 该方法虽在一定程度上减轻了重复计算的代价, 但范围查询代价仍旧高, 且内存效率受输入参数s/N影响.

总之, 现在算法对数据规模、数据分布和查询参数较为敏感, 无法保证在流环境下高效工作. 鉴于此, 本文提出查询处理框架GBEH解决这一问题.

2 离群点检测框架GBEH

本节提出框架GBEH支持数据流环境下基于距离阈值的离群点检测. 本节首先提出GQBI索引管理数据流, 随后提出算法PBH实现离群点检测.

2.1 框架GBEH概述

给定滑动窗口W<N, k>和离群点检测请求q<r, k>, 算法首先构建索引维护窗口中的数据流. 随后, 算法针对每一个对象o执行范围查询. 如果o有k个后邻居, 则将其标记为安全对象. 如果o有少于k个邻居, 则将其标记为离群点. 否则, 将o标记为非安全对象, 并构建关于o的最小邻居队列. 当窗口滑动时, 算法依次扫描窗口中的元素, 针对每一个对象o'执行半径为r的范围查询, 为其构建最小邻居队列.与此同时, 对于窗口中的非安全对象o'', 如果它跟o的距离小于r, 则更新关于o''的最小邻居队列. 当o''的最小邻居队列为空时, 算法将其标记为安全对象.

为实现数据流的高效维护, 本文首先提出索引GQBI. 它是以网格为基础提出的索引. 与树形结构相比, 由于不用更新其拓扑结构, 基于网格的索引更适合在数据流下工作. 与此同时, GQBI维护了数据流之间的时序关系, 这为实现安全对象、非安全对象的高效维护奠定了基础.

为了实现最小邻居队列的高效构建, 本文进一步提出算法PBH. 其核心思想是利用网格单元格中数据的分布筛选优先访问的单元格, 从而达到通过访问少量对象构建最小邻居队列的目的. 在接下来的内容中, 本节首先介绍索引GQBI, 随后介绍算法PBH.

2.2 索引GQBI

如图3所示, 它是一个两层索引结构. 给定GQBI I, 索引的第1层为网格, 用于管理数据流的位置信息. 索引的第2层为队列, 管理数据的时序关系. 给定单元格c, GQBI为各单元格分配元组c<n, q>维护c中对象. 在这里, c.n表示单元格c中包含的对象数目, c.q表示用于维护c中对象的队列.

图 3 索引GQBI

为了提高离群点检测效率, GQBI根据参数r设置单元格的划分粒度. 在这里, 如果单元格的面积较大, 则导致每个单元格包含对象数目较多, 产生高昂的单元格访问代价. 反之, 则导致算法需访问大量单元格. 本文将单元格的长度设置为2r. 分析可知, 给定任意位置的范围查询, 查询区域最多与2d个单元格相交. 这样一来, GQBI一方面保证了单元格的面积不至于过大而导致高昂的对象访问代价, 另一方面保证了算法需访问的单元格数目不至于过多.

算法1. GQBI维护算法

输入: 数据集O, 流入窗口的s个对象集合sm, 流出窗口的s个对象集合s0

1. foreach oi∈sm do

2. 　 c = calPosition(oi);

3.　 c.insertObject(oi);

4.　 add oi to c.q;

5.　 ++c.n;

6. 　 end for

7. 　 for each oj∈s0 do

8. 　 c'.deleteObject(oj);

9.　　 delete oj to c'.q;

10.　　 – –c'.n;

11. end for

算法1给出了GQBI框架的伪代码. 给定当前窗口W0{s0, s1, …, sm–1}和与之对应的GQBI I, 当窗口滑动时, sm中对象流入窗口, 对象s0流出窗口. 算法首先将s0中对象从I中删除. 接下来, 算法将sm中对象根据其坐标插入I. 假设sm中对象o被插入单元格c, 算法将o插入到c对应的队列c.q中, 最后将c.n设置为c.n+1 (第5行). 对于流出窗口的对象o', 算法首先将其从相应的单元格c'中删除, 随后将其从队列c'.q中删除. 最后, 算法将c'.n设置为c'.n–1. 和传统索引相比, GQBI具备以下优势: 1)和传统的树形结构相比, GQBI无需调整索引的平衡. 这导致对象的插入代价为O(1). 2) 索引利用查询参数设置单元格的大小. 这一方面保证了单元格内不会因划分粒度过小而导致对象数目过多. 另一方面, 不会因划分粒度过大而导致算法需访问单元格数目较多.

2.3 PBH算法

为提高离群点检测算法的计算效率, 本节提出算法PBH. 它的核心思想是利用查询区域与单元格的相交面积计算该单元格包含于查询区域对象数目的数学期望, 从而降低范围查询所需访问的对象数目.

如图4所示, 给定新流入窗口的对象o, 算法以o的位置为圆心, r为半径执行范围查询. 假设查询范围为q.r, 与之相交的单元格为c1, c2, c3, c4. c1包含了10个对象, c2包含了12个对象, c3, c4分别包含2了个对象. c1与查询区域相交的面积为0.5|c|, c2与查询区域相交的面积为0.1|c|, c3与查询区域相交的面积为0.4|c|, c4与查询范围相交的面积为0.2|c|, 那么包含于q.c的对象的数学期望分别为5, 1.2, 0.8, 0.4. 因此, c1能为对象o贡献邻居的数学期望大于其他单元格. 假设各单元格中数据的到达时间符合均匀分布, 那么{c1,c2,c3,c4}中最晚到达的对象存在于c1的概率最大. 因此, 算法应首先访问c1中队列的队首元素. 基于上述观察, 本节提出基于小顶堆的邻居查询算法, 判断对象是否为离群点.

具体地, 算法以各单元格中包含于查询范围的对象的数学期望为键值建立小顶堆. 随后, 算法访问堆顶单元格所对应的队列队首元素. 假设它包含于查询范围, 则将其插入对象的邻居集合. 随后调整键值. 在这里, 假设单元格中包含的对象数目为u, 算法将新的键值更新为(u–1)|s|. 其中, |s|表示单元格和查询范围相交的面积. 最后, 算法根据更新结果更新小顶堆. 当o的邻居达到k或者小顶堆为空集时算法终止. 同时, 根据邻居的到达时间将其分为对象o的前邻居和后邻居, 记录后邻居个数o.scnt和前邻居列表o.preNei, 当o的前邻居过期时重新执行邻居查询.

算法2. PBH算法

输入: 数据集O, 新流入窗口对象o, 查询半径R和邻居阈值个数k

输出: 对象o的离群点检测结果isOutlier

1. 初始化: bool isOutlier ← true

2. for each ci≠Ø do

3.　 o.calAreas(ci);

4. o.minHeap = o.bulidMinHeap;

5. while (o.neiborNum < k && o.minHeap != null) then

6.　 c = o.minHeap.top();

7.　 oi = c.q.top();

8.　 if (dist(o, oi) ≤ R) then

9.　 ++ neiborNum;

10.　 if (oi.arriveTime < o.arriveTime) then

11.　　 add oi to o.preNei

12.　 else

13.　　 ++o.scnt;

14. o.minHeap = o.updateMinHeap;

15. if (o.neiborNum ≥ k) then

16. isOutlier = false;

17. return isOutlier;

算法2给出了PBH算法的伪代码. 给定任意流入窗口的对象o, 算法以o的位置为圆心, R为半径执行范围查询q. 算法利用查询范围与单元格的相交面积计算该单元格中包含于查询范围的对象数目的数学期望(第3行). 随后, 以各单元格中包含于查询范围的对象的数学期望为键值建立小顶堆(第6–14行). 当o的邻居达到k或者小顶堆为空集时算法终止. 此时, 若o的邻居达到k算法返回false, 否则, 返回true (第15–16行).

图 4 范围查询

以图4为例, 给定查询对象o, 其小顶堆的初始状态如图4右侧所示, o与图中部分对象间距离如表1所示. 假设R=3, k=2, PBH算法首先计算o1与对象o之间的距离dist(o, o1)=2.6<3, 将o1插入o的对象集合中, o的邻居个数o.neiborNum更新为1<2, 算法继续; 随后, 更新c1的键值为(10–1)×0.5=4.5, 而c3的键值为12×0.4=4.8, 因此调整c3为堆顶单元格; 此时计算c3队列首元素o2与o之间距离dist(o, o2)=4.2>3,o2非对象o邻居; 之后更新c3键值为(12–1)×0.4=4.4<4.5, 调整c1为堆顶单元格; 此时c1队列首元素为o3, 两者间距离为2.7<3, 将其插入邻居集合, 更新邻居个数为k=2, 算法终止返回false.

表 1 o与部分对象间距离

3 实验分析 3.1 实验准备

本节首先讨论数据集的获取, 接下来讨论参数的设置和实验方法. 本节实验使用以下3个真实数据集: Stock包含1 048 575条具有单一属性的股票交易记录; Tao包含575 648条记录, 每条记录包含3个属性; HPC包含从家庭用电量数据中抓取的具有7个属性的1 289 534条记录.

接下来, 本小节介绍参数的设置和默认值的选取. 本文实验测试4个重要指标. 它们分别是滑动窗口大小N, 滑动对象个数s, 范围阈值R和邻居个数k. N和s决定数据流的容量和流动速度; R决定查询对象与其邻居间的距离范围. 本文将窗口大小N从变化到 $ \text{2}\text{×}{\text{10}}^{{-3}} $ |D|到 $ \text{4}\text{×}{\text{10}}^{{-2}} $ |D|. 其中, |D|表示数据集的大小. s从窗口的 ${\text{10}}^{{-2}}{N}$ 变化到N; k从5变化到100; n从窗口的 ${\text{10}}^{{-3}}{N}$ 变化到 ${\text{3}\text{×}\text{10}}^{{-3}}{N}$ . 表2说明了3个数据集的默认参数设置. 为保证实验的公平性, 所有数据集参数k的默认值设为50.

表 2 基于距离的离群点检测默认参数设置

本文的实验方法是按照数据集内的数据排列顺序将数据一次性读入内存. 随后, 实验依次将内存中的数据插入窗口. 在处理过程中, 实验统计每个对象的平均处理时间和在处理过程中的内存峰值. 实验环境详见表3.

表 3 实验环境

3.2 实验分析

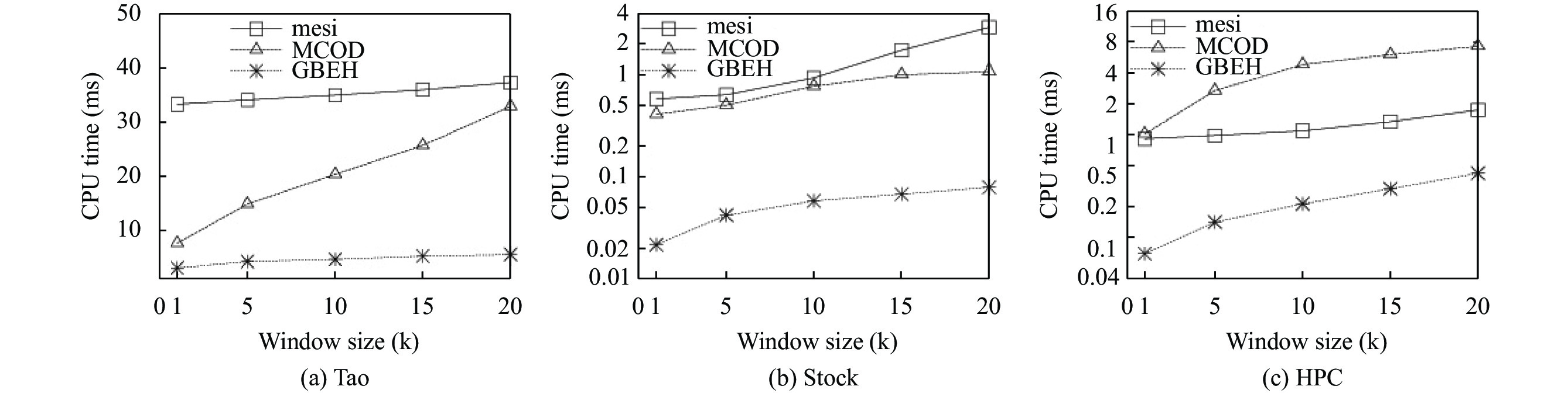
本节将mesi和MCOD算法作为对比实验, Tao、Stock和HPC这3个真实数据集作为测试数据. 本节首先测试了窗口长度对算法性能的影响, 其他参数均使用默认参数. 如图5, 图6所示, 随着窗口长度的增加, 本文有以下发现: 首先, GBEH的计算代价最小. 在最好情况下, 它的运行时间是mesi算法的0.1倍, MCOD的0.16倍; 其次, 3个算法的运行时间都随窗口大小的增加而增加, 但GBEH的增长幅度最小. 其原因在于: 与mesi相比, GBEH算法利用网格将临近位置的对象划分在同一单元格中, 节省了大量的计算代价; 与MCOD相比, 利用队列维护了数据流间的时间关系, 通过对安全点的筛选和候选对象最佳邻居的搜索, 降低了范围查询所需访问的对象数目. 其次, GBEH的空间代价较小. 原因在于, GBEH利用网格维护窗口中的数据流. 和传统树形结构相比, GBEH无需维护节点之间的拓扑关系. 这导致GBEH只需消耗较低的空间代价便可维护窗口中的数据流.

接下来, 本节测试数据流速对算法性能的影响. s从 $\text{1}\text{×}{\text{10}}^{{-2}}$ N扩大到0.1N, 如图7, 图8所示, 其他参数均使用默认参数. 随着s增加, 本文有以下发现: (1) GBEH算法性能最好, 在最好情况下它的运行时间是其他两个算法的0.05倍; (2) GBEH和MCOD的运行时间都随滑动对象个数的增加而增加, 但GBEH的涨幅最小, mesi的表现则不稳定. 其原因是: 和其他两个算法相比, PBH维护了数据流间的位置关系和时序关系, 这使得范围查询算法可以高效找到到达时间有限访问包含在查询范围内对象数目多的单元格, 降低由数据滑动引起的重复查询次数. 其次, 最坏情况下GBEH的内存峰值是mesi的5倍, 但此时mesi的运行时间是GBEH的6倍. 其原因是: (1)随着滑动对象个数的减少, 对象间时间关系的维护代价在降低; (2)与其他两个算法相比, GBEH对于数据流间时序关系的维护代价更大, 随着滑动对象个数的增加, 该代价减少.

图 5 不同窗口大小下算法的CPU运行时间

图 6 不同窗口大小下算法的内存峰值

图 7 不同滑动对象个数下算法的CPU运行时间

图 8 不同滑动对象个数下算法的内存峰值

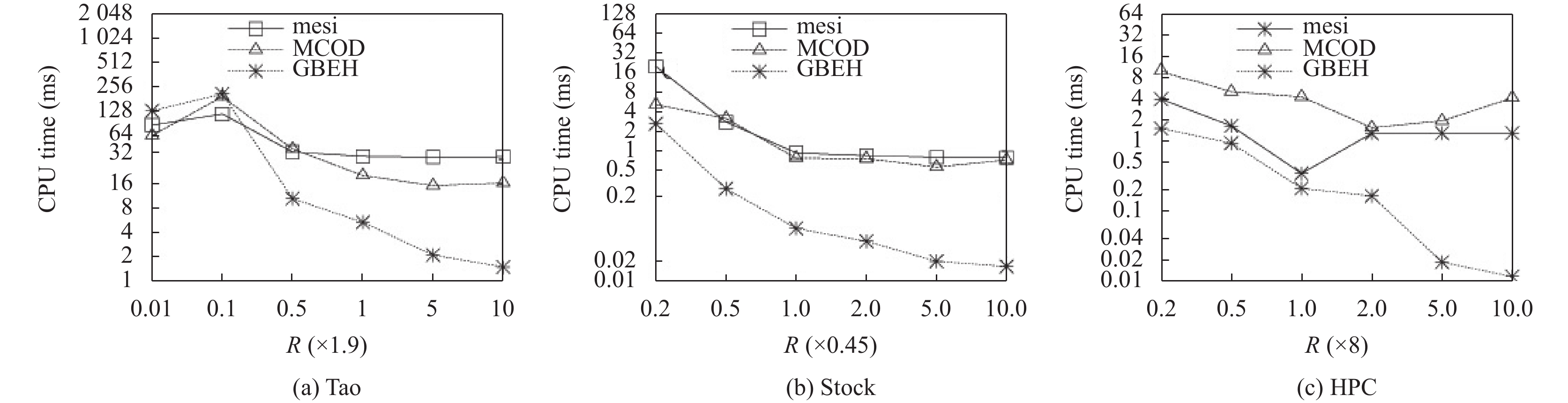
第3组实验测试距离阈值R对算法性能的影响, 其他参数均使用默认参数. 如图9和图10所示, 随着距离阈值R的增大, 本文有以下发现: (1) GBEH算法的性能最好, 在最好情况下它的运行时间是mesi的0.04倍, MCOD的0.08倍; (2) 3个算法的运行时间随距离阈值R的增加呈下降趋势, 当R增加到0.5r时, 运行时间骤降, 随后趋于平稳. 其原因是: (1)与mesi相比, GBEH算法利用虚拟网格维护位置信息, 随着R的增加大部分数据对象都可直接过滤, 由此节省了大量的计算代价; (2)当R增大至0.5r后, 离群点的数量降幅趋于平稳, 因此3个算法的运行时间也平稳下降. 其次, 3个算法的内存峰值在3个数据集上的表现不同, 但GBEH的表现最为稳定. 最坏情况下, GBEH约是MCOD的2.3倍, 但此时运行时间是其0.25倍. 原因是: (1)随着R增大至10r, 对于GBEH算法大部分对象均可划分到同一单元格中, 节省了大量的对象维护代价; (2) GBEH维护更多的邻居信息保证重复查询和数据维护代价的降低.

图 9 不同距离阈值下算法的CPU运行时间

图 10 不同距离阈值下算法的内存峰值

第4组实验测试邻居个数k对算法性能的影响, 其他参数均使用默认参数. 3个数据集的邻居个数k从5扩大到100. 如图11和图12所示, 随着邻居个数的增加, 本文有以下发现: (1) GBEH性能最好, 运行时间约是mesi的0.1倍, MCOD的0.5倍; (2) 3个算法的运行时间虽然都随邻居个数增加而增加, 但GBEH运行时间的涨幅最小. 其原因是: GBEH算法候选对象的平均维护代价与k大小无关. 其次, 3种算法的内存峰值随k的增大而增大, 但GBEH的内存峰值最为稳定, 尤其在测试Stock和HPC数据时, GBEH内存峰值几乎无变化; 约是mesi的6–7倍, 但运行时间是其0.1倍; 最坏情况下, GBEH内存峰值约是mesi的6倍, 但运行时间是其0.1倍. 由此得知, 综合来看GBEH具有可用性、高效性.

4 总结

本文首先对目前已有离群点检测方法进行归纳和分类, 并对各类方法进行分析, 找出其不足. 通过对现有的基于距离的数据流离群点检测算法的分析和对比, 发现现有算法具有时间复杂度高、受数据分布影响等缺陷, 为本文研究指明了方向. 随后本文针对数据流环境下基于距离的离群点检测问题, 提出了查询处理框架GBEH. 其主要工作包括设计高效索引GQBI维护数据流间的位置关系和时间关系, 支持高效范围查询; 提出基于GQBI的离群点检测算法PBH, 减少查询次数, 降低范围查询代价. 最后, 基于大量的实验证明了GBEH框架的高效性、可用性和稳定性.

图 11 不同阈值邻居个数下算法的CPU运行时间

图 12 不同阈值邻居个数下算法的内存峰值

参考文献
[1]
Muthukrishnan S. Data streams: Algorithms and applications. Proceedings of the 14th Annual ACM-SIAM Symposium on Discrete Algorithms. New York: ACM Press, 2003. 413.
[2]
Hawkins DM. Identification of Outliers. Dordrecht: Springer, 1980. 978–1007.
[3]
Knorr EM, Ng RT. Algorithms for mining distance-based outliers in large datasets. Proceedings of the 24th International Conference on Very Large Data Bases. New York: Morgan Kaufmann Publishers Inc., 1998. 392–403.
[4]
Ramaswamy S, Rastogi R, Shim K. Efficient algorithms for mining outliers from large data sets. Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. Dallas: ACM, 2000. 427–438.
[5]
Sadik S, Gruenwald L. DBOD-DS: Distance based outlier detection for data streams. Proceedings of the 21st International Conference on Database and Expert Systems Applications. Bilbao: Springer, 2010. 122–136.
[6]
Angiulli F, Pizzuti C. Outlier mining in large high-dimensional data sets. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(2): 203-215. DOI:10.1109/TKDE.2005.31
[7]
Angiulli F, Pizzuti C. Fast outlier detection in high dimensional spaces. Proceedings of the 6th European Conference on Principles of Data Mining and Knowledge Discovery. Helsinki: Springer, 2002. 15–27.
[8]
Bay SD, Schwabacher M. Mining distance-based outliers in near linear time with randomization and a simple pruning rule. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington: ACM, 2003. 29–38.
[9]
Angiulli F, Fassetti F. Distance-based outlier queries in data streams: The novel task and algorithms. Data Mining and Knowledge Discovery, 2010, 20(2): 290-324. DOI:10.1007/s10618-009-0159-9
[10]
Kontaki M, Gounaris A, Papadopoulos AN, et al. Continuous monitoring of distance-based outliers over data streams. Proceedings of the 2011 IEEE 27th International Conference on Data Engineering. Hannover: IEEE, 2011. 135–146.
[11]
Cao L, Yang D, Wang QY, et al. Scalable distance-based outlier detection over high-volume data streams. Proceedings of the 2014 IEEE 30th International Conference on Data Engineering. Chicago: IEEE, 2014. 76–87.
[12]
Cao L, Wang QY, Rundensteiner EA. Interactive outlier exploration in big data streams. Proceedings of the VLDB Endowment, 2014, 7(13): 1621-1624. DOI:10.14778/2733004.2733045
[13]
Sheng B, Li Q, Mao WZ, et al. Outlier detection in sensor networks. Proceedings of the 8th ACM International Symposium on Mobile Ad Hoc Networking and Computing. Montreal: ACM, 2007. 219–228.
[14]
Carmona J, Lopez I, Mateo J, et al. A distance-based method for outlier detection on high dimensional datasets. IEEE Latin America Transactions, 2020, 18(3): 589-597. DOI:10.1109/TLA.2020.9082731
[15]
Yu KQ, Shi W, Santoro N. Designing a streaming algorithm for outlier detection in data mining—An incremental approach. Sensors, 2020, 20(5): 1261. DOI:10.3390/s20051261
[16]
Toliopoulos T, Bellas C, Gounaris A, et al. PROUD: Parallel outlier detection for streams. Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. Portland: ACM, 2020. 2717–2720.
[17]
Tran L, Mun MY, Shahabi C. Real-time distance-based outlier detection in data streams. Proceedings of the VLDB Endowment, 2020, 14(2): 141-153. DOI:10.14778/3425879.3425885
[18]
Yoon S, Shin Y, Lee JG, et al. Multiple dynamic outlier-detection from a data stream by exploiting duality of data and queries. Proceedings of the 2021 International Conference on Management of Data. Online: ACM, 2021. 2063–2075.
[19]
Tran L, Fan LY, Shahabi C. Distance-based outlier detection in data streams. Proceedings of the VLDB Endowment, 2016, 9(12): 1089-1100. DOI:10.14778/2994509.2994526
[20]
Angiulli F, Fassetti F. Detecting distance-based outliers in streams of data. Proceedings of the 16th ACM Conference on Conference on Information and Knowledge Management. Lisbon: ACM, 2007. 811–820.