函数回归是机器学习核心问题之一, 通常可以采用两种方法解决: 一方面可以将目标函数视为一个确定性函数, 借助深度神经网络训练, 高效地逼近单个目标函数, 但这一方法需要大量标记准确的数据; 另一方面可以对函数分布进行建模, 以高斯过程回归(Gaussian process regression, GPR)^[1]为例, 通过对少量观测数据进行推理, 获得函数概率分布, 而后对该分布采样, 逼近真实的目标函数, 但目前该方法最优算法的计算复杂度仍高达 ${\rm{O}}({n^2})$ , 且可用的核函数在形式上受限, 需要进行额外优化.

神经过程(neural process, NP)结合以上两种思路, 利用深度神经网络的计算优势, 模仿了高斯过程回归的功能^[2], 且神经过程计算复杂度仅有 ${\rm{O}}(n)$ , 克服了高斯过程回归高计算复杂度的缺点; 另外, 它借助神经网络强大的函数拟合能力学习到隐式核函数, 避免了高斯过程回归模型中固定核函数影响其适用性的问题. 随后, 一系列结构类似于NP的函数估计模型被提出来, 统称为NP家族, 例如, Foong等人针对离网时空数据(off-the-grid spatio-temporal data), 先后提出卷积条件神经过程(convolutional conditional neural processes, ConvCNP)^[3]和卷积神经过程(convolutional neural processes, ConvNP)^[4], 并使用简化的最大似然目标代替了NP中的证据下界(evidence lower bound, ELBO), 提升了NP的预测能力. 目前, 神经过程家族被用以解决包括函数回归、分类、数据补全在内的多类任务, 已在自动驾驶^[5]、视频预测^[6]、机器人路径规划^[7]等领域得到应用.

作为图像处理领域的研究热点, 图像补全问题获得了一系列解决方案. 一是基于卷积神经网络对图像进行补全系列方法, 包括: 上下文编码器^[8]、部分卷积^[9]和门控卷积^[10]等经典法; 二是利用生成器和判别器博弈生成图像的生成式对抗网络(GAN)^[11]系列模型, 包括: 深度卷积生成对抗网络(DCGAN)^[12]、样本生成对抗网络(ExGAN)^[13]及上下文感知语义修复方法^[14]等. 三是基于深度自编码器^[15]的自监督模型, 包括去噪自编码器^[16]、变分自编码器 (variational auto-encoder, VAE)^[17]系列模型, 该类模型相较于GAN系列具备更好的理论基础, 可解释性更强, 但视觉效果相对来说弱于GAN. 神经过程作为具有完备推导保证的回归模型, 其结构更接近于自编码器模型, 同样可以用于解决图像补全等二维数据回归问题, 但该模型提出时间较短, 且经典NP模型采用全连接神经网络(fully connected neural network, FCN)作为编码器、解码器, 相对于天然适于处理图像的卷积神经网络(convolutional neural network, CNN)^[18], FCN结构并不具备优势. 因此, 神经过程家族模型在解决图像回归问题方面仍有缺憾.

实际上, 卷积神经网络已经具备丰富的基础操作和成熟的图像数据处理模型, 如: 空洞卷积^[19]在扩大感受野的同时捕获多尺度上下文信息, 可变卷积^[20]可以灵活应对物体复杂形变的场景; 残差网络^[21]以跨层连接的方式解决退化问题, 增加了网络深度, 获得更具语义信息的特征; 非局部神经网络^[22]通过直接计算嵌入空间中相似度矩阵, 获取全局信息. 为此, 本文尝试将CNN与NP相结合, 构建出面向图像的神经过程(image-faced neural process, IFNP), 以便于处理图像数据. IFNP在保留NP优势的同时, 也搭建起CNN和NP之间的桥梁, 使得丰富、成熟的图像处理技术得以应用到NP中.

本文的主要工作包括:

(1)通过结合CNN和NP, 构建了面向图像的神经过程(IFNP)基础模型; 并利用随机梯度变分推断方法^[22]推导出IFNP的证据下界(ELBO)表达式及训练损失函数.

(2)设计局部池化聚合(local pooling adduction, LPA)模块和全局交叉注意力(global cross attention, GCA)模块改进本文提出的IFNP, 构建出一种面向图像的注意力神经过程(image-faced attention neural process, IFANP), 拓展了IFNP模型在图像处理中的应用前景.

(3)将IFANP模型应用于图像补全任务, 与变分自编码器(variational auto-encoder, VAE)^[17]、NP等相关模型的补全结果进行比较, 显示IFANP模型更强的数据补全和细节拟合能力; 并对采用不同形式注意力的IFANP进行实验对比, 分析了更优的IFANP模型结构.

1 研究背景

神经过程(NP)是一种能够将输入映射到输出的回归函数族模型, 于2018年由DeepMind公司首次提出^[2], 这一模型利用神经网络的拟合能力和并行计算优势, 模仿了高斯过程回归(GPR)功能, 通过少量观测数据即可推断出目标函数的概率分布, 同时避免了高计算复杂度和固定核函数适用范围的问题.

NP解决回归问题时, 假设数据集由高斯过程 $ F $ 生成, 符合函数族 $ f:X \to Y $ , 函数族中的任一函数 $ f(x) $ 均采样自高斯过程, 即 $f(x)\sim\mathcal{G}\mathcal{P}$ . 数据集中的 $({x_i}, {y_i})$ 元组满足 ${y_i} = f({x_i})$ . 为了使用NP表示高斯过程, 模型使用神经网络来近似函数族分布, 并假设 $F$ 可以由一个高维向量 ${\textit{z}}$ 参数化, 写作 $F(x) = f(x, {\textit{z}})$ , 其中 $f$ 为固定、可学习函数, ${\textit{z}}$ 为全局隐变量且服从高斯分布, 假定 $F$ 的随机性来自于变量 ${\textit{z}}$ 的随机性. 在训练阶段, 模型通过对观测数据训练参数化隐变量 $ {\textit{z}} $ 的后验分布. 在预测阶段, 通过对该后验分布采样确定 ${\textit{z}} = {{\textit{z}}_i}$ , 从而得到确定性函数 $ {f_{{{\textit{z}}_i}}}(x) $ , 并预测出目标输入 $ {x^*} $ 的结果 $ {y^*} = {f_{{{\textit{z}}_i}}}({x^*}) $ .

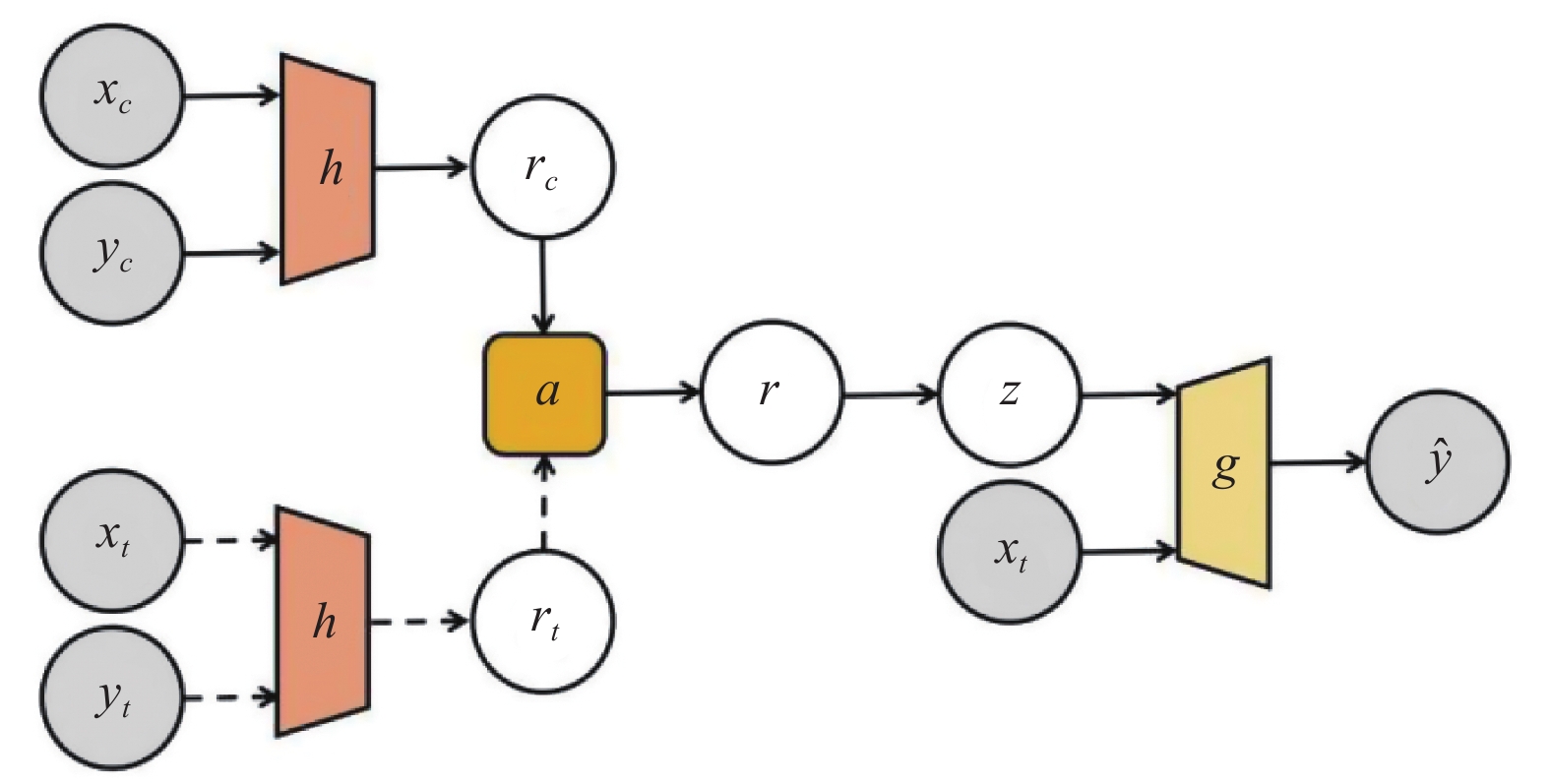
NP模型结构如图1所示, 结构图整体表示训练阶段, 实线部分表示生成阶段, $({x_c}, {y_c})$ 为上下文数据, 表示已知的观测数据, $({x_t}, {y_t})$ 为目标数据, 模型假设已知上下文数据, 预测目标输入数据 ${x_t}$ 对应的目标输出数据 ${y_t}$ . 模型总体主要包括编码器、聚合器和条件解码器3个部分, 其中, 编码器 $h$ 可以接收上下文数据 $({x_c}, {y_c})$ , 并通过神经网络为每对上下文数据生成对应的表征向量 ${r_i} = h(({x_i}, {y_i}))$ ; 聚合器 $a$ 通过取均值的方式对表征向量进行聚合, 获得全局表示: $r = a({r_i})$ , $a( \cdot )$ 为取均值操作. $r$ 将全局隐变量 ${\textit{z}}$ 的分布参数化, 使得隐变量 ${\textit{z}}$ 满足 $p({\textit{z}}|{x_c}, {y_c}) = N(\mu (r), \sigma (r))$ ; 条件解码器 $g$ 以 ${\textit{z}}$ 分布的采样值和目标输入 ${x_t}$ 作为输入, 通过采样隐变量 ${\textit{z}}$ 值, 得到确定函数 $f(x)$ , 从而在输入 ${x_t}$ 后获得其对应的预测值 ${\hat y_t} = f({x_t})$ .

训练阶段, 完整数据划分为上下文集 $({x_c}, {y_c})$ 和目标集 $({x_t}, {y_t})$ , 假设通过上下文数据分布 $p({\textit{z}}|{x_c}, {y_c})$ 采样得到 ${{\textit{z}}_c}$ , 由 ${{\textit{z}}_c}$ 确定的回归函数为 ${f_c}(x)$ ; 通过完整数据分布 $p({\textit{z}}|x, y)$ 采样得到 ${\textit{z}}$ , 由 ${\textit{z}}$ 确定的回归函数为 $f(x)$ . 那么, 通过训练编码器 $h$ , 并控制 $p({\textit{z}}|{x_c}, {y_c})$ 和 $p({\textit{z}}|x, y)$ 分布的差异, 可以使 ${{\textit{z}}_c}$ 与 ${\textit{z}}$ 接近, 从而确保回归函数 ${f_c}(x)$ 与 $f(x)$ 非常接近. 因此, 训练结束后, 可以仅使用 ${f_c}(x)$ 对目标输入数据 ${x_t}$ 对应 ${y_t}$ 进行预测. 由于 ${\textit{z}}$ 的先验分布难以求得, 可以使用近似先验分布 $q({\textit{z}}|{x_c}, {y_c})$ 来代替 $p({\textit{z}}|{x_c}, {y_c})$ .

编码器 $h$ 与解码器 $g$ 经过充分训练后, 在生成阶段, 由观察数据中的上下文集获得 ${\textit{z}}$ 的近似分布 $p({\textit{z}}|{x_c}, {y_c})$ , 从该分布中采样隐变量 ${{\textit{z}}_c}$ , 将 ${{\textit{z}}_c}$ 输入解码器 $g$ , 可以确定映射方程 ${f_c}(x)$ . 模型经过前期的充分训练, 可以认为由上下文数据集获得的回归函数 ${f_c}(x)$ 接近 $f(x)$ , 此时, 结合目标输入 ${x_t}$ 便可获得其对应输出 ${\hat y_t} = {f_c}({x_t})$ .

将神经过程应用于图像补全任务时, 一般以上下文坐标值为 ${x_c}$ , 对应的 ${y_c}$ 为上下文像素值, 同理, ${y_t}$ 为目标坐标值 ${x_t}$ 对应的目标像素值. 经典NP模型将图像展平并拆分为单一像素值, 结合像素值对应的坐标值, 以二元组的形式, 输入采用全连接神经网络(FCN)中, 并按照聚合、采样、解码的顺序做后续计算. 尽管使用FCN编码简单、直接、高效, 但卷积神经网络(CNN)与之相比, 具有的大量前期研究成果可以针对性解决图像补全问题, 给予模型更大的改进空间. 因此, 下文中构造了更适用于图像处理的面向图像的神经过程.

2 面向图像的神经过程(IFNP)

与神经过程(NP)中对图像和坐标二元组处理形式不同, 本文提出的面向图像的神经过程(IFNP), 通过对完整数据集进行随机遮罩处理, 使用整张图像完成模型的训练与生成. 在第2.1节首先利用随机梯度变分推断(SGVI)方法^[22,23]对IFNP的证据下界(ELBO)和损失函数进行推导, 并在随后的第2.2节对模型结构进行介绍.

2.1 证据下界和模型损失函数推导

本文假设图像数据集 $\mathcal{D}$ 中图像分辨率为 $h \times w$ , 且数据集由随机过程 $F$ 生成, 存在隐变量 $f$ 与数据集中的图像一一对应, $f$ 为函数且 $f\sim F$ .

定义 $M$ 为全部坐标元组集合, 图像中任一像素坐标为 ${m_{i, j}} = (i, j) \in M$ , 其中, $1 \leqslant i \leqslant h$ , $1 \leqslant j \leqslant w$ .

若图像中像素值相互独立且引入随机噪声, 噪声值 ${\epsilon}_{i, j}\sim \mathcal{N}(0, {\sigma }^{2})$ , 则坐标 ${m_{i, j}}$ 处图像像素值为 ${y}_{i, j}= f({m}_{i, j})+ {\epsilon}_{i, j}$ . 像素值的条件概率分布可以表示为:

$ p({y_M}|M) = \begin{array}{*{20}{c}} {\int p (f){\mkern 1mu} \displaystyle \prod\limits_{i = 1}^h { \displaystyle \prod\limits_{j = 1}^w {\mathcal{N}({y_{i, j}}|f({m_{i, j}}), {\sigma ^2})} } df} \end{array} $

(1)

为了使用神经过程建模随机过程 $F$ , 便于用神经网络近似, 假设 ${\textit{z}}$ 是一个足以表示 $F$ 的高维向量, 记 $F(M) = g(M, {\textit{z}})$ , 通过该方法, 将随机过程 $F$ 的随机性转移到隐变量 ${\textit{z}}$ 上, 对 ${\textit{z}}$ 采样可以获得了其对应函数 $f = g( \cdot , {\textit{z}})$ . 所以, 由式(1)可以获得:

$ p({\textit{z}}, {y_M}|M) = p({\textit{z}}){\mkern 1mu} \begin{array}{*{20}{c}} {\displaystyle \prod\limits_{i = 1}^h {\displaystyle \prod\limits_{j = 1}^w {\mathcal{N}({y_{i, j}}|g({m_{i, j}}, {\textit{z}}), {\sigma ^2})} } } \end{array} $

(2)

受变分自编码器启发, 设式(2)中 $p({\textit{z}})$ 为多元标准正态分布, $g({m_{i, j}}, {\textit{z}})$ 是一个卷积神经网络. 因为解码器 $g$ 是非线性的, 本文尝试用随机梯度变分推断优化似然函数.

根据 $p({y_M}|M) = \begin{array}{*{20}{c}} {\int p ({\textit{z}}, {y_M}|M){\mkern 1mu} d{\textit{z}}} \end{array}$ 可得:

$\begin{split}& \ln p({y_M}\left| M \right.) = \ln \left[ {\int {\frac{{p({\textit{z}}, {y_M}|M)}}{{q({\textit{z}}|{y_M}, M)}}} q({\textit{z}}|{y_M}, M){\mkern 1mu} d{\textit{z}}} \right] \\& \geqslant {E_{q({\textit{z}}|{y_M}, M)}}\left[ {\ln \frac{{p({\textit{z}})}}{{q({\textit{z}}|{y_M}, M)}}} \right.\left. {{\text{ + }}\ln \prod\limits_{i = 1}^h {\prod\limits_{j = 1}^w {p({y_{i, j}}|{\textit{z}}, {m_{i, j}})} } } \right] \end{split} $

(3)

式(3)中不等号右项即为边界下界ELBO.

为了便于训练和测试, 验证模型效果, 下面将数据集拆分为上下文集 $M{{+}}$ 、 ${y_{M{{+}}}}$ 和目标集 $M - $ 、 ${y_{M - }}$ 两部分. $M{{+}}$ 、 $M - $ 分别为图像已知像素坐标集合和未知像素坐标集合, 以坐标矩阵的形式输入, $M + , M - \subset M$ . 在计算过程中, 由于条件先验 $p({\textit{z}}|{y_{M{{+}}}}, M + )$ 难以直接求得, 因此, 可以使用近似分布 $q({\textit{z}}|{y_{M{{+}}}}, M + )$ 来代替. 那么, 以上下文集合作为条件时, 目标输出的条件分布为:

$\begin{split}& \ln p(\left. {{y_{M - }}} \right|{y_{M - }}, M + ) \geqslant {E_{q({\textit{z}}|{y_M}, M)}}[\ln \frac{{q({\textit{z}}|{y_{M + }}, M + )}}{{q({\textit{z}}|{y_M}, M)}} \\& +\sum\nolimits_{(i, j) \in \{ (i, j)|{m_{i, j}} \in M - \} } {\ln p({y_{i, j}}|{\textit{z}}, {m_{i, j}})} ] \\ \end{split} $

(4)

由式(3)可知, ELBO越大, 像素值 ${y_M}$ 的条件概率 $p({y_M}|M)$ 越大, 对应于模型训练过程中损失值越小. 为便于损失函数推导, 对式(4)中 ${\textit{z}}$ 进行蒙特卡洛^[14]采样, 得到:

$\begin{split}& \ln p(\left. {{y_{M - }}} \right|{y_{M + }}, M + ) \\& \geqslant - KL(q({\textit{z}}|{y_M}, M)||q({\textit{z}}|{y_{M + }}, M + )) \\& + \begin{array}{*{20}{c}} {\dfrac{1}{K} \displaystyle \sum\nolimits_{k = 1}^K { \displaystyle \sum\nolimits_{(i, j) \in \{ (i, j)|{m_{i, j}} \in M - \} } {\ln p({y_{i, j}}|{{\textit{z}}_k}, {m_{i, j}})} } } \end{array} \\ \end{split}$

(5)

其中, ${{\textit{z}}_k}\sim \;q({\textit{z}}|{y_M}, M)$ .

因此, 式(5)中大于等于号右项即为模型损失函数负值, 即:

$ \begin{split}& Loss = KL(q({\textit{z}}|{y_M}, M)||q({\textit{z}}|{y_{M + }}, M + )) \\& - \begin{array}{*{20}{c}} {\dfrac{1}{K} \displaystyle \sum\nolimits_{k = 1}^K { \displaystyle \sum\nolimits_{(i, j) \in \{ (i, j)|{m_{i, j}} \in M - \} } {\ln p({y_{i, j}}|{{\textit{z}}_k}, {m_{i, j}})} } } \end{array} \\ \end{split} $

(6)

2.2 模型结构

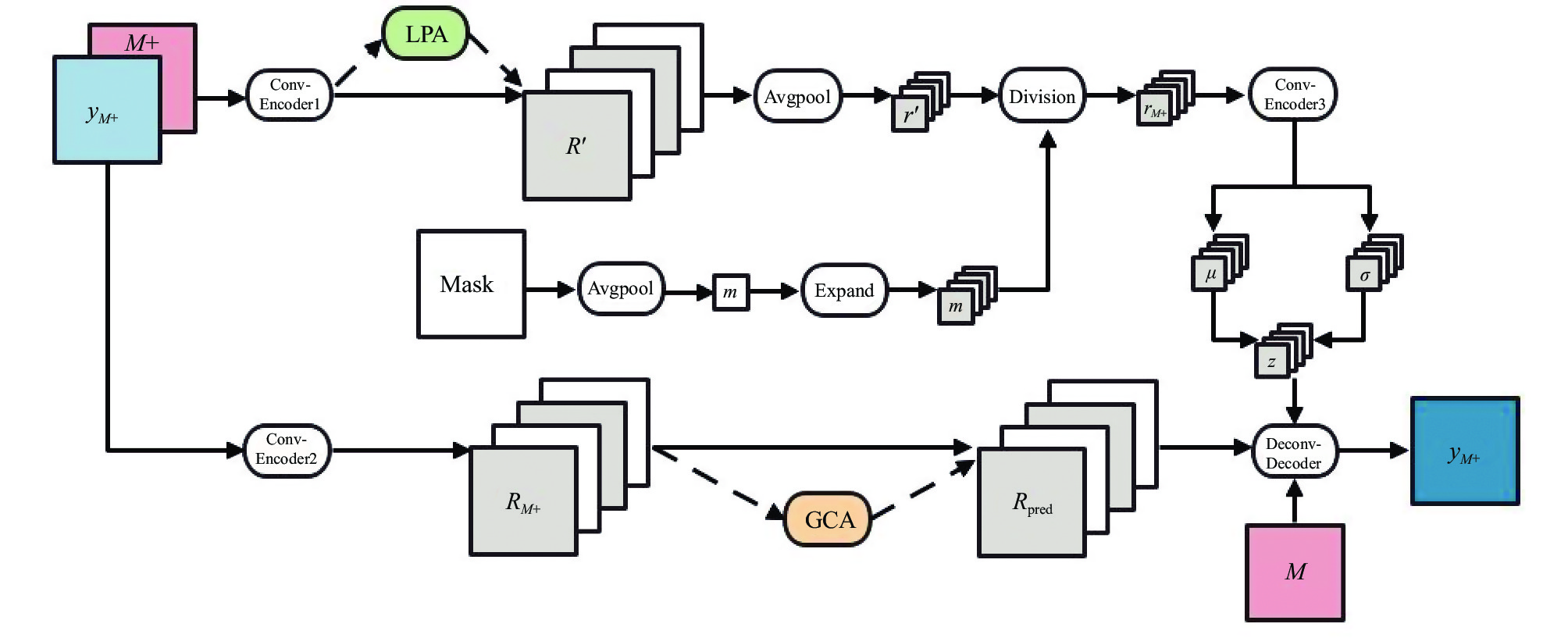
IFNP在保持图像结构及完整性的条件下, 以图像矩阵、坐标矩阵、未知点遮罩矩阵作为输入, 使用卷积神经网络及相关操作进行计算, IFNP结构见图2实线部分.

在训练阶段, 完整图像 $({y_M}, M)$ 及坐标分为上下文图像及坐标 $({y_{M{{+}}}}, M{{+}})$ 和目标图像及坐标 $({y_{M - }}, M - )$ 两部分, 以随机概率对完整图像进行采样获得 $({y_{M{{ + }}}}, M{{ + }})$ . 由于采样概率值随机产生, 且采样点均为随机采样, 因此采样获得的上下文数据对完整数据具有一定代表性和概括性; 其中, 上下文图像及坐标矩阵未知点元素值为0. 图2中显示仅以 $({y_{M{{ + }}}}, M{{ + }})$ 作为输入时模型流程说明, 完整图像 $({y_M}, M)$ 与其处理流程相同.

训练过程中, 完整图像及坐标 $({y_M}, M)$ 和上下文图像及坐标 $({y_{M{{ + }}}}, M{{ + }})$ 输入模型, 分别通过同一个卷积编码器(ConvEncoder1)获得两部分数据的高维特征矩阵 $R$ 和 $R'$ , 而后经过平均池化(Avgpool)获得表征向量 $r$ 和 $r'$ . 由于 $r'$ 生成过程中, 受到图像及坐标矩阵中0值的干扰. 因此, 与上下文图像所对应的遮罩矩阵(Mask)通过中间路径同步输入, 经过平均池化后在通道维度复制扩张, 利用除法模块(Division)与 $r'$ 按位相除获得上下文数据真实表征向量 ${r_{M{{ + }}}}$ . 遮罩矩阵元素与上下文数据一一对应, 矩阵中已知点设为1、未知点设为0, 长宽与图像完全相同. 训练时, 通过卷积编码器(Conv-Encoder3), 获得参数化的隐变量分布的均值和方差, 通过控制它们的KL散度, 可以使上下文数据集与完整图像数据集的分布更加接近, 确保在生成过程中, 仅使用上下文数据集即可参数化全局隐变量 ${\textit{z}}$ 真实分布; 从完整数据集近似分布 $q({\textit{z}}|{y_{M, }}M)$ 中采样得到的全局隐变量 ${\textit{z}}$ , 与目标坐标矩阵一同输入反卷积解码器(Deconv-Decoder), 获得对应输出.

在生成阶段, $({y_M}, M)$ 部分不参与数据预测. 经过前期的训练, 由模型参数化得到上下文集隐变量分布与完整图像数据集对应的全局隐变量 ${\textit{z}}$ 的分布非常接近. 此时, 以上下文集 $({y_{M{{ + }}}}, M{{ + }})$ 作为输入得到表征向量 ${r_{M{{ + }}}}$ , 将 ${r_{M{{ + }}}}$ 输入卷积编码器(ConvEncoder3), 获得全局隐变量 ${\textit{z}}$ 的近似分布 $q({\textit{z}}|{y_{M{{ + }}}}, M{{ + }})$ . 对该分布进行采样得到隐变量 ${{\textit{z}}_{M + }}$ , 随后结合完整坐标矩阵 $M$ 作为输入, 可以实现对图像像素的预测.

以第2.1节ELBO和损失函数推导为基础, 利用卷积、池化、反卷积等操作, 本文设计出IFNP基础模型结构. 在保证输入图像完整性、捕捉像素点空间联系的同时, 为进一步改造基础模型、提升模型性能留下更多空间.

在使用IFNP进行图像补全实验过程中(第4.1节), 可以发现, 虽然IFNP能够实现对缺失信息的补全, 但对于已知上下文信息的拟合不尽人意, 且补全效果仅与NP持平. 其原因是, 在面向图像的神经过程(IFNP)中, 图像表征信息 $r$ 是由全局平均池化操作得到, 该操作限制了不同上下文表征向量 ${r_i}$ 对预测目标差异性贡献, 无法在像素级上突出重点关注的信息表征, 影响补全效果. 因此需要进一步改进面向图像的神经过程, 区分主次、有针对性地使用表征向量 ${r_i}$ , 提升图像补全能力.

3 基于注意力的面向图像的神经过程改进

当人类观察图片获取信息的过程中, 视觉系统并没有同时接收图片的全部内容, 而是将有限的注意力集中在少部分重点信息上^[24]. 这一方式引导我们基于注意力对前文中设计的面向图像的神经过程(IFNP)改进. 受池化操作和非局部神经网络的启发, 本文利用局部池化聚合(LPA)和全局交叉注意力(GCA)模块构建了一种面向图像的注意力神经过程(IFANP). 在IFANP中, 局部池化自注意力在池化窗口范围内, 对像素间相似信息进行聚合, 实现对特征图的平滑操作, 便于抽取图像本质特征, 避免了背景信息的干扰; 全局交叉注意力则利用上下文数据对待补全数据的响应, 区分主次获取全局上下文数据, 预测未知数据表征, 便于补充图像细节特征. 通过局部特征聚合和全局信息响应相结合的方式, 模型数据补全及细节拟合能力得到增强, 图像重建损失进一步下降.

3.1 模型结构

图2中原始IFNP模型结合虚线部分插入的两个模块描述的是一种基于注意力机制的面向图像的神经过程改(IFANP)进模型结构.

整体上看, 模型包括隐藏路径(上侧路径)和确定路径(下侧路径)两部分, 两条路径分别对应全局隐变量 ${\textit{z}}$ 和确定性目标表征 ${R_{{\rm{pred}}}}$ 的生成; 解码器通过解码全局隐变量 ${\textit{z}}$ 、确定性目标表征 ${R_{\rm{{pred}}}}$ 和全局坐标 $M$ , 得到完整补全图像 $y_M^*$ .

具体来说, 隐藏路径中, 上下文数据经过卷积编码器(ConvEncoder1)编码后, 不直接采取全局平均池化操作, 而是通过LPA模块, 使高维表征矩阵 $R'$ 中的单个元素可以聚合池化窗口范围内的邻域信息, 同时实现了特征数据的平滑, 便于模型抽取图像数据集更为一般、普遍的特征; 确定性路径中, 上下文数据输入卷积编码器(ConvEncoder2)后, 获得上下文表征矩阵 ${R_{M{{ + }}}}$ , 该矩阵与上下文坐标矩阵 $M{{ + }}$ 、完整坐标矩阵 $M$ 结合, 输入GCA模块, 上下文表征矩阵与上下文坐标矩阵中的已知元素按位置一一对应. 在GCA模块中, 上下文坐标矩阵 $M{{ + }}$ 与完整坐标矩阵 $M$ 通过矩阵展平、通道变换、矩阵相乘等操作计算出 $M{{ + }}$ 与 $M$ 中所有元素的相似度矩阵, 相似度矩阵中任一元素为上下文表征矩阵元素与 $M$ 中元素在嵌入空间的相似系数, 输出 ${R_{{\rm{pred}}}}$ 为 ${R_{M{{ + }}}}$ 与相似度矩阵的矩阵乘积, ${R_{\rm{{pred}}}}$ 中元素为 ${r_{i, j}} = GCA({y_{M{{ + }}}}, M{{ + }}, {m_{i, j}})$ , 这一模块允许目标输入 $M$ 获取与其更加接近的上下文数据信息, 使预测结果更加精准; 在实际应用中, 可以通过堆叠GCA模块, 获取关注更加全面的目标表征 ${R_{{\rm{pred}}}}$ . 隐藏路径中的隐变量 ${\textit{z}}$ 保持全局特性, 建模随机过程的全局结构, 确定性路径中的确定性目标表征 ${R_{{\rm{pred}}}}$ , 细粒度建模像素级细节特征. 通过二者的结合, IFANP实现了相较于面向图像的神经过程(IFNP)更加精准的图像补全.

解码器部分除增加确定性目标表征 ${R_{{\rm{pred}}}}$ 作为解码器的输入, 其他部分仍然保持与面向图像的神经过程一致. 损失函数与面向图像的神经过程(IFNP)相同.

3.2 局部池化聚合模块

在卷积神经网络中, 由于图像中的相邻像素倾向于具有相似的值, 因此, 经过卷积后的输出中仍然包含了冗余信息. 而池化是一个特征选择和信息过滤的过程, 能够降低相邻像素的相似信息, 在二次提取特征的同时减少参数量和计算量^[25]; 由于池化操作的下采样作用, 输出结果中的一个元素对应原输入数据的一个子区域, 该元素获得邻域信息, 使得模型可以抽取更大范围内的特征.

池化往往紧随卷积层后, 池化对输入数据的一个固定的窗口(又称池化窗口)中的元素按照一定规则直接计算输出, 包括平均池化、最大池化、随机池化等多种形式. 以3×3的平均池化窗口对像素为3×3的图像进行池化操作为例, 当池化窗口滑动到某一位置时, 将原输入数据的一个子区域的平均值汇合到输出中的某一个元素上, 窗口中输入子数组的平均值即为输出数组中相应位置的元素.

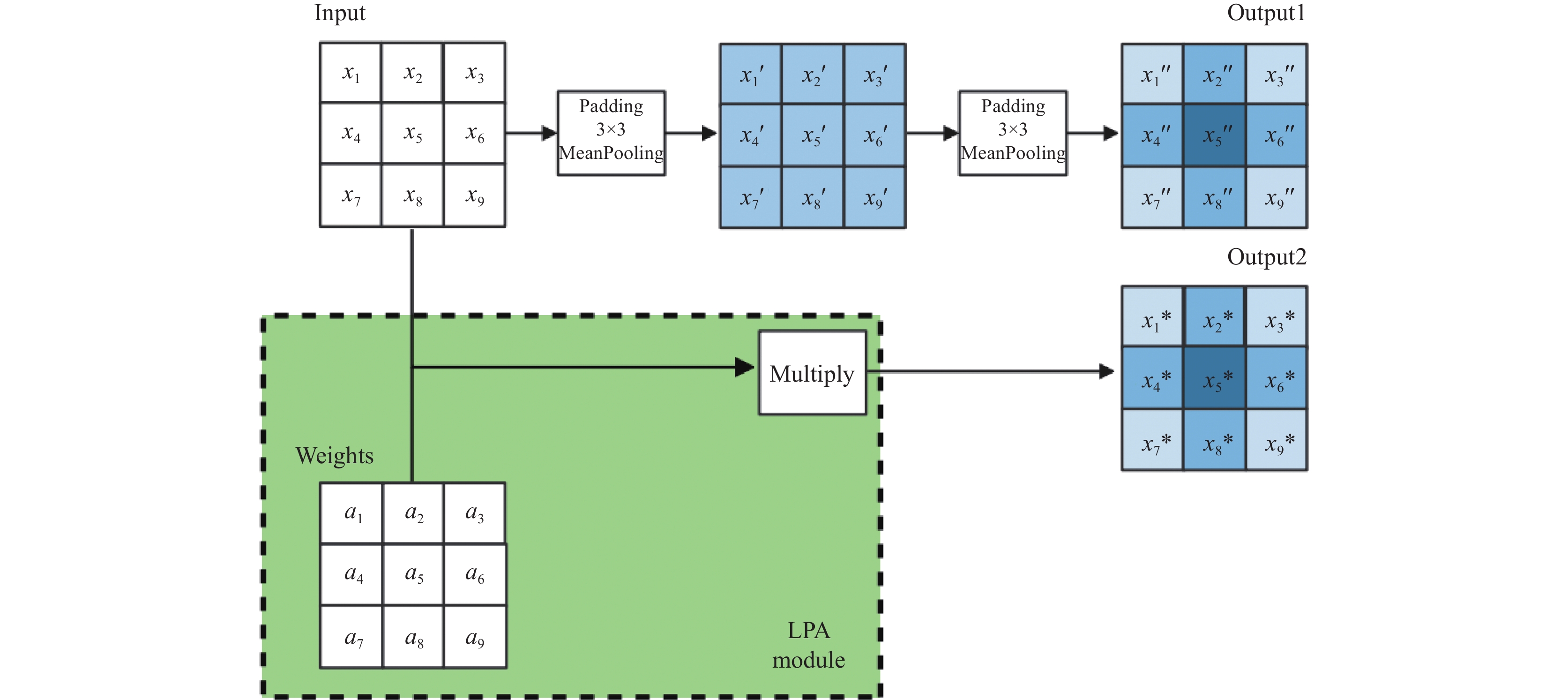
如图3中, 获得输出1 (Output1)路径所示, 以中心元素作为观察结点, 某一元素所在位置颜色越深, 代表初始值对观察结点的输出影响越大, 即所占权重越高. 对输入矩阵连续进行两次填充为1的池化, 观察结点对应输出为:

第1次池化后:

$ {x'_5} = \dfrac{1}{9}\begin{array}{*{20}{c}} { \displaystyle \sum\nolimits_{i = 1}^9 {{x_i}} } \end{array} $

第2次池化后:

$ {x''_5} = \frac{1}{{81}}(4{x_1} + 6{x_2} + 4{x_3} + 6{x_4} + 9{x_5} + 6{x_6} + 4{x_7} + 6{x_8} + 4{x_9}) $

随着池化层堆叠深度增加, 在像素更高的图像中, 邻域信息将按不同权重逐层汇合至观察结点, 且邻域范围不断增大, 权重不断减小. 同理, 当使用池化操作实现局部自注意力时, 池化窗口范围内的输入值对输出应当均有贡献, 但其贡献度会受与中心像素距离影响而有所区别. 对于图像而言, 从直观上来看, 距离中心像素越近的邻域像素, 其相似度越高, 使用池化注意力计算下一层输出时, 其贡献度或对应的权值也应当越大, 以更合理的方式筛选像素信息, 减少平均池化层的堆叠和计算开销, 更高效获得类似堆叠池化层的输出结果, 如图4获得输出2 (Output2)所示. 因此, 本文构建的局部池化聚合输出值遵循:

$ x_i^* = \begin{array}{*{20}{c}} { \displaystyle \sum\nolimits_j {{\alpha _j}{x_j}} } \end{array} $

(7)

$ {\alpha _j} = \dfrac{{{{\rm{e}}^{ - d({x_i}, {x_j})}}}}{{\begin{array}{*{20}{c}} { \displaystyle \sum\nolimits_k {{{\rm{e}}^{ - d({x_i}, {x_k})}}} } \end{array}}} $

(8)

式(8)基于坐标之间的欧式距离 $d({x_i}, {x_j})$ 衡量像素的近似程度, 并通过归一化处理获得每个输入点对应的权值 ${\alpha _j}$ , 形成一个参数化的池化窗口, 如图3中权重矩阵(weights), 窗口中的元素为权重参数, 且所有参数在相同通道内共享.

3.3 全局交叉注意力模块

卷积神经网络中, 卷积运算仅能处理空间局部邻域, 需要不断堆叠卷积层才能获得全局信息. 而非局部神经网络提出通过非局部运算建立长距离像素之间的联系, 捕获两个像素之间的依赖.

非局部运算是计算机视觉中经典的非局部均值运算的一种泛化结果. 直观上看, 非局部运算将某一处位置的响应作为输入特征映射中所有位置的特征加权和来进行计算(如图4所示). 当计算 ${x_1}$ 对应的输出 ${y_1}$ 时, 先计算任一位置 ${x_j}$ 对 ${x_1}$ 的响应 ${s_{1, j}} = sim({x_1}, {x_j})$ , 响应值作为特征映射 $r({x_j})$ 的权重, 通过逐个 ${s_{1, j}}$ 与 $r({x_j})$ 相乘并求和得到对应位置输出 ${y_1}$ , 同理可得其他任一 ${x_i}$ 对应输出 ${y_i}$ .

非局部神经网络模块可以通过关注图片或特征图中所有位置, 在嵌入空间中直接计算相似度矩阵, 可以考虑包括该位置自身在内的所有位置特征的加权, 不必局限于邻域空间, 避免堆叠运算, 因此能够高效汇聚信息. 同时, 该模块可以保证输入、输出尺度不变, 易于嵌入各种网络框架中, 在静态图像识别和视频分类任务中展现出其强大能力^[22].

受非局部神经网络结构的启发, 本文定义了全局交叉注意力通式如下:

$ {y_i} = \begin{array}{*{20}{c}} { \displaystyle \sum\nolimits_j {\frac{{{{\rm{e}}^{sim({x_i}, {x_j})}}}}{{ \displaystyle \sum\nolimits_j {{{\rm{e}}^{sim({x_i}, {x_j})}}} }}{r_j}} } \end{array} $

(9)

其中, $i$ 是一个图像空间中目标输出的位置索引, $j$ 是枚举所有上下文位置的索引. ${r_j}$ 是上下文像素表征向量, 与非局部神经网络中特征映射 $r({x_j})$ 相类似; ${x_i}$ 是坐标值, $sim( \cdot , \cdot )$ 函数接受成对坐标值作为输入, 所有上下文坐标值 ${x_j}$ 对 ${x_i}$ 进行响应并计算二者之间的相似关系, 由 $\displaystyle \sum\nolimits_j {{{\rm{e}}^{sim({x_i}, {x_j})}}}$ 进行归一化后, 与对应的特征映射 $r({x_j})$ 相乘、求和, 输出确定性目标表征向量 ${y_i}$ .

本文采用嵌入空间点积作为 $sim( \cdot , \cdot )$ 函数:

$ sim({x_i}, {x_j}) = \theta {({x_i})^{\rm{T}}}\theta ({x_j}) $

(10)

其中, $\theta ({x_i}) = {W_\theta }{x_i}$ 为 ${x_i}$ 的高维空间嵌入, ${W_\theta }$ 为嵌入矩阵. 全局交叉注意力模块结构如图5所示.

上下文坐标矩阵 $M{{ + }}$ 和完整坐标矩阵 $M$ 通过编码器获得其相对应的高维空间嵌入, 且通道数与上下文表征矩阵 ${R_{M{{ + }}}}$ 相同, 上下文坐标高维空间嵌入经过展平、通道变换, 并通过压缩消除元素值为0的未知信息干扰, 获得维度为 $(h' \times w', c)$ 的矩阵 ${M_1}$ , 完整坐标高维空间嵌入经展平得到维度为 $(h \times w, c)$ 的矩阵 ${M_2}$ . ${M_1}$ 、 ${M_2}$ 通过矩阵乘法, 获得元素值为 $sim({x_i}, {x_j})$ 的权重矩阵, 并经过 ${\textit{Softmax}}$ 归一化处理, 得到元素值为 ${{{\rm{e}}^{sim({x_i}, {x_j})}}} \mathord{\left/ {\vphantom {{{{\rm{e}}^{sim({x_i}, {x_j})}}} { \displaystyle \sum\nolimits_j {{{\rm{e}}^{sim({x_i}, {x_j})}}} }}} \right. } { \displaystyle \sum\nolimits_j {{{\rm{e}}^{sim({x_i}, {x_j})}}} }$ 的权重矩阵 ${M_c}$ . 上下文表征矩阵 ${R_{M{{ + }}}}$ 经过展平、压缩处理, 得到维度为 $(c, h' \times w')$ 的矩阵 ${R_1}$ . ${R_1}$ 与 ${M_c}$ 通过矩阵乘法和行列重组(reshape)获得确定性目标表征 ${R_{{\rm{pred}}}}$ . 全局交叉注意力模块灵活性高, 可以便捷地插入面向图像的神经过程中进行使用, 经过全局交叉注意力模块的处理, 确定性目标表征 ${R_{{\rm{pred}}}}$ 中的每个元素, 均为全部上下文信息的特征映射对某一位置响应的加权和, 便于任一位置关注与其密切相关的上下文信息, 也可以通过模块堆叠, 进一步建模细粒度的局部结构, 通过解码获得更加精准的细节特征.

上下文表征矩阵 ${R_{M{{ + }}}}$ 经过展平、压缩处理, 得到维度为 $(c, h' \times w')$ 的矩阵 ${R_1}$ . ${R_1}$ 与 ${M_c}$ 通过矩阵乘法和行列重组获得确定性目标表征 ${R_{{\rm{pred}}}}$ . 全局交叉注意力模块灵活性高, 可以便捷地插入面向图像的神经过程中进行使用, 经过全局交叉注意力模块的处理, 确定性目标表征 ${R_{{\rm{pred}}}}$ 中的每个元素, 均为全部上下文信息的特征映射对某一位置响应的加权和, 便于任一位置关注与其密切相关的上下文信息, 也可以通过模块堆叠, 进一步建模细粒度的局部结构, 通过解码获得更加精准的细节特征.

基于注意力的面向图像的神经过程模型形式多种多样, 本文设计的IFANP模型仅仅是利用局部池化聚合和全局交叉注意力对IFNP进行改进的一种方式. 由于在具体实验过程中, 该模型相较于IFNP和其他形式注意力面向图像的神经过程表现出更强的图像补全能力(详见实验分析第4.2节), 因此特地做以下介绍.

4 实验分析

本节按照上文设计搭建了面向图像的神经过程(IFNP)模型和面向图像的注意力神经过程(IFANP)模型. 为了便于评估模型性能, 本文复现了神经过程(NP)作为基准进行对比, 同时复现了同样基于自编码器结构的自监督模型变分自编码器(VAE)进行比较分析, 且以上模型结构和参数量均相近, 具有较强的可比性.本节分为两个部分, 在第4.1节中以视觉感官为标准, 定性分析VAE、NP、IFNP和IFANP模型在图像补全任务中数据补全能力的差异, 展示IFANP模型在拟合上下文数据方面的明显优势; 在第4.2节中, 通过调整IFANP模型中注意力模块, 定量比较基于不同形式注意力机制的面向图像的神经过程图像性能差异.

实验使用手写数字图片MNIST和人脸数据CelebA^[26]两种数据集, 其中MNIST为28×28大小的黑白灰度图像, CelebA为32×32大小的RGB彩图; 数据集均使用60000张图片作为训练集, 5000张图片作为测试集.

4.1 数据补全及上下文细节拟合能力比较

在面对图像补全任务时, IFNP的优势之一是可以从上下文数据中灵活迅速地学习出函数近似分布, 特别是IFANP, 可以通过采样函数、输入目标像素坐标, 实现像素级预测, 因此在数据补全方面展现出更强的性能; 而变分自编码器以整张图片为预测目标, 在应对复杂纹理图片时, 预测结果的细节方面不佳.

为比较不同模型的图像补全能力, 本文先后使用MNIST数据集和CelebA数据集进行实验. 如图6(a)对手写数字图片补全, 在只给定少量上下文数据(20%)条件下, 使用4个模型对图像分别进行预测. 整体上看, 4个模型能够根据上下文点抽取先验信息, 基本实现了对手写数字的正确推断预测; 相对而言, 由VAE补全的图像细节信息表达不够完全, 数字7腰部手写斜杠未能在补全图像中得到还原, NP和IFNP补全的图像能体现出一定细节拟合能力, 在对手写数字补全时, 视觉效果差距不大, IFANP补全图像的特征则更为鲜明, 数字4、数字9的整体大小、长宽比例和倾斜角度与真实图像最为接近, 直观上看相似度最高.

在对人脸数据集补全实验中, 如图6(b)所示, 可以发现VAE补全效果差距更加明显, 仅可以生成人脸, 但却无法体现头部姿态甚至性别. 而NP和IFNP受限于上下文数据量, 模型会从大量的训练样本中寻找与上线文点可能相近的图像, 并最终收敛于较为相似的面孔, 如对人脸2的补全中, 两个模型不仅在肤色、脸型、五官等方面无法体现出个性化特征, 对上下文数据的拟合也表现出明显差距, 人脸的大小、位置与真实图像差异明显. 这一结果验证了在NP和IFNP模型中, 上下文表征经取平均值(或均值池化)操作, 限制了预测不同目标像素时上下文数据差异性表达, 面对更为复杂的人脸数据集时, 表现不佳. IFANP利用局部池化聚合(LPA)模块平滑图像表征获得更为普遍的人脸特征的同时, 通过全局交叉注意力(GCA)模块充分利用上下文数据, 对不同目标像素的预测给予差异化的上下文数据权重, 因此能够对人脸数据集表现出更好的补全效果.

为了进一步验证IFANP的数据补全和上下文点拟合能力, 本文使用人脸图像的上半部分作为上下文数据, 遮罩后未知像素更加集中, 补全任务难度更大. 如图7(a)所示, 通过多次采样补全结果, 以采样2为例, 可以发现IFANP补全结果与真实图像在发型、脸型等方面相似度更高, 拟合能力更强; 而IFNP的补全结果趋于“大众脸”, 整体上看, 3次采样均未体现出真实图像的面部特征. 在图7(b)中, 真实图像上半部分与采样图像下半部分拼接, 结果显示IFANP与真实图像衔接更加自然, 面部轮廓与真实图像更加接近, 表现出该模型在细节拟合方面的明显优势.

4.2 基于不同形式注意力机制的面向图像的神经过程性能比较

第4.1节实验说明, IFANP对图像补全时, 由于加入注意力机制, 在细节刻画方面显示出优于VAE、NP和IFNP的补全能力. 那么注意力机制是如何影响到模型效果的. 本文以各注意力模块组合为对比, 将面向图像的神经过程(IFNP)、基于压缩激活网络(squeeze-and-excitation networks, SENet)^[27]的面向图像的神经过程(IFANP (SENet))、基于局部池化聚合模块的面向图像的神经过程(IFANP (LPA))、基于全局交叉注意力模块的面向图像的神经过程(IFANP (GCA))和本文提出的注意力面向图像的神经过程(IFANP)继续应用于人脸数据集补全任务, 结合KL散度、均方误差(mean squared error, MSE)、峰值信噪比(peak signal-to-noise ratio, PSNR)指标和视觉效果做以说明.

KL散度(见式(6))是衡量两个概率间差异的非对称性度量, 其数值越小, 代表补全图像和真实图像的隐变量 ${\textit{z}}$ 服从的概率分布差异越小, 其数值越大, 代表模型的生成能力越强. MSE是反映估计量与被估计量之间差异程度的一种度量; PSNR指标^[28]则提供了一个衡量图像失真或是噪声水平的客观标准, 单位为dB, 数值越大表示失真越小. 假设完整图像 $y$ 和补全图像 $\hat y$ 分辨率为 $h \times w$ , 图像中可能出现的最大像素值为MAX, 那么MSE和PSNR分别表示为:

$\begin{split} & {\textit{MSE}} = \frac{1}{{hw}}\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^w {{{({y_{i, j}} - {{\widehat y}_{i, j}})}^2}} } \\ &{\textit{PSNR}} = 10 \cdot {\log_{10}}\left(\frac{{{{\textit{MAX}}^2}}}{{{\textit{MSE}}}}\right) \end{split} $

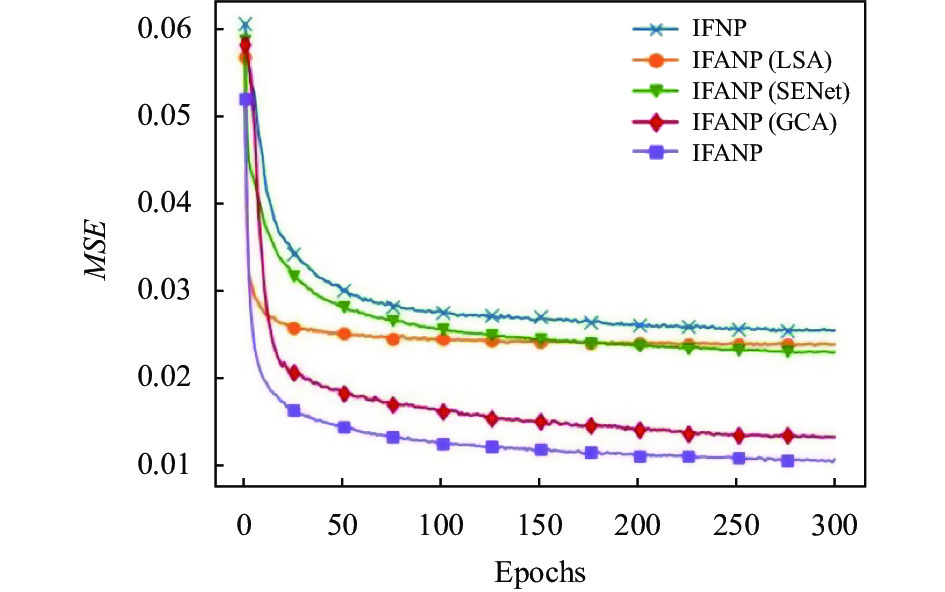
实验训练过程中, 每次迭代采用数量相同且随机采样30%至60%比例范围的图像像素作为上下文数据; 测试阶段, 不同模型采用完全相同的上下文数据, 数量分别占比真实图像20%、40%、60%. 训练和测试阶段以完整图像作为补全目标. 除注意力模块外, 均采用相同的表征变量维度和编码器、解码器结构. 实验结果如图8、图9及表1所示.

图8中, 5种模型最终基本都达到收敛, 与面向图像的神经过程相比, 4种基于注意力机制的面向图像的神经过程均方误差下降速度更快. 基于不同形式注意力机制的面向图像的神经过程中, 本文提出的IFANP模型收敛速度更快, 收敛时PSNR值更高.

结合表1, 对收敛的模型进行测试, IFANP使用不同比例上下文数据条件下, 补全图像的MSE值更小、PSNR更大, 说明补全图像失真更小、质量更高, 进一步说明IFANP补全图像与真实图像更为接近.

另外, 由图9中可以看到, IFNP、IFANP (LPA)和IFANP (SE-Net)在少量上下文数据(20%)情况下, 能生成不同预测结果, 具有更强的生成能力, 这与表1中, 以上3个模型测试结果KL散度更大相吻合. 而IFANP (GCA)和IFANP与前三者的补全效果相比, 质量更高, 直观上看与原始图像更加接近.

分析以上实验结果, 不难看出, 以VAE为代表的生成模型与IFNP相比有较大差距, 在图像信息更为复杂的人脸数据集上, IFANP的细节信息更为丰富, 与上下文数据的拟合能力更强. 不同形式的注意力机制中, IFNP、IFANP (LPA)和IFANP (SE-Net)在生成能力更强; 而本文改进提出的IFANP在保持一定生成能力的情况下, 具备更强的预测精准度.

5 结束语

本文将卷积神经网络(CNN)与神经过程(NP)相结合, 提出了一种用于图像补全的神经过程模型: 面向图像的神经过程(IFNP). 作为一种适用于图像处理的基础模型, IFNP继承了NP灵活抽取先验知识和线性复杂度的优势, 并展现出易于拓展的特点. 在IFNP基础上, 本文借鉴池化操作和非局部神经网络思想, 设计局部池化聚合和全局交叉注意力模块对其改进, 构建了面向图像的注意力神经过程(IFANP)模型. 与VAE、NP等其他生成模型相比, IFANP在以少量数据为上下文点条件下, 获得与真实图像相似度更高、图像轮廓衔接更加流畅的补全效果, 展现出了更强的数据补全和细节拟合能力. 通过基于不同注意力机制的IFANP模型比较, 本文提出的IFANP模型补全图像质量更高、损失更小.

本文提出的IFNP模型侧重于处理图像数据, 但直观上看, IFNP与IFANP都未能避免NP补全图像结果视觉效果不够清晰的问题. 下一步将会尝试实现对补全图像的超分重构和锐化, 以解决现有模型补全图像清晰度不高的问题. 另外, IFNP及IFANP均使用像素作为模型的输入, 而近期ViT (vision transformer)^[29]及遮罩自编码器(masked auto-encoder, MAE)^[30]等模型均尝试将图像切分为小块(patch), 以此作为模型输入, 克服了输入序列长度对注意力模块的影响. 因此, 在接下来的工作中, 拟采用类似手段改进模型.