随着城市化的演进, 地铁以快速便捷, 载客量大等优势, 逐步发展为城市公共交通的首选. 作为城市发展的标志, 地铁不仅为人民日常出行带来了便利, 也为拉动经济做出卓越的贡献, 然而, 由于工程施工周期长, 风险系数高及地质多样性、施工技术限制和过程规范性不足等因素会导致隧道结构发生形变, 而累积形变则会影响结构安全, 发生重大安全事故, 因此需要对施工期隧道的结构进行全方位监测, 以保障人民生命财产安全.

地下环境对通信网络具有很强的限制, 且存在环境恶劣, 作业空间小的缺陷, 施工期隧道主要依赖高精度传感器, 但传感器所收集的数据并不能直接用于分析或安全评估, 主要原因如下: (1) 测量环境存在随机噪声; (2)施工现场存在电磁干扰; (3) 传输线存在信号衰减; (4) 电源电压存在波动; (5) 传感器本身存在硬件误差. 因而需要对传感器直接采集到的数据进行过滤和清洗, 去除测量之中存在的噪声, 尽可能的“还原”出真实值, 以供后续的数据分析工作.

针对传感器监测数据的去噪方法主要有时域滤波和频域滤波^[1]. 常用时域滤波方法如算数平均滤波、中值滤波、滑动平均滤波等都是设置一个滑动窗口, 并基于数据的统计特性进行平滑, 这些方法虽然原理简单, 但计算量较大, 且在实时处理中若对数据一无所知则易发生严重偏移; 传统的频域滤波器 (高通/低通/带通) 需要把信号从时域变换到频域再设定相应阈值进行去噪, 这类方法通常无法还原信号序列的细节; 小波理论是时域-频域滤波的一个新发展, 其克服了傅里叶变换的缺陷, 将信号经过小波变换后得到一系列分解的小波, 再通过分析小波系数对信号进行重构从而达到消噪. 但小波理论在分解过程中的基函数、阈值函数及每一层的阈值选取方面困难较大.

施工隧道结构安全监控数据具有强实时、无先验知识及存在少量异常突变的特点, 以上方法难以直接使用. 卡尔曼滤波器(Kalman filter, KF)^[2] 作为一种针对传感器数据的无监督滤波算法, 通过结合模型的估计值来动态调整观测数据, 从而剔除随机干扰、逼近真实值, 达到去除噪声的目的. 该方法基于系统状态空间模型, 仅需 $ k-1 $ 时刻的估计值及 $ k $ 时刻的观测值即可计算出 $ k $ 时刻的估计值, 其递归特性也彰显了KF适用于在线实时动态系统的数据处理. 另外, 由于KF算法针对线性系统进行设计, 在非线性系统方面, 多位学者进行了研究, 其中应用最为广泛的当属扩展卡尔曼滤波器(extended Kalman filter, EKF)^[3] 和无迹卡尔曼滤波器 (unscented Kalman filter, UKF)^[4]. KF及其扩展算法自被提出起就广泛应用于定位导航、目标检测与追踪、信号处理以及数据融合等多个领域.

1 基本原理与研究现状 1.1 线性卡尔曼滤波器 1.1.1 基本原理

线性离散系统的系统方程可以描述为:

$ {x}_{k}={F}_{k-1}{x}_{k-1}+{B}_{k-1}{u}_{k-1}+{w}_{k-1} $

(1)

$ {{\textit{z}}}_{k}={H}_{k}{x}_{k}+{v}_{k} $

(2)

式(1)为状态更新方程. $ {x}_{k} $ 为 $ k $ 时刻信号的状态变量, 即信号的真实值; $ {F}_{k-1} $ 为从 $ k-1 $ 时刻到 $ k $ 时刻的转移矩阵; $ {u}_{k-1} $ 和 $ {B}_{k-1} $ 是系统外部已知的控制输入及其对应的矩阵; $ {w}_{k-1} $ 表示从 $ k-1 $ 时刻到 $ k $ 时刻系统自身产生的过程噪声. 式(2)为观测方程. $ {{\textit{z}}}_{k} $ 为 $ k $ 时刻的实际观测值; $ {H}_{k} $ 为量测矩阵, 表示真实值与观测值之间的变化关系; $ {v}_{k} $ 表示 $ k $ 时刻观测时的随机噪声. 其中, KF对过程噪声和观测噪声做了严格的假设: $ {w}_{k} $ 和 $ {v}_{k} $ 均为高斯白噪声, 即它们分别服从均值为0, 协方差为 $ {Q}_{k} $ 和 $ {R}_{k} $ 的高斯分布.

KF的原理即为通过不断地预测和更新校正来去除噪声、获取信号的真实值, 算法实现主要可以分为2个过程: 预测和更新.

预测步是直接使用 $ k-1 $ 时刻校正过的后验估计值得到的, 其结果称为 $ k $ 时刻的先验估计, 也可称为预测值, 计算公式为式(3)、式(4), 其中 $ {P}_{k|k-1} $ 是先验误差协方差.

$ {\widehat{x}}_{k|k-1}={F}_{k-1}{\widehat{x}}_{k-1}+{B}_{k-1}{u}_{k-1} $

(3)

$ {P}_{k|k-1}={F}_{k-1}{P}_{k-1}{F}_{k-1}^{\rm T}+{Q}_{k-1} $

(4)

更新步的主要思想为引入观测值对预测步中的先验估计进行修正, 其原理为式(5)–式(7). $ {K}_{k} $ 为卡尔曼增益, 它是在误差协方差最小的原则上求出来的, 作用为引入观测值并动态调整估计值, $ {K}_{k} $ 的大小决定了滤波结果的偏向性; $ {\widehat{x}}_{k} $ 则为结合了预测值和观测值的 $ k $ 时刻滤波后的真实值, 而 $ {P}_{k} $ 则为校正后的误差.

$ {K}_{k}={P}_{k|k-1}{H}_{k}^{\rm T}{({H}_{k}{P}_{k|k-1}{H}_{k}^{\rm T}+{R}_{k})}^{-1} $

(5)

$ {\widehat{x}}_{k}={\widehat{x}}_{k|k-1}+{K}_{k}({{\textit{z}}}_{k}-{H}_{k}{\widehat{x}}_{k|k-1}) $

(6)

$ {P}_{k}= (I-{K}_{k}{H}_{k}){P}_{k|k-1} $

(7)

1.1.2 参数设置

首先针对系统方程的参数设置, $ {F}_{k-1} $ 联系了 $ k-1 $ 到 $ k $ 时刻的状态变化过程, 当监测数据为一维标量值时, 可设置此值为1^[5]; 在系统没有外部控制时, $ {u}_{k-1} $ 和 $ {B}_{k-1} $ 为0; 在传感器所得观测值与所求状态值一致时, $ {H}_{k} $ 为1.

$ {w}_{k-1} $ 和 $ {v}_{k} $ 的协方差矩阵 $ {Q}_{k} $ 和 $ {R}_{k} $ 分别表示对模型和观测的信任程度, 它们的值间接影响 $ {K}_{k} $ , 故对滤波结果精度影响较大; $ {R}_{k} $ 可以从传感器的精度参数得出, 而 $ {Q}_{k} $ 则通常根据经验设置.

另外, 递归算法的推动还需要设定第1个估计值 $ {\widehat{x}}_{0} $ 及其误差 $ {P}_{0} $ , 它们的设置对滤波结果的影响效果很小^[6], 实际工程中 $ {\widehat{x}}_{0} $ 通常取第1个观测值, 而 $ {P}_{0} $ 则可以用测量数据的波动情况表示.

1.2 非线性卡尔曼滤波器

非线性离散系统的系统方程可以描述为:

$ {x}_{k}=f({x}_{k-1}, {u}_{k-1}, {w}_{k-1}) $

(8)

$ {{\textit{z}}}_{k}=h({x}_{k}, {v}_{k}) $

(9)

EKF是一种针对非线性系统常用的滤波算法, 其核心思想为通过一阶泰勒展开将非线性的函数 $ f\left(x\right) $ 和 $ h\left(x\right) $ 展开为线性函数, 从而转入KF计算流程. 其预测和更新过程如下:

$ {\widehat{x}}_{k|k-1}=f({x}_{k-1}, {u}_{k-1}, \mathrm{ }0) $

(10)

$ {P}_{k|k-1}={F}_{k-1}{P}_{k-1}{F}_{k-1}^{\rm T}+{{w}_{k-1}Q}_{k-1}{w}_{k-1}^{\rm T} $

(11)

$ {K}_{k}={P}_{k|k-1}{H}_{k}^{\rm T}{({H}_{k}{P}_{k|k-1}{H}_{k}^{\rm T}+{{v}_{k}R}_{k}{v}_{k}^{\rm T})}^{-1} $

(12)

$ {\widehat{x}}_{k}={\widehat{x}}_{k|k-1}+{K}_{k}[{{\textit{z}}}_{k}-h\left({\widehat{x}}_{k|k-1}, \mathrm{ }0\right)] $

(13)

$ {P}_{k}=(I-{K}_{k}{H}_{k}){P}_{k|k-1} $

(14)

1.3 卡尔曼滤波器在隧道数据处理中的研究

在隧道变形监测方面, KF常常用于变形趋势的预测. 陈冠宇等人^[7]和陈大勇等人^[8]直接将KF应用于隧道沉降数据, 实验证明滤波前后的降噪效果明显, 数据曲线更为平滑; Han等人^[9]针对过程噪声 $ Q $ 和观测噪声 $ R $ 结合滑动窗口根据极大似然估计推导出 $ Q $ 和 $ R $ 的计算公式, 算法可自适应调整 $ Q $ 和 $ R $ 的值, 提高了滤波器的精度和容错性; 钱建国等人^[10]和王宾宾等人^[11]对比了经典KF和基于方差补偿的自适应KF在沉降数据的去噪效果, 结果表明自适应算法的滤波和预测效果更好; Yi等人^[12]针对有色噪声通过Yule-Walker算法计算出自适应参数, 并借助KF结构提出一种在线去噪算法, 在混凝土结构监测数据上证明了算法的有效性.

本文通过研究经典卡尔曼滤波器, 发现其在抗野值, 噪声估计以及非线性系统的适应性方面性能较差, 从而导致滤波数据发生严重偏移, 针对以上问题, 提出了一种自适应噪声优化的可靠卡尔曼算法, 通过对野值数据的合理补偿及对噪声的实时估计, 进一步优化了系统的建模精度, 获得更准确的滤波结果.

2 可靠卡尔曼过滤算法设计 2.1 野值处理

在施工掘进过程中, 传感器的传输线不可避免地会被破坏, 系统将此时的测量值定义为与正常测量范围有巨大偏差的数值, 称这样的值为野值^[13]. 在一个相对稳定的环境, KF可获得很好的去噪效果, 但若系统中存在野值, 会严重影响滤波效果, 甚至导致滤波发散, 从而影响后续数据分析.

2.1.1 野值检测

根据野值的定义, 其检测准则归结到底即为合适的阈值设计. 常用的野值检测方法如奈尔准则^[14]等都需要提前获知整个数据列的统计特性, 不适用于动态系统; 而根据统计特性设计的SD、MAD和IQR方法^[15]在野值严重偏离正常数据时, 会直接影响计算结果从而使阈值失效.

在KF中, 将观测值与预测值的差值称为新息, 其定义为式(15). 观测野值也正是通过影响新息值从而影响卡尔曼增益, 并最终使滤波结果出现巨大偏差, 因而从新息值角度选取合适阈值进行野值的检测与判断.

由于土压力数据中野值与正常测量值差距悬殊, 根据工程制定的报警阈值和传感器自身量程, 当 $ {\widehat{e}}_{k} > 300 $ kPa时, 判断为野值.

$ {\widehat{e}}_{k}={{\textit{z}}}_{k}-{H}_{k}{\widehat{x}}_{k|k-1} $

(15)

2.1.2 野值补偿

在判断出野值后, 一种简单的想法是直接用KF滤波值代替, 但这种方法存在着以下问题: (1)直接使用预测值, 使得观测值丧失意义, 若野值连续长时间出现甚至可能导致滤波发散; (2) KF虽然能在一定程度上“拉回”野值, 但其作用有限, 使用预测值在后续工作中依然无法消除异常值带来的影响.

由于数据带有明显的趋势性, 常用的填充方法不再适用^[16], 本文依数据特点选取结合滑动窗口的最小二乘法进行野值补偿.

最小二乘法是一种经常用于工程领域的曲线拟合方法, 其根本思想为遵循最小化误差平方原则(式(16)), 根据数据特点选取合适的基函数, 构造合适的拟合函数, 并代入已有的观测数据并求解该函数的参数, 从而得到最佳拟合方程. 其中 $ {y}_{i} $ 为已知的观测数据, $ f\left({x}_{i}\right) $ 为最佳拟合函数上的计算值.

$ \epsilon=\sum _{i=\mathrm{ }1}^{n}{\left(f\left({x}_{i}\right)-{y}_{i}\right)}^{2} $

(16)

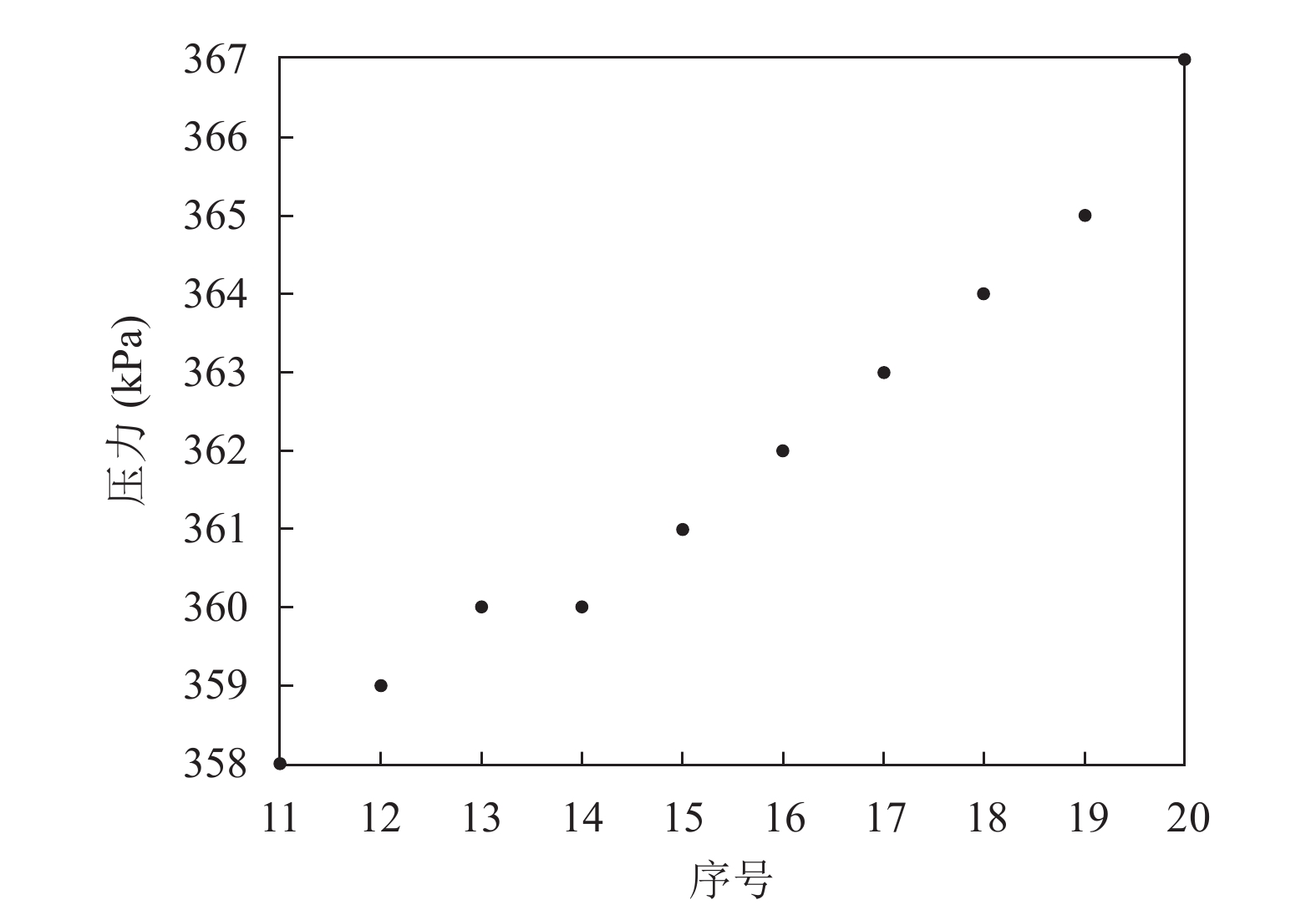
通过分析数据可以发现: 如图1所示, 在局部范围内, 数据变化的趋势基本为线性. 故本文采用线性最小二乘法进行计算, 选取基函数为 $1, x, {x}^{2},\cdots, {x}^{n}$ , 阶数为1.

由于系统为实时采集的动态系统, 且传输线在损坏后修复需要一定的时间, 故野值通常连续出现, 鉴于此, 使用滑动窗口进行局部拟合数据, 以更好地适应数据趋势. 设置滑动窗口初始大小为0, 最大值为11, 结合滑动窗口的野值检测与补偿算法如算法1.

算法1. 野值检测与补偿算法

1) 读入 $\scriptstyle {{\textit{z}}}_{k} $ , 计算 $\scriptstyle {\textit{size}}\left(window\right)$ .

2) 计算 $\scriptstyle k $ 时刻的新息值 $\scriptstyle {\widehat{e}}_{k} $ , 若 $ \scriptstyle {\widehat{e}}_{k} > 300 $ 则转入3), 否则转入6).

3) $\scriptstyle {{\textit{z}}}_{k} $ 是野值, 若 $\scriptstyle {\textit{size}}\left(window\right)=11$ 则转入4), 否则转入5).

4) 将 $\scriptstyle {{\textit{z}}}_{k-10} $ 至 $\scriptstyle {{\textit{z}}}_{k-1} $ 作为最小二乘的参数, 拟合函数为 $\scriptstyle f\left(x\right)={a}_{k}x+{b}_{k} $ , $\scriptstyle {{\textit{z}}}_{k}=f\left(11\right) $ , 转入6).

5) 将 $\scriptstyle {{\textit{z}}}_{k-{\textit{size}}\left(window\right)+1}$ 至 $\scriptstyle {{\textit{z}}}_{k-1} $ 作为最小二乘的参数, 拟合函数为 $ \scriptstyle f\left(x\right)={a}_{k}x+{b}_{k} $ , $ \scriptstyle {{\textit{z}}}_{k}=f\left(k\right) $ 转入6).

6) 若 $\scriptstyle {\textit{size}}\left(window\right)=11$ , 窗口向后滑动, 否则转入7).

7) 若 $\scriptstyle k $ 为最后一个检测时刻, 则结束算法, 否则转入8).

8) $\scriptstyle k++ $ , 转入1)进入下一轮迭代.

2.2 自适应噪声的卡尔曼滤波器

由第1节可知, 滤波后真实值的校正信息主要由卡尔曼增益决定, 即归根到底是由系统中的噪声决定的, 在KF中, 不仅假定噪声为高斯白噪声, 而且需要在初始化时对噪声协方差进行赋值. $ {Q}_{k} $ 和 $ {R}_{k} $ 的取值直接影响滤波效果, 若直接定值为常数, 存在以下缺陷: (1)实际工程往往无法得知较为准确的噪声值; (2)动态系统的噪声并非固定不变.

由此提出改进的卡尔曼滤波器, 递推过程如下:

$ {\delta }_{1}\left(k\right)=\sqrt{{{E}_{k-1}}^{2}+{({x}_{k-1}-{x}_{k-2})}^{2}} $

(17)

$ {\delta }_{2}\left(k\right)=\sqrt{{({{\textit{z}}}_{k-1}-{x}_{k-1})}^{2}} $

(18)

$ {K}_{k}=\frac{{{\delta }_{1}\left(k\right)}^{2}}{{{\delta }_{1}\left(k\right)}^{2}+{{\delta }_{2}\left(k\right)}^{2}} $

(19)

$ {x}_{k}={x}_{k-1}+{K}_{k-1}({{\textit{z}}}_{k}-{x}_{k-1}) $

(20)

$ {E}_{k}=\sqrt{1-{K}_{k-1}}{\delta }_{1}\left(k\right) $

(21)

算法从自适应噪声变化规律角度提出改进, $ {E}_{k} $ 为第 $ k $ 次测量的误差, 即通过增益矫正过的后验误差; $ {\delta }_{1}\left(k\right) $ 为预测误差, 系统动态估计过程中, 过程噪声主要由硬件误差引起, 假设噪声为白噪声, 则噪声协方差 $ {Q}_{k} $ 可以描述为 $ {({x}_{k-1}-{x}_{k-2})}^{2} $ , 则第 $ k $ 次的预测误差构造为第 $ k-1 $ 次测量的误差值向量与第 $ k $ 次的噪声向量的和; $ {\delta }_{2}\left(k\right) $ 为测量噪声, 在第 $ k $ 次测量时, 其系统累积的测量噪声可直接由第 $ k-1 $ 次测量的观测值和真实值得出; $ {K}_{k} $ 和 $ {x}_{k} $ 分别为校正增益和真实值, 与KF计算思想一脉相承.

在初值设定方面, 设 $ {x}_{0}={{\textit{z}}}_{1} $ , $ {x}_{-1}={{\textit{z}}}_{-1}=0 $ , $ {E}_{0}=0 $ .

该可靠卡尔曼算法 (reliable Kalman filter, RKF)摒弃了传统算法中在初始化时对噪声的常数式假定, 从噪声产生的物理意义出发, $ {Q}_{k} $ 和 $ {R}_{k} $ 直接由上一时刻结果得到, 遵循KF的“一步调整”思想, 自适应地调整系统噪声, 从而达到更精确的建模和估计.

3 实验分析

本文数据来源为北京某在建地铁线, 种类为拱肩土压力, 共6 380条, 数据有以下特点: (1)前期为断面区域施工期, 后期为基本稳定期, 整体呈先上升后下降最后逐渐平稳; (2)存在极少量野值, 占数据总量≤0.3%. 由于数据量较大, 图形不易辨别, 取前100条数据进行研究, 其中第29–44条为野值.

3.1 野值对滤波结果的影响

在传输线被破坏时, 传感器收集的数据显示为1 500 kPa, 为极度偏离正常值的野值. 虽然野值出现的概率非常低, 但若不加处理直接使用KF, 观测值对滤波结果的影响依然很大. 经实验, 原始数据直接使用KF, 此时RMSE高达195.484 6; 由于野值数量极低, 若直接删除, RMSE则骤降至4.989 0, 彰显了野值处理的重要性.

为了验证本文所提野值补偿方法的有效性, 首先将第11至20条数据设置为干扰野值(1 500 kPa), 分别对其使用本文方法及常用的均值补偿方法, 结果对比如表1所示, 使用滑动最小二乘法补偿后数据的最大误差为3.20, 而传统均值补偿后最大误差为10.40, 这也证明了统计特性方式的补偿方法难以用于趋势性数据.

由此, 将此方法应用于实际野值数据, 图2为补偿数据前后的数据对比. 图2(a)为补偿效果图, 补偿前后数据的方差从171 483.809 6下降至197.485 3, 数据趋势明显更加平稳; 图2(b)中的实线即为补偿后的数据, 可以看出数据整体呈先上升后下降, 且局部还有不少波动, 非线性特征明显. 在补偿效果具体细节方面, 表2为野值补偿前后的数据值, 可以看出, 结合滑动窗口的最小二乘拟合补偿的数据基本符合原始数据段递增的变化规律. 从工程角度来看, 野值出现的原因是传感器传输线被破坏, 即施工操作较剧烈, 经与工程进度记录相比较, 此时间段内断面挖掘频繁, 土压力理应愈来愈大, 与补偿值趋势一致.

遵循第1节中初值的设置规范以及KF的基本原理可以得到: 在处理一维数据时, $ {Q}_{k} $ 和 $ {R}_{k} $ 退化为常数 $ Q $ , $ R $ . KF的滤波结果与初值设置息息相关. KF需要的初值有4个: $ {P}_{0} $ , $ Q $ , $ R $ 和 $ {x}_{0} $ , 其中, $ {x}_{0} $ 通常设置为第一个监测值^[5], 即 $ {x}_{0}=358 $ ; $ {P}_{0} $ 的大小对结果影响不大, 故采用常规方式将其设置为平稳段数据(第3968–6380号数据)的方差值, 值为8.222 6; $ Q $ 和 $ R $ 为过程噪声和测量噪声, 为可调超参数. 表3为调节 $ Q $ 值时的滤波结果对比, 其中计算所用到的 $ R $ 为9: 当用于工程项目时, $ R $ 通常由仪器本身决定, 根据传感器出厂说明可知土压力计测量范围为1 000 kPa, 精度等级为0.3%, 即可计算出测量噪声协方差为9. $ Q $ 为系统噪声协方差, 即建立的状态空间模型和实际值的差距. 由表3数据变化情况可以看出, $ Q $ 越小, 滤波后曲线越平滑, 距离测量值越远; ${Q}$ 越大, 则越接近观测曲线. 在 $ Q $ 值的选取上通常依赖于经验值, 本系统为标量输入, 即状态转换过程确定, 此时 $ Q $ 的取值越小越好, 这样可以保证结果收敛快; 而若 $ Q $ 值过大时, 则有可能收敛过慢甚至发散. 由于在土压力滤波方面目前国内外研究情况较少, 且土体运动情况的局限性较强, $ Q $ 的取值没有过多可参考的经验值, 本文采用常用的标量卡尔曼 $ Q $ 值设定经验, 将 $ Q $ 值固定在[0.01, 1]区间, 并将MAE作为重要参考进行 $ Q $ 值选取: MAE为平均绝对误差, 若MAE<仪器绝对误差, 则选取此值作为 $ Q $ 值. 由仪器精度等级可以得出绝对误差为3 kPa, 即选取MAE<3 kPa时的 $ Q $ 值作为过程噪声协方差, 由表3可得 $ Q=0.55 $ . 另外, 为了验证测量噪声 $ R $ 对滤波结果的影响, 将 $ R $ 作为变量进行调参实验, 结果为表4, 可以看出 $ R $ 对滤波结果的调控与 $ Q $ 相反: $ R $ 越小越接近观测值, $ R $ 越大则越信任估计值.

图3为处理野值前后使用KF的对比. 图3(a)为直接使用KF时的滤波效果, 可以看出含野值的数据对滤波结果的影响巨大, 未经野值处理直接使用KF时, 检测值远远超过正常的400 kPa. 另外, 由于KF的估计值与观测值相互交织的特性, 使得野值造成的巨大误差会长久地在系统中累积, 影响时间较长. 通过分析整体6 380条数据发现: 第29–44条数据为野值, 而仅16个野值在此之后持续影响近200条数据才通过观测值将真实值“拉回”; 图3(b)为最小二乘法补偿后使用KF的滤波结果, 可以看出, KF滤波后数据明显平缓, 达到去噪效果, 但同时其在局部细节方面表现很差, 例如第40–100条数据明显的趋势波动在滤波后直接被平滑, 抹去了变化痕迹, 与实际土体运动情况差距过大.

虽然整体效果不算理想, 但在滤波效果方面, 直接使用KF滤波时MAE = 80.1058, MSE = 38214.2423, RMSE = 195.4846, 而补偿野值滤波后MAE = 2.9761, MSE = 15.8522, RMSE = 3.9815, 有了明显的提升.

3.2 不同滤波器对滤波结果的影响

由图3(b)可以看出, 由于原始数据的非线性较强, 滤波后数据与原始数据差异较大, 而这在结构安全监测方面有较大的影响, KF有可能将本应该出现报警的值平滑为安全值, 从而导致严重的后果; 也有可能将未达到告警阈值的数据平滑至报警边缘, 从而误报警.

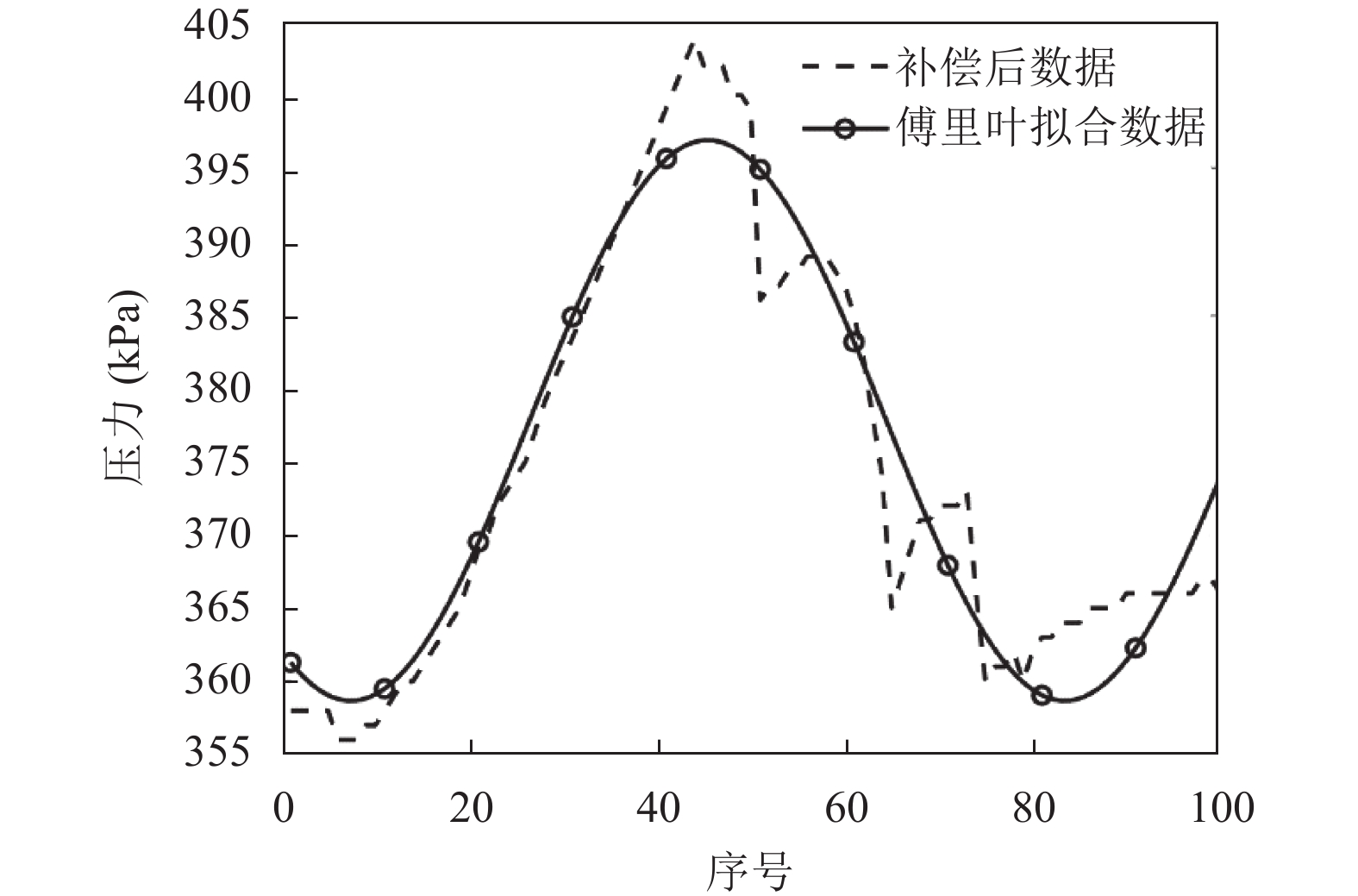
分别使用KF, EKF和本文所提的RKF对数据进行滤波实验. 其中EKF实验中使用Matlab进行傅里叶逼近进行拟合, 拟合函数为: $ f\left(x\right)= 377.8-15.65\mathrm{cos} \left(0.08265x\right)- 11.01\mathrm{s}\mathrm{i}\mathrm{n} \left(0.08265x\right) $ . 拟合后与原始数据的对比如图4所示, 模型拟合优度 $ {R}^{2} $ 为0.931 8.

使用不同滤波器的滤波效果如图5所示, 具体结果如表5所示. 结合图表可以看出, 3种算法滤波后数据都较滤波前更加平滑, 即都具备降噪能力, 而滤波精度则可由滤波值与观测值的接近程度来描述. 由于数据段为非线性, KF滤波结果与实测值差距过大, 尤其在反复波动的情况下, KF无法跟随信号细节, 这也突出了KF在处理非线性问题时的缺陷; EKF在高度拟合的情况下, 大体上能够跟随真实数据变化趋势, 但由于系统非线性程度较高, 在仅进行一次泰勒展开的情况下, RMSE依然较大, 说明EKF在面对强非线性系统时的不足. 实际上, 高精度拟合在工程中难以实现, 从图4中可以看出, 即使是在高精度拟合的情况下, 拟合函数依然很难跟随观测曲线, 第40–80条数据中的3次剧烈变化都被抹去, 而这可能在力学分析中有重要的意义; 另外, 整体数据变化趋势伴随施工过程的进行而呈明显分段, 显然不能用同一个函数拟合所有数据, 这也大大增加了EKF使用的难度; 而RKF直接动态跟踪噪声, 突破了强非线性的限制, 从图5中也可以看出RKF跟踪观测曲线的效果最好, 即精度最高. 表5是3种滤波器的滤波效果对比, 最终结果显示: 由于系统的强非线性, KF和EKF的滤波精度不够高; 而对于RKF来说, 即使是在强非线性环境, 算法依然可以得到很好的滤波效果, 比KF和EKF更加接近观测值, 其RMSE = 0.7068, 比EKF提高了74.53%, 进一步提高了滤波精度.

4 结论与展望

本文在经典卡尔曼滤波器的基础上, 针对其无法有效处理野值及应用于强非线性系统的缺陷, 从实时动态跟踪系统噪声的角度出发, 将新息值作为野值检测指标, 结合滑动窗口使用线性最小二乘方法进行野值补偿, 并将原本需要确切知晓并以常数表示的噪声 $ {Q}_{k} $ 和 $ {R}_{k} $ 用上一时刻的硬件误差及测量误差作为替代, 通过融入最终误差进行分析和计算, 实现了系统噪声的自适应估计, 从而解决野值补偿及精确追踪信号细节的问题. 经实际工程数据的实验分析可知, 本文算法较经典算法有了明显的提升, 具有一定的实用价值.