2. 天津市人工影响天气办公室, 天津 300074;
3. 天津市气象探测中心, 天津 300061
2. Tianjin Weather Modification Office, Tianjin 300074, China;
3. Tianjin Meteorological Observation Center, Tianjin 300061, China
风廓线雷达是利用大气湍流对电磁波的散射作用对大气风场进行探测的设备, 可连续获得测站上空较高时间、空间分辨率的垂直风廓线资料, 研究其在不同天气条件下的变化规律对于改善气象预报服务质量具有重要意义, 因此许多专家学者开展了风廓线雷达数据特征的分析研究.
杨引明等[1]讨论了风廓线雷达的垂直速度和温度资料在强对流天气中的应用. 郑石等[2]运用风廓线雷达数据对南京浦口区短时暴雨过程进行分析, 发现了风廓线雷达产品的水平风廓线、垂直气流和折射率结构常数等在降水过程不同阶段的精细特征. 董保举等[3]利用云南大理的一次暴雨过程, 研究了风廓线雷达资料在降水前和降水期间的不同特征. 陈楠等[4]利用2005–2008年两部风廓线雷达风场数据对南京地区低空急流的活动特征进行了统计分析. 史珺等[5]基于天津地区一次短时强降雨过程, 利用3部风廓线雷达资料和降水实况资料, 对比分析了降水发生、维持和消亡期间风廓线雷达资料的变化特征, 探讨了风廓线雷达对降水天气的监测能力. 王彦等[6]联合应用5部风廓线雷达、多普勒天气雷达组网观测资料、海河流域自动气象站资料详细分析了2012年7月21日海河流域强降水发生、发展过程中温度场、风场演变特征. 周芯玉等[7]利用风廓线雷达对广东前汛期短时强降水类暴雨过程低空风场特征进行了研究. 王佳津等[8]分析了成都两次暴雨期间风廓线雷达观测的低空风场特征.
总体来看, 目前针对不同天气条件下风廓线雷达数据特征的研究多采用的是少量典型天气个例和常规的统计分析, 利用挖掘技术的研究较少. 数据挖掘是从大量数据中发现有价值信息的有效手段, 通信、电力、气象等领域的诸多专家学者将数据挖掘技术引入实际应用, 取得了不错的效果. 林勤等[9]将双聚类算法引入电信高价值客户细分, 实验结果表明, 可挖掘出更多高价值客户群体. 周笑天等[10]、史静等[11]基于关联规则、聚类, 提出了气象数据质量控制的新方法. 刘伟东等[12]利用K均值聚类方法, 将北京地区2007–2010年123个自动气象站夏半年小时降水分为4个区, 进而分析得到了北京地区降水的精细化时空分布特征. 熊亚军等[13]开展了KNN数据挖掘算法在北京地区霾等级预报中的应用研究. 杜良敏等[14]提出了基于聚类分区的中国夏季降水预测模型. 雷景生等[15]利用模糊C均值算法得到了不同区域用户的用电特征. 苟浩峰等[16]基于聚类方法得到了兰州地区自动站降水的精细化特征. 李宗飞等[17]基于聚类开展了X波段双偏振雷达相态识别的研究, 取得了良好的效果. 兰荣亨等[18]以斗鱼直播平台为例, 聚焦于直播平台上的高消费群体, 通过构建观众特征, 采用聚类方法分析高消费群体的行为. 任禹丞等[19]将聚类分析技术应用在电力客户用电问题分析领域, 挖掘出了隐藏的客户用电问题关键信息, 为改进电力客服质量与潜在服务风险预测提供了数据支撑.
天津静海边界层风廓线雷达站已积累了大量的观测资料, 探索基于数据挖掘技术的风廓线雷达数据特征分析方法, 揭示风廓线雷达数据更具普遍性的规律, 为气象预报预测、防灾减灾提供更多参考, 具有非常重要的意义.
本文主要研究了将聚类分析技术应用在风廓线雷达数据特征分析领域, 通过数据预处理及改进的聚类方法, 对风廓线雷达观测数据进行分析. 文中基于聚类技术, 以天津静海风廓线雷达观测数据为基础, 提出了针对风廓线雷达数据分析的改进聚类算法, 并通过实验验证了该方法可快速准确地实现风廓线雷达数据的自动聚类, 挖掘出风廓线雷达数据中更具普遍性的规律, 从而为风廓线雷达数据特征分析提供了新思路, 为气象预报服务提供了新参考依据.
1 聚类模型设计 1.1 K-means算法原理及适用性分析聚类包括基于划分、基于层次、基于密度、基于网格等多种方法, 本文采用基于划分的聚类方法中较为经典的K-means算法. K-means算法把类的形心定义为类的均值, 对包含N个对象的数据集D的聚类处理流程如下:
Step 1. 从数据集中随机选取K个样本作为初始聚类中心C={c1, c2, …, ck}.
Step 2. 针对数据集中每个样本xi, 计算它到K个聚类中心的距离并将其分到距离最小的聚类中心所对应的类中.
Step 3. 针对每个类别ci, 重新计算它的聚类中心.
Step 4. 重复第2步和第3步直到聚类中心不再变化.
K-means方法适合处理数值型数据集, 可对大量数据根据属性进行高效分类. 风廓线雷达数据的探测高度、垂直速度属性均为数值型. 边界层风廓线雷达工作在L波段, 在无降水天气条件下, 接收的信号主要是大气湍流运动造成折射率分布不均匀而产生的散射; 在降水天气条件下, 接收的信号主要是雨滴在入射电磁波极化下作强迫的多极震荡而产生的散射[20, 21]. 不同天气条件下, 风廓线雷达探测能力差别很大. 风廓线雷达的探测原理决定了其在不同天气条件下的探测数据会存在较大差异, 已有个例研究也表明, 风廓线雷达数据的探测高度、垂直速度在降水、晴天等天气条件存在不同规律, 因此, 可将K-means方法应用于风廓线雷达数据探测高度、垂直速度属性的聚类划分.
1.2 基于K-means改进的风廓线雷达数据聚类算法本文选用K-means算法对风廓线雷达数据进行聚类分析, 考虑到传统K-means算法的初始聚类中心随机生成, 容易陷入局部最优, 本文针对初始聚类中心的选择进行了改进, 采用K-means++算法初始化聚类中心, 具体步骤如下:
(1) 从输入样本中随机选择一个样本作为初始聚类中心Ur.
(2) 首先计算每个样本与当前已有聚类中心间的最短距离(即与最近一个聚类中心的距离), 用D(x)表示; 接着计算每个样本被选为下一个聚类中心的概率P, P的计算如式(1)所示. 最后, 按照轮盘法选择出下一个聚类中心.
| P=D(x)2∑x∈XD(x)2 | (1) |
(3) 重复第2步直到选择出K个聚类中心.
1.3 数据规范化方法对于基于距离度量的聚类方法, 数据标准化可以赋予所有属性相等的权重, 避免值域较大的属性与较小值域的属性相比权重过大, 保障聚类效果, 包括最小-最大规范化、Z-score规范化、按小数定标规范化等方法, 本文选用Z-score规范化方法对聚类指标进行预处理, Z-score规范化方法公式如下.
首先计算均值绝对偏差和平均值:
| Sf=1nn∑i=1|Xif−Mf| | (2) |
| Mf=1nn∑i=1Xif | (3) |
其中, Mf为第f个属性的平均值; Sf为第f个属性的均值绝对偏差; Xif表示第i条记录的第f个属性.
然后计算标准化度量值, Zf为标准化后的第f个属性值, 计算公式为:
| Zf=Xif−MfSf | (4) |
对于K-means算法, 聚类数K的选取非常重要. 为避免K值选取上的主观性, 本研究运用肘部法则和轮廓系数两种方法确定最优K值, 这两项指标综合考虑了聚类结构中不同类别样本的离散性和同类别样本的凝聚性.
肘部法则(elbow method)基于如下观察: 增加类个数有助于降低每个类的类内误差平方和(sum of the squared errors, SSE), 这是因为有更多的类可以捕获更细的数据对象类, 类内对象间更为相似. 然而, 如果形成太多的类, 则降低SSE的边际效应可能下降, 因为把一个凝聚的类分裂成两个引起SSE的降幅较小. 绘制SSE关于聚类数K的曲线, 曲线的第一个(或最显著的)拐点即手肘处对应最佳聚类数.
对于包含N个对象的数据集D, 假设D被划分为K个类C1, C2, …, Ck. 对于每个对象o∈D, 其轮廓系数(sihouette coefficient) s(o)的定义如下:
| s(o)=b(o)−a(o)max{a(o),b(o)} | (5) |
其中, a(o)代表对象o与o所属类的其他对象间的平均距离, b(o)代表o与除自身所在类外对象的最小平均距离. a(o)反映了o所属类的紧凑性, b(o)反映了o与其他簇的分离程度.
由定义可知, 轮廓系数值在−1和1之间. 我们计算数据集中所有对象轮廓系数的平均值, 以评估聚类质量. 轮廓系数值越接近1, 代表聚类效果越好.
2 风廓线雷达数据聚类及结果分析 2.1 总体流程本研究针对风廓线雷达数据聚类分析的步骤主要包括: (1)构建风廓线雷达观测信息数据库: 基于风廓线雷达观测的小时数据文件, 解析提取其中不同高度的观测数据, 建立风廓线雷达观测信息数据库. (2)数据预处理: 对存储在风廓线雷达观测信息数据库中的数据, 首先剔除不合理数据, 并按时次统计得到逐时最大探测高度、最大垂直速度; 其次将最大探测高度、最大垂直速度进行规范化处理, 得到聚类指标. (3)聚类分析及特征提取: 利用改进后的K-means算法, 对预处理后的风廓线雷达数据进行聚类, 根据聚类结果、自动站观测的降水及人工观测的云量、天气现象等数据归纳总结出不同天气条件下风廓线雷达数据特征.
2.2 数据来源及预处理研究选取天津静海的风廓线雷达观测数据, 同时结合自动站观测的降水及人工观测的天气现象、云量数据标记各时次天气条件. 天津静海风廓线雷达为CFL-03B型边界层风廓线雷达, 雷达基本技术性能如表1所示. 静海自动站与风廓线雷达站距离在1 km以内, 自动站降水量数据可代表风廓线雷达上空降水情况, 风廓线雷达及自动站皆选用1 h频次数据. 天津地区降水主要发生在5–9月, 故研究时段选取2017–2019年5–9月. 由于静海站相关时段无云量人工观测, 因此云量数据选用距静海站最近的西青站人工观测数据.
| 表 1 风廓线雷达基本性能参数 |
静海风廓线雷达小时观测数据包括66个高度层, 2017–2019年5–9月小时产品数据文件解析入库后得到逐时、分高度层观测数据共计697008条. 通过剔除无效数据, 对风廓线雷达小时观测数据按时次统计得到10553条记录. 本文所使用的垂直速度是风廓线雷达探测到的垂直速度(定义垂直速度向下为正, 向上为负), 未经订正, 所以降水时代表了空气的垂直运动和降水粒子下沉运动的总和, 探测高度指距离地面的高度.
按照GB/T 35663-2017中定义的天气预报基本术语, 根据自动站观测的过去1 h降水量及人工观测的天气现象、云量, 将各时次划分为晴、少云、多云、阴、降水形成(降水发生前1–6 h)、降水期间、降水结束(降水结束后1–3 h) 7种状态, 详细划分规则如下:
(1)若当前时次自动站观测的过去1 h降水量≥0.1 mm或人工观测的天气现象记录有降水, 标记为降水期间; 否则, 转(2).
(2)当前时次未来1至6 h为降水阶段, 标记为降水形成阶段. 否则, 转(3).
(3)当前时次前推1至3 h为降水阶段, 标记为降水结束阶段. 否则, 转(4).
(4)根据人工观测的日均总云量标记天气条件. 日均总云量0–2成, 标记为晴; 3–5成, 标记为少云; 6–8成, 标记为多云; 9–10成标记为阴.
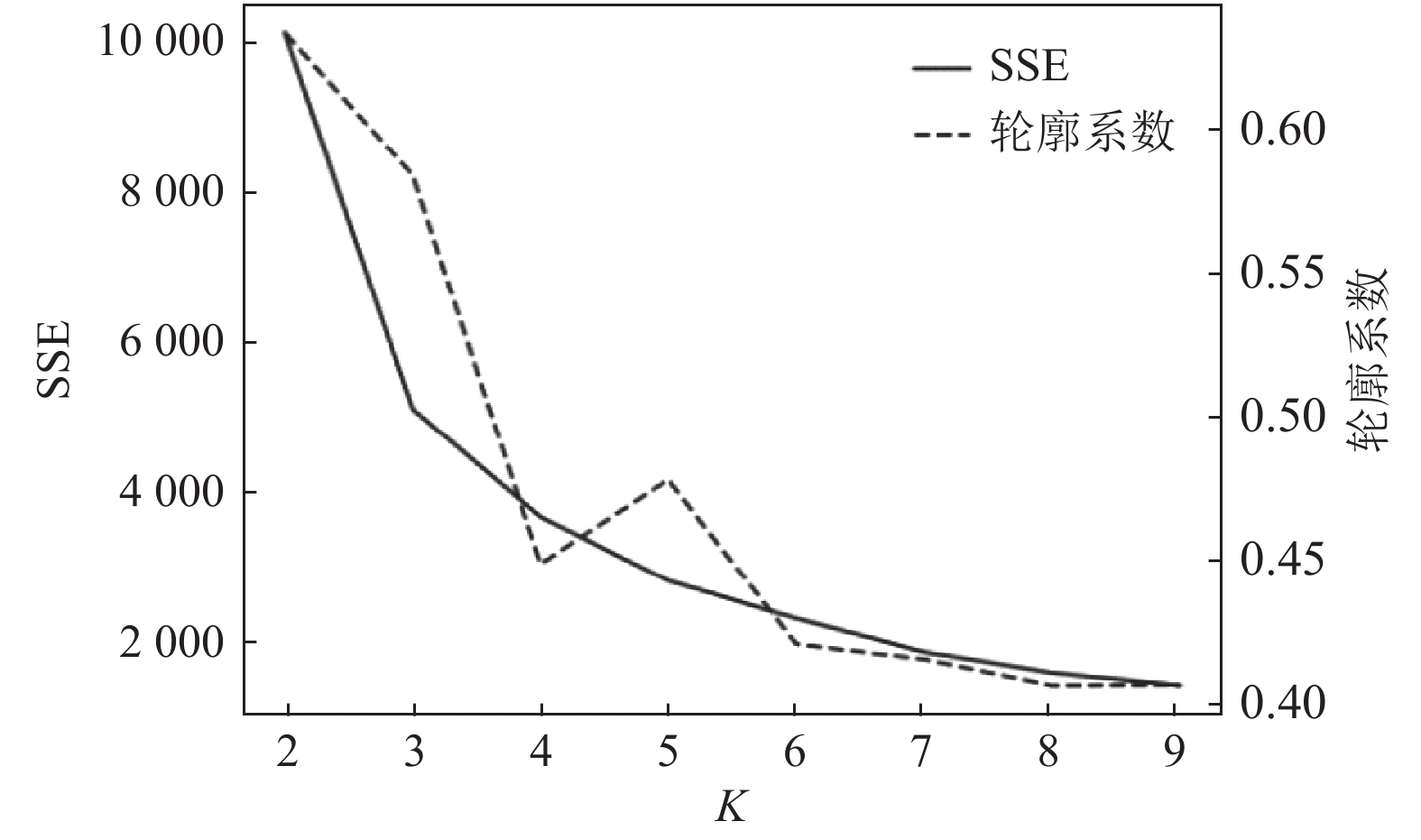
2.3 最佳聚类数K值确定轮廓系数值越大聚类效果越好, 肘部法则中理论上最佳K 值在肘处取得. 聚类数K的范围设定为[2, 9], 轮廓系数及聚类误差平方和(sum of the squared errors, SSE)随聚类个数K的变化如图1所示. 由图1可知, 聚类数K与误差平方和的拐点出现在K=3处, 此时轮廓系数也较大, 综合考虑轮廓系数、肘部法则, 确定聚类数K为3.
|
图 1 不同K值的SSE及轮廓系数变化 |
2.4 传统K-means算法与改进算法对比分析
分别利用原K-means算法和改进后的K-means算法对风廓线雷达数据进行聚类, K值选取最佳聚类数3, 每种算法运行10次, 选取平均值进行对比, 对比指标包括轮廓系数、迭代次数、运行时间3方面, 对比结果如表2所示. 由对比结果可见, 改进后的算法在迭代次数和运行时间均明显降低的情况下, 可获得与原K-means算法同等聚类效果.
| 表 2 K-means和改进后的K-means算法聚类对比 |
2.5 基于聚类的风廓线雷达数据特征分析
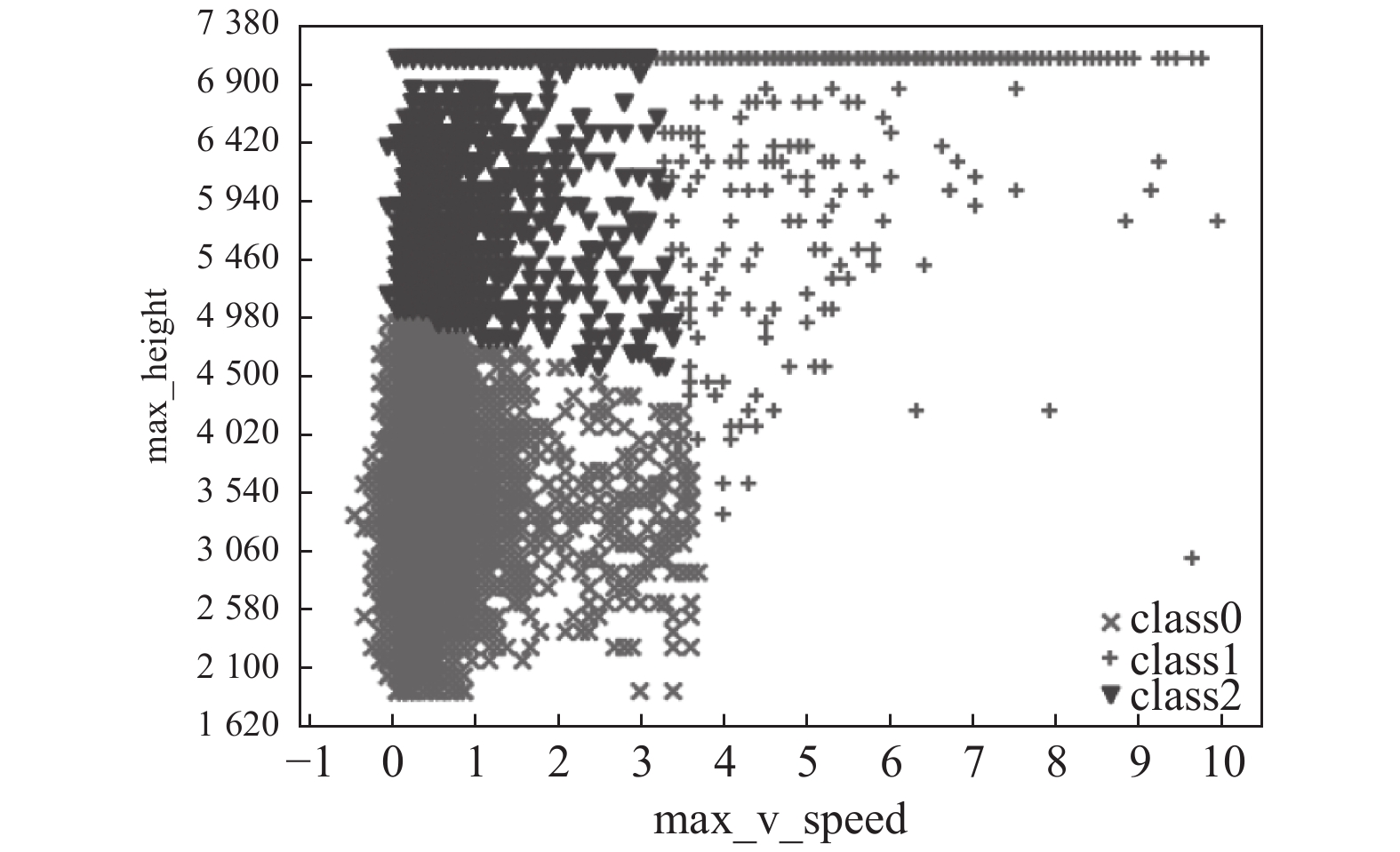
应用改进后的K-means算法对10 553个时次风廓线雷达数据进行聚类, K值选取最佳聚类数3, 聚类结果如图2所示, 计算每类各特征统计描述, 结果如表3所示. 根据表3可知, class0包含7 669个时次数据, 占比72.7%. class1包含615个时次数据, 占比仅5.8%. class2包含2 269个时次数据, class0的最大探测高度、最大垂直速度均最低, 最大探测高度均值低于3 500 m, 最大值低于5 000 m, 最大垂直速度均值在0.5 m/s. class1的最大探测高度和最大垂直速度皆最高, 最大探测高度均值为6 718 m, 该类近70%的时次最大探测高度可达静海风廓线雷达的最大探测高度7 080 m, 最大垂直速度均值在5.5 m/s. class2的最大探测高度和最大垂直速度介于class0和class1之间, 最大探测高度远高于class0, 均值亦在6 000 m以上, 但达到7 080 m的仅占38%, 最大垂直速度均值略高于class0, 为1 m/s, 明显低于class1.
经分析, class0主要为晴、少云天气观测数据, class1主要为降水期间的观测数据. class2主要为多云、阴天及降水前1–6 h、降水后1–3 h的观测数据.
探测高度方面, 晴天、少云天气的最大探测高度均值在3 562 m, 多云、阴天的最大探测高度均值为4 414 m, 降水前1–6 h、降水后1–3 h的最大探测高度均值为5 480 m, 降水期间的最大探测高度均值为6 548 m. 多云、阴天探测高度高于晴天及少云天气, 降水前1–6 h、降水后1–3 h风廓线雷达的探测高度较多云、阴天更高, 降水期间探测高度最高且多数可达静海风廓线雷达的最大探测高度. 风廓线雷达主要以晴空大气作为探测对象, 利用大气湍流对电磁波的散射作用来探测大气风场等要素. 其探测高度除了和雷达技术指标有关之外, 受天气状况的影响很大[22], 当有天气系统的时候, 大气湍流活动加强, 高层的水汽含量增加, 雷达探测高度会增加[23], 聚类结果表明风廓线雷达的最大探测高度对于大气高层水汽含量增大有较好的指示作用.
|
图 2 聚为3类的风廓线雷达数据分布 |
| 表 3 各类最大探测高度、最大垂直速度特征 |
垂直速度方面, 晴天、少云天气的最大垂直速度均值为0.5 m/s, 多云、阴天的最大垂直速度均值为0.7 m/s, 降水前1–6 h、降水后1–3 h的最大垂直速度均值为1.4 m/s, 降水期间数据最大垂直速度均值为5.5 m/s. 降水期间数据最大垂直速度大于等于4 m/s的占74%, 而其他天气条件97%的时次最大垂直速度低于4 m/s. 杨引明等[1]分析发现, 4 m/s的垂直速度反映了降水开始和结束(定义垂直速度向下为正, 向上为负), 本文研究结果与其研究结论基本一致.
总体来说, 风廓线雷达的最大探测高度在天气状况由晴天、少云转变为多云、阴天、降水天气时, 会有明显的上升. 但最大垂直速度仅在降水开始时急剧增大, 在降水开始前增长趋势不明显.
两个典型天气个例也印证了本文的挖掘结果. 图3展示了2018年7月23日00时至2018年7月26日05时静海站最大探测高度、最大垂直速度与小时雨量的时序变化对比. 23日属于少云天气, 24日00时至12时, 静海本站出现大暴雨, 累计降水量153.6 mm, 最大小时降水量27.1 mm.

|
图 3 2018年7月23日至24日静海风廓线雷达最大探测高度、最大垂直速度与小时雨量对比图 |
由图3可见, 降水前24 h到降水开始, 探测高度不断上升. 降水前24–12 h最大探测高度均值在3.5 km左右, 降水前12–6 h最大探测高度均值升至 4.5 km, 之后探测高度有所下降, 23日22时后又开始升高, 到24日01时升至静海风廓线雷达最大探测高度7 km, 3 h增幅达4.3 km, 强降水期间一直维持在最大探测高度. 说明随着降水临近, 大气的湍流活动明显加强、大气高层的水汽含量急剧增加. 降水结束后, 由于属于多云天气, 最大探测高度在4.8 km以上维持了一段时间, 直到25日05时后, 才降低到3.5 km以下. 降水期间, 最大垂直速度均在4 m/s以上, 降水结束后最大垂直速度迅速降低.
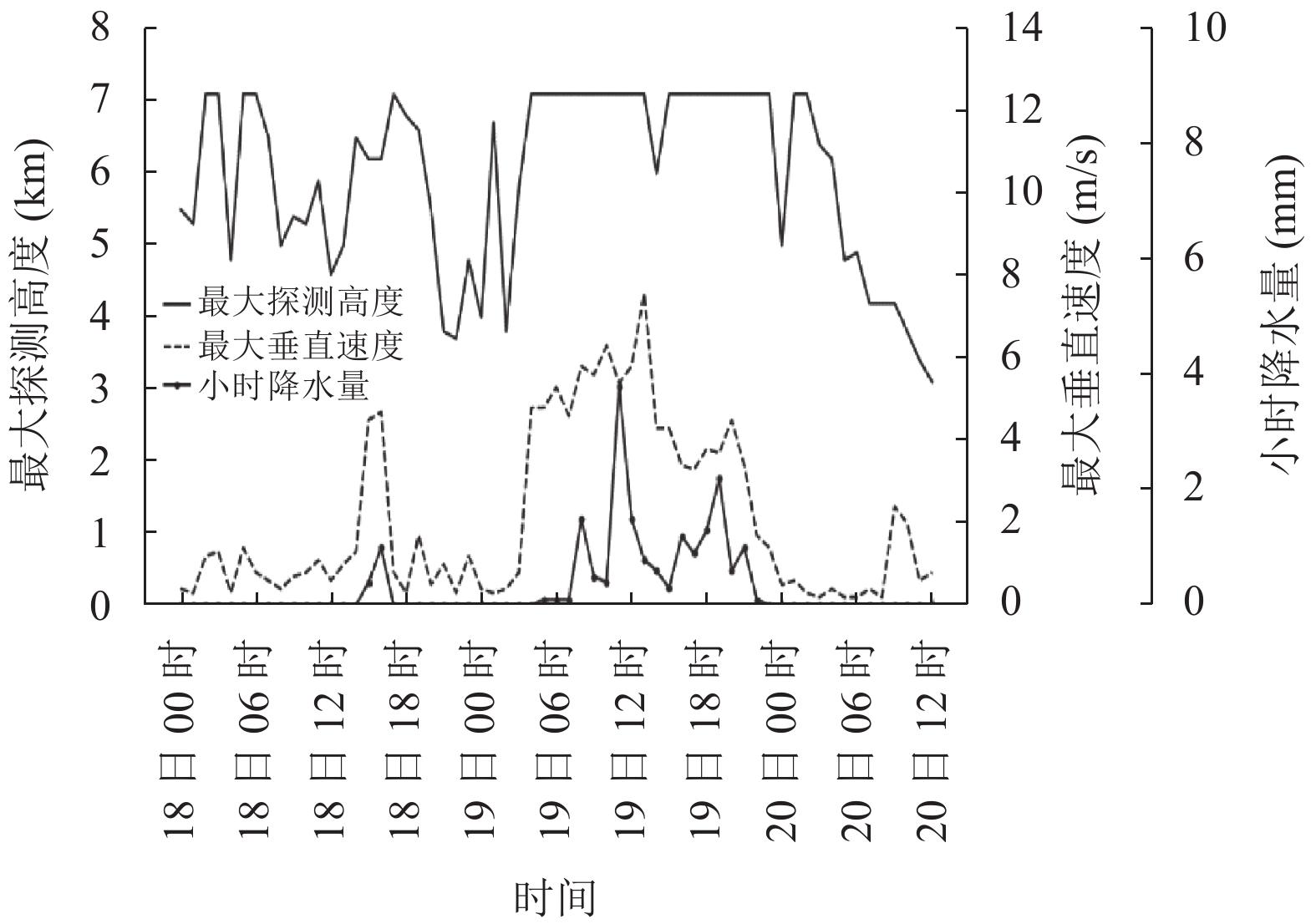
图4展示了2018年8月18日00时至2018年8月20日12时静海风廓线雷达在阴天及地面降水前后最大探测高度、最大垂直速度的时序变化.
|
图 4 2018年8月18日至20日静海风廓线雷达最大探测高度、最大垂直速度与小时雨量对比图 |
8月18日静海为阴天并在15时至16时发生1.4 mm小雨级别降水, 最大探测高度基本处于5 km以上, 18日12时降至4.5 km后又在降水前1 h的14时再次升至6.5 km, 2 h跃升2 km, 18日20时后逐渐下降. 探测高度从19日02时的3.7 km又开始升高, 到19日04时降水前1 h升至最大探测高度7 km, 19日05时至22时静海再次发生17 mm中雨级别降水, 降水期间探测高度基本维持在7 km, 20日03时之后开始逐渐下降. 从探测高度曲线图可以看出, 降水前6 h最大探测高度基本在5 km及以上, 即使有降低至4 km以下的时次, 也会在降水前1 h回升, 这可能是地面降水前高空先有水汽到达的缘故, 降水结束后, 探测高度没有立即降低, 在降水结束3 h或更长时间后才逐渐降至4 km以下, 可能是高空还有一定潮湿空气的缘故, 降水期间最大探测高度多在7 080 m. 对比最大垂直速度和小时降水量曲线图可知, 降水期间最大垂直速度多在4 m/s以上, 降水强度大时垂直速度较大, 但最大垂直速度值不一定出现在降雨最强时次. 垂直速度在降水开始会迅速增大, 降水结束会快速下降.
3 总结与展望针对风廓线雷达观测数据特点, 本文利用改进的K-means聚类算法建立了风廓线雷达数据特征聚类分析模型, 对天津静海边界层风廓线雷达2017–2019年(5–9月)的观测资料进行聚类, 挖掘出了风廓线雷达的最大探测高度、最大垂直速度在晴、阴天、降水前1–6 h、降水期间、降水后1–3 h等天气条件下的一些变化规律, 为气象预报服务提供了更具普遍性的参考依据, 为风廓线雷达数据特征分析提供了新思路. 但本文仅对探测高度、垂直速度特征进行了分析, 风廓线雷达还有水平风向、水平风速、折射率结构常数等观测要素, 下一步有必要对风廓线雷达其他观测信息继续开展挖掘分析, 以获取更多的数据特征为气象预报服务提供支撑.
| [1] |
杨引明, 陶祖钰. 上海LAP-3000边界层风廓线雷达在强对流天气预报中的应用初探. 成都信息工程学院学报, 2003, 18(2): 155-160. |
| [2] |
郑石, 黄兴友, 李艳芳. 一次短时暴雨WP-3000边界层风廓线雷达回波分析. 气象与环境学报, 2011, 27(3): 6-11. DOI:10.3969/j.issn.1673-503X.2011.03.002 |
| [3] |
董保举, 付志嘉, 李明, 等. 风廓线雷达资料在暴雨天气过程特征分析中的应用. 气象科技, 2012, 40(1): 74-78, 86. DOI:10.3969/j.issn.1671-6345.2012.01.015 |
| [4] |
陈楠, 胡明宝, 张柽柽, 等. 利用风廓线雷达资料对南京地区低空急流的统计分析. 热带气象学报, 2014, 30(3): 511-517. DOI:10.3969/j.issn.1004-4965.2014.03.012 |
| [5] |
史珺, 赵玉洁, 王庆元, 等. 风廓线雷达在一次短时暴雨过程中的应用. 气象与环境科学, 2017, 40(4): 83-89. |
| [6] |
王彦, 刘一玮, 孙晓磊. 利用风廓线雷达资料分析一次强降水过程的风垂直切变特征. 暴雨灾害, 2017, 36(2): 171-176. |
| [7] |
周芯玉, 廖菲, 胡东明. 利用风廓线雷达对广东前汛期短时强降水类暴雨过程低空风场特征的研究. 热带气象学报, 2019, 35(3): 332-342. |
| [8] |
王佳津, 张琪, 张涛, 等. 成都两次暴雨期间风廓线雷达观测的低空风场特征. 干旱气象, 2021, 39(1): 87-95. |
| [9] |
林勤, 薛云. 双聚类算法在电信高价值客户细分的应用. 计算机应用, 2014, 34(6): 1807-1811. DOI:10.11772/j.issn.1001-9081.2014.06.1807 |
| [10] |
周笑天, 褚希, 姚志平. 一种基于K-means聚类的实时气温动态质量控制方法. 气象, 2012, 38(10): 1295-1300. DOI:10.7519/j.issn.1000-0526.2012.10.016 |
| [11] |
史静, 党岳, 张永欣, 等. 自动站数据质量控制中关联规则挖掘的应用. 气象科技, 2014, 42(4): 612-616. DOI:10.3969/j.issn.1671-6345.2014.04.015 |
| [12] |
刘伟东, 尤焕苓, 任国玉, 等. 北京地区自动站降水特征的聚类分析. 气象, 2014, 40(7): 844-851. DOI:10.7519/j.issn.1000-0526.2014.07.008 |
| [13] |
熊亚军, 廖晓农, 李梓铭, 等. KNN数据挖掘算法在北京地区霾等级预报中的应用. 气象, 2015, 41(1): 98-104. DOI:10.7519/j.issn.1000-0526.2015.01.012 |
| [14] |
杜良敏, 柯宗建, 刘长征, 等. 基于聚类分区的中国夏季降水预测模型. 气象, 2016, 42(1): 89-96. DOI:10.7519/j.issn.1000-0526.2016.01.011 |
| [15] |
雷景生, 余修成. 基于模糊C均值聚类算法的区域用电特征分析. 上海电力学院学报, 2017, 33(2): 196-200, 209. |
| [16] |
苟浩锋, 王遂缠, 杨银, 等. 基于聚类分析的兰州地区自动站降水特征分析. 沙漠与绿洲气象, 2020, 14(1): 108-114. DOI:10.12057/j.issn.1002-0799.2020.01.014 |
| [17] |
李宗飞, 李祥海, 陈凯华, 等. 聚类分析在X波段双偏振雷达相态识别中的应用. 气象科技, 2021, 49(3): 315-321. |
| [18] |
兰荣亨, 朱格, 杨文, 等. 基于聚类的网络直播群体行为建模分析. 计算机系统应用, 2019, 28(1): 69-74. DOI:10.15888/j.cnki.csa.006728 |
| [19] |
任禹丞, 徐超, 赵磊, 等. 基于自适应特征权重聚类算法的用电问题分析. 计算机系统应用, 2020, 29(1): 29-39. DOI:10.15888/j.cnki.csa.007247 |
| [20] |
张培昌, 杜秉玉, 戴铁丕. 雷达气象学. 北京: 气象出版社, 2001, 7-20. |
| [21] |
王晓芳, 王成刚, 卜令兵, 等. 利用LAP-3000型风廓线雷达资料对深圳地区湍流耗散率特征的研究. 气象科学, 2011, 31(S1): 1-6. |
| [22] |
何平. 相控阵风廓线雷达. 北京: 气象出版社, 2006: 42–62, 104–121.
|
| [23] |
陈红玉, 高月忠, 尹丽云, 等. 强降水过程风廓线雷达资料的极值特征. 气象科技, 2016, 44(1): 87-94. DOI:10.3969/j.issn.1671-6345.2016.01.014 |
 2022, Vol. 31
2022, Vol. 31



