为应对全球化竞争加剧、原材料价格上涨以及外部经济环境的不确定性, 外包(outsourcing)成为众多制造型企业不可或缺的运营策略^[1]. 但外包策略的执行会增加企业作业调度的难度, 决策者一方面需要从现有待加工作业中确定外包作业, 另一方面还需对内部作业进行有效调度. 近年来, 带外包选择的调度问题(scheduling problems with outsourcing options, SPOO)引起了调度学者的关注. 现有针对该问题的研究成果中, 绝大多数都把单个转包商作为作业外包选择的对象. 不过, 企业实际运营中外包选择的对象往往是多个转包商, 并且随着企业经营范围的扩大会吸引越来越多的转包商参与其作业外包的竞争. 因此, 面向多转包商的作业外包选择才是企业外包运营管理的常态. 比起仅有单一转包商可供选择的情况, 企业在面对多个转包商时作业外包的选项更多, 优化决策的难度也更大. 如何得到作业的转包商选择与内部调度联合决策方案已成为当今企业外包运营管理的一项挑战性任务. 为此, 本文瞄准面向多转包商的可外包作业调度问题开展理论与方法研究. 这类问题不仅能为企业外包选择决策提供有效的解决方案, 还能帮助企业有效利用外包市场中的产能资源, 具有实践指导意义和应用价值.

带外包选择的调度问题的研究涌现出了丰硕的研究成果. 这些成果已经涉及单机^[2]、并行机^[3]、流水车间^[4]、作业车间^[5]等多种机器环境. 带多转包商外包选择的调度问题在带外包选择的调度问题的研究中占比较少. Chen等^[6]较早关注到带多转包商外包选择的调度问题, 他们对多转包商参与作业外包的并行机调度问题进行了深入研究, 并开发一种启发式算法求解该问题. Mokhtari等^[7]也注意到带多转包商外包选择的并行机调度问题, 构建了以总成本最小化为目标的数学模型, 并为该问题设计出一种团队过程算法. Ahmadiza等^[8]研究了面向双转包商的双机流水车间调度问题, 构建了以完工时间和外包及运输成本之和最小化为目标的数学模型, 并提出一种蚁群算法求解该问题. Goli等^[9]研究了带多转包商外包选择的流水车间调度问题, 通过考虑不同机器上加工作业工时的不确定性, 提出了一种鲁棒混合整数线性规划模型, 并通过实例验证了所构建模型的鲁棒性.

在并行批加工(parallel batch processing)环境下, 批处理机能同时加工多个作业, 同一批作业中最长的加工时间为此批作业的加工时间^[10]. 该环境能帮助企业提高机器利用率、降低能耗, 很多产品加工过程中的瓶颈工序都是在该环境加工完成^[11]. 并且在半导体制造、金属冶炼、陶瓷烧制等行业中十分常见^[12]. 从实际调研的情况来看, 在采用并行批加工模式的企业中, 加工时间相对较长的作业无论分配到哪个加工批次都会延迟同批次其他作业的完工时间并影响企业的整体交付服务水平. 在该情形下, 企业可考虑把这类作业分配给合适的转包商进行委外加工. 这样做既可以提高企业内部产能的利用效率, 又有助于缩短企业的完工期, 提升其交付服务水平. 可见, 并行批加工环境对外包策略的有效运用有着迫切的需求. 基于此, 本文针对并行批加工环境下带转包商选择的单机批调度问题(single-machine batch scheduling problem with subcontractor options, SBSP_SO)开展研究, 结合批处理机容量约束以及外包环节中的外包成本预算约束、外包作业最晚交付期约束构建了整数规划模型, 并设计改进型遗传算法和贪婪算法求解该模型. 最后, 通过对实例进行灵敏度实验分析, 为企业外包运营管理提供相关建议.

1 问题描述及数学模型 1.1 问题描述

待加工作业集合J中有n个作业亟待制造商实施联合调度, 这些作业均在0时刻可用. 现有两种生产资源可供选择, 可在其内部单台批处理机上加工或是外包给转包商. 现有外包市场上可供制造商选择的转包商有H个. 如果作业J_j外包给转包商S_h, 制造商则须向转包商S_h支付o_jh单位的外包成本, 转包商S_h完成对作业J_j的加工后会在l_jh时刻交付给制造商. 制造商需要确定外包给转包商S_h的外包作业集和内部作业集I在内部批处理机上的调度方案B.

本文所考虑的SBSP_SO问题可描述如下. 在满足外包成本预算约束、外包作业最晚交付期约束、机器容量约束的前提下, 得到最佳联合方案 $ \pi^{*} $ =[ ${\cup}_{h=1}^{H}O_{h}^{{\pi}^{*}}, B^{*}$ ]. 其中, $O_{h}^{{\pi}^*}$ 表示 $ \pi^{*} $ 中外包给转包商S_h的外包作业集, 以使得作业外包总成本OC与内部批加工总成本IBC之和(以下简称作业运营总成本)达到最小. 根据Graham等^[13]提出的调度问题三参数法和Qi^[14]提出的外包与调度联合优化问题简记法, 本文所考虑的SBSP_SO问题可表示为 1+H | batch, s_j≤Q, Budget |OC+IBC.

1.2 假设条件

(1) 每个作业的尺寸大小、内部加工时间均已知.

(2) 每个作业的尺寸都不超过批处理机的容量.

(3) 所有作业均在0时刻可用.

(4) 内部的批处理机采用并行批加工模式.

(5) 批处理机同一时刻仅能处理一个批次, 仅当一

个批次中所有作业都完工时才释放机器.

(6) 内部加工批次总数仅当所有批次都构建完成后才能确定.

(7) 转包商根据自身产能和市场条件主动将外包成本报价和交付时间信息提供给制造商.

1.3 符号定义

表1列出了SBSP_SO问题中若干符号表示及其说明.

1.4 数学模型

根据以上描述, 本文考虑的SBSP_SO问题的数学模型如下.

$ \min \lambda \cdot \sum\limits_{k = 1}^n {{{\max }_{1 \leqslant j \leqslant n}}} \left\{ {{x_{jk}} \cdot {p_j}} \right\} + \sum\limits_{h = 1}^H {\sum\limits_{j = 1}^n {{o_{jh}}} } \cdot {v_{jh}} $

(1)

$ \text { s.t. } \sum_{k=1}^{n} x_{j k}+\sum_{h=1}^{H} v_{j h}=1, \quad j=1,2, \cdots, n, \; h=1,2, \cdots, H $

(2)

$ x_{j k} \leqslant y_{k}, \quad j=1,2, \cdots, n, \; k=1,2, \cdots, n $

(3)

$ \sum_{j=1}^{n} x_{j k} \cdot s_{j} \leqslant Q \cdot y_{k}, \quad j=1,2, \cdots, n, \; k=1,2, \cdots, n $

(4)

$ \sum_{h=1}^{H} \sum_{j=1}^{n} o_{j h} \cdot v_{j h} \leqslant { Budget } $

(5)

$ \sum_{h=1}^{H} v_{j h} \cdot l_{j h} \leqslant D, \quad j=1,2, \cdots, n $

(6)

$ \begin{split} {x_{jk}},{y_k},{v_{jh}} \in \{ 0,1\} ,\quad &j = 1,2, \cdots ,n, \; k = 1,2, \cdots ,n\\ &h = 1,2, \cdots ,H \end{split} $

(7)

其中, 式(1)为SBSP_SO问题的目标函数; 式(2)排除了一个作业参与外包的同时又在制造商内部分批加工的可能性, 并保证当一个作业在制造商内部加工时只能安排到一个加工批次中, 当它参与外包生产时则仅能委托给一个转包商加工; 式(3)确保每个内部作业所在的加工批次一定不是空作业集; 式(4)保证每个内部加工批次中作业的尺寸之和不超过批处理机的容量 $ Q $ ; 式(5)表示作业外包总成本不能超过给定外包成本预算Budget; 式(6)表示各转包商对其加工的每个外包作业的交付时间不得超过事先预定的外包作业最晚交付期 $ D $ ; 式(7)指明了决策变量x_jk、y_k和v_jh的二元属性.

SBSP_SO问题的计算复杂性可通过一类特殊情形A₁获知. 其中, 各转包商S_h (h=1, 2, …, H)对每个作业J_j∈J的外包成本报价o_jh均相等且远远大于 $\lambda \cdot \displaystyle\sum\limits_{j=1}^{n} P_{j}$ . 由于作业的外包成本足够高, 导致无任何作业参与外包, 于是此时SBSP_SO问题退化为差异尺寸作业在单台批处理机上的调度问题, 即1 | batch, s_j≤Q|C_max (C_max表示最大完工时间). 该问题已被证明是强NP-hard问题^[15], SBSP_SO问题的计算复杂度不会低于该问题, 故SBSP_SO问题是强NP-hard问题.

SBSP_SO问题的求解过程包含两个决策环节: 一是确定出外包给各个转包商的作业集合, 即作业外包决策; 二是对制造商内部批处理机上加工的作业进行分批调度, 即内部批调度决策. 作业外包决策是SBSP_SO问题的首要环节, 包含外包与否和转包商选择两个任务. 事实上, 可根据下列性质直接判断符合特定条件的作业是否参与内部分批调度.

性质1. 如果作业J_j满足不等关系 $o_{jh} \gt \lambda \cdot p_j$ (h $ \in $ {1, 2, …, H}), 则它在最优联合方案 $\pi^*$ =[ $\bigcup_{h=1}^{H} O_{h}^{\pi^{*}}, B^{*}$ ]中不会分配给转包商S_h完成加工, 即J_j $\notin O_h^{\pi^*}$ .

性质2. 如果作业J_j满足不等关系 $ \min \left\{l_{j h} ; h= 1, 2, \cdots, H\right\}>D $ , 则它在最优联合方案 $\pi^*$ =[ $\bigcup_{h=1}^{H} O_{h}^{\pi^{*}}, B^{*}$ ]中参与内部分批调度, 即J_j∈ $ B^{*} $ .

以上性质均可通过反证法证明, 鉴于篇幅, 证明过程不在此详述.

2 改进型遗传算法和贪婪算法

本节为具备强NP-hard特性的SBSP_SO问题分别设计了改进型遗传算法(improved genetic algorithm, IGA)和贪婪算法(greedy method, GM). 本节先对IGA算法中染色体编码与初始种群生成、适应度函数与选择机制、交叉算子、变异算子和迭代终止条件这5个重要组成部分进行逐一详述, 然后给出IGA算法的总体流程. 最后对GM算法的设计思路和执行步骤进行表述.

2.1 染色体编码与初始种群生成

根据SBSP_SO问题的描述, 联合方案 $ \pi $ 须给出外包给转包商S_h的作业集和内部批处理机上的调度方案. 任意一个作业J_j $ \in $ J, 首先要决定其是否外包, 若是外包, 则须为其寻找合适的转包商; 若是在内部批处理机上完成加工, 则须确定其所属的内部加工批次. 因此, 在IGA算法中, 对染色体编码时需要兼顾单个作业可选择的外包对象与内部加工批次. 其中, 每条染色体表示一个可行联合方案 $ \pi $ , 为每个作业设置两个基因位, 分别用g₁和g₂表示. g₁表示作业可选择的外包对象, g₁可能取值为{0, 1, 2, …, H}, g₁=0表示作业在内部单台批处理机上加工, g₁=h则表示外包给转包商S_h加工; g₂表示作业的内部加工批次, 考虑到一批作业的尺寸大小均接近Q的极端情况, g₂可能的取值为{0, 1, 2, …, n}, 每条染色体的长度为2n. 任意一个作业要么参与外包, 要么在制造商内部加工, 故它的两个基因位不能同时取0且规定当g₁不等于0时g₂一定等于0.

以一个包含8个作业、3个转包商的问题为示例, 各作业的信息(即内部加工时间p_j、尺寸大小s_j)和转包商的信息(即外包成本报价o_jh、交付时间l_jh)如表2所示. 此外, 示例中统一取Q=10, Budget=7, D=15. 图1为该示例的一个可行联合方案的染色体表示结构图. 其中, J₄外包给转包商S₂, OC=5<Budget=7, l₄₂=13<D=15; 内部加工批次分为5个批次, J₂、J₈属于同一批次, J₁、J₇属于同一批次, J₃、J₅、J₆分别单独属于一个批次, 各内部加工批次中作业的尺寸之和也未超过机器容量Q.

IGA算法中的每一代种群由popSize条染色体组成, 每条染色体包含2n个基因位. 初始种群中的每条染色体均在每个基因位的有效范围内随机生成. 为进一步提高染色体的质量, 在染色体的生成时充分结合性质1和性质2, 将满足性质1、性质2中不等式条件的作业从外包作业集中排除.

2.2 适应度函数与选择机制

对于编码后的染色体, 在计算其适应度值之前需要判断它的合法性. 染色体合法性的判断需考虑以下4个方面:

(1) 外包成本预算约束Budget.

(2) 外包作业最晚交付期约束D.

(3) 机器容量约束Q.

(4) 每个作业的两个基因位不能同时为0且至少有一个为0.

文中规定不满足上述约束或条件的染色体为非法染色体, 记其适应度值为0; 反之, 将合法染色体转化为联合方案3, 并按式(1)计算联合方案3的目标函数值 ${\textit{z}}(\pi)$ . 染色体的适应度值按式(8)计算:

$ fitness (\pi)=\left\{\begin{array}{l} 0, \text { 如果染色体不合法 } \\ \dfrac{M-{\textit{z}}(\pi)}{M}, \text { 如果染色体合法 } \end{array}\right. $

(8)

其中, $M=\lambda \cdot \displaystyle\sum_{j=1}^{n} p_{j}$ .

本文采用结合精英保留策略的锦标赛选择机制. 该机制既保留了锦标赛选择简单易行、无需对所有适应度值进行有序排列的优点, 又能防止当前种群中的最优个体的基因在下一代丢失, 确保遗传算法随着迭代次数的增加一直收敛逐渐靠近最优解^[16]. IGA算法中选择操作的具体步骤如下:

步骤 1. 从上一代完成交叉、变异操作的种群Pop(t–1)中选择适应度值最大的elitismCount个染色体直接进入当代种群Pop(t).

步骤 2. 从上一代种群Pop(t–1)中随机选取tournamentSize个染色体进入选择池tournament.

步骤 3. 将选择池tournament中的个体按其适应度值从小到大排序, 从中选出适应度值最大的个体, 置于当代种群Pop(t)中.

步骤 4. 步骤2、步骤3重复执行popSize–elitismCount次, 直到形成Pop(t+1).

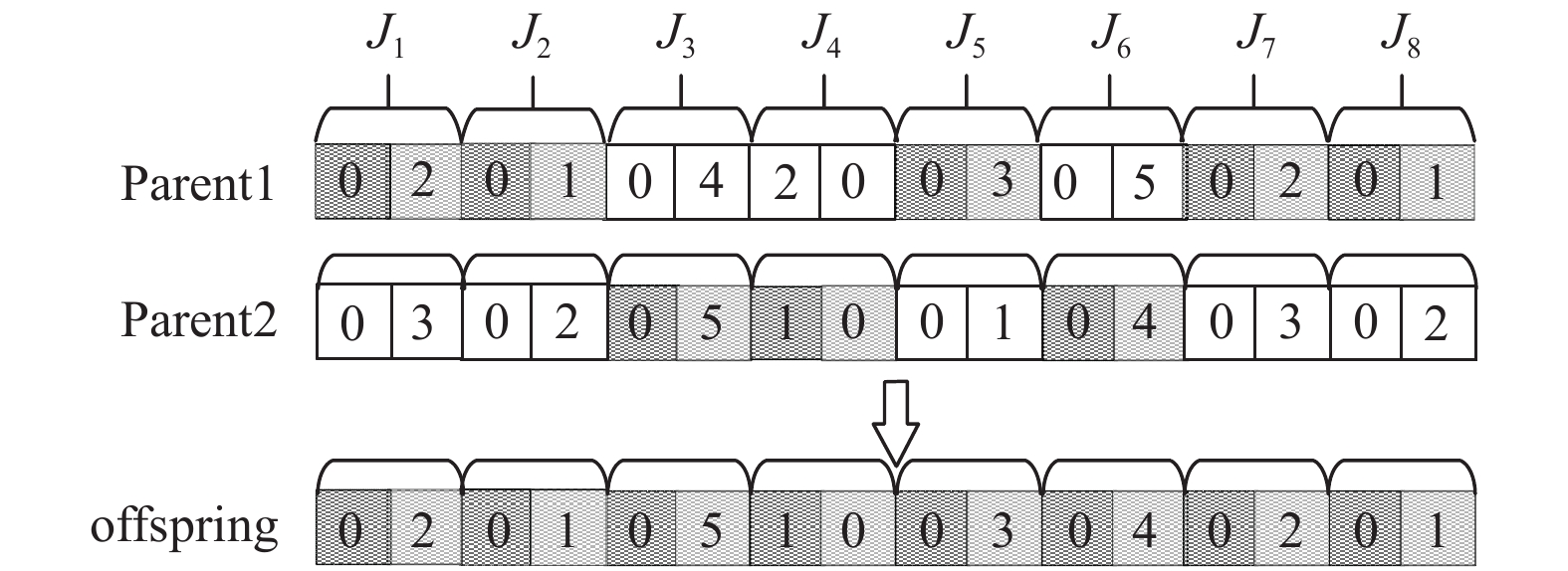
2.3 交叉算子

在上述染色体的编码结构中, 因每个作业对应两个基因位, 在执行交叉操作时需要两个基因位一起操作. 为了保证执行交叉操作后能以相对较高的概率获得合法染色体, 在 IGA算法中借鉴文献[17]中的均匀交叉方法实施逐代的染色体交叉操作. IGA算法中交叉操作的具体实施步骤如下.

首先, 从本代种群Pop(t)中随机选择2个亲代染色体, 分别表示为Parent1、Parent2. 然后, 判断是否满足交叉实施条件. 若交叉实施条件满足, 即p_c>random(a) (p_c表示交叉率, random(a) $\in $ [0, 1]), 为交叉实施后的后代染色体offspring分配2n个基因位, offspring中每个作业对应的两个基因位来自于Parent1或者Parent2的概率各有50%. 最后, 染色体offspring取代Parent1进入本代种群Pop(t) 中. 图2为上述示例的均匀交叉过程的示意图.

2.4 变异算子

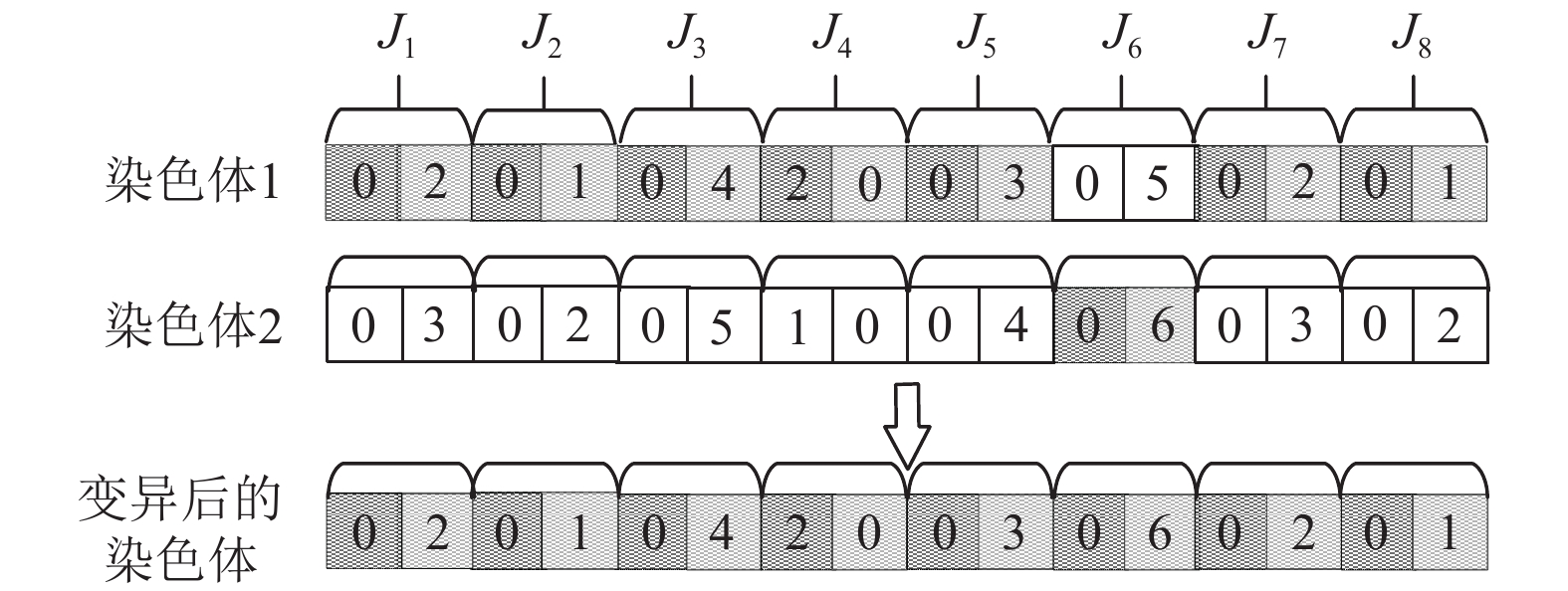
为尽量保证执行变异操作后的染色体为合法染色体, 在IGA算法中选用均匀变异的方式实施逐代的染色体变异操作, 以一个较小的概率来替换染色体原有的基因对. IGA算法中变异操作的具体实施步骤如下.

首先, 从本代种群Pop(t)中按顺序选择出一个染色体, 记作染色体1, 为保证有新的基因对进入现有种群, 按照初始种群中生成染色体的方式(见第2.1节)随机生成另一条染色体, 记作染色体2. 对于染色体1中的每个基因对, 若满足当前的变异实施条件, 即p_m>random(b) (p_m表示交叉率, random(b) $\in $ [0, 1]), 则将其替换为染色体2中对应的基因对, 否则, 基因对的值保持不变. 由此得到的染色体作为变异后的染色体进入种群Pop(t). 图3为上述示例的均匀变异过程的示意图.

2.5 终止条件

遗传算法中可选用的终止条件有最大迭代数或无改进最大迭代数终止、选取偏差度终止、评价准则终止等. 本文将无改进最大迭代数(t_max)作为所设计IGA算法的迭代终止条件, 令t_max=200n. 具体操作如下. IGA算法的每一次迭代中都记录并更新迄今最好解, 当迄今最好解的适应度值在连续的200n次迭代中都未改进时IGA算法终止.

2.6 算法步骤

本文所设计的IGA算法的具体步骤如下所示.

步骤1. 进行参数设置, 包括种群规模popSize、交叉率p_c、变异率p_m、精英保留个数elitismCount、锦标赛规模tournamentSize, 并设定迭代终止条件.

步骤2. 初始种群Pop(0)的生成按照第2.1节中初始种群生成的相关内容执行, 设置变量t, 其初始值设定为1.

步骤3. 先对种群Pop(t–1)执行结合精英保留策略的锦标赛选择操作, 具体的步骤按第2.2节的相关内容执行.

步骤4. 然后对选中的染色体进行均匀交叉操作, 具体的步骤按照第2.3节的相关内容执行.

步骤5. 最后, 对选中的染色体执行均匀变异操作, 具体的步骤按照第2.4节的相关内容执行, 生成新的种群Pop(t).

步骤6. t=t+1, 检验是否满足迭代终止条件, 即每一代记录的迄今最好解的适应度值是否在200n代内未得到改进; 若不满足迭代终止条件, 则返回步骤3.

步骤7. 输出联合方案 $ \pi $ 的目标函数值及求解时间、联合调度方案等信息.

2.7 贪婪算法

贪婪算法在求解复杂组合优化问题时, 通常不从整体最优解出发, 而总是基于当前条件做出最好的选择. 这种做法往往能在很多组合优化问题的求解中获得全局最优解或全局近似最优解^[18]. 本节应用所设计的GM算法完成SBSP_SO问题中的外包与否和转包商选择两个任务, 从而得到内部作业集 $ I' $ 和面向每个转包商的外包作业集 $ O_{h}^{\pi'} $ . 在外包作业集 $\bigcup_{h=1}^{H} O_{h}^{\pi'}$ 确定后, 可基于BFLPT (best-fit longest processing time)规则得出面向内部作业集 $ I' $ 的批调度方案 $ B' $ .众所周知, BFLPT规则能为差异尺寸作业批调度问题快速提供一个近似最优批调度解^[19], 文献[19]中给出了该规则的具体步骤, 在此不再赘述. 当外包作业集 $\bigcup_{h=1}^{H} O_{h}^{\pi'}$ 和内部作业集 $ I' $ 均确定后, 可根据式(1)计算出批调度方案 $ \pi' $ =[ $ \bigcup_{h=1}^{H} O_{h}^{\pi'}, B' $ ]的目标函数值 $ {\textit{z}}\left(\pi'\right) $ .

用于确定SBSP_SO问题中内部作业集 $I' $ 和外包作业集 $\bigcup_{h=1}^{H} O_{h}^{\pi'}$ 的GM算法步骤如下:

步骤1. 对于任意作业J_j $\in $ J, 按式(1)计算对应的比值 $ R $ :

$ {R_j} = \frac{{\lambda \cdot {p_j}}}{{\min \left\{ {{o_{jh}};h = 1, 2, \cdots , H} \right\}}} $

(9)

将作业集J中的全部作业按照对应的 $ R_j $ (j=1, 2, …, n)值降序排序, 形成作业排序方案 $ \tau $ .并且, 执行变量初始化操作: e←1、OC←0.

步骤2. 如果e>n, 那么输出内部作业集 $ I' $ 和外包作业集 $\bigcup_{h=1}^{H} O_{h}^{\pi'}$ , GM算法结束. 否则, 取出当前序列 $ \tau $ 中 $R_j$ 值最大的作业 $J_j$ , 并找出对该作业外包成本报价最低的转包商 $S_h$ .

步骤3. 确定转包商 $S_{h'}$ 对作业 $J_{j'}$ 的交付时间 $l_{j'h'}$ . 如果 $l_{j'h'}$ >D, 将作业 $J_{j'}$ 归入 $I'$ 中, 从序列 $\tau$ 中剔除作业 $J_{j'}$ , 置e←e+1, 并返回步骤2. 否则, 确定转包商 $S_{h'}$ 对作业 $J_{j'}$ 的外包成本报价 $o_{j'h'}$ .

步骤4. 更新当前的OC值: 置OC←OC+ $o_{j'h'}$ .如果OC > Budget, 将作业 $J_{j'}$ 归入 $I'$ 中, 从序列 $\tau$ 中剔除作业 $J_{j'}$ , 置e←e+1, 并返回步骤2. 否则, 将作业 $J_{j'}$ 归入 $O_{h}^{\pi'}$ 中, 从序列 $\tau$ 中剔除作业 $J_{j'}$ , 置e←e+1, 并返回步骤2.

3 实例分析

下面以某陶瓷制造企业的作业外包与批调度联合决策场景为例进行仿真实验分析, 整个实验分为两部分. 在第1部分, 通过对比实验考察IGA算法的优化性能, 以验证IGA算法对SBSP_SO问题的求解有效性. 在第2部分, 旨在运用IGA算法对SBSP_SO问题实例中的可控参数进行灵敏度实验分析, 以探寻影响作业运营总成本的关键可控参数及其影响效果.

3.1 实例介绍

所选取的实例来自于某陶瓷企业中进行胚体烧制的批加工生产线. 经实地调研发现: 该生产线采用并行批加工模式, 生产线烧制所使用的电炉的容量Q为25 m³; 企业内部单台批处理机单位时间的批加工成本 $ \lambda $ 为1; 外包市场上可供陶瓷厂选择的转包商有4个; 外包成本预算 $Budget = \eta \cdot \displaystyle\sum\limits_{j = 1}^n {\max } \left\{ {{o_{jh}}} \right\}$ , 其中 $ \eta \in $ [0, 1], 被称作外包成本容许率. 所关注的联合调度决策场景如下所述: 该批加工生产线共有35个待烧制作业; 各作业的内部加工时间p_j (以h为单位)、尺寸大小s_j (以m³为单位) 已知, 如表3所示; 各转包商对每个作业的外包成本报价o_jh (以RMB为单位)、交付时间l_jh (以h为单位)也已知, 如表3所示. 由于该厂自身的产能有限, 难以按时完成所有待烧制作业的加工任务, 不得不考虑将一部分待烧制作业外包, 以牺牲一定数额的外包成本, 使作业运营总成本下降.为保证完工的陶瓷品能按时送达客户, 该企业限定各个转包商在60 h内完成对委外烧制任务的交付.

3.2 改进型遗传算法的性能实验分析

下面选用商业优化软件 IBM ILOG CPLEX 12.8 和GM算法作为比较对象, 考察所设计IGA算法对SBSP_SO问题的优化性能表现. 运行环境如下: 计算机系统为Windows 10, 处理器为Intel^®Core™i7-7500@ 2.70 GHz 2.90 GHz, RAM内存为 4.0 GB. 另外, 实验中用到的各种算法、程序均采用Java语言编程实现. 在预实验中, 通过对所设计IGA算法的控制参数进行校准实验, 得出各参数的建议取值如下: popSize=50, p_c =0.95, p_m=0.01, elitismCount=5, tournamentSize=5.

当前性能实验中的6个测试算例源于第3.1节所述实例. 算例1中的待烧制作业数为30, 这30个作业的相关信息如表3中前30个作业所示; 算例2中的待烧制作业数为31, 这31个作业的相关信息如表3中前31个作业所示, 以此类推. 此外, 这6个算例中其他参数取值统一为: η=0.1, D=48 h , Q=25 m³. 随着作业规模的增大, CPLEX短时间内得不到精确解的可能性会提升. 为了便于比较IGA算法、GM算法和CPLEX的求解结果, 在当前实验中将CPLEX求解时间上限设置为3 600 s, 将迄今最好解的适应度值在连续200n次迭代中都未改进作为IGA算法的迭代终止条件. IGA算法本质上属于元启发式算法, 在IGA算法的性能实验中需要记录独立运行多次的求解结果(目标函数值和求解时间). 在本性能实验中, 为测算IGA算法和GM算法在求解能力上的差距, 特引入一个求解质量偏差度量指标Gap, 两算法的Gap指标值按下式计算:

$ {Gap_{HA}} = \frac{{{{\textit{z}}_{HA}}(\pi ) - {{\textit{z}}^*}(\pi )}}{{{{\textit{z}}^*}(\pi )}} \cdot 100 $

(10)

其中, HA为IGA算法和GM算法的通称变量, 即HA $ \in $ {IGA, GM}. ${\textit{z}}_{{\text{IGA}}}(\pi)$ 是IGA算法独立运行15次所得目标函数值的均值, ${\textit{z}}_{{\text{GM}}}(\pi)$ 是GM算法所得解的目标函数值. ${\textit{z}}^*(\pi)$ = $\min \left\{{\textit{z}}_{{\text{IGA}}}(\pi), {\textit{z}}_{{\text{GM}}}(\pi)\right\}$ .

表4给出的是改进型遗传算法、贪婪算法与CPLEX求解测试算例的统计结果. 其中, Obj1 和State分别表示CPLEX单独运行的求解结果、对应目标函数值的时间状态; Min、Max、AVG、SD、Time和Gap分别为改进型遗传算法独立运行15次的最小值、最大值、均值、标准差、求解时间以及 $Gap_{{\rm{ABA}}}$ 的值; Obj2 、Time和Gap分别表示贪婪算法单独运行的求解结果、对应目标函数值的求解时间以及 $Gap_{{\rm{GM}}}$ 的值.

由于CPLEX是基于数学规划法求解测试算例, 其耗时会随作业数n的增大而指数增长. 从表4可以看出, 对于作业数n≥31的算例, CPLEX在设定的3 600 s内无法得到精确最优解, 只能求得近似最优解. 而IGA算法却能在更短的时间得出更高质量的联合调度解, 运行时间仅为CPLEX所耗时间的1/500. 在n=30、31、32这3个算例的求解中, IGA算法全部15次实验中均得到和CPLEX相等的目标函数值. 在n=33、34、35这3个算例的求解中, 改进型遗传算法在全部15次实验中均达到或优于CPLEX求解结果水平. 可见, 与CPLEX相比, IGA算法在测试算例上的优化质量和时间上的表现更好.

另外, 从IGA算法和GM算法对上述6个算例的求解结果来看, 虽然IGA算法比GM算法花费的时间多, 但是这些时间并不是徒劳的, 而是有效提升了解的质量. IGA算法的Gap值均为0, 而GM算法的Gap值均在15%以上. 这说明IGA算法的优化质量明显优于GM算法, 进一步体现出IGA算法的收敛能力.

3.3 实例的灵敏度实验分析

本节力图利用灵敏度实验分析法找出影响企业作业运营总成本的关键可控参数, 通过对实例中关键可控参数的有效调整, 使企业所花费的作业运营总成本进一步降低. 实例中, 转包商提供的外包成本报价o_jh和交付时间l_jh、作业数n等属于不可控因素. 由于企业内部单台批处理机单位时间的批加工成本 $ \lambda $ 主要受人员工资、机器设备等影响, 在现实中改变的可能性不大, 也属于实例中的不可控参数. 实例中的可控参数主要有外包成本预算Budget和外包作业最晚交付期D, 而外包成本预算Budget的实际值由外包成本容许率η决定. 因此, 针对该实例的灵敏度实验主要围绕外包成本容许率η和外包作业最晚交付期D展开.

下面将使用IGA算法进行实例的灵敏度实验, 基于上述实例、基于外D和η的不同组合(D, η), 进而得到不同的作业运营总成本的值, 并将IGA算法独立运行15次的均值作为实验分析的数据. 其中, 作业运营总成本用TC表示, 外包作业最晚交付期上限用l_max表示. 考虑到企业预算不够充足更符合现实情况, 在进行灵敏度实验时, η的范围取[0.05, 0.5], 单位浮动数值为0.05. 把l_max作为基准, 将提前50%、25%作为间隔点, 将D划分为早(0, 30]、中(30, 45]、晚(45, 60]三个阶段. 在D范围的选取上, 考虑到D过早在现实中难以实现, 在此选取D $\in $ [20, 60]的范围进行实验, 单位浮动数值为3. 图4给出的是不同参数组合(D, η)所对应的作业运营总成本TC.

由图4可发现以下4个现象: (1) 外包作业最晚交付期D对作业运营总成本TC的影响较为明显, 而外包成本容许率η对作业运营总成本TC的影响不明显; (2) 当η>0.15时, 无论D取何值, TC的值几乎与η=0.15时TC的值持平. (3) 不建议企业将D定至早(0, 30]或中(30, 45]两个阶段. 究其原因在于外包作业最晚交付期的硬约束使得几乎所有作业在内部批处理机上加工, 企业无法从外包策略中获益. 四是在外包成本预算相对充足的情况下,D的取值越接近l_max, TC降低效果越明显. 当D=54, 57, 60 h时, 与早(0, 30]、中(30, 45]两个阶段相比,TC分别降低15.70%、21.07%、23.97%.

为验证上述第一个现象是否有统计学意义, 取外包成本容许率η和外包作业最晚交付期D作为自变量, 作业运营总成本TC作为因变量, 使用上述灵敏度实验得出的数据进行双因素方差分析检验. 表5给出的是双因素方差分析的检验结果. 从表5可以看出, 外包成本容许率η和外包作业最晚交付期D组成的交互项的p值大于0.05, 故没有统计学意义. 值得注意的是, 外包成本容许率η和外包作业最晚交付期D的p值分别为0.991、0.000, 可认为外包成本容许率η的不同对TC没有显著影响, 而外包作业最晚交付期D对TC有显著影响.

下面针对外包作业最晚交付期 $ D $ 接近l_max的4种情况即D=48, 51, 54, 57 h观测并分析外包成本容许率η在[0.01, 0.15]范围内对作业运营总成本TC的影响趋势, η的单位浮动值取0.01. 首先, 运用所设计的IGA算法在60种参数组合(D, η)下分别独立运行15次. 然后, 统计出每种参数组合(D, η)所得的15个目标函数值的均值, 并将其绘于图5中.

从图5可以看出, 当η≤0.15时, η对TC的影响明显, 并且外包作业最晚交付期D越接近l_max, IGA算法的作业运营总成本优化效果越显著. 此外, 在外包作业最晚交付期D的4种不同取值情况下, TC都是随着η的增大而先快速下降后又保持稳定. 在D的4种不同取值情况下, η的适宜取值范围也有所不同. 当D=48, 51, 54 h时, 建议外包成本容许率η的设定值不应低于0.07. 当D=57 h, η的取值维持在0.10以上较优.

4 结论与展望

本文研究了带转包商选择的单机批调度问题. 通过考虑该问题的特征并结合相关优化性质设计了改进型遗传算法和贪婪算法. 从算法性能实验结果可知, 贪婪算法的求解质量偏差即Gap值均超过15%. 这说明改进型遗传算法的优化质量明显优于贪婪算法. 在验证所设计改进型遗传算法有效性的基础上, 使用改进型遗传算法对实例中的可控参数进行灵敏度实验, 以找出关键可控参数并对其进行有效调整, 最大限度降低该企业的作业运营总成本, 为企业日常运营提供决策支持. 实例研究发现:

(1) 相较于外包成本容许率, 外包作业最晚交付期对作业运营总成本的影响更显著, 合理的外包作业最晚交付期设置可节省超过20%的作业运营总成本.

(2) 制造商不宜将外包作业最晚交付期设定太早, 否则无法从外包中获益, 在条件允许的情况下, 应让其设定值尽量接近外包作业最晚交付期上限.

(3) 外包成本容许率不宜低于0.1, 制造商可通过融资或银行贷款等方式增加外包成本预算, 以确保降本效果显著.

在下一步的研究中, 力求在外包运营实践方面为企业提供更多的管理启示, 并进一步寻找该问题的应用场景, 在其他行业的相关实例中验证所设计改进型遗传算法的适用性.