2. 中国科学院 沈阳计算技术研究所, 沈阳 110168
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China
采用虚拟仿真技术构建现实场景仿真系统已经是各行各业应用场景中比较成熟的一种技术应用模式. 虚拟仿真技术可以通过三维建模搭建可重复过程的特性很好的解决现实物理世界中不易复现的各类场景, 从而进行相关应用问题的分析. 应用虚拟仿真技术构建的仿真系统能够在降低实物成本和保证人员安全的前提下, 在逼真的虚拟环境中为用户提供高真实感的体验, 并全程实现量化数据的跟踪, 进而有效提高用户对实际场景的应变决策能力. 随着近几年各行业中信息化建设水平的不断提高, 在软硬件配套设施及相关工程管理技术发展创新的推动下, 虚拟仿真信息化过程也不断演进变化, 从单纯的三维模型建模、三维模型展示、三维场景过程展示向实景仿真及数据实时交互反馈评估等方向发展. 在此基础上, 与各行业相匹配的虚拟仿真系统应运而生, 作为评估过程、演练演习的重要手段.
Unity 是行业领先的跨平台实时3D开发引擎, 广泛的应用在各种专业技术领域, 可用于创作、运行实时互动的2D和3D内容. 基于 Unity3D开发的虚拟仿真系统为用户提供了丰富的学习条件与逼真的虚拟环境. Wang 等人[1] 提出Unity在虚拟仿真和虚拟现实等方面具有广泛应用的价值.
目前, 随着相关领域的迅速发展, 多旋翼无人机广泛的应用在警备、城市管理、农业、地质、气象、电力、抢险救灾、视频拍摄等行业. 多旋翼无人机集成了飞行控制、惯性导航、光电侦察等多种设备于一身的复杂装备, 其价格昂贵、寿命有限, 不便用户直接使用无人机进行训练来提高操作技术[2]. 在虚拟仿真技术发展背景下, 使用虚拟仿真无人机提高用户操作能力, 能够减少训练成本, 扩展无人机应用领域, 对探索更加科学有效的训练方法具有重大意义.
对于虚拟仿真来说, 根据仿真应用的需求, 对应用领域的相关属性进行科学的抽象和相应的描述, 是从现实世界迈进仿真世界的重要前提. 模型是仿真活动的基础. 仿真模型不仅仅是使用数学公式对系统模型的运行规律进行建模, 而且还对虚拟环境和虚拟对象的视觉外观、物理特性进行建模.
马忠丽等人[3] 、王小青等人[4]、彭玉元等人[5]的相关研究, 重点在于仿真平台系统的设计应用, 将重点放在系统的设计上, 取得了较好的成果, 但并没有对无人机的仿真模型进行深入的研究.
1 多旋翼无人机运动分析研究无人机仿真模型, 首先需要分析多旋翼无人机的基本组成和飞行原理.
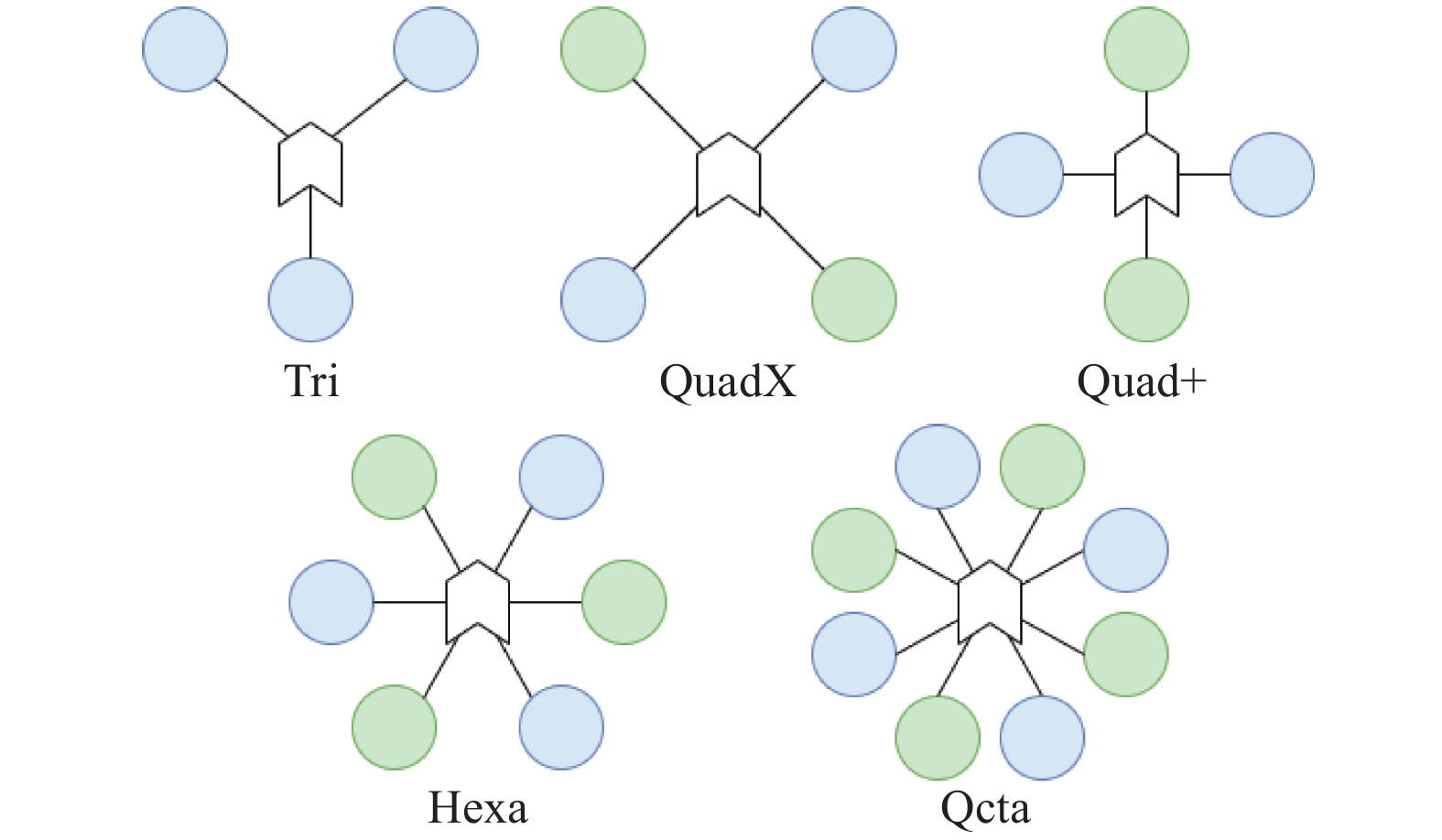
多旋翼无人机通常由机架、动力系统、控制系统组成. 多旋翼无人机机身常见布局如图1所示, 包括三旋翼、四旋翼、六旋翼和八旋翼等.
本文以QuadX型四旋翼无人机为例, 分析多旋翼无人机飞行原理. 无人机采用4个旋翼作为直接动力源, 通过改变机架上不同位置的电机转速来调整飞行器自身的姿态实现空间内6自由度运动, 即垂直、俯仰、滚转、偏航运动. 将机头前进方向右侧的电机命名为M1, 以机身逆时针方向将其与电机命名为M2, M3, M4. 通常M1, M3逆时针旋转、M2, M4顺时针旋转来使相邻电机的以不同转向来抵消扭矩.
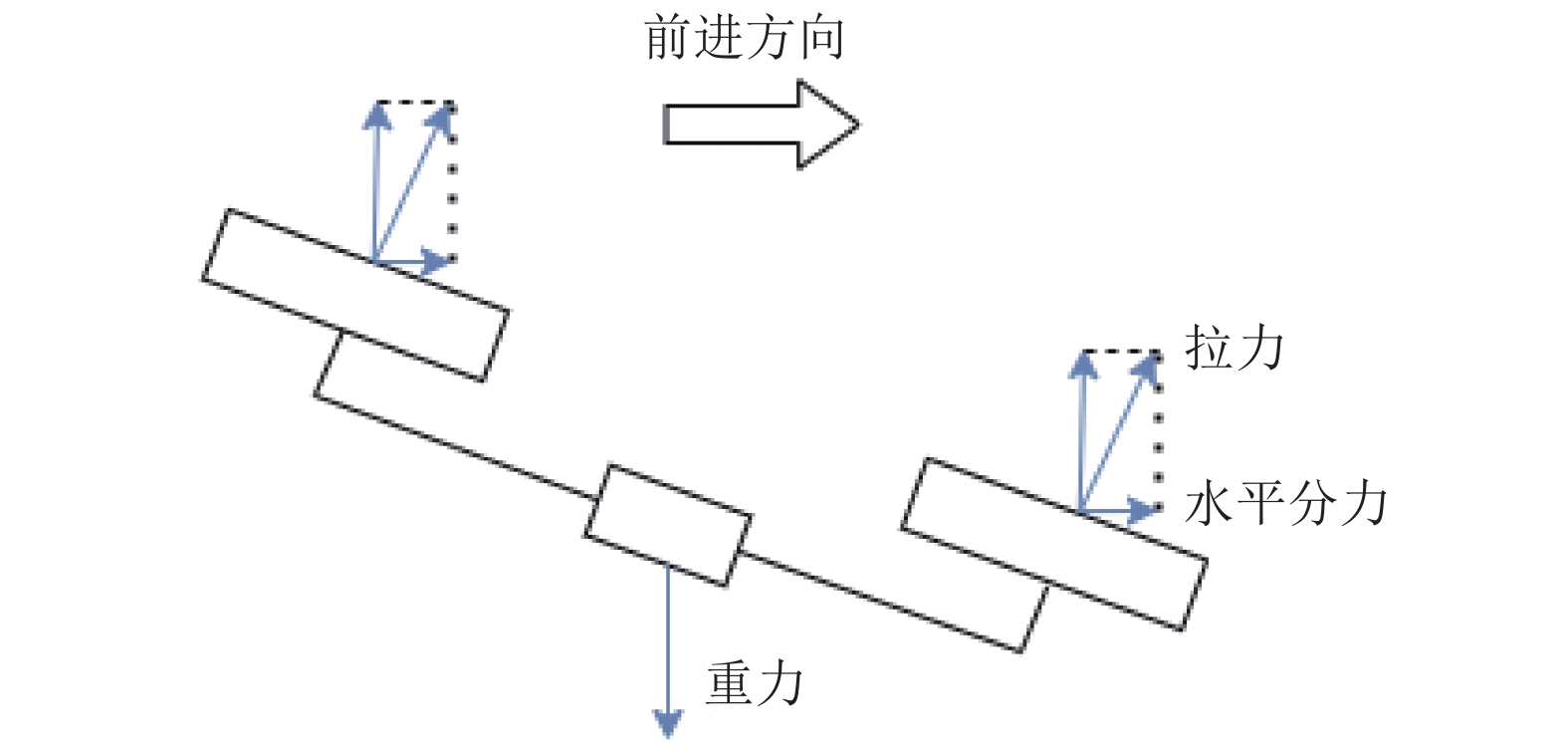
将4个电机的转速同时增大或减小即可实现垂直运动; 将M1、M3的转速增加或者将M2、M4的转速减小, 实现向右偏航. 反之, 实现向左偏航; 将M1、M2的转速减小或者将M3、M4转速增加时, 四旋翼会产生前倾的扭矩, 实现俯仰运动, 螺旋桨拉力的垂直分力抵消重力, 在前进方向的分力使四旋翼向前飞行, 如图2所示. 同理可知无人机左右飞行原理. 其他机身布局飞行原理相似.
|
图 1 多旋翼无人机旋翼常见布局 |
|
图 2 无人机前进运动 |
2 四旋翼无人机建模
本节就多旋翼无人机进行控制模型进行建模, 主要包含动力系统建模和控制系统建模. 其中信号传递如图3所示.

|
图 3 模型信号传递 |
2.1 无人机动力系统建模
无人机动力系统建模分为3部分: 螺旋桨建模、电机建模、电池建模.
多旋翼无人机常采用定桨距螺旋桨, 根据Dai等人[6]的螺旋桨建模方法, 螺旋桨拉力T(单位: N)和转矩M(单位: N·m)表示如下:
| T=CTρω2D4P | (1) |
| M=CMρω2D5P | (2) |
其中, CT为拉力系数, CM为转矩系数, ω为螺旋桨转速, DP为螺旋桨直径, ρ为空气密度. 文献[7]给出CT, CM的计算公式为:
| CT=0.25π3λξ2BPK0εarctanHPπDP−α0πA+K0 | (3) |
| CM=14Aπ2Cdζ2λ2BP | (4) |
| Cd=Cfd+πAK20e(εarctanHPπDP−α0)2(πA+K0)2 | (5) |
其中, HP为螺旋桨桨距, DP为螺旋桨直径, BP为桨叶数, 同时给出了参数的平均取值: A=5, ε=0.85, λ=0.75, ζ=0.5, e=0.83, Cfd=0.015, α0=0, K0=6.11.
目前, 多旋翼无人机使用无刷直流电机, 对于无刷直流电机转速N有:
| N=KV⋅U | (6) |
其中, KV为电机KV值, 定义为电机输入电压每增加1伏特电机空转转速增加的转速, 单位为RPM/V; U为电机输入电压. 在不考虑电机机械损耗和电机负载转矩情况下, 视电机转速N为螺旋桨转速.
对于电池模型, 主要目的是利用电池电压计算电机转速, 进而根据螺旋桨模型求得某电压下螺旋桨产生的拉力和转矩. 因此简化放电过程, 假设放电过程中电压保持不变, 忽略电池、电调、电机内阻的损耗, 只关注电池总电压.
考虑到模型的扩展性和易维护性, 根据模块化编程思想, 创建Propeller类实现螺旋桨模型的拉力、扭矩算法, 便于模型升级与扩展. 为了减少机器计算量, 在构造方法中将固定已知的参数提前计算存储. 电机类Motor、电池类Battery同理. 其中Motor类以引用的形式调用Propeller类、Battery类的方法, 以属性的形式获取或赋值当前电机的电压参数, 实现在Unity脚本生命周期中, 每固定0.02 s调用一次的FixedUpdate()方法, 部分代码如下:
var rotateSpeed = getRotateSpeed(EngineVol);
var Pull = _Propeller.getPull(rotateSpeed);
var counterTorque =
_Propeller.getTorque(rotateSpeed) * Mathf.Sign((float)Direction);
motorRigidbody.AddForce(transform.up * Pull); bodyRigidbody.AddTorque(bodyRigidbody.transform.up * counterTorque);
其中motorRigidbody、bodyRigidbody分别是电机三维模型、无人机三维模型的Rigidbody组件; Direction为枚举类型当前电机转向, 顺时针赋值1, 逆时针赋值−1, 调用Mathf.Sign()方法获得符号, rotateSpeed的值由式(6)求得.
Rigidbody.AddForce()、Rigidbody.AddTorque()方法是Unity脚本API, 作用分别是向 Rigidbody 添加力、相对扭矩.
至此, 无人机动力系统建模完毕.
2.2 无人机控制系统建模控制系统要解决机体在哪、姿态如何、如何飞行的问题, 其中姿态估计是控制模型的决策的基础, 姿态估计主要目的是估计姿态角, 测量加速度、角速度和位置等信息, 解决机体位置、机体姿态的问题.
多旋翼无人机通常使用IMU传感器单元进行无人机的姿态估计, 使用GPS传感器确定无人机的位置. 惯性测量单元(inertial measurement unit, IMU)包括加速度计和陀螺仪, 用来检测和测量物体加速度与旋转运动的传感器.
在Unity, 可直接调用Rigidbody.angularVelocity脚本API即可得物体的角速度, Transform.position可获得物体位置. 创建Sensors类封装该API, 但Unity的脚本API中并没有可直接获得加速度的方法, 因此根据加速度表达式(7)间接求出物体加速度, 角加速度同理.
| a=ΔvΔt | (7) |
在Unity脚本生命周期中, 每固定0.02 s调用一次FixedUpdate()方法, 调用间隔时间较短, 视为Δt. 线加速度计算代码如下:
previousVelocity = currentVelocity;
currentVelocity = rgb.velocity;
acceleration = new Vector3(
(currentVelocity–previousVelocity).x/FixedUpdateTime, (currentVelocity–previousVelocity).y/FixedUpdateTime, (currentVelocity–previousVelocity).z/ FixedUpdateTime);
将上述代码写入FixedUpdate()方法中, 即可计算出物体每一固定帧的运动线加速度, 其中rgb为物体刚体Rigidbody组件, previousVelocity、currentVelocity为Vector3类型变量, FixedUpdateTime为float型变量, 值为0.02f即FixedUpdate()的调用周期.
解决完机体在哪、机体姿态的问题后, 接下来需要解决如何飞行的问题, 这需要Controller类能够从Sensors类中获取机体姿态信息并根据输入的控制指令计算出达成目标姿态所需的拉力和力矩, 然后对无人机电机进行动力分配, 实现无人机的运动控制.
为了使输出能够符合期望的输入指令, 通常情况下选择PID控制器. PID控制是应用最广泛的一种工业控制算法, 距今已有近百年的历史. 由于四旋翼无人机为数字控制系统, 选用离散式PID. 离散式PID控制器分为位置式和增量式两种算法形式. 其中增量式计算结果只与最近3次的偏差有关, 解决位置式积分运算的误差积分积累问题, 因此该控制系统模型选用增量离式PID控制算法. 离散式PID控制其表达式如下:
| u(k)=KP×e(k)+KIk∑i=0e(i)+KD[e(k)−e(k−1)] | (8) |
由式(8)得:
| Δu(k)=u(k)−u(k−1) | (9) |
即:
| Δu(k)=KP[e(k)−e(k−1)]+KIe(k)+KD[e(k)−2e(k−1)+e(k−2)] | (10) |
其中, KP、KI、KD分别为比例系数、积分系数和微分系数, u(k)是第k次采样时刻的计算结果, e(k)是第k次采样时刻控制器的偏差. 实现代码实现如下:
float err = pid.exp–pid.act;
float increment =
pid.kp * (err–pid.errK1) + pid.ki * err +
pid.kd * (err–2.0f * pid.errK1+pid.errK2);
pid.output+=increment;
pid.errK2=pid.errK1;
pid.errK1=err;
代码中, 以结构体形式定义PID对象, 结构体内存储PID控制参数、期望值、目标值、两次误差值和输出值, 以引用形式传入PID算法中, 在算法中读写相关参数, 即代码中结构体变量pid.
当输出量与被控制系统呈线性关系时, 单极PID能获得较好的效果. 而多旋翼无人机通常可以简化为一个二阶阻尼系统[8], 是非线性系统. 螺旋桨转速和升力是平方倍关系, 单极PID在多旋翼无人机上很难取得好效果. 而串级PID控制系统提高了稳定性、可靠性和有效性, 克服了传统PID 精度不高的问题[9].
串级PID控制就是两级PID控制串联在一起, 分为内环PID控制和外环PID控制, 外环的输出作为内环的输入, 如图4所示. 对无人机的3个姿态角做PID控制, 外环输入反馈的是角度数据, 内环输入反馈的是角速度数据. 这样即使外环数据剧烈变化, 而内环数据不会发生突变.

|
图 4 串级PID控制系统示意图 |
确定了控制算法后, 分析控制输入值、输出值和反馈值的关系. 在姿态控制中, 需要控制俯仰、横滚、偏航3个姿态角, 即分别需要3个串级PID来控制无人机姿态. 这3个串级PID的外环的输入值都是其期望的姿态角度, 输出值是期望的角速度; 内环的输入是外环输出的期望角速度, 输出值是期望的角加速度. 最终作用于物体后, 外环的反馈值是物体当前的实际姿态角, 内环反馈的是物体当前的实际角速度. 在模型中, 期望值由输入控制脚本提供, 测量的实际值由前文提及的Sensors类提供. 同时还要对无人机的飞行高度进行串级PID控制, 以此实现无人机的悬停运动, 高度控制PID外环输入是无人机实际高度, 内环输入是无人机垂直方向上的速度.
在实际应用时发现, 俯仰、横滚运动中, 俯仰、横滚角取值范围在−90°~+90°控制幅度较小, 测量值即可作为输入的实际, 而偏航角取值范围在−180°~180°, 当测量值超过180°时测量值符号会相反, 此时会造成输入误差, 需要特殊处理. 这里以向量方法求偏航角, 构造单位向量:
| →vexp=(sin(θexp),cos(θexp))和→vact=(sin(θact),cos(θact)) |
由向量夹角公式:
| cosθ=→a→b|→a||→b| | (11) |
求得向量间夹角, 再由向量叉乘确定夹角方向, 其结果作为偏航角控制的测量值.
对3个姿态角分别采用串级PID控制, 使多旋翼无人机控制系统的非线性多变量输入多变量输出控制问题简化为两变量输入单变量输出问题.
根据QuadX形布局的多旋翼无人机的运动原理知, 电机M1转速对俯仰运动有负向作用、对横滚有正向作用, 对偏航有正向作用; 电机M2转速对俯仰运动有负向作用、对横滚有负向作用, 对偏航有负向作用; 电机M3转速对俯仰运动有正向作用、对横滚有负向作用, 对偏航有正向作用; 电机M4转速对俯仰运动有正向作用、对横滚有正向作用, 对偏航有负向作用. 于是有:
| {P1=Ph−Ppit+Prol+PyawP2=Ph−Ppit−Prol−PyawP3=Ph+Ppit−Prol+PyawP4=Ph+Ppit+Prol−Pyaw | (12) |
其中, P1、P2、P3、P4分别代表驱动电机M1、M2、M3、M4所需的PWM值, Ph为维持无人机飞行高度PWM值, Ppit、Prol、Pyaw分别为俯仰角、横滚角和偏航角的所需PWM值, 最后结果值限制在电机驱动器能接受的范围内. 将求得的输入电压分别驱动4个电机, 电机输入电压的改变引起电机转速的改变, 进而改变整个系统的受力情况, 实现对无人机的姿态控制.
在该模型中, 不考虑电机的饱和区, PWM值为电机输入电压占电池总电压的比值. 另外, 为了保证基本面姿态控制与抗风性需求, 一般多旋翼无人机在飞行时控留有制裕度, 油门指令应该小于0.9[7].
至此无人机控制系统建模完毕.
3 四翼无人机模型实现 3.1 Unity脚本实现确定了多旋翼无人机的算法模型后, 着手对模型算法的实现, 编写Unity脚本来实现对无人机对象的逻辑控制. 综合考虑各个脚本之间的关系, 设计UML时序图如图5.
UserInput脚本用于处理用户输入, 在多旋翼无人机中的遥控中, 需要控制3个姿态角和油门, 一共4个方向轴上的控制, 因此需要在Unity Input Manager中设置4个轴向控制来相应键盘输入. 由于无人机的姿态控制可以维持无人机的姿态, 在此设计油门输入实际是控制无人机的飞行高度. 依据航模遥控“美国手”手柄模式, 设置键盘w、s控制油门; 键盘a、d控制偏航; 方向键上下控制俯仰; 方向键左右控制横滚.

|
图 5 UML时序图 |
UserInput脚本的输入即为无人机的期望高度和期望姿态, Controller脚本获得无人机期望姿态后, 调用PID算法计算期望输出, 并将动力分配给Motor脚本, 而后将目标转速送入Propeller脚本中计算单个电机所产生的拉力和转矩, 直接作用在无人机对象的刚体上产生力的作用, Sensors脚本实时监控无人机对象的状态, 反馈给Controller脚本实现闭环控制. Controller脚本流程如图6.

|
图 6 Controller脚本流程图 |
3.2 Unity无人机对象组件设置
在Unity中使用包围盒碰撞检测, 在游戏对象上挂载Collider组件实现, 同时可以在脚本中实现碰撞后的受力效果, 无人机对象添加Collider效果如图7.

|
图 7 无人机对象 |
在多旋翼无人机的运动中, 仅有机体位置和螺旋桨旋转变化, 设置螺旋桨旋转动画会让仿真更加逼真, 给予用户沉浸体验. 创建Animator脚本, 该脚本获取Motor脚本的电机转速, 将其应用到螺旋桨上, 使螺旋桨产生旋转效果. 然而在现实中, 螺旋桨旋转由于视觉暂留而产生模糊效果, 转速越快模糊效果越明显, 而在Unity的旋转是在每渲染帧刷新对象状态, 使对象“瞬移”看起来不够真实, 对此可以使用模糊纹理贴图的代替三模模型旋转, 当螺旋桨低速旋转时使用真实三维模型旋转, 当转速逐渐提高时, 隐藏三维模型, 使用平面网格模型, 其材质使用提前绘制出模糊纹理的透明图片(图8), 实际旋转效果如图9, 其中M1, M2没有使用模糊纹理替换, 看出有很明显差别.

|
图 8 模糊纹理 |

|
图 9 模糊纹理替换旋转效果 |
为了实现Unity中无人机的控制逻辑, 需要对无人机对象挂载所需的脚本及相关组件, 挂载组件方式如图10.
Rigidbody刚体组件是实现游戏对象物理特性必不可少的组件, 刚体为游戏对象赋予物理属性, 使游戏对象在Unity物理引擎的驱动下产生力的作用, 实现真实世界中的运动效果. 本文将无人机受力模型直接应用在电机对应位置, 来仿真现实物体的受力状态, 从而免去了对模型的刚体数学建模.
|
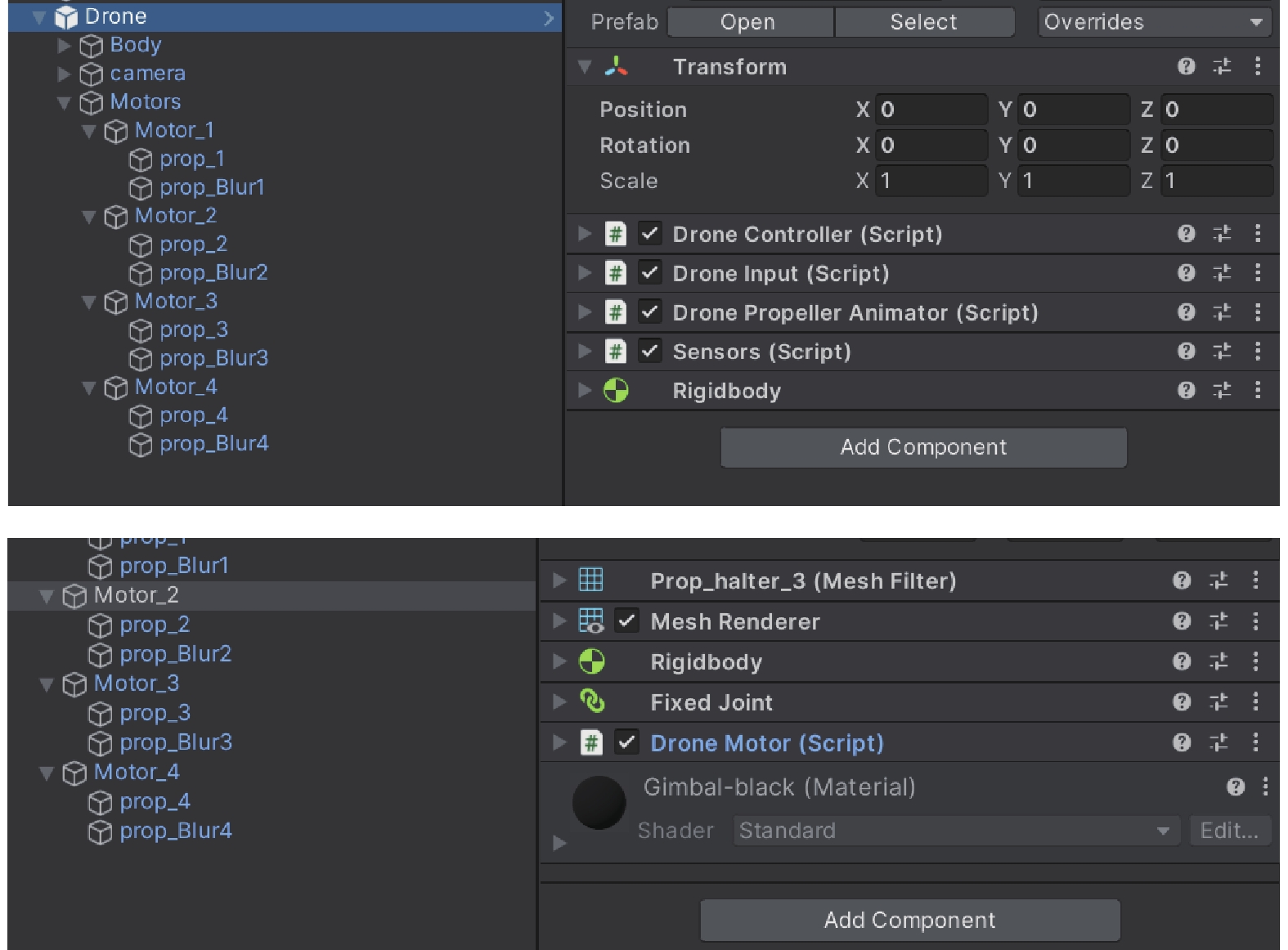
图 10 无人机GameObject组件挂载关系 |
在Drone对象中, Body是无人机机体三维模型对象, Camera是云台相机三维模型对象, Motors是所有电机、螺旋桨三维模型对象的父物体.
Motors对象中, Motor_1等是无人机的电机对象, 每个电机对象中的Fixed Joint组件将电机刚体和父物体刚体固定在一起; 其中Motor脚本用于对父物体产生实际的力和扭矩.
在Motor脚本中, 计算螺旋桨产生的拉力扭矩并直接作用电机的刚体上, 电机模型刚体带动整个无人机刚体运动. 所有的电机模型所产生的总拉力、总扭矩的作用效果由Unity物理引擎实现. 值得注意的是, 在Controller脚本的初始化中, 根据4个电机的位置将无人机的重心设置在对角电机连线的交点处, 否则无人机在飞行过程中可能产生不稳定的效果.
另外Prop_1等是螺旋桨三维模型, 以Motor_1等对象作为父物体, 这样可以使螺旋桨跟随电机对象; 而Prop_Blur1等为上述模糊纹理螺旋桨对象.
4 运行效果实验分别以无人机悬停、俯仰、滚转、偏航运动效果作为实验结果, 实验中无人机数据参数如表1.
4.1 PID参数整定无人机的姿态控制采用串级PID控制算法, 内环的输出是最终结果, 所以先调内环参数, 再调外环参数. 经过实验测试, 确定该无人机姿态控制PID参数如表2.
| 表 1 无人机数据参数 |
| 表 2 无人机PID参数 |
在PID参数整定过程中, 使用Unity调用Debug.Log()方法将无人机姿态数据实时打印出来, 将打印结果使用 Matlab 描绘控制曲线如图11.

|
图 11 PID姿态控制曲线 |
由图11可见, 在调整偏航角时会影响到俯仰和滚转运动, 产生较大波动. 为解决此问题, 使机体在一定误差范围内调整完俯仰、滚转运动后再调节偏航运动, 实验结果如图12所示, 可见限制偏航运动在一定程度上增加了稳定性, 同时限制偏航运动的俯仰滚误差与偏航响应时间呈现负向关, 限制误差值越小, 偏航响应越慢.

|
图 12 限制偏航运动的PID姿态控制曲线 |
运行场景, 使用键盘控制无人机飞行, 进行姿态控制, 无人机能够实现俯仰控制前进后退、滚转控制左移右移、偏航实现左转右转, 如图13所示.
5 结论与展望本文基于Unity物理引擎, 对四旋翼无人机这种典型非线性、多变量、欠驱动系统进行建模, 将无人机受力直接应用在电机对应位置, 更贴近现实物体受力状态, 免去了对模型的刚体数学建模, 使建模化繁为简; 在模型的姿态控制采用串级PID算法对无人机姿态进行控制, 飞行实验结果证明控制该模型的稳定性、有效性, 满足无人机仿真要求. 该模型既满足了仿真模拟的真实性又简化了建模过程, 为无人机仿真模拟提供了一条新思路. 不过本文没有考虑电机、电调、电池等物理特性、螺旋桨的气动阻力等, 有待进一步研究.

|
图 13 无人机模型实际运行效果 |
| [1] |
Wang S, Mao ZL, Zeng CH, et al. A new method of virtual reality based on Unity3D. Proceedings of 2010 18th International Conference on Geoinformatics. Beijing: IEEE, 2010. 1–5.
|
| [2] |
褚丽娜, 李建增, 谢志刚. 基于Unity3D的无人机交互式课件开发. 现代计算机, 2015(24): 39-42. |
| [3] |
马忠丽, 吴丽丽, 李嘉迪, 等. 基于Unity3D的多旋翼飞行器模拟训练系统设计. 应用科技, 2021, 48(3): 111-117. |
| [4] |
王小青, 吴兆轩, 马岩. 基于Unity的无人机三维视景系统设计与实现. 长江信息通信, 2021, 34(2): 12-14. DOI:10.3969/j.issn.1673-1131.2021.02.004 |
| [5] |
彭玉元, 李敏敏, 鲁家亮, 等. 无人机飞行虚拟训练平台设计应用. 大众科技, 2019, 21(5): 1-3. DOI:10.3969/j.issn.1008-1151.2019.05.001 |
| [6] |
Dai XH, Quan Q, Ren JR, et al. An analytical design-optimization method for electric propulsion systems of multicopter UAVs with desired hovering endurance. IEEE/ASME Transactions on Mechatronics, 2019, 24(1): 228-239. DOI:10.1109/TMECH.2019.2890901 |
| [7] |
全权. 多旋翼飞行器设计与控制. 杜光勋, 赵峙尧, 戴训华, 等, 译. 北京: 电子工业出版社, 2018, 68. |
| [8] |
赵亮, 王强, 徐立攀, 等. 四旋翼飞行器的串级PID姿态控制. 电脑知识与技术, 2018, 14(8): 248-249. |
| [9] |
张静, 刘恒, 郑采薇. 串级PID控制在微型无人机姿态控制中的应用. 电子世界, 2014, 16: 271-272. DOI:10.3969/j.issn.1003-0522.2014.16.267 |
 2022, Vol. 31
2022, Vol. 31



